5
Tools for Damage Assessment and Prediction
There are three principal methods for assessing and predicting the damage caused to spacecraft by the impact of orbital debris: observation of such impacts in space, ground-based hypervelocity impact testing, and analytical or numerical (computer) simulation of impacts. Since it is very difficult to gather data from the rare impacts of medium-sized or large debris in space, assessment of the potential damage such debris can cause to space systems is accomplished primarily through experimental testing and analytic/numeric methods. Experimental testing generally provides the majority of information on these effects; analytic or numerical tools currently mainly supplement and extend experimental results.
GROUND-BASED HYPERVELOCITY TESTING
Experimental laboratory testing can simulate and/or verify three major types of orbital debris-related phenomena: (1) the effects of orbital debris impacts on spacecraft component performance, reliability, lifetime, and survivability; (2) the capabilities and performance of impact damage mitigation techniques, such as shielding and shuttering; and (3) the creation of orbital debris in collision-induced breakups of spacecraft and rocket bodies. The principal technique used to simulate these phenomena is hypervelocity impact testing.
Ground-based hypervelocity impact testing provides a means to determine how well various components, subsystems, or entire spacecraft will survive a collision with debris. Since it is infeasible to build entire
spacecraft to be destroyed in ground tests, most tests are performed on components or on assemblies of components. Items tested can range from isolated fuel tanks and wiring harnesses to multicomponent assemblies including insulation materials and structural members (Christiansen, 1990; Christiansen and Ortega, 1990; Whitney, 1993; Schneider and Stilp, 1993). Although it is economically infeasible to test all components against all possible combinations of debris impact conditions, critical components can be evaluated with nominal impacts, and analytic or numerical techniques can then be used to extrapolate these results to other types of collisions.
Hypervelocity impact tests are also used to test and design debris shields. As with component testing, it is economically infeasible to test all possible shield configurations against all possible impact conditions, so a mixture of experimental testing, analytic methods, and numerical methods is used. Because the debris threat is not well enough known to "optimize" debris shielding against any particular type of impactor, shield designers develop shields to protect spacecraft against a wide range of impactor sizes, shapes, and velocities without greatly increasing the spacecraft's mass.
Finally, impact tests can be performed to examine the creation of fragmentation debris from breakups caused by hypervelocity collisions in space. This type of debris creation may play an important role in the evolution of the future debris population (as discussed in Chapter 8), but as mentioned in Chapter 2, only a few such tests have been performed to date. Such tests can be expensive, but since current data are very limited, a few well-planned and instrumented tests could add considerably to our knowledge of collision products and provide the basis for better estimates of the future debris population. Again, analytic and numerical methods can be used to extrapolate the limited test data to a wider range of possible situations.
The mass and velocity regimes required of an impactor in a hypervelocity test vary depending on the objective of the test. Obviously, the closer the tests come to matching real impactors' velocities, masses, materials, and shapes, the more accurate and useful the information acquired will be. For tests to determine the amount of debris created by a collision-induced breakup of a space object, it is necessary to use impactors large enough to fragment the target completely. For tests of spacecraft components and damage mitigation techniques, it is usually only necessary to use impactors that might feasibly be shielded against. The impactors used in such tests can range from millimeter to centimeter size, with masses ranging from much less than a gram up to several grams. Impactor shape must also be considered; since many potential debris impactors are fragments from rocket body or spacecraft explosions, the geometry of
possible impacting objects can vary greatly. Finally, the tests must simulate the typical impact velocities for debris, which can range up to about 15 km/s in LEO and up to about 800 m/s in GEO.
Hypervelocity Test Capabilities
A wide range of experimental facilities have some capability to simulate orbital debris impact conditions. Table 5-1 summarizes the principal generally available hypervelocity impact facilities, and Figure 5-1 displays the capabilities of these facilities in terms of the projectile sizes they launch and the impact velocities that these projectiles reach. Figure 5-1 also points out size and velocity regimes of debris impacts that could potentially be shielded against but that cannot be achieved with current hypervelocity impact capabilities.
As seen in Figure 5-1, the capability exists to perform impact tests with even fairly large masses at velocities typical of collisions in high-altitude orbits. The U.S. military has conducted many tests (primarily for antiaircraft and armor/antiarmor purposes) in these mass and velocity
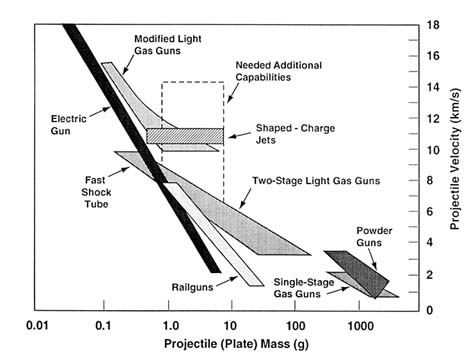
FIGURE 5-1 Capabilities of hypervelocity launch facilities.
TABLE 5-1 Experimental Test Facilities
|
|
Maximum Mass (gm) at Maximum Velocity |
Maximum Velocity (km/s) |
Spheres |
Rods |
|
Single stage guns |
2,000 |
1.4 |
X |
X |
|
Propellant guns |
1,000 |
2.5 |
X |
X |
|
Two-stage light gas guns |
0.01 to 250 |
8 |
X |
X |
|
Explosive Techniques |
||||
|
Inhibited shaped charge |
~1 |
~11 |
|
|
|
Staged explosives |
~0.1 |
14 |
|
|
|
Advanced Hypervelocity Launchers |
||||
|
Modified two-stage light gas gun (HVL) |
0.2 |
15.8 |
|
|
|
Fast shock tube |
~1 |
~10 |
|
|
|
Railgun |
~1 |
~8 |
|
X |
|
Other |
||||
|
Electric discharge gun |
0.01 |
~20 |
X |
|
|
Plasma drag accelerator |
1E-07 |
~20 |
X |
|
|
Van de Graaff accelerator |
1E-12 |
~100 |
X |
|
|
NOTE: Projectile masses and velocities are typical for the given capability. Increased mass capabilities have been achieved in modified scaled systems. "Other" refers to shapes that are not controlled (e.g., a slug in a jet tip). For more information on the velocity and size ranges achievable with various facilities, see Figure 5-1. |
||||
regimes. For example, some work done on "hit-to-kill" missile impacts could possibly be applied to collisions between large bodies at a few kilometers per second. However, the applicability of these data to orbital debris issues has not been studied, and in any case, the data may be considered too sensitive for wide release.
For studies of debris impacts at higher velocities, the standard laboratory tool is the two-stage light gas gun. Conventional light gas guns come in a variety of sizes and typically can accelerate impacting objects from less than 1.5 mm to more than 50 mm in diameter to about 8 km/s,
|
Plates |
Other |
Comments |
|
X |
|
Typically used for material property studies. Typical projectile diameter is 100 mm. |
|
X |
|
Typically used for material property studies. Typical projectile diameter is 90 mm. |
|
X |
|
Maximum size is customized for each gun. Microgram spheres have been launched to about 10.5 km/s using special designs. |
|
|
X (hollow cylinders) |
Projectile length to diameter difficult to control. |
|
X |
|
Computer analysis required to establish thermodynamic state. Typically used for material property studies. |
|
X |
X |
Computer analysis necessary to characterize thermodynamic state of the projectile. Photography necessary to characterize projectile shape. |
|
X |
X |
Still in development. Different variations claim capability to launch gram-size projectiles to several tens of kilometers per second or 100 projectiles to about 10 km/s. |
|
|
|
Still in development stage. Plastic rods have been launched to velocities approaching 8 km/s. |
|
|
|
Thermodynamic state of projectile not well characterized. |
|
|
|
Thermodynamic state of projectile not well characterized. |
|
|
|
Thermodynamic state of projectile not well characterized. |
although some facilities have been able to accelerate smaller particles to 10 km/s or more (often damaging the gun in the process). The standard projectile used in a two-stage light gas gun is a sphere, although various other shapes, including thin plates, cylinders, and long rods, can be launched (Piekutowski, 1986).
Light gas guns cannot launch impactors to the velocities typical of LEO debris impacts (10-15 km/s), but several ultrahigh-speed launchers have been developed that extend the impact velocity range for debris impact studies. One is a modified light gas gun technique, referred to as the Hypervelocity Launcher (Chhabildas et al., 1992a). This technique recently launched 1-mm thick, 6-mm diameter titanium plates to velocities of 15.8 km/s (Chhabildas, in press). Similarly modified larger light gas guns have launched 2-mm-thick, 30-mm-diameter titanium plates to
velocities greater than 10 km/s. This resultant capability covers the velocity and mass regime of a large fraction of space debris (see Figure 5-1) but is limited to plate-shaped impactors, and numerical methods are needed to specify the thermodynamic state of the impacting particle. A technique with the potential to further extend the range of debris impact studies is the electromagnetic railgun (Asay et al., 1989), which may eventually have the capability of launching spheres up to a centimeter in diameter to velocities of 15 km/s.
Launchers using explosives also have potential use in debris studies. One such technique employs an inhibited shaped-charge explosive to launch objects with dimensions in the tens of millimeters to velocities of about 11 km/s (Walker et al., 1992). Velocities relevant to space debris studies are therefore realizable, but the objects launched by such explosives are typically hollow cylinders with varying length-to-diameter ratios. This unusual shape complicates analysis of the data because analytical models for the damage caused by objects of this shape have not yet been developed. NASA is using a light gas gun to launch hollow cylinders at velocities of up to 8 km/s in order to learn more about the damage caused by this type of projectile. Russian investigators (Isbell et al., 1992) used a different staged-explosive technique to launch thin plates at high velocities for equation-of-state studies. This method has launched flat plates with centimeter diameters to velocities greater than 15 km/s. Finally, Russian and American investigators are developing a fast shock-tube device with the potential to launch larger flat plates to velocities of 15 km/s.
Other advanced launcher techniques have been developed to extend the range of small particle impacts to even higher velocities. Plasma drag launchers can launch microgram particles to velocities of nearly 20 km/s, and electrostatic launchers have extended this range to more than 100 km/s for particle masses of 10-15 gram (Stradling et al., 1992). Capacitor discharge techniques can launch thin flyers of metal and plastic with masses of a few tens of milligrams to velocities of 20 km/s (Lee et al., 1992). These techniques are most commonly used to simulate the damage caused to particular components by the impact of small debris and micrometeoroid particles. They have not, however, been widely used to develop damage prediction or degradation models; such models are based primarily on data analysis of returned spacecraft surfaces.
Techniques also have been developed to simulate high-velocity debris impacts without actually launching impactors at orbital velocities. One such technique, developed to overcome the velocity and mass limitations of existing hypervelocity test facilities, is ''dissimilar materials"
|
BOX 5-1 Two-Stage Light Gas Guns Two-stage light gas guns pressurize and accelerate gas to launch small projectiles to high velocities. A first-stage launch tube, typically 80-100 mm in diameter, contains a low molecular weight gas (such as hydrogen or helium) pressurized to a few atmospheres. An explosive charge accelerates a heavy piston to about 0.5 km/s, which accelerates the gas through a conical section to a smaller diameter launch tube (the second stage) containing the projectile. The accelerated gas produces a loading pressure of about 10,000 atmospheres, which accelerates the projectile to velocities of 8-10 km/s. The projectile then strikes the target in an evacuated chamber. In the Hypervelocity Launcher, the second-stage projectile impacts a thin plate at the end of the launch tube. The projectile is designed to impact so as to create a nearly isotropic pressure loading, accelerating the plate to velocities of up to 15 km/s, depending on its mass. |
testing (Holsapple, 1992). This method simulates the impact of aluminum particles on aluminum plates at velocities exceeding 12 km/s (where vaporization of the impacted materials occurs) by impacting cadmium (or another low-melting-point material) particles on cadmium plates at velocities of about 6 km/s. This method may be useful in investigating aspects of hypervelocity impact phenomena encountered during high-speed impact on aluminum, but determining the extent to which the results of dissimilar materials testing are applicable to damage prediction at velocities of about 10 km/s requires further detailed investigation and evaluation.
Russian investigators have developed a more radical method to simulate target conditions produced by ultrahigh-velocity particles; rather than launching an impactor, they have used electron beams and laser deposition to simulate the kinetic energy of high-velocity particles (Anisimov et al., 1985). Researchers in the United States, Germany, and Israel have also done extensive work on simulating impacts using ion beams and lasers (Gilath et al., 1992; Krueger, 1993) and have worked on laser ablation techniques for accelerating particles to high velocities (Trott and Meeks, 1990). To accurately simulate high-velocity impact, such techniques must not only match the impacting particle's kinetic energy but also impart such energy over a similar time frame to that of an impact and account for such effects of impact as momentum transfer and changes of state. Currently, these experiments cannot achieve such an accurate simulation of an impact, so analytic and numerical methods are used to convert their data into damage assessment predictions.
Sharing Hypervelocity Impact Information
One of the main reasons for the lack of good models of hypervelocity impact damage is that hypervelocity test data are not formally shared, and the capabilities of many facilities involved in hypervelocity testing are not commonly known. The general inaccessibility of facility capabilities and impact data generated at these facilities has resulted in duplication of effort, expense, and delays. Although information about the capabilities of laboratory facilities able to study debris impacts can usually be obtained from a variety of sources, such as published journals, company brochures, and word of mouth, there is no systematic process for obtaining this information. Detailed information regarding the capabilities of a specific laboratory is usually acquired through individual visits by researchers. Often, this information is published in trip reports and other company documentation and is not widely disseminated. This is especially true of facility capabilities outside the United States and of "alternative" techniques for simulating debris impact conditions, such as the laser and electron-beam facilities that Russian investigators use.
Attempts to disseminate information about the capabilities of hypervelocity impact facilities have been made; information on U.S. impact testing capabilities was at one point compiled in the "Facilities Handbook" (Malley and Nicols, 1987). The goal of this handbook was to (1) determine where impact testing could be conducted; (2) identify "holes" in test capabilities, facilities, and instrumentation; and (3) provide a mechanism to identify the most effective test facilities and methods for filling these holes. There was a great deal of useful information in this report, but it did not cover all U.S. facilities and covered none outside the United States. In addition, it did not include "alternative" test facilities, such as shaped charges, Van de Graaff accelerators, and electron beam deposition. Finally, distribution was limited to U.S. Air Force facilities, and the information was not entered into a database for easy retrieval.
Even more pressing than the lack of information about facility capabilities is the general inaccessibility of debris impact data generated at various facilities. Many test facilities have extensive collections of data (sometimes going back 30 to 40 years), most of which are not computerized or stored in databases for easy access. Often, these data are published in company reports that have limited distribution and are not archived for public access. In addition, technical information from many countries is published in journals that are not easily accessible in other nations or, in some cases, is not published at all because of potential or past military secrecy constraints. This inaccessibility of a great deal of data has surely limited the development of good models of debris impact damage.
Analytical And Numerical Modeling Of Debris Impacts
Analytic/numeric methods of various levels of complexity are used to predict the response of spacecraft to hypervelocity debris impacts. Analytic methods developed to aid spacecraft designers in the design of protective shields are the least complex. These include (1) "ballistic limit" equations (Cour-Palais, 1986; Herrman and Wilbeck, 1986; Reimerdes et al., 1993), which calculate the size of a particle stopped by a particular shield as a function of impact speed, impact angle, and impactor density; and (2) shield sizing equations (Christiansen, 1993), which provide estimates of shield thicknesses and spacings required to protect against particles of given sizes, velocities, densities, and impact angles. Shield sizing equations may incorporate ballistic limit equations to determine the effects of impact on the individual walls that make up the shield.
Analytic methods available to spacecraft designers for predicting the damage caused by impacts, and the effects of that damage, are slightly more complex. These include (1) impact damage and effects equations derived from physical principles (Watts et al., 1993, Watts et al., in press) and (2) semiempirical impact cratering, perforation, and spallation equations (e.g., Cour-Palais, 1979; Carey et al., 1984; Hörz et al., 1994). Other analytic models that are useful for providing a qualitative understanding of impact damage include the Grady model (Grady, 1987; Grady and Passman, 1990), the Tate model (Tate, 1967, 1969), and the Ravid and Bonder model (Ravid and Bonder, 1983; O'Donoghue et al., 1989).
There are, however, currently no standardized risk assessment models to determine the probability of component degradation or failure due to orbital debris impacts. Performance degradation models are also not standardized and currently exist for only a few component types. Because of this, spacecraft degradation due to debris impact is currently modeled by combining basic engineering model predictions of the expected environment with empirical scaling models for damage prediction. These empirical scaling laws, though, must often be applied via unproven extrapolations to materials and velocities that were not included in the original data sets on which the empirical models were based. After predicting damage, simple performance degradation "rules" relating degradation to damage area can be applied to determine whether performance will remain within specifications.
Empirical equations based on ballistic limit curves or other experimental data are often used to predict the performance of debris shields. These equations can produce good results if experimental data have been generated for similar particle configurations and velocities (Christiansen,
1993). A current deficiency of these methods is their typically being based on empirical data obtained over limited velocity and impactor shape regimes. This produces considerable uncertainty in extrapolating these equations to other materials, higher velocities, or velocity regimes where phase changes (such as vaporization) occur.
Numerical simulations also can be used to predict the damage to spacecraft from debris impacts or to determine the characteristics of the fragmentation debris released in spacecraft or rocket body breakups. Some such computer codes, usually referred to as "hydrocodes," can model the spacecraft and impact in three dimensions, though many calculations are performed in two dimensions, particularly when the code is being used for "phenomena scoping" and "parameter sensitivity" calculations (i.e., to determine the degree to which changes in material properties would change the size or shape of the impact damage).
The accuracy of results derived from these codes depends on the resolution with which the components are modeled and the material models used in the computations. Good models of the properties of materials and equations of state do not exist for many of the newer materials used on spacecraft, including many composites, ceramics, and coatings. If such models are not developed, these codes may have limited future value. Good material models must also accurately represent phase changes caused by the impact (such as vaporization) as well as material strength effects (such as compressive and tensile failure behavior).
The memory and speed of available computers limited the numerical resolution of early computer simulations of debris damage. Recent developments in computer capabilities have mitigated these problems; it is now possible to model individual components, such as debris shields and hull plates, with sufficient numerical resolution to predict debris impact damage (if good material models of all components are used) with reasonably good accuracy (Hertel et al., 1992; Hertel, 1993; Farenthold, 1992; and Katayama et al., 1993).
Computer simulations are most reliable, however, when benchmarked against experimental data obtained with materials, particle shapes, and velocity regimes similar to those being simulated (Chhabildas et al., 1992b) and used to interpolate between good experimental data. Often, though, experimental data are not available, so numerical analyses provide the only information available for specific impact conditions. In these cases, predictions of debris impact damage must be used with caution. When combined, hypervelocity testing and computer modeling are powerful tools for assessing the survivability of space systems to debris impacts.
LIMITATIONS IN DAMAGE ASSESMENT AND PREDICTION CAPABILITIES
As Figure 5-1 and Table 5-1 show, the range of capabilities for launching particles of the correct mass, velocity, and shape to simulate space debris impacts is limited. This has led to some limitations in current damage assessment and prediction capabilities that have serious implications for the debris field. These are (1) that the full variety of debris shapes and compositions likely to exist in orbit cannot yet be tested in all velocity regimes, and (2) that there is difficulty in launching larger impactors to typical LEO collision velocities. The first limitation makes shield design against the actual debris environment difficult. The second limitation not only reduces the accuracy of damage predictions for the impact of centimeter-size objects, but also contributes to the uncertainty in predictions of the future debris population.
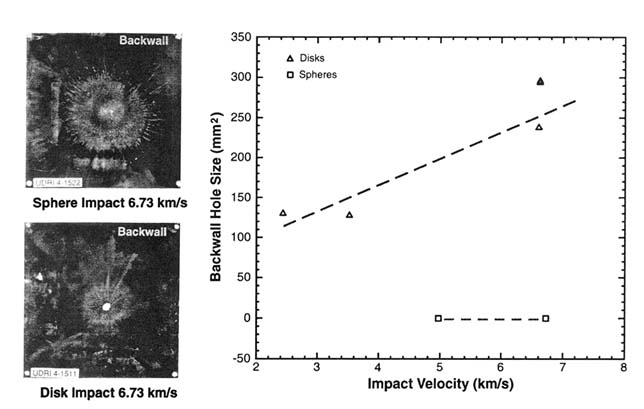
Many analytic theories and measures of impact damage, such as the ballistic limit, are based on the impact of spherical particles. While this is a reasonable assumption for meteoroid impacts, space debris exhibit a much wider assortment of shapes. It has been known for some time that nonspherical impactors can do more damage than spherical impactors in many situations. For example, penetration depth and crater volume from impacts in thick plate targets are strongly influenced by the length of the projectile along its flight axis (Gehring, 1970). Figure 5-2 illustrates how crater depth and volume in a thick target can vary by impactor shape. For Whipple bumper shields (described in Chapter 6), flat plate projectiles are generally more damaging than spherical projectiles of the same mass and velocity (Boslough et al., 1993). Figure 5-3 illustrates how the size of the rupture on the backwall of a Whipple bumper shield can vary greatly with impactor shape. Because of these shape effects, shields designed based on experience with spherical impactors may not be as effective as predicted in protecting spacecraft from actual orbital debris impacts.
Another weak link in current meteoroid and debris shield development efforts is that, because of the limited data available regarding the distribution of material types in the debris environment, models used for shielding design generally assume that large objects are composed of aluminum and small objects are composed of aluminum oxide. Some debris, however, is composed of higher-density materials; LDEF detected impacts by stainless steel, copper, and silver particles (Hörz and Bernhard, 1992). This is a problem because a shield that is designed to withstand only aluminum projectiles could potentially be perforated by high-density debris or meteoroids.
It is not feasible, however, to solve these problems by testing shields
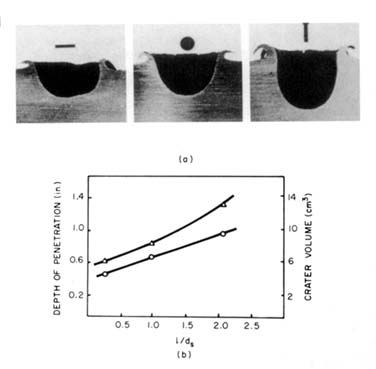
FIGURE 5-2 Variation of crater size with impactor shape for a thick target. SOURCE: Gehring, 1970.
and other components against all possible debris shapes and compositions (and sizes, masses, or velocities). Instead, analytic and numerical methods can be used to extend a limited set of experimental results to other configurations, shapes, compositions, etc., to identify worst-case conditions that can be used in the design of spacecraft protection systems. If these computer simulations are validated with sufficient experimental data, reasonable confidence could then be assigned to the computed results. This approach could increase the reliability of a given protection system and minimize the possibility of serious over- or under-design.
The inability to launch large impactors at typical LEO collision velocities not only causes the same type of problems described above but also limits the accuracy of breakup models. Currently, masses capable of breaking up even the smallest spacecraft can be launched only to low
velocities (<7 km/s). Because of this lack of capability, all breakup models use data from tests at impact velocities lower than the typical LEO collision velocities. In addition, few facilities can perform large-scale collision tests in a controlled environment. (A very large chamber capable of conducting both explosion- and collision-induced breakup experiments has, however, been constructed in Russia [Fortov, 1993].) As mentioned in Chapter 2, without a controlled environment, data on the distribution of small particles generated by a breakup are suspect and data on the breakup-induced velocities of any size particle become difficult to obtain.
FINDINGS
Finding 1: High confidence in the validity of (1) assessments of the response of spacecraft components and shield configurations to debris impacts and (2) component and shield qualification and acceptance tests can presently be provided only by hypervelocity impact testing, but current hypervelocity impact facilities cannot simulate the full range of debris impactor sizes, compositions, shapes, and velocities. As a result, spacecraft protection systems currently are designed to resist the type of projectiles that can be launched by these facilities (most typically aluminum spheres). Because actual debris objects typically have more complex shapes that are very likely to do more damage than spheres at LEO collision velocities, current spacecraft surfaces and shield designs may not provide the desired level of protection.
Finding 2: Facilities in a number of nations are capable of carrying out hypervelocity impact tests for debris research but information about and access to these facilities is often difficult to obtain, there is no coordinated interfacility approach to either impact research or new facility development, and the results of experiments are not widely available. The general inaccessibility of facility capabilities and of the impact data generated at these facilities has resulted in considerable duplication of effort, slowing the development of good models of debris impact damage.
Finding 3: Analytical models can be used to design spacecraft shielding and to predict impact damage for regimes that hypervelocity testing cannot simulate. Numerical simulations can be useful tools for predicting damage to spacecraft and determining the characteristics of breakup debris. Unless both of these methods are validated by comparison to experimental data, however, significant variability in predicted results can occur. When used together, hypervelocity testing and computer model
ing are powerful tools for assessing the survivability of space systems to debris impacts.
REFERENCES
Anisimov, S.I., B.A. Demidov, L.I. Rudakow, R.Z. Sagdeyev, and V.Ye. Fortov. 1985. Modeling the destruction of protective screens of the Vega spacecraft with the aid of high-current relativistic electron beams. Journal of Experimental and Theoretical Physics Letters 41(11):455.
Asay, J.R., T.G. Trucano, and R.S. Hawke. 1989. The use of hypervelocity launchers to explore previously inaccessible states of matter. International Journal of Impact Engineering 10:51–66.
Boslough, M.B., J.M. Ang, L.C. Chhabildas, W.D. Reinhardt, C.A. Hall, B.G. Cour-Palais, E.L. Christiansen, and J.L. Crews. 1993. Hypervelocity testing of advanced shielding concepts for spacecraft against impacts to 10 km/s. International Journal of Impact Engineering 14:95–106.
Carey, W.C., J.A.M. McDonnell, and D.G. Dixon. 1984. An empirical penetration equation for thin metallic films used in capture cell techniques. Pp. 131–136 in Properties and Interactions of Interplanetary Dust. Proceedings of the 85th Colloquium of the International Astronomical Union, Marseille, France, July 9–12. Volume 19 of the Astrophysics and Space Science Library. Dordecht, Holland: D. Reidel Publishing Company.
Chhabildas, L.C. In press. To be published in Proceedings of the 1994 Hypervelocity Impact Symposium, Santa Fe, New Mexico, October 16–19. International Journal of Impact Engineering.
Chhabildas, L.C., J.E. Dunn, W.D. Reinhart, and J.M. Miller. 1992a. An impact technique to accelerate flier plates to over 12 km/s. International Journal of Impact Engineering 14:121–132.
Chhabildas, L.C., E.S. Hertel, and S.A. Hill. 1992b. Hypervelocity impact tests and simulations of single Whipple bumper shield concepts at 10 km/s. International Journal of Impact Engineering 14:133–144.
Christiansen, E.L. 1990. Investigation of hypervelocity impact damage to space station truss tubes. International Journal of Impact Engineering 10:125–133.
Christiansen, E.L. 1993. Design and performance equations for advanced meteoroid and debris shields. International Journal of Impact Engineering 14:145–156.
Christiansen, E.L., and J. Ortega. 1990. Hypervelocity Impact Testing of Shuttle Orbiter Thermal Protection System Tiles. AIAA Paper No. 90-3666. American Institute of Aeronautics and Astronautics Space Programs and Technologies Conference, Huntsville, Alabama, September 25–28. Washington, D.C.: American Institute of Aeronautics and Astronautics.
Christiansen, E.L., R. Bernhard, J. Hyde, J. Kerr, K. Edelstein, J. Ortega, and J. Crews. 1993. Assessment of high velocity impacts on exposed shuttle surfaces. Pp. 447–452 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5–7 April 1993. Darmstadt: European Space Operations Center.
Cour-Palais, B.G. 1979. Space Vehicle Meteoroid Shielding Design. ESA SP-153. Paris: European Space Agency.
Cour-Palais, B.G. 1986. Hypervelocity impacts in metals. International Journal of Impact Engineering 5:221–238.
Farenthold, E.P. 1992. A Lagrangian model for debris cloud dynamics simulation. International Journal of Impact Engineering 14:229–240.
Fortov, V. 1993. Hypervelocity Impact in Space Debris Problem. Briefing presented to the Committee on Space Debris Workshop, National Research Council, Irvine, California, November 18.
Gehring, J.W. Jr. 1970. Engineering considerations in hypervelocity impact. Pp. 466–468 in High-Velocity Impact Phenomena, R. Kinslow, ed. New York-London: Academic Press.
Gilath, I., S. Eliezer, T. Bar-Noy, R. Englman, and Z. Jaeger. 1992. Material response at hypervelocity impact conditions using laser induced shock waves. International Journal of Impact Engineering 14:279.
Grady, D.E. 1987. Fragmentation of rapidly expanding jets and sheets. International Journal of Impact Engineering 5:285–292.
Grady, D.E., and S.L. Passman. 1990. Stability and fragmentation of ejecta in hypervelocity impact. International Journal of Impact Engineering 10:192–212.
Herrman, W., and J.S. Wilbeck. 1986. Review of hypervelocity penetration theories. International Journal of Impact Engineering 5:307–322.
Hertel, E.S. 1993. Simulation of orbital debris impacts on bumper shields. Pp. 413–418 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5–7 April 1993. Darmstadt: European Space Operations Center.
Hertel, E.S., L.C. Chhabildas, L. Yarrington, and S.A. Hill. 1992. Computational determination of ballistic limits for a simple Whipple shield. Pp. 15–18 in Hypervelocity Impacts in Space, J.A.M. McDonnell, ed. Canterbury, United Kingdom: University of Kent.
Holsapple, K.A. 1992. Hypervelocity impact experiments in surrogate materials. International Journal of Impact Engineering 14:335–345.
Hörz, F., and R.P. Bernhard. 1992. Compositional Analysis and Classification of Projectile Residues in LDEF Impact Craters. NASA TM-104750. Houston, Texas: National Aeronautics and Space Administration Johnson Space Center.
Hörz, F., M. Cintala, R.P. Bernhard, and T.H. See. 1994. Dimensionally scaled penetration experiments: Aluminum targets and glass projectiles 50 µm to 3.2 mm in diameter. International Journal of Impact Engineering 15(3):257–280.
Isbell, W.M., C.E. Anderson, J.R. Asay, S.J. Bless, D.E. Grady, and J. Sternberg. 1992. Penetration Mechanics Research in the former Soviet Union. Unpublished Foreign Applied Sciences Assessment Center Technical Assessment Report. September. McLean, Virginia: Science Applications International Corporation.
Katayama, M., T. Aizawa, S. Kibe, and S. Toda. 1993. A numerical simulation of hypervelocity impact of space debris against the Whipple bumper system. Pp. 419–424 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5–7 April 1993. Darmstadt: European Space Operations Center.
Konrad, C.H., L.C. Chhabildas, M.B. Boslough, A.J. Piekutowski, K. Poorman, S.A. Mullin, and D.L. Littlefield. 1993. Dependence of debris cloud on projectile shape. Pp. 1845–1848 in High Pressure Science and Technology, S.C. Schmidt, J.W. Shaner, G.A. Samara, and M. Ross, eds. Woodbury, New York: American Institute of Physics.
Krueger, F.R. 1993. Hypervelocity impact physics—Plasma discharge phenomena on solar generators. The Behavior of Systems in the Space Environment, NATO ASI Series E: Applied Sciences 245:273–290.
Lee, R., J. Osher, H. Chau, M. Gerassimenko, G. Pomykal, and R. Spear. 1992. The impact of flat, thin plates on aluminum targets in the 5-10 km/s velocity range. International Journal of Impact Engineering 14:451–466.
Malley, M.M., and W.G. Nicols. 1987. Survey of Laser and Hypervelocity Test Facilities for the Defensive Shields Demonstration. Air Force Weapons Laboratory report AFWL-NTC-ITR-87-02 June (unpublished, distribution limited to Air Force Weapons Laboratories only).
O'Donoghue, P.E., S.R. Bonder, C.E. Anderson, Jr., and M. Ravid. 1989. Comparison of a high velocity impact model with numerical simulation. International Journal of Impact Engineering 8(4):289–301.
Piekutowski, A.J. 1986. Debris clouds generated by hypervelocity impact of cylindrical projectiles with thin aluminum plates. International Journal of Impact Engineering 5:509–518.
Ravid, M., and S.R. Bonder. 1983. Dynamic perforation of viscoplastic plates by rigid projectiles. International Journal of Engineering Science 21(6):577–591.
Reimerdes, H., K. Stecher, and M. Lambert. 1993. Ballistic limit equations for the Columbus double-bumper shield concept. Pp. 433–439 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5-7 April 1993. Darmstadt: European Space Operations Center.
Schneider, E., and A. Stilp. 1993. Meteoroid/debris simulation at Ernst-Mach-Institute (EMI): Experimental methods and recent results. Pp. 401–404in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5–7 April 1993. Darmstadt: European Space Operations Center.
Stradling, G.L., G.C. Idxorek, B.P. Shafer, H.L. Curling, Jr., M.T. Collopy, A.A. Hopkins Blossom, and S. Furerstenau. 1992. Ultra-high velocity impacts: Cratering studies of microscopic impacts from 3 km/s to 30 km/s. International Journal of Impact Engineering 14:719–728.
Tate, A. 1967. Theory for the deceleration of long rods after impact. Journal of Mechanical Physics Solids 15:387–399.
Tate, A. 1969. Further results in the theory of long rod penetration. Journal of Mechanics Physics Solids 17:141–150.
Trott, W.M., and K.D. Meeks. 1990. Acceleration of thin foil targets using fiber-coupled optical pulses. Pp. 997–1000 in Shock Compression of Condensed Matter—1989. Amsterdam: Elsevier Science Publishers.
Walker, J.D., D.J. Grosch, and S.A. Mullin. 1992. A hypervelocity fragment launcher based on an inhibited shaped charge. International Journal of Impact Engineering 14:763–774.
Watts, A., D. Atkinson, and S. Rieco. 1993. Dimensional Scaling for Impact Cratering and Perforation. NASA NCR-188259. March 16, Houston, Texas: National Aeronautics and Space Administration Johnson Space Center.
Watts, A.J., D.R. Atkinson, L. Crowell, B. Tritz, and S. Rieco. In press. Impact Effects on Optics Survivability: Induced Optical Scatter. PL-TR-94-1046. Kirkland Air Force Base, New Mexico: Phillips Laboratory.
Whitney, J.P. 1993. Hypervelocity Impact Tests of Shielded and Unshielded Pressure Vessels. JSC-32294. Houston, Texas: National Aeronautics and Space Administration Johnson Space Center.