8
The Future Orbital Population and the Effectiveness Of Debris Reduction Measures
THE FUTURE ORBITAL POPULATION
As described in Chapter 1, the number of cataloged space objects has increased nearly linearly since 1960, at an average rate of about 220 objects per year. New spacecraft, the mission-related debris and rocket bodies associated with those spacecraft, and the fragments caused by the breakup of objects in space have contributed to this growth. Without the effect of orbital decay caused by atmospheric drag, the increase in the space object population would have been much large. To date, more than 15,000 cataloged objects (about twice the current cataloged population in orbit) have decayed into the atmosphere and, at the peaks of the 11-year solar activity cycle, the overall losses of cataloged space objects have occasionally outnumbered the increases, resulting in an overall decline in the cataloged population.
It is this balance between the creation of new debris and the orbital decay of existing debris that will determine the magnitude and distribution of the future debris population. For each altitude region, this balance will determine if the debris population will rise or fall and the rate at which this change will occur. The balance obviously will vary greatly at different altitudes; in circular orbits below about 500 km, where orbital decay is fairly rapid, major long-term increases in the debris population are unlikely, while at higher altitudes and in some high-eccentricity orbits, medium and large debris added to the population may remain for tens, thousands, or even millions of years.
As described in Chapter 2, models have been developed to predict
the future debris population. Many of these models are loosely based on population "birth and death" models, which assign the debris population to a number of "bins," each characterizing the number of particles of a given mass range within a given altitude range. The simplest models (e.g., Talent, 1992) use one bin for all masses and altitudes to represent the entire LEO population, but more complex models have used more mass and altitude ranges (Rossi et al., 1993). NASA's EVOLVE model (Reynolds, 1990) can use a variable number of bins, but typically uses 15 mass and 36 altitude ranges. Although these models incorporate a variety of different assumptions, they generally carry out similar procedures to predict the future debris population.
First, the initial debris population (to a certain limiting size or mass) is calculated for each altitude bin, based on measurements or models of the current debris population. Then the orbits of this initial population are propagated into the future (by using either deterministic or statistical methods), in the course of which some objects are removed from or added to the altitude bin as a result of perturbing forces such as atmospheric drag. Predictions of the amount and distribution of new objects launched into orbit, as well as of the results of possible explosions in orbit, are used to add new space objects to the population. When it is determined that a collision will occur, another model is used to determine the effects of the collision, including the creation of new debris. The entire process is then repeated, with the output of the first iteration used as the initial population for the next.
These models are generally useful only in predicting the magnitude and characteristics of the populations of medium-sized and large debris. As discussed in Chapter 3, knowledge of small debris is so limited that it is extremely difficult to estimate the current population, much less project future trends. About the only predictions that can be made about the future small debris population are that
-
the amount of small debris produced in breakups is likely to increase if the number of collisions grows, because collisions are predicted to produce very large numbers of small debris particles; and
-
the amount of very small debris (such as the particles expelled by solid rocket motors and the smallest products of breakups and degradation) in orbit may change markedly from year to year, due to the strong effect of perturbing forces on the orbits of these particles. Thus, regardless of the historical total amount of very small debris released into the environment, the population of these particles at any given time in the future will be strongly dependent on the amount produced during the preceding one or two years.
Uncertainties in the Models
As described in Chapter 2, models that predict the future debris population contain numerous uncertainties. These include uncertainties about
-
the number, characteristics, and distribution of the objects that are currently in orbit;
-
the number, characteristics, and initial distribution of objects that will be launched into orbit in the future;
-
the future level of solar activity and its effect on atmospheric drag; and
-
the characteristics of the fragments created in space object explosions and collisions.
These uncertainties have varying effects on the accuracy of models that predict the future space object population.
As discussed in Chapter 3, our knowledge of the current population of objects in orbit is very limited; the locations of only the largest are known. If a model of the future debris environment is going to include uncataloged objects in its initial population, it must extrapolate the number and distribution of the uncataloged population by using existing tracking and sampling data as well as estimates of the number and characteristics of debris created during known breakups. (Estimations of the amount of mission-related debris that has been released during spacecraft deployment and operations can also be employed to aid in this process, but they are currently not widely used.) This uncertainty about the uncataloged population, however, has only a limited effect on predictions of the future environment because (as is discussed later) it is the largest objects—most of which are cataloged—that drive the growth in the future population. Some studies show that the untrackable population has no detectable effect on the evolution of the future LEO debris population (Eichler, 1993; Kessler and Loftus, in press). Other models take advantage of this phenomenon and use only cataloged objects for their initial population (Kessler, 1991).
Predictions of the number and characteristics of space objects that will be added to various orbital regions as a result of future launches are also uncertain. The future launch rate, the size ranges of future spacecraft, and the distribution of orbits into which these spacecraft will be launched cannot be predicted in detail because they depend on such unpredictable factors as future mission requirements, technologies, economics, and global politics. Because of the limited predictability of future solar activity (and thus of atmospheric drag in LEO), it is also difficult to estimate the number of objects that will be removed by natural forces.
Finally, breakup models are a major source of uncertainty in any predictive model of the future debris environment. As discussed in Chapter 2, breakup models are based on a very limited set of data, and models of both explosions and collisions contain large uncertainties. Models of collisions, in particular, are supported by data from only two in-space collisions and a few ground tests conducted at velocities lower than typical LEO collision velocities. It is not at all certain how well current collision models
-
incorporate the effects of different space object configurations, different spacecraft materials, and different impact geometries on the results of a collision;
-
approximate the threshold size (in terms of mass and/or energy) of debris that can cause space objects of a given size to break up; or
-
estimate the distribution of the size and mass of particles produced in collisions (although the limited ground and space tests that have been conducted indicate that current models are fairly accurate at predicting the amount of large debris produced in a collision).
Models of the future debris population often deal with these uncertainties by treating them as variables. For example, a model of the future population can be run with the rate at which rocket bodies explode in the future set equal to current levels, and then run again with the rate set to zero, to predict the effects of implementing rocket body passivation measures on the future growth of the space object population. Treating these uncertainties as variables does not reduce the overall uncertainty in the model, of course, but it does serve to clarify the dependence of the model's results on each variable.
Predictions of the Future Orbital Environment
If the only additions to the future debris population were rocket bodies, nonfunctional spacecraft, mission-related debris, and the products of explosions and surface deterioration, the space object population would likely continue its roughly linear growth. Implementation of measures to reduce the number of explosions of spacecraft and rocket bodies, and to limit the amount of mission-related debris released as a result of spacecraft deployment and operations, might result in a slower rate of growth, just as changes in future launch patterns could result in a faster rate of growth. Collisions between space objects, however, threaten to add a potentially large and exponentially growing number of new objects to this population.
The probability that a collision will occur in any particular orbital region increases with roughly the square of the number of objects in that
region. Each orbital region has a ''critical density," at which point it contains enough objects with sufficient mass that the rate of fragment production from collisions is greater than the rate at which objects are removed due to such forces as atmospheric drag. Once this critical density is reached, fragments from collisions will cause an ever-increasing number of new collisions. This is sometimes referred to as a "cascading effect" or a "chain reaction," although the time frame involved is typically on the order of decades or centuries—not the nearly instantaneous reaction that the latter term often implies. Once collisional cascading has begun, it cannot be stopped by a reduction in launch rate because it is self-sustaining. If no new mass is added to the region, the number of collisions will eventually drop (perhaps over hundreds or thousands of years) as the large objects are broken into smaller pieces, but by that time, the collision hazard in the orbital region may be too high for most space operations.
Several independent models of the future debris population suggest that collisional cascading is likely to occur in Earth orbit (see Kessler and Cour-Palais, 1978; Kessler, 1991; Talent, 1992; Kessler et al., 1993; Rex and Eichler, 1993; Rossi et al., 1993; Su, 1993). Although these simulations use different methodologies and incorporate a number of different values for such parameters as the initial population and the amount of debris produced in collisions, their results are uniform in predicting a more-than-linear increase in the number of future space objects in LEO over the next century unless measures are taken to reduce the addition of new debris to the environment. Figures 8-1 and 8-2 show the results of two of these simulations.
These figures show predictions of the future growth in the population of objects larger than 1 cm, because this population is more relevant to the hazard to spacecraft than the population of large objects. However, it must be remembered that the collisional population growth is driven almost entirely by the population of large debris. The exponential growth visible in predictions of the 1-cm debris population is only a symptom, not the cause, of collisional population growth.
Though these models all show that an exponential rise in the orbital debris population will occur unless preventive measures are taken, the time frame over which this rise will occur cannot be determined precisely. The error bounds of the time frame for collisional growth are a result of all of the uncertainties (discussed earlier) that are incorporated into models of the future population growth. Figures 8-4 and 8-5 show how variations in the assumptions made in a model can affect that model's predictions of the rate at which the future space object population will rise. In Figure 8-4, different assumptions about the basic population growth rate (i.e., the growth rate not counting objects produced in
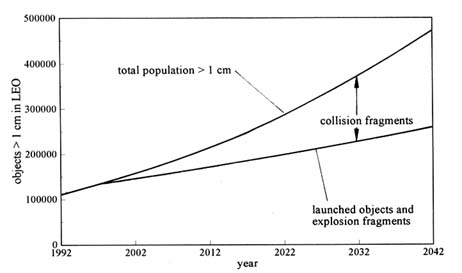
FIGURE 8-1 Model simulation of the contribution of collision fragments to the future LEO space object population. SOURCE: Rex and Eichler, 1993.
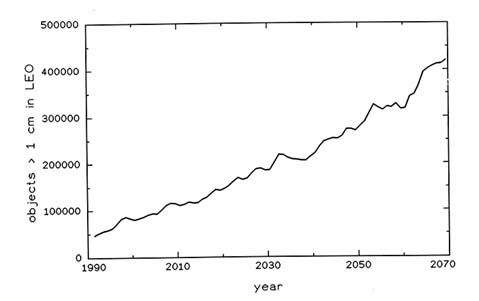
FIGURE 8-2 Different model simulation of the future LEO space object population (constant launch rate and explosion rate at current level, no mitigation measures).
SOURCE: National Aeronautics and Space Administration.
|
BOX 8-1 One Model of the Future Debris Environment The CHAIN program (Rex and Eichler, 1993) uses a combination of analytic and stochastic methods to predict the future number of orbital objects larger than a centimeter in diameter. Figure 8-3 shows the program's logic flow. First, the current number of orbiting space objects larger than 1 cm is estimated from measurements of the debris environment and is divided into 24 bins with six mass and four altitude ranges. The collision risk (for 21 different types of collisions) within each altitude bin is then calculated by using analytical formulas. A stochastic Monte Carlo method is used to randomly determine the number of collisions in each altitude bin based on these collision risks. Fragments from these collisions are then added to the population, along with newly launched objects and fragments from space object explosions. The effects of orbital decay on all of these objects are then calculated, and the new "initial" population is determined. The analytic formulas are then applied to this new population to calculate collision probabilities for the next iteration, and the entire process is repeated. This model predicts that a "business as usual" scenario, in which no debris reduction measures are implemented, would result in the population of objects larger than 1 cm increasing to about 250,000 in the next 50 years—not including the effects of collisions. When the effects of collisions are factored in, the further increase to the population is more than 200,000 additional fragments. Figure 8-1 shows the averaged output of this model. |
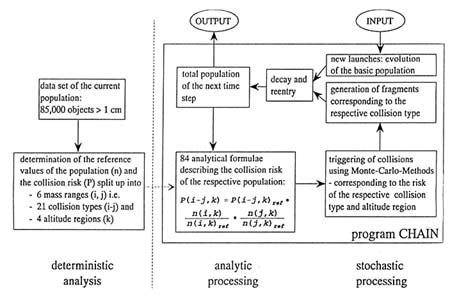
FIGURE 8-3 Logic flow of the CHAIN program. SOURCE: Rex and Eichler, 1993.
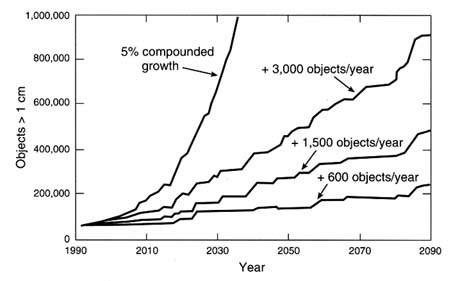
FIGURE 8-4 Effect of basic population growth rate on predicted future population of LEO objects larger than 1 cm. Initial basic population (launched objects plus collision fragments): about 60,000 > 1 cm. Lines are the result of Monte Carlo simulations run with the same stochastic numbers but with different basic population growth rates. SOURCE: Eichler et al., 1992.
collisions) change the predicted time it takes for the debris population to double from about 15 to 60 years. Figure 8-5 shows the effect of varying the mass distribution of collision fragments in a different simulation of the future environment; it is clear from the figure that this factor also introduces a large uncertainty into the predicted growth rate of the future debris population. Since models of the future debris population must incorporate both these uncertainties, as well as others, it is premature to suggest exactly when collisional growth will begin to occur; it may already be under way, or it may not begin for several decades.
Collisional growth will not, however, take place over the entire near-Earth orbital area. It is most likely to occur in regions that (1) have a high debris flux, (2) do not experience a high level of atmospheric drag, and (3) have high typical collision velocities. (These characteristics lead to a large number of energetic collisions that produce long-lasting fragments.) Figure 8-6 shows one assessment of how the critical density varies with altitude in LEO due to such factors as atmospheric drag and the size and inclination distribution of the current populations (Kessler, 1991). The shaded area shows the two LEO regions, at 900 to 1,000-km and around
1,500-km altitude, in which the cataloged population has already exceeded the calculated critical density.
In regions where the spatial density has already exceeded the critical density, the number of collision fragments produced will eventually rise exponentially. The launches of new spacecraft (and their accompanying rocket bodies and mission-related debris), as well as the explosion-induced breakup of orbiting rocket bodies and spacecraft, are also likely to contribute to the debris population in these regions. Launches to these regions will probably continue for some time because orbits within these regions have characteristics that make them valuable to spacecraft operators; this is, after all, the reason they became crowded. As discussed in Chapter 7, some level of residual explosions is also likely to continue, regardless of the passivation measures adopted. The addition of new objects to already crowded orbital regions will likely increase the collision probability for functional spacecraft in these regions, as well as the rate and magnitude of their future collisional population growth.
LEO regions that have not reached a critical density may still be af-
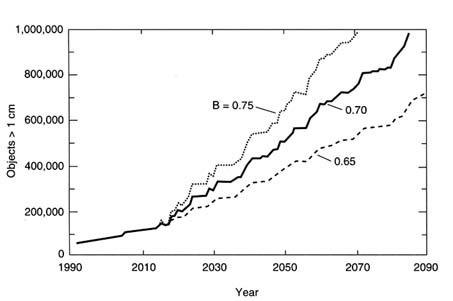
FIGURE 8-5 Effect of assumed mass distribution of collision fragments (B) on prediction of future population of objects larger than 1 cm. The three scenarios are the result of Monte Carlo simulations run with the same stochastic numbers but with different assumed mass distributions of collision fragments. In all scenarios, the basic population (launched objects plus collision fragments) increases by 3,000 objects >1 cm per year. SOURCE: Eichler, 1993.
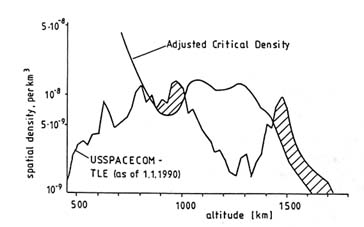
FIGURE 8-6 Critical density in LEO (shaded regions are above the adjusted critical density). SOURCE: Kessler, 1991.
fected by collisions in those regions that have surpassed their critical density. For example, as can be seen from Figure 8-6, the debris population at altitudes below about 700 km is not likely to exceed the critical density; at these altitudes, atmospheric drag typically will remove collision fragments before they collide with another object. Collision fragments produced in other orbital regions, however, could increase the debris hazard in these low-altitude orbits. Although most of the larger debris generated in collisions in higher orbits will tend to stay relatively close to their initial orbit, some smaller fragments will typically be rejected at greater velocities (as discussed in Chapter 4) and thus will be distributed widely, increasing collision probabilities over the entire LEO region. In addition, fragments from collisions at higher altitudes will eventually experience orbital decay, causing them to pass through lower orbital regions. Finally, fragments produced in collisions between objects in highly elliptical orbits and objects in LEO regions with high spatial densities may pass through other LEO regions at high velocities.
Even though atmospheric drag is only a minor factor in removing debris from orbits above LEO, the chance of collisional cascading does not necessarily increase with altitude as might be expected. There are a number of reasons for this. First, as shown in Figure 3-2, higher orbits typically have a much lower object flux than LEO. Second, the volume of a given altitude region increases with altitude so, even if additional objects are added, the spatial density will rise only slowly. Third, collision velocities in high-altitude orbits are generally slower than in LEO; this typically leads to the creation of fewer fragments in a collision. Finally (as discussed in Chapter 7), the debris created in collisions at high alti-
tudes is dispersed over a much wider area than debris from collisions in LEO, which reduces its chance of striking other objects in the initial orbital region.
In GEO, where collision velocities are lower than in LEO and debris produced in collisions will be spread over a wide volume of space, collisional cascading may not occur and, if it does, may not be noticeable for thousands to tens of thousands of years (Kessler, 1993). It thus seems probable that unlike the situation in LEO, the future debris population in GEO could be driven more by explosions and continued launch traffic than by collisions. Because of this dependence on inherently unpredictable factors, it is difficult to make accurate predictions of the future GEO population.
EFFECTIVENESS OF DEBRIS REDUCTION MEASURES
There are two major types of methods to reduce the debris hazard in Earth orbit. One set of methods aims at limiting the number of potentially harmful objects in orbit, primarily by reducing the release of mission-related debris and by preventing further explosions of spacecraft and rocket bodies. The other methods seek to limit the total mass and cross-sectional area of objects in orbit by deorbiting or reorbiting spacecraft and rocket bodies. These two approaches to debris reduction have very different effects on the short- and long-term orbital debris hazard.
Limiting the number of potentially harmful objects in orbit can sharply reduce growth in the short-term debris hazard and can restrict growth in the long-term hazard to some regions, but it will have little effect on slowing or preventing collisional cascading. Limiting the total mass and cross-sectional area added to orbit, on the other hand, can prevent or slow the onset and growth of collisional cascading and can also ameliorate the short-term collision hazard. Limiting cross-sectional area plays an important role in reducing the long-term potential for collisional cascading because the total cross-sectional area in orbit represents the total "target area" for collisions. Limiting the amount of mass is important because, in the long-term, the mass in orbit determines the maximum number of collision fragments capable of causing further breakups.
The same models used to predict the future evolution of the debris population can also be used to predict the effectiveness of various measures in limiting the growth in that population. Although all of the uncertainties in these models (discussed earlier in this chapter) also apply to such predictions, that does not prevent a rough assessment of the effectiveness of various debris reduction methods from being made. These
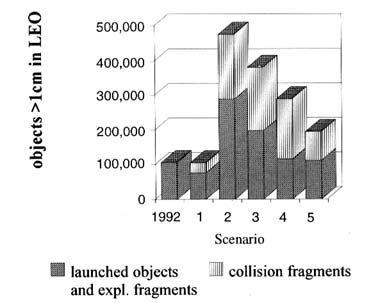
FIGURE 8-7 Predicted effect of debris reduction measures on population of collision fragments and other debris in 2042. SOURCE: Rex and Eichler, 1993.
models simulate only the LEO environment, however; similar models with the capability to predict the effectiveness of debris reduction measures on the semisynchronous or GEO environment have not yet been developed.
Figures 8-7 and 8-8 show the result of one of these model simulations (Rex and Eichler, 1993). Figure 8-7 shows the predicted effect of various debris reduction methods on the LEO population of collision fragments and other types of debris in 2042, and Figure 8-8 shows how these measures are predicted to affect the total LEO debris population over time. In Figure 8-7, the first bar shows the estimated population of LEO objects larger than 1 cm in 1992, and the other bars show the predicted 2042 population of debris if various reduction methods are implemented. Scenario 1 shows the predicted 2042 LEO population resulting from an immediate and complete cessation of all space launches. The model suggests that in this case, although the population of launched objects and explosion debris would decrease as a result of orbital decay, some collision debris and some debris from explosions of objects already in orbit would be generated, keeping the total population nearly constant over the 50 years of the simulation. Scenario 2 represents the other extreme, in which the linear growth of space activity drives the population of objects
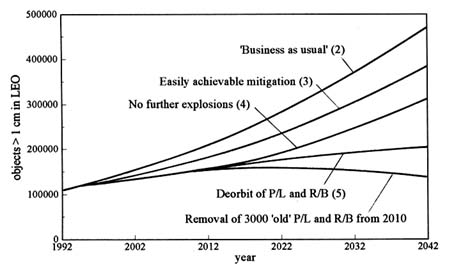
FIGURE 8-8 Predicted effect of debris reduction measures over fifty years on space object population. SOURCE: Rex and Eichler, 1993.
larger than 1 cm in LEO from about 100,000 to close to 500,000 over the 50 years of the simulation.
Scenarios 3, 4, and 5 explore the effects of various debris reduction measures on the future LEO population. Scenario 3 shows the effect of cutting the explosion rate and the release of mission-related debris in half, and scenario 4 shows the effect of completely ending all explosions in orbit (starting in 1998). These measures are shown to significantly cut the predicted number of objects added to orbit, but since they do nothing to reduce the total mass or cross-sectional area added to orbit, it is not surprising that the model predicts that they will not greatly reduce the number of additional collision fragments. Figure 8-8 shows that neither scenario 3 nor scenario 4 prevents the eventual exponential growth of the debris population.
Scenario 5 shows the combined effect of preventing explosions, reducing the release of mission-related debris, and performing EOL deorbiting of rocket bodies (after 2003) and spacecraft (after 2010). Even in this scenario, the total debris population still doubles in 50 years. In this case, however, unlike the previous cases, the population does not increase rapidly near the end of the simulation, which suggests that exponential growth has at least been delayed. Finally, the bottom curve in Figure 8-8 shows how (for this model) it would take the active removal of 3,000 old payloads and rocket bodies to actually prevent the population from growing.
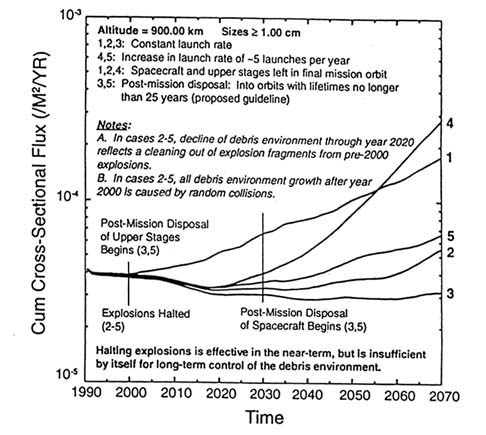
FIGURE 8-9 Predicted effect of debris mitigation measures on the debris environment. SOURCE: Loftus, 1993.
Figures 8-9 and 8-10 show the results of a different model's predictions of the effect of debris reduction measures (Loftus, 1993). This model incorporates different initial assumptions than the previous model and examines the effect of a different set of potential debris reduction methods. The figures focus on the object flux in the 900-km-altitude regime, which (as discussed earlier) is believed to already have a spatial density that exceeds the region's critical density. Like the previous model, this model predicts that the debris population will rise much more rapidly if the number of explosions is not reduced and that the debris population will rise exponentially unless some types of reorbiting maneuvers are performed. (Figure 8-9 also shows the strong influence of the assumptions about the future launch rate on the future hazard; scenario 4, which assumes that the number of launches increases from the present level at a
rate of five additional launches each year, predicts double the flux in 2070 than does scenario 2, which is identical except that it assumes a constant launch rate at current levels.) Figure 8-10 further explores the effect on the debris flux of reducing the orbital lifetime of spacecraft and rocket bodies. It is clear from this figure that orbital lifetime reduction measures can slow the rate at which the debris population increases and that the greater the reduction in orbital lifetime, the less will the debris environment grow. However, given all the uncertainties involved, the model does not suggest that any one particular chosen target lifetime is more cost-effective than another. It must be remembered that all of these models incorporate high levels of uncertainty. This can be seen just by comparing Figure 8-8 and Figure 8-9. In Figure 8-9, the debris hazard for a ''no-explosion" scenario
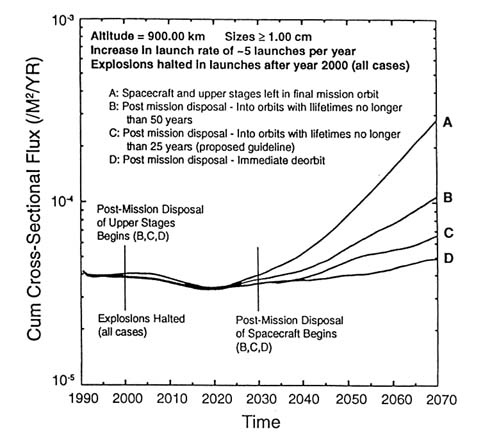
FIGURE 8-10 Predicted effect of disposal orbit lifetime on the debris environment. SOURCE: Loftus, 1993.
with a linear traffic growth actually declines until about 2020. In the equivalent scenario (4) in Figure 8-8, the population almost doubles over the same time frame. Detailed comparisons of the two models (Reynolds and Eichler, in press) indicate that the differences are mostly due to different assumed initial conditions for the amount of mass in orbit and, to a lesser extent, the number of bins used. Nevertheless, both models predict that (1) reducing the number of explosions in orbit will help contain the growth in the debris hazard, and (2) deorbiting or lifetime reduction maneuvers (in addition to reducing the number of explosions) may be required to prevent an eventual exponential rise in the debris population.
FINDINGS
Finding 1: If the only additions to the future debris population were rocket bodies, nonfunctional spacecraft, mission-related debris, and the products of explosions and surface deterioration, the space object population would probably continue its roughly linear growth. Several models using different methodologies and different assumptions, however, predict that collisions between space objects will add a potentially large and exponentially growing number of new objects to this population. Because of the numerous uncertainties involved in models of the debris environment, it is premature to suggest exactly when collisional growth will begin to occur; it may already be under way, or it may not begin for several decades.
Finding 2: Collisional growth is most likely to occur in regions that (1) have a high debris flux, (2) do not experience a high level of atmospheric drag, and (3) have high typical collision velocities. Two LEO regions that meet these criteria, at around 900- to 1,000-km and around 1,500-km altitude, are believed to already have exceeded their critical density, the point at which they will continue to experience population growth due to collisions even if no further objects are added. Fragments from collisions in regions experiencing collisional growth may be widely distributed, increasing the collision probability even in regions that are not threatened by collisional growth.
Finding 3: Although debris fragments represent the greatest short-term debris hazard to current spacecraft, it is the large objects in orbit (generally spacecraft and rocket bodies) that drive the potential for collisional cascading. Thus, although eliminating the explosion of objects in orbit can reduce the short-term growth in the debris population, it is necessary to take measures to remove spacecraft and rocket bodies from crowded orbital regions at the end of their functional lifetimes in order to reduce the potential for collisional growth.
REFERENCES
Eichler, P. 1993. The necessity and efficiency of mitigation measures to limit the debris population in LEO. Presented at the National Research Council Committee on Space Debris Workshop, Irvine, California. November 18.
Eichler, P., H. Sdunnus, and J. Zhang. 1992. Reliability of Space Debris Modelling and the Impact on Current and Future Space Flight Activities. World Space Congress paper B.8-M.3.11. Washington, D.C.
Kessler, D.J. 1991. Collisional cascading: The limits of population growth in low Earth orbit. Advances in Space Research 11(12):63–66.
Kessler, D.J. 1993. Orbital debris environment. Pp. 251–262 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5–7 April 1993. Darmstadt: European Space Operations Center.
Kessler, D.J., and B.G. Cour-Palais. 1978. Collision frequency of artificial satellites: The creation of a debris belt. Journal of Geophysical Research 83(A6):2637–2646.
Kessler, D.J., and J.P. Loftus, Jr. In press. Orbital Debris as an Energy Management Problem. Paper presented at the 31st Plenary Meeting of COSPAR, Hamburg, Germany, July 14. To be published in Advances in Space Research.
Kessler, D.J., R.C. Reynolds, and P.D. Anz-Meador. 1993. Review of Various Models to Describe the Orbital Debris Environment. IAA-6.3-93-744. Paper presented at the 44th Congress of the Astronautical Federation, Graz, Austria, October 16–22.
Loftus, J.P. 1993. The NASA debris handbook. Presented at the National Research Council Committee on Space Debris Workshop, Irvine, California. November 18.
Rex, D., and P. Eichler. 1993. The possible long term overcrowding of LEO and the necessity and effectiveness of debris mitigation measures. Pp. 604–615 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany, 5–7 April 1993. Darmstadt: European Space Operations Center.
Reynolds, R. 1990. A review of orbital debris environment modeling at NASA/JSC. AIAA 90-1355. Paper presented at the AIAA/NASA/DoD Orbital Debris Conference, Baltimore, Maryland, April 16–19. Washington, D.C.: American Institute of Aeronautics and Astronautics.
Reynolds, R., and P. Eichler. In press. A comparison of debris environment projections using the EVOLVE and CHAIN models. Paper presented at the 31st Plenary Meeting of COSPAR, Hamburg, Germany, July 14. To be published in Advances in Space Research.
Rossi, A., L. Anselmo, C. Pardini, A. Cordelli, P. Fannella, and T. Parinello. 1993. Approaching the exponential growth: Parameter sensitivity of the debris evolution. Pp. 287–289 in Proceedings of the First European Conference on Space Debris, Darmstadt, Germany , 5–7 April 1993. Darmstadt: European Space Operations Center.
Su, S.-Y. 1993. On runaway conditions of orbital debris environment. Advances in Space Research 13(8):221–224.
Talent, D. 1992. Analytical model for orbital debris environment management. Journal of Spacecraft and Rockets 29(4):508–513.


















