10
Simulation And Modeling
Overview
Analytical simulation and modeling of unit manufacturing processes based on knowledge of the underlying process physics and validated by experimental results is becoming a powerful tool to advance the optimization of unit processes. In this context, simulation is defined as the "representation or model of the operation of a system on a digital computer" (NRC, 1988). The availability of high-powered engineering workstations allows simulation of many complex unit processes that often require three-dimensional solutions. Examples cited in Part II range from polymer injection molding to high-temperature forging of jet-engine components.
In many process development and design situations, simulations are beginning to replace full-scale process trials, reducing development time and cost compared with those of the normal iterative methods. Tooling and dies and material specifications can also be optimized based on the results developed from the preliminary design and geometric modeling stages (NRC, in press). The most important task is selecting the optimum processing conditions, which will ensure that the required mechanical and physical characteristics of the product design can be produced at a high-quality level.
The mathematical underpinnings of unit process simulations typically involve the solution of the classical laws of conservation of mass, momentum, and energy, coupled with constitutive formulations of the material behavior during its residency in the unit process. The solution procedure is governed by initial and boundary conditions that represent the process conditions of the situation being modeled. The complexity of the simulation model may be simplified with first-order assumptions that provide solutions with reasonable accuracy and converge to the correct solution.
Simulations of unit processes are largely based on the computer-aided approaches that include three important activities: modeling, visualization, and design. Simulation output consists of information on the processed component characteristics of geometry, surface, and microstructure, including defects. The finite-element method is widely used for modeling unit processes. Presently available software for computation includes a variety of three-dimensional elements and offers a coupled thermomechanical and fluid-flow analysis capability. A wide variety of analysis options, material models, and interface elements are supported. Three of the desirable analysis options include Lagrangian or Eulerian formulation; implicit/explicit solution algorithms; and automatic, time-step control. In addition, the analysis packages have robust nonlinear solution algorithms that guarantee convergence and are able to take into account complex displacement, velocity, stress, and thermal boundary conditions.
With the present requirement of representing a variety of physical phenomena that occur during unit processes, the constitutive modeling capabilities of the analysis packages have become extremely important. For example, as discussed in Chapter 9, analytical packages used in deformation process simulations should provide both elastic-viscoplastic and elastic-plastic material models, so that rate-dependent and rate-independent phenomena can be modeled. In addition, models should be capable of using constitutive equations that can evolve specific metallurgical features during the simulation.
The suitability of a finite-element package to model the interface phenomena of a unit process is critical, because only accurate representation of the interface situation (e.g., friction, heat transfer, etc.) can provide an accurate set of boundary conditions for the modeling of the bulk workpiece behavior. For example, the robustness of deformation process models is influenced by contact modeling capabilities. Current generalized three-dimensional contact algorithms include general three-dimensional sliding capability, automatic detection of element contact and release, contact between deformable bodies, and single surface contact capability for modeling the formation of defects such as lap formation. A future enhancement of contact algorithms would be the representation of interface phenomena such as friction and heat transfer. In addition, this deformation process representation should include detailed interface models that are functions of various process parameters. A particular need for analysis of unit processes with large strain deformations is adaptive finite element meshing, which rezones the mesh as needed (i.e., automatically redefines the finite element grid) and continues the analysis with little or no user interaction.
Most of the previously discussed modeling requirements are currently addressed at a two-dimensional level by available finite-element method computer codes. These programs are usually general purpose packages capable of handling the nonlinear partial differential equations typical of unit process
models, as well as the traditional linear partial differential equation required to solve thermal and mechanical problems. The constitutive descriptions of material behavior are limited in most of these packages; however, some user-defined formulations can be inserted into the more advanced programs. The versatility of these packages is traded off against the efficiency of the problem solution, particularly in the three-dimensional versions of the codes. The programs are available on most workstations; mainframes; super computers; and, more recently, on reduced instruction set computing processor workstations and parallel processor machines.
As in any computation, the use of physical insight to eliminate less important variables can simplify a solution with little loss of accuracy. In addition, consideration of revised variables that incorporate coupled or related variable groups ("super variables") may also simplify the partial differential equations and their solution. Simplified equations can result in faster computation times with a minimal loss in simulation accuracy. Further increases in simulation performance may be attainable with the development of specialized processors that are tailored for the numerical solution of process simulations. These processors trade program versatility for enhanced precision, speed, and accuracy of their solutions.
The use of knowledge-based engineering systems in unit process simulation relies on past experience to estimate the behavior of the process. For example, this approach has been used for tooling and die design and input stock geometry estimation for two-dimensional simulation of forming processes (Tang and Oh, 1988). This technique, however, has had limited success, because it has not yet addressed three-dimensional problems and does not include consideration of the workpiece material behavior. Application of knowledge-based engineering systems to the prediction of defects and microstructure has been reported for forming processes (Demeri, 1989). Future simulation tools should incorporate both knowledge-based engineering systems and analytical techniques.
Validation of simulation results with data obtained from critical experiments is necessary to establish confidence in the predictive capabilities of simulations. This is a critical, and continuing, activity. The range of the validation (i.e., process conditions) should be based on the robustness of the assumptions in the simulation to identify the limits of process conditions for future application of the simulation.
Application of simulation tools to the design of unit processes (e.g., tooling configuration, input material characteristics, and process parameter operational scheme) is an increasingly important element in successful product manufacture. In general, unit process design evolves as experiences are gained from product to product. Limited confidence is normally assigned to design situations outside of the region of past experiences. The design procedure draws upon different
types and levels of knowledge at different stages of the design sequence and relies heavily on the creativity and intuition of the user (Richmond, 1986).
Hence, from a user's perspective, the modeling system should be user-friendly and should provide a user interface that enhances productivity. In addition, it should contain features that ease a user's task burden during iterative process design. The modeling system should assist the user differently at different stages of the design process, since the needs vary.
In a concurrent engineering environment, the modeling system should provide a framework to establish, in the early stages of product development, the technical feasibility of manufacturing the product. The processes can be optimized once the final design is completed. Incorporation of such an iterative capability allows the system to be a true design tool rather than a verification tool (Richmond, 1986).
Unit process design can be viewed as comprising three distinct stages: preliminary design, geometric modeling, and process modeling. Typical activities that occur during each of the stages include part design for assembly, preliminary part design for processing and producibility (or net shape manufacturing), preliminary die/mold design (if process uses dies or molds as in forging, stamping, die casting, or injection molding), and process simulation to verify die/mold as well as product and process design. Figure 10-1 is an example of the design steps that occur for discrete part manufacture (Altan and Oh, 1987).
Each design stage uses particular tools and information about the product under design, as well as information about past product development. An integrated unit process modeling system would seamlessly transfer information and data among the three stages, so that the effect on the other two stages of decisions made during preliminary design could be visualized.
Preliminary design is heavily influenced by the geometry of the product's components. Limited consideration is given at this stage to how selected material properties will be affected during processing or how difficult a material will be to process. Preliminary design typically draws extensively on previous design experience. If a knowledge-based engineering system were available, the following important areas could be addressed interactively during preliminary design:
- selection of suitable unit processes;
- optimum sequencing of the unit processes;
- preliminary estimation of the unit process operational parameters; and
- preliminary tooling design for each unit process.
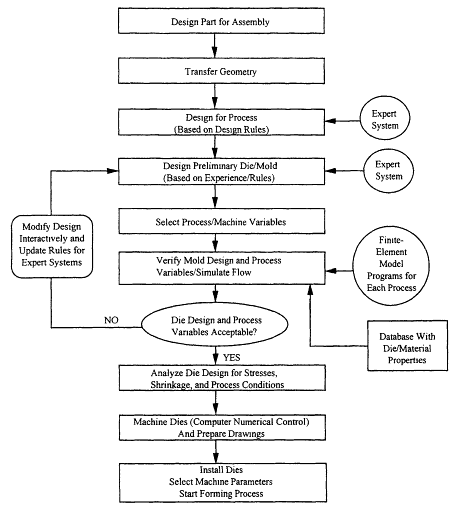
Figure 10-1
Schematic illustration of steps involved in manufacturing discrete parts via a unit manufacturing process (adapted from Altan and Oh, 1987).
The importance of a robust geometric modeler and reliable transfer of three-dimensional geometry as a part of the integrated modeling system cannot be overemphasized in light of some of the difficulties in three-dimensional modeling
mentioned earlier. The geometric modeler should also allow the creation of process geometry specific to a particular unit process to aid the design engineer in visualizing the process. The geometric modeler should also provide accurate information concerning assembly details, such as interference between different parts and tools. Current geometric modeling tools utilize advanced solid modeling techniques for creation of part and tool geometries and include automatic mesh generation. The modelers also include several geometric manipulation functions for process geometry visualization.
Automatic mesh generation assumes a special importance in process simulations that have severe material distortions because of the problems with remeshing that were discussed in Chapter 9. Hence, a three-dimensional remeshing utility for arbitrarily shaped geometries is needed, especially for complex components.
Important elements of a geometric modeler include the following.
- Feature definition. Features provide the mechanical detail to the geometry of the part and the process. Through features, the geometric model is supplemented with a variety of essential nongeometric data (e.g., surface-finish information, material type, heat treatment requirements, etc.) that result in a complete product model. An ideal geometric modeler would support these three basic modes of inputing feature information: design by features, automatic recognition of features, and interactive identification of features.
- User specification of product and process attributes at the solid model level. This information should be transferred to the downstream applications, such as finite-element mesh generation and process modeling. The attributes of interest include material properties and boundary conditions (e.g., mechanical loading and heat transfer across an interface).
- Three-dimensional contact information. The information required for finite-element methods analysis should be generated at this stage from the solid model after classifying the geometry into different features, namely workpiece and tooling. Once the workpiece and the tools are identified, intersections can be calculated and appropriate contact information generated. This contact information can be supplied to each node after the finite-element methods mesh is generated.
- Electronic data transfer. The data should be transferred according to standard procedures, such as those based on the Initial Graphic Exchange Standard or the newly emerging Product Data Exchange Standard/Standard Exchange Protocol standards.
Research Opportunities
The preceding discussion of research status and needs of unit process simulation and modeling has identified certain issues that should be addressed by future research.
- Development of comprehensive, fully interactive geometry modelers . Geometric modelers are needed that can bridge the capabilities of computer-aided design and analysis. Such model should provide less-detailed models with clearly defined topological characteristics and be capable of easily linking to finite element models.
- Engineering design tools. Advanced design tools are required that employ knowledge-based engineering systems and analytical techniques to aid in selecting and developing the specification for unit processes.
- Low-cost, dynamic, three-dimensional, finite-element meshing techniques . Simulations of processes exhibiting large strain deformations often result in very distorted finite elements. A remeshing capability that requires little or no user interaction is needed to provide for computational efficiency with no compromise to accuracy.
- Representation of dynamic interface phenomena. Contact algorithms must be improved to include interface phenomena, such as friction and heat transfer.
- Improved computational performance. Research is needed to accelerate the run-time performance of the computer models with no loss of fidelity to the real world. Promising directions include streamlining of the partial differential equations and the use of revised variables that incorporate physically coupled behavior.
- Specialized computer processors. There is a demand for computer processors that are specialized for handling process simulations.
References
Altan, T., and S.I. Oh. 1987. Computer Aided Process Modeling. Chapter 24 in Manufacturing High Technology Handbook, O. Tijunelis and K. McKee, eds. New York: Marcel Dekker, Inc.
Demeri, M.Y., ed. 1989. Expert Systems in Forming Processes, Expert System Applications in Materials Processing and Manufacturing. Warrendale, Pennsylvania: The Metallurgical Society.
NAE (National Academy of Engineering). 1988. F.H. Grant, Simulation in designing and scheduling manufacturing systems. Pp. 139-147 in Design and analysis of integrated manufacturing systems. Washington, D.C.: National Academy Press.
NRC (National Research Council). In press, Computer-Aided Materials Selection During Structural Design. Washington, D.C.: National Academy Press.
Richmond, O. 1986. Microstructure-based modeling of deformation processes. Journal of Metals 38(4): 16-18.
Tang, J.P, and S.I. Oh. 1988. AFD: An automated forging design system. From Volume 16 of the Proceedings of the North American Manufacturing Research Conference held 24-27 May 1988. Urbana, Illinois: University of Illinois.








