Appendix C: Review of Selected Knowledge-Representation Techniques and Tools
Expert system implementations employ many different knowledge-representation techniques and tools. Each technique provides an abstraction that is useful in describing some aspect of expert behavior or an improved implementation of an abstraction concept. Just as words, numbers, graphs, and sketches are different but useful abstractions, the techniques described in this appendix are various ways of describing relationships and reasoning. Tools are implementations of knowledge-representation techniques. This appendix reviews several of the currently used representation technologies and tools discussed in the report and is not meant to be exhaustive. References are provided so that interested readers can further explore the techniques discussed here, as well as many others.
CASE-BASED REASONING
Case-based reasoning is a method for decision making based on the retrieval and adaptation of prior recorded cases. Tool functionality can range from retrieval, which only finds relevant cases in response to a user's input, to analogical reasoning, which finds and adapts a prior solution to the current situation. As such, case-based systems provide at least a primitive form of learning. Commercial tools for associative retrieval and case-based retrieval are available and significant applications are beginning to emerge.
CONSTRAINT-BASED REASONING
In constraint-based reasoning, knowledge is encoded as constraints that express qualitative or quantitative relationships between design parameters. Various algorithms exist to provide varying support of constraints ranging from violation detection, to enforcement, to propagation, to satisfaction.
When reasoning about constraints, the expert system must decide which constraints are relevant to the problem and then interpret them. Constraints and constraint reasoning can support design analysis by identifying problem areas. During design synthesis, constraints can be exploited to propose a solution that is acceptable within the problem domain, provided that the problem is not overly constrained. As an aid to search, constraints can be used to confine the search space. Systems that symbolically solve mathematics problems have been investigated since the early days of artificial intelligence (McCarthy, 1968; Minsky, 1968). Constraint reasoning is a more recent technology that has evolved in several different styles. In particular, reasoning about geometric invariance is critical to spatial reasoning. Linking geometric reasoning to symbolic reasoning will be critical for expert system technology in material selection.
Constraint-based algorithms vary in complexity as support ranges from detection of violations through satisfaction. Violation detection can be and has been done with a variety of rule-based languages as well as procedural code. Constraint propagation is available in several commercial products. Constraint satisfaction or solution is an active research area, although some algorithms with limited capabilities are available and in use.
ACTIVE DATA DICTIONARIES
Data dictionaries are organized references to data contained in other programs, systems, databases, or collections of files. Whereas databases store and process ordinary data about objects, data dictionaries contain data about data, or metadata. Active data dictionaries are used to coordinate and support data retrieval and analysis between different systems or databases. Although the implementation of active data dictionaries is predominantly a research area, some limited capabilities are currently available and in use as part of database systems.
DATABASES
Simply defined, databases store information according to a specified schema. Relational databases are commonly used today, and they store data like that represented by tables in reference works. Database management systems are an important component of most expert systems. They support dynamic factual recall, updating, and user access control, which may be thought of as a form of intelligent behavior. Furthermore, many of the recent advances in state-of-the-art database management systems have incorporated advanced concepts from expert database systems.
Relational electronic databases are organized as rigid tables, where each record of the database is assigned an equal number of fields, each containing a specified type of entry. Such rigid formatting is no longer necessary with the flexibility afforded by implementations such as association lists or structures and even arrays of structures. Free-format databases can save storage space when most records in the database contain entries only for a few of the many possible fields. Free-format databases are also preferred when the database is unstable and updated frequently, not only by adding records but also by adding fields or by modifying the requirements on a field. However, rigid formatting saves space and query time when most records of the database contain values for the same number of fields and allows nonprocedural queries to be made that automatically link together multiple tables.
Modern database packages are so versatile and easy to use that the materials scientist hardly needs to worry about database formats as long as the data are well-defined quantities or arbitrary text. However, analysis must be done in the design of a database or knowledge base. Factors to be considered include expected query scenarios and unusual data sets (e.g., default values, multiple entries, data ranges, incidental information such as warnings and comments, derived values, constraint ranges, quality, unit conversions, and educated guesses for missing entries).
Most expert system applications involve extracting information from existing databases. Some existing database packages may be able to handle certain types of reasoning about data within the database structure itself, but in most cases the knowledge engineer must either select a different form of knowledge representation to support reasoning requirements or design a new database to handle special problems. New technology for knowledge discovery in databases shows promise for making the information more useful in the construction of more advanced reasoning systems (Piatetsky-Shapiro and Frawley, 1993; see ''Active Data Dictionaries"). Object-oriented databases are adding the security and access facilities of databases with the flexibility of artificial intelligence data structures and may overcome performance limitations to be widely used in the future.
A strength of computers is the ability to retrieve items stored in a database for use in other forms of knowledge representation or for display to inform the user. However, the quantity of data available for most advanced materials is inadequate for the types and depth of analyses needed for knowledge base systems, including statistically based design values. Database technology has outstripped the effort to build and distribute reliable data.
FUZZY LOGIC
Fuzzy logic is a method for dealing with the inherent ambiguities in concepts and an attempt to build a formal logic for plausibility. Fuzzy logic does not deal with probabilities but, rather, with the type of reasoning people use when faced with inconclusive or contradictory evidence. Fuzzy logic involves four basic elements: (1) schemes to convert stimuli signals to strength of belief, (2) simple rules expressed in logical terms, (3) algorithms for computing strength of belief for the conclusion of rules, and (4) output functions to convert the belief in conclusions to a control signal. Unlike the rules found in typical expert systems, which are complex and designed to support deep logical chains, fuzzy logic rules are very simple and do not involve the combination of conclusions to infer other conclusions.
Recent computing advances have led to successful applications of fuzzy logic in areas ranging from manufacturing controls to consumer electronic products. The main advantage of fuzzy logic is that it provides a simple formulation of simple reasoning processes. The simplicity of the reasoning restricts the application of fuzzy logic to narrowly scoped problems, however.
GEOMETRIC AND MICROSTRUCTURAL INFORMATION REPRESENTATION
There are three levels of geometric modeling common in industry. One-dimensional (wireframe modeling), two-dimensional (surface modeling), or three-dimensional (solid modeling) analytical elements are used in constructing spatial representations. Figure C-1 displays the essential difference in the representational domain of each of the three levels of modeling. It should be clear that solid modeling has the most explicit representation of the objects in real-world and includes the lower levels of representation. This implicit embodiment, however, does not necessarily mean that any solid modeling approach can uniformly manipulate entities of the lower dimensions as well as solids.
Several taxonomies for solid modeling have been proposed, but one way of categorizing most of the existing solid model approaches is to perceive them in three classes:
-
cell-based representations;
-
constructive solid geometry representations; and
-
surface boundary representations.1
Two distinct approaches in the category of cell based representations are the cell enumeration technique and the octree approach. In both of these cases, a solid is defined as a union of a selection of space-based cubical volumes. In constructive solid geometry schemes, objects are obtained by combining a set of solid primitives with boolean operators. In surface boundary representations, the objects are represented by their enclosing shell.
HYPERDOCUMENTS
Hyperdocuments are multimedia files in which the pieces of the documents are linked to one another to capture important relationships between concepts presented in the documents. Several commercial systems have led to numerous successful applications. The capturing of the relationships between objects acts as a primitive form of semantic network (see "Objects and Taxonomies").
MACHINE LEARNING
Machine-learning techniques allow a system to acquire knowledge automatically. Some simple techniques have been successfully applied and are commercially available, such as in the areas of case-based reasoning and neural networks, but most are still in the research phase.
MATHEMATICAL RELATIONS
Mathematical relations are equations, inequalities, approximations, and iterations that designers use to determine the properties of materials under certain conditions. Mathematical relations appear in exactly the same format in electronic knowledge bases as they do in books. The great advantage that computers have, however, is that they can actually compute values using equations, whereas books can only describe how to compute the values. One disadvantage of computers is that the covert use of equations to represent knowledge can be dangerous. Many equations, particularly in the materials and design fields, are based on approximations that are only valid for one application or within a specific range of variables. Good knowledge representation demands the existence of a mechanism, commonly referred to as "explanation," to permit the user to inspect the equations that are invoked and the assumptions that are inherent in the choice of the equations used in the calculation to avoid potential problems.
When dealing with mathematical relations, the knowledge engineer must decide whether these relations are to be used as symbolic expressions or simple computations. If they are to be used as computations only, then conventional programming languages can be used to perform the
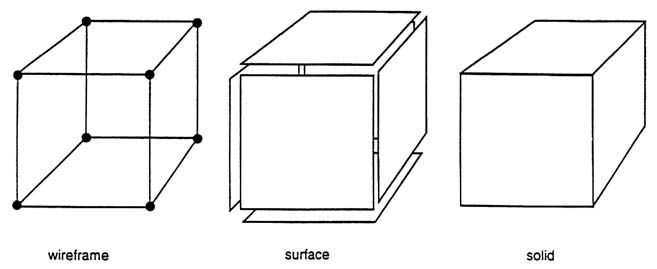
Figure C-1 The differences between wireframe, surface model, and solid model representational domains (Source: Gursoz and Prinz, 1990; Reprinted courtesy of Elsevier Science Publications).
NEURAL NETWORKS
Neural networks attempt to mimic brain-like systems via simplified mathematical models. Researchers have found that simple mathematical stimulus-response equations can be used to simulate the behavior of neurons in the brain. Like the brain, the most basic processing unit of neural networks is the neuron, which is characterized by "an activity level (representing the state of polarization of a neuron), an output value (representing the firing rate of the neuron), a set of input connections (representing synapses on the cell and its dendrite), a bias value (representing an internal resting level of the neuron), and a set of output connections (representing a neuron's axonal projections)" (Rumelhart et al., 1994). Neural networks analyze data by mapping input data into output patterns based on maps produced by previous runs.
A major advantage of neural networks is that the simple mathematical representation lends itself to learning algorithms. Using feedback, these algorithms adjust the set coefficients used to reinforce and combine stimuli to minimize an error score. Neural network learning algorithms require very large training sets and typically work best when the network connectivity has been properly organized in advance by an expert. Successful applications have been developed mainly in pattern recognition.
There are two main drawbacks with neural networks, however. In addition to requiring large training sets, neural networks do not have strong mechanisms for explaining the results of a computation. The latter problem is particularly troublesome in areas of engineering where tractability of design decisions is a requirement, such as in the design of products that affect public safety.
While many of the concepts of neural networks have been investigated for quite some time, this technology is in its early stages of application. Applications have only now become feasible because of low-cost computing developments.
OBJECTS AND TAXONOMIES
Objects and taxonomies are knowledge base tools that allow programmers to represent knowledge of physical or conceptual entities with many attributes in an abstract manner that mimics the way people organize knowledge about concepts and classes of objects. Objects and taxonomies are probably the most general and flexible form of knowledge-capture scheme available. They can handle databases, mathematical relations, rules, and anything that can be classified, including design features such as shapes and colors. Object-oriented programming requires a different software design approach than conventional programming and is still evolving.
There are many concepts that have been explored in artificial intelligence and programming language research that are similar to objects and taxonomies, some of which are commercially available in many forms as well as embedded in knowledge base engineering tools. Abstract data types, frames, schema, relational tables, and semantic networks are the most commonly referred to variants of the technology. All of these provide a means to describe facts and meaningful relationships between facts. They differ from data types found in conventional programming languages and databases in the expressive power regarding relationships. The price paid for this is less efficient programming and difficulty in providing shared access to data. Objects and abstract data types provide an additional benefit to the programmer or knowledge engineer by associating the processing or functional elements of the implementation with the kinds of data that the functions can manipulate. Thus, they provide more structure and understandability.
One disadvantage of maximizing generality and flexibility in a system is that a great deal of expertise is usually required to operate the system, so that the user effectively becomes a computer specialist as well as a materials scientist or design specialist.
REASONING WITH UNCERTAINTY
Reasoning with uncertainty is a knowledge-representation technique for combining contradictory, incomplete, or inconclusive knowledge. This is not the same as fuzzy knowledge or fuzzy logic, however. Expert systems can accommodate uncertainty by several approaches, including maintaining multiple problem formulations, qualitative methods, and quantitative methods involving uncertainty measures. Many applications have used some form of uncertainty logic.
RULE-BASED REASONING
Rules are representations of knowledge about which patterns of information experts use to make decisions and what are the decisions that follow. Rule-based reasoning provides automatic combination of rules to chain to a conclusion. One popular way to represent knowledge is the "if-then" rule. A rule can formally be represented as the logical relation:
p ![]() q
q
p represents a set of conditions or premises, and q represents a set of consequences or conclusions. Many different algorithms have been developed to implement and support the basic notion of rule-based reasoning. The differences between various approaches are in the domain of knowledge-engineering. For example, forward chaining rules facilitate programming synthesis, while backward chaining rules are more suited for analysis or search.
Rules are well suited for the type of reasoning that can typically be represented by a tree or a flow diagram. Rules typically represent reasoning about facts and data rather than the facts or data themselves (i.e., metadata). Expert systems based on rules include an implementation of an algorithm that governs what the rules can do, when they are activated or triggered, and what order of priority they are checked and executed. The software component controlling the rules is commonly referred to as an inference engine, since it controls the inferences of the system. Knowledge about materials can usually be stated in the "if-then" form. Rule-based knowledge representations can also handle limited forms of uncertain reasoning, such as by adding or subtracting confidence while appraising a hypothesis or by providing mechanisms to handle alternative lines of reasoning.
Many commercial tools are available that provide forward or backward chaining or both types of rules.
Rule-based tools are often characterized as expert system shells. Many successful applications have been developed in combination with other tools (e.g., objects). The main advantages of software packages that represent knowledge in rule form are that they allow the user to inspect the rules in near-natural language and provide an explanation of why a decision was made. Although it is easy for a human expert to understand a rule about material properties and to judge whether the rule is acceptable (a definite plus when one needs to know what knowledge has been brought to bear), knowledge engineers tend to clutter their rules with computing tricks that ultimately make reading, managing, modifying, or updating the rules by the user extremely difficult. This practice has led to unfair criticism of the underlying technology. Thus, rules should be used as appropriate in conjunction with other knowledge-representation forms.
SPATIAL SYNTHESIS AND LAYOUT
Conceptual layout is usually one of the first steps in creating a structure. These structures may be in the electrical, mechanical, architectural, or microstructural domain. The nature of the problem of formulating a layout is discussed, and some of the emerging computer technologies are described that can either automatically or with user guidance synthesize structures in two or three dimensions. The earlier described geometric representations can be used to implement such algorithms.
Layout design deals with many of the complex issues that typically arise in the design of artifacts that have to satisfy specified constraints and are composed of parts that have shape and occupy space. A large (potentially infinite) number of location and orientation combinations are available for placing any single object. In each combination, design objects interact in intricate ways through their shapes, sizes, and the spatial or topological relations that exist between them. These characteristics also interact in complex patterns with multiple performance criteria or functional attributes demanded of the artifact being designed. Layout design decisions must simultaneously satisfy global requirements (e.g., usage of space) and local requirements (e.g., adjacencies between pairs of objects with certain microstructures, as required in the design of sliding components); acceptable spatial arrangement often exhibits a complex pattern of tradeoffs.
For these reasons, there is no known direct method that is guaranteed to produce feasible solutions without iterations of trial and error for most application domains. Some amount of exploration of the structure, formulation of the layout task, and searching for candidate solutions is required. However, due to cognitive limitations, human designers do not have the capability for making systematic explorations of alternative arrangements. This shortcoming in human performance has motivated numerous attempts to apply computational methods to layout. What is desired is a structured method for producing multiple alternatives, each of which embodies tradeoffs that can be understood, justified, and indicative of a range of possible variations within which optimization can take place.
Attempts to arrive at such a method confront the challenges mentioned above. Consequently there is a long history of attempts to develop an effective, "closed-solution" computational-based method reflecting a variety of representations, system architectures, and planning strategies for layout design. Finding an effective representation to support the efficient generation and evaluation of design alternatives has been a difficult undertaking and has dominated the evolution of the field. The representation must support the creation of a space of possible designs by capturing meaningful differences between design alternatives at a manageable level of detail (or abstraction). Layouts for a given design problem are typically very large; therefore, the representation must allow for the employment of effective planning and search strategies to enable reasonable examination of the best alternatives (e.g., through the evaluation of partial solutions and the incremental specification of designs).
The layout operating system (LOOS; Coyne and Flemming, 1990), for example, enables the systematic generation of layout alternatives and their evaluation over multiple performance criteria. The system utilizes a graph-based representation that separates topological issues (spatial relations between objects) from metrical issues (dimensions and dimensional positions of objects) in layout. The representation uses basic spatial relations (i.e., above, below, to the right of, and to the left of) to define the structure or topology of a layout as a set of relations between pairs of rectangles. It represents this structure formally through an arc-colored directed graph, the vertices of which represent the rectangles in a layout and the arcs of which represent the spatial relations between the rectangles. Figure C-2 shows an example in
which solid arrows indicate above/below relations, dashed arrows indicate left/right relations, and E represents the minimum enclosing rectangle that is above, to the right of, to the left of, and below all other rectangles in the layout. Using this representation, a set of rules or operations are defined that can generate all possible arrangements of rectangles in a plane by insertion of one rectangle at a time. The layouts produced by the LOOS are loosely packed arrangements of rectangles (e.g., the rectangles are nonoverlapping and need not fill the surrounding rectangle). Therefore, the approach is general enough to encompass a broad class of layouts and is useful over a wide range of domains. These rectangular arrangements are given meaning as layouts in a particular domain by attributing the layout objects or components from the domain to respective rectangles. In addition, tests or performance requirements for the layout are attached to these objects enabling the layouts produced to be comparatively evaluated. Those that fail requirements may be discarded, while those that show promise can be further developed.
Laying out abstract objects does not make a design; it only gives a spatially feasible configuration of the objects considered. The next step involves incorporating all detailed features of the design, both geometric as well as nongeometric ones. To facilitate this step, it is convenient to introduce a formal language with a grammar to express the intentions of where to generate what entity in what shape and size, and to determine what other nongeometric entity should be assigned to it.
Solids can be described through the surface boundary representation as previously introduced. Boundary solid grammar provides a means of generating complex models of rigid solid objects. Solids are represented by their boundary elements (i.e., vertices, edges, and faces with coordinate geometry associated with the vertices). Labels may be associated with any of these elements. Rules match conditions of a solid or collection of solids and may modify them or create additional solids. A boundary solid grammar uses an initial solid and a set of rules to produce a language of solid models.
Mountain grammar is defined by using a lamina as the initial solid and eight rules to modify the mountain's surface. A rule of the grammar subdivides an existing face and randomly moves the position of the vertices of the face. This produces random variation of the surface of the mountain, while the rules recursively subdivide its faces.
Although this application may initially not sound very useful, it may be quite attractive if the creation of novel material structures and compositions are imagined within structures that are designed to behave in a predefined way. Variations on this technique may be used to produce a wide variety of textures on the surface of the interior of
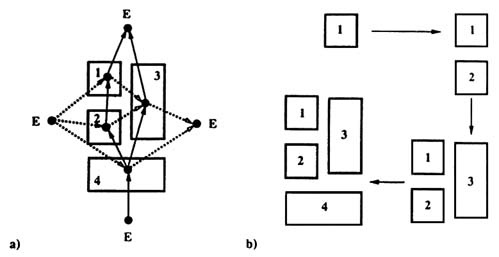
Figure C-2 An example of the LOOS system to define the structure or topology of a layout (Coyne, 1991; reprinted courtesy of Robert F. Coyne).
STRUCTURE SELECTION
Structure selection is a technique for selecting components from a finite list of candidates and ensuring compatibility. Many problems have been formulated with approach in mind and there are a variety of techniques that are used to provide structure to the process and the information needed to perform the task. Many of the early success of expert systems employed structured selection.
TRUTH MAINTENANCE
Truth maintenance is a knowledge-representation technique that records the justification for information so that the fact is removed if the support for a fact is negated or removed. Truth maintenance techniques have been included in several commercial knowledge-engineering tools. The technique is particularly useful in exploring multiple options but has not had the impact that was expected.








