4
MATHEMATICAL RESEARCH OPPORTUNITIES FROM THEORETICAL/COMPUTATIONAL CHEMISTRY
Introduction
This chapter highlights some of the most prominent research challenges from theoretical/computational chemistry that appear to be amenable to attack with the help of reasonable advances in the mathematical sciences. Most of the sections have as their starting point a challenge facing the chemical sciences, which is described in terms that should be accessible to the nonspecialist. The remaining sections—"Molecular Dynamics Algorithms," "Multivariate Minimization in Computational Chemistry," and "Fast Algebraic Transformation Methods"—contain discussions of topics from the mathematical sciences with specific insight into their relevance to theoretical/computational chemistry. Expositions and references are meant to give the mathematical reader sufficient insight and direction to be able into subsequently investigate the topic via deeper reading and especially by discussions with colleagues from the chemical sciences. Note that the topics surveyed in Chapter 3 are also sources of continuing research opportunity, some of which are identified therein.
As an overview of this chapter and a guide for navigating through it, the matrix in Figure 4.1 displays a subjective assessment of the depth of potential cross-fertilization between major challenges from theoretical and computational chemistry and relevant topics in the mathematical sciences. This matrix is based to some extent on intuition because it is an assessment of future research opportunities, not past results. An "H" in the matrix implies an overlap that appears clearly promising, while an "M" suggests that some synergy between the areas is likely. The absence of an H or an M should not be taken to imply that some clever person will not find an application of that technique to that problem at some point.
Two topics, polymers and protein folding, are consciously underrepresented in this report because the mathematical research opportunities related to these topics have been surveyed very recently by other reports from the National Research Council. For a discussion of mathematical opportunities related to the frontiers of polymer science, see pages 153–168 of Polymer Science and Engineering: The Shifting Research Frontiers (National Research Council, 1994). A chapter devoted to mathematical research into protein folding may be found in Calculating the Secrets of Life (National Research Council, 1995).
References
National Research Council, 1994, Polymer Science and Engineering: The Shifting Research Frontiers, National Academy Press, Washington, D.C.
National Research Council, 1995, Calculating the Secrets of Life, National Academy Press, Washington, D.C., in press.
Numerical Methods for Electronic Structure Theory
Most of the recent progress in theoretical chemistry has come from computation of numerical approximations to the solutions of realistic model problems. This has largely replaced earlier approaches based on analytic solutions to simplified model problems. Although there are interesting
|
Adaptive and multiscale methods |
H |
M |
M |
|
|
|
M |
M |
M |
M |
M |
|
Special bases |
H |
|
M |
M |
|
|
|
H |
|
|
|
|
Differential geometry |
|
M |
|
|
|
M |
M |
|
M |
H |
H |
|
Functional analysis |
H |
|
M |
H |
H |
|
H |
M |
|
M |
M |
|
Graph theory |
M |
M |
M |
|
|
H |
|
|
M |
M |
M |
|
Group theory |
H |
|
M |
|
M |
M |
|
M |
M |
|
M |
|
Optimization |
H |
H |
H |
H |
M |
H |
H |
M |
H |
H |
H |
|
Numerical linear algebra |
H |
H |
|
M |
|
|
M |
|
|
M |
|
|
Number theory |
|
|
M |
|
|
|
|
M |
|
M |
|
|
Pattern recognition |
M |
M |
H |
|
|
H |
|
M |
H |
H |
H |
|
Probability and statistics |
H |
|
H |
|
M |
H |
|
M |
H |
H |
H |
|
Several complex variables |
H |
|
H |
M |
|
|
|
M |
|
M |
M |
|
Topology |
M |
M |
H |
|
|
H |
M |
M |
H |
H |
H |
|
Dynamical systems |
|
M |
H |
|
|
|
|
H |
M |
H |
M |
|
|
Quantum electronic structure |
Molecular mechanics |
Condensed-phase simulations |
Density functionals |
N-representability |
Design of molecules |
Construction of potential energy functions |
Gas-phase dynamics |
Polymers |
Topography of potential energy surfaces |
Biological macro-molecules (including protein folding) |
FIGURE 4.1. Subjective assessment of depth of potential cross-fertilization between major areas of the mathematical sciences and theoretical and computational chemistry. An "H" implies an overlap that is clearly promising and an "M" suggests some synergy is likely.
intellectual problems involved with analytic properties of the exact solutions, progress to date with this approach has had little impact on chemistry.
In quantum chemistry, improved numerical approximations made possible by the greatly decreased cost (in dollars and personnel time) of computing have had an enormous impact. The Journal of the American Chemical Society, which once reluctantly accepted a limited number of articles reporting computational results, now has some computational aspect coupled with experimental results in more than half of the articles published.
The Schrödinger wave equation was introduced earlier, in Box 2.1. The primary method now used to obtain useful results may be described briefly as follows. The time-independent, nonrelativistic Schrödinger equation for a system of N electrons in the Coulomb field generated by K nuclei may be written in the Born-Oppenheimer approximation (using reduced units to eliminate mass and Planck's constant) as
where
is the Hamiltonian operator with
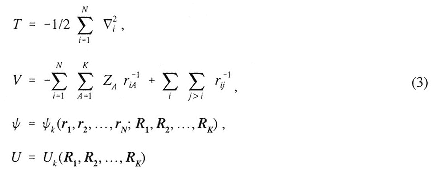
where ri is the position vector for the ith electron and Ri is the position vector for the ith nucleus with charge Zi.
This is a partial differential eigenvalue equation in 3N variables. The equation and its solutions are parameterized by the nuclear positions and charges. The eigenvalues Uk, viewed as functions of Ri, yield the potential energy surfaces for the molecule in its ground and excited states after including the repulsive internuclear interactions. The lowest eigenvalue, in particular, plays a fundamental rule in understanding the chemical properties of a chemical system.
Equation (1) may be solved subject to either bound state or scattering boundary conditions. For a bound state, the function ψ should give finite values for the integrals ![]() ψ*qyd3r1d3r2 ... for θ = 1, T, or V, where the asterisk denotes complex conjugation. For a scattering state, the wavefunction may have an exp (ikr) behavior for large |r|. The wavefunction is further subject to conditions of continuity everywhere and differentiability except at the singularities in V.
ψ*qyd3r1d3r2 ... for θ = 1, T, or V, where the asterisk denotes complex conjugation. For a scattering state, the wavefunction may have an exp (ikr) behavior for large |r|. The wavefunction is further subject to conditions of continuity everywhere and differentiability except at the singularities in V.
The Hamiltonian is symmetric under permutation of the electron coordinates. Consequently, the eigenfunctions can be chosen to form bases for irreducible representations of the permutation group. It has been found empirically that only a few irreducible representations actually correspond to physical reality and the rest are ''excluded." This observation is summarized in the Pauli exclusion principle. In the standard labeling of the irreducible representations of the symmetric group by a partition of N into the sum of integers, only those partitions containing no integers greater than 2 are observed.
In quantum chemistry, this observation is usually implemented by introducing an additional discrete value, called the spin ξi, for each electron. This variable takes only the values ±1/2. The permutation operator is then defined to interchange the spin and position of a pair of electrons in the extended function ψ(r1,ξ1, r2ξ2, . . .). The Pauli exclusion principle then is simply stated by observing that the only ψ that occur in nature change sign under every pairwise permutation of the electron coordinates.
Equation (1) has no closed-form solutions for nontrivial chemical systems. The most important problem in electronic structure theory is the rapid construction of useful approximate solutions to this equation. While chemists have made much progress on this problem, there is always the possibility that a fresh approach by mathematicians would lead to novel approaches. There is less possibility that changing the implementation of the methods now in use would lead to great improvement.
The dominant approach for obtaining approximate solutions at present is based on multiple expansions. First, a basis set is selected in three-dimensional space. Then this is transformed by a similarity transform to an orthonormal set of functions called "molecular orbitals." These orbitals are then used to construct Slater determinants, which are the simplest functions in 3N dimensions that obey the Pauli condition of antisymmetry under permutation of the positions and spins of the electrons. Finally, the wavefunction ψ is expanded as a linear combination of Slater determinants. Often, the transformation from basis functions to molecular orbitals is chosen to optimize an approximation to the wavefunction from a severely truncated expansion in Slater determinants. The coefficients in the Slater determinant expansion and the approximate eigenvalue U may be computed by the Rayleigh-Ritz variational principle, perturbation theory, cluster expansions, or some combination of those methods.
Slater determinants are determinants whose elements are n distinct orbitals for n distinct electrons.
In the Hartree-Fock approximation an exact Wavefunction is replaced with an antisymmetrized product of single-particle orbitals (i.e., a Slater determinant).
All of these methods require formation of matrix elements of the Hamiltonian in the Slater determinant basis,
where Φ is a Slater determinant and the integration is over 3N dimensions. For a finite basis of orthonormal molecular orbitals, it is possible to replace this equation by a different one that gives the same matrix element
This is accomplished by utilizing an operator algebra that facilitates manipulation of Slater determinants, in which ai is an annihilation operator and ai![]() is a creation operator. A correspondence can be established between the function space formed by all possible linear combinations of Slater determinants and the vector space formed by the creation operators so that
is a creation operator. A correspondence can be established between the function space formed by all possible linear combinations of Slater determinants and the vector space formed by the creation operators so that
That is, the Slater determinant, ΦI, in which the orbital labels i1 . . . iN appear, corresponds to the abstract element |ΦI>. The operator ![]() , called the "second quantized Hamiltonian," takes the form
, called the "second quantized Hamiltonian," takes the form
where, in terms of the orbitals φi,
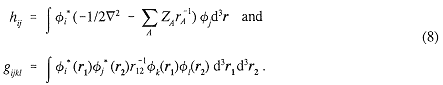
A major bottleneck in the present approach is the calculation of a large number of six-dimensional integrals gijkl. The choice of basis set is limited to those functions for which these integrals are readily computed.
The second major bottleneck is the actual calculation of U for this second quantized Hamiltonian. Although the values of |U| for various chemical systems vary from 0 to several thousand, the range of U for interesting variations in the parameters for a given system is typically only 10-1 to 10-3. Most programs determine U to a precision of 10-6, regardless of the absolute magnitude. Because of the multiple expansions involved, the error in U is often 10-1 to 10-2, but the error is often constant over the interesting range of nuclear position parameters to within ±10%.
A major advantage of some of these procedures for obtaining U is that first and second derivatives with respect to the nuclear coordinate parameters can be obtained analytically. This has greatly facilitated searching U in this parameter space for minima, saddlepoints, and so on. The major disadvantage has been the very steep dependence of computer time on the number of electrons. Evaluating U for one set of parameters typically takes computing time proportional to Nk, with k ranging from 3 for the least accurate methods to 7 for the best methods now in common use. Finding one eigenvalue of ![]() in the full vector space is even more costly, with computer time proportional to MN+4, where M is the number of basis functions. Consequently, accurate calculations are limited to about 40 electrons and an improvement of a factor of 10 in computer speed will not change this very much.
in the full vector space is even more costly, with computer time proportional to MN+4, where M is the number of basis functions. Consequently, accurate calculations are limited to about 40 electrons and an improvement of a factor of 10 in computer speed will not change this very much.
Although this approach is very productive, it is also limited to small chemical systems. Progress for somewhat larger systems can be made by use of the Hohenberg-Kohn and Kohn-Sham theorems to give a useful density functional theory. These assume that it is possible to find an effective one-body potential σ so that, by solving the one-electron Schrödinger equation
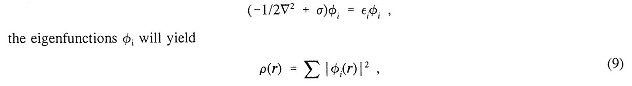
where ρ is the exact charge density of the system as defined by Equation (13) below, using the exact wavefunction defined by Equation (1). As before, σ, φ, and εi are parameterized by the nuclear charges and positions. Here σ is a functional of ρ. From ρ, the lowest potential energy surface U can be formed. The difficulty is that there is only an existence proof for σ and no systematic constructive procedure is yet known. Nevertheless, much progress has been made by choosing σ empirically so it will correctly reproduce the properties of simple model systems such as the uniform electron gas and free atoms. The attraction of this method is that the computational cost grows only as N3. Effort is being made to improve this even further to obtain methods whose costs grow as N2 or N.
Progress with density functional theory has been rapid in recent years. Direct solution of the Kohn-Sham equation on a three-dimensional grid now is possible, although basis set expansions are still more commonly used. The major limitation in this field is still the lack of a scheme for finding the effective potential that can guarantee the desired accuracy in U for all chemical systems of interest.
For even larger systems, solution of the Schrödinger equation seems hopeless. In this case, U is usually directly approximated by taking advantage of empirically observed near-transferability of parameters between similar chemical systems. This requires some input from the user of these programs to decide which atoms are bonded. Then, near a local minimum in U, it is possible to approximate U as a sum,

Each pair of nonbonded atoms can be assigned parameters transferred from experimental data to allow a calculation of a ΔU(RAB) energy contribution. Similarly, each chemically distinct type of bond can be assigned an energy for displacement from its usual bond length. Functions constructed in this way have accuracy approaching the desired 10-3 level needed for chemical prediction. This approach is now used for widely different problems, such as rational drug design, structure of liquids, predicting the shape of moderate-sized organic molecules, and protein folding.
There are many problems in numerical analysis and data handling associated with the present methods. These include the generation and manipulation of large numbers of six-dimensional integrals, finding eigenvalues and eigenvectors of large matrices, and searching a complicated function for global and local minima and saddle points. There are also important questions about the construction of optimum expansion functions for most rapid convergence. At present, there are no useful error bounds for the energy or other properties derived from the wavefunction.
The N-and V-Representability Problems
Conventional approaches for computing the solution to the wavefunction have a strong dependence on the number of electrons. Therefore, searches are constantly under way for methods of comparable accuracy with a better scaling. In this regard, people have considered methods based on density matrices, density functionals, Monte Carlo diffusion equations, effective core potentials, and so on. In particular, because the energy of an atom or molecule is a linear function of the density matrix and the one-and two-body distribution functions derived from it, density matrix methods raise the hope that one could dispense with computing the associated 3N-dimensional Wavefunction and deal with simpler three-dimensional density functions. A number of mathematical issues are raised by the attempt to reformulate computational chemistry in terms of particle distribution functions instead of wavefunctions.
The N-body distribution function is given simply as the product of the wavefunction and its complex conjugate,
Here, x symbolizes the collection of coordinates x1, x2, . . ., xN, describing the positions ri and spins ξi of all N particles. In the chemical literature, this quantity is usually called the N-body density
matrix. This may be averaged over an ensemble with an arbitrary set of probabilities (weights) wi to give the ensemble distribution,
Because of permutational symmetry, all identical particles enter this distribution in an equivalent way. From the N-body distribution, one-and two-body position distribution functions can be obtained by integration over the other coordinates:
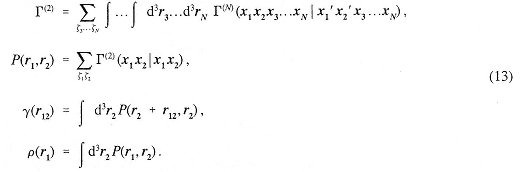
The distribution function P(x1,x2) is also called the two-body reduced density matrix. Similarly, the density matrix may first be Fourier transformed and then used to derive the one-body momentum distribution
For most cases of interest, knowledge of the one-and two-body position distribution functions and the one-body momentum distribution function suffices to determine the energy. For the Hamiltonian H with given external potential Vex(ri) and given two-body interaction potentials g(rij),
the energy is given by
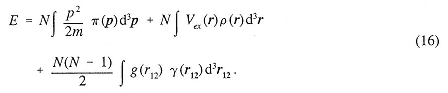
There are a number of outstanding mathematical problems associated with these distributions. For many potentials, the behavior of ρ( r) is known near the singularities of the potential. Similarly, the behavior of γ(r12) is known for a Coulomb interaction near the singularities, and the form of π(p) is known for large and small p. The N-representability problem consists of finding the conditions on this set of three functions such that they could all come from the same N-body density matrix. Many inequalities are known, but no general solution has been obtained. The V-Representability problem consists of determining the further restriction imposed by considering only those distributions that can come from a wavefunction that is the eigenfunction of some H for a fixed g.
The two-body reduced density matrix Γ(2) can be integrated to give the one-body reduced density matrix
Density matrices may be treated as integral kernels and factored in terms of their eigenfunctions
where
These functions fi are known as natural orbitals. It is conjectured, but not proved, that they form a complete set when Γ(1)(1) is derived from an exact eigenfunction of H with Coulomb interactions. The complementary functions
are certainly not complete in the 3(N — 1) dimensional space. The extended Koopmans theorem claims, however, that if ψ is the exact eigenfunction of H for an N-electron system, then the ground state wavefunction of the N — 1 electron system may be expanded exactly in the set of Fi. Both ''proofs" and "disproofs" of this conjecture exist in the literature (see Morrison, 1993, and Sundholm and Olsen, 1993, for a recent exchange of opinions and a list of relevant earlier papers).
Because the energy is a linear function of the one-and two-body distribution functions, the variational minimum will lie on the boundary determined by the N-representability conditions. Unfortunately, only an incomplete set of necessary conditions are known, but these are already so complex that further work in this area has been abandoned by chemists.
In density functional theory, only the density ρ (r) is used. Hohenberg and Kohn showed that the energy is a functional of this density for a fixed two-body potential g(rij). Density functional theory has become of practical importance, but progress is hindered by lack of knowledge of the properties of the functional and lack of a systematic procedure for constructing a convergent sequence of functionals. Some past work in this field has been summarized in several monographs (Davidson, 1976; Dahl and Avery, 1984; Kryacho and Ludena, 1989; March, 1989; Parr and Yang, 1989; Sham and Schlinter, 1989; Gadre and Pathah, 1991).
References
Dahl, J.P., and J. Avery, 1984, Local Density Approximations in Quantum Chemistry and Solid State Physics, Plenum Press, New York.
Davidson, E.R., 1976, Reduced Density Matrices in Quantum Chemistry, Academic Press, New York.
Gadre and Pathah, 1991, Advances in Quantum Chemistry 22:211.
Kryacho, E.S., and E.V. Ludena, 1989, Density Functional Theory of Many-Electron Systems, Kluwer Press, Dordrecht.
March, N.H., 1989, Electron Density Theory of Atoms and Molecules, Academic Press, New York.
Morrison, R.C., 1993, The oxactness of the extended Koopmans Theorem—A numerical study—Comment, J. Chem. Phys. 99:6221.
Parr, R.G., and W. Yang, 1989, Density Functional Theory of Atoms and Molecules, Oxford University Press,
Oxford.
Sham, L.J., and M. Schlinter, 1989, Principles and Applications of Density Functional Theory, World Scientific, Teaneck, N.J.
Sundholm, D., and J. Olsen, 1993, The exactness of the extended Koopmans theorem—A numerical study—Response, J. Chem. Phys. 99:6222.
Melding of Quantum Mechanics with Simpler Models
A daunting challenge for the future is to accurately model chemical reactions in phases and at the active site of enzymes. An ability to do so would be of great importance in designing new biological catalysts as well as fully understanding the chemical mechanism of those that already exist. This would be of significant technological as well as scientific importance. One could imagine that many new molecules could be made and made much more efficiently by such catalysts.
Methods to do this in an approximate way have been available since 1976 (Warshel and Levitt, 1976) and have involved using the Schrödinger equation (Equation 1 or a variant or empiricized form of it) for the parts of the system where bonds are being made or broken and thus the electronic structure is changing, combined with representations such as Equation (10), which assume transferable electronic structure, for the remaining atoms of the system. Typically, the number of atoms for which Equation (1) must be solved is much smaller, of the order of 20 to 30, than the number in the whole system, which for the chemical reactions mentioned is typically more than a thousand.
In fact, some exciting results for simple reactions involving organic molecules in different solvents have been achieved (Blake and Jorgensen, 1991). In these cases, one has solved Equation (1) to high accuracy for a simple reactive pathway in vacuo and then, employing these energies, has used free energy calculation methods to evaluate the solvation free energy of different structures along the reactive pathway. This is in some sense a proof of concept for the combined application of Equations (1) and (10) because impressive agreement with experiment has been achieved in these simple, welldefined cases.
For more complex cases, such as enzyme reactions, the reaction pathway might involve many steps, and some of the reacting groups are chemically bonded to the protein, thus requiring some additional technical challenges in simulating the atoms at the junction between those that are participating in the chemical reactions and those that are not. In addition, one might have to consider many conformations of the enzyme and its substrate and accurately represent their relative energy by using the energy function of Equation (10), all the while considering the electronic energy (Equation 1) and the relative total free energy of the system.
As noted above, progress on this problem has been made when employing much simplified representations of the electronic structure of the system, which enable the solution of equations such as Equation (1) for the few "quantum mechanical" atoms as rapidly or more so than the classical molecular dynamical equations of motion, using Equation (10) as a potential energy (Field et al., 1990; Warshel, 1991).
These methods use semi-empirical or empirical valence bond approximations to solve Equation (1). Although these methods are not highly accurate, the use of non-empirical quantum mechanical
|
BOX 4.1 Electronic Phase Transitions The electronic properties of extended bulk materials such as metals and superconductors have been studied extensively by physicists. However, as the field has progressed from simple elemental materials to more complex synthetic ones, computational chemistry has come to the fore in addressing these problems. The "exotic materials" include the organic superconductors such as Bechgaard salts, polyacetylene, the fullerenes, and the high-temperature superconductors based on copper oxides. In addition, many new amorphous materials are technologically interesting in their electronic properties. For instance, electronic conduction in polymers, such as polyvinylcarbazole, is essential to some xerographic processes. The chemical complexity of these systems puts a premium on understanding the fundamental physics in new ways that do not usually rely on the simple symmetries present in elemental materials. All of these systems exhibit electronic phase transitions as the chemical composition or doping is changed: their electronic states change qualitatively. Sometimes this transition is from being an insulator to a metal, sometimes from a metal to a superconductor or to some complex magnetically ordered structure. One of the simplest electronic phase transitions is the transition between extended and localized states of a single electron moving in a random potential. Even though this problem is at the heart of the study of the electronic properties of any disordered material, the traditional methods of simply combining rough semiquantitative theories and experiment have been insufficiently powerful to resolve all of the important issues. One reason is that real materials have many physical influences in addition to disorder, such as interactions of vibrations and interactions between different electrons in the same material. Some mathematical work, such as rigorous theorems related to one-dimensional Anderson localization, has already helped in understanding this problem. On the other hand, loopholes in these theorems have been uncovered when the disorder is of a special, correlated kind. For instance, certain 1-D systems do not have only localized states as the simple theorems had indicated. These unusual sorts of extended states arise in systems with certain kinds of correlated disorder or with quasi-periodic Hamiltonians. Interestingly, far from being a mathematical curiosity, these exceptions to the simple theorems about one-dimensional localization seem to be at the heart of understanding the behavior of materials such as polyacetylene. In two-or three-dimensional materials, experiment has amply demonstrated the existence of both extended and localized states. However, there are still numerous controversies about the applicability of simple phase transition ideas to these electronic phase transitions. Are they described by the usual scaling phenomenology of ordinary thermal phase transitions? It has been argued that, in fact, such descriptions may break down because the wavefunctions at the transition are multifractal. Thus, the study of these electronic phase transitions has much in common with problems addressed in quantum chaos, where the structure of the wavefunctions needs to be understood in a statistical way. The interacting electron systems and their phase transitions also carry mathematical challenges. In one dimension, the interactions between electrons again can cause them to behave as if they were insulating. These one-dimensional many-electron problems lead to exactly solvable Schrödinger equations. The exact integrability of these classical models is connected with conformal invariance and the existence of solitons of nonlinear partial differential equations in one dimension. The question of whether such electronic interaction effects give rise to new phases for higher-dimensional systems doubtless has connections with the problem of solitons and exact integrable systems in higher dimensions—a problem that has attracted many in the area of partial differential equations. Finally, a large number of interesting phase transitions occur in disordered systems that also have interactions. These include the Kondo effect in which isolated electronic sites behave as if they have spins that can be quenched, as well as the exotic spin glass phases that have proved useful at least as analogies in many other areas of chemistry and biology. At the moment, the most useful theory of these system is based largely on the use of the unrestricted Hartree-Fock approximation. There are numerous mathematical questions connected with the Hartree-Fock problem for such disordered systems. Many of the ideas invented by Lieb in his proof of the stability of matter may have practical use here. Again, the rigorous mathematical analysis can be of significant help in understanding whether or not certain approximations can be used confidently in elucidating the qualitative physics. In addition, the same issues will arise when quantitative calculations are contemplated for specific materials. The study of electronic phase transitions in dusters will make these issues even more pronounced. The usual theory of phase transitions concentrates on infinite systems, and only dominant thermodynamic contributions are computed. For clusters, the finite size effects and the asymptotics of the approach to the infinite limit become important mathematical problems. |
methods for systems of 20 to 30 atoms (the traditional ab initio approach) requires 104 to 106 more computations than the semi-empirical or empirical approaches and much more time than it takes to solve the classical equations of motion for the rest of the system (Singh and Kollman, 1986).
To elaborate, calculation of the free energy of a complex chemical system by using classical molecular dynamics (Kollman, 1993) requires one to calculate the energy of the system and its gradient with respect to all the 3N coordinates. This can be done for noncovalent processes (those using only Equation 10) quite efficiently because the energy function in Equation (10) is very simple and its derivatives are quick and easy to evaluate. When one adds quantum mechanical (bond making or breaking) effects via Equation (1), in order to make the calculation of the free energy tractable, one must be able to evaluate the quantum mechanical energy and its gradient for the few quantum mechanical atoms as rapidly as the classical molecular mechanical energy and gradient for the thousands of atoms in the remainder of the system. This can be done by using simpler empirical (Warshel, 1991) and, to a reasonable approximation, semi-empirical (Field et al., 1990) quantum mechanical methods, but not with the first principle ab initio methods.
Density functional methods (Labanowski and Andzelm, 1991), particularly the divide-and-conquer strategy (Yang, 1991), show promise in leading to accurate and rapid solutions of Equation (9) for the electronic structure, but they are still a long way from being fully developed, so one cannot tell how efficient and useful they will be in this regard.
Thus, accurate simulation of chemical reactions at the active sites of macromolecules will likely require significant progress in the conformational search problem, even if one considers only the active site of the enzyme. As should be emphasized, the "conformational search problem" requires one not only to consider many conformations, but also to rank their relative free energy in solution. On top of this, one places the problem of accurate and very rapid electronic structure calculations. The above problems are very challenging conceptually, practically, and computationally.
References
Blake, J.F., and W. Jorgensen, 1991, Solvent effects on a Diels-Alder reaction from computer simulations, J. Am. Chem. Soc. 113:7430–7432.
Field, M.J., P.A. Bash, and M. Karplus, 1990, A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations, J. Comput. Chem. 11:700–733.
Kollman, P., 1993, Free energy Calculations—Applications to chemical and biochemical phenomena, Chem. Rev. 93:2395–2417.
Labanowski, J., and J.W. Andzelm, eds., 1991, Density Functional Methods in Chemistry, Springer-Verlag, New York.
Singh, U.C., and P.A. Kollman, 1986, A combined ab initio QM/MM method for carrying out simulations on complex systems: Application to the CH3Cl + Cl- exchange reaction and gas phase protonation of polyethers, J. Comput. Chem. 7:718–730.
Warshel, A., 1991, Computer Modeling of Chemical Reactions in Enzymes and Solutions, John Wiley, New York.
Warshel, A., and M. Levitt, 1976, Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme, J. Mol. Biol. 103:227–249.
Yang, W., 1991, Direct calculation of electron density in density-functional theory-implementation for benzene and a tetrapeptide, Phys. Rev. A. 44:7823–7826.
Molecular Dynamics Algorithms
Enhanced Sampling
The multiple minima problem, discussed elsewhere in this report, can be addressed by approaches other than optimization. Specifically, reasonable sampling strategies can be devised to scan configuration space in the hope of obtaining information about many local minima, maxima, and saddlepoints. Moreover, these strategies can incorporate a variety of chemical information, such as interproton distances from NMR, van der Waals radii (for hard-core exclusion), and secondary-structure elements. Useful search strategies today involve Monte Carlo, molecular dynamics (MD), Brownian and Langevin dynamics, calculations of free-energy perturbations, high-temperature simulations, normal-mode analyses, and various enhanced sampling techniques that involve hybrids of all of the above. As reflected by those many approaches, the problem of inadequate sampling of configurational space is receiving increasing attention as a realization emerges that faster and more powerful computers alone cannot solve this problem in the near future. New methodologies and a hierarchy of approaches at different levels of resolution—in combination with experiment—are needed to attack this sampling problem to advance current capabilities of computational chemistry in connection with biomolecules.
A specific problem involves numerical integration in the context of MD simulations. In this technique, molecular motion is propagated by numerically integrating the classical equations of motion governing a molecular system under the influence of a specified force field (McCammon and Harvey, 1987; Allen and Tildesley, 1990). In theory, MD simulations can provide extensive spatial and temporal information. However, inadequate sampling limits the scope of the results that can be obtained in practice. Similar issues arise in other chemical applications, such as quantum mechanics, and the development of improved integration schemes will advance the systems and types of processes that can be simulated on modern computers.
Numerical Methods for Solving Ordinary Differential Equations
Many problems in chemistry can be reduced to the solution of systems of coupled ordinary differential equations (ODEs). Examples include classical and Langevin dynamics, rate equations of kinetic theory, and the time-dependent Schrödinger equation when expanded in a basis set. Thus, numerical integrators used to solve these equations are fundamental tools in computational/theoretical chemistry, and any significant improvement in these integrators (e.g., speedup, long-time stability) results in advances throughout the field.
The technology of numerical integrators for solving ODEs has a long history with significant interplay among mathematics, physics, and chemistry. Many of the earliest integrators, such as Runge-Kutta and predictor-corrector integrators, are still in common use, but there have also been recent advances, driven in part by the need for methods that can treat multiple time scales and have greater stability for large-scale coupled nonlinear oscillators commonly found in MD of polymers and biological macromolecules. The long-time stability of integrators for such systems is a challenging area of mathematical analysis research; perhaps the chemical applications described here will stimulate important developments.
Symplectic Integrators
Symplectic integrators have recently gained attention in the mathematical community and were quickly adapted for use in dynamics calculations in chemistry because of their favorable properties. In applications to Hamiltonian systems, symplectic integrators have the property of building in Liouville's theorem, whereby areas in phase space are preserved as the system evolves in time. This strong conservation property translates into stability over long-time integrations, an important
property in MD calculations involving millions and more steps. One consequence of this for constant-energy MD simulations is that except for fluctuations, symplectic integrators with small time steps conserve energy for very long times, whereas nonsymplectic integrators typically introduce a systematic drift in the total energy. Time reversibility is another useful practical property of symplectic integrators.
A symplectic integrator is any of a class of numerical algorthms for the integration of classical many-body equations of motion that possess favorable properties such as area preservation, energy conservation, and time reversiblity.
Symplecticness may also be used in determining numerical solutions to the Schrödinger equation. There is an equivalent representation of quantum mechanics in terms of Hamilton's equations (Gray and Verosky, 1994) that makes possible the use of integrators for the quantum dynamics studies that are used for classical dynamics. Area-preserving mapping are also of interest in their own right in studies of dynamical systems (Meiss, 1992).
Symplectic integrators may be implicit or explicit. In explicit methods, the solution at the end of the time step is obtained by performing operations on the variables at the beginning of each time step. Symbolically, we write yn+1 = f(yn, Δt, ...), where f is some nonlinear function, Δt is the time step, yn is the approximation to the solution y at time nΔt, and the dots indicate other parameters or previous solutions (e.g., yn-1, yn-2). With implicit integrators, the final solutions are functions of both the initial and the final variables (yn+1 = f(yn+1,yn, Δt, ...)), and so coupled nonlinear equations must generally be solved at each time step to propagate the trajectory. The explicit versions generally involve simple algorithms that (for propagation only) use modest memory, while implicit methods involve more complex algorithms but are often more powerful for treating systems with disparate time scale dynamics, as discussed below.
The development of symplectic integrators has involved significant interplay among mathematicians, physicists, and chemists. Seminal work on symplectic integrators was done by both physicists and mathematicians (Ruth, 1983; Feng, 1986; Candy and Rozmus, 1991; McLachlan and Atela, 1992; Okunbor and Skeel, 1992; Calvo and Sanz-Serna, 1993) based on second-and third-order explicit approaches and Runge-Kutta methods. Implicit approaches were developed in parallel (Channell and Scovel, 1990; De Frutos and Sanz-Serna, 1992). Recently, these ideas have found their way into the chemistry community (Gray et al., 1994) with promising results. The Verlet integrator (Verlet, 1967), already in common use, was found to be symplectic, thereby explaining the good associated stability observed in practice. However, symplectic integrators that improve on previously available methods have also been developed (Gray et al., 1994). Initial applications using these methods suggest that they may become favored for simulations of polymer dynamics and related problems with small time steps.
The Time Step Problem in Molecular Dynamics
Although standard explicit schemes, such as the Verlet and related methods, are simple to formulate and fast to propagate, they impose a severe constraint on the maximum time step possible. Instability—uncontrollable growth of coordinates and velocities—occurs for step sizes much larger than 1 femtosecond (10-15 second). This step size is determined by the period associated with high-frequency modes present in all macromolecules, and it contrasts with the much longer time scales (up to 102 seconds) that govern key conformational changes (e.g., folding) in macromolecules. This disparity in time scales urges the development of methods that increase the time step for biomolecular simulations. Even if the stability of the numerical formulation can be ensured, an important issue concerning the reliability of the results arises, since vibrational modes in molecular systems are
intricately coupled.
Standard techniques of effectively freezing the fast vibrational modes by a constrained formulation (Ryckaert et al., 1977; van Gunsteren and Berendsen, 1977; van Gunsteren, 1980; Miyamoto and Kollman, 1992) increase the time step by a small factor such as two, still with added complexity at each step. The multiple time step approaches for updating the slow and fast forces provide additional speedup (Streett et al., 1978; Grubmüller et al., 1991; Tuckerman and Berne, 1992; Watanabe and Karplus, 1993), although some stability issues are also involved (Biesiadecki and Skeel, 1993).
Implicit Integration Schemes
There are well-known numerical techniques for solving differential equations describing physical processes with multiple time scales (Gear, 1971; Dahlquist and Björck, 1974). Various implicit formulations are available that balance stability, accuracy, and complexity. However, the standard implicit techniques used by numerical analysts (Kreiss, 1991) have not been directly applicable to MD simulations of macromolecules, for the following reasons.
First, such implicit schemes are often designed to suppress the rapidly decaying component of the motion. This is a valid approach when the contribution of these components becomes negligible for sufficiently long times, as is the case for the second term in y(t) = exp (-t) + exp (-100t). However, this situation does not hold for biomolecular systems because of the intricate vibrational coupling. It is well recognized that concerted conformational transitions (e.g., in hinge-bending proteins) require a cooperative mechanism driven by small-scale fluctuations to make possible a large-scale collective displacement. Thus, although the absence of the positional fluctuations associated with these high-frequency modes may not by itself be a severe problem, the absence of the energies associated with these modes may be undesirable for proteins and nucleic acids, since cooperative motions among the correlated vibrational modes may rely on energy transfer from these high-frequency modes.
Second, implicit schemes with known high stability (e.g., implicit Euler) can introduce numerical damping (Zhang and Schlick, 1993). This has prompted the application of such implicit schemes to the Langevin dynamics formulation, which involves frictional and Gaussian random forces in addition to the systematic force to mimic molecular collisions and therefore a thermal reservoir. This stabilizes implicit discretizations and can be used to quench high-frequency vibrational modes (Peskin and Schlick, 1989; Schlick and Peskin, 1989), but unphysical increased rigidity can result (Zhang and Schlick, 1993). Therefore, more rigorous approaches are required to resolve the subdynamics correctly, such as by combining normal-mode techniques with implicit integration (Zhang and Schlick, 1994); significant linear algebra work in the spectral decomposition is necessary for feasibility for macromolecular systems. For example, banded structures for the Hessian approximation (see related discussion in the section on multivariate minimization beginning on page 68) can be exploited in the linearized equations of motion. There has also been some work on implicit schemes that do not have inherent damping, but preliminary experience suggests that for nonlinear systems, desirable energy conservation properties can be obtained only up to moderate time steps (Simo et al., 1992; Zhang and Schlick, 1995). In particular, serious resonance problems have been noted (Mandziuk and Schlick, 1995).
Third, implicit schemes for multiple time scale problems increase complexity, since they involve solution of a nonlinear system or minimization of a nonlinear function at each time step. Therefore, very efficient implementations of these additional computations are necessary, and even then, computational gain (with respect to standard ''brute-force" integrations at small time steps) can be realized only at very large time steps.
Future Prospects
The preceding subsections have described several recent accomplishments in the development of integration methods in MD simulations and have also outlined several important challenges for the future. What makes these integration problems particularly challenging is the fact that solutions demand much more than straightforward application of standard mathematical techniques. At this point it appears that the optimal algorithms for MD will require a combination of methods and strategies discussed above, including symplectic and implicit numerical integration schemes that have minimal intrinsic damping, and correct resolution of the subdynamics of the system by some other technique (e.g., normal-mode analysis). Undoubtedly, high-performance implementations will make possible a gain of several orders of magnitude in the simulation times, and there are certainly additional gains to be achieved by clever programming strategies.
References
Allen, M.P., and D.J. Tildesley, 1990, Computer Simulation of Liquids, Oxford University Press, New York.
Biesiadecki, J.J., and R.D. Skeel, 1993, Dangers of multiple-time-step methods, J. Comput. Phys. 109:318–328.
Calvo, M.P., and J.M. Sanz-Serna, 1993, The development of variable-step symplectic integrators, with application to the two-body problem, SIAM J. Sci. Comput. 14:936.
Candy, J., and W. Rozmus, 1991, A symplectic integration algorithm for separable Hamiltonian functions, J. Comput. Phys. 92:230.
Channell, P.J., and J.C. Scovel, 1990, A symplectic integration of Hamiltonian systems, Nonlinearity 3:231.
Dahlquist, G., and Å. Björck, 1974, Numerical Methods, Prentice Hall, Englewood Cliffs, N.J.
De Frutos, J., and J.M. Sanz-Serna, 1992, An easily implementable fourth-order method for the time integration of wave problems, J. Comput. Phys. 103:160.
Feng, K., 1986, Difference schemes for Hamiltonian formalism and symplectic geometry, J. Comput. Math. 4:279–289.
Gear, C.W., 1971, Numerical Initial Value Problems in Ordinary Differential Equations, Prentice Hall, Englewood Cliffs, N.J.
Gray, S.K., and J.M. Verosky, 1994, Classical Hamiltonian structures in wave packet dynamics, J. Chem. Phys. 100:5011–5022.
Gray, S.K., D.W. Noid, and B.G. Sumpter, 1994, Symplectic integrators for large scale molecular dynamics simulations: A comparison of several explicit methods, J. Chem. Phys. 101:4062–4072.
Grubmöller, H., H. Heller, A. Windemuth, and K. Schulten, 1991, Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions, Mol. Simul. 6:121–142.
Kreiss, H.-O., 1991, Problems with different time scales, Acta Numerica 1:101139.
Mandziuk, M., and T. Schlick, 1995, Resonance in chemical-system dynamics simulated by the implicit-midpoint scheme, Chem. Phys. Lett., in press.
McCammon, J.A., and S.C. Harvey, 1987, Dynamics of Proteins and Nucleic Acids, Cambridge University
Press, Cambridge.
McLachlan R.I., and P. Atela, 1992, The accuracy of symplectic integrators, Nonlinearity 5:541.
Meiss, J.D., 1992, Symplectic maps, variational principles, and transport, Rev. Mod. Phys. 64:795.
Miyamoto, S., and P.A. Kollman, 1992, SETTLE: An analytical version of the SHAKE and RATTLE algorithm for rigid water models, J. Comput. Chem. 13:952–962.
Okunbor, D.I., and R.D. Skeel, 1992, Canonical numerical methods for molecular dynamics simulations, Math. Com. 59:439.
Peskin, C.S., and T. Schlick, 1989, Molecular dynamics by the backward-Euler method, Commun. Pure Appl. Math. 42:1001–1031.
Ruth, R.D., 1983, A canonical integration technique, IEEE Trans. Nucl. Sci. NS-30:26–69.
Ryckaert, J.P., G. Ciccotti, and H.J.C. Berendsen, 1977, Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes, J. Comput. Phys. 23:327–341.
Schlick, T., and C.S. Peskin, 1989, Can classical equations simulate quantum-mechanical behavior? A molecular dynamics investigation of a diatomic molecule with a Morse potential, Commun. Pure Appl. Math. 42:1141–1163.
Simo, J.C., N. Tarnow, and K.K Wong, 1992, Exact energy-momentum conserving algorithms and symplectic schemes for nonlinear dynamics, Computer Methods in Applied Mechanics and Engineering 100:63–116.
Streett, W.B., D.J. Tildesley, and G. Saville, 1978, Multiple time step methods in molecular dynamics, Mol. Phys. 35:639–648.
Stuart, A.M., and A.R. Humphries, 1994, Model problems in numerical stability theory for initial value problems, SIAM Review 36:226–257.
Tuckerman, M.E., and B.J. Berne, 1992, Molecular dynamics in systems with multiple time scales: systems with stiff and soft degrees of freedom and with short and long range forces, J. Comput. Chem. 95:8362–8364.
van Gunsteren, W.F., 1980, Constrained dynamics of flexible molecules, Mol. Phys. 40:1015–1019.
van Gunsteren, W.F., and H.J.C. Berendsen, 1977, Algorithms for macromolecular dynamics and constraint dynamics, Mol. Phys. 34:1311–1327.
Verlet, L., 1967, Computer "experiments" on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules, Phys. Rev. 159:98.
Watanabe, M., and M. Karplus, 1993, Dynamics of molecules with internal degrees of freedom by multiple time-step methods, J. Chem. Phys. 99:8063–8074.
Zhang, G., and T. Schlick, 1993, LIN: A new algorithm to simulate the dynamics of biomolecules by combining implicit-integration and normal mode techniques, J. Comput. Chem. 14:1212–1233.
Zhang, G., and T. Schlick, 1994, The Langevin/implicit-Euler/normal-mode scheme (LIN) for molecular dynamics at large time steps, J. Chem. Phys. 101:4995–5012.
Zhang, G., and T. Schlick, 1995, Implicit discretization schemes for Langevin dynamics, Mol. Phys., in press.
N-and V-Representability Problems in Classical Statistical Mechanics
Classical equilibrium statistical mechanics presents a class of unsolved N-representability problems analogous to those in the quantum mechanical regime discussed earlier in this chapter. In this case, N refers to the number of particles (atoms or molecules) present, rather than the number of electrons The most straightforward version of this classical problem concerns a single-species monatomic system (i.e., spherically symmetric identical particles) and revolves the pair correlation function g(r). This nonnegative function of interparticle distance r is defined by the occurrence probability of particle pairs at r, relative to random expectation, Consequently, deviations of g(r) greater than 1 indicate that interparticle interactions have biased the distance distribution to a greater-than-random expectation, while deviations less than 1 indicate the Opposite.
For many cases of interest, the interparticle potential energy function V can be regarded as a sum of terms arising from each pair of particles present:
The pair potentials v(r) typically are taken to satisfy the following criteria:
(b) v(r) is bounded, and is piecewise continuous and differentiable for r > 0;
Under these circumstances, g(r) plays a special rule in the thermodynamic properties of the N-particle system (Hansen and McDonald, 1976). This fundamental quantity appears in closed-form expressions giving the pressure and mean energy at the prevailing temperature and density. Furthermore, it appears in expressions for the X-ray and neutron diffraction patterns for the substance; consequently, these diffraction measurements constitute an experimental means for measuring g(r) for real substances. It should be added that g(r) is also one of the traditional results reported from computer simulations of N-body systems (Ciccotti et al., 1987).
The experimentally, or computationally, adjustable parameters are temperature; particle number density; container size, shape, and boundary conditions; and number N of particles. For most cases of interest, one focuses on the infinite-system limit, where the container size and N diverge, while temperature, number density, and container shape are held constant. The central problem then concerns the mapping between the pair of functions v(r) and g(r), where the latter is interpreted as the infinite-system limit function.
Historically, the fundamental theory of classical systems (particularly in the liquid state) concentrated heavily on prediction of g(r) for a given v(r), that is, the mapping from v to g. This has generated several well-known approximate integral equation predictive theories for g(r), including those conventionally identified in the theoretical chemistry literature by the names Kirkwood (1935), Bogoliubov-Born-Green-Yvon (Born and Green, 1949), Percus and Yevick (1958), and hypernetted chain (van Leeuwen et al., 1959) integral equations, each of which has spawned successor refinements. However, in all cases the respective approximations invoked have, strictly speaking, been uncontrolled. Consequently, the local structure and thermodynamic property predictions based on these various integral equations have had only modest success in describing the dense liquid state,
|
BOX 4.2 Tutorial on Statistical Mechanics and the Importance of Minima and Saddlepoints in Condensed Matter Systems A large part of computational chemistry is concerned with the properties of systems at or near thermal equilibrium. The statistics of configurations at thermal equilibrium therefore dominate many of the questions studied by chemists. The principles of the statistical mechanics of equilibrium systems are quite simple to state but are profound and sometimes surprising in their results. A fundamental postulate of equilibrium statistical mechanics is that in the long run, all states of an isolated system that are consistent with conservation of energy will be observed with equal probability. The thermodynamic quantity S, the entropy, is simply a measure of the number Ω of these equally probable states that the system might access, S = kB log Ω. Here kB is Boltzmann's constant. Thus, combinatorial and various counting problems play a special rule in our thinking about the thermodynamics of chemical systems. Although each of the states of an isolated system is equally probable, this is not the case when we consider only a part of a system. When only part of a system is being examined, we must ask the question, How many states of the entire system are accessible when a subsystem is in a given configuration? The answer is given by where X refers to the specified subsystem and the entropy refers to the subsystem's environment. A very interesting and powerful special case of his formula is used constantly in equilibrium statistical mechanics. If the subsystem considered is only weakly coupled to the rest of a much larger system, we can decompose the total energy of the entire system into parts: The energetic coupling is small and can be neglected if we are considering a system that is itself fairly large and therefore has a relatively small surface of interaction with the remainder of the system. In this case the counting problem can be solved since we know that the entropy of the environment is a smooth function of its total energy. This then gives a count of states expressed by The probability then of an exactly specified state of a subsystem that is part of a larger one is proportional to this number of states. It is given by the Boltzmana distribution law The temperature entering here is the thermodynamic derivative of the entropy and is proportional to the average kinetic energy of each particle in the system. This distribution law contains within it many of the great phenomena of chemistry and physics. First we see that the most important states are those that have the lowest energy. If the energy then is a continuous function of the coordinates of part of the system, the most probable configurations are those that give minima this potential. Indeed, the coefficient 1/kBT in the Boltzmann distribution law ensures that at the lowest temperatures only the deepest or global minima are |
|
important. Chemistry is usually a low-temperature phenomenon—most chemical reactions are studied around room temperature, although, of course, many do occur under greater extremes of conditions—and room temperature corresponds to only one-fortieth of the typical energy scale of chemical bonds. Thus, the Boltzmann distribution law tells us that chemistry will mostly concern itself with the specific configurations that minimize the energy. Of course, if molecular systems remained entirely at their energy minima, little would go on. Occasionally, a molecular system must make a transition between one minimum on the energy surface and another. To do this, the system must occasionally find itself in an intermediate high-energy configuration, which the Boltzmann distribution law tells us is rather improbable. If we ask which of the relatively improbable intermediate states between two minima are the most probable, it is clear that these should correspond to saddlepoints of the energy. These saddlepoint configurations are known as transition states to chemists. The probability of a system being found at a transition state determines the rate of a chemical transformation. We see, therefore, that the geometry of minima and saddlepoints of potential energy surfaces is extremely important in determining the chemical properties of a molecular system. Sometimes only certain aspects of a system are considered explicitly. For example, when we study the shapes, structures, and motions of a biological molecule (e.g., a protein immersed in water), we are interested only secondarily in the configurations of the water molecules around this macromolecule. A special case of these geometrical problems arises when the subsystem being considered is itself rather large and involves strong interactions between its molecular subunits. In this case, it sometimes happens that the minimum-energy saddlepoint actually possesses an extremely high energy. We then say that the transformation between two minima has a large barrier and the transformation will be extremely slow. Sometimes as the subsystem studied grows larger and larger, the transformation barrier itself also grows larger and larger. Thus, for a macroscopic system, certain transformations may actually take place effectively only on infinite time scales. We can then treat each part of the configuration space very nearly as separate regions. This situation arises when a phase transition occurs. The theory of phase transitions is then concerned with the problem of how a many-dimensional configurational space gets fragmented into parts that are separated by very high energy barriers. The Boltzmann distribution law applies only to a completely specified subsystem that is interacting weakly with its environment. The biological macromolecule is interacting strongly with its solvent environment, and so the Boltzmann distribution law using the energy alone is inappropriate for describing its configurations. On the other hand, for different configurations of the biomolecule, we can in principle compute the number of configurations of the surrounding solvent that are compatible with that configuration of the biomolecule. Thus, the probability of a particular configuration of the biomolecule would have the form where the probability has been rewritten in a Boltzmann-like form in which the energy of the molecular system is combined with the entropy in its environment to form a free energy F(x) = E(X)-TS(X), which gives the probability of the subsystem's configuration. For this reason, the geometry of free energy surfaces is often also of great interest to chemists and physicists. Occasionally the distinction between energies and free energies is blurred in offhand writing by chemists and physicists, and the uninitiated reader must be careful about these distinctions when applications are made. |
they have failed to predict the so-called nonclassical singular behavior at the liquid-vapor critical point (Widom, 1965), and they have been largely useless for the study of freezing and melting transitions. Perhaps as a result of these shortcomings, the recent trend in classical statistical mechanics has been to rely heavily on direct computer simulation of condensed-phase phenomena. Because these simulations often require massive computational resources, a case can be made that revival of analytic predictive theory for g(r) would be favorable from the point of view of the ''productivity issue" in theoretical and computational chemistry.
In some respects, the inverse mapping of g to v is even more subtle, intriguing, and mathematically challenging. At the outset, one encounters the obvious matter of defining the space of functions g(r) that in fact can be generated by a pairwise additive potential energy function V. A few necessary conditions are straightforward; as already remarked, g(r) cannot be negative. It is generally accepted (but not rigorously demonstrated) that g must approach unity as r diverges if the temperature is positive, even though the system itself may be in a spatially periodic crystalline state. In addition, the Fourier transform of g(r) — 1,
is also subject to necessary conditions stemming from the nature of the linear equilibrium response of the system to weak external perturbations: for all k > 0 one must have (Percus, 1964)
1 + ρ G(k) ≥ 0 (ρ = number density).
These generic conditions can be supplemented by others that are necessary if v(r) has an infinitely repelling hard core, that is,
This hard-core property prevents neighbors from clustering too densely around any given particle, and from the geometry of hard-sphere close packings it is possible to bound the integral of r2g(r) over finite intervals of r.
A primary challenge concerns formulation of sufficient conditions on g(r), given that V possesses the pairwise-additive form displayed above. At present we have no rational criterion for deciding whether a given g(r), however "reasonable" it may appear to be by conventional physical standards, corresponds to the thermal-equilibrium short-range order for any pairwise additive V. It is not even clear at present how to construct a counterexample, namely, a g(r) meeting the necessary conditions above that cannot map to a v(r) of the class described. In any case, formulation of sufficient conditions would likely improve prospects for more satisfactory integral equation (or other analytical) predictive techniques for g(r).
Several directions of generalization exist for this classical V-Representability problem; these include the following matters:
-
Properties of triplet and higher-order correlation functions gn for occurrence probabilities of particle n-tuples;
-
Properties of correlation functions for particles (molecules) with internal degrees of freedom (rotation, vibration, conformational flexibility);
-
Effects of specific nonadditive potentials, which would be the case when including
-
three-particle contributions in V; and,
-
Multicomponent (several species, or mixture) systems, in particular the important case of electrostatically charged particles (ions) with their long-ranged Coulombic interactions.
References
Born, M., and H.S. Green, 1949, A General Kinetic Theory of Liquids, Cambridge, London.
Ciccotti, G., D. Frankel, and I.R. Kirkwood, 1987, eds., Simulation of Liquids and Solids, North-Holland, Amsterdam.
Hansen, J.P., and I.R. McDonald, 1976, Theory of Simple Liquids, Section 2.6, Academic Press, New York.
Kirkwood, J.G., 1935, Statistical mechanics of fluid mixtures, J. Chem. Phys. 3:300–313.
Percus, J.K., 1964, in The Equilibrium Theory of Classical Fluids, H.L. Frisch and J.L. Lebowitz, eds., W.A. Benjamin, New York, pp. II-33 to II-170 (see particularly II-41).
Percus, J.K., and G.J. Yevick, 1958, Analysis of classical statistical mechanics by means of collective coordinates, Phys. Rev. 110:113.
van Leeuwen, J.M.J., J. Groeneveld, and J. De Boer, 1959, New method for the calculation of the pair correlation function, Physica 25:792–808.
Widom, B., 1965, Equation of state in the neighborhood of the critical point, J. Chem. Phys. 43:3898–3905.
Implications of Topological Phases
The Born-Oppenheimer approximation dates from the 1920s, and the entire notion of molecular structure can be based upon it. It is thus a surprise that significant qualitative physics has been ignored by most chemical physicists in applying the Born-Oppenheimer approximation to systems with degenerate electronic states. The basic idea behind the Born-Oppenheimer approximation is that nuclei move much more slowly than electrons. Thus, the Schrödinger equation for electrons can be solved at fixed nuclear configuration and the resulting energy can be used as a potential for studying the motions of the nuclei themselves.
Generally, when nuclear motion itself is quantized, one assumes the usual Schrödinger equation with a classical scalar potential for the nuclear motions. This has proved valid for systems that do not have significant electronic degeneracy. A serious mathematical problem is the uniqueness of the wave function for the nuclei. The Born-Oppenheimer approximation really assumes a single path for the slowly moving nuclei. If there is an electronic degeneracy, topologically distinct paths may connect two different positions on the same electronic surface. Thus, in addition to the phases that one develops for the quantum dynamics through the simple scalar potential dynamics, there is an additional topological phase. The existence of this topological phase, which depends on the path between two points, has been known since at least the p, when Longuet-Higgins studied it in the context of Jahn-Teller distortions. Only in recent years has its significance been truly appreciated, however. One of the leaders in bringing out the significance of topology in quantum molecular dynamics was M. Berry. However, it was appreciated somewhat earlier by Truhlar and Mead that this topological phase plays a rule in chemical reactions. Indeed it is important even in the most fundamental of chemical reaction problems, the H + H2 reaction. Very recently, the discrepancy
|
BOX 4.3 Implications of Dynamic Chaos for Quantum Mechanical Systems Many phenomena in chemistry are at the border of applicability of classical mechanics. Quantum mechanical phenomena, such as tunneling and interference, certainly are relevant to many chemical reactions. Thus, in addition to purely classical dynamical methods, semiclassical approximations are used quite commonly in chemical physics. Semiclassical methods work fairly well for low-dimensional systems such as those encountered in gasphase chemical reactions, because the collisions that act as randomizers are infrequent and the chaotic character of the processes may often be neglected. On the other hand, in attempting to extend semiclassical methods to condensed-phase systems, one is immediately faced with the problem of the underlying classical chaos, No completely adequate semiclassical quantization of chaotic systems yet exists. Most of the effort of theoretical chemists working in this area has been devoted to understanding simple themes that may give some qualitative insight to phenomena that occur in the quantum mechanics of systems that are classically chaotic. Several important themes have been developed, one of the most notable being the connection of quantum chaos to random matrix theory. The notions behind this have their roots in Wigner's use of random matrices to describe nuclear systems, but the application of these ideas to molecules has been equally rewarding. One can examine the evolution of the energy levels of a system under perturbation in order to understand its quantum chaotic nature. It has been shown that a random matrix description could arise from multiple level crossings. This approach has also been shown to be related to some exactly integrahie systems of particles moving in one dimension. The great irony is that the random matrix description arises from a problem that, in another guise, leads to exactly integrable equations. Very interesting connections exist to the theory of solutions of nonlinear partial differential equations. Classical systems in many dimensions, when they are chaotic, often exhibit diffusive dynamics. Arnold has shown how weakly coupled systems of dimension higher than 2 exhibit such diffusion. It has recently been argued that a phenomenon analogous to Arnold diffusion in the classical limit arises in quantum problems and that weakly coupled systems of quantized oscillators are analogous to local random matrix models. These local random matrix models are closely tied to the problem of Anderson localization, which concerns itself with the nature of eigenfunctions of random differential operators. A most enticing development in the understanding of quantum chaos has been the connection of problems in quantum chaos with deep problems in number theory. One of the most picturesque approaches for obtaining quantum mechanical energy levels is to calculate the Green's function of the Schrödinger equation through a sum over classical paths. For chaotic systems these classical paths are extremely numerous and the Green's function is indeed the sum of a statistically fluctuating quantity that itself presents interesting mathematical problems to be discussed later. One model for the classical paths represents them as repetitions of some fundamental periodic orbits. Some very simple special models of the actions of these orbits lead to a Green's function that is closely tied to the Riemann zeta function. The prime numbers represent the fundamental periodic orbits. This has suggested that the zeros of the Riemann zeta function are related to the quantum mechanical eigenvalues of some Hamiltonian that is classically chaotic. This ansatz has led to interesting predictions about the spacing of zeros of the Riemann zeta function and other statistics that seem very much in keeping with the random matrix theories being used to describe quantum chaos. Thus, it seems that problems in quantum chaos might be clarified considerably by considerations from probabilistic number theory and, conversely, that deep number theoretic questions might be addressed by using ideas from the quantum mechanics of chaotic systems. Although significant progress has already been made in developing conjectures based on these ideas, there is still a tremendous amount to do and many deep mysteries remain. |
between experimental results for H + H2 and large-scale computations of the scattering cross sections was shown to arise from neglect of this topological phase.
For problems with small amounts of degeneracy, the topological phase is easy to handle with little mathematical sophistication. Either a trajectory encircles a conical intersection (of Born-Oppenheimer energy surfaces) or it does not, leading to two values of the phase. This encircling of singularities can be described by using the idea of a gauge potential. With higher degeneracies, however, very difficult topological problems may be encountered since many surfaces can make avoided crossings in many locations. The paradigm of such complicated topology problems may well be metal clusters. For metals in the thermodynamic limit, there are numerous energy levels corresponding to the excitation of electrons just below the Fermi sea to just above it. Since the electronic levels are highly delocalized, these energy changes are quite small and the energy surfaces are close together. The actual dynamics of the nuclei must involve the coupling of several surfaces. There are many possible interchanges of the metallic ionic cores, and complicated topologies can result.
Another place in which topology enters is when an underlying approximate wave function is built up out of many degenerate electronic wave functions and the dynamics of electronic excitations is studied. The paradigm for this is the recent interest in resonating valence bond descriptions of metallic and superconducting materials. Here, reorganization of the different valence bond structures as an excited electron or hole moves around gives rise to topological phases and gauge fields. It has been argued that these effects are at the heart of the new high-temperature superconductors and represent a real breakdown of the traditional band structure picture of metals. Most models studied by physicists, however, have been very simple, and it will be necessary to understand how the topological phases arise in completely realistic electronic structure calculations if one is to make predictions of new high-temperature superconductors on the basis of these ideas.
Theoretical and Computational Chemistry in Spaces of Noninteger Dimension
A major mathematical landmark in the eighteenth century was Euler's introduction and exploitation of the famous gamma function. One of its basic and striking properties is that it provides a natural "smooth" extension of the factorials n! that are defined nominally just for the positive integers to all positive numbers, and indeed even into the complex plane. The pervasive appearance of the Euler gamma function throughout classical mathematical analysis constitutes a powerful paradigm suggesting that analogous extensions from the discrete positive integers to the complex plane in other contexts might generate analogous intellectual benefits.
During roughly the last two decades, simultaneous developments in several distinct areas of physical science appear to point to the necessity (or at least the desirability) of just such an extension. Specifically, this involves generalizing the familiar notion of Euclidean D-dimensional spaces from positive integer D at least to the positive reals, if not to the complex D-plane. This is not an empty pedantic exercise; at least one serious proposal has been published (Zeilinger and Svozil, 1985) claiming that accurate spectroscopic measurements of the electron "g-factor" indicate that the space dimension of our world is less than 3 by approximately 5 x 10-7. Furthermore, in various theoretical applications that have so far been suggested for the continuous-D concept, D itself or its inverse appears to be a natural expansion parameter for various fundamental quantities of interest. However, most of the work along these lines thus far has been ad hoc, lacking rigorous mathematical underpinning. Naturally this calls into question the validity of claimed results.
Three physical science research areas deserve mention in this context. The first is quantum field theory; dimension D has been treated as a continuously variable "regularizing parameter" whose
manipulation avoids embarrassing divergences in perturbation expansions (Bollini and Giambiagi, 1972; t'Hooft and Veltman, 1972; Ashmore, 1973). The second is the statistical mechanics of phase transitions (specifically involving critical point phenomena); because of rigorously known results for D = 2 and D = 4, 5, 6, . . . , series expansions in the quantity 4 — D have been developed for various quantities of interest to access the physical case D = 3 (Wilson and Fisher, 1972; Gorishny et al., 1984). The third area holds perhaps the greatest promise for chemical progress, namely, the development of atomic and molecular quantum mechanics (with useful computational algorithms) in spaces of arbitrary D (Goodson et al., 1992; Herschbach et al., 1992).
As in the other applications, the notion of atomic and molecular quantum mechanics is unambiguously defined for D a positive integer; in other words, the Schrödinger wave equation and
|
BOX 4.4 Nodal Properties of Wavefunctions Knowledge of the nodes of the many-fermion wavefunction would make possible exact calculation of the properties of fermion systems by Monte Carlo methods. Little is known about nodes of many-body fermion systems even though the one-dimensional case is ubiquitous in textbooks on quantum mechanics. The nodes referred to here are the nodes of the exact many-body wavefunction and are very different from the nodes of orbitals. In the absence of a rigorous simulation method for fermion systems, the fixed-node approximation has been found to be a useful and powerful approach. One assumes knowledge of where the exact wavefunction is positive and negative based on the nodes of a trial wavefunction. The Schrödinger equation in imaginary time is solved by simulating the diffusion process with branching within the regions bounded by the assumed nodes. For the ground state, Ceperley (1991) has proved that ground state nodal cells have the tiling property (i.e., there is only one type of nodal cell, all other cells being related by permutational symmetry). The tiling property is the generalization to fermions of the theorem that a bosonic ground state is nodeless. The nodal hypervolumes of a series of atomic N-body Hartree-Fock level electronic wavefunctions have been mapped by using a Monte Carlo simulation in 3N-dimensional configuration space (Glauser et al., 1992). The basic structural elements of the domain of atomic and molecular wavefunctions have been identified as nodal regions and permutational cells (identical building blocks). The results of this study on lithium-carbon indicate that Hartree-Fock wavefunctions generally consist of four equivalent nodal regions (two positive and two negative), each constructed from one or more permutational cells. A generalization of the fixed-node method has been proposed that could solve the fermion problem at finite temperature if only the nodes of the fermion density matrix were known (Ceperley, 1991). References Ceperley, D.M., 1991, J. Stat. Phys. 63:1237. Glauser, W.A., W.R. Brown, W.A. Lester, Jr., D. Bressanini, B.L. Hammond, and M.L. Koszykowski, 1992, J. Chem. Phys. 97:9200. |
its boundary conditions have an immediate and clear meaning. The desire to embed these problems in the arbitrary-D context arises primarily from the observation that solutions to the Schrödinger equation adopt a simple limiting form as D approaches infinity, namely, those for simple harmonic oscillators localized in multidimensional space (Goodson et al., 1992; Herschbach et al., 1992). Eigenfunction and eigenvalue expansions in 1/D have then been formally generated, with the hope
that series summation techniques (e.g., Padé approximants) would permit extension to the case of ultimate interest D = 3. This strategic approach to real chemistry in the real world is emboldened by the facts that (a) D = 1 is often an exactly solvable case (or at least amenable to very accurate numerical study), and (b) exact interdimensional identities for D and D + 2 are known (Herrick, 1975). These latter afford convenient fixed points for refining the series summation attempts.
The presumption that spaces with noninteger dimension were available as analytic tools for atomic and molecular quantum mechanics rests largely on simple observations such as the fact that the D-dimensional (hyper) spherical volume element,
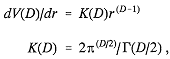
is an obvious analytic function of the variable D. The implicit assumption in the various applications to date, quantum mechanical and otherwise, seems to have been that the same expression can be invested with mathematical legitimacy for noninteger D, in the sense that it is an attribute of a family of precisely defined spaces. This is by no means an obvious proposition, since any quantity such as K(D) above could be augmented by any function of D that vanishes at the positive integers, such as sin (2πD), without affecting the situation for conventional Euclidean geometry.
The published literature reveals some attempts to axiomatize spaces of noninteger dimension (Wilson, 1973; Stillinger, 1977), but it is clear that the subject requires deeper mathematical insight than it has thus far experienced. In particular, it is desirable to determine the extent to which arbitrary-D spaces are uniquely definable as uniform and isotropic metric spaces and what their relation to conventional vector spaces might be. It has been suggested (Wilson, 1973) that noninteger-D spaces can be viewed as embedded in an infinite-dimensional vector space, but whether this is uniquely possible or even necessary to perform calculations remains open.
It is important to stress the distinction between the general-D spaces that may be obtained by interpolation between the familiar Euclidian spaces for integer D on the one hand and the so-called fractal sets to which a generally noninteger Hausdorff-Besicovitch dimension can be assigned (Mandelbrot, 1983). The latter are normally viewed as point sets contained in a Euclidean host space; furthermore, they fail to display translational and rotational invariance, and are therefore not uniform and isotropic.
References
Ashmore, J.F., 1973, On renormalization and complex space-time dimensions, Commun. Math. Phys. 29:177–187.
Bollini, C.G., and J.J. Giambiagi, 1972, Dimensional renormalization: The number of dimensions as a regularizing parameter, Nuovo Cimento B 12:20.
Goodson, D.Z., M. Lopez-Cabrera, D.R. Herschbach, and J.D. Morgan III, 1992, Large-order dimensional perturbation theory for two-electron atoms, J. Chem. Phys. 97:84–81.
Gorishny, S.G., S.A. Larin, and F.V. Tkachov, 1984, Phys. Lett. 101A:120.
Herrick, D.R., 1975, Degeneracies in energy levels of quantum systems of variable dimensionality, J. Math. Phys. 16:281.
Herschbach, D.R., J. Avery, and O. Goscinski, eds., 1992, Dimensional Scaling in Chemical Physics, Kluwer Academic, Dordrecht, Holland.
Mandelbrot, B.B., 1983, The Fractal Geometry of Nature, W.H. Freeman, San Francisco.
Stillinger, F.H., 1977, Axiomatic basis for spaces with noninteger, J. Math. Phys. 18:12–24.
t'Hooft, G., and M. Veltman, 1972, Nuclear Phys. B 44:189.
Wilson, K.G., 1973, Phys. Rev. D 7:29–11.
Wilson, K.G., and M.E. Fisher, 1972, Phys. Rev. Lett. 28:240.
Zeilinger, A., and K. Svozil, Measuring the dimension of space-time, Phys. Rev. Lett. 54:25–53.
Multivariate Minimization in Computational Chemistry
Introduction
Mathematical optimization is a branch of mathematics that seeks to answer the question ''What is best?" for problems in which the quality of the answer can be expressed as a numerical value (see, e.g., Gill et al., 1983b; Fletcher, 1987; Ciarlet, 1989). This question might refer to the "best" approximation in some local sense (i.e., a local solution) or to the global solution over the entire feasible space (i.e., the global minimum) (see, e.g., Nemhauser et al., 1989; Floudas and Pardalos, 1991). A common problem arises when a complex physical system is described by a collection of particles, or combinations of states, in a multidimensional phase space. An energy or cost function is associated with each different configuration, and the challenge is to find sets of points that minimize (or maximize)1 the objective function. Such applications arise frequently in molecular modeling, rational drug design, quantum mechanical calculations, mathematical biology models, neural networks, combinatorial problems, financial investment planning, engineering, electronics, meteorology, and computational geometry. In applications that arise in computational chemistry (Scheraga, 1992; Schlick, 1992), the feasible space is often very high in dimensionality and complexity, so both local and global minima are of interest.
There are many optimization techniques available for the computational scientist. Nonetheless, implementation of the more sophisticated techniques requires considerable computing experience, algorithm familiarity, and intuition. While software vendors offer a variety of "black-box" codes, serious practitioners frequently discover that a good deal of understanding and modification is required for successful applications. Such modifications involve tailoring the algorithm to features of the problem at hand—such as function separability—or exploiting available experimental information that might guide the optimization path—such as nuclear magnetic resonance (NMR) distance restraints in molecular mechanics. Moreover, successful new optimization schemes may be not be known or available to nonspecialist mathematicians, let alone to scientists in allied fields.
Thus, the transfer of knowledge, its application to real problems, and its further developments will greatly benefit from increased interdisciplinary interactions. In particular, it may be useful to
stimulate algorithmic developments in optimization toward important scientific problems, such as arise in chemistry, that would involve synergistic efforts on both parts: the application-oriented scientist and the algorithm developer. Such collaborations are likely to be fruitful to both parties, since testing of new methods will be possible on real-life problems and might generate an evolving body of solutions that take into account the available physical data. There is recent evidence (e.g., in special sessions of meetings of the Society for Industrial and Applied Mathematics) that mathematicians have discovered the challenges in "mathematical chemistry problems" and protein folding, but many frontiers lie ahead.
Problem Classification
The available optimization algorithms are classified according to the features of the target problem. The objective function to be minimized (or maximized) may be formulated in terms of integer variables (discrete optimization), integers in permutations (combinatorial optimization), continuous real numbers (continuous optimization), or both continuous real numbers and integers (mixed integer optimization). Examples from these four classes involve, respectively, order planning for organizations (the integers may denote, for example, the number of units of each item to be purchased monthly for a restaurant); the traveling salesman problem (the ordered list of N integers represents a cyclical itinerary for visiting N cities); molecular structure prediction (the real numbers may denote nuclear or electronic positions of the particles, or a set of internal variables describing the molecular system); and airline crew scheduling (the integers may identify particular flight routes and the real numbers may refer to the hours of shift for the flight crew). For computational chemistry, continuous optimization is the most important type of problem.
In addition to the nature of the control (or independent) variables, the objective function may be linear, quadratic, or nonlinear (the latter in varying extent). The problem may be formulated as unconstrained or constrained, with constraints involving equality or inequality conditions, which may be linear, quadratic, or nonlinear. Thus, for the above examples, constrained formulations may introduce upper and lower bounds for the Cartesian positions or specified values for certain internal variables that should remain fixed; the airline crew scheduling problem will incorporate into the optimization formulation the total number of scheduled flights, lower and upper bounds for the lengths of shifts, enforced limits on gaps between transatlantic flights, and so on. In addition to functional form and constraints, other important considerations involve the cost of evaluating the objective function and the availability (or lack) and associated cost of derivatives. In some cases, the derivatives may be discontinuous, and special techniques may be required. Derivative information can often be exploited significantly for the optimization algorithm, but the benefits must be balanced with the additional costs involved.
The Complexity of Computational Chemistry Problems
Optimization problems frequently arise in molecular and quantum mechanical calculations in chemistry. These problems are typical of optimization applications seeking favorable configurational states of a physical system. The large-scale nature of these problems together with the lack of convexity rules out exhaustive sampling in the feasible space except for very small systems. Therefore, clever optimization methods are a necessity, and their improvement translates into the ability to model larger physical systems and generate important structural predictions.
The expense of calculating the function and the associated derivatives also introduces difficulties that limit the type of algorithm that may be utilized. In many molecular mechanics applications, it may be tedious but possible to calculate the derivatives; often, the additional computational cost involved in computing the gradient is only a small factor more (e.g., 4 to 5) than computing the function (and guaranteed by automatic differentiation, which also saves coding efforts; see Box 4.5).
Computational intensity often stems from the long-range interactions among the N particles in the system (e.g., Coulombic forces). In molecular mechanics, the direct evaluation requires on the order of N2 operations, and even if a cutoff radius is introduced, computation of the nonbonded terms dominates computation time. Implementation of fast particle methods (Greengard, 1994) in molecular mechanics and dynamics calculations (Grubmüller et al., 1991; Board et al., 1992) is clearly important for reducing the severity of this problem and allowing more accurate representation of the
|
BOX 4.5 Automatic Differentiation Automatic differentiation, essentially a new algebraic construct (Rall, 1981; Griewank, 1988; Griewank and Corliss, 1991), provides a way to compute exact derivatives of a function whose calculation is expressed by a computer program. This technique may be useful for minimization of computational chemistry problems. Finite-difference techniques have been used for this purpose for a long time, but they require judicious choices in the finite-difference interval (Gill et al., 1983a); even with optimal choices, errors are inevitable in regions where the gradient is very small or in those where function curvature changes very rapidly. Finite differences also become very expensive in large dimensions, unless partial separability is exploited. There have been some "computer algebra" approaches based on symbolic computations (e.g., packages like Macsyma, Mathematica, or Maple) that can actually handle some differentiation tasks when the functional form is specified. Parenthetically, the reduction in mathematical errors and ready availability of graphics due to such symbolic computing tools have enhanced productivity in a number of areas of chemistry. However, while simplifying the programmer's work considerably, symbolic programs are not practical to use in the context of large-scale computer programs that require repeated evaluation and differentiation of a complex function. Moreover, this approach cannot be applied to full Fortran, C, or C++ programs directly, only to simplified or special syntax. In contrast to finite differences and symbolic algebra, the more recent approach of automatic differentiation is based on compiler techniques. Specifically, compiler transformations are applied to compute rigorously the derivative of a function defined by a program. The basic idea is to use the chain rule from calculus to compute the derivative of a composition of functions. Mathematically, this is similar to using symbolic algebra, but the chain rule is applied to the numerical intermediate results instead of to the expressions themselves, which makes it much more efficient. Automatic differentiation can be applied to complete programs including common blocks, equivalence statements, GOTO statements, and other features beyond the scope of existing symbolic algebra systems. Any code can be viewed as such a composition of elementary functions and algebraic operations, with the dependencies of one variable upon another being traced with modern compiler techniques. A code may have conditional branches that depend on the values of the independent variable (either explicitly or implicitly). The differentiation software must generate corresponding conditional branches. Originally, packages were developed for programs written in C and C++, but recent efforts have extended this to include Fortran programs as well (Bischof et al., 1992). Because the derivatives are expressed in exact symbolic form, their calculation is subject only to rounding errors. However, if a function is nondifferentiable at some point, it is not entirely clear what the result of automatic differentiation will be; in many cases, it corresponds to the derivative computed from one side of the nondifferentiability. If a function is defined by table-lookup, then the derivative returned by automatic differentiation may well be zero. Some cases of anomalous behavior in differentiating specific codes are the subject of ongoing research. Significantly, automatic differentiation techniques turn out to be competitive with the finite difference approach computationally. Their application to computational chemistry codes is just beginning. |
long-range interactions; the advantage of such an approach has already been demonstrated in other scientific applications (Greengard, 1994), for example in the context of integral equations in engineering problems (Nabors et al., 1994).
The multiple-minimum problem is a severe hurdle in many large-scale optimization applications. The state of the art today is such that only for small and reasonable problems do suitable algorithms exist for finding all local minima for linear and nonlinear functions. For larger problems, however, many trials are generally required to find local minima, and finding the global minimum cannot be ensured. These features have prompted research in conformational-search techniques independent of, or in combination with, minimization (Leach, 1991). To illustrate, consider a simple model for an alkane chain of m units (residues). From combinations or rough partitions in favorable structures of the individual building blocks, the number of possible starting points produces 3m starting configurations. For polypeptides and polynucleotides, the flexibility of the monomer (building block) configurations increases, producing a rough range of 10m to 25m reasonable starting points by coarse subdomain partition (e.g., combinations of typical side chain, main chain, backbone, or sugar dihedral angles). Exhaustive searches are clearly not feasible.
A molecular configuration is described by a list of numbers that specifies the relative position of the atoms in space. By definition, the configuration is unchanged when the molecule as a whole is subjected to rigid-body motion (translation or rotation). If the molecule consists of N atoms, 3N-6 numbers are required to specify its configuration uniquely. These numbers may consist of 3N-6 Cartesian positions (with 6 values fixed for uniqueness) or some combination of bond lengths, bond angles, and dihedral angles (angles defining the rotation between two groups with respect to the bond connecting them). The term conformation is typically used by chemists to describe the spatial configuration of a molecular system—strictly speaking, one with fixed bond lengths and valence angles.
The buildup technique is a related configurational search strategy, used in studies of proteins (Pincus et al., 1982) and nucleic acids (Hingerty et al., 1989). Reasonable starting points are constructed by combining minima of conformational building blocks. This rational strategy has performed rather well in practice, but there is no guarantee that all biologically important local minima, much less the global minimum, are revealed. One of the problems is the nonlocal nature of the interactions in the folded macromolecule. That is, segments far apart in the linear sequence will make close contact upon folding; thus, the collective minimum may not correspond to any minima of the constituent building blocks. Furthermore, the number of starting points is still exponential in the number of building blocks. This buildup technique might be an interesting mathematical area to explore further, perhaps through techniques of interval analysis (see below under global optimization methods).
Molecular dynamics, discussed on pages 54–58, can also be viewed as a technique for obtaining structural information (e.g., mean atomic fluctuations, dynamical pathways, isomerization rates) that is complementary to potential energy minimization. While in theory information on all thermally accessible states should be observable, the restriction of the integration time step to a very small value with respect to time scales of collective biomolecular motions limits the scope of molecular dynamics in practice.
Local Optimization Methods
Local methods are defined by an iterative procedure that generates iterates {x0, x1, ..., Xk,... } intended to converge to a local minimum x* from a given x0. Their performance is clearly sensitive to the choice of starting point in addition to search direction and algorithmic details. In the
line-search subclass, a search vector pk is computed at each step by a given strategy, and the objective function f is minimized approximately along that direction so that ''sufficient decrease" is obtained (see, e.g., Dennis and Schnabel, 1983; Luenberger, 1984). In trust-region approaches, a local quadratic model of the function is minimized at every step using current Hessian information, and an optimal step is chosen to lie within the "trust region" of the quadratic model (Dennis and Schnabel, 1983).
Local deterministic optimization methods have experienced extensive development in the last decade (e.g., Nocedal, 1991; Wright, 1991). Studies have produced a range of robust and reliable techniques tailored to problem size, smoothness, complexity, and memory considerations. Many variants of Newton's method have been produced that extend applicability far beyond small or sparse problems. Nonderivative methods are generally not competitive, but significant developments have been made in nonlinear conjugate gradient (CG) methods (generally recommended for very large problems whose function is very expensive to evaluate) and Newton methods.
The classes and extensions of Newton's method, the prototype of second-derivative algorithms, include discrete Newton, quasi-Newton (QN) (also termed variable metric), and truncated Newton (TN) (e.g., Dennis and Schnabel, 1983; Gill et al., 1983b). Historically, because of the O(n2) memory requirements, where n is the number of variables in the objective function, and the O(n3) computation associated with solving a linear system directly, Newton methods have been most widely used (1) for small problems, (2) for problems with special sparsity patterns, or (3) when near a solution, after a gradient method has been applied. Fortunately, advances in computing technology and algorithmic developments have made the Newton approach feasible for a wide range of problems. Indeed, effective strategies have been tailored to available storage and computation, exhibiting good performance in theory and practice, and this trend will undoubtedly intensify.
Two specific classes are emerging as the most powerful techniques for large-scale applications: limited-memory quasi-Newton (LMQN) and truncated Newton methods. LMQN methods attempt to retain the modest storage and computational requirements of CG methods while approaching the superlinear convergence properties of standard (i.e., full memory) QN methods (Gilbert and Lemaréchal, 1989; Liu and Nocedal, 1989; Nash and Nocedal, 1991; Zou et al., 1993). Similarly, TN algorithms attempt to retain the rapid quadratic convergence rate of classic Newton methods while making computational requirements feasible for large-scale functions (Dembo and Steihaug, 1983; Nash, 1985; Schlick and Overton, 1987). With advances in automatic differentiation (see Box 4.5), the appeal of these methods will undoubtedly increase even further (Dixon, 1991).
Both limited-memory QN and TN methods are promising for computational chemistry problems. Moreover, they can be adapted to both constrained and unconstrained formulations and can exploit the special composition (distinct components) of the potential energy function to accelerate convergence (Derreumaux et al., 1994). This issue involves a natural separation of the objective function into components of differing complexity (e.g., local and nonlocal interactions). This special composition can be exploited to construct banded or other sparse preconditioners in the context of CG and TN. Such problem tailoring requires some familiarity with the algorithmic modules and also demands knowledge of the theoretical and practical strengths and weaknesses of the different minimization methods. With rapidly growing improvements in high-performance vector and massively parallel machines, application-tailored software may be even more important in combination with parallel architectures whose design is motivated by specific applications.
Global Optimization Methods
In their attempt to find a global rather than local minimum, global optimization methods tend to explore larger regions of function space (see, e.g., Dixon and Szegö, 1975; Floudas and Pardalos, 1991). The global minimum of a function can be sought through two classes of approaches:
deterministic and stochastic. Deterministic methods usually require the objective function to satisfy certain smoothness properties; they construct a sequence of points converging to lower and lower local minima. Ideally, they attempt to "tunnel" through local barriers. Local minimization methods are often required repeatedly in the framework; hence, developments in local methods are likely to have an important impact on global techniques as well. Computational effort tends to be very large, and a guarantee of success can be obtained only under specific assumptions.
Stochastic global methods, on the other hand, involve systematic manipulation of randomly selected points (Nemhauser et al., 1989; Rinnooy Kan and Timmer, 1989; Schnabel, 1989; Törn and Zilinskas*, 1989; Byrd et al., 1990). Success can be guaranteed only in an asymptotic, stochastic sense, although in practice many applications are very promising.
In the early days of global optimization (mid-1970s), most efforts focused on stochastic or heuristic approaches (Dixon and Szegö, 1975). In chemical applications, simulated annealing (Metropolis et al., 1953; Kirkpatrick et al., 1983; Dekkers and Aarts, 1991) is an appealing method of this class and is effective for small to medium molecular systems. It is also very easy to implement and generally requires no derivative computations. Indeed, there has been a wide application of this method to chemical systems.
More recent efforts have focused also on deterministic global optimization methods. Interesting examples include the tunneling method (Levy and Gomez, 1985; Levy and Montalvo, 1985) and several innovative deterministic approaches in chemical applications (Purisima and Scheraga, 1986; Piela et al., 1989; Scheraga, 1992; Shalloway, 1992). In particular, in the mathematical community, two recent powerful methods have been identified that might be useful to chemical applications. One exploits convex properties and is based on differences of convex functions (Pardalos and Rosen, 1987; Horst and Tuy, 1993); the other is based on interval analysis (Hansen, 1980, 1992; Neumaier, 1990; Schnepper and Stadtherr, 1993). The convexity approach has been successful for global quadratic problems of up to approximately 300 variables and 50 constraints (Pardalos and Rosen, 1987; Horst and Tuy, 1993). Interval analysis, a field little known even to mathematicians, was pioneered by Hansen, among others. It involves computation of strict bounds to bracket the global minimum of a function. The algorithms involve various branch and bound techniques that recursively split the configuration space, aiming at bracketing the minimum as tightly as possible. Other information, such as bounds on derivatives, may also be generated. This class of methods can be applied to the solution of nonlinear systems, as well as global constrained and unconstrained optimization. However, these methods require second-derivative information (Hessians for optimization problems) and, moreover, the inverse of a preconditioning matrix to produce realistic bounds. For these reasons, interval analysis has been applied only to relatively small problems thus far. However, future research may be promising with preconditioning techniques that are now well developed for local optimization.
Perspective
In sum, the optimization applications that arise in computational chemistry offer challenging and rewarding problems to mathematicians. There is a need for the development of both local and global methods (the latter stochastic as well as deterministic) and for transferring the technology rapidly from one discipline to another. In particular, optimization schemes will be more effective when all available chemical information (e.g., function separability, availability of derivatives, additional experimental data) is taken into account in design of the algorithm, as is possible by preconditioning in both limited-memory quasi-Newton and truncated-Newton algorithms. Multigrid approaches (Kuruvila et al., 1994) and functional transformations (e.g., Piela et al., 1989; Wu, 1994) appear promising to global optimization problems in computational chemistry, and further developments might be fruitful.
Areas of mathematics that may have an important impact on the field are interval analysis and automatic differentiation. While the field of deterministic global optimization is still in its infancy in terms of general large-scale applicability, it is anticipated that the exploitation of vector and massively parallel computing environments for algorithm design will lead to significant progress in the coming years. Technological advances will clearly improve the range of global optimization strategies that can be considered, but greater efforts in parallel programming skills will be essential so that these high-performance platforms will have a true impact on these important scientific problems.
References
Bischof, C.H., A. Carle, G.F. Corliss, A. Griewank, and P. Hovland, 1992, ADIFOR: Generating derivative codes from FORTRAN programs, Scientific Programming 1:129.
Board, J.A., Jr., J.W. Causey, T.F. Leathrum, Jr., A. Windemuth, and K. Schulten, 1992, Accelerated molecular dynamics simulations with the parallel fast multiple algorithm, Chem. Phys. Lett. 198:8994.
Byrd, R.H., C.L. Dert, A.H.G. Rinnooy Kan, and R.B. Schnabel, 1990, Concurrent stochastic methods for global optimization, Math. Program. 46:129.
Ciarlet, P.G., 1989, Introduction to Numerical Linear Algebra and Optimization, Cambridge University Press, Cambridge.
Dekkers, A., and E. Aarts, 1991, Global optimization and simulated annealing, Math. Program. 50:367–393.
Dembo, R.S., and T. Steihaug, 1983, Truncated-Newton algorithms for large-scale unconstrained optimization, Math. Prog. 26:190–212.
Dennis, Jr., J.E., and R.B. Schnabel, 1983, Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Prentice-Hall, Englewood Cliffs, N.J.
Derreumaux, P., G. Zhang, B. Brooks, and T. Schlick, 1994, A truncated Newton minimizer adapted for CHARMM and biomolecular applications, J. Comput. Chem. 15:532–552.
Dixon, L.C.W., 1991, On the impact of automatic differentiation on the relative performance of parallel truncated Newton and variable metric algorithms, SIAM J. Opt. 1:475–486.
Dixon, L.C.W., and G.P. Szegö, 1975, Towards Global Optimization, Elsevier, New York.
Fletcher, R., 1987, Practical Methods of Optimization, Second Edition, John Wiley & Sons, New York.
Floudas, C.A., and P.M. Pardalos, eds., 1991, Recent Advances in Global Optimization, Princeton Series in Computer Science, Princeton University Press, Princeton, N.J.
Gilbert, J.C., and C. Lemaréchal, 1989, Some numerical experiments with variable-storage quasi-Newton algorithms, Math. Prog. 45:407–435.
Gill, P.E., W. Murray, M.A. Saunders, and M.H. Wright, 1983a, Computing forward-difference intervals for numerical optimization, SIAM J. Sci. Stat. Comput. 4:310–321.
Gill, P.E., W. Murray, and M.H. Wright, 1983b, Practical Optimization, Academic Press, N.Y.
Greengard, L., 1994, Fast algorithms for classical physics, Science 265:909–914.
Griewank, A., 1988, On automatic differentiation, in Mathematical Programming 1988, Kluwer Academic Publishers, Norwell, Mass. pp. 83–107.
Griewank, A., and G.F. Corliss, eds., 1991, Automatic Differentiation of Algorithms: Theory, Implementation, and Application, Society for Industrial and Applied Mathematics, Philadelphia, Pa.
Grubmüller, H., H. Heller, A. Windemuth, and K. Schulten, 1991, Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions , Mol. Simul. 6:121–142.
Hansen, E.R., 1980, Global optimization using interval analysis—The multidimensional case, Numer. Math. 34:247–270.
Hansen, E.R., 1992, Global Optimization Using Interval Analysis, Dekker, New York.
Hingerty, B.E., S. Figueroa, T.L. Hayden, and S. Broyde, 1989, Prediction of DNA structure from sequence: A buildup technique, Bidpolymers 28:1195–1222.
Horst, R., and H. Tuy, 1993, Global Optimization: Deterministic Approaches, second edition, Springer, Berlin.
Kirkpatrick, S., C.D. Gelatt, Jr., and M.P. Vecchi, 1983, Optimization by simulated annealing, Science 220:671–680.
Kuruvila, G., S. Ta'asan, and M.D. Salas, 1994, Airfoil optimization by the one shot method, Lecture Notes on Optimum Design Methods for Aerodynamics, AGARD FDP/VKI Special Course, von Karman Institute for Fluid Dynamics, Rhode-Saint-Genese, Belgium, April, 2529.
Leach, A.R., 1991, A survey of methods for searching the conformational space of small and medium-sized molecules, in Reviews in Computational Chemistry, Vol. II, K.B. Lipkowitz and D.B. Boyd, eds., VCH Publishers, New York.
Levy, A.V., and S. Gomez, 1985, The tunneling method applied to global optimization, in Numerical Optimization 1984, P.T. Boggs, R.H. Byrd, and R.B. Schnabel, eds., SIAM, Philadelphia, pp. 213–244.
Levy, A.V., and A. Montalvo, 1985, The tunneling algorithm for the global minimization of functions, SIAM J. Sci. Stat. Comput. 6:1529.
Liu, D.C., and J. Nocedal, 1989, On the limited memory BFGS method for large scale optimization, Math. Program. 45:503–528.
Luenberger, D.G., 1984, Linear and Nonlinear Programming, Second Edition, Addison-Wesley, Reading, Mass.
Metropolis, N., A.W. Rosenbluth, M.N. Rosenbluth, A.H. Teller, and E. Teller, 1953, Equation of state calculations by fast computing machines , J. Chem. Phys. 21:1087–1092.
Nabors, K., F.T. Korsmeyer, F.T. Leighton, and J. White, 1994, Multipole accelerated preconditioned iterative methods for three-dimensional potential integral equations of the first kind, SIAM J. Sci. Comput. 15:713–735.
Nash, S.G., 1985, Solving nonlinear programming problems using truncated-Newton techniques in SIAM Numerical Optimization 1984, P.T. Boggs, R.H. Byrd, and R.B. Schnabel, eds., Philadelphia, pp. 119–136.
Nash, S.G., and J. Nocedal, 1991, A numerical study of the limited memory BFGS method and the truncated-Newton method for large-scale optimization, SIAM J. Opt. 1:358–372.
Nemhauser, G.L., A.H.G. Rinnooy Kan, and M.J. Todd, eds., 1989, Handbook in Operations Research Management Science, Vol. 1, Elsevier Science Publishers (North-Holland), Amsterdam.
Neumaier, A., 1990, Interval Methods for Systems of Equations, Cambridge University Press, Cambridge.
Nocedal, J., 1991, Theory of algorithms for unconstrained optimization, Acta Numerica 1:199–242.
Pardalos, P.M., and J.B. Rosen, 1987, Constrained Global Optimization: Algorithms and Applications, Lecture Notes in Computer Science 268, Springer, Berlin.
Piela, L., J. Kostrowicki, and H.A. Scheraga, 1989, The multiple-minima problem in conformational analysis of molecules. Deformation of the potential energy hypersurface by the diffusion equation method, J. Phys. Chem. 93:3339–3346.
Pincus, M., R. Klausner, and H.A. Scheraga, 1982, Calculation of the three-dimensional structure of the membrane bound portion of melittin from its amino acids, Proc. Natl. Acad. Sci. USA 79:51075110.
Purisima, E.O., and H.A. Scheraga, 1986, An approach to the multiple-minima problem by relaxing dimensionality, Proc. Natl. Acad. Sci. USA 83:2782–2786.
Rall, L.B., 1981, Automatic Differentiation—Techniques and Applications, Lecture Notes in Computer Science 120, Springer-Verlag, Berlin.
Rinnooy Kan, A.H.G., and G.T. Timmer, 1989, Global optimization, in Handbooks in Operations Research and Management Science, Vol. 1, G.L. Nemhauser, A.H.G. Rinnooy Kan, and M.J. Todd, eds., Elsevier Science Publishers (North-Hoiland), Amsterdam.
Scheraga, H.A., 1992, Predicting three-dimensional structures of oligopeptides, in Reviews in Computational Chemistry, Vol. III, K.B. Lipkowitz and D.B. Boyd, eds., VCH Publishers, New York, pp. 73–142.
Schlick, T., 1992, Optimization methods in computational chemistry, in Reviews in Computational Chemistry, Vol. III, K.B. Lipkowitz and D.B. Boyd, eds., VCH Publishers, New York, pp. 171.
Schlick, T., and A. Fogelson, 1992, TNPACK—A truncated Newton minimization package for large-scale problems: I. Algorithm and usage, and II. Implementation examples, ACM Trans. Math. Softw. 14:46–111.
Schlick, T., and M. Overton, 1987, A powerful truncated Newton method for potential energy minimization, J. Comput. Chem. 8:1025–1039.
Schnabel, R.B., 1989, Sequential and parallel methods for unconstrained optimization, in Mathematical Programming, M. Iri and K. Tanabe, eds., Kluwer Academic Publishers, Norwell, Mass., pp. 227–261.
Schnepper, C.A., and M.A. Stadtherr, 1993, Application of a parallel interval Newton/generalized bisection algorithm to equation–based chemical process flowsheeting, Interval Computations 4:40–64.
Shalloway, D., 1992, Application of the renormalization group to deterministic global minimization of molecular conformation energy functions, J. Global Opt. 2:281–311.
Törn, A., and A. Zilinskas*, 1989, Global Optimization, Lecture Notes in Computer Science 350, Springer-Verlag, Berlin.
van Laarhoven, P.J.M., and E.H.L. Aarts, 1987, Simulated Annealing: Theory and Applications, D. Reidel, Dordrecht.
Wright, M.H., 1991, Interior methods for constrained optimization, Acta Numerica 1:341–407.
Wu, Z., 1994, The Effective Energy Transformation Scheme as a Special Continuation Approach to Global Optimization with Application to Molecular Conformation, Argonne National Laboratory report MCS-P4420-694, July.
Zou, X., I.M. Navon, F.X. Le Dimet, A. Nouailler, and T. Schlick, 1993, A comparison of efficient large-scale minimization algorithms for optimal control applications in meteorology, SIAM J. Opt. 3:582–608.
Locating Saddlepoints
The potential energy hypersurface of an individual molecule describes its minimum energy (i.e., stable) states as well as the transition structures linking these states. In other words, the local minima on the potential energy surface correspond to the minimum energy conformations of a molecule, and first-order saddlepoints on the surface correspond to transition states. These concepts can be extended to interacting molecular assemblies as well (e.g., clusters, biomolecular systems with solvent).
With the advent of modern computational techniques, it has become possible to exhaustively search the potential energy surface of individual molecules containing fewer than about 12 rotatable bonds (i.e., degrees of freedom for the dihedral angles that define molecular geometry, along with bond lengths and bond angles, in internal coordinate space) when classical (molecular mechanics-based) potential energy functions are employed. The previous section has broadly described the issues and various algorithmic techniques for finding local and global minima on such complex multidimensional energy surfaces. This section focuses on another aspect of conformational searches: the identification of saddlepoints and their connection to chemical reactions.
In addition to a description of the conformational properties of individual molecules, the potential energy surface can be employed to describe the energetics of chemical reactions. Therefore, searches on the potential energy hypersurface of a molecule can extend to molecular reactions as well (Eksterowicz and Houk, 1993). Reactants and products correspond to energy minima, whereas transition states linking products to reactants usually correspond to first-order saddlepoints on the energy surface (although unusual symmetries can produce higher-order transition states, including those of the "monkey-saddle" type). Thus, the location of stationary points (particularly minima and saddlepoints) on potential energy surfaces represents an important and challenging problem in computational chemistry.
In chemical applications, special conformational-space search methods have been devised for locating minima on molecular mechanics-based potential energy surfaces. These methods include stochastic (Saunders, 1987; Chang et al., 1989; Ferguson and Raber, 1989) and deterministic, gridbased (Motoc et al., 1986; Lipton and Still, 1988; Dammkoehler et al., 1989) approaches. Yet, with rare exception (Kolossvary and Guida, 1993), conformational searches have not been performed in such a way that saddlepoints are located. Nonetheless, the utility and indeed necessity of determining the conformational transition states that link these minima have recently been emphasized (Anet, 1990). Whereas in the past, conformational searches have been synonymous with location of energy minima, it is clear that in order to adequately study the conformational properties of molecules it is essential to locate first-order saddlepoints as well.
Significant effort has addressed the problem of locating transition states on potential energy surfaces derived from quantum mechanics calculations. A number of algorithms have been developed such as those that rely on eigenvector-following techniques (Cerjan and Miller, 1981; Simons et al., 1983, 1984; Bell and Crighton, 1984; Simons, 1985; Baker, 1986). In these methods one begins a
saddlepoint search at or near a local minimum that is found by standard minimization techniques. A spectral decomposition is performed to find all the normal modes of the system (mass scaled eigenvalues and associated eigenvectors of the Hessian matrix (i.e., second-derivative matrix of the potential energy); then one of the normal modes is selected and followed in an ''uphill" direction (i.e., a direction that leads to an increase of potential energy) until a saddlepoint is located. Evaluation of the energy gradient and Hessian matrix at each step of the search is performed until a point on the surface is located at which the gradient is zero and the Hessian possesses only one negative eigenvalue. In another approach, the linear synchronous transit method (Halgren and Lipscomb, 1977) has been employed to aid in the location of saddlepoints. It locates a maximum along a path connecting two structures and thus can be used to provide an initial guess for the transition state structure that connects them. Methods that find the location of saddlepoints by beginning the search at points on the potential energy surface that are of higher energy than the saddlepoint one wishes to locate have also been described (Berry et al., 1988). Recent developments (Jorgensen et al., 1988; Culot et al., 1992) have led to improved efficiency in locating transition states in calculations based on quantum mechanics-derived potential energy surfaces. Nonetheless, the aforementioned saddlepoint searches sometimes fail to converge, or they converge to critical points that are minima. Clearly, more robust algorithms are still needed, and this is an area that mathematical optimizers may find very interesting.
It is conceivable that algorithms for locating transition states on potential energy surfaces derived from calculations based on quantum mechanics could be employed for the location of conformational transition states on molecular mechanics-derived potential energy surfaces once the minima have been located. However, these algorithms have generally been used to study mechanisms of chemical reactions and have not been adequately tested for locating such conformational transition structures. In a typical conformational search procedure, the potential energy surface is scanned randomly or systematically and a large number of trial structures are generated for energy optimization. These structures can be severely "distorted" geometrically in the sense that bond lengths and angles lie out of the ranges observed experimentally, and van der Waals radii of atoms may overlap. These structures must then be optimized by the standard, "greedy" descent methods of local minimization toward a local minimum or toward a saddlepoint. However, for the quantum chemical calculation of a reaction mechanism, the reactant and product are usually known, and uphill movement toward the interconnecting saddlepoint is sought.
Conformational search procedures that locate first-order saddlepoints and minima with equal efficiency would be of enormous utility. Even though advances in this area have been slow, some progress has been achieved. For example, the so-called self-penalty walk method (Czerminski and Elber, 1990) provides an example of an algorithm for the calculation of reaction paths in complex molecular systems when molecular mechanics-derived potential energy functions are employed. However, it is likely that additional work will be required to develop methods for the efficient conformational searching of saddlepoints. New algorithms for conformational searches in which firstorder saddlepoints are efficiently located are clearly urgently needed.
References
Anet, F.A.L., 1990, Inflection points and chaotic behavior in searching the conformational space of cyclononane, J. Am. Chem. Soc. 112:71–72.
Baker, J., 1986, An algorithm for the location of transition states J. Comput. Chem. 7:385.
Banerjee, A., N. Adams, and J. Simons, 1985, Search for stationary points on surfaces, J. Phys. Chem. 89:52.
Bell, S., and J.S. Crighton, 1984, Locating transition states, J. Chem. Phys. 80:24–64.
Berry, R.S., H.L. Davis, and T.L. Beck, 1988, Finding saddles on multidimensional potential surfaces, Chem. Phys. Lett. 147:13.
Cerjan, C.J., and W.H. Miller, 1981, On finding transition states, J. Chem. Phys. 75:2800.
Chang, G., W.C. Guida, and W.C. Still, An internal coordinate Monte Carlo method for searching conformational space, J. Am. Chem. Soc. 111:43–79.
Culot, P., G. Dive, V.H. Nguyen, 1992, Theor. Chim. Acta 82:189.
Czerminski, R., and R. Elber, 1990, Self-avoiding walk between two fixed points as a tool to calculate reaction paths in large molecular systems, Int. J. Quantum Chem. 24:67.
Dammkoehler, R., S.F. Karasek, E.F.B. Shands, and G.R. Marshall, 1989, Constrained search of conformational hyperspace, J. Computer-Aided Molec. Design 3:3.
Eksterowicz, J.E., and K.N. Houk, 1993, Transition-state modeling with empirical force fields, J. Chem. Rev. 93:24–39.
Ferguson, D.M., and D.J. Raber, 1989, A new approach to probing conformational space with molecular mechanics: Random incremental pulse search , J. Am. Chem. Soc. 111:43–71.
Halgren, T.A., and W.N. Lipscomb, 1977, Chemical Physics Letters 49:12–25.
Jorgensen, P., et al., 1988, Theor. Chim. Acta 73:55.
Kolossvary, I., and W.C. Guida, 1993, Comprehensive conformational analysis of the four- to twelve-membered ring cycloalkanes: Identification of the complete set of interconversion pathways on the MM2 potential energy hypersurface, J. Am. Chem. Soc. 115:21–07.
Lipton, M., and W.C. Still, 1988, The multiple minimum problem in molecular modeling. Tree searching internal coordinate conformational space, J. Comput. Chem. 9:343.
Motoc, I., R.A. Dammkoehler, D. Mayer, and J. Labanowslcki, 1986, Three-dimensional quantitative structure-activity relationships. I. General approach to the pharmacophore model validation, Quant. Struct.-Act. Relat. 5:99.
O'Neal, D., J. Simons, and H. Taylor, 1984, Potential surface walking and reaction paths for C2VBe + H2) Be + H2 → Be + 2H (1A1), J. Phys. Chem. 88:15–10.
Saunders, M., 1987, J. Am. Chem. Soc. 109:31–50.
Simons, J., P. Jorgensen, J. Ozment, H. Taylor, et al., 1983, Walking on potential-energy surfaces, J. Phys. Chem. 87:2745–2753.
Simons et al., 1984, J. Phys. Chem. 88:15–19.
Simons, J., N. Adams, A. Banerjee, and R. Shepard, 1985, Search for stationary-points on surface, J. Phys. Chem. 89:52–57.
Sampling of Minima and saddlepoints
Many problems in computational chemistry require a concise description of the large-scale geometry and topology of a high-dimensional potential surface. Usually, such a compact description will be statistical, and many questions arise as to the appropriate ways of characterizing such a surface. Often such concise descriptions are not what is sought; rather, one seeks a way of fairly sampling the surface and uncovering a few representative examples of situations on the surface that are relevant to the appropriate chemistry. Some specific examples include finding snapshots of crucial or typical configurations or movies of kinetic pathways. This allows what one might call an artistic description of the chemical situation. Such a description is often looked down upon by quantitative scientists as being "anecdotal," but it is important not to cut ourselves off from any route to understanding. To make this point one might compare the kinds of understanding of ancient cultures that are obtained from the numerous scholarly statistical studies of bookkeeping accounts and what we learn from the great paintings of the same periods, which give us different perspectives on social life. The main danger of such artistic representations is that one must have some guarantee that they do not simply represent a kind of beautiful propaganda for an incorrect qualitative viewpoint. Clearly, statistics must be used to validate such individual samples of a system's behavior.
Several chemical problems truly demand the solution of these mathematical problems connected with the geometry of the potential surface. Such a global understanding is needed to be able to picture long time scale complex events in chemical systems. One area in which this is clearly essential is the understanding of conformational transitions of biological molecules. The regulation of biological molecules is quite precise and relies on sometimes rather complicated motions of a biological molecule. The most well studied of these is the so-called allosteric transition in hemoglobin, but indeed, the regulation of most genes also relies on these phenomena. These regulation events involve rather long time scales from the molecular viewpoint. Their understanding requires navigating through the complete configuration space. Another such long time scale process that involves complex organization in the configuration space is biomolecular folding itself. By what process is the structure of a biological molecule determined? In order to function, enzymes require a fairly precise three-dimensional positioning of different chemical groups in the protein molecule. To achieve this precise positioning of only a few groups, the collective interactions of the rest of the molecule must conspire to form such a fairly rigid construction. Although the three-dimensional structures of protein molecules exhibit some symmetries, they are exquisitely complex, and in addition, the architectures of folded protein are formed from molecules that have no simple pattern in their one-dimensional sequence.
Understanding how the Brownian motion on an energy surface can funnel such a molecule to a very precise structure is a major puzzle requiring a global analysis of the many-dimensional energy surface. The global geometry of the potential energy surface also enters into the study of nonbiological chemical problems such as those involving the structure and mechanical properties of amorphous materials. While crystalline solids can be studied through the analysis of the ground state and the first few excited states, glasses and other amorphous materials have a huge number of local structural configurations. Unlike a typical liquid, however, these individual configurations last for incredibly long periods of time, and one must understand the statistics of the different minimal energy structures and the nature of the transitions between them in order to quantify the slow relaxations of such systems. The aging of amorphous materials in glasses shows that they do not obey the simple equilibrium statistical mechanical laws so often used to characterize simple materials. At the same time, these aging phenomena have great practical significance to the macroscopic properties (e.g., long time stability) of materials important to such applications as fiber optics. The local minima are the mathematically simplest objects to characterize statistically the potential energy surface. The
crucial questions here are first, what do the minima look like and, second, how many of the different kinds of minima exist on the surface? Sampling many minima of a potential energy surface can be carried out with gradient descent techniques, and a great deal has been learned about the qualitative structural characteristics of these minima for both biomolecules and glasses. The counting of minima seems to be of crucial importance as well, since at the phenomenological level, the kinetics of amorphous materials are highly correlated with their configurational entropy. At this point, no very good algorithm yet exists for doing this sort of counting in an objective and reliable way, even on a computer.
Statistical mechanics is the study of the collective behavior of large numbers of interacting particles. Properties of interests include those describing time-dependent, irreversible process. The basic principles of this discipline were laid down in the nineteenth century by Ludwig Boltzmann, James Clerk Maxwell, and Josiah Willard Gibbs.
The very deepest minima of systems can be characterized by using techniques superficially similar to those of thermodynamics and equilibrium statistical mechanics. Generalization of mean field theory for random Hamiltonians is used. The low-lying states of heteropolymeric biological macromolecules have been studied in this way. There is a very clear analogy to the phenomenon of broken ergodicity studied in spin glasses by the quasi-equilibrium statistical mechanical methods. The problem of broken ergodicity is one that is central to understanding the global topology of potential energy surfaces for such "random" systems. This problem plays a rule both in the issues discussed here of biological macromolecules and amorphous materials, and in other optimization problems as well. There are deep connections with the theory of NP-completeness, a fundamental question in theoretical computer science. The formal questions of broken ergodicity in spin glasses (i.e., the topology of low-energy states) have not been answered entirely unambiguously by experiment, and the question of the nature of the low-lying states is one that is still hotly debated. An important route to understanding this sort of broken ergodicity has been by the methods of rigorous statistical mechanics pioneered by mathematicians. It has been shown rigorously in some higher-dimensional problems that the broken ergodicity imagined in simple phenomenological theories of protein folding can, in fact, occur. It is still an open question, however, how ergodicity is broken for three-dimensional systems, spin glass systems, or for the random heteropolymers themselves.
Ergodicity is the capacity of a dynamical system spontaneously to sample all of its phase space.
One of the most interesting results of the theory of broken ergodicity based on quasi-equilibrium statistical mechanics is that the low-energy states of a typical Hamiltonian are related to each other in a fashion that is characterized by an ultrametric distance. This ultrametricity concept arose earlier in the study in pure mathematics. The ultrametric organization may well play a rule in the dynamics on such surfaces, and ultrametric hopping models have been widely discussed.
While the use of statistical energy surface topography is now coming to be accepted in the context of biomolecules, there is a still deeper mathematical question in its application to glasses. This question is, How does a Hamiltonian that is perfectly regular, having no explicit randomess, possess solutions that appear to be totally irregular and aperiodic? A long-standing issue for the purist has been whether even hard spheres have, as their most dense state, the simple regular packing characteristic of face-centered cubic (FCC) crystals. Recently a proof of this was announced, but it has apparently been retracted. In fact, for the three-dimensional situation there is little doubt from the experimental input that the dense state is in fact periodic. The question of the closest packings in
|
BOX 4.6 Comments on the Ambiguous Concept of ''Structure" for Complex Molecules and Macromolecules Owing to the special nature of their rules in life processes, biological macromolecules such as proteins, nucleic acids, and carbohydrates have evolved into systems exhibiting a high degree of structural diversity and complexity. Theoretical/Computational chemistry bears the responsibility of predicting, characterizing, and explaining the biological reasons for the three-dimensional shapes or "structures" adopted by those macromolecules. However, researchers should be aware (particularly on first entering this problem area) that the concept of "structure" has multiple interpretations that depend on the physical and chemical circumstances involved. As explained in the main text, prediction of the preferred structure adopted by any given molecule is usually reduced in principle, if not in practice, to the study of minima on a suitable energy surface in a multidimensional space of configurational coordinates. In many—but not all—cases, the global minimum corresponds to the biologically active structure, while higher-lying relative minima correspond to inactive denatured forms. The figure below shows, in simple cartoon fashion, three generic energy surfaces. The simplest (a) contains but a single minimum that would be easy to locate numerically. The next (b) shows multiple minima and requires more effort if a full classification of extrema is warranted by the problem it represents. Case (c) is most representative of the situation with biological macromolecules, with a vast array of minima arranged in basins or valleys over a wide range of length scales. In this last circumstance, the concept of "structure" depends in part on the level of accuracy that is warranted, and that level is strongly dependent on temperature. At very low temperature (e.g., a protein frozen in its aqueous medium), thermally excited vibrations will be so feeble that the system of protein and water molecules would be trapped in the vicinity of a single finegrained minimum. Raising the temperature stimulates transitions between neighboring microbasins, so the relevant notion of ''structure" entails the average configuration for the broadened distribution. A simple view would be that raising the temperature effectively smooths out the finer features of the complicated energy surface. This amounts to passage from (c) to (b) in the figure.  (a) simple 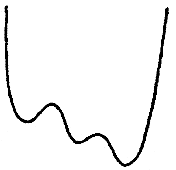 (b) complicated  (c) much more complicated |
|
In the vicinity of room temperature, where the aqueous medium is liquid, it is traditional to average over the solvent degrees of freedom and to utilize the resulting "free energy surface" for biological macromolecule studies. Consequently, the configuration space undergoes a reduction in dimensionality to that of just the macromolecule's flexible degrees of freedom. At the same time, the surface to be searched for minima becomes temperature dependent, so the number of minima it exhibits, where they are located, and indeed which is the absolute minimum can vary. Furthermore, interbasin transitions can produce substantial configurational fluctuations even in this reduced-dimensionality representation, requiring a correspondingly permissive definition of "structure." |
high-dimensional systems has many contacts with group theory and the theory of optimal coding.
The existence of quasicrystals has made the problem an even richer one since even the existence of such quasi-periodic structures was ruled out by "folk theorems" of physicists. It is likely that truly aperiodic crystals can, in principle, exist in three dimensions. An important argument for this is based on tiling theory. It has been shown that certain tiling problems are NP-complete. This implies that it is certainly very difficult to figure out whether a periodic packing of such a tiling is possible. Thus, it seems that the problem of totally aperiodic crystal phases for regular structures may be itself tied to the NP-completeness question.
The problem of transitions between minima on such a high-dimensional surface is in a still more primitive state than the characterization of minima. The search for minima is itself a relatively stable computational problem. The search for saddlepoints that connect individual minima is computationally much more difficult. This is certainly a consequence of the unstable mode at such saddlepoints. Despite numerous efforts, there are no entirely reliable methods for carrying out such a search. For many simple problems, finding a reasonably good transition state is possible, but these techniques become still more complicated and less reliable as system size increases. On the purely theoretical side, very simple models that relate the heights of barriers to the statistics of minima have been developed, but almost no truly rigorous work has been done. Simply characterizing the minima and the saddlepoints connecting a few of them does not give an entire description of significant processes on a complex energy landscape. It is clear that one must understand something more about the basin of attraction of any given minimum. If the nearby minima are not entirely uncorrelated, this basin of attraction will depend on their structure as well. A characterization of the size of such funnels in biomolecular problems is essential to understanding protein folding.
Similarly, in many such complex problems it has been imagined that specific kinetic pathways are important. Again some work has already been done on the question of how specific pathways can emerge on a statistical energy landscape. These ideas are, however, based on the quasi-equilibrium statistical mechanics of such systems, and there are many questions about the rigor of this approach. Similarly, a good deal of work has been carried out to characterize computationally pathways on complicated realistic potential energy surfaces.
Techniques based on path integrals have been used to good effect by Elber in studying the recombination of ligands in biomolecules and in the folding events involved in the formation of a small helix from a coiled polypeptide. These techniques tend to focus on individual optimal pathways, but it is also clear that sets of pathways are very important in such problems. How these pathways are related to each other and how to discover them and count them is still an open computational challenge.
|
BOX 4.7 Implications of Dynamical Chaos at the Classical Level A large part of modern computational chemistry is based on the solution of the equations of classical mechanics for many-body systems. For these problems, the standard numerical integration techniques found in classic textbooks only provide a simple framework for application and analysis. This is because most of the theory of numerical analysis provides criteria for long-time stability for these smaller systems with regular dynamics. Nevertheless, it is clear that for most many-body chemical systems, the differential equations may have chaotic solutions primarily. Thus, it is of little use to talk about the stability of an individual trajectory for tong times, particularly when methods with some stochastic elements (e.g., Langevin dynamics) are involved. A necessary mathematical advance is an understanding of error estimation and long-time stability for chaotic systems. In fact, one seeks a way of characterizing the accuracy in some statistical sense from such a simulation, or collection of simulations, since an individual trajectory's details are certainly predicted incorrectly. The classical theory of error estimates in numerical analysis is clearly inadequate for most purposes and the theory of long-time stability for complex systems is rather at its infancy (Stuart and Humphries, 1994). A most striking example is in the old simulations of hard-sphere molecular dynamics showing trajectories for times encompassing many, many collisions of a dilute gas (e.g., Alder and Wainwright, 1970). One can easily show that the trajectories were numerically inaccurate beyond the limit of machine precision, even after only 10 collisions. Nevertheless, when the velocity correlation function was computed, it exhibited a long-time tail that persisted out to 30 collision times, and this long-time tail's form as well as amplitude agreed precisely with kinetic theory calculations. Thus, statistical properties can be accurate even when individual trajectories are entirely incorrect. A similar problem enters when one considers the use of "stochastic dynamics" methods in simulation (e.g., pseudorandom forces are added to the systematic force to mimic a thermal reservoir). When only a subsystem of a larger system (e.g., biomolecule pius solvent) is being studied, the appropriate equations of motion are stochastic or Langevin equations. The most familiar example is the diffusion of biomolecules in water. The theory of quadratures for such stochastic equations has long been of interest, but comprehensive analyses of associated error estimates have been developed mainly from a relatively simple point of view, such as via analysis of harmonic oscillators (Pastor et ai., 1988; Tuckerman and Berne, 1991). However, there are many important mathematical issues that arise in this connection. What is the meaning of error analysis in this stochastic framework? Is it appropriate to compare results to parallel approaches, such as molecular dynamics, where the stochastic forces are zero? Are asymptotic results as the time step approaches zero relevant to practical problems? As discussed elsewhere in this report, the complexity of biomolecular systems involves multiple conformations and numerous biologically relevant pathways. And, given the severity of the time step problem in molecular dynamics (see pages 54–58), how can qualitative and quantitative theories for evaluating simulation results be merged? Clearly, there is a strong need for both aspects, but one can imagine that different numerical models in combination with different integration or propagation methods could be designed to address various aspects of the dynamical problems. Therefore, an organized theory for simulation evaluation, including local error analysis, longtime behavior, and some kind of broader or "global" framework for evaluation, would be extremely valuable. Such a theory could clearly aid in evaluating new models and methods as they arise, identifying the appropriate tests for the various simulation protocols, and putting in perspective the biological results that may emerge from any computer simulation. References Alder, B.J., and T.E. Wainright, 1970, Phys. Rev. A 1:1821. Pastor, R.W., B.R. Brooks, and A. Szabo, 1988, An analysis of the accuracy of Langevin and molecular dynamics algorithms, Mol. Phys. 65:14091419. Stuart, A.M., and A.R. Humphries, 1994, Model problems in numerical stability theory for initial value problems, SIAM Review 36:2262571. Tuckerman, M., and B.J. Berne, 1991, J. Chem. Phys. 95:4389. |
Efficient Generation of Points That Satisfy Physical Constraints in a Many-Particle System
Prototypical Problem
Consider N particles in a cube in three-dimensional space, each with x, y, and z coordinates in the range [O, L]. The state of the system is then given by specifying the positions ri of all N points.
In the statistical mechanics modeling of condensed phases, one typically is interested in restricted sets of particle configurations. For instance, one's interest is often restricted to only those states for which
Imagine that the points represent the locations of the centers of hard spheres of diameter unity. The conditions state that the hard spheres do not overlap one another; that is, the spheres repel each other strongly when they are close together, so that each center-center distance must be greater than unity.
For the present problem, we are interested in the regime where N is large, of the order of 102 to 106. The volume is large enough so that N/L3 is in the range (0,21/2). In the actual problem of common interest for computer simulation of materials, the system will satisfy periodic boundary conditions. In effect, this means that the restriction above is more precisely stated as
and all vectors n with integer components.
The problem is to generate efficiently states of the system that satisfy these constraints. The states will more than likely be generated by a stochastic process of some sort. A more ambitious goal is to generate states such that all states that satisfy the constraints are equally likely to be generated. (More precisely, if the set of positions {r1, ..., rN} is regarded as a set of random variables, the joint distribution function for these variables, which is zero when one or more of the constraints is violated, should be a constant for values that satisfy the constraint.)
This is an example of a problem for which each constraint is relatively easy to state and express in terms of a small number of the variables in the problem, and the number (or measure) of states that are consistent with the constraints is very small compared with the total number of states, in fact vanishing exponentially as N increases. This problem is related to that of generating possible states for an atomic fluid whose interatomic potential precludes two atoms from getting close to one another. The rigid-sphere interpretation relates to the challenging mathematical problem of existence and characterization of random sphere packings.
Variations on the Prototypical Problem
First Variation. Consider a random walk in a three-dimensional space that consists of N steps of unit length and random direction. Let si for i > 1 be the ith step. The position
is the location of the random walker after the ith step, with r0 being equal to the origin. The only
states of interest are those for which these positions never come close to one another. More precisely,
This problem is related to specifying the possible structures of a polymeric molecule. The goal is to generate random walks that satisfy these conditions. As in the previous problem, the method of generation is likely to be probabilistic. A stronger goal would be to generate states with a process such that all states that satisfy the constraint are equally likely to be generated. (More precisely, if each step si of the random walk is specified by a location on the surface of a unit sphere, the joint distribution function of the N steps should be zero for sets of steps that violate the constraints and a constant for sets that satisfy the constraints.)
Second Variation. In problems of interest, there may also be some additional constraints on the locations; for example, for some pairs of locations, there might be restrictions of the form
When the number of these restrictions is large enough to imply that only a small range of structures can satisfy all the constraints, the problem becomes a special case of the problems that are solved by using the methods of distance geometry, which is discussed in more detail in Chapter 3.
Third Variation. The various steps in the random walk of the previous problem might be correlated in the sense that the probability distribution for si might depend on the value of si-1 or perhaps both si-1 and si-2.
In these problems, there are some constraints that are "easy" to satisfy (e.g., in the first problem each particle must be inside the cubic box; in the second problem, each step must have unit length). Then there are others that are "harder" to deal with. Whether a constraint is hard or easy to deal with is related, in general, to whether it is concerned with just one of the basic vectors of the problem or with more than one.
Simplest Strategy
The simplest strategy for generating states that satisfy all the constraints is obviously to generate states that satisfy the easy constraints and then delete those states that violate the hard constraints. This solution is practical, if at all, only for relatively uninteresting situations. It works for the first problem, for example, only when the density N/L3 is much lower than the maximum density allowed. The problem is that almost all of the states generated will subsequently be deleted by this process.
More precisely, in the first problem one might imagine generating sets of N points, each of which is randomly distributed in the cube, and then discarding sets that violate the conditions specified. The sets not discarded then should be uniformly and randomly distributed among the states that do satisfy the conditions. The difficulty with this approach is that the probability that a set of randomly generated points satisfies the condition is of order exp(-aN) for large N, where a is a constant that depends on the density N/L3. For large N, therefore, much of the computational effort is wasted.
An obviously more efficient procedure is to generate the set of positions one at a time and test each one to ensure that it is far enough from the previous positions before generating the next position. If one violation of the conditions is found this way, no effort need be expended to generate the remaining positions in the set or to test them. Even this is not efficient enough. A significant
amount of effort will be expended in generating partial sets of positions, only to find that the set must be discarded because of the value of some position generated late in the sequence. This difficulty is sometimes referred to as the problem of "exponential attrition" because of the exponentially small fraction of sets of positions that are generated successfully.
Metropolis Monte Carlo Method
In this strategy one first generates one state that satisfies all the constraints; then this is used as the beginning of a Markov process whose transition probabilities are such that transitions are allowed only to other states that satisfy the constraints. In practice, this means that each transition typically involves a change of, at most, one of the coordinates by a very small amount. The two difficulties with this method are the following:
-
The set of states that satisfy the constraints may not be connected, so that with a particular initial state it will be impossible to generate a very large fraction of the states.
-
Even if the set of states that satisfy the constraints is connected, typical Markov processes explore the range of accessible states relatively slowly.
Therefore, some entirely new ideas for dealing with this class of problems would be worthwhile.
Relationship of These Problems to More General Optimization Problems
Some special cases of these problems, especially the first and second variations described above, are closely related to optimization problems that arise in chemical calculations. Chemical optimization problems typically involve minimization of an energy or free energy that depends on the positions of atoms or groups of atoms. (See pages 68–77 for a discussion of optimization problems and methods.) In more general problems, the object is not to minimize the energy or free energy but to calculate the typical properties of all the states of low enough energy that they might be populated at the temperature of interest. Such functions typically are very large and positive for certain configurations in which atoms or molecules are very close. It is typically true that a configuration in which any one pair of atoms is too close to one another has a high enough energy to make the total energy of the configuration so high that it cannot possibly be a solution of the optimization problem (or so high that it is not thermally populated). Thus, identification of states that are consistent with constraints of the type mentioned can be a useful first step toward solving optimization problems in chemistry.
Molecular Diversity and Cornbinatorial Chemistry in Drug Discovery
Overview of the Drug Discovery Process
The discovery of new drugs is a time-consuming, risky, and expensive process. These things are true even though in the past 15 years there has been a dramatic increase in the number of three-dimensional structures of proteins that can be used as scaffolds for the conceptual and computational aspects of drug design. The discovery traditionally moves through several stages once the biological target has been chosen (see Science, 1994).
First, a moderately active compound, a "lead," is identified from clues provided by the literature, through "random" screening of many compounds or through targeted screening of compounds identified by three-dimensional searching or docking. If the three-dimensional structure of the biological target macromolecule is known, then one may use three-dimensional searching to identify
existing compounds that are complementary to the binding site in the target (Kuntz, 1992; Martin, 1992). Alternatively, if a number of structurally unique compounds bind to the target, one may propose a three-dimensional pharmacophore and search databases for matches to it (Martin, 1992).
Once a lead has been identified, hundreds to thousands of additional compounds are designed and synthesized to optimize the biological profile. The cost and environmental impact of synthesis and patentability are also important issues. If the three-dimensional structure of the biological target is known, then molecular modeling might be used in the design (Erickson and Fesik, 1992). As testing data are accumulated, statistical three-dimensional quantitative structure-activity relationships (three-dimensional QSAR) may help set priorities for synthesis. Any attractive compounds found are tested in more detail through advanced protocols that more reliably forecast therapeutic and toxicity potential.
A pharmacophore is a chemical identity and geometrical arrangement of the key substituents of a molecule that confer biochemical or pharmacological effects.
Lastly, the surviving compounds are prioritized, and the best compound known at that time is prepared for clinical trial.
New mathematical techniques could have an impact on the rate of new compound discovery if the potency of compounds could be forecast more quickly and accurately before their synthesis. Many of the improvements in computational chemistry discussed elsewhere in this report would also impact the ability to forecast affinity based on the structure of the ligand and the macromolecular target. However, additional opportunities exist for cases in which the structure of the macromolecular target is not known, cases for which the forecast is based on three-dimensional QSAR investigations (Kubinyi, 1993). The most explored method is comparative molecular field analysis (CoMFA; Cramer et al., 1988). With CoMFA, molecules are aligned with each other; then for each molecule, the interaction energies with various probes are calculated at intersections of a three-dimensional lattice that encloses all the molecules. The relationships between these thousands of energy values and the potencies of the 10 to 100 molecules are established by the statistical method of partial least squares (PLS) with leave-one-out cross-validation (see Frank and Friedman, 1993, for background on PLS and comparisons of the method to other statistical procedures). When a CoMFA model is found, it generally has quite robust forecasting ability: the average error in forecasting the potency of 85 compounds in eight datasets is 0.55 logs or 0.8 kilocalories per mole (Martin et al., in press).
However, there are indications that one may fail to find a model, even though one exists, because of the coarseness of the lattice spacing (2 Å) and the sensitivity of PLS to noise. PLS can find only linear relationships between properties and biological potency; a method that could detect nonlinear relationships would be an improvement and might model more sets of data. Limited experiences with neural nets have shown no improvement over PLS. There might be an optimization method that could select the relevant variables from a pool of thousands. It would have to be roughly as fast as PLS (a minute or so to do leave-one-out cross-validation on 25 compounds) since one of the elements of the analysis is to compare results with different properties calculated at the lattice points, adding whole molecule properties, comparing alignment rules, investigating outliers, and combining and separating subseries of molecules.
Sources of Molecular Diversity
The weak point in the whole scenario of new drug discovery has been identification of the "lead." There may not be a "good" lead in a company's collection. The wrong choice can doom a project to never finding compounds that merit advanced testing. Using only literature data to derive the lead may mean that the company abandons the project because it cannot patent the compounds found. These concerns have led the industry to focus on the importance of molecular diversity as a key
ingredient in the search for a lead. Compared to just 10 years ago, orders of magnitude more compounds can be designed, synthesized, and tested with newly developed strategies. These changes present an opportunity for the imaginative application of mathematics.
Automated testing methods employing, simplifed assays, mixing strategies, robotics, bar-coding, etc., have led many pharmaceutical and biotechnology companies to test every available compound, perhaps 105 to 106 of them, in biological assays of interest (Gallop et al., 1994; Gordon et al., 1994). Testing a collection generally takes approximately six months. This operation presents several challenges: (1) Is it really necessary to test all of the compounds in order to identify the series of compounds that will show the activity? (2) Should a pilot set of compounds be tested first to adjust the assay conditions and forecast how many active compounds will be found? If so, how would this set be selected (3) What compounds, available from outside vendors, should be selected for purchase to complement the set of in-house compounds? Is there a way to quantify their worth other than the cost to synthesize in-house?
Concurrently, synthetic chemists developed new strategies that provide large numbers of compounds for biological testing typically as mixtures. Such libraries, synthesized in a few months, can contain 104 to 10 7 different chemical structures (Baum, 1994). Although this number of compounds seems high, note that it has been estimated that there are 10200 stable chemical compounds of molecular weight less than 750 that contain only carbon, hydrogen, nitrogen, oxygen, and sulfur. Even factoring in their possibility of synthesis and realistic chemical and physical properties still leaves on the order of 10180 compounds to consider. How, then, does one choose which 104 compounds should be included in the first library, or the second?
A final strategy to enhance molecular diversity results from computer programs that design molecules to meet specified three-dimensional criteria, typically based on the experimental structure of a protein binding site (Rothstein and Murcko, 1993). The programs design molecules to meet geometric criteria and include electrostatic complementarity at the level of force fields such as those used for molecular dynamics. The diversity arises from the combinatorics: a protein binding site usually contains at least four or five hydrogen-bonding or charged groups; a ligand might interact with most or all of them, and many different templates might be able to fit into the binding site and orient polar groups for optimal interaction. Hence, it is expected that a huge number of nicely fitting molecules might be designed. Although design programs could be set up to produce only those molecules that could be synthesized readily, this severely limits the diversity. Hence, it is likely that the designed molecules will have to be made by traditional synthesis. This places a realistic upper limit of 25 molecules to be selected. Even if binding affinity could be forecast precisely, we are a long way from forecasting every type of toxicity or drug metabolism quirk that a molecule might possess. Again, we face the problem of selection of the most diverse sample from a population.
Current Computational Approaches to Compound Selection
There are three aspects to the problem of selecting samples from large collections of molecules: First, what molecular properties will be used to describe the compounds? Second, how will the similarity of these properties between pairs of molecules be quantified? Third, how will the molecules be grouped or clustered?
For datasets of size 104 and higher, the standard method of describing the molecules for clustering encodes the presence or absence of substructural features in a bit-string, typically of length 256–1024 (Willett, 1987; Hodes, 1989). In modern systems, these substructural features are recognized by enumerating all paths of length 07 in the molecular graph and using these to populate one or more of the bits (Weininger et al., 1994). It typically takes one to two hours on a modern workstation to generate such fingerprints of a database of 105 compounds. The time required for this process increases linearly with the number of compounds.
|
BOX 4.8 Possibility of Intelligent Algorithms to Detect Novel Phenomena Automatically The total amount of numerical information generated in a typical computer simulation is immense. Whether the model system under study is inorganic or biological, classical or intrinsically quantum mechanical, in thermal equilibrium or violently nonstationary, the processing of the data created is usually structured to address a small set of often conceptually orthodox questions that have been selected beforehand. Given the inappropriateness of trying to examine raw numerical information in tabular form, this is entirely reasonable. Nevertheless, serendipitous discoveries that fall outside the preselected query set indeed do occasionally occur, and their consequences can produce significant advances. The usual procedures for carrying out computer simulations probably are far from optimal in detecting initially unsuspected correlations and phenomena. This leads one to suspect that generic pattern-recognizing algorithms might be constructed that would operate in conjunction with Monte Carlo or molecular dynamics simulations and would effectively amplify the human scientist's limited capacity to pull novel correlations out of huge files of numerical data. Generally speaking, humans are best at recognizing visual patterns—after all, the human visual apparatus has been honed to exquisite sensitivity by approximately a billion years of evolutionary trial. But in the scientific context this requires that just the right graphs or figures be presented to the investigator, and in one respect it presupposes something about the nature of the correlations to be examined. One hopes to transcend such human limitations, perhaps with a carefully crafted form of open-ended artificial intelligence that incorporates pattern-detecting capacity free from our human biases and limitations. In particular, computers ought to be able to "see" in spaces of dimension higher than three and pick out significant patterns whose projection into two or three dimensions would obscure the phenomena of interest. This opportunity is not so much intended as an attempt to replace human researchers as it is to magnify their wisdom and insight. In this respect, generic pattern-detecting software could be a powerful device operating to maximize productivity. And it should not escape notice that such a tool is not restricted just to simulation data, but in principle could also apply to other classes of large chemical databases discussed elsewhere in this report. |
The second step is to calculate the similarity of every molecule to every other molecule in the dataset. The similarity measure traditionally used, the Tanimoto coefficient, is expressed as
where Simij is the similar i to molecule j, Fij is the number of features (bits set to 0 or 1) in common between molecule i and molecule j, Fi is the number of bits set in molecule i, and Fj is the number of bits set in molecule j. For the same 105 compounds, this process takes on the order of 24 hours. Since every molecule is compared with every other, it scales as the square of the number of compounds. Lastly, the Jarvis-Patrick clustering method (Jarvis and Patrick, 1973) is used to group the compounds. This method is based on comparing the nearest neighbors of compounds and is very fast, taking only seconds to accomplish. Although each of these steps is feasible, none is optimal.
Opportunities for Improvements in Computational Approaches to Compound Selection
Molecular fingerprints are not the best descriptor to use to select compounds for bioactivity since the biological properties of compounds depend on their three-dimensional complementarily of shape and electronic properties with those of the target biomolecule. Clearly, we would like to consider the
three-dimensional structures of the molecules—shape, the location of intermolecular recognition sites such as hydrogen-bonding or charged groups, and the way in which the position of these features changes with changes in conformation. Speeding up such calculations or representations of the results would be a big help.
However, the problem of how to represent conformational flexibility in this context is a bigger challenge—do we need a totally different way to represent the structures than coordinates or distances between pairs of atoms? It is important to recognize that two-dimensional molecular structure is the basis of both chemical synthesis strategy and patent claims, and so the representation must also include the two-dimensional structure. This is a clear example where the choice of model is significant and must be the result of close collaboration between mathematical and chemical scientists.
Any new molecular descriptor will require that one define a corresponding metric for the similarity or distance between compounds to be used in grouping them. For example, in contrast to substructural features, which are either present or absent, distances are continuous and do not fall so easily into a bit-string. Should distances be binned—if so, should the bins be fuzzy or overlapping? How is similarity evaluated in such cases?
On the other hand, one might quantitate the similarity of two molecules by the size and composition of the maximum common substructure. Experience with the Bron-Kerbosh algorithm (Bron and Kerbosh, 1973) has shown a rate of 106 comparisons per hour. For a dataset of size 105, it would take 1010 comparisons or 104 hours to prepare the similarity matrix! Similarly, 106 molecules would require 1012 comparisons and 106 hours. Although parallelization might allow one to perform the calculations, a better algorithm might accomplish the same thing with greater efficiency. It might be possible to eliminate most of the comparisons while retaining all important ones.
Improvements in the grouping of compounds are sorely needed. The Jarvis-Patrick algorithm performs poorly on sets of very diverse compounds. For example, a typical result produces a few large clusters, each containing very different compounds, and many singletons. There are sometimes clusters that contain compounds with a similarity of 0.2 on a scale of 0.0 to 1.0, with 1.0 the upper limit. Clearly, this is not clustering similar compounds together.
Much better results are found, albeit with datasets of 1000, by using statistically based agglomerative clustering methods. For 1000 compounds, the clustering takes approximately one day and would scale roughly as the square of the number of compounds. Since we typically would expect to investigate no more than 1/100 as many clusters as original compounds, divisive methods might have an advantage because in this approach, clustering starts with one huge cluster, divides clusters into tighter ones, and could stop once the target number of clusters was formed.
At this time, no method other than Jarvis-Patrick is known to the computational chemistry community that will group 105 or 106 objects in a time scale of less than a week (Willett et al., 1986; Willett, 1987; Whaley and Hodes, 1991). There are unpublished reports that the divisive Guenoche (1991) algorithm classifies 104 compounds overnight on a personal computer once the pairwise similarities have been calculated. However, it seems possible that there may be better ways to discover the groups of compounds in a dataset.
References
Baum, R.M., 1994, Combinatorial approaches provide fresh leads for medicinal chemistry, Chemical and Engineering News (February 7) 20–26.
Bron, C., and J. Kerbosch, 1973, Algorithm 457. Finding all cliques of an undirected graph. Commun. ACM 16:575.
Cramer III, R.D., D.E. Patterson, and J.D. Bunce, 1988, Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins, J. Am. Chem. Soc. 110:5959–5967.
Erickson, J.W., and S.W. Fesik, 1992, Macromolecular X-ray crystallography and NMR as tools for structure-based drug design, In Annual Reports in Medicinal Chemistry, Vol. 27, M.C. Vernuti, ed., Academic Press, New York, pp. 271–289.
Frank, I.E., and J.H. Friedman, 1993, A statistical view of some chemometrics regression tools, Technometrics 35:109–135.
Gallop, M.A., R.W. Barrett, W.J. Dower, S.P.A. Fodor, and E.M. Gordon, 1994, Applications of combinatorial technologies to drug discovery. 1. Background and peptide combinatorial libraries, J. Medicinal Chem. 37:1233–1251.
Gordon, E.M., R.W. Barrett, W.J. Dower, S.P.A. Fodor, and M.A. Gallop, 1994, Applications of combinatorial technologies to drug discovery. 2. Combinatorial organic synthesis, library screening strategies, and future directions, J. Medicinal Chem. 37:1387–1401.
Guenoche, A., P. Hansen, and B. Jaumard, 1991, Efficient algorithms for divisive hierarchical clustering with diameter criterion, J. Classification 8:530.
Hodes, L., 1989, Clustering a large number of compounds. 1. Establishing the method on an initial sample, J. Chem. Inform. Comput. Sciences 29:66–71.
Jarvis, R.A., and E.A. Patrick, 1973, Clustering using a similarity measure based on shared nearest neighbors, IEEE Trans. Comput. C-22:1025–1034.
Kubinyi, H., 1993, 3D QSAR in drug design, Theory, Methods, and Applications, ESCOM, Leiden, 759 pp.
Kuntz, I.D., 1992, Structure-based strategies for drug design and discovery, Science, 257:1078–1082.
Martin, Y.C., 1992, 3D database searching in drug design, J. Medicinal Chem. 35:2145–2154.
Martin, Y.C., K.-H. Kim, and C.T. Lin, in press, Comparative molecular field analysis: CoMFA , in Linear Free Energy Relationships in Biology, M. Charton, ed.
Rothstein, S.H., and M.A. Murcko, 1993, Group Build: A fragment-based method for de novo drug design, J. Medicinal Chem. 36:1700–1710.
Science, 1994, Research news: Drug discovery on the assembly line, 264:399–1401.
Weiniger, D., C. James, and J. Yang, 1994, Daylight Chemical Information Systems, Manual to Version 4.34, Daylight Chemical Information Systems, Irvine, Calif.
Whaley, R., and L. Hodes, 1991, Clustering a large number of compounds. 2. Using the connection machine, J. Chem. Inform. Comput. Sciences 31:345–347.
Willett, P., 1987, Similarity and Clustering in Chemical Information Systems, Research Studies Press, Letchworth.
Willett, P., V. Winterman, and D. Bawden, 1986, Implementation of nonhierarchic cluster analysis methods in chemical information systems, J. Chem. Inform. Comput. Sciences 26:109–118.
Statistical Analyses of Families of Structures
The diversity of chemical structures is one of the hallmarks of modern experimental chemistry. The problems of diversity and similarity are most prevalent in the study of biological molecules for which very different sequences—that is, fundamental structures—give rise to molecules that have very similar overall three-dimensional structures and often very similar functional properties. The Human Genome Project is devoted to characterizing the myriad of proteins encoded in humans, but a still larger universe of proteins exists in other living beings. Furthermore, it is easy to understand that the existing proteins are just a small subset of all possible random heteropolymers. The same type of combinatorial complexity exists for many other classes of molecules. In nature, we are familiar with the complexity of alkaloids or terpenes.
More and more molecular scientists are trying to understand how to use the information from a variety of different molecules to understand the structure and function of a given one. It is now becoming possible, by using combinatorial syntheses in the laboratory, to make 10 million variants of a single protein or 10,000 covalently connected frameworks such as those in a natural product. The most well known of these techniques is that employed to make catalytic antibodies, but many other approaches are possible. A variety of mathematical problems arise when one tries to make use of these resulting longitudinal data about molecular systems.
For naturally occurring biomolecules, one of the most important approaches is to understand the evolutionary relationships between macromolecules. This study of the evolutionary relationship between biomolecules has given rise to a variety of mathematical questions in probability theory and sequence analysis. Biological macromolecules can be related to each other by various similarity measures, and at least in simple models of molecular evolution, these similarity measures give rise to an ultrametric organization of the proteins. A good deal of work has gone into developing algorithms that take the known sequences and infer from these a parsimonious model of their biological descent.
Similar analyses based on the three-dimensional structure of molecules also present ongoing mathematical problems. At the moment, the use of evolutionary similarity to infer three-dimensional structure is a common and very important algorithm for people who have practical interests in the prediction of biomolecular structure. Use of the theory of spin glasses to characterize random heteropolymers has also allowed the phrasing of interesting questions such as the probability in a single experiment of obtaining a foldable protein molecule. This is a question in which the statistics of low-lying energy states on the surface and the statistics of sequences must be analyzed jointly and related to each other. Experiments of this type have recently been done and seem to agree in many respects with the results of theory, but there are many questions of physicochemical principle and of mathematical analysis for this theory.
An emerging technology is the use of multiple rounds of mutation, recombination, and selection to obtain interesting macromolecules or combinatorial covalent structures. Very little is understood as yet about the mathematical constraints on finding molecules in this way, but the mathematics of such artificial evolution approaches should be quite challenging. Understanding the navigational problems in a high-dimensional sequence space may also have great relevance to understanding natural evolution. Is it punctuated or is it gradual as many have claimed in the past? Artificial evolution approaches may obviate the need to completely understand and design biological macromolecules, but there will be a large number of interesting mathematical problems connected with the design of efficient artificial evolution experiments.
Quantum Monte Carlo Solution of the Schrödinger Equation
Many-body problems in physics are often treated by a Monte Carlo (MC) approach (e.g., Hammersley and Handscomb, 1964; Kalos and Whitlock, 1986). The Monte Carlo method is statistical and draws its name from the famous gambling casinos of Monaco because of the rule of random numbers or coin tosses in the method.
Problems handled by Monte Carlo are generally of two types, probabilistic or deterministic, depending on whether they are connected with random processes. In the probabilistic case, the simple Monte Carlo approach is to observe the occurrence of random numbers, chosen in a way that they directly simulate the physical random processes of the original problem, and to infer the desired solution from the behavior of these random numbers. In the deterministic case, the power of the Monte Carlo approach is the capability of carrying out numerical calculations in cases where the equations that describe the essence of a problem and its underlying structure are not solvable by alternative means. The underlying structure or formal expression also describes some unrelated random process, and therefore the deterministic problem can be solved numerically by a Monte Carlo simulation of the corresponding probabilistic problem.
The essential feature common to all Monte Carlo computations is that at some point one will need to substitute for a random variable a corresponding set of values with the statistical properties of the random variable. The values that are substituted are called random numbers. They are not really random, however, because if they were it would be impossible to repeat a particular run of a computer program. An absolute requirement in debugging a computer code is the ability to repeat a particular run of the program. If real random numbers were used, no calculation could be repeated exactly, and attempts to check for errors would be extremely difficult. It is essential that one be able to repeat a calculation when program changes are made or when the program is moved to a new computer.
For electronic computation it is desirable to calculate easily by a completely specified rule a sequence of numbers as required that will satisfy reasonable statistical tests for randomness for the Monte Carlo problem of interest. Such a sequence is called pseudorandom and clearly cannot pass every possible statistical test.
Most of the pseudorandom number generators now in use are special cases of the relation (Heermann, 1986; Kalos and Whitlock, 1986)
One initiates the generator by starting with a vector of j + 1 numbers x0,x1, . . . , xj. The generators are characterized by a period τ that in the best case cannot exceed Pj+1. The length of τ and the statistical properties of the pseudorandom sequences depend on the values of aj, b, and P.
With the choice of aj = 0, j >1, and b = 0, one obtains the multiplicative congruential generator,
Recent work has shown that a set of parameters λ and P can be chosen with confidence to give desired statistical properties in many-dimensional spaces (Kalos and Whitlock, 1986). There are many other generators available; the interested reader should consult the references.
With parallel computers and supercomputers capable of very large calculations, very long pseudorandom sequences are necessary. In addition, there remains the desire to have reproducible
runs. The question of independence of separate sequences to be used in parallel remains a research issue.
Quantum Monte Carlo (QMC), as used here, refers to a set of methods to solve the Schrödinger equation (exactly, in two of the three variants listed below) to within a statistical error by random walks in the many-dimensional space. These methods—variational MC, diffusion MC, and Green's-function MC—are based on the formal similarity between the Schrödinger equation in imaginary time and a multidimensional classical diffusion equation.
Variational Monte Carlo (VMC)
For ΨT(R) a known approximate (trial) wavefunction, where R is the 3N set of coordinates of the N-particle system, VMC (Kalos and Whitlock, 1986; Hammond et al., 1994) uses the Metropolis algorithm (Hammersley and Handscomb, 1964; Heermann, 1986; Kalos and Whitlock, 1986; Hammond et al., 1994) to sample | ΨT|2. Therefore, any expectation value with respect to this trial function can be computed including the variational energy of ΨT. To begin a calculation, an initial distribution of walkers is generated. In order to create a distribution of |ΨT| 2, these walkers take a series of Metropolis steps to equilibrate, followed by another series of Metropolis steps at which the local energy
is calculated for each walker; here H is the Hamiltonian. Averaging the local energy over the walkers at the sampling points yields the variational energy, which is an upper bound to the exact energy of the ground state. An alternative strategy is to minimize the variance of the local energies. A strength of the VMC method is the capability of treating trial functions that depend explicitly on interelectronic coordinates—there is no integral problem associated with the use of trial functions containing such coordinate dependence for many-electron systems.
Diffusion Monte Carlo (DMC)
If one multiplies the time-dependent Schrödinger equation in imaginary time by ΨT and rewrites it in terms of a new probability distribution f(R,t) ![]()
![]() Φ(R,t)ΨT(R), one obtains
Φ(R,t)ΨT(R), one obtains
where Di![]()
![]() 2/2mi, EL is the local energy, and ET (the trial energy) represents a constant shift in the zero of energy. At large simulation (imaginary) time, the function Φ(R,t) tends to the ground state wavefunction.
2/2mi, EL is the local energy, and ET (the trial energy) represents a constant shift in the zero of energy. At large simulation (imaginary) time, the function Φ(R,t) tends to the ground state wavefunction.
The algorithm (Hammond et al., 1994) is initiated with a distribution (ensemble) of several hundred walkers taken from f(R,0) = |ΨT(R)|2, which is then evolved forward in time after a sequence of equilibration steps. The three terms on the right-hand side then correspond to diffusion with diffusion constant Di, a drift term associated with the trial function, and a branching term that derives this designation from the DMC equation being, in the absence of the first two terms on the right-hand side, a first-order kinetic equation. Because f can, in general, assume both positive and negative values, which would preclude the interpretation of f as a probability for fermion systems, one alternative is to impose the nodes of the ground state wavefunction ΨT on Φ so that f is always positive. This is the fixed-node approximation, which can be shown to give an upper bound to the ground state energy.
After sufficiently long simulation time in which the steady-state solution of the DMC equation has been attained, the ground state energy is obtained as the average value of the local energy now averaged over the mixed distribution Φ(R)ΨT(R). This is an improvement over VMC and associated sampling from |ΨT|2 because DMC contains information on the exact ground state Φ (in the fixednode approximation). The ground state energy has the zero-variance property of QMC; that is, in the limit that ΨT approaches Φ, the variance of the MC estimate of the energy approaches zero.
Green's Function Monte Carlo (GFMC)
The integral equation form of the Schrödinger equation can also be modeled by a stochastic process, which leads immediately to the consideration of Green's functions. GFMC approaches (Kalos and Whitlock, 1986) have been investigated for the time-independent as well as the time-dependent Schrödinger equations. In practice, however, there are only convergent when the Fermi energy is close to the Bose energy and the trial function has sufficiently accurate nodes. New directions with GFMC that overcome these limitations still encounter limitations that restrict their application, at present, to first-row atoms. Nevertheless, GFMC remains an area for continued scrutiny.
Research Opportunities
The various forms of Monte Carlo for solving the Schrödinger equation (VMC, DMC, and GFMC) could each be improved by better sampling methods. Wavefunctions typically used for importance sampling often recover at best 80 to 95% of the correlation energy, the energy difference between the Hartree-Fock approximation and the nonrelativistic limit, for molecules consisting of first-row atoms. Beyond the first row, computer time dependence on atomic number, which has been estimated as za where α = 5.5 to 6.5, is a major limiting factor that has led to the introduction of analytical functions to describe inner-shell electrons (i.e., pseudopotentials or effective core potentials). Another area in which improvements are eagerly sought is in methods that go beyond the fixed-node approximation. Currently, these methods are limited to atoms and molecules containing no more than 6 to 10 electrons.
References
Hammersley, J.M., and D.C. Handscomb, 1964, Monte Carlo Methods, Methuen, London.
Hammond, B.L, W.A. Lester, Jr., and P.J. Reynolds, 1994, Monte Carlo Methods in Ab Initio Quantum Chemistry, World Scientific, Singapore.
Heermann, D.C., 1986, Computer Simulation Methods, Springer-Verlag, Berlin.
Kalos, M.H., and P.A. Whitlock, 1986, Monte Carlo Methods, Volume 1: Basics, John Wiley & Sons, New York.
Nonadiabatic Phenomena2
The Born-Oppenheimer (BO) adiabatic approximation is the basis of the well-known separation of the many-body problem of electronic and nuclear motion into two separate many-body problems. It is
also applied to separate other ''fast'' and "slow" subsystems including vibrational and rotational modes of molecules. The combination of these approximations leads to the double adiabatic approximation that has been applied in the study of solids as well as molecules.
For most applications, the approximation of separation of electronic and nuclear motion does not lead to appreciable error. For high precision, however, the BO energy has to be corrected for the coupling of electronic and nuclear motions. The coupling is important if, for example,
-
two potential energy surfaces of the same symmetry cross in the BO approximation— correction terms prevent such crossings—or are close and more-or-less parallel over a moderate range of configuration space;
-
the electronic state of a polyatomic molecule is degenerate for a symmetric arrangement of nuclei; coupling leads to Jahn-Teller and Rennet-Teller effects;
-
the nuclear velocities are large as in high-energy molecular collisions;
-
the molecule is in a high rotational state and has nonzero electronic angular momentum.
There are two kinds of correction terms for the coupling of electronic and nuclear motions. The diagonal corrections shift the energy levels. The nondiagonal corrections produce and broaden the natural line width to the energy levels and cause transitions between quantum states. The energy corrected for the diagonal coupling terms is called the adiabatic energy and gives the best possible energy curves and surfaces.
A number of problems arise in the inclusion of nondiagonal corrections. They occur because of divergences in coupling matrix elements in regions where potential energy surfaces approach very closely or because the BO electronic basis functions may not be appropriate for the region of close approach.
BO deviations arise for two reasons. First, coupling terms appear in the kinetic energy when the coordinates are transformed from the laboratory-fixed axes to the body-fixed (molecular) axes. Second, the Breit-Pauli relativistic corrections to the electrostatic Hamiltonian lead to spin-spin, spin-orbit, and other magnetic coupling terms. The present discussion neglects the latter and focuses on the former.
The Hamiltonian in the laboratory-fixed frame may be written
where primes denote the laboratory frame, ma is the mass of the α-th nucleus in units of electron mass, and U is the potential energy given by the Coulomb interactions (nuclear, electronic-nuclear, and electronic) of all the particles of the system. Since U is a function only of relative distances between the particles, one separates out the center-of-mass motion and is left with 3(n+N)-3 relative coordinates for an n-electron and N-nucleus molecular system. The choice of optimum coordinates for polyatomic molecules is not straightforward, and so the focus here, for simplicity, is on the diatomic molecule case. Then the Hamiltonian takes the form
where μ = ma. mb/(ma + mb) and
Here Za and Zb are the nuclear charges, rai is the distance separating nucleus a from electron i, and R is the distance between nuclei a and b.
If one assumes that the electronic Schrödinger equation,
can be solved exactly for the complete set of eigenfunctions ψk (r,R) and eigenvalues Ek(R), then the total Schrödinger equation for nuclear and electronic motions,
can be solved by expanding Ψ as follows,
Here r represents all the coordinates of the electrons and k is the set of electronic quantum numbers. This leads to a set of equations for the functions φk(R) that determine the nuclear motion of the system,
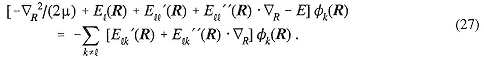
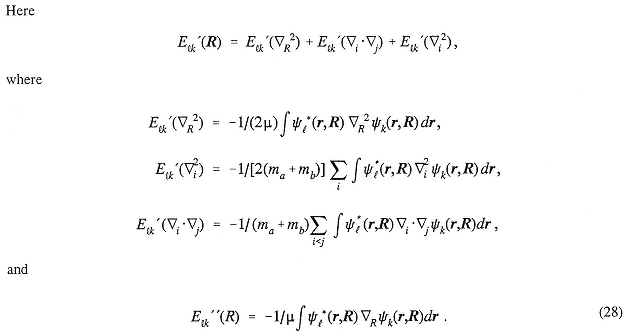
An a sterisk denotes complex conjugate. The quantities defined by Equation (28) give rise to velocity-
dependent forces on the nuclei. For real ψl, however, the diagonal term vanishes.
In practice, Equation (27) is extremely difficult to solve and various approximations to it are introduced. The BO approximation corresponds to neglecting all of the coupling terms. Equation (27) then becomes a Schrödinger equation for nuclear motion,
In this approximation, the El(R) determined from Equation (24) become the potential energy for the nuclear motion.
The adiabatic approximation corresponds to neglecting all nondiagonal terms in Equation (27), which results in a Schrödinger-type equation for nuclear motion,
where the potential for nuclear motion is
The diagonal elements Ell'(R) are effectively a correction to the potential energy due to the coupling between the electronic and nuclear motions.
The adiabatic approximation gives the best potential energy function. As defined here the adiabatic approximation to the energy is an upper bound to the true energy since it can be expressed as the expectation value to the correct Hamiltonian for the molecule evaluated with an approximate wave function.
The nonadiabatic approximation corresponds to consideration of the nondiagonal as well as the diagonal elements Elk'(R). This is extremely difficult to carry out but has been accomplished for H2 by using variational basis set (Kolos and Wolniewicz, 1960) and quantum Monte Carlo approaches (Traynor et al., 1991; see also Ceperly and Alder, 1987).
For processes occurring in excited states, it appears clear that for molecules more complicated than H2 alternative approaches must be found. This is an area demanding fundamental improvements if breakthroughs are to be achieved.
References
Ceperley, D.M., and B.J. Alder, 1987, Phys. Rev. B 36:20–92.
Hirschfelder, J.O., and W.J. Meath, 1967, Adv. Chem. Phys. 12:1.
Kolos, W., and L. Wolniewicz, 1960, Rev. Mod. Phys. 35:13–23.
Traynor, C.A., J.B. Anderson, and B.M. Boghosian, 1991, A quantum Monte-Carlo calculation of the ground-state energy of the hydrogen molecule, J. Chem. Phys. 94:3657–3664.
Evaluation of Integrals with Highly Oscillatory Integrands: Quantum Dynamics with Path Integrals
The solutions of many quantum dynamics problems can be formulated in terms of path integrals. Indeed, there is a formulation of quantum mechanics (less familiar than the Schrödinger wave function formulation, the Heisenberg matrix formulation, or the Dirac Hilbert space formulation) based
entirely on the use of path integrals (Feynman and Hibbs, 1965). Path integrals are closely related to some of the mathematical approaches used to describe classical Brownian motion. A prototypical mathematical problem and a class of methods for solving it are described first; then a more general discussion of the problem is presented.
Prototypical Problem
This discussion of the prototypical problem follows closely the discussion of Doll et al. (1988). Consider the integral I(t) = ![]() dx ρ(x) eitf(x) where t is a real parameter corresponding to the time, x is the set of coordinates for a many-dimensional space, and ρ(x) and f(x) are functions in that space. The function ρ(x) is positive semidefinite and can without loss of generality be taken as normalized to unity. Thus, it can be regarded as a probability density in the space. The function f(x) is real (for this prototype problem).
dx ρ(x) eitf(x) where t is a real parameter corresponding to the time, x is the set of coordinates for a many-dimensional space, and ρ(x) and f(x) are functions in that space. The function ρ(x) is positive semidefinite and can without loss of generality be taken as normalized to unity. Thus, it can be regarded as a probability density in the space. The function f(x) is real (for this prototype problem).
For problems of interest, the dimensionality of the space can be very large (from 1 to a hundred to thousands), and the complexity of the function precludes analytic integration. For any particular x, ρ(x) and f(x) can be evaluated numerically, and typically there is much more computation required for the evaluation of ρ than f.
The range of the x integration may be bounded, but more often it is unbounded. For typical problems of interest, however, integrals of the form ![]() dx ρ(x) (f(x))n exist for all positive integers n.
dx ρ(x) (f(x))n exist for all positive integers n.
The goal is usually to evaluate the integral for a specific value of t (or for a set of values of t) by making use of calculated values of ρ and f at appropriately chosen points and to estimate the accuracy of the answer. In some cases, the desired quantity is the area under the function
or perhaps the Fourier transform
Techniques for evaluation of such integrals of I would be extremely worthwhile, but this discussion focuses on the evaluation of I(t) for specific values of t.
Discussion of the Problem
A standard way of attacking this problem would be a Monte Carlo integration scheme in which points x are generated with a probability distribution of ρ(x) and f is evaluated at these points. Then
where N points are generated and xn is the nth point. For small values of t, this can be a practical procedure. For large values of t, however, this procedure is extremely inefficient because of the large amount of cancellation among the various terms.
If t is large and f is not a constant, it is clear that the integrand is highly oscillatory; thus, small regions of space where f is varying will tend to contribute small net amounts to the integrand for large t. Nevertheless, individual points in such a region will contribute to the sum an exponential whose magnitude is unity. Cancellation among the various terms will give an accurate and small answer only when each such small region is sampled many times in the Monte Carlo evaluation.
The regions of the space in which df(x)/dx is zero or small will make the major contributions to the integral for large t. Thus, a scheme that concentrates the Monte Carlo sampling at and near such regions would be desirable. Such schemes are useally called "stationary-phase" methods, since at such points the phase of the exponential is stationary.
Stationary-Phase Monte Carlo Methods
A variety of sampling methods have been developed that focus on the stationary-phase points (Doll, 1984; Filinov, 1986; Doll et al., 1988). Here the approach of Doll et al. (1988), which is similar to the others, is outlined.
The integral of interest can be rewritten identically as
where
and P(y) is an arbitrary normalized probability distribution. (This result is exact if the range of integration is over all positive and negative values of the integration variables.) The function P( y) is typically chosen to be a Gaussian distribution centered at y = 0. D(x,t) is called a "damping function," because for such a typical choice of P(y), D(x,t) is largest where f is stationary and hence it damps the integrand in Equation (29) away from the stationary points.
An evaluation of D(x,t) poses the same problems as evaluation of I(t). However, for specific choices of P, various approximations for D can be constructed and used as the basis for a more efficient sampling method for the evaluation of I. For example, if P(y) is a narrow Gaussian function with a maximum at y = 0, then for large t an approximation can be constructed by replacing ρ(x-y)/ρ(x) by unity and performing a Taylor expansion of the exponent. One then obtains an approximation for D called the "first-order gradient approximation":
Then
This integral, which is the major contribution to the correct answer, is generally more amenable to evaluation by sampling, in this case by using ρ(x)D0(x,t) as the probability distribution. A complete method would require the development of procedures to estimate the correction terms that must be added on the right to make this an equality (see Doll et al., 1988, for additional details). The essential idea of these procedures is that use of a precise approximate formula for D automatically includes much of the cancellation responsible for decreasing the value of I.
The stationary-phase Monte Carlo methods provide some useful ideas for formulating tractable sampling methods for solving some problems of interest. It would be worthwhile to develop better versions of these methods both for I(t) and for its Fourier transform.
Alternative Approaches to the Prototype Problem
In many cases of interest, the function I(t) is known to be an analytic function of t at the origin. This knowledge may be of use in developing approximate evaluation techniques based on analytic continuation. Most analytic continuation methods are based on a more detailed formulation of the problem of interest that is tied closely to the physical nature of the problem. But even for this simple formulation of the prototype problem, one might ask whether the fact that I(t) is an analytic function of (complex) t for some region that includes the origin suggests any alternate ways of calculating I(t) accurately.
For example, one might consider the use of Padé approximants (i.e., ratios of polynomials; Baker and Gammel, 1970), which are often used for approximate analytical continuation of analytic functions, especially meromorphic functions. Expanding the exponential in I(t) gives
where
The first few Taylor series coefficients can then be estimated by sampling on ρ(x) in the usual way, but the difficulty of making accurate estimates grows as n increases. These coefficients might then be used to fit I(t) with a Padé approximant.
This approach raises a number of mathematical questions.
-
Are there any sampling techniques that would be especially effective in evaluating the coefficients for large n?
-
Does the statistical error in the αn make it inappropriate to use Padé approximants to fit the function? Are there better alternatives?
-
If the Padé approximant method is valid, how is the uncertainty in I(t) related to the statistical uncertainty of the individual αn?
-
Does the fact that the integral expression for I(t) is dominated by stationary points in the x space give any insights into how to evaluate αn or how to construct appropriate Padé approximants?
Other Formulations and Solutions of the Basic Problem
The nature and dimensionality of the x space and the specific form of the ρ(x) function are determined by the nature of the quantum mechanical problem to be solved. In general, however, the coordinates of x are Cartesian (or other) coordinates for a mechanical system. Similarly, the form of the function f(x) is determined by the nature of the problem. Various analytic continuation techniques have been applied to attack specific special cases of the prototype problem. The question then arises as to whether these are isolated solutions of specific problems or special cases of an underlying, not yet discovered, general method for solving problems of this type. This is not the place to delve into the details of specific problems; instead, some of the relevant mathematical principles involved are highlighted. For additional discussion of related problems, the reader is referred to Doll (1984), Makri (1991), and Wolynes (1987).
Analytic Continuation in Time. In some problems, the goal is to evaluate a function of time t of the form

More generally, there is a function of a complex variable z of the form

that is analytic in a region including the positive real axis and part of the positive imaginary axis, and for which h(t) = lim ![]()
![]() 0+H(
0+H(![]() + it). The function g(z,x) is an analytic function of all its arguments, and f(x) is real (for real x]). In many cases, the formulation in Equation (31) is required to make the problem well defined, because g(it, x) is purely imaginary and the integrals in Equation (30) are not absolutely convergent (for an infinite range of integration).
+ it). The function g(z,x) is an analytic function of all its arguments, and f(x) is real (for real x]). In many cases, the formulation in Equation (31) is required to make the problem well defined, because g(it, x) is purely imaginary and the integrals in Equation (30) are not absolutely convergent (for an infinite range of integration).
The calculation of H(z) for real z presents a tractable sampling problem because g(z,x) is real for real z. Then, sampling a set of points distributed with a probability density proportional to g(z, x) and calculating f at those points allow H to be calculated for real z. In fact, as long as z has a positive real part, the problem of evaluating H can be converted to a well-defined sampling problem, because ![]() g(z,x)
g(z,x) ![]() -
-![]() for large positive and negative values of the integration variables. Then
for large positive and negative values of the integration variables. Then ![]() g(z,x) can be used as a probability distribution, and the right side of Equation (31) can be expressed as a ratio of two averages over this distribution:
g(z,x) can be used as a probability distribution, and the right side of Equation (31) can be expressed as a ratio of two averages over this distribution:
For complex values of z, however, this sampling problem may become intractable because the quantities to be averaged, exp [i![]() g(z,x)]f( x) and exp [i
g(z,x)]f( x) and exp [i![]() g(z,x)], are complex and oscillatory. This can pose the same difficulty as that discussed for the prototypical problem above. This difficulty becomes acute in the limit that z becomes purely imaginary, because the "probability distribution function" approaches unity and is not normalizable.
g(z,x)], are complex and oscillatory. This can pose the same difficulty as that discussed for the prototypical problem above. This difficulty becomes acute in the limit that z becomes purely imaginary, because the "probability distribution function" approaches unity and is not normalizable.
A variety of analytic continuation methods have been used to solve problems of this type. One strategy is to perform tractable sampling calculations to obtain H(z) for real z and then use Padé approximant techniques to estimate H as z approaches the imaginary axis (Miller et al., 1983; Thirumalai and Berne, 1983; Jacquet and Miller, 1985; Yamashita and Miller, 1985; Makri and Miller, 1989). These techniques motivate the same sorts of mathematical questions as those listed above for a different approach to analytic continuation.
Deformation of the Integration Contours. Another technique has been used in certain situations in which the integrand is an analytic function of all the variables in x. The integration is from-![]() to
to ![]() along the real line for each of these variable. Deformation of these contours of integration and evaluation of the resulting integrals by sampling methods can be an effective technique if the deformed contours come near or pass through stationary-phase points of the integrand (Chang and Miller, 1987; Mak and Chandler, 1991). In one situation in which this was used (Mak and Chandler, 1991), the contour was described by a set of parameters that were varied during the calculation to maximize some measure of the success of the sampling process being used to calculate the integral.
along the real line for each of these variable. Deformation of these contours of integration and evaluation of the resulting integrals by sampling methods can be an effective technique if the deformed contours come near or pass through stationary-phase points of the integrand (Chang and Miller, 1987; Mak and Chandler, 1991). In one situation in which this was used (Mak and Chandler, 1991), the contour was described by a set of parameters that were varied during the calculation to maximize some measure of the success of the sampling process being used to calculate the integral.
Most General Formulation. Perhaps the most general formulation of these problems is the following one. Given a set of complex variables z1, ..., zn and a function of these variables g(z1, ...., Zn) that is an analytic function of all these variables for a domain that includes the real axis for each of them, calculate the following complex function of m complex variables:
The method should work for highly oscillatory functions and should take into account the fact that each evaluation of g and the location of stationary-phase points are expensive. Here z1, . . . , zm are analogous to the t in previous examples, and zm+1, ..., zn are the integration variables.
References
Baker, Jr., G.A., and J.L. Gammel, 1970, The Padé Approximant in Theoretical Physics, Academic Press, New York.
Chang, J., and W.H. Miller, 1987, Monte-Carlo path integration in real-time via complex coordinates, J. Chem. Phys. 87:16–48.
Doll, J.D., 1984, Monte Carlo Fourier path integral methods in chemical dynamics, J. Chem. Phys. 81:35–36.
Doll, J.D., Thomas L. Beck, and David L. Freeman, 1988, Quantum Monte-Carlo dynamics—The stationary phase Monte-Carlo path integral calculation of finite temperature time correlation-functions, J. Chem. Phys. 89:5753–5763.
Feynman, R.P., and A.R. Hibbs, 1965, Quantum Mechanics and Path Integrals, McGraw-Hill, New York.
Filinov, V.S., 1986, Calculation of the Feynman integrals by means of the Monte-Carlo method, Nucl. Phys. B 271:717–725.
Jacquet, R., and W.H. Miller, 1985, J. Phys. Chem. 89:21–39.
Mak, C.H., and D. Chandler, 1991, Coherent-incoherent transition and relaxation in condensed-phase tunneling systems, Phys. Rev. 44:2352–2369.
Makri, N., 1991, Feynman path integration in quantum dynamics, Computer Physics Communications 63:389.
Makri, N., and W.H. Miller, 1987, Monte-Carlo integration with oscillatory integrands: implications for Feynman path integration in real time, Chem. Phys. Lett. 139:10–14.
Makri, N., and W.H. Miller, 1989, Exponential power series expansion for the quantum time evolution operator, J. Chem. Phys. 90:904–911.
Miller, W.H., S.D. Schwartz, and J.D. Tromp, 1983, Quantum mechanical rate constants for bimolecular reactions, J. Chem. Phys. 79:488–990.
Thirumalai, D., and B.J. Berne, 1983, On the calculation of time correlation functions in quantum systems: path integral techniques, J. Chem. Phys. 79:502–933.
Wolynes, P.G., 1987, Imaginary time path integral Monte Carlo mute to rate coefficients for nonadiabatic barrier crossing, J. Chem. Phys. 87:65–59.
Yamashita, K., and W.H. Miller, 1985, "Direct" calculation of quantum mechanical rate constants via path integral methods: Application to the reaction path Hamiltonian, with numerical test for the H + H2 reaction in 3D, J. Chem. Phys. 82:5475–5484.
Fast Algebraic Transformation Methods
Numerous problems require rapid evaluation of a product of a matrix and a vector,
This arises in the transformation from one basis in a linear space to another. If computed as written, this transformation computes the n values of the transform in an amount of work proportional to n2. However, there are both exact and approximate methods that can compute such a transform much more efficiently in a variety of cases.
One of the most famous is the Fourier transform, which is frequently used to transform from physical space to frequency space. The fast Fourier transform (FFT) is a well-known algorithm for computing the n values of the transform in an amount of work proportional to n log2n. The FFT is an exact method, not an approximation: in exact arithmetic, it computes the sum exactly by a reordering of the summands. Although this algorithm is remarkably successful, recent advances have been made by further exploiting its algebraic structure.
Efficient implementation of large multidimensional FFTs on modern computers is memory bound This can be seen from the following timings for a Sun Sparcstation 10 performing an FFT on a two-dimensional image of size 2K by 2K words using the standard FFT algorithm. When carried out on a machine with 64 megabytes of random access memory (RAM), the algorithm executes in 66 seconds. However, on a machine with only 32 megabytes of RAM, the algorithm takes more than two hours, due to the fact that the 2K by 2K dataset cannot fit in RAM and data must be moved in and out of memory during the calculation. Recently, J.R. Johnson and R.W. Johnson (private communication, June 1994) reported that a truly multidimensional version of the FFT algorithm has been developed that accomplishes the same computation in only 75 seconds on a 32-megabyte machine and 47 seconds on a 64-megabyte machine.
A recent example of approximate methods is the fast multipole expansion technique, which takes advantage of special properties of the matrix (aij). This technique has been successfully applied to evaluate Coulombic potentials in molecular dynamics simulations (Ding et al., 1992). This idea has been extended (Draghicescu, 1994) to a broad class of matrices using a general approximation procedure. These more general techniques would apply directly to the non-Coulombic potentials
arising in periodic problems through the use of Ewald sums.
A closely related algebraic operation occurs in the evaluation of multilinear forms such as those that appear in density functional methods for calculating ground electronic states in quantum electronic structures. A bilinear form B((zi), (xi)) can always be written in terms of a matrix:
As written, the bilinear form would require O(n2) operations to evaluate. It can be computed instead by using the intermediate vector (yi) defined above, calculation of which requires O(n) operations, as
This way of evaluating a bilinear form can greatly reduce overall computation time, depending on how efficiently yi can be computed.
In density functional methods for calculating ground electronic states in quantum electronic structures, it is desired to approximate multilinear forms including integrals of the form
where
(Here, μi denotes a multi-index, say (pi,qi, ri) so that ![]()
In particular, such a representation arises via an expansion
Hence,
The evaluation of ρ at a single point provides an example of the alternatives for evaluating a bilinear form. Using the representation involving the matrix (Cijrequires n2 operations, whereas the expression involving the χ's requires m·n operations. If m ![]() n, the latter approach will be more efficient.
n, the latter approach will be more efficient.
The above integral can be viewed as a quadrilinear form involving the coefficients ![]() Multilinear forms can be evaluated in a variety of ways. It is tempting to represent them in terms of a precomputed tensor (a matrix for a bilinear form). Recently, Bagheri et al. (1994) have observed that it can be more efficient, in both time and memory, not to precompute expressions.
Multilinear forms can be evaluated in a variety of ways. It is tempting to represent them in terms of a precomputed tensor (a matrix for a bilinear form). Recently, Bagheri et al. (1994) have observed that it can be more efficient, in both time and memory, not to precompute expressions.
The original integral can be written
By using a suitable quadrature rule, this could be approximated via
Let Q = q2 denote the total number of quadrature points; the quadrature approximation can be calculated in an amount of work proportional to Qnm.
On the other hand, the original integral can be expressed as
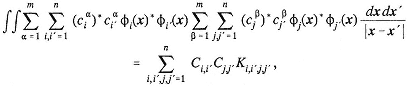
where computation of the intermediate quantities
has been introduced, which adds only O(n2m) work. The summation over i, i', j, j' requires an amount of work and storage proportional to n4 to evaluate. It would be more efficient to use the former technique if the quadrature could be done sufficiently accurately with Q ![]() n3 /m points.
n3 /m points.
The integral form involving ρ can be written as
where K is an operator defined by
If one thinks of an integral simply as a very large summation, the analogy between the integral form and the original bilinear form is apparent. With a rapid way to evaluate K, there might be a faster way to evaluate the bilinear form. (Alternative ways to evaluate ρ, based on similar considerations, have already been discussed.)
Observe that K is simply the solution operator for Poisson's equation
With this in mind, there are numerous ways to evaluate the action of K approximately, using discrete methods for approximating the solution of Poisson's equation. For example, the multigrid method can be used to do this in a very efficient way. The analogy with quadrature suggests using a grid with q points and solving Poisson's equation, with a multigrid method in O(q) work. Then the complete evaluation could be done in O(qmn) work. This potentially would be faster than direct evaluation of the integrals.
References
Bagheri, B., L.R. Scott, and S. Zhang, 1994, Implementing and using high-order finite element methods, Finite Elements in Analysis and Design 16:175–189.
Ding, Hong-Qiang, Naoki Karasawa, and William A. Goddard III, 1992, Atomic level simulations on a million particles: The cell multipole method for Coulomb and London nonbond interactions, J. Chem. Phys. 97:4309–4315.
Draghicescu, C.I., 1994, An efficient implementation of particle methods for the incompressible Euler equations, SIAM J. Numer. Anal. 31: 1090–1108.


































































