8
Morphological Evolution Through Complex Domains of Fitness
Karl J. Niklas
… the central problem of evolution … is that of a mechanism by which the species may continually find its way from lower to higher peaks.
Sewall Wright
The history of life is to be studied by a great variety of means, among which special importance attaches to the actual historical record in rocks and the fossils contained in them.
George Gaylord Simpson
A powerful metaphor, proposed by Sewall Wright (Wright, 1931, 1932; Provine, 1986), conceives of evolution as a ''local search" for "adaptive peaks" by progressively fitter mutants. This image of a walk over a fitness-landscape forcefully draws attention to the relation between the number and location of fitness peaks, on the one hand, and the number and magnitude of phenotypic transformations among neighboring variants required to increase fitness, on the other (Kauffman, 1993; Maynard Smith, 1970). However, comparatively few attempts have been made to quantify the relation between the topology of landscapes and the dynamics of walks (Eigen, 1987; Gillespie, 1983; Kauffman and Levin, 1987). Among the numerous obstacles to quantitative analyses of Wright's metaphor are (i) the de minimus requirement for mapping all possible genotypes onto their corresponding pheno-
Karl J. Niklas is professor of botany at Cornell University, Ithaca, New York.
types for a complete analysis of phenotypic variation (Scharloo, 1991), (ii) the possibility that the fitness contributed by performing one task depends upon the ability to perform other tasks simultaneously (i.e., epistatic fitness-contributions; Ewens, 1979; Franklin and Lewontin, 1970; Lewontin, 1974), (iii) the likelihood that the dynamics of a walk depend upon the walk's point of origin on the landscape in addition to intrinsic genetic or developmental barriers to phenotypic transformations, and (iv) the requirement to treat biological realistic temporal and spatial variations in the topology of fitness-landscapes, as well as (v) the complex interactions among a panoply of physical and biological variables that collectively define fitness (Kauffman, 1993; Gould, 1980; Levin, 1978).
Nonetheless, the image of the fitness-landscape continues to inspire questions about the tempo and mode of evolution—for example, what is the relation between the number of fitness peaks and the number of functional tasks that an organism must simultaneously perform to grow, survive, and reproduce? Although there is no a priori reason to assume that the number and location of phenotypic optima depend upon the number of tasks an organism must perform, there are good reasons to believe that manifold functional obligations author "course-grained" landscapes with many phenotypic optima. For example, engineering theory shows that the number of equally efficient designs for an artifact generally is proportional to both the number and the complexity of the tasks than an artifact must perform (Meredith et al., 1973) because the efficiency with which each of many tasks is performed must be relaxed due to unavoidable conflicting design specifications for individual tasks (Gill et al., 1981), and, as the number of tasks increases, the number of configurations that achieve equivalent or nearly equivalent performance levels increases (Brent, 1973). If such relationships hold true for organisms, these relations may account for the morphological and anatomical diversity seen among even closely related species. Indeed, the sharp logical distinction between "optima" and "maxima," on the one hand, and the observation that a multi-task artifact may assume diverse appearances, on the other, suggest the hypothesis that the imposition of manifold obligations increases the number of equally fit phenotypes.
Although the problematic analogy between engineered and biological systems speaks to the topology of fitness-landscapes, it sheds no light on questions related to the dynamics of walks—for example, what is the relation between the number of tasks that an organism must perform and the magnitude of the morphological transformations between neighboring variants required to reach fitness optima? Are walks confined to nearest-neighbor variants or are they free to reach compara-
tively distant morphologies? At some level, the number and magnitude of phenotypic transformations comprising a walk must depend upon both the location of fitness peaks and the extent to which the fitness of neighboring variants are correlated. However, it is evident also that the extent to which a walk proceeds depends upon the ability of an organism to alter its phenotype. Although the developmental repertoire of most organisms permits some latitude in external shape and internal structure, walks undoubtedly are governed by genetic or developmental mechanisms that establish barriers to transformations among neighboring variants on the landscape (Alberch, 1980, 1981, 1989; Odell et al., 1981; Oster et al., 1980). Thus, morphological transformations among phenotypes are not equiprobable, and walks cannot be governed exclusively by the topology of the fitness-landscape.
Plants as a Venue for Simulated Walks
The extent to which walks are genetically or developmentally unfettered is a matter of relative rather than absolute degree because it undoubtedly varies among organisms and changes over evolutionary time. For example, the developmental "plasticity" of plants appears extremely high in comparison with most animals (Schmid, 1993; Sultan, 1987; Van Tienderen, 1990). By the same token, certain periods of evolutionary time are characterized by exceptionally high rates of phenotypic innovation as, for example, the colonization of the terrestrial landscape by the first vascular plants (Figure 1). Indeed, one is left with the impression that the walks of plants, in general, and those of early tracheophytes, in particular, feature phenotypic transformations sufficient to achieve many, perhaps most, of the morphological optima widely scattered over their fitness-landscapes.
An added advantage to dealing with plants is that their fitness calibrates closely with the operation of physical laws and processes governing the exchange of mass and energy between the plant body and the external environment, which have remained constant over evolutionary time (Gates, 1965; Brent, 1973; Alberch, 1980, 1981, 1989; Oster et al. , 1980; Gill et al., 1981; Odell et al., 1981; Nobel, 1983; Sultan, 1987; Van Tienderen, 1990; Niklas, 1992; Schmid, 1993). Thus, the broad outlines of the fitness-landscape for plants likely have remained comparatively constant. If so, then plants may be the ideal venue for examining the relation between the topology of fitness-landscapes and the dynamics of more or less unrestricted walks.
The assumption that walks are unimpeded over stable fitness-landscapes greatly simplifies attempts to explore the relation between
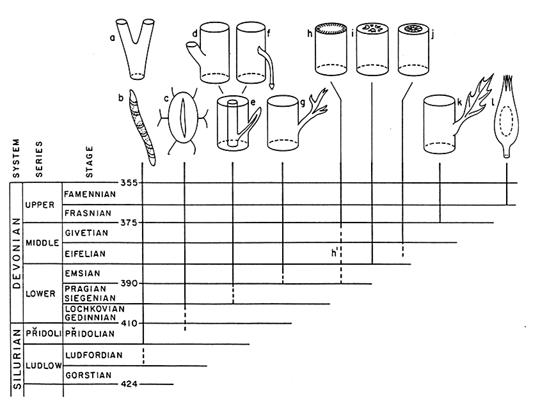
Figure 1 First occurrences of some morphological and anatomical features in the fossil record of Upper Silurian and Devonian Period vascular land plants (Niklas, 1992): (a) equal branching, (b) tracheids, (c) stomata, (d) unequal branching, (e) vascularized appendages, (f) adventitious roots, (g) planated lateral branches, (h) continuous periderm, (h') patches of periderm, (i) dissected steles, (j) secondary xylem, (k) planated, webbed leaves, (l) ovules.
landscape topology and the dynamics of walks, particularly in terms of computer simulations. The first step is to simulate a multidimensional domain of all conceivable phenotypes—a "morphospace" (sensu Thomas and Reif, 1993). The next step is to determine the ability of every hypothetical phenotype to perform each of a few biologically realistic tasks, in addition to its ability to simultaneously perform various combinations of these tasks—that is, the fitness of phenotypes must be mapped to establish and quantify the topology of the fitness-landscape. Then, beginning with the same ancestral phenotype, a computer algorithm can be used to search the morphospace for successively more fit phenotypes. Simulations of this sort are brought to closure when each phenotypic maximum or optimum within the morphospace is reached by a walk, after which the number and magnitude of the phenotypic transformations in a walk, as well as the number of phenotypic maxima or optima within different fitness-landscapes, are computed and compared. Clearly, to be useful, this heuristic protocol requires nonarbitrary definitions for "morphology," "function," and "ancestor.'' It also must be cast in terms of a real evolutionary episode against which simulated walks and predicted phenotypic maxima or optima can be compared and contrasted with the actual morphological trends established by the fossil record.
The early evolution of vascular land plants is a case in point. The most ancient tracheophytes had cylindrical, bifurcating axes that lacked leaves and roots (Banks, 1975; Edwards et al., 1992; Stewart and Rothwell, 1993; Taylor and Taylor, 1993). These morphologies are easily simulated by means of a computer with only six variables (Niklas and Kerchner, 1984; Niklas, 1988). Referring to Figure 2, in which each axis of a bifurcate pair is distinguished by the subscript 1 or 2, the six variables are the probabilities of branching P1 and P2, the rotation angles subtended between each axis and the horizontal plane γ1 and γ2, and the bifurcation angles subtended between the longitudinal axis of each axial member and the longitudinal axis of the subtending member ø1 and ø2. Indeed, a morphospace containing 200,000 phenotypes, encompassing virtually the entire spectrum of early vascular land-plant morphology, can be simulated by establishing the limiting conditions (and increments) for these six variables: 0 ≤ P ≤ 1 (in increments of 0.01), and 0° ≤ g ≤ 180° and 0° ≤ ø ≤ 180° (both in increments of 1°). Within this morphospace, the simplest phenotype (i.e., a Y-shaped plant) results when P1 = P2 = 0 and ø1 = ø2. Higher values of P produce more complex, highly branched morphologies. Morphologies with equal (isometric) branching are simulated when P1 = P2. Plants with anisometric (unequal) branching, very much like those that appear in the Devonian Period, are obtained when P1![]() P2 . And phenotypes with
P2 . And phenotypes with
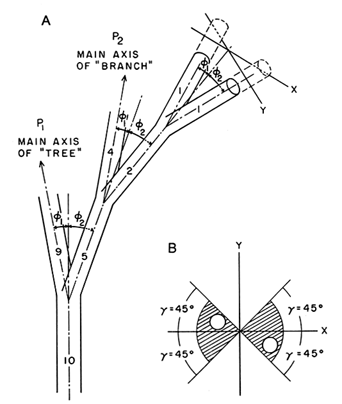
Figure 2 Variables used to simulate branched morphology of early vascular land plants: P, probability of branching; ø, bifurcation angle; γ, rotation angle (subscripts 1 and 2 distinguish parameters for each axis in a branch-pair). (A) Three-dimensional bifurcate pattern of branching for which the orientation of each axis is prescribed by ø and γ. (B) Transverse view of terminal branch-pair in A showing the geometric affect of γ.
horizontally flattened (planated) branching systems are simulated when γ1 = γ2 = 0°.
Because six variables are required to simulate ancient tracheophytes, hypothetical phenotypes occupy a multidimensional space. Although this makes the graphic display of simulated walks somewhat difficult, the situation is greatly simplified by initiating simulations of walks in the isometric domain of the morphospace (i.e., P1 = P2) and permitting optima within this domain to enter the anisometric domain of the morphospace (i.e., P1![]() P2). Conceptually, this simulation is illustrated in Figure 3A.
P2). Conceptually, this simulation is illustrated in Figure 3A.
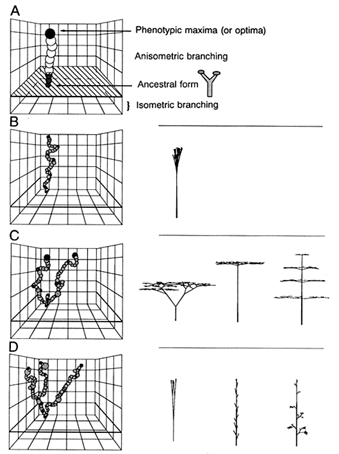
Figure 3 Multidimensional domain (morphospace) of simulated branching patterns (A) and simulated walks through three single-task fitness-landscapes (B-D). (A) Simplified version of the morphospace represented in Cartesian space (x, y, z) consisting of two subdomains of shape (isometric and anisometric branching). Each walk is "seeded" with the simplest shape in the isometric domain (i.e., a Y-shaped ancestral form) and represents a series of genetically and developmentally unfettered steps that obtain phenotypic maxima or optima (shown at right). (B) A walk through a reproductive-success landscape. (C) A walk through a light interception landscape. (D) A walk through a mechanical stability landscape (see Table 1).
Turning attention to the topology of the fitness-landscape, the functional obligations assuring growth, survival, and reproduction must be known and quantified. For early vascular land plants, these obligations can be inferred from living tracheophytes and undoubtedly include the requirement to intercept sunlight, to mechanically sustain the weight of aerial organs, and to be able to produce and disperse diaspores some distance from parental plants. Fortunately, each of these tasks can be quantified by means of closed-form equations derived from biophysics or biomechanics. For example, the efficiency E of a computer-simulated phenotype to intercept solar irradiance (of intensity I measured perpendicular to its surfaces) is given by the formula
where Sp is the total unshaded surface area of the phenotype projected toward incident light, S is the total surface area of the phenotype, and Θ is the incident solar angle, which varies between 0° and 180° in each diurnal cycle (Niklas and Kerchner, 1984). Because the magnitude of I is independent of Θ (assuming atmospheric conditions are clear), Eq. 1a reduces to
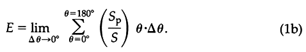
Although the total projected area Sp of each morphology varies as a function of Θ, it also depends upon the orientation of axes in addition to the extent to which neighboring axes shade one another. All of these variables can be dealt with by even the most simple computer.
In terms of mechanical stability, the maximum bending stresses σmax that develop in a cylindrical plant axis may be computed from the formula
where M is the bending moment, which has units of force times length, and + and - denote tensile and compressive stresses, respectively (Niklas, 1992). For any value of d, the bending stresses are directly proportional to the bending moment that, when expressed in terms of Φ and γ, is given by the formula
where ρ is the bulk density of tissues used to fabricate a plant and g is gravitational acceleration. Assuming that the bulk density varies little from one plant to another, M α γ-1 sin Φ. Thus, the bending moment and therefore the maximum bending stresses are minimized when Φ = 90° (i.e., a vertically oriented axis).
In terms of spore dispersal, an elementary ballistic model suffices:
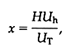
where x is the lateral distance of transport, H is the height at which spores are released from the parent plant, UT is the average settling velocity of spores, and Uh is the horizontal wind speed averaged between H and ground level, which is assumed to parabolically diminish from the top to the base of the plant (Okubo and Levin, 1989). Assuming that UT is independent of H and that Uh is proportional to H, the maximum lateral transport distance for spores is proportional to the square of plant height, x α H2, indicating that even a small increase in plant height confers a selective advantage to spore dispersal. However, the number of spores a plant produces is as important to its reproductive success as the distance spores are transported (Niklas, 1986). Thus, the fitness contribution of the number of spores produced per plant must be considered in addition to the fitness contributed by elevating spores above ground level. Assuming that spores are produced at the tips of branches and that the number of spores per sporangium varies little among hypothetical phenotypes, reproductive fitness R is maximized by maximizing both the number n and height of branch tips: R = f(n, H).
The foregoing implicitly assumes that fitness is proportional to E and R and inversely proportional to M. Assuming that each of these three functional obligations contributes equally and independently to fitness, the most parsimonious mathematical expression for the total fitness F of a phenotype is the geometric mean of E and R divided by M—i.e., F = [(E)(R)]1/2M-1. Importantly, the topology of the fitness-landscape for each of the three functional tasks differs because different functional obligations can have different phenotypic requirements. For example, phenotypes that maximize light interception also maximize their bending moments. However, a phenotype with a high fitness in terms of its ability to garner irradiate energy for photosynthesis will have a low fitness in terms of its high probability for mechanical failure. Consequently, when both of these functions are considered simultaneously, the objective of a walk is to optimize E/M. Although E cannot be maximized without maximizing M, some functional obligations reinforce the same morphological solution because their phenotypic require-
ments are very similar. Phenotypes that maximize the potential for long-distance spore dispersal tend to minimize the bending moment on their vertical axes. Theoretically, therefore, walks that optimize R/M are comparatively direct and simple. From the formula for total phenotypic fitness F, the topology of the fitness-landscape resulting when all three tasks are considered simultaneously is more complex than those resulting when only one or two tasks are considered. Specifically, phenotypes that maximize long-distance spore dispersal (high fitness) also minimize their bending moments (high fitness) but minimize their ability to intercept sunlight (low fitness) because most of their branches are vertically oriented and therefore bunched together.
Once the topology of the fitness-landscape has been quantified, walks must be "seeded"—that is, they must be assigned a nonarbitrary point of origin. Once again, the fossil record for early tracheophytes is invaluable in this regard. The simplest and most ancient phenotype known for vascular land plants is epitomized by the Silurian fossil remains of Cooksonia. The sporophyte of this genus consisted of one, or more than one, short-branched cylindrical axes that terminated in sporangia and lacked leaves or roots (Banks, 1975; Edwards et al., 1992). This morphology can be taken as the point of origin for each walk, regardless how fitness is mathematically defined. Each walk proceeds as a sequence of N number of steps, each representing a morphological transformation to a more fit phenotype from the preceding phenotype. The sequence of steps in a walk, therefore, serves to identify more fit phenotypes. The magnitude of each phenotypic transformation can be depicted as the volume of the morphospace that must be searched by a computer-driven algorithm until the next more fit phenotype is reached. The volume searched by each step in a walk can be quantified by its diameter D. Each walk is permitted to branch when two or more phenotypes with equivalent fitness are identified by the algorithm. Each walk is brought to closure when it obtains all the phenotypic maxima within a single-function landscape or all the phenotypic optima within multi-function landscape. The mean diameter ¯D and the SE of D for all the steps in a walk quantify the mean variation in the phenotypic transformations required to achieve all maxima or optima within a particular fitness-landscape. The volume fraction VF of the entire morphospace occupied by a walk can be computed from the formula VF = [(ΣDi)V-1/T] × 100%, where VT is the total volume of the morphospace. Because the sample statistics obtained from single-and multiple-function fitness-landscapes (i.e., N, n, ¯D, VF) have unequal variances, the approximate t test, ¦t's¦, can be used to test for equality of sample means (Snedecor and Cochran, 1980; Sokal and Rohlf, 1981).
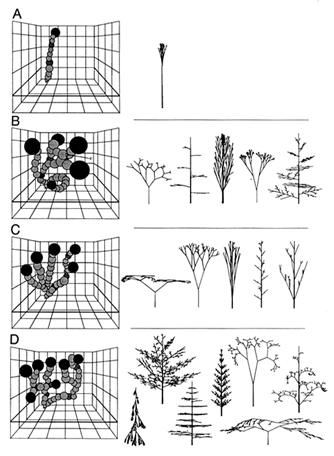
Figure 4 Walks within four multi-task landscapes (Left) and phenotypic optima (Right). (A) A walk through a mechanical stability and reproductive success landscape. (B) A walk through a light interception and mechanical stability landscape. (C) A walk through a light interception and reproductive success landscape. (D) A walk through a light interception, mechanical stability, and reproductive success landscape (see Table 1).
Single- Versus Multi-task Walks
Unfettered walks over stable fitness-landscapes are illustrated in Figs. 3 and 4 for a morphospace containing 200,000 phenotypes mimicking early vascular land plants. As noted, the morphospace is multidimensional, consisting of a domain occupied by "ancient" isometrically branched phenotypes and another occupied by more "derived" anisometrically branched morphologies (Figure 3A). Consequently, the plots
TABLE 1 Sample statistics for simulated walks in Figs. 3 and 4
|
|
Sample statistics* |
|||
|
|
N |
n |
D(± SE) |
VF |
|
Single-task walks |
|
|
|
|
|
Light interception, E |
116 |
3 |
5.81 ± 0.152 |
0.568 |
|
Mechanical stability, M |
81 |
3 |
5.49 ± 0.186 |
0.335 |
|
Reproductive success, R |
56 |
1 |
4.37 ± 0.130 |
0.117 |
|
|
84.3 ± 17.4 |
2.33 ± 1.15 |
5.22 ± 0.44 |
0.34 ± 0.13 |
|
Multi-task walks |
||||
|
E-M-R |
49 |
7 |
14.4 ± 0.58 |
3.65 |
|
E-R |
41 |
5 |
15.1 ± 1.02 |
3.53 |
|
E-M |
40 |
5 |
21.6 ± 1.26 |
10.1 |
|
M-R |
13 |
1 |
13.7 ± 1.63 |
0.84 |
|
|
35.8 ± 7.85 |
4.50 ± 1.26 |
16.2 ± 1.82 |
4.52 ± 2.26 |
|
*N, number of steps in walk; n, number of phenotypic maxima or optima in landscape; D, mean diameter of steps in walk; VF, volume fraction of morphospace occupied by walk. |
||||
of walks are graphic reactions of mathematically more complex features. Every walk proceeds through the same morphospace; walks differ solely as a consequence of differences in fitness topologies. Specifically, walks are shown for three single-task and four multi-task-defined fitness-landscapes. The three individual tasks are light interception E, mechanical stability M, and reproduction R (Figure 3). In turn, these tasks have four combinatorial permutations (Figure 4), three of which give two-task landscape (i.e., E-M, E-R, M-R) and one of which is a three-task landscape (i.e., E-M-R).
The most apparent differences between simulated single- and multi-task walks are the number and magnitude of their phenotypic transformations, on the one hand, and the number of phenotypic maxima and optima they reach within landscapes, on the other (Table 1). Single-task walks have many small phenotypic transformations within landscapes that contain what appear to be comparatively few phenotypic maxima. By contrast, multi-task walks have few, but large, transformations within landscapes that, at first glance, appear to contain comparatively many phenotypic optima. Also, the mean morphospace volume occupied by multi-task walks is greater than that occupied by single-task walks (Table 1). Statistical comparisons indicate that the hypothesis that multi-task walks require significantly larger phenotypic transformations than those of single-task walks can be accepted (Table 2). However, statistical comparisons show that the mean number of phenotypic maxima in single-task landscapes does not significantly differ from that of optima in multi-task landscapes. In part, this is due to the small sample sizes for each of these two categories of fitness-landscape and to
TABLE 2. Summary of ![]() tests for the equality of
tests for the equality of ![]() values (see Table 1)
values (see Table 1)
|
|
Parameter* |
|||
|
|
N |
n |
D |
VF |
|
|
1.55 |
2.17 |
5.87 |
9.46 |
|
|
3.66 |
3.69 |
3.25 |
3.19 |
|
* |
||||
the fact that the topology of fitness resulting from performing two tasks, mechanical stability and reproduction, contains a single phenotypic optimum (Figure 4A) that dramatically depresses the mean and inflates the SE for the mean number of optima. Nonetheless, the largest number of optima observed among all simulated landscapes is attained when fitness is quantified in terms of all three tasks, suggesting that the hypothesis would have been accepted had walks been simulated in landscapes for which fitness was defined in terms of other biological tasks in addition to light interception, mechanical stability, and reproduction.
It is instructive to compare the fitness of phenotypic maxima with the fitness of phenotypic optima. Although every simulated walk is permitted to reach all the maxima or optima in a particular landscape, the elevation of peaks (maxima or optima) differs from one landscape to another because fitness is defined in different terms in each landscape. Because phenotypic maxima and optima occupy fitness peaks, their absolute fitnesses define a landscape's elevation and, therefore, the gradient of the phenotypic transformations attending a walk. In theory, the magnitudes of the fitness of phenotypic maxima are greater than the magnitudes of the fitness of phenotypic optima. Therefore, the observation that the fitness of phenotypic maxima is greater than that of phenotypic optima is somewhat trivial. What is not unimportant, however, is that the "currency" in which fitness is measured differs among landscapes—that is, fitness was measured in different units (e.g., quanta of light absorbed, probability of mechanical failure, distance of spore dispersal). Therefore, comparisons among the elevations of different landscapes can be made only in relative, rather than absolute, terms. The ratio of the fitness of a phenotypic maximum (or optimum) and the fitness of the ancestral phenotype is useful because it normalizes the elevation of peaks and can be used to crudely compare the topologies of very different landscapes.
Noting that the normalized fitness values are ratios, a comparison for the fitness-landscapes shown in Figure 3 with those shown in Figure 4 indicates that the topologic relief of single-task landscapes is, on the average, 10 times greater than that of multi-task landscapes—that is, the fitnesses of phenotypic maxima with respect to the fitnesses of their ancestral condition are 10 times greater than the fitnesses of phenotypic optima with respect to their ancestral condition. Thus, the fitness of phenotypic optima apparently falls closer to the mean fitness of all the phenotypes within a landscape as the functional complexity of the phenotypes under selection increases. As noted, this result is consistent with engineering theory that indicates that the performance levels of artifacts designed to perform individual functional tasks are higher than those of artifacts designed to simultaneously perform two or more of the same tasks. Additionally, within both categories of fitness-landscapes, the relative fitness values of phenotypes occupying fitness peaks decreases as the number of peaks increases (r = 0.82; N = 25 maxima and optima)—that is, the number of phenotypic maxima (or optima) increases as the elevation of a landscape declines.
These observations are crudely summarized in Figure 5; they suggest that both the number and the accessibility of phenotypic optima increase as the number of functional obligations contributing to total fitness increases. Put differently, as the complexity of optimal phenotypes increases, the fitness of these optima falls closer to the mean fitness of all the phenotypes under selection. One implication of this conclusion is that the majority of walks over complex fitness-landscapes occurs over fitness plateaus and, therefore, is largely undirected by gradients of fitness until walks approach the foothills of fitness peaks.
Weaknesses and Strengths of Simulated Walks
However entertaining they may be, computer-simulated walks have four obvious weaknesses. First, "fitness" was measured in terms of comparatively few biological tasks that were further assumed to contribute to fitness in an independent and equal manner. The obvious epistatic relation between photosynthesis and reproduction (Gates, 1965; Nobel, 1983), therefore, was entirely neglected, as was the possibility that some tasks are more important to fitness than others (Franklin and Lewontin, 1970; Lewontin, 1974; Ewens, 1979). Second, walks were simulated as continuous processions among more fit phenotypes. Alternatively, plausible types of walks were not considered (Gillespie, 1983, 1984; Kauffman, 1993). Third, fitness-landscapes were assumed to be spatially stable in pointed neglect of evident changes in the environment that are predicted to shift the location of fitness optima
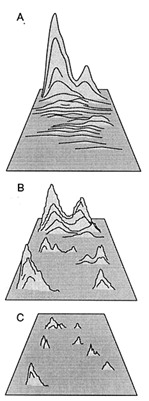
Figure 5 Diagrammatic relations among relative phenotypic fitness, the number of phenotypic maxima or optima, and the coarseness of fitness-landscapes. As phenotypic complexity (i.e., the number of biological tasks to be simultaneously performed by organisms) increases, the relative elevation of fitness peaks declines, but the number of phenotypic maxima (or optima) and the coarseness of the landscape increase (A-C).
and accelerate evolution, particularly in very large panmictic populations (Wright, 1932). And fourth, all walks were assumed to be unfettered by genetic or development constraints. Even for plants, which arguably may be more phenotypically ''plastic" than animals, this is a naive expectation (Maynard Smith et al., 1985).
On the other hand, the approach taken here has some obvious strengths. First, walks were simulated over a dimensionally complex morphospace containing phenotypes representative of the entire spectrum of vascular land-plant morphology. Second, although only three were considered, the functional obligations elected to define and quantify fitness are biologically realistic for the majority of past and present terrestrial plant species. Third, although the environment, living and nonliving, is in constant flux, the particular episode of plant evolution focused upon here most likely was dominated by the operation of physical laws and processes. Metaphorically, the fitness-landscape of the first occupants of the terrestrial landscape was painted in the primary colors of biophysics rather than the subtle hues of complex
biotic interactions characterizing subsequent plant history. And fourth, the morphological trends predicted by the phenotypic transformations attending simulated walks are, in very broad terms, compatible with those actually seen in the fossil record of early tracheophytes. This correspondence is important on two accounts. First, it suggests that the developmental repertoire of early vascular plants was capable of phenotypic transformations sufficiently dramatic to warrant the assumption that the walks entertained by these organisms were largely developmentally unfettered. Second, if the hypothetical relations between fitness topologies and the dynamics of walks forecast by computer simulations have any relevancy, then they must, at the very least, mimic trends evinced in the fossil record of plants.
There can be little doubt that the phenotypic optima reached by simulated walks, particularly those over the tripartite fitness-landscape, are morphologically complex (Figure 4D) nor that all phenotypic maxima or optima are attainable by walks proceeding essentially from the archetypal vascular land plant (i.e., Cooksonia). Fossil remains from the Late Silurian Period indicate that the first tracheophytes were comparatively short, consisting of equally branched, naked axes that simultaneously functioned as photosynthetic and reproductive organs. During much of the Devonian Period, the maximum stature of sequentially younger plant taxa steadily increased. This intertaxonomic trend in plant size was attended by significant evolutionary changes in branching morphology, among which unequal branching and horizontally planated lateral branching systems are notable. Importantly, unequal branching is a requisite for and, therefore, prefigures the elaboration of a main vertical axis for mechanical support. By the same token, the planation of lateral branches, which facilitates light interception, has been traditionally interpreted as a precursor to the evolution of megaphylls (Stewart and Rothwell, 1993). Therefore, it is not unreasonable to suppose that the transition from equal to unequal branching, which was evolutionarily rapid and invariably adopted by simulated walks, was a requisite for subsequent morphological trends and likely positioned derived phenotypes at the foothills near (rather than within the valleys between) fitness peaks (Figure 6).
By the latest Devonian Period arborescent species bearing planated lateral branching systems and true leaves were not uncommon (Stewart and Rothwell, 1993; Taylor and Taylor, 1993). This fact is consistent with the observation that the majority of the phenotypic maxima in multi-task landscapes have horizontally planated lateral branching systems, as do the phenotypic maximum in the fitness-landscape defined by light interception. Virtually every major vascular land-plant lineage evolved arborescent, leaf-bearing species, although these species obviously
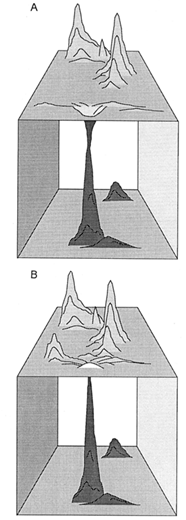
Figure 6 Alternative hypothetical topologies of a complex fitness-landscape. In both cases, the ancestral phenotype resides within the lower (boxed) domain, and descendent phenotypic variants must ascend the prominent (darkly shaded) fitness peak in this domain before a walk can proceed over the upper (unboxed) domain. (A) The first phenotypic variant entering the upper domain occupies a fitness minimum (valley) distant from fitness peaks. (B) The first phenotypic variant entering the upper domain resides on a local fitness-maximum (foothill) near fitness peaks.
differed in morphological, as well as anatomical, details. In very broad terms, the appearance of ancient tracheophyte lineages evincing parallel or convergent phenotypic evolution is a feature mimicked by simulated walks. In all but two fitness-landscapes, walks repeatedly branched to obtain many phenotypic maxima or optima, most of which have a tree-like appearance (i.e., unequally branched with a main vertical "stem") with many lateral, planated "branches" or "leaf-like appendages." Some walks even converge on and cross through the same
regions in the hypothetical morphospace of early vascular land plants (see Figure 4B).
Another, although highly problematic, parallel that can be drawn between simulated walks and the early evolution of tracheophytes relates to the "dilated" terminal steps of each branch in the walks through multi-task landscapes. These terminal steps indicate that the last phenotypic transformations required to reach optima within a landscape are more sensational compared with prior phenotypic transformations. This hypothesis is consistent with the fact that the highest-per-taxon origination rates as well as the highest rates of appearance of morphological (as well as anatomical) characters occur toward the end of the Devonian Period, which marks the closure of early land-plant evolution (Niklas et al., 1980; Knoll et al., 1984). Interestingly, a significant temporal lag between the first appearance and rapid taxonomic diversification of animal, as well as plant, lineages is not atypical (Sepkoski, 1979; Tiffney, 1981). It should be noted, however, that simulated walks have no temporal component—steps in walks are vectors whose magnitudes are measured in space, not time. Although the volume of the morphospace occupied by a step denotes the phenotypic variance required to reach the next more fit phenotype, the "time" required to achieve this variance cannot be specified.
However tantalizing the similarities between simulated walks and the broad morphological trends seen in early land-plant evolution, they cannot be taken as prima facie evidence that the mathematical and statistical properties of simulated walks reflect reality, nor can they be taken as evidence that the early evolution of vascular plant shape was governed by the biological obligations to intercept sunlight, remain mechanically stable, or to disperse large numbers of spores over great distances. However important these biological tasks may be to plant growth, survival, and reproductive success, the correspondence between simulated and empirically determined morphological trends for early tracheophytes may be simply fortuitous. And, under any circumstances, correlation can never be taken as evidence for a cause-effect relationship.
With these caveats clearly in mind, the following hypotheses are tentatively proposed for future study: (1) The fitness-landscapes defined by a single biological task require comparatively small, but numerous, morphological transformations to reach phenotypic maxima (i.e., single-task landscapes are "fine-grained," yet steep), whereas manifold functional obligations obtain "course-grained," but less steep, fitness-landscapes; (2) course-grained landscapes contain a greater number of phenotypic optima than the number of phenotypic maxima in fine-grained landscapes; (3) multi-task-driven walks occupy a greater volume
of the morphospace than do single-task-driven walks; (4) multi-task optima have a lower overall fitness than single-task phenotypic maxima; (5) organisms evincing developmental plasticity (and therefore the potential for significant phenotypic variation) (i) evolutionarily benefit by their ability to walk "rapidly" through and occupy a greater volume of the theoretically available morphospace, (ii) will be at increasing advantage as the number of manifold functional obligations increases, but (iii) are at a disadvantage whenever circumstances abruptly change to favor a single functional obligation rather than the full complement of functions.
Wright's metaphor suggests a "trial and error mechanism on a grand scale by which the species may explore the region surrounding the small portion of the fitness field which it occupies" (Wright, 1932). Attempts to cast this and other evolutionary mechanisms in terms of biologically realistic models by means of computer simulations are still very much in their infancy. As heuristic tools, however, simulations designed to forecast opportunistic phenotypic transformations over the topologies of fitness-landscapes illustrate some of the initial steps required to adapt Wright's metaphor to understanding the evolution of plant morphology.
Summary
Computer simulated phenotypic walks through multi-dimensional fitness-landscapes indicate that (1) the number of phenotypes capable of reconciling conflicting morphological requirements increases in proportion to the number of manifold functional obligations an organism must perform to grow, survive, and reproduce, and (2) walks over multi-task fitness-landscapes require fewer but larger phenotypic transformations than those through single-task landscapes. These results were determined by (1) simulating a "morphospace" containing 200,000 phenotypes reminiscent of early Paleozoic vascular sporophytes, (2) evaluating the capacity of each morphology to perform each of three tasks (light interception, mechanical support, and reproduction) as well as the ability to reconcile the conflicting morphological requirements for the four combinatorial permutations of these tasks, (3) simulating the walks obtaining all phenotypic maxima or optima within the seven "fitness-landscapes," and (4) computing the mean morphological variation attending these walks. The results of these simulations, whose credibility is discussed in the context of early vascular land-plant evolution, suggest that both the number and the accessibility of phenotypic optima increase as the number of functional obligations contributing to total fitness increases (i.e., as the complexity of optimal phenotypes in-
creases, the fitnesses of optima fall closer to the mean fitness of all the phenotypes under selection).
References
Alberch, P. (1980) Ontogenesis and morphological differentiation. Am. Zool. 20, 653–667.
Alberch, P. (1981) Convergence and parallelism in foot morphology in the neotropical salamander Bolitoglossa. I. Function. Evolution 35, 84–100.
Alberch, P. (1989) The logic of monsters: Evidence for internal constraints in development and evolution. In Ontogenèse et Evolution, eds. David, B., Dommergues, J. L., Chaline, J. & Laurin, B. (Geobios, Lyon, France), Vol. 12, pp. 21–57.
Banks, H. P. (1975) Early vascular land plants: proof and conjecture. BioScience 25, 730–737.
Brent, R. P. (1973) Algorithms for Minimization Without Derivatives (Prentice-Hall, Englewood Cliffs, NJ), p. 195.
Edwards, D., Davies, K. L. & Axe, L. (1992) A vascular conducting strand in the early land plant Cooksonia. Nature (London) 357, 683–685.
Eigen, M. (1987) New concepts for dealing with the evolution of nucleic acids. In Cold Spring Harbor Symp. Quant. Biol. 52, 307–320.
Ewens, W. (1979) Mathematical Population Genetics (Springer, New York), p. 325.
Franklin, I. & Lewontin, R. C. (1970) Is the gene the unit of selection? Genetics 65, 707–717.
Gates, D. M. (1965) Energy, plants, and ecology. Ecology 46, 1–16.
Gill, P. E., Murray, W. & Wright, M. H. (1981) Practical Optimisation (Academic, London), p. 401.
Gillespie, J. H. (1983) A simple Stochastic gene substitution model. Theor. Popul. Biol. 23, 202–215.
Gillespie, J. H. (1984) Molecular evolution over the mutational landscape. Evolution 38, 1116–1129.
Gould, S. J. (1980) The evolutionary biology of constraint. Daedalus 109, 39–52.
Kauffman, S. A. (1993) The Origins of Order (Oxford Univ. Press, Oxford), p. 709.
Kauffman, S. A. & Levin, S. A. (1987) Towards a general theory of adaptive walks on rugged landscapes. J. Theor. Biol. 128, 11–45.
Knoll, A. H., Niklas, K. J., Gensel, P. G. & Tiffney, B. H. (1984) Character diversification and patterns of evolution in early vascular plants. Paleobiology 10, 34–47.
Levin, S. A. (1978) On the evolution of ecological parameters. In Ecological Genetics: The Interface, ed. Brussard, P. F. (Springer, New York), pp. 3–26.
Lewontin, R. C. (1974) The Genetic Basis of Evolutionary Change (Columbia Univ. Press, New York), p. 346.
Maynard Smith, J. (1970) Natural selection and the concept of protein space. Nature (London) 225, 563–564.
Maynard Smith, J., Burian, R., Kauffman, S., Alberch, P., Campbell, J., Goodwin, B., Lande, R., Raup, D. & Wolpert, L. (1985) Developmental constraints and evolution. Q. Rev. 60, 265–287.
Meredith, D. D., Wong, K. W., Woodhead, R. W. & Wortman, R. H. (1973) Design and Planning of Engineering Systems, eds. Newmark N. M. & Hall, W. J. (Prentice-Hall, Englewood Cliffs, NJ), p. 393.
Niklas, K. J. (1992) Plant Biomechanics: An Engineering Approach to Plant Form and Function (Univ. of Chicago Press, Chicago), p. 607.
Niklas, K. J. (1988) Biophysical limitations on plant form and evolution. In Plant Evolutionary Biology, eds. Gottlieb, L. D. & Jain, S. K. (Chapman and Hall, London), pp. 185–220.
Niklas, K. J. (1986) Computer-simulated plant evolution. Sci. Am. 254, 78–86.
Niklas, K. J. & Kerchner, V. (1984) Mechanical and photosynthetic constraints on the evolution of plant shape. Paleobiology 10, 79–101.
Niklas, K. J., Tiffney, B. H. & Knoll, A. H. (1980) Apparent changes in the diversity of fossil plants: A preliminary assessment. In Evolutionary Biology, eds. Hecht, M., Steere, W. & Wallace, B. (Plenum, New York), Vol. 12, pp. 1–89.
Nobel, P. S. (1983) Biophysical Plant Physiology and Ecology (Freeman, New York), p. 608.
Odell, G. M., Oster, G., Alberch, P. & Burnside, B. (1981) The mechanical basis of morphogenesis. I. Epithelial folding and invagination. Dev. Biol. 85, 446–462.
Okubo, A. & Levin, S. A. (1989) A theoretical framework for data analysis of wind dispersal of seeds and pollen. Ecology 70, 329–338.
Oster, G. F., Odell, G. & Alberch, P. (1980) Mechanics, morphogenesis and evolution. In Lectures on Mathematics in the Life Sciences, ed. Oster, G. (Am. Math. Soc., Providence, RI), pp. 165–255.
Provine, W. B. (1986) Sewall Wright and Evolutionary Biology (Univ. of Chicago Press, Chicago), p. 545.
Scharloo, W. (1991) Canalization, genetic and developmental aspects. Annu. Rev. Ecol. Syst. 22, 265–294.
Schmid, B. (1993) Phenotypic variation in plants. Evol. Trends Plants 6, 45–60.
Sepkoski, J. J. (1979) A kinetic model of Phanerozoic taxonomic diversty. II. Early Phanerozoic families and multiple equilibria. Paleobiology 5, 222–251.
Snedecor, G. W. & Cochran, W. G. (1980) Statistical Methods (Iowa State Univ. Press, Ames), 7th Ed., p. 507.
Sokal, R. R. & Rohlf, F. J. (1981) Biometry: The Principles and Practice of Statistics in Biological Research (Freeman, San Francisco), p. 859.
Stewart, W. N. & Rothwell, G. W. (1993) Paleobotany and the Evolution of Plants (Cambridge Univ. Press, Cambridge, U.K.), p. 521.
Sultan, S. E. (1987) Evolutionary implications of phenotypic plasticity in plants. Evol. Ecol. 21, 127–178.
Taylor, T. N. & Taylor, E. L. (1993) The Biology and Evolution of Fossil Plants (Prentice-Hall, Englewood Cliffs, NJ), p. 982.
Thomas, R. D. K. & Reif, W.-E. (1993) The skeleton space: A finite set of organic designs. Evolution 47, 341–360.
Tiffney, B. H. (1981) Diversity and major events in the evolution of land plants. In Paleobotany, Paleoecology, and Evolution, ed. Niklas, K. J. (Praeger, New York), Vol. 2, pp. 193–230.
Van Tienderen, P. H. (1990) Morphological variation in Plantago lanceolata : limits of plasticity. Evol. Trends Plants 4, 35–43.
Wright, S. (1932) The role of mutation, inbreeding, crossbreeding, and selection in evolution. Proc. Int. Congr. Genet. 6th 1, 356–366.
Wright, S. (1931) Evolution in Mendelian population. Genetics 16, 97–159.
| This page in the original is blank. |






















