13
Dynamics of Adaptation and Diversification: A 10,000-Generation Experiment with Bacterial Populations
Richard E. Lenski and Michael Travisano
Fifty years after the publication of Simpson's Tempo and Mode in Evolution (1944), evolutionary biologists are still fascinated by—and struggling to understand—the dynamics of adaptation and diversification, especially for those traits that affect the reproductive success of individual organisms. How quickly do populations change in these traits, and are their rates of change constant or variable? How rapidly do populations diverge from one another in these traits, and are rates of adaptation and diversification tightly or loosely coupled? How repeatable is evolution, and how sensitive are evolutionary outcomes to a population's initial genetic state? What are the relative roles of chance, phylogeny, and adaptation in evolution? How do the answers to these questions depend on the genetic system of an organism and on the traits examined?
We have embarked on an experimental program to investigate these questions. We believe that experiments complement historical and comparative studies and, when appropriately designed, may forge an important link between micro- and macroevolutionary studies. Before describing our experiments, however, we present an imaginary framework for such research. This imaginary framework illustrates the profound problems of inference inherent in purely observational ap-
Richard E. Lenski is the John Hannah Professor of Microbial Ecology at Michigan State University, East Lansing, Michigan. Michael Travisano is a postdoctoral researcher at the RIKEN Institute, Wako, Japan.
proaches to studying evolutionary dynamics, while also highlighting the power of our particular experimental system.
Imagine, then, that you have discovered a well-preserved and clearly stratified fossil bed that provides a record of evolution extending thousands of generations for the particular organism that you study. You could measure the size and shape of the organisms that were preserved and perhaps deduce the rate of change in these traits. But even from a near-perfect record, you would have great difficulty inferring the evolutionary processes—selection, drift, mutation, recombination, and migration—affecting these morphological traits. It might be difficult even to exclude the hypothesis that any phenotypic trends reflect nonheritable changes caused by the direct effects of a changing environment on the organism.
But imagine that you could infer that the environment had not changed for thousands of generations, so that any phenotypic trends must have resulted from underlying genetic changes. Moreover, you could be sure that there was no influx of genotypes from other populations and that the population was initially homogeneous, so that all of the genetic variation in the fossil population must have arisen in situ. You could then confidently assess the tempo and mode of morphological evolution.
Now imagine that you found many fossil beds, all in identical environments and having the same initial genetic state. You could evaluate the repeatability of evolution by examining the parallelism or divergence of the populations from one another. Any repeatability (or lack thereof) would also bear on the success of specific hypotheses that sought to address the adaptive significance of particular phenotypic trends.
And the fantasy continues. Imagine that you could resurrect these organisms (not merely bits of fossil DNA but the entire living organisms) and reconstruct their environment exactly as it was during the thousands of generations preserved in the fossil bed. You could measure not only the organism's morphology, but also its functional capacities and genetic composition. You could even place derived and ancestral forms in competition to determine their relative fitness in the "fossil" environment. You could assess which phenotypes promoted ecological success, and you could evaluate the similarity of the adaptive solutions achieved by the replicate populations, thereby disentangling the roles of "chance and necessity" (Monod, 1971) in evolutionary dynamics.
Still more opportunities exist in this fantastic world. You could travel back in time and manipulate populations by altering their evolutionary history or their environment, and then return to the present to examine the effect of these conditions on the dynamics of adaptation and
diversification. With this power, you could gain insight into the potency of phylogenetic constraints, examine the effects of environmental constancy or complexity, and pursue a host of other evolutionary questions.
Yet this fantasy is not fiction; it is fact. We have many such "fossil beds" preserved, and we have "traveled in time" to manipulate populations with respect to their history and environment. The fossil beds are preserved in a freezer and contain populations of the bacterium Escherichia coli. Our time travel thus far extends over 5 years, representing > 10,000 generations in this system, and we have manipulated many populations each comprising millions of individual organisms. In essence, our approach might be called experimental paleontology.
The following section gives a quick overview of our experimental system. We then analyze and interpret our experiments, which are organized around the analogy to an increasingly fantastic exploration of fossil beds. The discussion relates our findings on the dynamics of adaptation and diversification to theories of micro- and macroevolution. Finally, we briefly discuss tensions that inevitably encroach on any effort to forge an experimental link between micro- and macroevolution.
Experimental Overview
Twelve populations of E. coli B were propagated in replicate environments for 1500 days (10,000 generations). Each population was founded by a single cell from an asexual clone, and so there was initially no genetic variation either within or between replicate populations (except for a neutral marker used to identify populations). The experimental environment consisted of a serial transfer regime, in which populations were diluted (1:100) each day into 10 ml of a glucose-limited minimal salts medium that supports ![]() 5 × 107 cells per ml. Populations were maintained at 37°C with aeration. Every day, the bacteria underwent a lag phase prior to growth, followed by a period of sustained growth, eventual depletion of the limiting glucose, and starvation until the next serial transfer. The 1:100 dilution permits
5 × 107 cells per ml. Populations were maintained at 37°C with aeration. Every day, the bacteria underwent a lag phase prior to growth, followed by a period of sustained growth, eventual depletion of the limiting glucose, and starvation until the next serial transfer. The 1:100 dilution permits ![]() 6.6 (log2 100) cell generations per day. Samples from each population were periodically stored at -80°C, along with the common ancestor.
6.6 (log2 100) cell generations per day. Samples from each population were periodically stored at -80°C, along with the common ancestor.
In this paper, we report the dynamics of two properties of the evolving bacterial populations, cell size and mean fitness. Size is a morphological trait commonly studied by paleontologists and influences many functional properties of organisms. Fitness is the most important property of any organism according to evolutionary theory. The mean fitness of a population was obtained by allowing it to compete against the common ancestor. Relative fitness was then calculated as the ratio of the competitors' realized rates of increase (Malthusian parameters). Cell
sizes were obtained by using an electronic device that measures the volume displaced by a particle (Lenski and Bennett, 1993; Vasi et al., 1994). Prior to assays of either fitness or cell size, bacteria were removed from the freezer and allowed to acclimate for 1 day (several generations) to the experimental conditions. This procedure eliminates confounding effects of different physiological states of organisms and thereby establishes that phenotypic differences between populations have an underlying genetic basis.
We emphasize that our experiments employ natural selection, and not artificial selection as practiced by breeders and many experimentalists. That is, we do not select individual organisms based on any particular trait, but rather impose an environment on the experimental populations. Any heritable properties that systematically enhance an individual's reproductive success in that environment can respond to natural selection.
Except as indicated otherwise, materials and methods are identical to those previously published. In particular, see Lenski et al. (1991) for details concerning the ancestral strain, culture conditions, methods for exclusion of contamination from external sources and cross-contamination between replicate populations, and procedures for estimating mean fitness of derived populations relative to their ancestor.
Analyses and Interpretation
It may seem peculiar that we begin with analyses of morphological data (given that we have data on fitness) and that we focus initially on a single population (given that we have replicate populations). We do so to emphasize the potential difficulties of drawing inferences from morphological data (without information on fitness) and from single populations (without independent replication). This organization also facilitates comparison of anagenetic (within a lineage) and cladogenetic (diversifying) trends. We conclude our analyses by examining the relationship between morphology and fitness.
The Record of Morphological Evolution in One Fossil Bed. Figure 1 shows the trajectory for average cell size in one bacterial population during 10,000 generations of evolution. For ![]() 2000 generations after its introduction into the experimental environment, cell size increased quite rapidly. But after the environment was unchanged for several thousand generations more, any further evolution of cell size was imperceptible. A hyperbolic model [y = x0 + ax/(b + x)] accounts for
2000 generations after its introduction into the experimental environment, cell size increased quite rapidly. But after the environment was unchanged for several thousand generations more, any further evolution of cell size was imperceptible. A hyperbolic model [y = x0 + ax/(b + x)] accounts for ![]() 99% of the temporal variation in average cell size [r = 0.995, n = 9, P < 0.001; relative to linear model, partial F = 162.9, 1 and 6 df (df = degrees of
99% of the temporal variation in average cell size [r = 0.995, n = 9, P < 0.001; relative to linear model, partial F = 162.9, 1 and 6 df (df = degrees of
freedom), P < 0.001]. These data therefore indicate a rapid bout of morphological evolution after the population was placed in the experimental environment, followed by evolutionary stasis (or near stasis).
From these data, one might speculate that selection had favored larger cell size per se, although one could not exclude the possibilities that size was a correlated response to selection on some other trait or, more remotely, that cell size was subject solely to random genetic drift. If cell size was indeed a target of natural selection, then the eventual stasis might be interpreted either as a genetic/developmental constraint (such that no new mutations appeared that could increase cell size further) or as stabilizing selection (such that both larger and smaller variants continued to appear but were purged by natural selection). And whether or not cell size was a target of selection, the population may have continued to adapt to the environment (after size was static) by changing other traits.
Replicating History. Inferences concerning the tempo of morphological evolution and the adaptive significance of cell size would be greatly strengthened if similar trends were seen in several independent fossil beds. This opportunity is not usually possible: even when several contemporaneous fossil beds exist, one cannot exclude the possibility
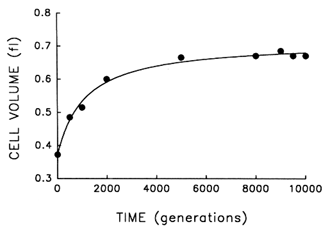
Figure 1 Trajectory for average cell volume in one population of E. coli during 10,000 generations of experimental evolution. Each point is the mean of two assays. Curve is the best fit of a hyperbolic model. Averages were calculated after removing particles of 80.25 fl, except for the ancestor (t = 0) where particles of 80.15 fl were removed; these criteria gave a clear separation between cells and background particles. Cell sizes were measured in stationary-phase populations, at the end of the 24-h serial transfer cycle.
that the several populations responded similarly because they shared genetic variation (i.e., alleles identical by descent that were either present in the common ancestor or introduced by migration), or that they diversified because they were in subtly different environments. But our experimental system affords the opportunity to examine rigorously the repeatability of evolutionary dynamics, including the origin as well as the fate of phenotypic modifications.
Figure 2 shows the estimated trajectories for average cell size in the replicate populations during 10,000 generations. All 12 independently evolved larger cells and, moreover, all 12 underwent much more rapid change soon after their introduction into the experimental environment than when their environment had been constant for several thousand generations.
Despite their superficial similarity, these trajectories also suggest that the replicate populations were approaching somewhat different plateaus for cell size. This inference must be made cautiously, however, because the parameters for each fitted curve have an associated statistical uncertainty. We performed analyses of variance on the raw data used to obtain these trajectories in order to estimate directly the among-population variance component for average cell size at each time point. We know that the populations were initially identical; if they are, in fact, approaching different plateaus for average cell size, then the among-population variance component must increase from zero to some
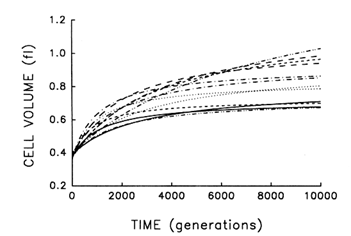
Figure 2 Trajectories for average cell volume in 12 replicate populations of E. coli during 10,000 generations. Each curve represents the best fit of a hyperbolic model to data obtained for one population at intervals indicated in Figure 1.
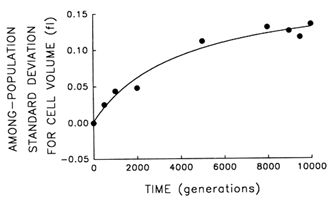
Figure 3 Trajectory for diversification of the 12 populations in their average cell volume. Analyses of variance were performed to partition the observed variation in cell size into its components. Each point represents the among-population SD for cell volume (i.e., the square root of the among-population variance component). Curve shows the best fit of a hyperbolic model.
plateau. Figure 3 shows the trajectory for the among-population standard deviation (i.e., square root of the variance component). The fit of the hyperbolic model to these data is very good (r = 0.987, n = 9, P < 0.001; relative to linear model, partial F = 15.6, 1 and 6 df, P = 0.008). Thus, we conclude that the populations have diverged, not only from their common ancestor but from one another, in cell size. After 10,000 generations, the among-population standard deviation was ![]() 0.14 fl, as compared with the average change in cell size from the ancestral state of
0.14 fl, as compared with the average change in cell size from the ancestral state of ![]() 0.44 fl.
0.44 fl.
The observation that all 12 independently evolving populations responded similarly, even if not identically, seems to rule out random genetic drift, unless we invoke some profound asymmetry in mutational effects on cell size. However, we still cannot determine whether cell size was the actual target of selection (or merely a correlated response to selection on other traits), nor can we discern whether adaptation to the environment continued apace for the entire 10,000 generations (but without producing further changes in cell size).
The Quick and the Dead. A remarkable feature of our experimental system is that we can measure the mean fitness of a derived population relative to its actual ancestor. That is, populations of cells can be ''resurrected from the dead" (i.e., removed from the freezer) at any time and placed in direct competition. This ability to measure fitness permits investigation of a host of intriguing questions. Has mean fitness im-
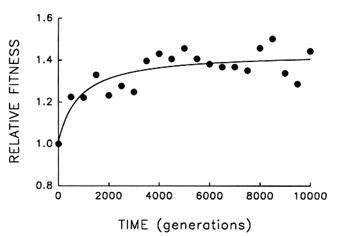
Figure 4 Trajectory for mean fitness relative to the ancestor in one population of E. coli during 10,000 generations of experimental evolution. Each point is the mean of three assays. Curve is the best fit of a hyperbolic model.
proved, thus demonstrating adaptation by natural selection? Is the evolutionary trajectory for fitness similar to that for cell size, or did fitness improve at a constant rate throughout the experimental evolution? Have the replicate populations also diverged from one another in mean fitness, suggesting that they scaled different adaptive peaks? Or have the populations converged on similar fitnesses, implying that their differences in cell size are inconsequential for fitness? How tightly correlated are morphology and fitness?
Figure 4 shows the dynamics of mean fitness relative to the ancestor for the same population whose evolutionary trajectory for average cell size is shown in Figure 1. Mean fitness evolved rapidly for ![]() 2000 generations in the experimental environment but was nearly constant for the final several thousand generations. Although the fitness data are subject to more "noise" than the data on cell size, the hyperbolic model explains
2000 generations in the experimental environment but was nearly constant for the final several thousand generations. Although the fitness data are subject to more "noise" than the data on cell size, the hyperbolic model explains ![]() 70% of the variation in mean fitness (r = 0.843, n = 21, P < 0.001; relative to linear model, partial F = 17.9, 1 and 18 df, P < 0.001). The fact that fitness shows the same decelerating trajectory belies the hypothesis that adaptation continued apace for the 10,000 generations but was not reflected in further changes in cell size.
70% of the variation in mean fitness (r = 0.843, n = 21, P < 0.001; relative to linear model, partial F = 17.9, 1 and 18 df, P < 0.001). The fact that fitness shows the same decelerating trajectory belies the hypothesis that adaptation continued apace for the 10,000 generations but was not reflected in further changes in cell size.
Figure 5 provides finer resolution of the fitness trajectory for the first 2000 generations in the same population; fitness was estimated every 100 (rather than 500) generations and with 10-fold (rather than 3-fold) replication. A step model (Lenski et al., 1991) [y = c0 + c1 (if t > T1) +
c2 (if t > T2) + … + cn (if t > Tn)] with three steps provides an excellent fit to the trajectory (r = 0.978; 3 and 17 df; P < 0.001). What accounts for the initial delay and the seemingly discontinuous jumps? Both features are expected from population genetic theory, given the uniformity of the founding population, its asexuality, and the resulting dependence of the selection response on new mutations (Muller, 1932; Lenski et al., 1991). Any favorable allele must first appear and then increase from a very low frequency. Assuming constant selection, it takes as long for a favored new allele to increase from a frequency of 10-7 to 10-6 as it takes it to increase from 10% to 90%; and yet only after the allele has reached high frequency does it appreciably affect the mean properties of a population. Thus, the smoothness of the trajectories shown in Figures 1 and 4 is, to some extent, a product of relatively infrequent sampling; discontinuities revealed by more frequent sampling (Figure 5) indicate nothing more than the dynamics of selection when a population depends on new mutations (rather than abundant standing variation) for its response.
The Adaptive Landscape. Wright's (1932, 1982, 1988) concept of the adaptive landscape (or fitness surface) provides one of the most vivid images in all of evolutionary theory, but it is also one of the most difficult to firmly grasp and study. The essential idea is that natural selection tends to drive a population to a local optimum, which is not necessarily a global optimum. Thus, a population may be stuck with a suboptimal solution to its environment because natural selection (which is not goal
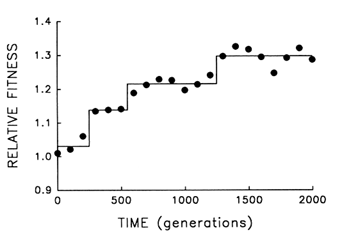
Figure 5 Finer scale analysis of the trajectory for mean fitness in one population of E. coli during its first 2000 generations of experimental evolution. Each point is the mean of 10 assays. Solid lines indicate the fit of a step model.
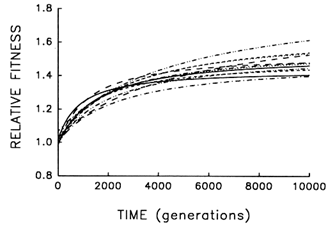
Figure 6 Trajectories for mean fitness relative to the ancestor in 12 replicate populations of E. coli during 10,000 generations. Each curve represents the best fit of a hyperbolic model to data obtained for one population every 500 generations.
directed) opposes passage through a "valley" of maladapted intermediate states, even though a better solution may exist across the way. Theoreticians have identified processes that might facilitate peak shifts, but empiricists know very little about the structure of adaptive landscapes. A key question is, how often are there nearby fitness peaks of unequal height?
To address this question, we examine whether the evolving populations diverged from one another in mean fitness, as they did in morphology. Figure 6 shows the estimated trajectories for mean fitness in the replicate populations during 10,000 generations. All 12 adapted much more rapidly soon after their introduction into the experimental environment than they did subsequently, when their environment had been constant for several thousand generations. We performed analyses of variance to estimate the among-population variance component for mean fitness at each time. If the populations were approaching different fitness peaks from the same initial state, then this variance component should increase from zero to some plateau. Figure 7 shows the fit of the hyperbolic model to the trajectory for the among-population standard deviation for mean fitness. The fit of the model is poor (r = 0.286). However, the twenty separate analyses of variance (after t = 0) yielded estimated variance components > 0 in 18 cases. The associated significance levels were <0.05 in 7 cases and between 0.05 and 0.25 in 8 others.
The joint probability of obtaining, by chance, so many low-probability outcomes is very remote [P < 0.001, based on Fisher's technique for combining probabilities from independent tests of significance (Sokal and Rohlf, 1981)]. Therefore, although we cannot discern any clear trend in the among-population variance for mean fitness, we know it was initially equal to 0 and that significant variation arose early in the experiment and persisted throughout the 10,000 generations.
Nonetheless, we cannot absolutely exclude the possibility that the populations might eventually converge in mean fitness. In fact, when similar analyses were performed after 2000 generations, we suggested that the populations might have diverged in mean fitness only transiently, owing to stochastic variation in the timing of a series of substitutions leading to the same fitness peak (Lenski et al., 1991). The reason for our earlier caution in claiming sustained divergence was not because the among-population genetic variance was much smaller in the first 2000 generations (Figure 7), but rather because the rate of adaptation continued at a much more rapid pace (Figure 6), leaving open the possibility that the less fit populations would soon catch up to their better-adapted cousins. But with an additional 8000 generations, the rate of fitness improvement has become so slow that eventual convergence now seems very unlikely. Whereas the average rate of improvement between generations 1000 and 2000 was 0.108 (±0.020 SEM) per 1000
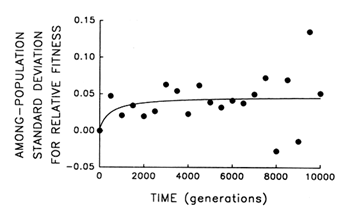
Figure 7 Trajectory for diversification of the 12 populations in their mean fitness. Analyses of variance were performed at 500-generation intervals to partition the observed variation in mean fitness into its components. Each point represents the among-population SD for mean fitness (i.e., the square root of the among-population variance component); negative values indicate that the estimated variance component was negative. Curve shows the best fit of a hyperbolic model.
generations (Lenski et al., 1991), the rate of further improvement had fallen to only 0.008 (±0.004 SEM) per 1000 generations between generations 5000 and 10,000. Also, using the hyperbolic models for each population, there is a positive correlation between fitness and the rate of continued improvement at 10,000 generations (r = 0.848; n = 12; P < 0.001), suggesting that the replicate populations will become more divergent in fitness, not less.
Thus, the replicate populations have approached distinct fitness peaks of unequal height (or, just maybe, they are climbing slowly along different ridges of unequal elevation toward the same peak). After 10,000 generations, the among-population standard deviation for fitness was ![]() 0.05, while the average fitness gain from the ancestral state was
0.05, while the average fitness gain from the ancestral state was ![]() 0.48.
0.48.
The Relationship of Size and Fitness. One cannot help but notice the similarity of the trajectories for cell size and fitness. Does this correspondence imply that cell size was a "target" of selection? Or might size merely be correlated with other traits responsible for the improved fitness? Is the relationship between cell size and fitness rigidly fixed or is it evolutionarily malleable?
Even with this powerful experimental system, these questions are vexing and difficult to resolve. Ideally, one would like to manipulate cell size, holding all other traits constant. But this proposition presumes an atomization of traits that is implausible, given the pleiotropic action of alleles and the functional interconnections inherent in any organism. Thus, for the time being, we are forced to rely on statistics to describe the relationship between size and fitness.
To describe the functional relationship between two traits, it is necessary to use a regression coefficient (the slope in a linear model) rather than a correlation coefficient. A problem arises, however, because standard regression methods require that one of the variables either be manipulated experimentally or measured without error (Sokal and Rohlf, 1981), whereas both average cell size and mean fitness of a population are measured with error. Although there is no general solution to this problem of "model II" regression, a precise solution exists when the error variances associated with measurement of each variable are known (Mandel, 1964). Fortunately, we can estimate the error variances associated with both variables, because each size/fitness datum in our analysis is the mean of two (size) and three (fitness) independent assays.
Figure 8A shows the correspondence between mean fitness and average cell size over all populations and time points. Figure 8B illustrates the hypothesis that size and fitness are tightly coupled, as
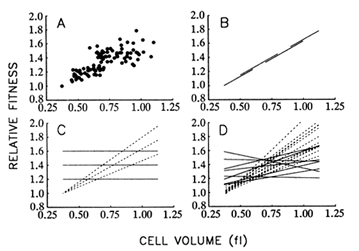
Figure 8 Relationship between mean fitness and average cell size. (A) Data from all 12 populations and 9 time points for which both fitness and size were measured. (B) Hypothesis I: There exists a rigid functional relationship between average cell size and mean fitness, such that the latter can be improved only by increasing the former. Longitudinal (one population over all time points) and cross-sectional (all populations at one time point) regressions would yield the same slope. (C) Hypothesis II: The functional relationship between size and fitness is malleable, so that replicate populations may diverge in the relationship between size and fitness. Although longitudinal regressions (dashed lines) may be strong, cross-sectional regressions (solid lines) need not show any systematic coupling between size and fitness. (D) Dashed and solid lines show actual longitudinal and cross-sectional regressions, respectively, using the data shown in A. All regressions were performed according to model II procedures that are applicable when both variables are measured with error, but the corresponding error variances are known (Mandel, 1964). From analyses of variance performed on repeated measures, the ratio of the error variances for average cell size and mean fitness was 0.138 (adjusted for sample sizes of two and three, respectively, and averaged over all populations and generations).
though size were the actual target of natural selection. According to this hypothesis, one should obtain the same regression line whether the data are analyzed longitudinally (i.e., using a single population over all time points) or cross-sectionally (i.e., using all populations at a single time point). Put another way, any variation among populations in fitness is because some have achieved larger cells than others.
Figure 8C illustrates an alternative hypothesis, which states that traits other than cell size are the actual targets of selection; larger size is correlated with some of the selected traits, but there is no rigid coupling
between size and fitness. Thus, the replicate populations may diverge not only in size and fitness, but also in the functional relationship between size and fitness. In that case, there need not be any systematic relationship between size and fitness in cross-sectional regressions, even if the longitudinal regressions are strong.
Figure 8D shows the results of the 12 longitudinal (1 for each population) and 8 cross-sectional (1 for each time point) regressions. The mean of the longitudinal slopes is 1.063 fl-1. (That is, relative fitness, which is a dimensionless quantity, increases by 1.063 per fl increase in cell volume.) This mean is significantly greater than 0 (t = 11.72; 11 df; P < 0.001). In contrast, the mean of the cross-sectional slopes is only 0.187 fl-1, which is not significantly different from 0 (t = 1.61; 7 df; P = 0.150) but is significantly less than the mean of the longitudinal slopes (t = 6.01; 18 df; P < 0.001). Therefore, these analyses do not support the hypothesis that the functional relationship between size and fitness is causal and rigidly fixed (Figure 8B) but suggest instead that the replicate populations have diverged in this relationship (Figure 8C). These results therefore also challenge the controversial assumption of certain evolutionary analyses that genetic covariances between traits are constant over long periods (Lande, 1975, 1979; Kohn and Atchley, 1988; Turelli, 1988).
Conclusions and Discussion
Chance and Necessity. The 12 bacterial populations had similar trajectories for both cell size and fitness (Figures 2 and 6). It is perhaps surprising that the populations evolved in such a parallel fashion, given that their evolution depended on mutations that arose independently in each population. Of course, a critical factor promoting parallel evolution was the simple fact that populations evolved in identical environments. A second factor promoting parallelism may have been large population sizes, which would give rise to identical mutations in the replicate populations. Each population underwent ![]() 7.5 × 1011 cell replications (5 × 107 cell replications per ml per day × 10 ml × 1500 days). The estimated rate of mutation in E. coli (Drake, 1991) is
7.5 × 1011 cell replications (5 × 107 cell replications per ml per day × 10 ml × 1500 days). The estimated rate of mutation in E. coli (Drake, 1991) is ![]() 2.5 × 10-3 mutation per genome replication (5 × 10-10 mutation per bp replication × 5 × 106 bp per genome). Thus, each population experienced
2.5 × 10-3 mutation per genome replication (5 × 10-10 mutation per bp replication × 5 × 106 bp per genome). Thus, each population experienced ![]() 2 × 109 mutations. With 5 × 106 bp per genome and three alternative point mutations at each bp (ignoring more complex mutations), this translates to >100 occurrences, on average, for every point mutation in the whole genome! (Of course, drift eliminates many mutations shortly after they occur, but even so this figure suggests redundancy.)
2 × 109 mutations. With 5 × 106 bp per genome and three alternative point mutations at each bp (ignoring more complex mutations), this translates to >100 occurrences, on average, for every point mutation in the whole genome! (Of course, drift eliminates many mutations shortly after they occur, but even so this figure suggests redundancy.)
However, it is also important that the replicate populations diverged somewhat in both morphology and mean fitness (Figures 3 and 7). After 10,000 generations, the standard deviation for mean cell size among the derived populations was ![]() 30% of the average difference between the derived populations and their common ancestor. For mean fitness, the standard deviation among the derived populations was
30% of the average difference between the derived populations and their common ancestor. For mean fitness, the standard deviation among the derived populations was ![]() 10% of the average improvement from the common ancestor. Moreover, the populations also diverged in the functional relationship between cell size and fitness (Figure 8D).
10% of the average improvement from the common ancestor. Moreover, the populations also diverged in the functional relationship between cell size and fitness (Figure 8D).
Evolutionary biologists usually regard diversification as being caused by either (i) adaptation to different environments, which often produces conspicuous phenotypic variation, or (ii) random genetic drift, which is usually seen in molecular genetic variation. Yet our experiments demonstrate diversification, in identical environments and with very large populations, of no less selected a trait than fitness itself. Someone confronted with the variability among our derived populations (and unaware of the experimental design) might attribute this diversity to environmental heterogeneity or phylogenetic constraints, but any such "just-so story" would clearly be misguided in this case. Instead, our experiment demonstrates the crucial role of chance events (historical accidents) in adaptive evolution.
In a previous analysis of the first 2000 generations of this experiment (Lenski et al., 1991), it was not possible to reject the hypothesis that the populations had diverged only transiently in mean fitness but would soon converge on the same mean fitness. It was proposed that this hypothesis could be rejected, in favor of sustained divergence, "if the level of between-population variance of mean fitness remains significant indefinitely, even in the absence of further increases in mean fitness" (Lenski et al., 1991, p. 1337). We have shown here that variation among populations in mean fitness does persist for thousands of generations, even after improvement in mean fitness has slowed to an almost imperceptible rate.
Sustained divergence in mean fitness supports a Wrightian model of evolution (Wright, 1932, 1982, 1988; Barton and Hewitt, 1989; Mani and Clarke, 1990; Wade and Goodnight, 1991), in which replicate populations found their way onto different fitness peaks. Although the experimental populations were so large that the same mutations occurred in all of them, the order in which various mutations arose would have been different (Mani and Clarke, 1990). As a consequence, some populations may have incorporated mutations that were beneficial over the short-term but led to evolutionary dead ends.
Beyond promoting the idea of fitness surfaces with adaptive peaks separated by maladapted intermediate states, Wright (1932, 1982, 1988)
identified processes by which populations might move from one peak to another. One process that can produce a peak shift, without environmental change, is random genetic drift (including founder effects). Although this hypothesis has been highly influential [e.g., for models of speciation (Mayr, 1954; Templeton, 1980)], the mathematical conditions conducive to such peak shifts appear to be restrictive (Barton and Rouhani, 1987). In this respect, it is important that, in our experiment, populations were not on one adaptive peak and asked to "jump" to another peak; instead, they were thrown into an arbitrary environment and asked to climb any accessible peak.
Adaptation, Diversification, and Stasis. For about 2000 generations after their introduction into the experimental environment, all 12 populations underwent rapid changes in both morphology and fitness, whereas these properties were nearly static between generations 5000 and 10,000. The initially rapid evolution was presumably due to intense selection triggered by the sudden environmental changes imposed at the start of our experiment. Although the ancestors of the founding bacterium used in this study had been "in captivity" for several decades, they were not systematically propagated under the experimental conditions that we imposed (serial dilution in glucose-minimal medium). The experimental regime was thus a novel environment. Unfortunately, we cannot say anything quantitative about the evolutionary dynamics of the study organism before the start of our experiment. However, in two other studies, we have used derived bacteria from this study to found new populations, which were introduced into environments that differed either in temperature (Bennett et al., 1992) or in limiting nutrient (Travisano, 1993). In both cases, these environmental changes led to more rapid adaptive evolution.
Our results also reveal the quasi-punctuated dynamics expected when selection depends on new mutations. However, we saw no compelling evidence for any more radical punctuation, such as when one adaptive change sets off a cascade of further changes [cf. "genetic revolutions" (Mayr, 1954; Templeton, 1980) and "epochal mutations" (Kubitschek, 1974)]. Such an effect might have been manifest by a period of renewed, rapid evolutionary change in a population that had previously been at or near stasis. Perhaps 12 populations and 10,000 generations were too few to see such rare events.
If environmental change and the dynamics of selection caused the initially rapid changes in morphology and fitness, then the eventual stasis (or near stasis) presumably resulted from the constancy of the environment and a paucity of mutations that would produce further improvements comparable to those seen earlier in the experiment. The
trajectories for cell size and fitness are superficially similar to data from other experiments, wherein stasis results from a depletion of the genetic variation present in a base population (Falconer, 1983). However, this interpretation is not relevant to our experiment, because there was no initial variation and mutation is an ongoing process. One might also suggest that the eventual stasis in cell size was a consequence of stabilizing selection, although it is not clear why selection would stabilize the replicate populations at different sizes. And the idea that there might be stabilizing selection for intermediate fitness is an evolutionary oxymoron. Hence, the most reasonable interpretation for the eventual stasis in our experimental populations is that the organisms have ''run out of ways" to become much better adapted to their environment. Either further major improvements (with fitness increments of more than a few percent in this environment) do not exist or else they are evolutionarily inaccessible (e.g., adaptations requiring multiple genetic changes in which the intermediate states are unfit).
A common pattern in the fossil record is that periods of rapid change in a lineage from its ancestral state (anagenesis) are also periods of rapid diversification (cladogenesis). This association is a central issue in the debate over the theory of punctuated equilibrium (Eldredge and Gould, 1972; Charlesworth et al., 1982; Levinton, 1988; Gould and Eldredge, 1993). In our experiment, rates of anagenetic and cladogenetic evolution were tightly coupled, with the most rapid anagenetic change and diversification both occurring shortly after the populations were introduced into the experimental environment. Thus, our experiment recreates one of the major features taken as evidence for the theory of punctuated equilibrium. We believe the explanation for this concordance of anagenetic and cladogenetic rates is that environmental change (i.e., introduction of the study organism into the experimental environment) radically perturbed the adaptive landscape. This perturbation precipitated rapid adaptive evolution, while diversification resulted from the stochastic effects of mutation and drift that pushed replicate populations into the domains of attraction of different adaptive slopes and fitness peaks. [Diversification would presumably be even more pronounced if the populations were not only isolated but in different environments (Bennett et al., 1992).] This explanation is similar to that put forward by Charlesworth et al. (1982, p. 482): "Ecological opportunities offered by the opening of new niches, either by changes in the environment or by the evolution of a key adaptation, will [in the] classical view, generate an association between rapid morphological evolution and the proliferation of species."
Coda
[Experiments] may reveal what happens to a hundred rats in the course of ten years under fixed and simple conditions, but not what happened to a billion rats in the course of ten million years under the fluctuating conditions of earth history. (Simpson, 1944, p. xvii)
We acknowledge the severe limitations inherent in our study of evolutionary dynamics. Foremost among these are the short time span (even 10,000 generations is but a brief moment in evolution) and the simple environment (which ignores the complexity and changeability of nature). The former limitation reflects our lack of access to better machines for time travel, and the latter our desire as experimentalists to keep things simple enough that we may understand the results. In terms of these limitations, we are certainly studying the tempo and mode of microevolution.
But our studies begin to explore macroevolution, insofar as we address the repeatability of adaptation, the diversification of lineages, and thus the causes and consequences of the uniqueness of evolutionary history. Moreover, it is important that, in our experimental system (unlike other model systems more widely used in population genetics), all of the genetic variation available to selection is generated de novo, by mutation, during the course of the experiment. Thus, our study is concerned with the origin of novelties as well as their fate. And although our experiments are small in the evolutionary scheme of things, their duration and size are nonetheless such that each population explores literally millions of genetic changes and at least several of these changes eventually go to fixation (or near fixation). Therefore, our experiment reflects more complex and encompassing evolutionary dynamics than studies of responses to selection that depend either on quantitative variation already present in a population or on a single allele of major effect.
In fact, we observed several hallmarks of macroevolutionary dynamics, including periods of rapid evolution and stasis, altered functional relationships between traits, and concordance of anagenetic and cladogenetic trends. For now, the generality of our results remains an open question: one might well wonder what outcomes would be observed with a sexual organism, with larger or smaller population sizes, with different population structures, or with a more complex environmental regime. We believe that, with appropriate experimental systems and designs, all of these questions can be rigorously addressed.
The differences between microevolution and macroevolution are ones of spatial and temporal scale, of course, but they are also more than that. Microevolution deals primarily with the fundamental "laws" of evolu-
tion (the processes of selection, drift, mutation, recombination and migration), whereas macroevolution typically focuses on the uniqueness (the accidental nature) of evolutionary history. But we would argue that the uniqueness of evolutionary history is itself amenable to careful experimental analysis, and that this uniqueness may be an inevitable consequence of the "laws" of microevolution.
Summary
We followed evolutionary change in 12 populations of Escherichia coli propagated for 10,000 generations in identical environments. Both morphology (cell size) and fitness (measured in competition with the ancestor) evolved rapidly for the first 2000 generations or so after the populations were introduced into the experimental environment, but both were nearly static for the last 5000 generations. Although evolving in identical environments, the replicate populations diverged significantly from one another in both morphology and mean fitness. The divergence in mean fitness was sustained and implies that the populations have approached different fitness peaks of unequal height in the adaptive landscape. Although the experimental time scale and environment were microevolutionary in scope, our experiments were designed to address questions concerning the origin as well as the fate of genetic and phenotypic novelties, the repeatability of adaptation, the diversification of lineages, and thus the causes and consequences of the uniqueness of evolutionary history. In fact, we observed several hallmarks of macroevolutionary dynamics, including periods of rapid evolution and stasis, altered functional relationships between traits, and concordance of anagenetic and cladogenetic trends. Our results support a Wrightian interpretation, in which chance events (mutation and drift) play an important role in adaptive evolution, as do the complex genetic interactions that underlie the structure of organisms.
This research is supported by a grant from the National Science Foundation to R.E.L. (DEB-9249916) and by the National Science Foundation Science and Technology Center for Microbial Ecology (BIR-9120006). We thank S. C. Simpson for excellent technical assistance; A. F. Bennett, D. E. Dykhuizen, D. L. Hartl, R. Korona, M. H. Lenski, M. R. Rose, P. D. Sniegowski, D. R. Taylor, and F. Vasi for helpful comments and discussion; and F. J. Ayala and W. M. Fitch for organizing a stimulating conference.
References
Barton, N. H. and Hewitt, G. M. (1989) Adaptation, speciation and hybrid zones. Nature (London) 341, 497–503.
Barton, N. H. and Rouhani, S. (1987) The frequency of shifts between alternative equilibria. J. Theor. Biol. 125, 397–418.
Bennett, A. F., Lenski, R. E. and Mittler, J. E. (1992) Evolutionary adaptation to temperature. I. Fitness responses of Escherichia coli to changes in its thermal environment. Evolution 46, 16–30.
Charlesworth, B., Lande, R. and Slatkin, M. (1982) A neo-Darwinian commentary on macroevolution. Evolution 36, 474–498.
Drake, J. W. (1991) A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA 88, 7160–7164.
Eldredge, N. and Gould, S. J. (1972) Punctuated equilibria: an alternative to phyletic gradualism. In Models in Paleobiology, ed. Schopf, T. J. M. (Freeman, San Francisco), pp. 82–115.
Falconer, D. S. (1983) Introduction to Quantitative Genetics (Longman, London), 2nd Ed., pp. 194–206.
Gould, S. J. and Eldredge, N. (1993) Punctuated equilibrium comes of age. Nature (London) 366, 223–227.
Kohn, L. A. P. and Atchley, W. R. (1988) How similar are genetic correlation structures? Data from mice and rats. Evolution 42, 467–481.
Kubitschek, H. E. (1974) Operation of selective pressure on microbial populations. Symp. Soc. Gen. Microbiol. 24, 105–130.
Lande, R. (1975) The maintenance of genetic variability by mutation in a polygenic character with linked loci. Genet. Res. 26, 221–234.
Lande, R. (1979) Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 33, 402–416.
Lenski, R. E. and Bennett, A. F. (1993) Evolutionary response of Escherichia coli to thermal stress. Am Nat. 142, S47–S64.
Lenski, R. E., Rose, M. R., Simpson, S. C. and Tadler, S C. (1991) Long-term experimental evolution in Escherichia coli. I. Adaptation and divergence during 2,000 generations. Am. Nat. 138, 1351–1341.
Levinton, J. (1988) Genetics, Paleontology and Macroevolution (Cambridge Univ. Press, New York).
Mandel, J. (1964) The Statistical Analysis of Experimental Data (Wiley, New York), pp. 288–292.
Mani, G. S. and Clarke, B. C. (1990) Mutational order: a major stochastic process in evolution. Proc. R. Soc. London B 240, 29–37.
Mayr, E. (1954) Change of genetic environment and evolution. In Evolution as a Process, eds. Huxley, J., Hardy, A. C. and Ford, E. B. (Allen and Unwin, London), pp. 157–180.
Monod, J. (1971) Chance and Necessity (Knopf, New York).
Muller, H. J. (1932) Some genetic aspects of sex. Am. Nat. 66, 118–138.
Simpson, G. G. (1944) Tempo and Mode in Evolution (Columbia Univ. Press, New York).
Sokal, R. R. and Rohlf, F. J. (1981) Biometry, 2nd Ed. (Freeman, San Francisco).
Templeton, A. R. (1980) The theory of speciation via the founder principle. Genetics 94, 1011–1038.
Travisano, M. (1993) Adaptation and divergence in experimental populations of the
bacterium Escherichia coli: the roles of environment, phylogeny and chance. Dissertation (Michigan State Univ., East Lansing, MI).
Turelli, M. (1988) Phenotypic evolution, constant covariances, and the maintenance of additive variance. Evolution 42, 1342–1347.
Vasi, F., Travisano, M. and Lenski, R. E. (1994) Long-term experimental evolution in Escherichia coli. II. Changes in life history traits during adaptation to a seasonal environment. Am. Nat. 144, 432–456.
Wade, M. J. and Goodnight, C. J. (1991) Wright's shifting balance theory: an experimental study. Science 253, 1015–1018.
Wright, S. (1932) The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. 6th Int. Congr. Genet. 1, 356–366.
Wright, S. (1982) Character change, speciation, and the higher taxa. Evolution 36, 427–443.
Wright, S. (1988) Surfaces of selective value revisited. Am. Nat. 131, 115–123.
| This page in the original is blank. |






















