their own conclusions because they know that their objective must be to try to convince their ablest colleagues.

The social mechanisms of science do more than validate what comes to be known as scientific knowledge. They also help generate and sustain the body of experimental techniques, social conventions, and other ''methods" that scientists use in doing and reporting research. Some of these methods are permanent features of science; others evolve over time or vary from discipline to discipline. Because they reflect socially accepted standards in science, their application is a key element of responsible scientific practice.
EXPERIMENTAL TECHNIQUES AND THE TREATMENT OF DATA
One goal of methods is to facilitate the independent verification of scientific observations. Thus, many experimental techniques—such as statistical tests of significance, double-blind trials, or proper phrasing of questions on surveys—have been designed to minimize the influence of individual bias in research. By adhering to these techniques, researchers produce results that others can more easily reproduce, which promotes the acceptance of those results into the scientific consensus.
If research in a given area does not use generally accepted methods, other scientists will be less likely to accept the results. This was one of several reasons why many scientists reacted negatively to the initial reports of cold fusion in the late 1980s. The claims were so physically implausible that they required extraordinary proof. But the experiments were not initially presented in such a way that other investigators could corroborate or disprove them. When the experimental techniques became widely known and were replicated, belief in cold fusion quickly faded.
In some cases the methods used to arrive at scientific knowledge are not very well defined. Consider the problem of distinguishing the "facts" at the forefront of a given area of science. In such circumstances experimental techniques are often pushed to the limit, the signal is difficult to separate from the noise, unknown sources of error abound, and even the question to be answered is not well defined. In such an uncertain and fluid situation, picking out reliable data from a mass of confusing and sometimes contradictory observations can be extremely difficult.
In this stage of an investigation, researchers have to be extremely clear, both to themselves and to others, about the methods being used to gather and analyze data. Other scientists will be judging not only the validity of the data but also the validity and accuracy of the methods used to derive those data. The development of new methods can be a controversial process, as scientists seek to determine whether a given method can serve as a reliable source of new information. If someone is not forthcoming about the procedures used to derive a new result, the validation of that result by others will be hampered.
Methods are important in science, but like scientific knowledge itself, they are not infallible. As they evolve over time, better methods supersede less powerful or less acceptable ones. Methods and scientific knowledge thus progress in parallel, with each area of knowledge contributing to the other.
A good example of the fallibility of methods occurred in astronomy in the early part of the twentieth century. One of the most ardent debates in astronomy at that time concerned the nature of what were then known as spiral nebulae—diffuse pinwheels of light that powerful telescopes revealed to be quite common in the night sky. Some astronomers thought that these nebulae were spiral galaxies like the Milky Way at such great distances from the earth that individual stars could not be distinguished. Others believed that they were clouds of gas within our own galaxy.
One astronomer who thought that spiral nebulae were within the Milky Way, Adriaan van Maanen of the Mount Wilson Observatory, sought to resolve the issue by comparing photographs of the nebulae taken several years apart. After making a series of painstaking measurements, van Maanen announced that he had found roughly consistent unwinding motions in the nebulae. The detection of such motions indicated that the spirals had to be within the Milky Way, since motions would be impossible to detect in distant objects.
Van Maanen's reputation caused many astronomers to accept a galactic location for the nebulae. A few years later, however, van Maanen's colleague Edwin Hubble, using the new 100-inch telescope at Mount Wilson, conclusively demonstrated that the nebulae were in fact distant galaxies; van Maanen's observations had to be wrong. Studies of van Maanen's procedures have not revealed any intentional misrepresentation or sources of systematic error. Rather, he was working at the limits of observational accuracy, and his expectations influenced his measurements.
|
THE SELECTION OF DATA Deborah, a third-year graduate student, and Kathleen, a postdoc, have made a series of measurements on a new experimental semiconductor material using an expensive neutron source at a national laboratory. When they get back to their own laboratory and examine the data, they get the following data points. A newly proposed theory predicts results indicated by the curve. 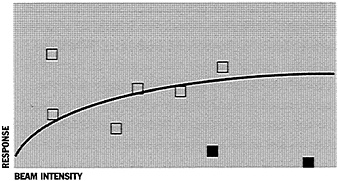 During the measurements at the national laboratory, Deborah and Kathleen observed that there were power fluctuations they could not control or predict. Furthermore, they discussed their work with another group doing similar experiments, and they knew that the other group had gotten results confirming the theoretical prediction and was writing a manuscript describing their results. In writing up their own results for publication, Kathleen suggests dropping the two anomalous data points near the abscissa (the solid squares) from the published graph and from a statistical analysis. She proposes that the existence of the data points be mentioned in the paper as possibly due to power fluctuations and being outside the expected standard deviation calculated from the remaining data points. "These two runs," she argues to Deborah, "were obviously wrong."
|
Though van Maanen turned out to be wrong, he was not ethically at fault. He was using methods that were accepted by the astronomical community as the best available at the time, and his results were accepted by most astronomers. But in hindsight he relied on a technique so susceptible to observer effects that even a careful investigator could be misled.
The fallibility of methods is a valuable reminder of the importance of skepticism in science. Scientific knowledge and scientific methods, whether old or new, must be continually scrutinized for possible errors. Such skepticism can conflict with other important features of science, such as the need for creativity and for conviction in arguing a given position. But organized and searching skepticism as well as an openness to new ideas are essential to guard against the intrusion of dogma or collective bias into scientific results.
VALUES IN SCIENCE
Scientists bring more than just a toolbox of techniques to their work. Scientist must also make complex decisions about the interpretation of data, about which problems to pursue, and about when to conclude an experiment. They have to decide the best ways to work with others and exchange information. Taken together, these matters of judgment contribute greatly to the craft of science, and the character of a person's individual decisions helps determine that person's scientific style (as well as, on occasion, the impact of that person's work).
Much of the knowledge and skill needed to make good decisions in science is learned through personal experience and interactions with other scientists. But some of this ability is hard to teach or even describe. Many of the intangible influences on scientific discovery—curiosity, intuition, creativity—largely defy rational analysis, yet they are among the tools that scientists bring to their work.
When judgment is recognized as a scientific tool, it is easier to see how science can be influenced by values. Consider, for example, the way people judge between competing hypotheses. In a given area of science, several different explanations may account for the available facts equally well, with each suggesting an alternate route for further research. How do researchers pick among them?
Scientists and philosophers have proposed several criteria by which promising scientific hypotheses can be distinguished from less fruitful ones. Hypotheses should be internally consistent so that they do not generate contradictory conclusions. Their ability to provide accurate experimental predictions, sometimes in areas far removed from the original domain of the hypothesis, is viewed with great favor. With disciplines in which experimentation is less straightforward, such as geology, astronomy, or many of the social sciences, good hypotheses should be able to unify disparate observations. Also highly prized are simplicity and its more refined cousin, elegance.
Other kinds of values also come into play in science. Historians, sociologists, and other students of science have shown that social and personal beliefs—including philosophical, thematic, religious, cultural, political, and economic beliefs—can



