6
Adaptive Finite Element Methods for the Helmholtz Equation inExterior Domains
James R. Stewart
Thomas J.R. Hughes
Stanford University
|
This paper addresses the development and application of adaptive methods for finite element solution of the Helmholtz equation in exterior domains. Adaptivity allows for efficient resolution of both large- and small-scale solution features by minimizing the necessary computational degrees of freedom. This provides a cost-effective mechanism for application of domain-based procedures to large-scale structures. Although we restrict attention to the frequency domain, adaptivity can likewise be beneficial in the time domain. The use of unstructured meshes allows for efficient representation of geometric complexities. Finite element computations in exterior domains are enabled by applying the Dirichlet-to-Neumann (DtN) condition on an artificial exterior boundary. Two finite element formulations are considered: the Galerkin and the Galerkin Least-Squares (GLS) methods. Computational efficiency is achieved by applying an explicit residual-based a posteriori error estimator coupled with a global h-adaptive strategy. An hp-adaptive strategy, in which the element size h and polynomial order p can be refined simultaneously, is also presented. Through two-dimensional simulation of nonuniform radiation from a rigid infinite circular cylinder, it is shown (using h-refinement only) that the adaptive process produces a final mesh with a greatly reduced number of elements for any given accuracy. Based on a solution error of 1 percent, the adaptive mesh contains 3.5 times fewer elements than a uniform mesh (for the Galerkin formulation). When adaptivity is coupled with the GLS formulation, the number of elements required for any given accuracy is reduced even further. |
Note: This research was supported by the Office of Naval Research under Grant N000 14-92-J-1774.
INTRODUCTION
Adaptive Methods
The purpose of this work is to apply previously developed adaptive finite element methodologies to the solution of the Helmholtz equation in exterior domains. In doing so, the viability of adaptivity in reducing the cost of computation will be demonstrated. We compute solutions to a model problem of acoustics in two dimensions, using Galerkin and Galerkin Least-Squares (GLS) finite element formulations with the fully coupled (truncated) DtN boundary condition (Givoli and Keller, 1989; Harari and Hughes, 1994). The development of the DtN boundary condition has allowed the exterior problem to be posed on a finite domain, which enables a finite element analysis. The finite element meshes consist of linear triangles. We present a general hp-adaptive strategy, which allows specification of simultaneous refinement in both the element size h and spectral order p. However, we show results for h-refinement only. In addition, we consider only the Helmholtz equation, which governs the frequency domain; adaptive solutions in the time domain are not addressed. Although adaptivity in the time domain is more complex due to the need to track solution features over time, much of the methodology contained herein could be adapted for that purpose.
Traditionally, the Helmholtz equation in exterior domains has been solved using boundary element formulations applied to the boundary integral form of the equation (see, e.g., Burton and Miller, 1971; van den Berg et al., 1991; Kleinman and Roach, 1974; Seybert and Rengarajan, 1987; Cunefare et al, 1989; Kirkup, 1989; Demkowicz et al., 1991; Demkowicz and Oden, 1994). Another approach is the application of infinite elements to the exterior problem (Bettess, 1977; Burnett, 1995). One of the main issues concerning the choice of solution methodologies is the cost of achieving a desired level of accuracy. Boundary element formulations engender considerable savings in that the problem size is much smaller, requiring meshing of only the domain boundary. However, these formulations require significant costs in equation formation, solution of the linear system (since the coefficient matrix is full and not symmetric), and so on. Harari and Hughes (1992a) have compared the costs of boundary element formulations to the costs of finite element formulations using the fully coupled DtN boundary condition, and have found that finite element methods are competitive. Burnett (1995) has shown a significant cost advantage of the infinite element approach compared to boundary element methods.
There are several ways in which the cost competitiveness of finite element techniques can be increased. The first is to change the finite element discretization. For example, Harari and Hughes (1990, 1991, 1992b) developed a GLS method that provides higher accuracy than Galerkin, and maintains stability even on coarse meshes. We will compare GLS and Galerkin solutions in this paper. A second means of decreasing the cost of finite element methods is to use a local DtN boundary condition (Harari and Hughes, 1991; Bayliss and Turkel, 1980; Givoli, 1991; Givoli and Keller, 1990), which leads to savings in both equation formation and solution time, since much smaller bandwidths are obtained in the coefficient matrix. The penalty for such an approach seems to be a reduced accuracy, or the need for C1-continuous shape functions across element interfaces on the artificial boundary. Still other cost-saving measures are possible. Among these are development of iterative solution techniques and parallelization, as well as reducing the cost of mesh generation. The meshing needs of finite element methods can be formidable, particularly in three dimensions. Mesh generation is currently an area of intensive research, and much progress has been made in recent years (see, e.g., Shephard and Georges, 1991; Schroeder and Shephard, 1989, 1990; Peraire et al., 1988; Cavendish et al., 1985; Lohner and Parikh, 1988; Baker, 1989; Blacker and Stephenson, 1991).
Another cost-saving approach is adaptivity, and it is the focus of this paper. The goal of adaptivity is efficiency of the finite element mesh, in that a solution of a given accuracy is to be obtained with a minimum number of degrees of freedom. The role of adaptivity depends heavily on the problem if highly localized solution features are present, then adaptivity will lead to a larger cost reduction. Adaptivity can be used in conjunction with most of the other cost-saving approaches discussed above. It involves the development and application of technologies outside the finite element solver. In addition to reliable mesh generation and mesh refinement techniques, the primary technologies are a posteriori error estimation and adaptive strategies.
Figure 6.1 provides a simplistic illustration of how adaptivity works; all adaptive computations fit more or less into this general framework. The diagram shows how the various components of adaptivity work together to drive the efficient placement of the mesh nodes. The a posteriori error estimator takes the finite element solution as input and computes an estimate of the solution error. The adaptive strategy then uses the estimated error distribution to compute a new, more efficient, distribution of element sizes (in the case of h-refinement), element spectral orders (in the case of p-refinement), or combination thereof (hp-refinement). The mesh generator then creates the adaptive mesh with the requested size distribution (in our case by regenerating the mesh globally), and the process repeats until a suitable stopping criterion is satisfied. The idea is to begin with a relatively coarse, uniform mesh, and drive the adaptive refinement through the selection of smaller and smaller error tolerances in each adaptive iteration. Usually three or four iterations of this loop are sufficient. Efficiency is attained by placing more degrees of freedom in areas where solution errors are large, and fewer degrees of freedom in areas of comparatively smaller errors. In doing so, the adaptive strategy attempts to compute a distribution of degrees of freedom such that the error is equidistributed among the elements of the adaptive mesh.
Each of the component technologies mesh generation, finite element methods, a posteriori error estimation, and adaptive strategies—individually plays a critical role in the realization of an efficient mesh. The meshes in this paper were generated using an advancing front mesh generator written by Jaime Peraire (Peraire et al., 1987). The error estimator and adaptive strategy are derived in Stewart and Hughes (1995). The derivation of the error estimator is based on a general methodology developed by Johnson and coworkers in other contexts, such as model elliptic and advection-diffusion operators and nonlinear conservation laws (see Johnson and Hansbo, 1992; Eriksson and Johnson, 1988; Johnson, 1990, 1992, and references therein). The error estimator is an explicit function of residuals, and provides an upper bound on the L2 -norm of the error. In addition, it does not assume positive-definiteness of the operator. This is important for the propagating case (k2 > 0), in which the Helmholtz operator may lose positivity. Adaptive computation of propagating waves is thus made possible. The adaptive strategy computes simultaneous hp-refinement, and for the problem shown in this paper we specialize to the case of h-refinement only.
The outline of this paper is as follows. In the second section the problem statement is given. In addition, the mesh generator, finite element formulations, a posteriori error estimator and hp-adaptive strategy are described. The remainder of the paper is dedicated to the presentation of results (for h-refinement only). Through solution of nonuniform radiation from an infinite circular cylinder (kα = 2π), we demonstrate the adaptive solution procedure. Galerkin results are presented in the first part of section 3 and GLS results are presented in the second part of that section. Comparisons are made throughout the third section to the case of uniform refinement, providing a context for the adaptive results. Finally, conclusions are given in the fourth section.
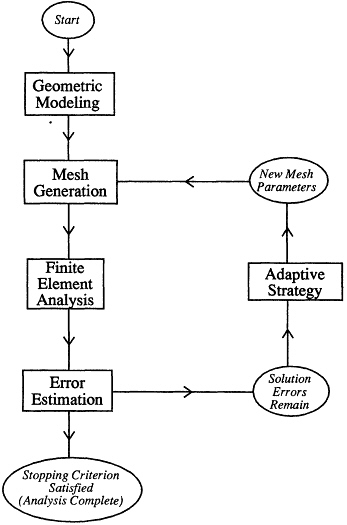
Figure 6.1 Schematic diagram of adaptive solution algorithm, showing the critical technologies involved.
PROBLEM STATEMENT AND ADAPTIVE SOLUTION METHODOLOGIES
In this section we present the problem statement (in the first part) and briefly describe the technologies used to perform the adaptive computations mesh generation, finite element methodologies, a posteriori error estimation, and the hp-adaptive strategy (in the second part).
Problem Statement
The continuous problem is as follows: Find ![]() , the spatial component of the acoustic pressure or velocity potential, such that
, the spatial component of the acoustic pressure or velocity potential, such that
where ![]() is the Helmholtz operator,
is the Helmholtz operator, ![]() is the wave number, and a comma denotes partial differentiation. The interior boundary of Ω is
is the wave number, and a comma denotes partial differentiation. The interior boundary of Ω is
where we assume
The outward normal to Ω is n, ![]() is the imaginary unit, and
is the imaginary unit, and ![]() , and
, and ![]() are the prescribed data. The DtN boundary condition is given by (6.4), where M is the DtN map and
are the prescribed data. The DtN boundary condition is given by (6.4), where M is the DtN map and ![]() is the artificial exterior boundary of Ω. The geometry is depicted in Figure 6.2.
is the artificial exterior boundary of Ω. The geometry is depicted in Figure 6.2.
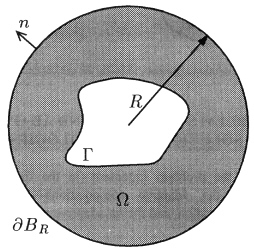
Figure 6.2 Problem geometry for the solution of the Helmholtz equation in an exterior domain.
The weak form of the continuous problem is now stated: Find ![]() such that
such that ![]()
where
and S and V denote the usual spaces of trial solutions and weighting functions, respectively, and an overbar denotes conjugation. In addition, (.,.): ![]() is the L2(Ω)inner product (with the first argument conjugated), and subscripts on inner products denote domains of integration other than Ω.
is the L2(Ω)inner product (with the first argument conjugated), and subscripts on inner products denote domains of integration other than Ω.
Adaptive Solution Methodologies
Mesh Generation
The adaptive meshes are produced via global regeneration; i.e., for each adaptive refinement, the old mesh is discarded and a completely new mesh is generated. This allows us to use the same mesh generator for the initial mesh and the adaptive meshes. All meshes in this paper were generated using a 2d advancing front mesh generator written by Jaime Peraire (Peraire et al., 1987). The method utilizes a background mesh to provide a discrete distribution of element sizes. This is particularly convenient for adaptive mesh generation, since the adaptive element size distribution can be specified using the old mesh. The h-adaptive strategy, presented below, is used to compute a new element size at each xK, where K is an element of the old mesh. The element sizes are scattered to the nodes (where they are stored), and the old mesh then serves as the background mesh.
Finite Element Formulations
The Galerkin form of the continuous problem (6.7) is as follows: Find ![]() such that
such that ![]()
where ![]() And
And ![]() are finite dimensional spaces containing continuous piecewise linear polynomials, and h refers to a suitable measure of element length.
are finite dimensional spaces containing continuous piecewise linear polynomials, and h refers to a suitable measure of element length.
The Galerkin least-squares (GLS) form of (6.7) is given by
Where
and the subscript ![]() denotes integration over the union of element interiors. The parameter τ has dimensions of length-squared and is given by
denotes integration over the union of element interiors. The parameter τ has dimensions of length-squared and is given by
A detailed derivation is given in Harari (1991). The GLS formulation was designed to provide phase accuracy for propagating solutions with fewer mesh points than required for comparable Galerkin solutions. In addition, consistency and stability are maintained. Later we compare GLS and Galerkin results.
A Posteriori Error Estimation
The a posteriori error estimator was derived by Stewart and Hughes (1995) using the method developed by Johnson and coworkers (see, e.g., Johnson and Hansbo, 1992; Johnson, 1992; Eriksson and Johnson, 1988; Johnson, 1990). It is in the form of an upper bound on the global L2 -norm of the error, and is an explicit function of residuals (no local problems need to be solved). Important attributes of the error estimator, in the context of the Helmholtz equation in exterior domains, are that nonpositive operators are easily handled (due to the use of the L2 -norm) and the DtN boundary condition is incorporated in a natural way. The a posteriori error bound for the Galerkin formulation is given by
and for the GLS formulation,
The first term on the right-hand side of (6.16) is the error contribution from element interiors, and the second term is the error contribution from element boundaries (which is assigned a constant value over each element interior for the purpose of computing the norm). Ci, Cs, and CGLS are constants.1 Thus, the GLS bound (6.17) is equal to the Galerkin bound (6.16) plus an additional contribution from the error on element interiors.
The residual on element interiors, rh, is given by
The element boundary residual, Rh, is defined as
where
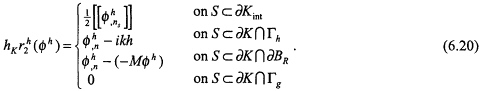
In two dimensions, S denotes an element edge and ![]() denotes an interior mesh edge belonging to element K. In words, (6.19) states that Rh on element K is the maximum value of the boundary residual,
denotes an interior mesh edge belonging to element K. In words, (6.19) states that Rh on element K is the maximum value of the boundary residual, ![]() , over all the edges (i.e., the boundary) of the element. The boundary residual involves a jump in the normal derivative of
, over all the edges (i.e., the boundary) of the element. The boundary residual involves a jump in the normal derivative of ![]() across interior edges, which emanates from the use of C0-continuous shape functions. It is assumed that on
across interior edges, which emanates from the use of C0-continuous shape functions. It is assumed that on ![]() the given data are exactly representable by the finite element functions, i.e.,
the given data are exactly representable by the finite element functions, i.e., ![]()
hp-adaptive Strategy
The hp-adaptive strategy is derived in detail in Stewart and Hughes (1995). We summarize the main results here. For h-refinement only, p is unchanged from the old mesh and the new element size h is given by

where the subscript K refers to quantities in the old mesh, ![]() is a user-defined element error tolerance for the subsequent adaptive mesh solution, and β = 2 for 2D and β = 2.5 for 3D. Thus, (6.21) computes a new h for the location xK of element K in the old mesh. The quantity
is a user-defined element error tolerance for the subsequent adaptive mesh solution, and β = 2 for 2D and β = 2.5 for 3D. Thus, (6.21) computes a new h for the location xK of element K in the old mesh. The quantity ![]() is the (scaled) estimated error in element K, given by
is the (scaled) estimated error in element K, given by
Note that (6.22) does not require the constants CiCs or CGLS (see (6.16) and (6.17)) to be known. This engenders considerable computational savings. The computation of these constants is not discussed herein, but will be the focus of a future paper. The element error ![]() , therefore, represents the approximate element contribution to the scaled global error, where the scaling is with respect to CiCs (for GLS, CGLS is essentially ignored in order for the scaling to be carried out). The element error
, therefore, represents the approximate element contribution to the scaled global error, where the scaling is with respect to CiCs (for GLS, CGLS is essentially ignored in order for the scaling to be carried out). The element error
tolerance ![]() must reflect this scaling. We compute
must reflect this scaling. We compute ![]() using a formula given in Stewart and Hughes (1995),
using a formula given in Stewart and Hughes (1995),
where nel is the number of elements in the old mesh, and ![]() is a user-defined parameter.
is a user-defined parameter.
If p is variable, then the dependence of C, on p can be accounted for by incorporating Ci into the definition of element error:
where Ci,K is the interpolation constant on element K, and ![]() represents an error scaled only by Cs instead of CiCs (compare with (6.22)). This change must be suitably accounted for in the specification of
represents an error scaled only by Cs instead of CiCs (compare with (6.22)). This change must be suitably accounted for in the specification of ![]() . For p-refinement only, h is unchanged from the old mesh and the new element shape function polynomial order for location xK is given by
. For p-refinement only, h is unchanged from the old mesh and the new element shape function polynomial order for location xK is given by
where ![]() has been used instead of
has been used instead of ![]()
For a general hp-refinement, where h and p can be changed simultaneously, pnew is computed using (6.25) and this result is incorporated into the computation of hnew:
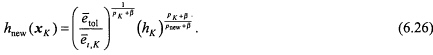
The hp-adaptive strategy is given in Box 6.1.
Remarks:
-
Computation of the dual problem stability constant, Cs, is not necessary.
-
The hp-adaptive strategy allows for either increasing or decreasing h, but p can only be increased (or held constant). In addition, Pnew must be an integer, but hnew is generally a noninteger. Directional stretching of the mesh is not accounted for.
-
It may be necessary to smooth the distribution of Pnew, and/or enforce a limit on the maximum value.
|
Box 6.1 - hp-Adaptive Strategy
|
-
The parameter εp defines the relative amounts of p-refinement and h-refinement. For example, εp > 1 favors h-refinement, and εp > 1 essentially prevents any p-refinement. On the other hand, εp < 1 favors p-refinement.
-
The problem of generating the mesh with the requested {hnew, Pnew}distribution has not been addressed. The method used to refine the mesh dictates what form this distribution must take, and significantly influences the achievability of the requested adaptive mesh. As given in Box 6.1, the adaptive strategy defines {hnew, Pnew} at discrete locations xK, which may be taken as the centroids of elements K in the old mesh. This is a convenient form for an advancing front mesh generator, for example, in which the {h,p} distribution is interpolated from a background mesh. If a finite quadtree/octree mesh generator is used, the hnew distribution may have to be converted to desired quadrant/octant levels. If, instead, a local mesh enrichment procedure is used, in which existing elements are subdivided, hnew (xk) may have to be converted to an integer value, indicating the number of new elements to form from element K. Other techniques can also be used for mesh refinement.
-
As mentioned previously, a sequence of several meshes is used to obtain a complete adaptive solution, where in each step the solution becomes gradually more resolved. The parameter α in (6.23) controls how fast this resolution takes place, or, in other words, the amount of error reduction in each subsequent mesh. This parameter plays an important role in the overall efficiency of the adaptive algorithm. The goal is to drive down the error as quickly as possible without sacrificing efficiency of the adaptive mesh. If α is too low, then the adaptive meshes will contain large areas of overrefinement, decreasing their efficiency. On the other hand, if α is too high, then error reduction will be slow and too many meshes will be necessary. One can also change α from mesh to mesh, or derive an alternative formula for computing
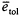
For the computations herein, p is fixed (for linear elements, p = 1), β = 2 (for 2D), and a distribution of the new mesh size, hnew, is all that is required. From (6.21), the computation of hnew reduces to

The same adaptive strategy is used for both the Galerkin and the GLS formulations. This does not imply, however, that the element errors are equivalent. Note that ![]() depends on residuals, which are not necessarily the same for Galerkin and GLS. This will be further explored in the GLS results section below.
depends on residuals, which are not necessarily the same for Galerkin and GLS. This will be further explored in the GLS results section below.
As discussed previously, the h-adaptive strategy computes a pointwise distribution of hnew. The values are stored at the nodes of the old mesh, which in turn provides the necessary input for the mesh generator to build the new, adaptive mesh.
NONUNIFORM RADIATION FROM A RIGID INFINITE CIRCULAR CYLINDER
In this section we compute nonuniform radiation from a rigid infinite circular cylinder for a wave number of ka = 2π, where a is the radius of the cylinder. This problem was previously solved in (Harari and Hughes, 1991) for ka = π on a coarse mesh of quadrilateral elements, and Galerkin and GLS results were compared. Here we examine the problem in more detail, focusing on convergence with both adaptive and uniform mesh refinement. Galerkin results and Galerkin Least-Squares results are presented below.
A brief description of the problem is now given. Referring to Figure 6.2, the interior boundary γ represents the cross section of the cylinder. Dirichlet boundary conditions are applied to the cylinder surface—the portion ![]() is assigned a unit value, while the remaining portion is assigned a homogeneous value. The exact solution is given by
is assigned a unit value, while the remaining portion is assigned a homogeneous value. The exact solution is given by
where here we choose ![]() . Highly localized features are present, namely the discontinuities in the boundary values at
. Highly localized features are present, namely the discontinuities in the boundary values at ![]() . The challenge of the adaptive analysis is to efficiently capture these features.
. The challenge of the adaptive analysis is to efficiently capture these features.
Galerkin Results
The solution was computed on a sequence of 5 meshes. Figure 6.3 shows the real part of the solution along with the corresponding mesh, for each of the 5 meshes. The number of elements and nodes in each mesh are given in Table 6.1. The computation begins with a coarse uniform mesh, while
the subsequent adaptive meshes are obtained by gradually decreasing the element error tolerance, ![]() . The value of α for each adaptive mesh, used in (6.23) to compute
. The value of α for each adaptive mesh, used in (6.23) to compute ![]() , is also listed in Table 6.1.
, is also listed in Table 6.1.
The solution becomes highly attenuated to the left of the cylinder, and the error estimator records a very small error there. This is reflected in the second mesh, as the adaptive strategy computes a large element size. The refinement capturing the radiated wave is also evident in the second mesh. This problem contains highly localized features, namely the discontinuities in the boundary values at ![]() . It can be seen in the fourth and fifth meshes that they are efficiently captured. A high degree of refinement exists at the discontinuities, and a lesser degree of refinement resolves the radiated wave.
. It can be seen in the fourth and fifth meshes that they are efficiently captured. A high degree of refinement exists at the discontinuities, and a lesser degree of refinement resolves the radiated wave.
The mesh gradually coarsens towards the left side of the cylinder, efficiently adapting to the attenuating solution.
Table 6.1 Number of Elements and Nodes in the Sequence of Meshes Shown in Figure 6.3, for the Adaptive Solution of Nonuniform Radiation from a Rigid Infinite Circular Cylinder, ka = 2π
|
Mesh |
nel |
nnd |
α Eq. (6.23)a |
|
1 |
184 |
124 |
— |
|
2 |
323 |
194 |
.15 |
|
3 |
797 |
458 |
.13 |
|
4 |
1812 |
1001 |
.14 |
|
5 |
2791 |
1521 |
.25 |
|
a The value of α for each adaptive mesh, used in (6.23) to compute |
|||
In the second mesh in Figure 6.3, it is apparent that the coarsening of the elements has caused a degradation of the geometry. This is not seen to be a problem, since the subsequent refinement restores the geometrical representation. However, if it is desired to maintain geometrical integrity throughout the refinement process, this can easily be accomplished by limiting the maximum allowable element size. In doing so only the extremely large elements are affected; thus, very few elements would be added to the mesh.
Figure 6.4 shows the final adaptive mesh and a uniform mesh with nearly the same number of elements. Alongside the full mesh is an enlargement of the region near the upper boundary condition discontinuity. The elements in the uniform mesh are extremely large in this region compared to the adaptive mesh, leading to a relatively poor resolution of the discontinuity. This contributes to a global error (![]() ) over 3 times greater than that in the adaptive mesh (
) over 3 times greater than that in the adaptive mesh (![]() ).
).
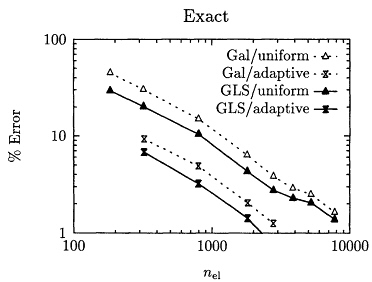
Convergence with increasing number of elements is shown in Figure 6.5, comparing the adaptive and uniform mesh (exact) errors for the entire sequence of mesh refinements.
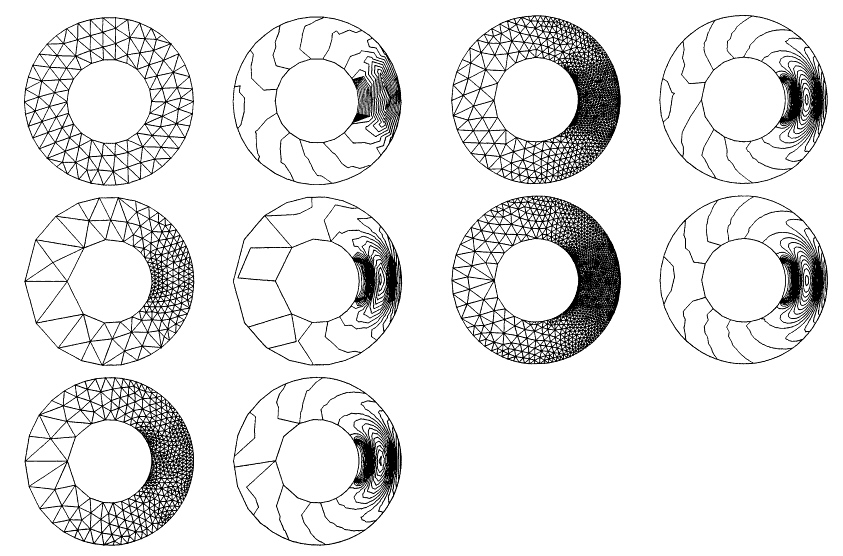
Figure 6.3 Nonuniform radiation from an infinite circular cylinder, ka = 2π: real part of solution along with corresponding mesh, showing the five meshes used in the adaptive solution. The number of elements and nodes in each mesh is given in Table 6.1.
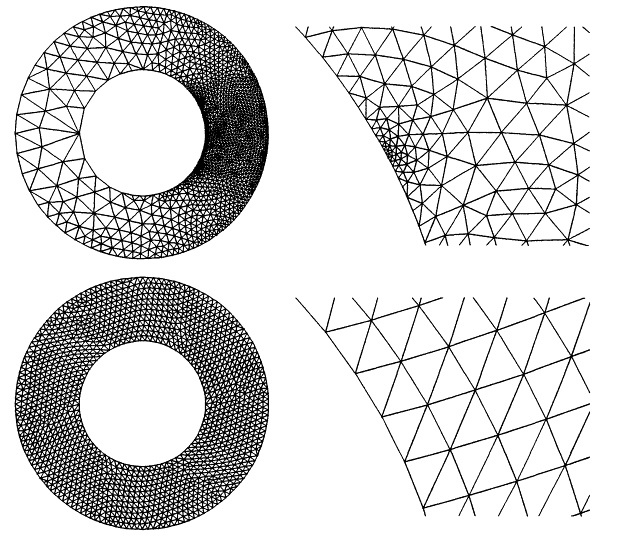
Figure 6.4 Nonuniform radiation from an infinite circular cylinder, ka = 2π: final adaptive mesh (fifth mesh in adaptive sequence; 2,791 elements, ![]() ) and uniform mesh (2,792 elements,
) and uniform mesh (2,792 elements, ![]() ), along with detailed view of meshes in region of upper boundary condition discontinuity.
), along with detailed view of meshes in region of upper boundary condition discontinuity.
Recall that the analytical solution is given by (6.28). To get an idea of required mesh sizes for further decreases in error, linear fits of the convergence data are also shown. The slopes of these lines, indicated in the figure, show that the convergence rate of adaptive refinement is roughly the same as the convergence rate of uniform refinement. It is easily seen that the uniform mesh requires a much larger number of elements to achieve a given error tolerance, compared to the required adaptive mesh size. For example, to attain ![]() requires just under 4,000 elements in the adaptive mesh, but over 13,000 elements in the uniform mesh.
requires just under 4,000 elements in the adaptive mesh, but over 13,000 elements in the uniform mesh.
Figure 6.5 Nonuniform radiation from an infinite circular cylinder, ka = 2π: exact error vs. number of elements in the mesh. The solid lines are curve fits of the data.
Remarks:
-
Convergence studies are often presented in terms of the mesh parameter, or element size, h, as it asymptotically approaches 0. The definition of h becomes confusing, however, in adaptive meshes where h can vary considerably throughout the mesh and approach 0 at different rates. For this reason it is more convenient to present convergence studies in terms of nel. An intuitive conversion from nel to h can be made for uniform mesh convergence. In two dimensions, nel is proportional to 1/h2. Therefore, the slope of -0.91 indicated in Figure 6.5 roughly translates to a slope of +1.82 if
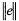 is plotted versus h. In other words, the error decreases at a rate slightly lower than the square of h; the latter is the optimal rate of convergence for the Galerkin method. Since the slope of
is plotted versus h. In other words, the error decreases at a rate slightly lower than the square of h; the latter is the optimal rate of convergence for the Galerkin method. Since the slope of 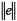 vs. nel, for adaptive refinement is -0.93, it is concluded that nearly optimal convergence is also obtained in this case. The primary effect of h-adaptivity is to reduce the constant of proportionality between solution error and problem size.
vs. nel, for adaptive refinement is -0.93, it is concluded that nearly optimal convergence is also obtained in this case. The primary effect of h-adaptivity is to reduce the constant of proportionality between solution error and problem size. -
For computing the exact error, 200 terms were used in the series given by (6.28). This provided a reasonable approximation of the discontinuities on the wet surface at
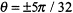 , where the series converges to the average value
, where the series converges to the average value 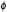 = 0.5 (note that the term ''discontinuities'' is used loosely the truncated series representation of them is actually smooth but very steep). To provide consistency and meaning to the term "exact error," the truncated series solution was used as the Dirichlet boundary condition. In addition, a node was fixed at each discontinuity and assigned a value
= 0.5 (note that the term ''discontinuities'' is used loosely the truncated series representation of them is actually smooth but very steep). To provide consistency and meaning to the term "exact error," the truncated series solution was used as the Dirichlet boundary condition. In addition, a node was fixed at each discontinuity and assigned a value 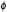 h = 0.5. This was found to be critical since if the discontinuities were not "captured," the convergence rate would be reduced (i.e., suboptimal convergence would occur when the mesh became refined enough for the overall error to be dominated by the error at the discontinuities).
h = 0.5. This was found to be critical since if the discontinuities were not "captured," the convergence rate would be reduced (i.e., suboptimal convergence would occur when the mesh became refined enough for the overall error to be dominated by the error at the discontinuities). -
Note that the boundary condition
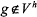 , which violates the assumption in (6.16). Nonetheless, as seen in foregoing results, the error estimator has enough robustness to adapt to the boundary solution. As
, which violates the assumption in (6.16). Nonetheless, as seen in foregoing results, the error estimator has enough robustness to adapt to the boundary solution. As
-
the mesh is refined, the approximation of g improves. With respect to the analytically discontinuous problem, i.e., the problem described by computing an infinite number of terms in the analytical solution, the only error incurred by the piecewise linear representation of g would be at the two discontinuities. With respect to the truncated series form of the analytical solution, additional error (assumed to be small) is incurred away from the "discontinuities."
GLS Results
In addition to applying adaptive procedures, the efficiency of the mesh (uniform or adaptive) can be increased by improving the finite element formulation. This is precisely the goal of the Galerkin Least-Squares (GLS) formulation, given by (6.6), which was designed to enhance accuracy while maintaining stability and consistency (Harari and Hughes, 1991). The method provides nodal exactness (for a 1D model problem) for propagating solutions up to the limit of mesh resolution (4 elements per wave). In addition, GLS is trivial to implement; for details, see Harari and Hughes (1991). In this section, we compare CLS and Galerkin results for the nonuniform radiation problem.
Contours of Re(![]() h) on a coarse uniform mesh are shown in Figure 6.6, comparing Galerkin and GLS formulations. It is clear that the GLS solution is more resolved, as evidenced by a more defined wave pattern to the right of the cylinder. The exact error in the Galerkin solution is 50 percent higher.
h) on a coarse uniform mesh are shown in Figure 6.6, comparing Galerkin and GLS formulations. It is clear that the GLS solution is more resolved, as evidenced by a more defined wave pattern to the right of the cylinder. The exact error in the Galerkin solution is 50 percent higher.
Figure 6.7 shows the exact error as a function of nel, for GLS with both uniform and adaptive refinement, as well as Galerkin with both uniform and adaptive refinement. The Galerkin convergence curves are the same ones that were presented in Figure 6.5, and are included here for comparison with GLS convergence. We consider first the GLS convergence with uniform refinement, and hereafter refer to it as GLS/uniform (analogous notation is used for the other cases). As expected, the GLS/uniform curve lies below the Galerkin/uniform curve, indicating improved accuracy using GLS.
The convergence of GLS (on uniform meshes) is now compared to that of (Galerkin) adaptive refinement. Referring again to Figure 6.7, the GLS/uniform convergence curve lies above the Galerkin/adaptive curve, indicating (at least for this problem) that adaptivity results in higher computational efficiencies relative to GLS. Finally, adaptivity is combined with GLS to produce the greatest gains in efficiency; this is shown by the GLS/adaptive curve in Figure 6.7. It is seen that adaptivity and GLS are complementary in that their effects are additive. It is also evident that the convergence rates of GLS mirror those of Galerkin.
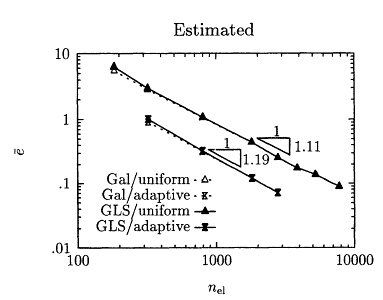
The preceding conclusions are based on analysis of the exact error. We now focus on the estimated error. Figure 6.8 repeats the convergence study of Figure 6.7, this time showing the estimated error as a function of mesh refinement. The estimated error ![]() is obtained by dividing the right-hand side of (6.16) by CiCs, viz.,
is obtained by dividing the right-hand side of (6.16) by CiCs, viz.,
Therefore, ![]() represents the scaled error:
represents the scaled error:
Note for GLS, CGLS is essentially ignored in order for the scaling to be carried out. We examine, therefore, only relative magnitudes of ![]() . It is immediately evident from Figure 6.8 that
. It is immediately evident from Figure 6.8 that ![]() is nearly identical to
is nearly identical to ![]() , for both uniform refinement (top curve) and adaptive refinement (bottom curve). This is in contrast to the conclusions of Figure 6.7, where GLS significantly improves upon the accuracy of Galerkin. Since
, for both uniform refinement (top curve) and adaptive refinement (bottom curve). This is in contrast to the conclusions of Figure 6.7, where GLS significantly improves upon the accuracy of Galerkin. Since ![]() is essentially a function of the residual, it must be concluded here that the GLS residual is nearly identical to the Galerkin residual, even when the two solutions are different.
is essentially a function of the residual, it must be concluded here that the GLS residual is nearly identical to the Galerkin residual, even when the two solutions are different.
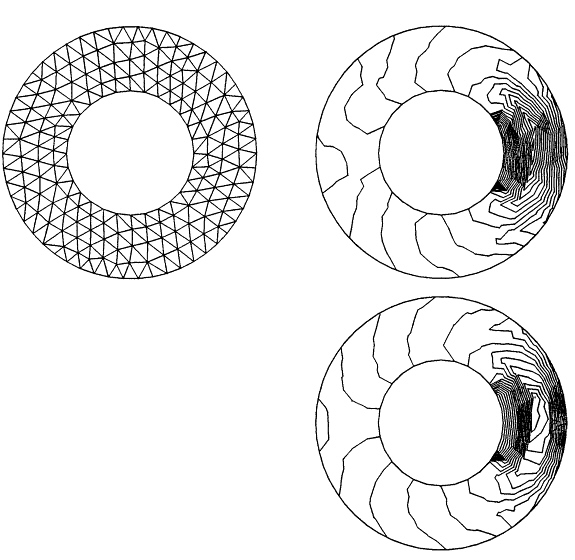
Figure 6.6 Nonuniform radiation from an infinite circular cylinder, ka = 2π: comparison of Re(![]() h) for the Galerkin (top) and GLS (bottom) formulations, on a relatively coarse uniform mesh (320 elements, 201 nodes). For the Galerkin solution,
h) for the Galerkin (top) and GLS (bottom) formulations, on a relatively coarse uniform mesh (320 elements, 201 nodes). For the Galerkin solution, ![]() ; for the GLS solution,
; for the GLS solution, ![]()
The convergence rates with respect to the estimated error (indicated by the slopes shown in Figure 6.8) are about 20 percent higher than the exact convergence rates (Figure 6.7). This is likely due to the error estimator being less accurate on coarser meshes, by overpredicting the error to a greater extent.2
From these results we can draw conclusions regarding the absolute value of the estimated GLS error. Computation of the absolute error entails including the heretofore ignored parameters CiCs and Cots appearing in the error estimates. Comparing the GLS error expression (6.17) to the Galerkin error expression (6.16), it is clear that the estimated GLS error will be larger than the estimated Galerkin error since
The overprediction of the GLS error estimator is actually greater upon noting, as discussed above, that the exact GLS error is lower than the exact Galerkin error.
A common measure of the absolute accuracy of error estimators is the global effectivity index, θ, given by
Thus θGLS is larger than θGalerkin, since for GLS the numerator is larger and the denominator is smaller than the corresponding Galerkin values. In other words, the Galerkin a posteriori error bound is (globally) sharper than the GLS bound.
In a forthcoming paper, we will compute CiCs and CGLS as well as θ (including distributions of local, or elementwise, effectivity indices); we will also compute the robustness index (Babuska et al., 1994a,b), and perform a detailed analysis of the quality of the error estimator.
CONCLUSIONS
In this paper, we demonstrated finite element solution-adaptive methodologies on a model time-harmonic exterior acoustics problem in two dimensions. The results indicate that adaptivity can provide a substantial increase in mesh efficiency for these types of problems namely, propagating solutions at moderate wave numbers. A significantly reduced computation cost can therefore be realized. The adaptive computations involved application of an advancing front mesh generator (which generates linear triangles), a Galerkin and Galerkin Least-Squares finite element code, an explicitly residual-based a posteriori error estimator, and an h-adaptive strategy (p and hp-adaptive strategies were also presented, but computations were not performed using these types of refinement). Each of these component technologies, briefly described above, is critical in achieving an efficient adaptive solution.
Results were obtained for the problem of nonuniform radiation from an infinite circular cylinder, for ka = 2π. Galerkin and GLS solutions were compared, and it was shown that the GLS formulation is more efficient (i.e., accurate) on any mesh, adaptive or uniform. Thus GLS can be combined with adaptivity to produce the most efficient computations.
A specific goal in the design of the adaptive strategy was to avoid requiring knowledge of the constant appearing in the error estimator. This led to much simplification and cost savings; however, the issue of how to define a stopping criterion is perhaps made more difficult. The computation of the constant appearing in the error estimator will be discussed in a future paper.
ACKNOWLEDGMENT
We would like to thank Jaime Peraire and Ken Morgan for allowing us to use their mesh generator.
REFERENCES
Babuska, I., T. Strouboulis, C.S. Upadhyay, S.K. Gangaraj, and K. Copps, 1994a, "Validation of a posteriori error estimators by numerical approach,"Int. J. Numer. Methods Eng.37,1073-1123.
Babuska, I., T. Strouboulis, and C.S. Upadhyay, 1994b, "A model study of the quality of a posteriori error estimators for linear elliptic problems. Error estimation in the interior of patchwise uniform grids of triangles,"Comput. Methods Appl. Mech. Eng.114,307-378.
Baker, T.J., 1989, "Automatic mesh generation for complex three-dimensional regions using a constrained Delaunay triangulation,"Engineeringwith Computers5,161-175.
Bayliss, A., and E. Turkel, 1980, "Radiation boundary conditions for wave-like equations,"Commun. Pure Appl. Math.33, 707-725.
Bettess, P., 1977, "Infinite Elements,"Int. J. Numer. Methods Eng .11, 53-64.
Blacker, T.D., and M.B. Stephenson, 1991, "Paving: A new approach to automated quadrilateral mesh generation,"Int. J. Numer. MethodsEng.32, 811-847.
Burnett, D., 1995, "A 3-D acoustic infinite element based on a generalized multipole expansion," submitted to J. Acoust. Soc. Am.
Burton, A.J., and G.F. Miller, 1971, "The application of integral equation methods to the numerical solution of some exterior boundary-value problems,"Proc. R. Soc. London Ser.A323, 201-210.
Cavendish, J.C., D.A. Field, and W.H. Frey, 1985, "An approach to automatic three-dimensional finite element mesh generation,"Int.J. Numer. Methods Eng.21,329-347.
Cunefare, K.A., G. Koopman, and K. Brod, 1989, "A boundary element method for acoustic radiation valid for all wave numbers,"J. Acoust.Soc. Am.85 (1), 39-48.
Demkowicz, L., and J.T. Oden, 1994, "Recent progress on application of hp-adaptive BE/FE methods to elastic scattering,"Int. J. Numer.Methods Eng.37, 2893-2910.
Demkowicz, L., J.T. Oden, M. Ainsworth, and P. Geng, 1991, "Solution of elastic scattering problems in linear acoustics using h-p boundary element methods,"J. Comput. Appl. Math.36, 29-63.
Eriksson, K., and C. Johnson, 1988, "An adaptive finite element method for linear elliptic problems,"Math. Comp.50, 361-383.
Givoli, D., 1991, "Non-reflecting boundary conditions—a review,"J. Comput. Phys.94 (1), 1-29.
Givoli, D., and J.B. Keller, 1989, "A finite element method for large domains,"Comput. Methods Appl. Mech. Eng.76, 41-66.
Givoli, D., and J.B. Keller, 1990, "Non-reflecting boundary conditions for elastic waves,"Wave Motion12, 261-279.
Harari, I., 1991, "Computational methods for problems of acoustics with particular reference to exterior domains,"Ph.D. Thesis, Division of Applied Mechanics, Stanford University, Stanford, Calif.
Harari, I., and T.J.R. Hughes, 1990, "Design and analysis of finite element methods for the Helmholtz equation in exterior domains,"Appl. Mech. Rev.43 (2), 366-373.
Harari, I., and T.J.R. Hughes, 1991, "Finite element methods for the Helmholtz equation in an exterior domain: model problems,"Comput.Methods Appl. Mech. Eng.87, 59-96.
Harari, I., and T.J.R. Hughes, 1992a, "A cost comparison of boundary element and finite element methods for problems of time-harmonic structural acoustics,"Comput. Methods Appl. Mech. Eng.97, 77-102.
Harari, I., and T.J.R. Hughes, 1992b, "Analysis of continuous formulations underlying the computation of time-harmonic acoustics in exterior domains,"Comput. Methods Appl. Mech. Eng.97, 103-124.
Harari, I., and T.J.R. Hughes, 1994, "Studies of domain-based formulations for computing exterior problems of acoustics,"Int. J. Numer. MethodsEng.37, 2935-2950.
Johnson, C., 1990, "Adaptive finite element methods for diffusion and convection problems,"Comput. Methods Appl. Mech. Eng.82, 301-322.
Johnson, C., 1992, "Finite element methods for flow problems." In: AGARD Report 787 (AGARD, 7 Rue Ancelle, 92299 Neuilly sur Seine, France), 1.1-1.47.
Johnson, C., and P. Hansbo, 1992, "Adaptive finite element methods in computational mechanics,"Comput. Methods Appl. Mech. Eng.101, 143-181.
Kirkup, S.M., 1989, "Solution of exterior acoustic problems by the boundary element method,"Ph.D. Thesis, Department of Mathematical Sciences, Brighton Polytechnic, Brighton, U.K.
Kleinman, R.E., and G.F. Roach, 1974, "Boundary integral equations for the three-dimensional Helmholtz equation,"SIAM Review16 (2), 214-236.
Lohner, R., and P. Parikh, 1988, "Generation of three-dimensional grids by the advancing-front method,"Int. J. Numer. Methods Fluids8, 1135-1149.
Peraire, J., M. Vahdati, K. Morgan, and O.C. Zienkiewicz, 1987, "Adaptive remeshing for compressible flow computations,"J. Comput. Phys.72 , 449-466.
Peraire, J., J. Peiro, L. Formaggia, K. Morgan, and O.C. Zienkiewicz, 1988, "Finite element Euler computations in three dimensions,"Int.J. Numer. Methods Eng.26, 2135-2159.
Schroeder, W.J., and M.S. Shephard, 1989, "An O(N) algorithm to automatically generate geometric triangulations satisfying the Delaunay circumsphere criteria,"Engineering with Computers5, 177-193.
Schroeder, W.J., and M.S. Shephard, 1990, "A combined Octree/Delaunay method for fully automatic 3-D mesh generation,"Int. J. Numer. MethodsEng.29, 37-55.
Seybert, A.F., and T.K. Rengarajan, 1987, "The use of CHIEF to obtain unique solutions for acoustic radiation using boundary integral equations,"J. Acoust. Soc. Am.81, 1299-1306.
Shephard, M.S., and M.K. Georges, 1991, "Automatic three-dimensional mesh generation by the finite octree technique,"Int. J. Numer. MethodsEng.32, 709-749.
Stewart, J.R., and T.J.R. Hughes, 1995, "An a posteriori error estimator and hp-adaptive strategy for finite element discretizations of the Helmholtz equation in exterior domains," to appear in Finite ElementsAnal. Des.
van den Berg, P.M., A.P.M. Zwamborn, G.C. Hsiao, and R.E. Kleinman, 1991, "Iterative solutions of first kind integral equations." In: Direct and Inverse Boundary Value Problems, R.E. Kleinman, R. Kress, and E. Martensen (eds.), New York: P. Lang, 213-232.