10
An Overview of the Application of the Method of Moments to LargeBodies in Electromagnetics
Edward H. Newman
I. Tekin
Ohio State University
|
This paper presents an overview of recently developed techniques that improve the efficiency of the method-of-moments (MM) solution of electromagnetic radiation and scattering problems and thus allow it to be applied to electrically larger bodies. The techniques reviewed include fast iterative methods, recursive methods, sparse matrix methods, and the use of different unknowns or expansions. It is concluded that only with a hybrid method that combines a "low-frequency" technique, such as the MM, with an asymptotic "high-frequency" technique can problems of arbitrary size and complexity be treated. |
INTRODUCTION
The frequency-domain method of moments (MM) is possibly the most well developed and widely used of the numerical methods for the analysis of electromagnetic radiation and scattering problems (Harrington, 1982, 1987; Hansen, 1990; Miller, 1988; Miller et al., 1991; Wang, 1991). As it is typically applied in electromagnetics, the MM is used to solve an integral equation for the currents on or in a body, by converting the integral equation to a matrix equation. For this reason, the MM is often referred to as an integral equation method. An advantage of integral equation methods is that the unknowns of the problem are limited to the surface or volume of the radiating or scattering body, as compared to differential equation methods (such as the finite element or finite difference methods), in which the unknowns can fill all space. A second advantage of integral equation methods is that the elements in the MM matrix equation are all expressed as integrals of fields, as opposed to derivatives of fields in the differential methods. The averaging process of integration tends to make integral equation methods more stable and reliable than differential equation methods. Finally, the MM is a method that is applicable to almost arbitrary geometries, and thus it has been implemented in a number of user-oriented general purpose computer codes. A disadvantage of the standard MM is that it generates full matrices. Thus, for an N unknown MM solution, the matrix fill time and storage requirements are O (N2), while the matrix
Note: This work was sponsored by the Joint Services Electronics Program under Contract N00014-78-C-0049 with the Ohio State University Research Foundation.
solution time (by direct methods) is O(N3) and dominates for large N. Recently, Canning (1991) has pointed out that this solution time can be reduced by a factor of 2 for symmetric matrices. Also, Cohoon (1980) has shown that group theory can be used to exploit problem symmetries and reduce computational expense.
The main limitation of the MM is that N is proportional to some power of frequency, and thus the required computer storage and CPU time increase dramatically as the frequency (and thus the electrical size of the body) increases. For this reason, the MM has always been viewed as a "low-frequency" method applicable when the radiating or scattering body is not too large in terms of the operating wavelength. Over the last several years, a number of methods have been studied to improve the efficiency of the MM and thus allow it to be applicable to electrically larger bodies. This paper will present a non-all-inclusive review of some of these techniques, including fast iterative methods, recursive methods, sparse matrix methods, and hybrid methods.
OVERVIEW OF THE METHOD OF MOMENTS
The method of moments (MM) is a numerical technique for solving a linear operator equation by transforming it into a system of simultaneous linear algebraic equations, i.e., a matrix equation (Harrington, 1982, 1987; Hansen, 1990; Miller, 1988; Miller et al., 1991; Wang, 1991). In electromagnetics, the linear operator equation is almost always a linear integral equation for the actual or equivalent current on or in a radiating or scattering body. Once these currents are known, most parameters of engineering interest, such as input impedance, efficiency and radiated (or scattered) fields, can be evaluated in a straightforward manner and with relatively small computer CPU time and storage (as opposed to that required to obtain the currents).
The first step in the MM solution of the integral equation is to approximate the unknown current J as
where JN is an N term approximation to the true current J, the Jn are a series of N known linearly independent expansion functions, and the In are a series of N unknown coefficients, n = 1,2,3,...,N. The next step is to select a series of N linearly independent weighting functions wm, m=1,2,...,N, and enforce N weighted averages of the integral equation to be valid. This procedure will reduce the integral equation to a system of N simultaneous linear algebraic equations that can be compactly written as the order N matrix equation
In analogy with Ohm's Law, [Z] is the N x N impedance matrix, V is the length N right-hand side or voltage vector, and I is the length N solution or current vector that contains the N unknown coefficients, In, from (10.1). Typical elements of the [Z] matrix and V vector are given by
where En is the electric field of expansion function Jn, Ei is the known incident electric field, and the integrals are over the region (line, surface, volume) of weighting function wm.
As it is usually applied in electromagnetics, there is no guarantee or proof that the MM solution will converge to the exact solution as N increases (Dudley, 1985). However, more than 30 years' experience has shown that it almost always does. In fact, except for classical shapes where exact convergent eigenfunction solutions are available (Bowman et al., 1987), the MM solution is often regarded as the most accurate and reliable method. In fact, it is often used as a reference solution to check other numerical methods and even measurements. Further, it is amenable to the analysis of very complex 2D and 3D geometries such as aircraft, buildings, biological bodies, and log periodic or spiral antennas.
In electromagnetics, the main limitation of the MM is that the number of unknowns, N, is proportional to the electrical size of the radiating or scattering body, i.e., its size in wavelengths. Assuming Nλ unknowns per wavelength (typically ![]() ) and a body of characteristic dimension Lλ wavelengths, then Table 10.1 shows the computer resources for problems in which the unknowns are along a line (thin wires or perfectly conducting 2D cylinders) on a surface (perfectly conducting plate or penetrable 2D cylinder) and through a volume (3D penetrable body). The table also shows the matrix storage and the order of the CPU time assuming a direct solution of the matrix equation. For even modest-sized problems, the storage is dominated by the N2 elements of the dense [Z] matrix. For small or modest-sized problems (say, up to a few hundred unknowns), the CPU time is usually dominated by that to fill the N2 elements of the [Z] matrix. However, for large problems, the O(N3) CPU time to solve the matrix equation 2 by direct LU decomposition always dominates. The important point is that as the electric size of the body increases, the computer resources increase very rapidly. For example, assuming a problem in which the unknowns are distributed along a surface, and Nλ = 10 unknowns per wavelength, then
) and a body of characteristic dimension Lλ wavelengths, then Table 10.1 shows the computer resources for problems in which the unknowns are along a line (thin wires or perfectly conducting 2D cylinders) on a surface (perfectly conducting plate or penetrable 2D cylinder) and through a volume (3D penetrable body). The table also shows the matrix storage and the order of the CPU time assuming a direct solution of the matrix equation. For even modest-sized problems, the storage is dominated by the N2 elements of the dense [Z] matrix. For small or modest-sized problems (say, up to a few hundred unknowns), the CPU time is usually dominated by that to fill the N2 elements of the [Z] matrix. However, for large problems, the O(N3) CPU time to solve the matrix equation 2 by direct LU decomposition always dominates. The important point is that as the electric size of the body increases, the computer resources increase very rapidly. For example, assuming a problem in which the unknowns are distributed along a surface, and Nλ = 10 unknowns per wavelength, then ![]() ,
, ![]() , and
, and ![]() . Note that a factor of 10 increase in frequency will result in a factor of 100 increase in N, a factor of 104 increase in storage, and a factor of 106 increase in CPU time! Clearly, as the frequency increases, the computer resources for the MM increase dramatically, and for this reason the MM is limited to bodies that are not too large in terms of a wavelength.
. Note that a factor of 10 increase in frequency will result in a factor of 100 increase in N, a factor of 104 increase in storage, and a factor of 106 increase in CPU time! Clearly, as the frequency increases, the computer resources for the MM increase dramatically, and for this reason the MM is limited to bodies that are not too large in terms of a wavelength.
Table 10.1 Computer Resources for a MM Solution
|
|
Line |
Surface |
Volume |
|
Unknowns = N |
NλLλ |
[NλLλ]2 |
[NλLλ]3 |
|
[Z] Storage = N2 |
[NλLλ]2 |
[NλLλ]4 |
[NλLλ]6 |
|
CPU Fill |
O[NλLλ]2 |
O[NλLλ]4 |
O[NλLλ]6 |
|
CPU Solve |
O[NλLλ]3 |
O[NλLλ]6 |
O[NλLλ]9 |
The MM is often referred to as a "low-frequency" method; however, this is not strictly correct. The MM can be applied at optical frequencies if the bodies are of micron size. It is not the frequency that is important, but rather the electrical size of the bodies. The next section will present an overview of several techniques to increase the efficiency of MM solutions and thus allow them to be applicable to electrically larger bodies.
SUMMARY OF METHODS
Iterative Solutions
Without doubt, the main obstacle to the application of the MM to electrically large bodies is the O(N3) CPU time to solve the matrix equation 2 by direct methods such as LU decomposition. The most obvious solution to this problem is to employ an iterative solution to the matrix equation (Sarkar et al., 1981; Ferguson et al., 1976; Sarkar, 1991). For example, to generate a simple iterative solution of (10.2), add I to both sides of the equation to yield
(10.5) suggests the iteration
where Iº is the initial guess for the I vector, Ik is the value of the I vector after k iterations of (10.6), and K is the number of iterations required to achieve some convergence criteria. The major computational effort in an iterative solution is the O(N2 ) [Z]Ik matrix product required in each step of the iteration, and thus the total CPU time is O(KN2). Recent research has centered on reducing the number of iterations, K, required to achieve convergence, and also on reducing the O(N2 ) operation count per iteration.
Reducing the Number of Iterations
Iterative solutions of the dense matrix equations generated by the MM can be extremely slowly convergent, or even nonconvergent. If ![]() , then the iterative solution is O(N3), and it is probably best to use a direct method. As illustrated in Figure 10.1, iterative solutions can exhibit stalling or stagnation in which the error initially drops rapidly, and then stalls for a number of iterations before again falling rapidly. As pointed out by Kalbasi and Demarest (1993), the stalling is due to the fact that the rapidly varying or high spatial frequency components in the solution typically converge rapidly, while the slowly varying or low-frequency spatial components are more slowly varying.
, then the iterative solution is O(N3), and it is probably best to use a direct method. As illustrated in Figure 10.1, iterative solutions can exhibit stalling or stagnation in which the error initially drops rapidly, and then stalls for a number of iterations before again falling rapidly. As pointed out by Kalbasi and Demarest (1993), the stalling is due to the fact that the rapidly varying or high spatial frequency components in the solution typically converge rapidly, while the slowly varying or low-frequency spatial components are more slowly varying.
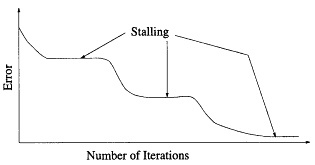
Figure 10.1 An illustration of the stalling or stagnation of an iterative solution.
As illustrated in Figure 10.2, one solution to the stalling problem is a multigrid or multilevel formulation of the MM (Kalbasi and Demarest, 1993). Figure 10.2(a) shows a strip split into N segments, where N is sufficiently large that the MM solution will yield acceptable results. This is referred to as level 1 or the fine level. Figure 10.2(a) also shows the strip split into N/2 and N/4 segments corresponding to the middle level 2 and coarse level 3. In the 3-level V formulation of Figure 10.2(b), the iterative solution is first solved at the fine level 1, then the coarser level 2, and finally the coarsest level 3. As the MM segment size is increased, low spatial frequency components are turned into high spatial frequency components, and stalling is hopefully avoided. The solution is continued by going back up to level 2, and then repeating the process. Results by Kalbasi and Demarest show that the multilevel MM can significantly reduce the number of iterations to obtain convergence, and even turn a nonconvergent iteration into one which does converge.
Murphy, Rokhlin, and Vassilou have developed a method that they term complexification to accelerate the convergence of iterative solutions (Murphy et al., 1993). When the MM is applied to electrically large bodies, the frequency is virtually always close to an interior resonance of the body. This results in a large condition number for the MM [Z] matrix, and slow convergence of the iterative solution. In the complexification method, one replaces the ambient medium, which is typically lossless
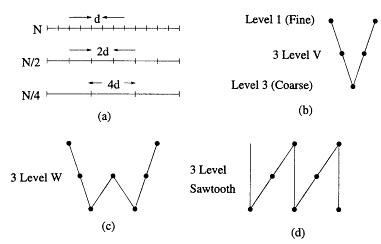
Figure 10.2 A three-level V-type multilevel formulation.
free space, by one with a small amount of loss. Adding loss to the problem reduces the matrix condition number, and thus accelerates convergence of the iterative solution. If the real wavenumber of the ambient medium is k, then one solves the problem in two lossy media of complex wavenumbers k -jk1 and k -jk2. One can then do a linear extrapolation of the currents from these two lossy media solutions, to obtain the currents for the lossless media with real wavenumber k. The same idea can be applied with solutions from three lossy media and quadratic extrapolation to real k. The results of Murphy et al. (1993) show that complexification does accelerate the convergence of the iterative solution, at times by an order of magnitude. An advantage of the complexification method is that it is relatively simple and straightforward to implement, since it typically requires relatively little additional effort to develop a computer code for a lossy, as opposed to lossless, medium.
The Fast Multipole Method
The fast multipole method (FMM), developed by V. Rokhlin and others, is a technique to perform a matrix vector product in O(N3/2) or fewer operations (Murphy et al., 1993; Rokhlin, 1983, 1990; Engheta et al., 1992; Coifman et al., 1993). In an iterative solution, one must perform a matrix vector product of the form Vk = [Z]Ik, where Ik is the known solution vector after k iterations. Element m of Vk is the inner product between row m of [Z] and Ik; i.e.,
When performed in the straightforward manner of (10.7), each inner product requires O(N) operations, and thus the matrix vector product requires O(N2) operations. The FMM provides a rapid method for performing those terms in the summation of (10.7), for which modes m and n are far removed.
As illustrated in Figure 10.3, in the FMM the basis functions are collected into P groups of p = N/P basis functions each. If the groups containing the expansion and weighting functions are in the far zone of each other, then the contribution from all of the expansion functions in the expansion group can be evaluated through the use of a multipoleexpansion that requires far fewer operations than the straightforward superposition indicated in (10.7). In electromagnetics, roughly kD multipoles are required, where k is the wavenumber and D is the size of the expansion group. If kD « p, then considerable time can be saved using the multipole expansions.
As a simple example of a multipole, consider the problem of computing the gravitational field of a large collection of p small masses, ml, i = 1,2,...p. If the observation point is far removed from the p masses, then the gravitational field will be close to that of a point mass
A Scatterer with N=32 Basis Functions
Split Into P=8 Sections of p=N/P=4 Basis Functions per Section
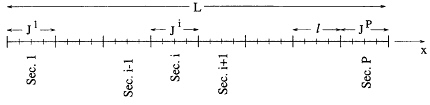
Figure 10.3 A scatterer is split into P sections of p = N / P unknowns.
located somewhere near the center of the p masses. M0 can be viewed as the 0th order multipole of the masses.
In an electrically large body, most of the groups will be in the far zone of each other, and thus most of the terms in the summation of (10.7) will be performed by the faster multipole expansions. Further, since the Zmn corresponding to modes m and n in far zone groups are never explicitly used, they need not be computed or stored. Thus, the CPU time to compute the [Z] matrix, and the memory to store it, can be dramatically reduced. Early results on problems with roughly N = 1000 unknowns show an order of magnitude reduction in CPU time and storage. More dramatic results may be possible for larger N.
Recursive Methods
Recursive methods are different from iterative methods. In an iterative method, one sets up the solution to the entire or global problem, and then attempts to generate in an iterative manner global solutions that approach the exact solution. By contrast, in a recursive solution the global problem is split into many smaller problems. The smaller problems are solved, and their solutions are combined in some recursive manner to build up to the solution to the global problem.
Exact Fixed Step Methods
Over the past several years W.C. Chew and others at the University of Illinois' Electromagnetics Laboratory (Chew, 1993) have developed a series of recursive algorithms for solving electromagnetic scattering problems that can be viewed as a large collection of N scattering bodies. In a recursive method, one begins by "analyzing" the individual scatterers. Typically, "analyzing" means determining the scatterer T-Matrix (Waterman, 1969), which defines the amplitude of the modal harmonics scattered by the body for a given incident mode. The N one body solutions are then combined to form N / 2 two body solutions, which are then combined to form N / 4 four body solutions, and the process is continued until the N body problem is solved. As opposed to the iterative methods described above, these recursive methods determine the exact (meaning the solution that would have been obtained if the N body problem were attacked directly) solution in a fixed number of steps. Several recursive algorithms have been developed by the group at the University of Illinois (Chew, 1989; Gurel and Chew, 1992a,b; Chew and
Yang, 1990; Chew et al., 1992, 1995; Lu and Chew, 1993; and Chew and Lu, 1993) and go under names such as "Recursive T-Matrix Algorithms" (RTMA). Depending upon the method, the complexity of the problem is reduced to ![]() , as compared to O(N3) for a standard MM solution with LU decomposition.
, as compared to O(N3) for a standard MM solution with LU decomposition.
Spatial Decomposition
As illustrated in Figure 10.3, in the spatial decomposition method, a large body is segmented into P smaller parts or sections, each having p = N / P unknowns (Umashankar et al., 1992). Let us denote

as the current on section i, and thus the current on the entire strip J = J1 + J2 +...+Jp. The method is begun by initializing J to the best estimate available. This might be the physical optics current ![]() , or it could simply be J = 0. The first recursion is begun by determining the current, J1 on section 1, induced by the incident fields and by the best estimate currents on Sections 2- P. These Section 1 currents are determined by a standard MM solution with LU decomposition. This is an order O(p3) = O[(N /P)3] process, which for large P is much less than the O(N3) direct MM solution of the entire problem. The next step is to determine the currents induced on Section 2 by the incident fields plus the best estimate currents on Sections 1 and 3- P (i.e., the just-determined J1, plus the initial guess for the currents on Sections 3 - P ). This process is continued until the currents on all sections have been updated once, thus completing the first recursion. The second recursion is identical to the first, except the first recursion has provided an update of the best estimate current. The recursive process must then be continued until some convergence criterion has been met. Assuming that as N increases, P also increases to keep p = N / P constant, the entire recursion is of order O(KP) = O(KN / p), where K is the number of recursions necessary to obtain convergence. On modest-size problems of a few hundred unknowns, the method has been shown to produce essentially the same results as a standard MM solution, but with up to an order of magnitude savings in CPU time.
, or it could simply be J = 0. The first recursion is begun by determining the current, J1 on section 1, induced by the incident fields and by the best estimate currents on Sections 2- P. These Section 1 currents are determined by a standard MM solution with LU decomposition. This is an order O(p3) = O[(N /P)3] process, which for large P is much less than the O(N3) direct MM solution of the entire problem. The next step is to determine the currents induced on Section 2 by the incident fields plus the best estimate currents on Sections 1 and 3- P (i.e., the just-determined J1, plus the initial guess for the currents on Sections 3 - P ). This process is continued until the currents on all sections have been updated once, thus completing the first recursion. The second recursion is identical to the first, except the first recursion has provided an update of the best estimate current. The recursive process must then be continued until some convergence criterion has been met. Assuming that as N increases, P also increases to keep p = N / P constant, the entire recursion is of order O(KP) = O(KN / p), where K is the number of recursions necessary to obtain convergence. On modest-size problems of a few hundred unknowns, the method has been shown to produce essentially the same results as a standard MM solution, but with up to an order of magnitude savings in CPU time.
Sparse Matrix Methods
Method-of-moments (MM) impedance matrices are generally dense. Referring to (10.3), this is a result of the fact that En is an entire domain function that fills all space, and drops off only as 1 / r from the expansion function Jn. An MM formulation that did produce a sparse [Z] matrix would save storage as well as CPU time by using sparse matrix methods for solving the matrix equation. Further, if the essentially zero elements could be determined a priori, then CPU time could also be saved in the matrix fill by simply not computing the essentially zero elements of [Z]. The methods presented below do not generate sparse matrices in the sense that most elements are exactly 0. Rather, they generate matrices in which most elements are much smaller than the largest or dominant elements. A threshold is set, and elements whose magnitude fall below that threshold are set to 0 and ignored. As the threshold level is raised, the [Z] matrix becomes sparser, and the method becomes more efficient but less accurate.
The Impedance Matrix Localization Method
In the impedance matrix localization method (IML) developed by Canning (1990, 1993), it is helpful to think of Zmn of (10.3) as the voltage induced in a receiving antenna with current wm by a transmitting antenna with current Jn. Thus, if modes m and n are not too close, Zmn is proportional to the product
where Rmn is the center to center distance between modes m and n and the patterns are evaluated at a look angle from the center of mode n to the center of mode m. The patterns of Jn or wm are the free space electric fields of the currents, Jn or Wm, respectively.
Typically MM solutions employ subsectional basis functions defined over an electrically small region of the body, not exceeding λ / 4. These small currents have essentially omnidirectional radiation (and receive) patterns, and thus by (10.10) produce a dense [Z] matrix. As illustrated in Figure 10.4 the idea of the IML is to use electrically large basis functions, and further to employ a traveling wave current distribution such that the basis functions have highly directional patterns. In Figure 10.4, it can be seen that Zmn will only be significant if wm falls within the main beam of Jn and vice versa. Otherwise Zmn will be relatively small, and can be ignored or set to 0. In a sample computation with a threshold of 0.001 (i.e., ignore elements of [Z] less than the threshold times the largest element), only 2 percent of the elements of [Z] were above the threshold, and yet the method produced excellent results for the far-zone scattered fields.
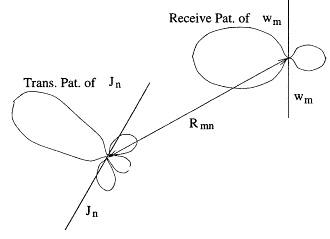
Figure 10.4 Zmn is proportional to the product of the transmit pattern of Jn times the receive pattern of Wm.
Pogorzelski developed a somewhat different method for obtaining a sparse MM [Z] matrix, which he termed near-field localization (Pogorzelski, 1993). Rather than use basis functions with highly directive far-field patterns as in the IML, Pogorzelski suggested the use of basis functions whose near-zone patterns are highly focused to a small region on the surface of the body. In this way there is only strong coupling between closed-spaced basis functions. As the electrical size of the body increases, and the total number of basis functions is increased, the total number of significant matrix elements remains approximately constant.
Wavelet Basis Functions
Although wavelets have many interesting properties that make them useful in signal processing applications and as basis functions for different numerical methods (Daubechies, 1992), the feature exploited by Steinberg and Leviatan (1993) to produce a sparse MM impedance matrix is that wavelets have 0 average value. Figure 10.5 illustrates the computation of the mutual impedance between expansion function Jn and Galerkin weighting function wm for the cases of simple pulse and wavelet type basis functions. Referring to (10.3), Zmn is the weighted average of the electric field of expansion n over the extent of weighting function m, and weighted by wm. For far separated modes, Zmn can be approximated by
where En (rm) is the electric field of Jn evaluated at the center of weighting function m, and
is the current moment of weighting function wm. Pulse basis functions (and virtually every other common subsectional basis function) have a finite current moment, and thus Zmn is reduced only by the 1 / r dependence of its far-zone fields. By contrast, wavelet basis functions have 0 average value, and thus 0 current moment. Although (10.11) predicts that for far separated wavelets Zmn = 0, this is not exactly true. The reason is that (10.11) is based upon the approximation that En is constant over the extent of weighting function m, which is not true for the phase even in the limit as the separation goes to infinity. The wavelet far separated mutual impedances are further reduced by the fact that, since the wavelet expansion function has 0 current moment, its far-zone fields drop off as 1/r2, rather than as 1/r for conventional subsectional basis functions. On a rather small problem with only N = 80 unknowns, as the threshold was adjusted lower from 0.01 to 0.001, the number of elements of [Z] above the threshold increased from 7 percent to 25 percent.
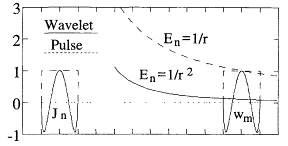
Figure 10.5 Mutual impedance computation for wavelet and pulse type basis functions.
Novel Expansion Methods
Traditionally the unknowns in integral equation methods have been the true electric currents flowing on perfectly conducting bodies, or rigorously obtained equivalent electric and/or magnetic currents flowing either on the surface of or through the volume of penetrable bodies (Balanis, 1989). In an attempt to reduce the number of unknowns in the MM solution, various authors have investigated the use of different unknowns.
Rather than use the true or rigorous equivalent currents to produce the fields scattered by the body, Leviatan and Boag have proposed the use of fictitious current filaments located inside (or outside) the scattering body (Leviatan and Boag, 1987). The use of these filaments avoids the time consuming numerical integrations typically needed to find the fields of the expansion functions. Also, since the filaments are removed from the surface on which the boundary conditions are being enforced, the usual singularity problem associated with computation of self-impedance terms is avoided.
Leviatan, Hudis, and Einziger have investigated the use of Gaussian beams as expansion functions in the MM (Leviatan et al., 1989). An advantage of the Gaussian beam expansion functions is that their fields can be expressed as a summation of analytic terms, thereby avoiding the necessity of a numerical integration. Boag and Mittra have investigated the use of multipole sources in complex space, and have found that the method not only reduces the number of unknowns in the MM solution, but also generates a banded (Z) matrix with a low condition number (Boag and Mittra, 1994).
Recently there has been work on using the electromagnetic fields rather than currents as the unknown. Ludwig developed the spherical-wave expansion technique (SPEX) (Ludwig, 1986, 1989), and Hafner developed the Generalized Multipole Technique (GMT) (Hafner 1990a,b) in which the unknowns are the electromagnetic fields, rather than currents. These fields are expanded in terms of a modal harmonics satisfying Maxwell's equations, and the unknown coefficients are determined by setting up a system of simultaneous linear equations that enforce boundary conditions at the surface of the scatterer. These modal expansion methods have the advantage that often the scattered field can be represented in terms of fewer unknowns than the current. These methods also totally avoid the sometimes numerically difficult problem of computing the fields of currents, since they deal directly with the fields.
Hybrid Methods
Despite all of the methods described above, the MM remains a ''low-frequency'' method, i.e., it is applicable only when the size of the radiating or scattering body is not too large in terms of a
wavelength. By contrast, there are a variety of "high-frequency" or asymptotic methods that are applicable when the radiating or scattering body, and all of its important features, are electrically large. At X-band (10 GHz) there is no available single method that could analyze the radiation from a simple monopole antenna on an aircraft. The MM would fail because the aircraft is electrically too large, and thus would be impractical due to limited computer resources, while the asymptotic methods would fail because the monopole antenna is too small. In the authors' opinion, the only hope for analyzing complex bodies at high frequencies is through the use of hybrid methods (Burnside, 1980) that combine a high-frequency technique, such as the Geometrical Theory of Diffraction (GTD) (Hansen, 1981; Pathak, 1988), to analyze most of the electrically large body with a low-frequency technique, such as the MM, to analyze the remaining small parts that cannot be treated by the high-frequency method.
The Hybrid MM/GTD Method
In a standard MM solution, equivalence theorems are used to replace the entire radiating or scattering body by free space and by equivalent currents (Balanis, 1989, secs. 7.7, 7.8). The advantage of doing this is that all currents radiate in homogeneous free space, and thus the kernel of the integral equation contains the relatively simple free space Green's function. As a result, En and Ei in Equations 10.3 and 10.4 are the free space fields of expansion function Jn and the impressed currents, respectively.
By contrast, in an MM/Green's function solution only a portion of the body is replaced by free space and by equivalent currents (Newman, 1988). For example, Figure 10.6 shows a body split into Sections 1 and 2 (shown disjoint for clarity, but they may be touching). As suggested in Figure 10.6, Section 1 is considered as the small part of the body and requires N1 expansion functions to approximate its current, while Section 2 is the large part and would require N2 » N1 expansion functions to approximate its current (N1 + N2 = N). The advantage of the MM/Green's function method is that one must only place N1 unknowns over that portion of the body that is being replaced by equivalent currents. Thus (10.1) is modified to
where J1 is that portion of J in Section 1. The MM matrix equation is still given by (10.2), however, now it is an order N1 « N matrix equation.
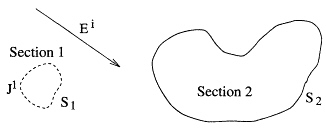
Figure 10.6 In the MM/Green's function method, Section 1, but not Section 2, of the body is replaced by free space and equivalent currents.
The disadvantage of the MM/Green's function method is that the kernel of the integral equation contains the Green's function for Section 2 of the body not replaced by equivalent currents, and thus En and Ei in (10.3) and (10.4) are the fields of expansion function Jn and the impressed currents, respectively, radiating in the presence of Section 2. A problem such as a dipole antenna (Section 1) radiating in the presence of a sphere (Section 2) would be ideal for the MM/Green's function method since the sphere is a classical shape whose Green's function is known, and also since many more unknowns would be required to model the current on the sphere as opposed to that on the dipole.
Of course, a limitation of the MM/Green's function method is that Section 2 must be of sufficiently simple shape that its Green's function is known, and there are only a few classical shapes with known Green's functions (Bowman et al., 1987). However, Thiele and Newhouse (1975) realized that the class of Section 2 geometries can be greatly extended if the GTD is used to approximate the Section 2 Green's function. The result is termed a hybrid MM/GTD method, and was applied by Thiele and Newhouse to analyze a small monopole antenna (Section 1) on a flat plate (Section 2). Today the GTD has been developed to the point where the asymptotic Green's function for a body as complex as an aircraft can be constructed.
The Hybrid GTD/MM Method
A virtual axiom in the MM, rooted in the Sampling Theorem, is that one needs at least 4 expansion functions per linear wavelength. Although one can develop "better" basis functions that can produce more accurate results with fewer unknowns per wavelength, in the end the number of unknowns is still proportional to the electrical size of the body (see Table 10.1) and the MM remains a "low-frequency" method. In an attempt to break this log jam, a technique known as a physicalbasis MM solution was developed by Richmond (1985). In a physical basis MM solution, one attempts to build the physics of the problem into the MM expansion functions so that their size can be increased to cover all or almost all of the body. For example, Richmond solved the problem of scattering by an electrically wide dielectric strip using only 3 expansion functions. Richmond's insight into the physics of the problem suggested that the fields or currents in an electrically wide strip are very close to the known currents in an infinitely wide strip, with the main difference coming from surface waves generated at either end of the strip. Thus, he expanded the current in terms of 3 expansion functions. The first had the form of the currents in an infinitely wide strip, while the second and third had the form of left and right propagating surface waves on the strip. The results for this 3-term physical basis expansion were in very close agreement with a standard pulse basis MM solution, except near the edges of the strip. However, the results for the far-zone fields were in essentially perfect agreement, since the far-zone fields are an integral of the current.
The problem with the physical basis MM solution is that, in general, one does not have enough physical insight into the problem to construct the physical basis expansion functions. However Burnside, Yu, and Marhefka (1975) recognized that, away from edges or other points of discontinuity on electrically large bodies, the form of the currents is closely approximated by the GTD. Thus, the GTD can be used to construct the physical basis expansion functions on a complex body, with the result being referred to as a GTD/MM solution. Near edges or other points of discontinuity they employed standard MM pulse functions. The result is a physical basis MM solution in which the number of unknowns is virtually independent of frequency.
Figure 10.7 illustrates the GTD/MM expansion for the current on a perfectly conducting strip. Note that the strip is divided into the GTD and MM regions. Away from the edges in the GTD region, the strip current will be closely approximated by the physical optics current ![]() plus currents of the form
plus currents of the form
corresponding to currents diffracted from the left and right edges. Here ρl and ρr denote distances from the left or right edges, respectively. In the MM regions near the edges, the shape of the current may be complex, and is represented in terms of standard MM expansion functions. Figure 10.7 illustrates a pulse expansion. Assuming Ne expansion functions are needed near each edge, the GTD/MM expansion for the current on the strip is
in the GTD region
in the left edge MM region
in the right edge MM region. (10.14)
Typically, the width of the MM region is about a wavelength, and thus Ne is typically about 10. Thus, the GTD/MM expansion for the strip requires ![]() unknowns, independent of the electrical width of the strip.
unknowns, independent of the electrical width of the strip.
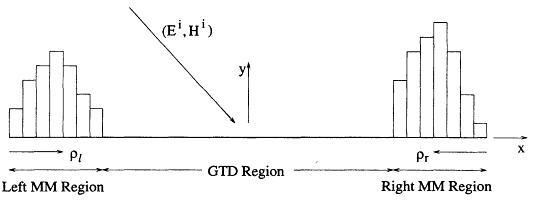
Figure 10.7 In the GTD/MM method, the strip is divided into GTD and MM regions for expanding the current.
CONCLUSIONS
This paper has presented a number of methods for improving the efficiency of the MM, in an attempt to permit it to be applicable to electrically large bodies. A number of interesting methods were described, each displaying the ability to reduce the CPU and/or storage requirements for MM solutions. However, in each case, the total CPU time and storage is still proportional to the electrical size of the body, and thus the MM remains a "low-frequency" technique applicable when the body is not electrically too large. Improvements in these techniques and the use of more and more powerful computers will permit the MM to be applied to higher and higher frequencies. However, at the same time, the operating frequency of radars and communication systems is being pushed to the millimeter or even terahertz band. Thus, the MM appears to be in a losing battle, and may never be able to cover the full range of desired operating frequencies.
Of the many methods presented, the authors feel that the fast multipole method (FMM) may be the best for arbitrary bodies and general purpose codes. The FMM not only reduces the matrix solution time to O(N3/2 ) (or less), but it also reduces [Z] matrix storage and fill time since only the "near-zone" elements need to be computed and stored. However, possibly the most attractive feature of the FMM is that it seems reasonably straightforward to apply it to arbitrary geometries, and it can even be implemented as a retrofit to an existing code.
The authors feel that the only hope of developing a computer code that is applicable at all frequencies is through the use of hybrid methods. In a hybrid solution a "high-frequency" method (such as the GTD) is used to treat most of the electrically large body. The remaining portions of the body that cannot be treated by the "high-frequency" method, because they are too small or are too close to discontinuities, are treated with a "low-frequency" method (such as the MM). Hybrid solutions offer the possibility of a solution in which, as the frequency is increased, the number of unknowns approaches a finite limit. The main problem with hybrid methods has been the difficulty in implementing them for arbitrary geometries.
REFERENCES
Balanis, C.A., 1989, Advanced Engineering Electromagnetics, New York: John Wiley and Sons.
Boag, A., and R. Mittra, 1994, "Complex multipole beam approach to electromagnetic scattering problems,"IEEE Trans. Antennas Propag.AP-42, 366-372.
Bowman, J.J., T.B.A. Senior, and P.L.E. Uslenghi, 1987, Electromagneticand Acoustic Scattering by Simple Shapes, New York: Hemisphere Publishing.
Burnside, W.D., 1980, "A summary of hybrid solutions involving moment methods and GTD." In: Applications of the Method of Moments to ElectromagneticFields, St. Cloud, Fla.: The SCEEE Press.
Burnside, W.D., C.L. Yu, and R.J. Marhefka, 1975, "A technique to combine the geometrical theory of diffraction and the moment method,"IEEE Trans. Antennas Propag.AP-23, 551-557.
Canning, F.X., 1990, "The impedance matrix localization (IML) method for moment calculations,"IEEE Trans. Antennas Propag.AP-32, 18-30.
Canning, F.X., 1991, "Direct solution of the EFIE with half the computation,"IEEE Trans. Antennas Propag.AP-39, 118-119.
Canning, F.X., 1993, "Improved impedance matrix localization method,"IEEE Trans. Antennas Propag.AP-41, 659-667.
Chew, W.C., 1989, "An N2 algorithm for the multiple solution of N scatterers,"Microwave Opt. Tech. Lett.2, 380-383.
Chew, W.C., 1993, "Fast algorithms for wave scattering developed at the University of Illinois' Electromagnetics Laboratory,"IEEETrans. Antennas Propag.AP-35, 22-32.
Chew, W.C., and C.C. Lu, 1993, "NEPAL—An algorithm for solving the volume integral equation,"Microwave Opt. Tech. Lett.6, 185-188.
Chew, W.C., and Y.M. Yang, 1990, "A fast algorithm for solution of a scattering problem using a recursive aggregate Tua matrix method,"Microwave. Opt. Tech. Lett.3, 164-169.
Chew, W.C., L. Gurel, Y.M. Yang, G. Otto, R. Wagner, and Q.H. Liu, 1992, "A generalized recursive algorithm for wave-scattering solutions in two dimensions,"IEEE Trans. Microwave Theory Tech.40, 716-723.
Chew, W.C., Y.M. Wang, and L. Gurel, 1995, "A recursive algorithm for wave-scattering using windowed addition theorem,"J. ElectromagneticWaves Appl., accepted for publication.
Cohoon, D.K., 1980, "Reduction of the cost of solving integral equations arising in electromagnetic scattering through the use of group theory,"IEEE Trans. Antennas Propag.AP-28, 104-107.
Coifman, R., V. Rokhlin, and S. Wandzura, 1993, "The fast multipole method for the wave equation: a pedestrian prescription,"IEEE Trans.Antennas Propag.AP-35, 7-12.
Daubechies, I., 1992, "Ten lectures on wavelets,"CBMS-NSF Seriesin Applied Mathematics, SIAM, Philadelphia.
Dudley, D.G., 1985, "Error minimization and convergence in numerical methods,"Electromagnetics5, 89-97.
Engheta, N., W.D. Murphy, and V. Rokhlin, 1992, "The fast multipole method (FMM) for electromagnetic scattering problems,"IEEE Trans.Antennas Propag.AP-40, 634-641.
Ferguson, T.R., T.H. Lehman, and R.J. Balestri, 1976, "Efficient solutions of large moments problems,"IEEE Trans. Antennas Propag.AP-24, 230-235.
Gurel, L., and W.C. Chew, 1992a, "A recursive T-matrix algorithm for strips and patches,"Radio Science27, 387-401.
Gurel, L., and W.C. Chew, 1992b, "Scattering solution of three-dimensional array of patches using the recursive T-matrix algorithm,"MicrowaveGuided Wave Lett.2.
Hafner, C., 1990a, The Generalized Multipole Technique, Boston: Artech House.
Hafner, C., 1990b, "On the relationship between the MoM and the GMT,"IEEE Trans. Antennas Propag.AP-34, 12-19.
Hansen, R.C., 1981, Geometric Theory of Diffraction, New York: IEEE Press.
Hansen, R.C., 1990, Moment Methods in Antennas and Scattering, Boston: Artech House.
Harrington, R.F., 1982, Field Computation by Moment Methods, Malabar, Fla.: Kricger.
Harrington, R.F., 1987, "Matrix methods for field problems,"Proc.IEEE55, 136-149.
Kalbasi, K., and K.R. Demarest, 1993, "A multilevel formulation of the method of moments,"IEEE Trans. Antennas Propag.AP-41, 589-599.
Leviatan, Y., and A. Boag, 1987, "Analysis of electromagnetic scattering from dielectric cylinders using a multi filament current model,"IEEE Trans. Antennas Propag.AP-35, 1119-1127.
Leviatan, Y., E. Hudis, and P.D. Einziger, 1989, "A method of moments analysis of electromagnetic coupling through slots using Gaussian beam expansions,"IEEE Trans. Antennas Propag.AP-37, 1537-1544.
Lu, C.C., and W.C. Chew, 1993, "Electromagnetic scattering of finite strip array on a dielectric slab,"IEEE Trans. Microwave Theory Tech .41, 97-100.
Ludwig, A.C., 1986, "A comparison of spherical wave boundary value matching versus integral equation scattering solutions for a perfectly conducting body,"IEEE Trans. Antennas Propag.AP-34, 857-865.
Ludwig, A.C., 1989, "A new technique for numerical electromagnetics,"IEEE Trans. Antennas Propag.AP-37, 40-41.
Miller, E.K., 1988, "A selective survey of computational electromagnetics,"IEEE Trans. Antennas Propag.AP-36, 1281-1305.
Miller, E.K., L.M. Mitschang, and E.H. Newman, 1991, ComputationalElectromagnetics-Frequency-Domain Method of Moments, New York: IEEE Press.
Murphy, W.D., V. Rokhlin, and M.S. Vassilou, 1993, "Acceleration methods for the iterative solution of electromagnetic scattering problems,"Radio Science28, 1-12.
Newman, E.H., 1988, "An overview of the hybrid MM/Green's function method in electromagnetics,"Proc. IEEE76, 270-282.
Pathak, P.H., 1988, "Techniques for High-Frequency Problems." In: Antenna Handbook: Theory, Applications, and Design, Y.T. Lo and S.W. Lee (eds.), New York: Van Nostrand Reinhold Co.
Peterson, B., and S. Strom, 1973, "T matrix for electromagnetic scattering from an arbitrary number of scatterers and representations of E(3),"Physical Rev.D8, 3661-3678.
Pogorzelski, R.J., 1993, "Improved computational efficiency via near-field localization,"IEEE Trans. Antennas Propag.AP-41, 1081-1087.
Richmond, J.H., 1985, "Scattering by thin dielectric strips,"IEEETrans. Antennas Propag.AP-33, 64-68.
Rokhlin, V., 1983, "Rapid solution of integral equations of classical potential theory,"J. Comput. Phys.60, 187-207.
Rokhlin, V., 1990, "Rapid solution of integral equations of scattering theory in two dimensions,"J. Comput. Phys.86, 414-439.
Sarkar, T.K., 1991, "Application of the conjugate gradient method to electromagnetics and signal analysis." In: Progress in ElectromagneticResearch5 (PIER 5), J.A. Kong (chief ed.), New York: Elsevier.
Sarkar, T.K., K.R. Siarkiewicz, and R.F. Stratton, 1981, "Survey of numerical methods for solutions of large systems of linear equations for electromagnetic field problems,"IEEE Trans. Antennas Propag.AP-29, 847-856.
Steinberg, B.Z., and Y. Leviatan, 1993, "On the use of wavelet expansions in the method of moments, "IEEE Trans. Antennas Propag.AP-41, 610-619.
Thiele, G.H., and T.M. Newhouse, 1975, "A hybrid technique for combining moment methods with the geometrical theory of diffraction,"IEEETrans. Antennas Propag.AP-23, 62-69.
Umashankar, K.R., S. Nimmagadda, and A. Taflove, 1992, "Numerical analysis of electromagnetic scattering by electrically large objects using spatial decomposition technique,"IEEE Trans. Antennas Propag .AP-40, 867-877.
Wang, J.J.H., 1991, Generalized Moment Methods in Electromagnetics , New York: John Wiley and Sons.
Waterman, P.C., 1969, "New formulation of acoustic scattering,"J. Acoust. Soc. Am.45, 1417-1429.

















