Large-Scale Structures in Acoustics and Electromagnetics: Proceedings of a Symposium (1996)

Richard W. Ziolkowski

Justin B. Judkins

University of Arizona

Laser pulses are continuing to be utilized in a variety of advanced commercial, civilian, and military systems. Their bandwidth and intensity have been increasing, to the point at which the materials they interact with no longer respond in a linear fashion. The material response is nonlinear and the properties of the materials depend on the shape of the pulse propagating in them. Moreover, the materials have memory effects so that trains of multiple pulses can produce effects similar to those occurring from one large pulse. Despite the increase in complexity of the associated physical properties, these nonlinear effects offer the potential for a variety of novel device and systems applications.

Nonlinear optical (NLO) devices are currently being explored for their applications in various systems associated with communications, remote sensing, optical computing, and so on. However, as the size of optical devices such as microcavity lasers is pushed to the size of an optical wavelength and less, the need for more exact materials and response models is paramount to the successful design and fabrication of those devices. Most current simulation models are based on known macroscopic, phenomenological models that avoid issues dealing with specific microscopic behavior of the materials in such NLO devices. Inaccuracies in the simulation results are then exacerbated as the device sizes shrink to subwavelength sizes and the response times of the excitation signals surpass the response times of the material. There are laser sources currently under development with submicron wavelengths that are pushing the boundaries of the subfemtosecond regime. Phenomenological nonresonant models lose their ability to describe the physics in this parameter regime; hence, they lose their accuracy there. Quantum mechanical effects begin to manifest themselves; the simulation models must incorporate this behavior to be relevant.

Until recently, the modeling of pulse propagation in and scattering from complex nonlinear media has generally been accomplished with one-dimensional, scalar models. These models have become quite sophisticated; they have predicted and explained many of the nonlinear as well as linear effects in present devices and systems. Unfortunately, they cannot be used to explain many observed phenomena; and expectations are that they are not adequately modeling multidimensional nonlinear phenomena. It is felt that vector and higher dimensional properties of Maxwell's equations that are not currently included in existing scalar models in addition to more detailed material and device structure models may significantly impact the scientific and engineering results. The associated propagation and scattering issues have a direct impact on a variety of applications, particularly on the design and engineering of integrated photonic components that have immediate utility to nonlinear soliton fiber optical communications systems currently under development. It is believed that the successful development of semi-classical simulators that combine numerical quantum mechanical models of materials and macroscopic Maxwell's equations solvers will significantly affect the concept and design stages associated with novel nonlinear optics phenomena.

The problem of accurate numerical modeling of the propagation of ultrafast pulses in nonlinear media and their use in NLO optical devices has been subject to increasing interest in recent years. Since the most interesting nonlinear phenomena are transient and superposition is not available, it is natural to try to carry out this modeling directly in the time-domain. For this reason the finite-difference time-domain (FDTD) method is receiving intensive study for modeling linear and nonlinear optical phenomena. In contrast to the case for frequency-domain linear analysis, a single value of permittivity ε is completely inadequate to describe nonlinear time-dependent phenomena, and it is essential to model the interaction of the electromagnetic field with the material medium.

Initial simulations of these ultrafast optical pulse interactions have been based upon several well-known phenomenological material models (Ziolkowski and Judkins, 1993a,b, 1994; Judkins and

Ziolkowski, 1995; Goorjian and Taflove, 1992; Goorjian et al., 1992; Joseph et al., 1993). They included the linear Lorentz dispersion model, the nonlinear Debye model, the nonlinear Raman model, and the instantaneous nonlinear Kerr model. This approach has allowed an investigation of the usually neglected longitudinal field component and polarization effects when optical beams self-focus in bulk materials, and of the physics underlying the design of optical beam steerers and output couplers constructed from corrugated linear and nonlinear waveguides. Nonetheless, while they have been adequate for the applications considered, these phenomenological material models do not handle well fully resonant interactions. To understand the physics underlying the small-distance scale and short-time scale interactions, particularly in the resonance regime of the materials and the associated device structures, a first principles approach is desirable. This in turn requires quantum-mechanical descriptions of the electronic states available in the medium. Accurate physical models must incorporate all propagation effects such as dispersion and nonlinearity, with the proper physical linkages between them.

A finite-difference time-domain (FDTD) technique-based simulation tool has been developed in two spatial dimensions to model the electromagnetic interaction of focused optical Gaussian beams incident on a corrugated surface coated with several layers of thin dielectric films and realistic metals. The technique is a hybrid approach that combines an intensive numerical method near the surface of the grating and that takes into account the optical properties of the dielectrics and metals, with a free space transform to obtain the radiated fields. It has been used to simulate a variety of configurations including the scattering behavior of an obliquely incident beam that is focused on a uniform grating and of a normally incident beam that is focused on a nonuniform grating. Both TE and TM polarization simulators have been developed and validated with solutions to canonical grating problems and with experimental results from actual grating structures. Using this hybrid FDTD technique results in a complete and accurate simulation of the total electromagnetic field in the near field as well as in the far field of the diffraction grating. Metal and dielectric gratings and corrugated surfaces are found in a wide variety of optics applications. Among them are optical storage disks, polarizers, and optical filters. Because lasers are often used in these systems, it is important to understand the interaction of finite optical beams with the grating surfaces associated with these devices. It has been shown (Judkins and Ziolkowski, 1995) that there are significant perturbations in the performance between the realistic metal and the perfect metal gratings, which necessitate the more detailed modeling offered by simulators such as ours.

Corrugated dielectric and metallic gratings have been modeled in the past by Fourier transform techniques and moment methods but these treatments have some disadvantages. They do not provide the mechanism for modeling beams in geometries containing both corrugated dielectrics and metal thin films. Furthermore, these methods do not work well for structures that are not strictly periodic, such as gratings with variations in the size or periodicity of the grating teeth. An FDTD modeling tool, which models the problem on a subsectional level, is ideally suited to these more complicated grating surfaces. This approach has been successfully applied in modeling near-field detection of subwavelength-sized rectangular wells in a perfect conductor surface in two dimensions (Kann et al., 1995). This model has been extended to simulate optical beams obliquely incident on a multi-layer thin film dielectric-metallic stack over a grooved dielectric backing. The hybrid FDTD approach gives a quick and accurate description of the near and radiated fields for almost any arbitrary grating design in two spatial dimensions. Extensions to three dimensions are straightforward, but computer intensive.

Devices in the optical regime which are constructed with nonideal materials do not always behave identically to the usual theoretical models, which treat the materials as ideal. An example of where a realistic metal model is important is when light impinges onto the surface of an optical disk. This geometry has a dielectric corrugated surface that is coated with a thin conducting film. A perfect conductor condition for the film layer does not allow energy to penetrate through it; and a conductivity σ model, for most good conductors at optical frequencies, gives the incorrect wave impedance for the corrugation. If this problem is to be examined from the perspective of an FDTD approach, then some physical considerations need to be taken into account in order to make the model complete. At optical frequencies the noble metals Au, Ag, and Cu and also the metal Al have dispersion relations similar to a free electron gas, which cannot be represented by a simple time independent ε, σ model. However, with a time-domain-based modeling approach, the time-dependent properties of materials can be taken into account allowing for a broader range of material possibilities. Thus, the metal regions can be modeled using an appropriate phenomenological relationship between the electric field and the polarization to give the correct refractive index.

In particular, we have numerically constructed solutions to the multidimensional, full-wave, vector form of Maxwell's equations describing the interaction of monochromatic beams with a dispersive material having a finite response time. These numerical solutions have been obtained in two space dimensions and time with a two-dimensional finite-difference time-domain (2D-FDTD) method, which combines a generalization of a standard, FDTD, full-wave, vector, linear Maxwell's equations solver with a Lorentz linear dispersion model. In particular, we are solving in a self-consistent manner the system of equations:

Maxwell Curl Equations

Lorentz Model

where is the polarization generated by the Lorentz model and does not contain the instantaneous permittivity, i.e., .

In two dimensions, and , Maxwell's equations decouple into two polarization sets, the TM set: , and the TE set: . Each field set can be modeled independently of the other. Maxwell's equations are rendered in discrete form and solved on a square mesh in a stepwise manner. Nodes for the electric and magnetic fields are staggered in space and time. The second-order Lorentz model is solved as a sequence of first-order equations for the polarization (bound) current in parallel with Maxwell's equations.

In addition, as with other hybrid approaches, our simulator uses a far-field transform to derive the far field pattern in free space from the fields generated in the vicinity of the geometry. This necessity arises because the FDTD mesh must be finite and all the structures relevant to the problem must be included in it, but the field patterns may be required at some great distance that the mesh cannot encompass due to

computational size limitations. Only the complete field amplitude and phase distribution is generated within this near-field region. On the other hand, a detector placed many diffraction lengths away from this simulation region will see only the far-field pattern. Furthermore, the geometry, in this case a grating with a very thin metal surface layer, might demand higher than normal spatial discretization and thus, for the same amount of computer memory, will require the mesh to be confined to an even smaller spatial region. These issues demand either a large number of cells to be used in the FDTD grid or an alternate hybrid approach be taken in producing the signal that a detector would see. With our approach, the computational grid can be restricted to a much smaller spatial region and a Fourier transform method can be used to generate the desired far-field patterns if the region between the actual FDTD simulation domain and the detector is a homogeneous medium.

Following the field/material interaction, the components of the field that do not represent stored energy propagate some distance from the scatterer and eventually evolve into the far field. The pattern in the far field of a grating, where the detector distance d is much larger than Λ / λ, where Λ is the grating period, represents the angular distribution of this energy. Simulating the propagation of energy over this distance with the FDTD algorithm, given the discretization requirements of a structure with large dielectric constants and/or detailed structures, requires an extremely large computational grid. For example, to model typical optical disk cases with adequate discretization (i.e., λ/20 in the material with the highest refractive index) all the way out to the far-field observation point would involve a 1000λ × 20λ grid and require in the TE case more than 40MB of memory. Truncating the mesh closer to the scatterer does not allow an adequate simulation region for the scattered field to develop into its far-field distribution.

The free space transform is one way to circumvent this problem. This transform takes a transverse component of the scattered field along a planar aperture near one of the four truncation boundaries in the simulation region and projects this field component onto a circle (in two dimensions, a sphere in three) a distance R away from this sampling plane. The method is accurate, within the limits of the Kirchoff approximation, for cases where nearly all the scattered energy generated in the total field region of the mesh is propagated back across the transform boundary and very little energy is leaked through the remaining three truncation boundaries of the FDTD domain. For problems where a beam impinges on a planar structure, the mesh does not need to be much bigger than the scattering object, but it must be large enough in one dimension to encompass in their entirety both the incident and the scattered beams. A diffraction grating configuration for a beam blazing at an angle from the diffraction grating is well suited to this method because the mesh can be made very long (along the grating) in comparison to its height (distance along the normal to the grating).

As shown in Figure 4.1, the simulation region is separated into a scattered field region and a total (incident plus scattered) field region where The juncture of these two regions is the source boundary. This source boundary is separated into two adjacent planes located a half cell apart. It runs parallel to the grating and is located inside the mesh, near to the outer boundary of the simulation region, which is also taken parallel to the grating. The transverse field distributions along this plane represent exact solutions for an incident Gaussian beam, and , that focuses to a desired location in space. The incident beam may have an arbitrary cross section; but for the cases we have modeled to date, it has been restricted to a lowest-order Gaussian cross-section beam. The incident beam is assumed to be focused at the grating surface (z = z_s). The beam focus is at the center of the mesh along the direction of the grating. The source is driven at the source boundary at the distance z_s above the grating surface. The desired incident beam is achieved by using the free space transform to back-propagate the complex field structure in the focal region to the source boundary. After the source is

turned on, it is allowed to run for the duration of the simulation, which is long enough for several cycles to scatter off the grating and reach the truncation boundary.

A variety of TE and TM cases for the metal film diffraction grating geometry have been considered and are reported in Judkins and Ziolkowski (1995). The basic problem configuration is summarized in Figure 4.2. The specific geometries are characterized by the grating period, the height of the grating teeth, the film thickness, the tooth size ratio, and the complex refractive index of the metal.

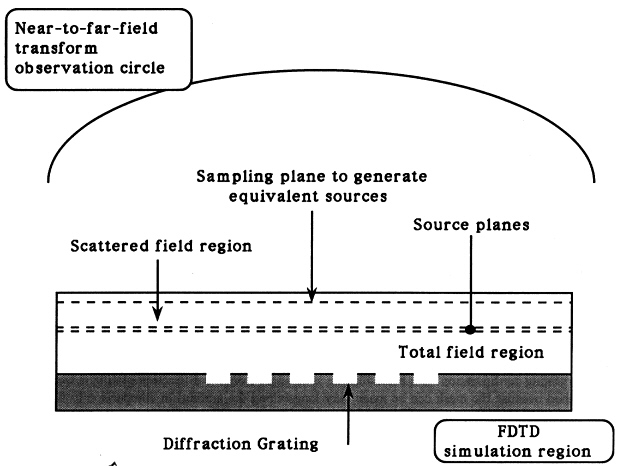
Figure 4.1 The FDTD-Lorentz Medium simulator allows one to model locally scatterers such as realistic multilayered thin film diffraction gratings and yet produce far-field patterns with a near- to far-field transform.

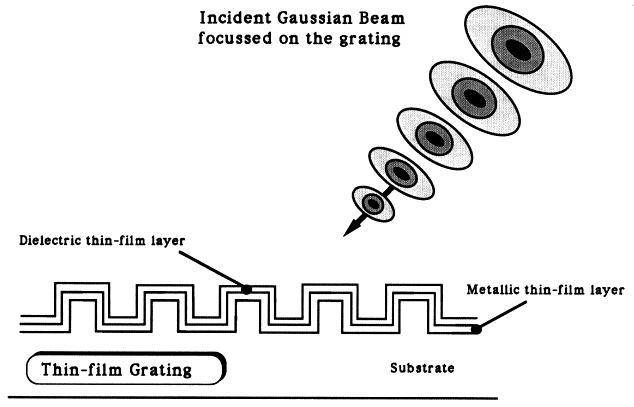
Figure 4.2 A typical optical grating problem involves a focused Gaussian beam and a multilayered thin film diffraction grating.

With the continuing and heightened interest in linear and nonlinear optically integrated devices, more accurate and realistic numerical simulations of these devices and systems are in demand. Such calculations provide an integrated optics/photonics testbed in which one can investigate new basic and engineering concepts, materials, and device configurations before they are fabricated. The time from device conceptualization to fabrication and testing should therefore be enormously improved with numerical simulations that incorporate more realistic models of the linear and nonlinear material responses and the actual device geometries. It is felt that vector and higher dimensional properties of Maxwell's equations that are not currently included in existing scalar models, in addition to more detailed materials models, may significantly impact the scientific and engineering results.

We have also been simulating a variety of linear and nonlinear corrugated waveguiding systems for their applications to integrated optics/photonics systems. For instance, corrugated waveguide structures have many potential uses as beam steerers and grating assisted couplers. We are developing a simulation toolbox that eventually will be used to design these and many other devices and systems. To meet self-imposed design goals that specify integrated optical/photonic devices that are only a few wavelengths or pulse lengths in size, we require a thorough understanding of the basic physics that we are modeling without the typical approximations generally used for this class of problems. This in turn has required

our simulations to be based upon numerically solving the full-wave, vector Maxwell's equations. We have shown that this approach leads to a superior understanding of the underlying physics and to improved engineering designs (Ziolkowski and Judkins, 1993a,b, 1994; Judkins and Ziolkowski, 1995). These numerical solutions have been obtained in two space dimensions and time with a nonlinear finite-difference time-domain (NL-FDTD) method that combines a generalization of the Lorentz linear dispersive medium-Maxwell's equations solver with a nonlinear Raman model and an instantaneous Kerr nonlinear model. In particular, we are solving in a self-consistent manner the system of equations (Judkins and Ziolkowski, 1995):

Lorentz Model

Raman Model

where and

the last term representing the instantaneous Kerr nonlinearity, χ^Kerr being the instantaneous Kerr susceptibility. The resulting NL-FDTD simulator can model pulse propagation in complex environments under the influence of linear and nonlinear dispersive, linear and nonlinear diffractive, and time retardation effects of the materials in and surrounding the electromagnetic structures. By coupling the linear and nonlinear dispersion models together simultaneously with the natural boundary conditions arising from dielectric and metallic discontinuities, we are able to handle the gratings and corrugated interfaces readily. Moreover, as in the linear dispersion cases, both the TE and TM polarization cases can be simulated. Consequently, more complex, realistic integrated optics/photonics structures are straightforwardly modeled with the NL-FDTD approach.

The NL-FDTD approach can handle ultrafast single-cycle cases as readily as multiple-cycle cases having an intrinsic carrier wave. Since most current optical systems deal directly with a carrier-wave type signal, the NL-FDTD approach can simulate the propagation and scattering effects associated with those narrow bandwidth systems. However, it can also simulate the behaviors of the interactions of ultrafast pulses. Ultrafast pulses are single-cycle or multiple-cycle envelopes containing fewer than 15 cycles. Sources in the laboratory have produced pulses compressed to as fast as 4fs and the optics community is already investigating the attosecond regime. By using these ultrafast sources we illustrate two advantages of the time-domain approach: (1) the ability to carry phase information over a wide spectrum, and (2) the ability to model transient effects that occur either quickly or slowly relative to the

time scale of the pulse. The evolution of the pulse in the medium can be dependent on both the material's resonances in the presence of the beam and the initial shape of the exciting pulse. Switching or steering of this type of pulsed beam requires one to take advantage of interference effects and the material's transient response.

The complex waveguiding structures we have considered (Judkins and Ziolkowski, 1995) are filled with either linear or nonlinear dispersive materials that have finite response times. The corrugations themselves can be modeled as dielectric teeth (an extension of the dielectric waveguide) or metallic teeth (deposited into or on top of the dielectric waveguide). A corrugated waveguide with these dielectric or metallic teeth can be viewed as a leaky-wave antenna. The corrugation section is a slow-wave structure whose impedance properties determine the properties of its radiated fields. The field radiated by an infinite linear or nonlinear corrugated structure can be modeled with a Floquet mode representation. The resulting fields have to satisfy a phase matching or Bragg condition resulting from the electromagnetic boundary conditions. Physically this means that because of the regular placement of the teeth in the corrugation section, the individual scattered fields will interfere constructively only along certain preferred directions and the ''leaked'' energy will appear in the form of pulsed beams that radiate at angles specified by the Bragg condition both into the air and into the substrate regions.

In particular, let θ_t be the angle that the radiated beam subtends with respect to the normal of the waveguide, n₀ be the index of refraction above the corrugations, and n_G = n_B + n₂I be the index of refraction in the waveguide, which includes the effective waveguide index n_B (which varies slightly from the TE and TM cases to achieve the desired TE₀ and TM₀ initial spatial amplitude distributions) and the intensity-induced index change n₂I. This Bragg condition then takes the form

or

This immediately translates into a practical device: the output-beam from the corrugation section can be steered away from the normal by the strength of the intensity of the input waveguide pulsed-beam, the size of the unit cell or the strength of the nonlinearity.

A special case of this relationship suggests a useful output coupler design. If we specify that the corrugation spacing be Λ = λ/n_B, then the first order (m = -1) output-beam from the corrugation section of the waveguide has the transmission angle:

Thus, the output-beam from the corrugation section can be steered away from the normal simply by adjusting the strength of the intensity of the input waveguide pulsed-beam or the nonlinear index. Our simulations have confirmed this effect (Judkins and Ziolkowski, 1995).

The multidimensional NL-FDTD model has been applied to the modeling of the extraction of energy from a variety of linear and nonlinear waveguiding structures using corrugated waveguide sections.

Expected conversion efficiencies from the guided mode energy to the radiated field energy have been observed in the linear case. The nonlinear waveguiding structures are presenting interesting challenges in their analysis and interpretation. A variety of TE and TM cases with metallic corrugations have been considered (Judkins and Ziolkowski, 1995) to illustrate the desired linear and nonlinear output coupler and beam steering effects. Typical simulation geometries are shown in Figures 4.3 and 4.4. Since the electric field behavior near the edges of these metallic corrugations is significantly different between the two polarizations, the resulting radiated field structures reflect this difference. Output beam characteristics depending on the medium response time, the polarization, and the material parameters, have been studied and reported (Judkins and Ziolkowski, 1995). Near-field simulations obtained with the NL-FDTD approach are translated into Fresnel and Fraunhofer regime information with the same near- to far-field transforms introduced for the FDTD Lorentz medium-Maxwell equations simulator. Particular emphasis has been given to ultrafast pulses whose time-record length is approximately the same size as the corrugation region. It has been found that even pulses that are short in comparison with the corrugation region can be effectively used to beam steer and couple energy through a grating-assisted coupler from one corrugated waveguide to another.

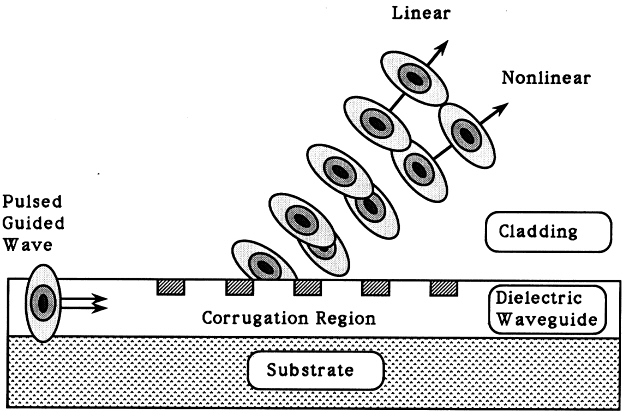
Figure 4.3 The output direction of nonlinear grating-assisted beam steering, integrated optics devices can be controlled by the intensity of the incident pulse.

Figure 4.4 The S-parameters of nonlinear grating-assisted, waveguide output couplers can be controlled by the intensity of the incident pulse, the grating period, and the material parameters.

We have also been developing a simulator that utilizes the Maxwell-Bloch system for multilevel atoms for our material models in Maxwell's equations. This effort is novel in that it combines a realistic material model that is quantum mechanically based with a full-wave, vector Maxwell's equations solver. The FDTD implementations of the Maxwell-Bloch modeling system in one space dimension and time have been accomplished (Ziolkowski et al., 1995) and have yielded some interesting physical consequences. In particular, in a density matrix approach to arrive at the Bloch equations describing a two-level atom medium we introduce the terms ρ₁, ρ₂, and ρ₃, which satisfy the relationship , and represent, respectively, the dispersive or in-phase component of the polarization, the absorptive or in-quadrature component of the polarization, and the fractional difference in the populations for the two energy levels. The near-resonant behavior of nonlinear systems cannot be meaningfully discussed unless dissipative effects are taken into account. The usual method of achieving this in simple systems is to include in the Liouville equations for these terms, phenomenologically obtained diagonal terms consisting of characteristic decay rates. If we take the incident electromagnetic field to be a uniform plane wave that is propagating along the z-axis and is polarized along the x-axis, i.e., and , and set the spatial orientation of the dipole to be , the polarization takes the form , where

N_atom being the number density of atoms and y the dipole coupling coefficient. The following one-dimensional Maxwell-Bloch system results from this reduction:

Maxwell Equations

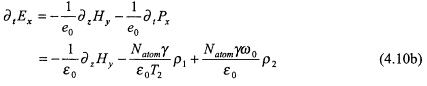
Bloch Equations

where T₁ is the excited state lifetime, T₂ is the dephasing time, and ρ30 is the initial population difference in the system. Note that the specification that ρ30 = -1(+1) represents all the atoms initially being in their ground (excited) states. This system of equations can be discretized using finite differences in several different ways. We have characterized the performance of several of these discrete approaches and feel that we know how to extend this semi-classical model to higher space dimensions and to more complex media such as a three-level atom medium.

Using this FDTD approach to solving the semiclassical Maxwell-Bloch system, we have studied in a more exact manner (without removing the carrier wave) self-induced transparency effects in a two-level atom medium (Ziolkowski et al., 1995). Standard self-induced transparency (SIT), the so-called π, 2π, 4π,.... results have been reproduced with this model. A SIT solution represents the nonlinear wave propagation dynamics in which a particular pulse shape, a carrier at the transition frequency with a hyperbolic secant envelope, having the appropriate high intensity completely loses its energy to a two-level atom medium by stimulating it from its ground state into its excited state, and then is completely reconstructed in a coherent manner via stimulated emission by having the excited medium completely decay back into its ground state. This SIT pulse thus propagates through the highly nonlinear two-level atom medium with no change in its shape, i.e., as though the medium is transparent; it is a soliton solution of the semiclassical Maxwell-Bloch system. The SIT effect is normally described with a rotating wave approximation of the Maxwell-Bloch system. As will be demonstrated, we have recovered these SIT pulse dynamics with our FDTD Maxwell-Bloch simulator. However, we have also found (Ziolkowski et al., 1995) novel features that appear at points where the electric field is null and have

been identified as being associated with the maximums of the time derivative of the electric field. These features are not present in standard approximate solutions (e.g., the rotating-wave approximation) to this problem.

These nonlinear time-derivative effects have been emphasized further (Ziolkowski et al., 1995) by considering a variety of ultrafast pulse cases. It has been demonstrated (Ziolkowski et al., 1995), during ultrafast pulse interactions with a two-level atom medium, that a single-cycle pulse can be designed that completely inverts the two-level atom medium. A multiple ultrafast pulse train has been given that can completely invert the medium from the ground to the excited state and then completely reverse the process. These results confirm that the time-derivative-driven nonlinear properties of the two-level atom medium have a significant impact on the time evolution of this system in the limit of ultrafast pulses.

We have also used (Ziolkowski et al., 1995) the FDTD Maxwell-Bloch simulator to recover expected small-signal gain results for sinusoidal input signals. The designed ultrafast inversion pulse has been combined with a sinusoid input signal to form a pump-probe signal set. It has been illustrated (Ziolkowski et al., 1995) that a two-level atom medium could be inverted by the leading ultrafast pulse to yield a gain medium for the trailing sinusoidal probe pulse.

Full device and system integration complexities are presently being introduced into our model by considering multidimensional (spatial) extensions. We are investigating several different amplifier and microcavity laser configurations with the resulting multidimensional FDTD Maxwell-Bloch simulator. Current progress in higher dimensions will be reported elsewhere.

We are developing full-wave, vector Maxwell equation solvers for use in studying the physics and engineering of linear and nonlinear integrated photonics devices and systems. These simulators and their applications have been described. Particular emphasis is given to time-domain problems describing the interaction of ultrafast optical pulses with nonresonant and resonant optical materials and structures. These problems pose severe difficulties to numerical modeling because of the many time and length scales involved. The global structures dealt with in integrated photonic systems are large relative to their operating wavelengths; but their substructures are subwavelength in size. The corresponding computational procedures for studying these large-scale structures are computationally large and entail an extremely large number of degrees of freedom. We have developed hybrid simulators that incorporate the linear and nonlinear dynamics of the substructures and the overall response of the integrated system. We discussed one such simulator which couples Maxwell's equations and a Lorentz linear dispersion model with a near- to far-field transform capability to generate the global far-field patterns associated with the scattering of optical Gaussian beams from diffraction gratings coated with multiple layers of realistic thin film dielectrics and metals. This simulator is being applied to a variety of wavelength-sized diffractive optic components. An extension of this simulator was also described that includes both the Raman and the instantaneous Kerr nonlinear material models. This simulator has been used to describe locally the behaviors of linear and nonlinear finite length corrugated optical waveguides for applications to grating-assisted couplers and beam steerers. We also described another simulator under development that combines a multilevel atom materials model with our Maxwell's equations simulator to model self-induced transparency and laser gain-medium effects. This resonant systems model requires a careful marriage between a microscopic (quantum mechanical) materials model and the macroscopic Maxwell's equations solver. This simulator is being developed to model microcavity lasers and waveguide amplifiers.

Integrated optics/photonics devices and systems are truly representative of large-scale structures. The associated simulations require a corresponding large amount of high-performance computing (HPC) efforts. The need for more accurate simulators will increase as the integrated optics/photonics devices and systems complexity increases. Examples from our efforts in this area, which have civilian and military relevance, have been given to illustrate what classes of simulators have been developed to model these structures. Future efforts in this area will require even more complete materials models appropriately integrated into the Maxwell equations solvers and the associated advanced HPC methods.

Goorjian, P.M., and A. Taflove, 1992, "Direct time integration of Maxwell's equations in nonlinear dispersive media for propagation and scattering of femtosecond electromagnetic solitons,"Opt. Lett .17(3), 180-182.

Goorjian, P.M., A. Taflove, R.M. Joseph, and S.C. Hagness, 1992, "Computational modeling of femtosecond optical solitons from Maxwell's equations,"IEEE J. Quantum Electron.QE-28(10), 2416-2422.

Joseph, R.M., P.M. Goorjian, and A. Taflove, 1993, "Direct time integration of Maxwell's equations in two-dimensional dielectric waveguides for propagation and scattering of femtosecond electromagnetic solitons,"Opt. Lett.18(7), 491-493.

Judkins, J.B., and R.W. Ziolkowski, 1995, "FDTD modeling of nonperfect metallic thin film gratings," submitted to J. Opt. Soc. Am. A.

Kann, J., T. Milster, F. Froehlich, R.W. Ziolkowski, and J.B. Judkins, 1995, "Near-field optical detection of asperities in dielectric surfaces,"J. Opt. Soc. Am. A.12(3), 501-512.

Ziolkowski, R.W., and J.B. Judkins, 1993a, "Full-wave vector Maxwell equation modeling of the self-focusing of ultrashort optical pulses in a nonlinear Kerr medium exhibiting a finite response time,"J.Opt. Soc. Am.B10(2), 186-198.

Ziolkowski, R.W., and J.B. Judkins, 1993b, "Applications of discrete methods to pulse propagation in nonlinear media: self-focusing and linear-nonlinear interfaces,"invited paper, special issue of RadioScience for the 1992 URSI EM Theory Symposium, Radio Sci.28(5), 901-911.

Ziolkowski, R.W., and J.B. Judkins, 1994, "NL-FDTD modeling of linear and nonlinear corrugated waveguides,"J. Opt. Soc. Am.B11(9), 1565-1575.

Ziolkowski, R.W., J.M. Arnold, and D.M. Gogny, 1995, "Ultrafast pulse interactions with two-level atoms," submitted to Phys. Rev. A.