Chapter 10
Value-Added Indicators of School Performance*
ROBERT H. MEYER
Harris Graduate School of Public Policy Studies,
University of Chicago
Educational outcome indicators are increasingly being used to assess the efficacy of American education. Reliance on such indicators is largely the result of a growing demand to hold schools accountable for their performance, defined in terms of outcomes, such as standardized test scores, rather than inputs, such as teacher qualifications, class size, and the number of books in a school's library. Unfortunately, most schools and districts have not developed and implemented entirely suitable performance indicators. Many scholars fear that these indicator/accountability systems could distort the behavior of educators and students, with worse results than when using no indicators at all. It is, therefore, very important to consider the attributes of an acceptable, valid performance indicator system.
Criteria for Performance Indicators
Outcome Validity
The set of tests and other measures of outcomes that underlie a performance indicator system must measure the types of skills demanded by society. Otherwise, a high-stakes accountability system could induce educators to design and implement a curriculum that emphasizes skills that are of minimal social value. Many educators believe that many of the standardized multiple-choice tests are flawed because they focus almost exclusively on low-level academic content, not
on specific curriculum objectives (Smith and O'Day, 1990; Clune, 1991). As a result of this criticism, many school districts, states, and professional test developers are experimenting with new types of assessments—for example, tests with open-ended questions, performance-based assessments, graded portfolios, and curriculum-based multiple-choice tests—more closely related to educational objectives.1 As new tests are developed, test developers and curriculum designers need to determine whether the new tests and assessments are valid, in the sense of measuring the skills that are highly valued by society.
Noncorruptability
Second, a performance indicator must accurately measure performance with respect to the outcome that it purports to measure. Test scores can be "corrupted" in various ways. For example, a test could be administered in such a way that it is easy for students and staff to cheat. Alternatively, a test form that is administered year after year could stimulate instructors to teach narrowly to the test, rather than to the broader domain of knowledge that underlies the test.2
Valid Measurement of School Performance
Finally, a performance indicator must accurately and reliably measure school performance, where school performance with respect to a particular test or other student outcome is defined as the contribution of the school to that outcome. In a recent paper Meyer (1994) demonstrated that the common indicators of school performance—average and median test scores—are highly flawed even though derived from valid assessments. The simulation results reported by Meyer indicate that changes over time in average test scores could be negatively correlated with actual changes in school performance.
The purpose of this chapter is to consider the class of educational indicators referred to as value-added indicators that satisfy the third criterion discussed above. For simplicity the focus here is entirely on value-added indicators derived from student test scores. The first section explains the theory and logic of value-added indicators, emphasizing the interpretation and reporting of value-added models and indicators rather than methods of estimating these models and other technical questions. The second section compares value-added and nonvalue-added indicators such as the average test score. The third part discusses policy considerations that are relevant to the use and nonuse of value-added and nonvalue-added indicators. Finally, conclusions are drawn and recommendations offered.
The Theory and Logic of Value-Added Indicators
Alternative Uses of Standardized Tests and Assessments
The results of standardized tests and assessments can be used to measure the achievement of individual students, produce aggregate indicators of the level and distribution of achievement for groups of students, evaluate the efficacy of specific school policies and inputs, and measure school performance. The focus here is on the latter application, although the tasks of measuring school performance and evaluating school policies and inputs are closely related.
It is not widely appreciated that properly constructed school performance indicators differ greatly from simple aggregate indicators such as average test scores, in part because test vendors have tended to focus attention on measuring student achievement rather than school performance. Increasingly, however, schools, states, and other groups are interested in assessing the performance of schools as well as students through standardized tests. It is therefore important to draw a sharp distinction between school performance indicators and simple aggregate indicators based on test scores.
The most common aggregate indicators are average and median test scores and the share of students scoring above or below a given threshold. These "level" indicators measure some feature of the level of student achievement rather than, for example, growth in student achievement (Meyer, 1994). Level indicators are widely reported by schools, states, test vendors, and national organizations such as the National Assessment of Educational Progress. If correctly constructed and based on appropriate tests or assessments, level indicators convey useful descriptive information about the proficiencies of students in particular classrooms, schools, or groups. It is appropriate to use indicators of this type to target assistance, financial or otherwise, to schools that serve students with low test scores. Such indicators are not a valid measure of school or classroom performance, however.
Value-Added Indicators: An Introduction
The question of how to measure school performance is, fundamentally, a technical statistical problem, similar to the task of measuring the efficacy of school policies and inputs, and one that has been addressed in the evaluation literature for well over three decades and continues to be an active area of research.3 The common characteristic of the value-added models used in the literature is that they measure school performance or the effect of school policies and
inputs using a statistical regression model that includes, to the extent possible, all of the factors that contribute to growth in student achievement, including student, family, and neighborhood characteristics. The key idea is to isolate statistically the contribution of schools from other sources of student achievement. This is particularly important in light of the fact that differences in student and family characteristics account for far more of the variation in student achievement than school-related factors. Failure to account for differences across schools in student, family, and community characteristics could result in highly contaminated indicators of school performance.
The basic logic of a value-added model, whether it is used to measure school performance or to evaluate alternative school policies, can be illustrated by using a simple two-level model of student achievement. 4 The first level of the model captures the influences of student and family characteristics on growth in student achievement. The second level captures the effect of school-level characteristics. Given this framework, it is straightforward to define one or more indicators of school performance—for example, one that is appropriate for school choice purposes or one that is appropriate for school accountability purposes, as follows.
Let us first consider a value-added model of growth in student achievement for a particular grade—say, grade 2. A simple level-one equation is5
Posttestis = θ Pretestis + α StudCharis + ηs + ∈is, (1)
where i indexes individual students and s indexes schools. Posttest is and Pretestis represent student achievement for a given individual in second grade and first grade, respectively; StudCharis represents a set of individual and family characteristics assumed to determine growth in student achievement (and a constant term); ∈is captures the unobserved student-level determinants of achievement growth; θ and α are model parameters that must be estimated; and ηs is a school-level effect that must be estimated.6 The model has been structured such that the
school effects (ηs) have an average value equal to zero in a given school year, the so-called benchmark year.
Parameter ηs is very important. It reflects the contribution of a given school (school s) to growth in student achievement after controlling for all student-level factors, pretest and student characteristics. Equivalently, it captures all of the achievement. Hence, it is a measure of total school performance (Meyer, 1994). Willms and Raudenbush (1989) refer to this indicator as a type A indicator.
As defined, the total performance indicator gives an unambigious ranking of schools, but the exact range and magnitude of the indicator are somewhat arbitrary. As a result, the indicator could appear to be divorced from the outcome that everyone ultimately cares about—student achievement. An alternative but equivalent strategy is to define the total performance indicator as the predicted mean achievement of a given school for a given benchmark group of students:
P(Total)s = {θ PretestBENCHMARK + α StudCharBENCHMARK} + ηs, (2)
where PretestBENCHMARK and StudCharBENCHMARK represent the mean values of Pretest and StudChar in the benchmark year and the term in brackets is a fixed number for all schools.7 For those accustomed to interpreting test scores reported on a given scale, it may be easier to interpret the total performance indicator when it is reported as a predicted mean than as an indicator centered around zero.8 In the remainder of this chapter the benchmark predicted mean form of the indicator is used.
The alternative predicted mean method of reporting value-added indicators opens up the possibility of reporting value-added indicators tailored to different types of students. In particular, Eq. (2) could be used to compute the predicted achievement of students given pretest scores and student and family characteristics other than those of the benchmark group. This method of reporting indicators may be termed the conditional mean format and has a number of advantages. First, students and families might pay more attention to indicators that are custom designed to suit their own circumstances. Second, the format provides information on the effects on student achievement of prior achievement and student, family, and neighborhood characteristics, as well as school performance. Third, this format readily handles value-added models that are more complicated than the one considered thus far.
One possible disadvantage of reporting indicators in the conditional format is that it might be burdensome and possibly confusing to distribute multiple versions of essentially the same indicator, especially if the number of reporting
|
7 |
In graphical terms, P(Total)s is simply the height of the student achievement regression/prediction line at the values PretestBENCHMARK and StudCharBENCHMARK (see Figure 10.1). |
|
8 |
Note that the term in brackets in Eq. (2) is equal to PosttestBENCHMARK = θ PretestBENCHMARK + α StudCharBENCHMARK. As a result, P(Total)s can also be interpreted as the total performance indicator centered around the overall mean achievement level in the benchmark year. |
categories is large. Suppose that an achievement growth model includes five control variables—prior achievement, parental education, parental income, race, and special education status. If each variable is split into five different values, the total number of reporting categories would equal 55 = 3,125.9 Clearly, it would be advantageous to find some creative ways of presenting these data without producing information overload.
How should the total performance indicator be interpreted? One interpretation is that it captures the effect at some past date of enrolling one additional student in a school, holding all school-level factors constant, including the composition of the student group that attends the school. If these characteristics are relatively stable from year to year, the total school performance indicator could provide reliable information on the future performance of schools and thus be very helpful to students and parents who are in the process of choosing a neighborhood to live in and/or a school to attend. In short, the total performance indicator is appropriate for purposes of informing school choice, but it is not the most appropriate indicator for holding schools accountable for their performance because it fails to exclude components of school performance that are external to the school.
For an indicator that serves the accountability function, let us turn to the second level of the value-added model. This equation captures the school-level factors that contribute to growth in student achievement. A simple level-two equation is:
ηs = δ1 Externals + δ2 Internals + us (3)
where ηs is the school effect (and total school performance indicator) for school s from the level-one equation; Externals and Internals represent all observed school-level characteristics assumed to determine growth in student achievement plus a constant term; us is the unobserved determinant of total school performance; and δ1 and δ2 are parameters that must be estimated. To be consistent with the level-one equation, it is assumed that the internal school characteristics all have mean zero in the benchmark year.
The distinction between the external and internal variables is crucial for the purpose of measuring school performance. Externals includes all observed school-level characteristics that could be considered external to the school (plus a constant term), including neighborhood and community characteristics and aggregate student characteristics such as the average socioeconomic status of all students in a school. Internals includes all observed school-level characteristics that could be considered internal to the school, principally school policies and inputs.
Given the distinction between internal and external school-level characteristics, a measure of school performance, controlling for all factors that are external to the school, is given by δ2 Internal s + us, where the first term, δ2 Internals, represents the component of school performance that is predictable given the observed school policies and inputs, and the second term, us, represents the unpredictable component of school performance. This indicator can also be written as
As in the case of the total performance indicator, the intrinsic performance indicator can be defined as the predicted mean achievement of a given school with benchmark characteristics:
P(Intrinsic)s={θPretestBENCHMARK + α StudCharBENCHMARK + δ1 External BENCHMARK} + δ2 Internals + us (4)
where ExternalBENCHMARK represents the mean value of External in the benchmark year and the term in brackets is a fixed number for all schools. This indicator can also be reported in the conditional mean format.
The intrinsic performance indicator can be interpreted in more than one way, depending on the types of variables that are considered external in the model and on which individuals and institutions are responsible for determining a school's policies and inputs at a given grade level. Let us assume that the external variables are limited to community characteristics and school-level student characteristics, such as average parental income and education. In schools where decisions are largely made by school staff, the intrinsic indicator can be viewed as a measure of the collective performance of these staff. In cases where significant school decisions are made by district staff and perhaps other parties, the indicator can be viewed as a joint measure of school and district performance. Finally, in cases where important school inputs are determined in part by state agencies or taxpayers, the indicator can be interpreted as a joint measure of the performance of the school and the institutions that affect the school's policies and inputs.
This analysis implies that it could be problematic to interpret the intrinsic performance indicator as a measure of the performance of school staff when there is substantial variation across schools in important school inputs such as class size. In this situation one alternative is to view school inputs that are determined outside the school as external school-level characteristics, along with the set of external characteristics listed above. Including these external characteristics in the value-added model would make it legitimate to compare the performance of schools that differ in these characteristics.
In any case, the intrinsic performance indicator is the appropriate indicator for the purpose of holding educational decisionmakers and providers accountable for their performance. Obviously, how this indicator is used as part of an ac-
countability system should depend on who has authority to make decisions that determine the performance of a school and the exact specification of the value-added model used to produce the indicators.
Although the discussion here has thus far focused on deriving measures of school performance from the two-level value-added model, the methodological similarities between analyses designed to produce value-added indicators and analyses designed to evaluate alternative school policies and inputs, as represented by the parameter δ2, should be apparent.10 There are, however, some potentially important differences between the two types of analyses.
First, large-scale evaluations tend to be based on samples that include a large number of schools and districts. The High School and Beyond Study, for example, includes over a thousand high schools. In contrast, most districts have less than 50 elementary schools and even fewer middle schools and high schools. This implies that in small to medium-sized districts it might not be feasible to produce reliable estimates of the level-two slope parameters and therefore estimates of intrinsic school performances using within-district data only.11 One possible alternative would be to estimate the slope parameters of the level-two model using data from several districts collected via some cooperative data-sharing arrangement among districts. As indicated in the next section, it is straightforward to construct estimates of total and intrinsic school performance given estimates of the slope coefficients in the level-one and -two value-added equations.
Second, when evaluating the effects of alternative policies and inputs, it is common to observe the same policies and inputs at more than one school or district, thus enabling researchers to estimate potentially small effects with a high degree of precision. In the case of value-added indicators, in contrast, the possibilities for replication are essentially eliminated because the objective typically is to estimate the performance of a single school. As a result, steps need to be taken to ensure that school performance indicators meet acceptable criteria for reliability—for example, aggregation of indicators across multiple grade levels and subject areas within a given school.
Third, the data typically used to construct school performance indicators are usually obtained from administrative records rather than extensive surveys of students and parents. As a result, the data will typically be quite limited and possibly either missing for large numbers of cases or subject to errors. This has
important implications for the accuracy of value-added indicators, as is discussed later in the paper.
Finally, some analysts might argue that, while it is accepted practice to use statistical methods to evaluate school policies, it is problematic to use them to construct performance indicators because they may not be comprehensible to students, families, educators, and other interested parties. This is an important concern, justifying considerable effort to make value-added indicators more comprehensible—for example, by using the predicted mean achievement format. A second way to make value-added indicators more comprehensible is to provide the public with some alternative ways of understanding the logic of value-added indicators.
Value-Added Indicators: Logic
To convey the logic of value-added indicators, it is useful to think of a two-stage process of estimating the indicators. In the first stage the so-called slope parameters in Eqs. (1) and (3) (θ, α, δ 1, and δ2) are estimated by using appropriate statistical procedures. 12 These coefficients reflect the contributions of prior achievement, individual characteristics, and school-level factors to growth in student achievement and thus can be used to adjust for the contributions of these factors to average differences across schools in student achievement growth. In the second stage, school performance is estimated, given estimates of the slope parameters from the first stage. Suppose that the first-stage slope parameters have already been estimated. An estimate of total school performance for a given school (school s) can then be given by:
![]() (Total)s = Mean(Posttest)s—AdjFactor(Total)s, (5)
(Total)s = Mean(Posttest)s—AdjFactor(Total)s, (5)
where AdjFactor(Total)s = θ[Mean(Pretest)s - PretestBENCHMARK] + α[Mean (StudChar)s - StudCharBENCHMARK and where Mean(Posttest)s denotes the mean posttest for all students in school s and the other variables are similarly defined. Note that estimated parameters are indicated by placing a circumflex (^) over the parameter. An estimate of intrinsic school performance is similarly given by
![]() (Intrinsic)s = Mean(PostTest)s - AdjFactor(Intrinsic)s (6)
(Intrinsic)s = Mean(PostTest)s - AdjFactor(Intrinsic)s (6)
where AdjFactor(Intrinsic)s = AdjFactor(Total)s + ![]() 1 [Externals -ExternalBENCHMARK].
1 [Externals -ExternalBENCHMARK].
The above formulas provide important insight into the meaning and mechanics of
value-added indicators. The total performance indicator can be viewed as an indicator that adjusts or controls for average differences across schools in student and family characteristics. In particular, the value-added approach purges the average test score—Mean(Posttest) in Eq. (5)—of the component of achievement growth that represents the within-school contribution of students and families to growth in student achievement. The adjustment factor is highest for schools with students who have disproportionately high entering achievement and student and family characteristics that are positively associated with growth in achievement. It is equal to zero for schools that serve students mirroring the overall group of students in the benchmark sample. This implies that the average test score overstates the true performance of schools that have high adjustment factors and understates the true performance of those that have low adjustment factors.
The intrinsic performance indicator has a similar interpretation. The sole difference between the two is that the intrinsic indicator adjusts for differences across schools in external school-level characteristics as well as student-level characteristics. In a sense the intrinsic indicator levels the ''playing field," so that it measures how much a given school adds to a student's achievement, controlling for all external differences across schools.
Note that the value-added indicators defined by Eqs. (5) and (6) are easy to compute, given prior estimates of the slope parameters. 13 This implies that it would be possible to implement an indicator system without placing undue emphasis on the statistical "machinery" that underlies the system—in particular, the first-stage estimation process. With sufficient training, most school administrators could learn to compute estimates of total or intrinsic school performance, resulting in a greater understanding and acceptance of the indicators. 14
Note that the formula for computing the intrinsic performance indicator, Eq. (6), does not require data on internal school characteristics. It may be sufficient to collect this information only periodically for the sole purpose of estimating the required parameters of the value-added model, especially δ1.15 On the other hand, information on internal school characteristics could be useful to schools as part of a diagnostic indicator system, helping identify a school's strong and weak
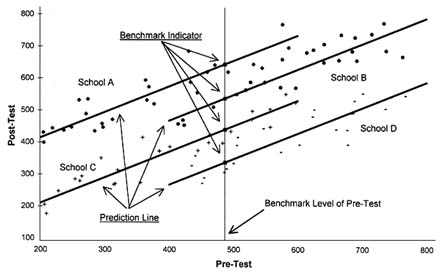
FIGURE 10.1 Plot of hypothetical test score data.
points and providing schools with a ready diagnosis of why their measured performance is high or low. To implement such a system would require a reasonably comprehensive set of school process and input indicators.16
Perhaps the best way to illustrate the logic and mechanics of the value-added approach is with an example. Let us consider a hypothetical dataset containing information on student achievement for students from four different schools. The data are based on a highly simplified model of growth in student achievement that contains only a single control variable—prior achievement.17 As a result, the data can conveniently be displayed on a two-dimensional graph. For simplicity, the discussion here is limited to the total performance indicator; analysis for the intrinsic performance indicator would be similar.
To interpret properly the indicators discussed below, it is important to know something about the distribution of the pre- and posttests that underlie them. Both tests were scored in a manner similar to the Scholastic Assessment Test; scores were centered around a national mean of 500, with a range of approximately 200 to 800. Figure 10.1 plots pre- and posttest scores for 25 students from
TABLE 10.1 Total Performance Indicator Reported as a Benchmark Predicted Mean and as a Conditional Mean, Given Selected Values of Prior Achievement
four different schools (schools A, B, C, and D). In all four schools there is a strong positive relationship between post- and prior achievement. Moreover, for each school the data points are clustered around a centrally located, upward-sloping regression or prediction line. For each school this prediction line can be used to compute the total performance indicator, ![]() (Total)s. This indicator is simply the height of the prediction line for each school at the benchmark level of prior achievement indicated by the vertical line. The value of this indicator for each school is indicated on the graph by a black box. The total performance indicator, reported as a set of conditional mean indicators, is the height of the prediction line for each school at selected values of prior achievement. Table 10.1 reports the total performance indicator in these two alternative formats.
(Total)s. This indicator is simply the height of the prediction line for each school at the benchmark level of prior achievement indicated by the vertical line. The value of this indicator for each school is indicated on the graph by a black box. The total performance indicator, reported as a set of conditional mean indicators, is the height of the prediction line for each school at selected values of prior achievement. Table 10.1 reports the total performance indicator in these two alternative formats.
The total performance indicator is higher for school A than school B, even though the average test scores tend to be higher for school B. This is a consequence of the fact that the pretest scores are substantially lower in school A than in school B. School A is rated a better school than school B because it produces greater achievement growth or adds more value than school B or either of the other two schools. It is easy to see this if one compares students with similar pretest scores, for example, in the range of 400 to 600. The power of the value-added method is that it makes it possible to compare the performance of schools that differ widely in terms of their student populations.
The basic logic of this method is illustrated in Figure 10.2, which reproduces the est score data from Figure 10.1. For each school, the average test score and the total school performance rating are indicated by black squares. These two points are connected by a right triangle. The horizontal segment of the triangle represents the difference between the average level of prior achievement in a given school and the average benchmark level of prior achievement (or Mean [Pre Test]s-PreTestBENCHMARK). In the case of schools B and D, for example, this difference is positive. As a result, the average test score overstates the performance of these two schools.
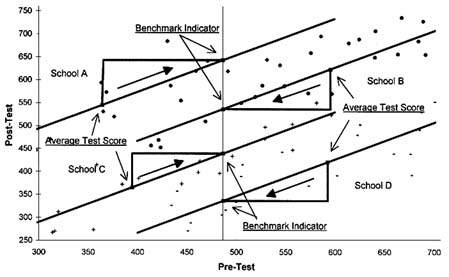
FIGURE 10.2 Graphical illustration of method of estimating value-added indicators.
As is evident in Figures 10.1 and 10.2, the value-added approach is based on two important related assumptions. First, the regression/prediction lines for all schools are linear and parallel. Second, it is possible to predict school performance, given any values of the control variables. The first assumption, in my experience, is consistent with the observed data.18 If not, it might be appropriate to use a more complex value-added model. With regard to the second assumption, one should be very careful in interpreting predicted school performance levels in cases where the values of the control variables are substantially beyond the range of the data for a given school. One might interpret the predicted levels of performance in these cases as indicative of the level that a school could reach in the long run, after it has adjusted to the particular needs of new students.19 This implies that parents should be wary of selecting schools solely on the basis of their predicted total performance if, in the past, the schools have not served students with similar individual and family characteristics. To assist school choice therefore, it is important to convey information about the composition of alternative schools. It is straightforward to incorporate this information into a report of conditional mean indicators, as indicated in Table 10.1. In the table the
predicted levels of school performance that involve extrapolation beyond existing data are italicized. For accountability purposes, the issue of extrapolation appears to be much less of a problem, since it is reasonable to evaluate schools on the basis of an indicator that reflects long-run performance potential.
Alternative Value-Added Models and Modeling Issues
As mentioned earlier, value-added modeling is an active area of research. Some of the modeling issues being addressed are discussed briefly below.
Adequacy of Control Variables
The principal obstacle to developing a high-quality indicator system, is the difficulty of collecting extensive information on student and family characteristics. Value-added indicators are often implemented by using the rather limited administrative data commonly available in schools, such as race and ethnicity, gender, special education status, limited English proficiency status, eligibility for free or reduced-price lunches, and whether a family receives welfare benefits. Researchers equipped with more extensive data have demonstrated that parental education and income, family attitudes toward education, and other variables also are powerful determinants of student achievement. The consequence of failing to control adequately for these and other student, family, and community characteristics is that feasible real-world value-added indicators are apt to be biased, if only slightly, because they absorb differences across schools in average unmeasured student, family, and community characteristics.
To see this, note that the error in estimating a total performance indicator is approximately equal to20
EstErrors ≂ Mean(∈)s, (7)
where Mean(∈)s is the average value of the student-level error term in school s. Because this error absorbs all unmeasured and random student-level determinants of achievement, including measurement error, the error in estimating a school's performance could tend to be high or low depending on whether the school has students with systematically high or low unmeasured characteristics. A similar problem affects the intrinsic performance indicator. In this case, however, the indicator captures all unmeasured student-level characteristics that are systematically high or low together with all unmeasured external school-level characteristics. The bottom line is that value-added models can control for differ
ences across schools in student, family, and community characteristics only if they include explicit measures of these characteristics.
It would be useful for school districts and states to experiment with alternative approaches for collecting the types of information on students that are frequently missing from administrative data. One possibility is to use U.S. census block group data—for example, average adult educational attainment in the block group—as a substitute for unobserved student-level data.
Reliability
An important implication of the above equation is that value-added indicators could be subject to possible errors in estimation owing to random factors. Note that the standard error of a school performance estimate is approximately equal to
StdErrors ≃ Standard Deviation(∈is) /ns1/2, (8)
where ns is the number of students in school s. As indicated, the magnitude of the error diminishes as the number of students in a given school or classroom increases. This implies that it could be very difficult to produce reliable estimates of school performance in a given grade or year in very small schools or at the classroom level. An alternative in such cases is to focus on indicators that are the product of aggregation across grades, years, classrooms, and possibly subject areas.21 If school performance in these different dimensions is highly correlated, aggregation could produce substantial improvements in reliability. There are, of course, other reasons to focus on aggregate indicators. For accountability purposes, for example, a school district might prefer to focus attention on the combined performance of all grade levels at a given school (e.g., grades K-6, 6-8, or 9-12).
Models in which School Performance Depends on Student Characteristics
As noted, the models presented thus far assume that the regression/prediction lines for all schools are parallel—that is, that the slope coefficients for all schools are identical. If this assumption is false, it could be quite misleading to report indicators that are based on it. The appropriate alternative in this case is to adopt a value-added model that allows one or more slope coefficients to vary across schools. Models of this type are often referred to as heterogeneous slope models.22
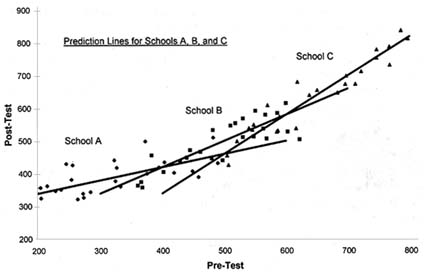
FIGURE 10.3 Plot of hypothetical test score data given heterogeneous slopes.
Figure 10.3 contains a plot of hypothetical pre- and posttest data in which the regression/prediction lines vary substantially across schools.23 The data suggest there is no single best-performing school. School A appears to be the best for students with low prior achievement. School B appears to be the best for students with medium prior achievement. School C appears to be the best for students with high prior achievement. In this situation it is impossible to characterize school performance with a single performance rating; the relative performance of schools is a function of student characteristics. As a result, it is necessary to report school performance information in something very much like the conditional mean format illustrated in Table 10.2. As noted earlier, the major disadvantage of this format is that the total number of reporting categories could be quite large. To minimize the number, it might be advantageous to limit the number of reporting dimensions to the control variables that exhibit significant variation across schools in their coefficients.
One potential problem with heterogeneous slope models is that the coefficients tend to be less precisely estimated than in models where the slope coefficients are the same in all schools. There are fewer data to estimate the model parameters in a single school than in an entire sample of schools. It makes sense to use the heterogeneous slope model only when the variation in slope coefficients across schools is substantively and statistically significant. As mentioned
TABLE 10.2 NAEP Mathematics Exam Data, by Grade/Age and Year
|
|
1973 |
1978 |
1982 |
1986 |
|
|
Average Test Score |
|
|
|
|
Grade 3/age 9 |
219.1 |
218.6 |
219.0 |
221.7 |
|
Grade 7/age 13 |
266.0 |
264.1 |
268.6 |
269.0 |
|
Grade 11/age 17 |
304.4 |
300.4 |
298.5 |
302.0 |
|
|
Average Test Score Gain |
|
|
|
|
|
73 to 78 |
78 to 82 |
82 to 86 |
|
|
Grades 3–7/ages 9–13 |
45.0 |
50.0 |
50.0 |
|
|
Grades 7–11/ages 13–17 |
34.4 |
34.4 |
33.4 |
|
|
SOURCE: Dossey et al. (1988). |
||||
previously, the assumption that slopes do not vary across schools is often a reasonable one.
Value-Added Versus Common Educational Indicators: Theory and Evidence
As discussed earlier, level indicators, such as average test scores, are frequently used to measure school performance even though they are not, in general, equivalent to either total or intrinsic performance indicators. Is the difference between level and value-added indicators substantial enough to worry about? For simplicity, consider a single-level indicator, the average test score.
The average test score, measured at a given grade level, is the product of growth in student achievement over a potentially large number of grades and years. It therefore reflects the contributions to student achievement of schools and other inputs to the learning process from multiple grades and multiple points in time. For several reasons the average test score is potentially a highly misleading indicator of how productive a school is at a given point in time. First, the average test score is, in general, contaminated by factors other than school performance, primarily the average level of student achievement prior to entering first grade and the average effects of student, family, and community characteristics on student achievement growth from first grade through the grade in which students are tested. It is likely that comparisons across schools of average test scores primarily reflect these differences rather than genuine differences in total or intrinsic school performance. Average test scores are highly biased against schools that serve disproportionately higher numbers of academically disadvantaged students.
Second, the average test score reflect information about school performance that tends to be grossly out of date. For example, the average test scores for a group of tenth-grade students reflect learning that occurred from kindergarten, roughly 10 1/2 years earlier, through the tenth grade. If the variability over time of school performance is higher in elementary school than in middle or high
school, a tenth-grade-level indicator could be dominated by information that is five or more years old. The fact that the average test score reflects outdated information severely weakens it as an instrument of public accountability. To allow educators to react to assessment results in a timely and responsible fashion, performance indicators presumably must reflect information that is current.
Third, average test scores at the school, district, and state levels tend to be highly contaminated because of student mobility in and out of different schools. The typical high school student is likely to attend several different schools over the period spanning kindergarten through grade twelve. For these students a test score reflects the contributions of more than one, even several, schools. The problem of contamination is compounded by the fact that rates of students mobility may differ dramatically across schools and is likely to be more pronounced in ones that undergo rapid population growth or decline and in ones that experience significant changes in their occupational and industrial structure.
Finally, unlike the grade-specific value-added indicator, average test score fails to localize school performance to the natural unit of accountability in schools—a specific classroom or grade level. This lack of localization is, of course, most severe at the highest grade levels. A performance indicator that fails to localize school performance to a specific grade level or classroom is likely to be a relatively weak instrument of public accountability.
A simulation vividly demonstrates how the average test score is determined in large part by past gains in achievement and hence is apt to be quite misleading as an indicator of current school performance.
To focus on the consequences of variations in school performance over time assume that (1) average initial student achievement and average student characteristics are identical for all schools at all points in time, (2) school performance is identical at all grade levels in a given year, (3) growth in student achievement is determined by a linear growth model, and (4) there is no student mobility.24 The technical details of the simulations and the simulation data reported in the figures are presented in Meyer (1994). Figure 10.4 charts average tenth-grade achievement and school performance before and after the introduction of hypothetical academic reforms in 1992. This analysis is particularly relevant in evaluating the efficacy of school reform efforts. Figure 10.4(a) depicts a scenario in which academic reforms reverse a trend of gradual deterioration in school performance across all grades and initiate a trend of gradual improvement in school performance in all grades. Figure 10.4(b) depicts a scenario in which academic reforms have no effect on school performance. The reforms are preceded, how-
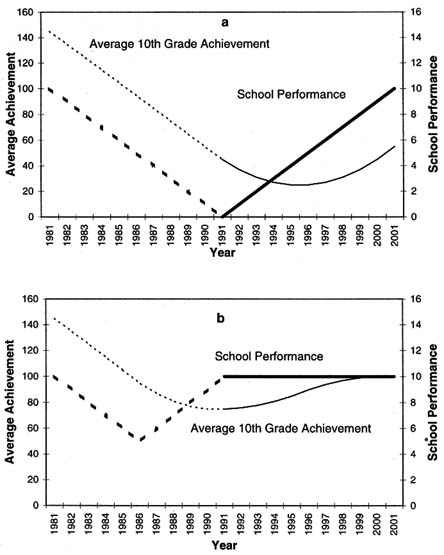
FIGURE 10.4 Average 10th grade achievement versus school performance.
ever, by an era of gradual deterioration in school performance across all grades, followed by a brief period (1987–1991) of gradual improvement.
Figure 10.4 illustrates that the average tenth-grade test score provides a totally misleading view of the effectiveness of the hypothetical academic reforms implemented in 1992. In Figure 10.4(a) the average tenth-grade test score declined for five years after the introduction of successful reforms. In Figure 10.4(b)
the average tenth-grade test score increased for a decade after the introduction of reforms that have no effect on growth in student achievement. These results are admittedly somewhat counterintuitive. They arise from the fact that tenth-grade achievement is the product of gains in achievement accumulated over a 10-year period. The average tenth-grade test score is, in fact, exactly equal to a 10-year moving average of school performance. This stems from the simple assumption that school performance is identical at different grade levels in the same year. The noise introduced by this type of aggregation is inevitable if school performance is at all variable over time.
The problem of aggregation of information that is grossly out of date also introduces noise into the comparisons of different schools at the same point in time. The degree to which noise of this type affects the relative rankings of school depends on whether the variance over time in average achievement growth is large relative to the variance across schools in achievement growth. To illustrate this point, Figure 10.5 considers the consequences of aggregation over time and grade levels for two schools that are identical in terms of school performance in the long-term. In the short-term, however, school performance is assumed to vary cyclically. For school 1, performance alternates between 10 years of gradual decline and 10 years of gradual recovery. For school 2, performance alternates between 10 years of gradual improvement and 10 years of gradual decline. These patterns are depicted in Figure 10.5(b). The correct ranking of schools, based on school performance, is noted in the graph. Figure 10.5(a) depicts the associated levels of average tenth-grade achievement for the two schools. The rankings of schools based on this indicator are also noted. The striking aspect of Figure 10.5 is that the average tenth-grade test score ranks the two schools correctly only 50 percent of the time. In short, the noise introduced by aggregation over time and grade levels is particularly troublesome if comparing schools that are roughly comparable in terms of long-term performance. On the other hand, the problem is less serious for schools that differ dramatically in terms of long-term average performance. It is also less serious if cycles of decline and improvement are perfectly correlated across schools—an unlikely phenomenon.
Example Based on Data from the National Assessment of Educational Progress
To consider whether the average test score exhibits these problems in real-world data, consider average mathematics scores from 1973 to 1986 from the National Assessment of Educational Progress (NAEP) (see Table 10.2). Unfortunately, the NAEP is not structured in such a way that it is possible to construct a value-added measure of school performance,25 so we compare average test scores with the simple average growth in achievement from one test period to the next for the same cohort of students. This measure is typically referred to as a gain
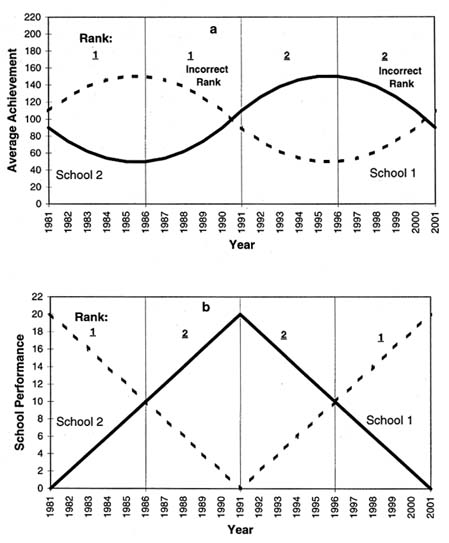
FIGURE 10.5 Average 10th grade achievement given alternative cycles of school performance.
indicator.26 It differs from a true value-added indicator in that it fails to control for differences across schools and over time in average student and family characteristics. In general, it makes sense to compute a gain indicator only when the tests administered at different grade levels are scored using a common scale. The NAEP tests fulfill this criterion.
As indicated in Table 10.2, average tests scores for eleventh graders exhibit the by-now familiar pattern of sharp declines from 1973 to 1982 and then partial recovery between 1982 and 1986. The eleventh-grade data, by themselves, are fully consistent with the premise that academic reforms in the early and mid-1980s generated substantial gains in student achievement. In fact, an analysis of the data based on a more appropriate indicator than average test scores suggests the opposite conclusion. The gain indicator reveals that achievement growth during the 1982–1986 period was actually no better than that during the 1978–1982 period and that gains from grades 7 through 11 were actually slightly lower from 1982 to 1986 than in previous periods! The rise in eleventh-grade math scores from 1982 to 1986 stems from an earlier increase in achievement for the same cohort of students rather than from an increase in achievement from grades 7 through 11. In short, these data provide no support for the notion that high school academic reforms during the mid-1980s generated significant increases in test scores. Moreover, the analysis underscores that in practice, not just in theory, average test scores can be a highly fallible measure of school performance.
Policy Implications
Consequences of Using Flawed Indicators
The fact that level indicators measure school performance with potentially enormous error has important implications for their use in making education policy, informing students and parents about the quality of schools, and evaluating school performance as part of an accountability system. With respect to policymaking, it is clear that level indicators potentially provide wholly incorrect information about the success or failure of educational interventions and reforms. They could lead to the expansion of programs that do not work or to the cancellation of ones that are truly effective. Similarly, level indicators are likely to give students and parents erroneous signals about which schools to attend. Either academically advantaged and disadvantaged students could be fooled into abandoning an excellent neighborhood school simply because the school served stu
dents who were disproportionately academically disadvantaged. At the other extreme, families whose children attend a school that serves a disproportionately higher number of academically advantaged students could be lulled into complacency about a school that is contributing relatively little to growth in student achievement. Overall reliance on average test scores or other level indicators is likely to yield lower levels of student and school performance.
The adverse effects of level indicators on the behavior of teachers and administrators are likely to be particularly acute if they are in any way rewarded or penalized on the basis of their performance with respect to a given indicator. In a high-stakes accountability system, teachers and administrators are likely to respond to the incentive to improve their measured performance by exploiting all existing avenues. It is well known, for example, that teachers may ''teach narrowly to the test," although some tests are more susceptible to this type of corruption than others. For tests that are relatively immune to such corruption, teaching to the test could induce teachers and administrators to adopt new curricula and teaching techniques much more rapidly than they otherwise would. On the other hand, if school performance is measured by using a nonvalue-added indicator, teachers and administrators have the incentive to raise measured school performance by teaching only those students who rate highly in terms of average student and family characteristics, average prior achievement, and community characteristics—a phenomenon referred to as creaming.
The tendency toward creaming is stronger at schools that have the authority to admit or reject prospective students and to expel already enrolled students. But the problem also exists in more subtle forms. For example, schools sometimes create an environment that is relatively inhospitable to academically disadvantaged students, provide course offerings that predominantly address the needs of academically advantaged students, fail to work aggressively to prevent students from dropping out of high school, err on the side of referring "problem" students to alternative schools, err on the side of classifying students as special education students where the latter are exempt from statewide testing, or make it difficult for low-scoring students to participate in statewide exams. These practices are designed to improve average test scores in a school, not by improving school quality but by catering to high-scoring students while ignoring or alienating low-scoring ones.
Value-Added Indicators and School Performance Expectations
Some commentators have expressed the concern that value-added indicators, because they control or adjust for student, family, and community characteristics associated with growth in student achievement, reduce performance expectations for schools and states that serve disproportionately higher numbers of disadvantaged students.27 This is obviously an important concern, but noth
ing in the value-added method discourages a district or state from establishing high-performance expectations for all students. To avoid creating an incentive for schools to engage in creaming, however, it is essential to translate student performance expectations into the corresponding school performance goals. This can be accomplished by using Eqs. (5) and (6). For this application, however, Mean(Posttest)s represents the average student achievement goal rather than the actual average level of student achievement, and the performance indicators represent the school performance goals rather than the actual levels of performance.
Note that for a given student achievement goal the corresponding school performance goal will always be higher, not lower, for schools that serve disproportionately higher numbers of disadvantaged students. The reason is straight-forward: to reach a given student achievement goal, it is necessary for schools that serve disproportionately higher numbers of disadvantaged students to outperform other schools. If expectations for student achievement are sufficiently high, this procedure will almost certainly produce school performance goals that are extremely ambitious for schools that serve disproportionately higher numbers of disadvantaged students—a strength rather than a weakness of the value-added approach. If the nation is serious about setting high expectations for all students, it is important to translate these performance expectations into accurate school performance goals.
A second response to concerns about lowered performance expectations is that the conditional mean format for reporting value-added indicators makes it easy to separate the tasks of measuring school performance and setting student performance expectations (see Table 10.1). It would be straightforward, for example, to augment Table 10.1 to include a separate student achievement goal for each type of student or to include a common student achievement goal for all students.
Value-Added Indicators: Data Requirements
In view of the problems associated with average test scores and other level indicators, is it appropriate to consider using value-added indicators as the core of school district, state, and national performance indicator/accountability systems? There are at least two reasons to be optimistic in this regard. First, value-added models have been used extensively over the past three decades by evaluators and other researchers interested in education and training programs. Second, a number of districts and states, including Dallas (see Webster et al., 1992), South Carolina (Mandeville, 1994), and Tennessee (Sanders and Horn, 1994), have successfully implemented value-added indicator systems.
Despite their promise, such systems require a major commitment on the part of school districts and states. Districts and states must be prepared to test students frequently, ideally at every grade level, as is done in South Carolina, Tennessee, and Dallas. They also must develop comprehensive district or state data
systems that contain information on student test scores and student, family, and community characteristics.
Annual testing at each grade level is desirable for at least three reasons. First, it maximizes accountability by localizing school performance to the most natural unit of accountability—the grade level or classroom. Second, it yields up-to-date information on school performance. Finally, it limits the amount of data lost because of student mobility. As the time interval between tests increases, these problems become more acute. Indeed, for time intervals of more than two years, it may be impossible to construct valid and reliable value-added indicators for schools with high mobility rates. Mobile students generally must be excluded from the data used to construct value-added and gain indicators, since both indicators require pre- and posttest data. In schools with high student mobility, infrequent testing diminishes the prospect of ending up with student data that are both representative of the school population as a whole and large enough to yield statistically reliable estimates of school performance.28 Less frequent testing—for example, in kindergarten29 and grades 4, 8, and 12—might be acceptable for national purposes, since student mobility is less prevalent at the national level; but to evaluate local school performance, frequent testing is highly desirable.
Conclusions and Recommendations
Average test scores, one of the most commonly used indicators in American education, are an unreliable indicator of school performance. Average test scores fail to localize school performance to the classroom or grade level, aggregate information on school performance that tends to be grossly out of date, are contaminated by student mobility, and fail to distinguish the distinct value-added contribution of schools to growth in student achievement from the contributions of student, family, and community factors. Average test scores are a weak, if not counterproductive, instrument of public accountability.
The value-added indicator is a conceptually appropriate indicator for measuring school performance. This chapter presents two basic types of value-added indicators: the total school performance indicator, which is appropriate for purposes of school choice, and the intrinsic performance indicator, which is appropriate for purposes of school accountability. The quality of these indicators is determined by the frequency with which students are tested, the quality and appropriateness of the tests, the adequacy of the control variables included in the
appropriate statistical models, the technical validity of the statistical models used to construct the indicators, and the number of students and schools available to estimate the slope parameters of value-added models. States should consider testing students at every grade level, as is currently done in South Carolina, Tennessee, and Dallas, or at least at every other grade level, beginning with kindergarten. They should also make an effort to collect extensive and reliable information on student and family characteristics and to develop state tests that are technically sound and fully attuned to their educational goals. Further research is needed to assess the sensitivity of estimates of school performance indicators to alternative statistical models and alternative sets of control variables. In particular, it would be helpful to know more about the empirical differences between total and intrinsic school performance indicators. Finally, in order to improve the reliability of estimates of school performance, particularly intrinsic performance, small and medium-sized school districts should consider combining their data to create school performance indicator systems that serve multiple districts.
References
Boardman, A. E., and R. J. Murnane. 1979. "Using panel data to improve estimates of the determinants of educational achievement." Sociology of Education 52:113–121.
Bock, R. D. 1989. Multilevel Analysis of Educational Data, San Diego: Academic Press.
Bryk, A. S., and S. W. Raudenbush. 1992. Hierarchical Linear Models: Applications and Data Analysis Methods. Newbury Park, Calif.: Sage Publications.
Coleman, J. S., and others. 1966. Equality of Educational Opportunity . Washington, D.C.: U.S. Department of Health, Education, and Welfare.
Clune, W. H. 1991. Systemic educational policy. Madison: University of Wisconsin, Wisconsin Center for Educational Policy.
Darling-Hammond, L. 1991. "The implications of testing policy for quality and equality." Phi Delta Kappan 73:220–225.
Dossey, J. A., I. V. Mullis, M. M. Lindquist, and D. L. Chambers. 1988. The Mathematics Report Card: Are We Measuring Up? Princeton, N.J.: Educational Testing Service.
Dyer, H. S., R. L. Linn, and M. J. Patton. 1969. "A comparison of four methods of obtaining discrepancy measures based on observed and predicted school system means on achievement tests." American Educational Research Journal 6:591–605.
Finn, C. E., Jr. 1994. "Drowning in Lake Wobegon." Education Week, pp. 31, 35.
Haladyna, T. M., S. B. Nolen, and N. S. Hass. 1991. "Rising standardized achievement test scores and the origins of test score pollution." Educational Researcher 20:2–7.
Hanushek, E. A. 1972. Education and Race. Lexington, Mass.: D. C. Health.
Hanushek, E. A., and L. Taylor. 1990. "Alternative assessments of the performance of schools." Journal of Human Resources 25:179–201.
Hsiao, C. 1986. Analysis of Panel Data. Cambridge: Cambridge University Press.
Koretz, D., B. Stecher, S. Klein, and D. McCaffrey. 1994. "The Vermont portfolio assessment program." Educational Measurement: Issues and Practice 13(3):5–16.
Lord, F. M. 1980. Applications of Item Response Theory to Practical Testing Problems . Hillsdale, N.J.: Lawrence Erlbaum Assoc.
Mandeville, G. K. 1994. The South Carolina experience with incentives. Paper presented at the conference entitled "Midwest Approaches to School Reform," Federal Reserve Bank of Chicago, Chicago.
Meyer, R. H. 1992. Applied versus traditional mathematics: new econometric models of the contribution of high school courses to mathematics proficiency. Discussion Paper No. 966-92, University of Wisconsin-Madison, Institute for Research on Poverty.
Meyer, R. H. 1994. Educational performance indicators: a critique. Discussion Paper No. 1052-94, University of Wisconsin-Madison, Institute for Research on Poverty.
Murnane, R. J. 1975. The Impact of School Resources on the Learning of Inner-City Children. Cambridge, Mass.: Ballinger Publishing Co.
Nolen, S. B., T. M. Haladyna and N. S. Haas. 1992. "Uses and abuses of achievement test scores." Educational Measurement: Issues and Practice 11:9–15.
Raudenbush, S. W. 1988. "Educational applications of hierarchical linear models: a review." Journal of Educational Statistics 13:85–116.
Raudenbush, S. W., and A. S. Bryk. 1986. "A hierarchical model for studying school effects." Sociology of Education 59:1–17.
Raudenbush, S. W., and J. D. Willms. 1991. Schools, Classrooms, and Pupils. San Diego: Academic Press.
Sanders, W. L., and S. P. Horn. 1994. "The Tennessee value-added assessment system (TVAAS): mixed-model methodology in educational assessment." Journal of Personnel Evaluation in Education 8:299–311.
Shepard, L. A. 1991. "Will national tests improve student learning?" Phi Delta Kappan 73:232–238.
Smith, M. S., and J. O'Day. 1990. "Systemic school reform." Pp. 233–267 in The Politics of Curriculum and Testing: 1990 Yearbook of the Politics and Education Association, S. Fuhrman and B. Malen, eds. London: Taylor and Francis.
Smith, M. L., and C. Rottenberg. 1991. "Unintended consequences of external testing in elementary schools." Educational Measurement: Issues and Practice 10:7–11.
Webster, W. J., R. L. Mendro, and T. O. Almaguer. 1992. Measuring the effects of schooling: expanded school effectiveness indices. Paper presented at the annual meeting of the American Educational Research Association, San Francisco.
Wiggins, G. 1989. "A true test: toward more authentic and equitable assessment." Phi Delta Kappan 70:703–713.
Willett, J. B. 1988. "Questions and answers in the measurement of change." Pp. 345–422 in Review of Research in Education, E.Z. Rothkopf, ed. Washington, D.C.: American Educational Research Association.
Willms, D. J., and S. W. Raudenbush. 1989. "A longitudinal hierarchical linear model for estimating school effects and their stability." Journal of Educational Measurement 26:209–232.




























