Insights from Ambient Toxicity Testing
Arthur J. Stewart
Introduction
Ambient toxicity tests assess the toxicity of stream or river water by exposing organisms to the water and measuring their survival, growth, or reproduction. The performance of organisms in ambient toxicity tests can thus be used to directly assess the biological quality of waters that receive industrial or other effluents. This paper examines the types of insights that can be derived from ambient toxicity testing, based on lessons learned from several large-scale ambient toxicity testing programs established for streams that receive effluent from U.S. Department of Energy (DOE) facilities near Oak Ridge, Tenn.
In contrast to ambient toxicity tests that expose organisms to stream or river water, effluent toxicity tests (Goulden, this volume) expose organisms directly to effluent or diluted effluent. Regulations frequently require the use of effluent toxicity tests to document the biological quality of receiving waters. Standard methods approved by the U.S. Environmental Protection Agency (EPA) are available for both effluent and ambient toxicity tests (Kszos and Stewart, 1992; Weber et al., 1989).
Effluent and ambient toxicity tests use similar procedures but have different objectives. Both use "reagent grade" organisms as biodetectors, under standardized conditions, to provide a direct assessment of water quality. A subtle but important difference between effluent and ambient testing is this: In effluent testing, the key objective is usually to determine how toxic an effluent is, whereas in ambient testing, the main objective is usually to determine whether the water is toxic. A clear understanding of the differences between the two is necessary to design statistically rigorous, cost-effective, ambient toxicity testing programs.
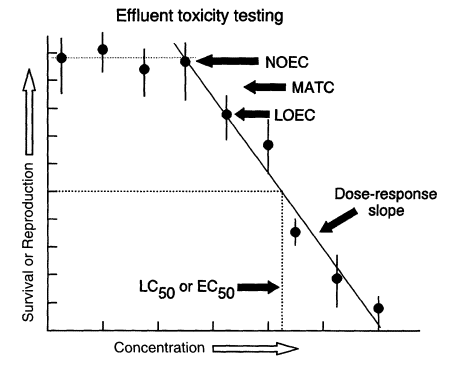
Figure 1
Generalized dose-response relationship suitable for estimating no-observed-effect concentration (NOEC), lowest-observed-effect concentration (LOEC), maximum-allowable toxicant concentration (MATC, equal to mean of NOEC and LOEC values), and LC50 and EC50 values (concentrations needed to kill 50 percent of the test organisms, or reduce the response variable by 50 percent, respectively).
In effluent testing, organisms are reared in various dilutions of effluent for a specified period of time with specified food, temperature, and light conditions. The ability of the organisms to survive, grow, and (in some cases) reproduce is measured and compared with the responses of organisms reared in a negative control (i.e., water known to be of good biological quality). The highest effluent concentration that causes no adverse effect is referred to as the no-observed-effect concentration (NOEC). The next-higher tested concentration, which shows the first statistically detectable effect of the effluent on the organisms, is referred to as the lowest-observed-effect concentration (LOEC). For regulatory purposes, effluent testing is used to establish a reliable estimate of an effluent's NOEC, LOEC, or LC50 (concentration of effluent that is lethal to half of the test organisms in a specified period of time) (Figure 1). The statistical procedures for estimating these concentrations are well defined (Figure 2). The NOECs can be
compared with expected effluent concentrations in receiving streams to predict the likelihood of in-stream toxicity. Despite recent strong challenges to the concept of NOEC and LOEC on statistical grounds (see, for example, Kooijman, 1996), NOECs and LOECs are widely used and are likely to remain so for regulatory purposes in the United States for years to come.
The key difference between effluent toxicity data and ambient toxicity data may be best conceptualized in terms of signal-to-noise ratio. Compared with most receiving waters, most effluents have a strong toxicity ''signal." On the other hand, the "noise level" for effluents tends to be lower than that of ambient waters. Thus, in general, the toxicity signal-to-noise ratio is higher for effluents than it is for ambient tests of receiving waters. This is important because it determines how the tests should be applied to maximize the information gained per dollar spent.
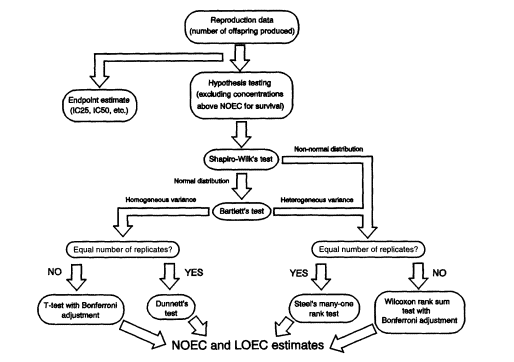
Figure 2
Statistical analysis flow path for reproduction data from Ceriodaphnia effluent toxicity tests (redrawn from Weber et al., 1989). NOTES: IC25 and IC50 refer to the concentrations of effluent or chemical that inhibits the measure of interest (such as growth or reproduction) by 25 or 50 percent, respectively. NOEC = no-observed-effect concentration. LOEC = lowest observed-effect concentration.
Waste treatment operators have a good understanding of their operations and know from experience and instrumentation feedback when treatment processes are operating correctly. In this situation, many water-quality conditions that can affect the outcome of a toxicity test (e.g., hardness, conductivity, suspended solids, pH, temperature) are relatively constant and predictable. In contrast, hardness, conductivity, and concentration of suspended solids can vary greatly in ambient waters with rainfall or snow-melt; pH can vary two standard units or more in response to season or even over daily cycles due to algal photosynthesis; and temperature can increase or decrease rapidly in response to weather conditions. Water-quality conditions in receiving streams can also change rapidly due to upstream spills or intermittent releases of batch-process effluents (e.g., cooling tower operations, which typically release a large volume of ion-rich waste water over a short period of time). In short, temporal variation in water quality is an important source of background noise that can complicate quantification of low levels of ambient toxicity.
Aquatic organisms are about as good at detecting toxicants in receiving waters as they are at detecting toxicants in effluents. However, the apparent or actual sensitivity of the organisms to some toxicants can be affected by other chemicals or water-quality factors. The sensitivity of test organisms to toxicants and their vulnerability to nontoxicant interferences are particularly important in ambient testing where the signal-to-noise ratio is low. Specific examples demonstrate this point. High but nontoxic concentrations of sodium can lower the toxicity of lithium to Ceriodaphnia (Stewart and Kszos, 1996). Thus, lithium at a concentration of 5 parts per million (ppm) in a sodium-rich waste water (e.g., 140 ppm sodium) might show no evidence of toxicity, whereas lithium is distinctly toxic at a concentration of 1 ppm in low-sodium (e.g., 5-10 ppm) ambient water. Calcium or other hardness-contributing materials can also lower the toxicity of nickel (Kszos et al., 1992) and other metals.
Physical variables also can affect the apparent sensitivity of test organisms. For example, naturally occurring particulate matter (algae, bacteria, and/or sediment) can lower the apparent sensitivity of organisms in two ways. First, some particulate matter (notably, algae, bacteria, and detritus) can be used as food by freshwater microcrustaceans. The nutritional benefits of the "extra food" can be important. For ambient toxicity tests of water samples from two sites in East Fork Poplar Creek (EFPC) (a stream that receives various waste waters from the DOE's Oak Ridge Y-12 Plant), we found that filtering the water to remove naturally occurring particulate matter significantly lowered Ceriodaphnia reproduction. The mean reduction in Ceriodaphnia reproduction caused by filtering the water was slightly larger at one site (9.7 percent) than it was at the other site (7.4 percent), but the effect of filtration was statistically significant at both sites (p = 0.030 for 15 tests at km 24.1 of EFPC; p = 0.019 for 21 tests at km 23.8 of EFPC, Student's T test). (Sites in East Fork Poplar Creek are identified by distance upstream from its confluence with Poplar Creek, a tributary of the Clinch River.) In contrast to many
stream and river waters, most industrial effluents do not contain significant quantities of particulate matter because specific treatment operations such as polymer-enhanced flocculation or filtration remove solids from the water.
Particulate matter can also alter the bioavailability or biological activity of some contaminants. Chlorine (measured as total residual chlorine), for example, is very toxic to daphnids (Taylor, 1993) but is rapidly detoxified when it reacts with algae, detritus, or chemically labile dissolved organic matter. Organic and inorganic particles also are important sinks for relatively insoluble contaminants such as polychlorinated biphenyls, hydrophobic hydrocarbons, and various metals. In general, naturally occurring particulate matter lowers the concentrations of dissolved pollutants, thereby lowering the water's toxicity.
Monotonic response to an increase in the signal of interest is an important consideration in any detector system. The dose-response concept in toxicity testing embodies this consideration and has been very influential in the development of effluent toxicity tests. Dose-response patterns, where organism responses are a function of toxin concentration, are fundamental to effluent and pure-chemical toxicity testing. It is through adherence to an expected dose-response relationship that effluent toxicity testing gains predictive value. Therefore, much effort in the development of toxicity tests has gone into the selection of test procedures that generate smooth dose-response curves. Procedures for establishing regulatory limits on effluent toxicity are based on the premise that a monotonic dose-response relationship can be determined (Figure 1). This premise dominates every aspect of effluent toxicity testing: Adherence to a linear dose-response pattern allows extraction of the toxicity signal. The statistical procedures for estimating toxicity of effluents that yield smooth dose-response curves are clearly outlined in EPA manuals (Kooijman, 1996; Weber et al., 1989) (Figure 1).
A weak toxicity signal and relatively high background noise are typical of ambient toxicity test conditions. Low signal-to-noise ratios prevent effective quantification of ambient toxicity using the statistical framework of the dose-response model that works so well for effluent toxicity tests. The difference in appropriate statistical procedures for analysis of test results is the crucial distinction between the analytical procedures for ambient and effluent toxicity tests. This difference is central to the formulation of a cost-effective strategy for ambient toxicity testing.
Applications
Ambient toxicity tests using Ceriodaphnia dubia (a freshwater microcrustacean) and Pimephales promelas (fathead minnow) larvae have been used to support biological monitoring programs for 12 receiving streams at DOE facilities in Oak Ridge, Tenn. and Paducah, Ky. (Stewart and Loar, 1994). The tests used EPA-approved procedures for estimating chronic toxicity (Mount and Norberg, 1984; Norberg and Mount, 1985; Weber et al., 1989), specifically, rear-
ing replicate groups of fathead minnow larvae, or individual Ceriodaphnia , in full-strength (i.e., nondiluted) samples of water from the site(s) being evaluated. During the 7-day tests, fresh samples of water were collected daily from each site being evaluated. The water was then warmed to the test temperature (25°C) and used to replace the previous day's water in the test chambers. This procedure is referred to as static renewal of test cultures. In almost every case, we evaluated the sites for ambient toxicity by testing both species concurrently. The ambient toxicity tests include negative controls (i.e., tests with mineral water, diluted to an acceptable ionic strength with distilled water) and water samples from reference sites, located upstream of known point- or area-source inputs of pollutants. We estimated toxicity using survival and growth of minnow larvae and survival and reproduction of Ceriodaphnia. We also measured the pH, conductivity, alkalinity, hardness, and total residual chlorine of all freshly collected water samples.
Ambient toxicity tests were run on water from as many as 10 sites per stream, but in some cases one site was sufficient for effective monitoring. At one of the DOE facilities near Oak Ridge (the Oak Ridge National Laboratory), 15 sites on 5 receiving streams have been tested 42 times (concurrently with both species) since 1986. A total of 630 site and test-period combinations were represented by the sampling and testing strategy used for the five receiving streams (i.e., 15 sites in each of 42 test periods). For each stream or suite of streams that is monitored for ambient toxicity, the primary unit of statistical analysis is the mean response for each site-date combination. The response parameters include Ceriodaphnia survival (percentage, based on 10 animals per site-date combination) and reproduction (number of offspring per female, for females that survive all 7 days), and fathead minnow survival (percentage, based on 4 replicates, each containing 10 fish) and growth (mean milligrams dry mass per surviving fish, per replicate, corrected for initial weight). Survival data for the minnows are generally arc-sine square-root transformed before analysis; growth data for the minnow larvae can be corrected for growth of larvae in the controls or reference sites, depending on the objective of the analysis. We do not normally transform Ceriodaphnia survival values because each test generates only a single value (e.g., 100 percent, 90 percent, 80 percent) derived from 10 individual animals, each of which constitutes a replicate.
We have explored various methods for analyzing the results of ambient toxicity tests. The case-study examples below summarize these methods, the key findings revealed through their use, and their major advantages and disadvantages. Most of these examples are derived from studies published elsewhere (e.g., Kszos et al., 1992; Stewart, 1996; Stewart et al. ,1990, 1996). In general, the results of ambient tests are used either to reveal differences among sites (e.g., a longitudinal pattern within a stream or differences among streams) or to demonstrate the occurrence of water-quality changes over time.
Analysis of Variance Methods
Analysis of variance (ANOVA) can be conducted using site, test period, and the interaction between site and test period as explanatory factors for Ceriodaphnia survival or reproduction, or fathead minnow survival or growth. ANOVA (SAS-GLM, available for use on personal computers; SAS Institute, 1985) provides an estimate of the amount of variation in survival, reproduction, or growth that is explained (R2) by the three factors together. Duncan's multiple-range test (a SAS-GLM option) or other multiple-comparison tests can be used to identify sites or test periods where the response factor is low. When Duncan's multiple-range test is used to identify differences among sites, sites are sorted according to mean responses. Sites that have an unusually low mean value for any of the four response parameters can be considered as suspect for toxicity. If the study involves a linear array of sites below a discharge, and the effects attributable to date and the interaction of site and test period are small, the procedure could permit the investigator to identify a "no-observed-effect site," analogous to the NOEC of effluent toxicity tests.
If data for a sufficiently large number of test periods are available, and one or two of the test periods have unusually low mean values for a response parameter, the data set can be pruned by eliminating data from the suspect test period(s). This procedure may be justified if the response parameter in question (e.g., fathead minnow growth) is unusually low in water from all sources, including references sites, and the control. The elimination of data for test periods that have suspiciously low values for the response factors should increase R2 for the full model (site, test period, and the interaction between site and test period) and lower the significance of test period. An analysis reported in Boston et al. (1994) showed an increase in the amount of explained variance in Ceriodaphnia survival and reproduction by eliminating suspect dates from the data set. In contrast, neither the results for minnow survival or growth did not benefit much from data pruning. Pruning should be used only when it is thoroughly justified. In such cases, the justification should be explained, and the consequences of the act of pruning should be considered carefully. The objective of pruning is not to increase the R2 of a linear model but to reveal temporal or spatial patterns in biological quality of the water that may otherwise be obscured by excessive variance due to test dates where growth, survival, or reproduction of test organisms was low in control or reference conditions.
When using toxicity test methods to assess ambient water quality, a bioassay should simultaneously meet two key objectives: It should discriminate readily among sites, and it should exhibit little variation from test period to test period, when applied to noncontaminated control water or to water from a noncontaminated reference site. An ANOVA-based analysis of results of 285 site and test-period combinations was used to determine which test organism—Ceriodaphnia or fathead minnow larvae—best fulfilled these objectives (Boston et al., 1994). That analysis
considered rank values of sites within test periods and of test periods within sites for all four measures of toxicity (minnow survival and growth, and Ceriodaphnia survival and reproduction). The suitability of these two types of tests for ambient applications was evaluated in a two-step process. First, for each of the four measures of toxicity (dependent variables), a site specificity over time term was computed by dividing the proportion of variation in the dependent variable explained using site as the explanatory factor (i.e., the R2 for site) by the proportion of variation explained by using test period as the explanatory factor (i.e., the R2 for test period). The relative utility of each test organism was then computed by summing its two "site specificity over time" terms (one term for each measure of toxicity). This computation showed that the Ceriodaphnia test was about 3.8 times more specific than the fathead minnow test. One significant conclusion from the study by Boston et al. (1994) was that, for ambient water-quality assessments, greater testing frequency with Ceriodaphnia might be more effective than less frequent testing with both species.
The examples described above use ANOVA with site and test period as explanatory factors. This approach allows one to determine if site or test period has a statistically significant effect on fathead minnow larvae survival or growth, or on Ceriodaphnia survival or reproduction. These methods cannot be used to infer that toxicants cause a response, even if one site differs greatly from the others with respect to survival, reproduction, or growth. Other data must be considered to ascertain the cause of the observed response. Using two-way ANOVA, responses of organisms in the controls can be used qualitatively, to support the idea of pruning results from a particular test date from the data set, or quantitatively, as though controls were merely an additional site. When used in the latter fashion, some of the sites frequently appear significantly better than controls and some sites worse than the controls. In effluent testing, controls are essential; in ambient testing, controls are useful, but reference sites are critical.
Contingency-Table Analysis Methods
We have used contingency-table methods to establish lower-bound values for "passing" an ambient toxicity test of Ceriodaphnia survival. The procedure is simple and practical in concept and its computation is similar to Fisher's Exact Test, which EPA recommends for assessing Ceriodaphnia survival in effluent toxicity tests. The main drawback of contingency-based methods is that generating strong conclusions requires data from a large number of ambient tests at one or more reference sites.
Basically, the contingency-table method involves categorizing and tabulating Ceriodaphnia test results to reveal the distribution of survival values for ambient tests of water from several reference sites pooled through time. The distributions of the test outcomes can be used in two ways. First, they can be used as
TABLE 1 Distribution of Survival Values for Ceriodaphnia
a reference for identifying suspiciously low survival or mean reproduction values for tests of nonreference sites. Second, the distribution of survival values for reference-site tests can be compared formally with the distribution of survival values in control tests through application of an appropriate test (e.g., Chi-square).
Table 1 gives an example of the distribution of Ceriodaphnia survival values for controls and ambient tests of reference sites in three streams near the Oak Ridge National Laboratory. Inspection of this table shows that the distribution of Ceriodaphnia survival values in reference-site tests is very similar to their distribution in control water (diluted mineral water). Thus, the probability that a reference-site ambient-water test would yield a Ceriodaphnia survival value that is equal to or lower than 60 percent can be estimated as 100 x (1 case ÷ 121 cases) (see Table 1), or 0.008. Accordingly, if Ceriodaphnia survival is 50 percent in a 7-day test of water collected from a receiving stream, the low survival value is unlikely to be due to chance alone.
A contingency-table analysis method also could be used to establish a lower pass-or-fail criterion for Ceriodaphnia reproduction or fathead minnow survival or growth. Using data for reference sites in the three streams near Oak Ridge National Laboratory, we found that Ceriodaphnia mean reproduction values were less than or equal to 10 offspring per surviving female in only 6 of 121 tests (Table 2), or about 5 percent of the cases. Thus, one could use 10 offspring per surviving female as the lower-bound criterion for passing a Ceriodaphnia reproduction ambient toxicity test. However, within a given test, each surviving daphnid serves as a replicate and yields a value for reproduction. Replicate values are also available for fathead minnow survival and growth. The information from replicates permits the use of other, more powerful methods of analysis, such as ANOVA.
TABLE 2 Distribution of Ceriodaphnia Reproduction Values
Assessment of Concordance Patterns
The ANOVA and contingency-table methods described above consider responses of a particular species (e.g., Ceriodaphnia dubia or Pimephales promelas) separately, in relation to site. Ambient toxicity data may also answer the question, Are site-to-site differences in responses for one species similar to the site-tosite differences in responses for a second species? A similar spatial response pattern for two or more species strengthens the argument that biological water quality is site specific. It is intuitively clear that a strongly polluted site should adversely affect various species and that various species should do "better" in water that lacks pollutants. For 180 site and test-period combinations (15 sites, 12 test periods) of five receiving streams at Oak Ridge National Laboratory, we found that the correlation between Ceriodaphnia survival and fathead minnow survival was positive and significant (p < 0.0001); Ceriodaphnia reproduction and fathead minnow growth were also correlated, but less strongly (p = 0.026) (Stewart et al., 1990). This finding supports the idea that testing more than one species has some value and provides evidence for the notion that biologically significant differences in water quality may be revealed through assessment of concordance.
One simple method for using concordance ranks sites according to responses for each species separately, then tabulates the number of cases in which each site is best or worst for each species, for either species, or for both species together. Table 3 shows an example of this approach, using Ceriodaphnia and fathead minnow toxicity test results for eight test periods and six sites in East Fork Poplar Creek. In this example, no site stood out as being consistently better or worse in terms of fathead minnow growth or Ceriodaphnia reproduction. This analysis
showed no detectable longitudinal pattern to water quality in the stream, based on either fathead minnow growth or Ceriodaphnia reproduction in 7-day tests (Boston et al., 1993). Water from km 13.8 of East Fork Poplar Creek, however, appeared to be consistently better than water from the other sites: It was never the worst for either species and was the best for one or the other of the two species in six of the eight test periods.
Multivariate Analyses
The ANOVA, contingency-table, and concordance-pattern methods can be used to reveal biologically based water-quality differences among sites. A more powerful and predictive framework for the analysis of ambient toxicity test outcomes can be established by linking responses of the test organisms specifically to chemical measurements of water quality. Various statistical methods are available for this purpose. Examples of two such methods—principal components analysis followed by multiple regression analysis, and logistic regression—are summarized below.
Principal components analysis (PCA) and multiple regression analysis were used to inspect relationships between ambient toxicity test outcomes and chemical variables for 180 site and test-period combinations (15 sites each tested 12 times) in receiving streams near Oak Ridge National Laboratory (Stewart et al., 1990). Ceriodaphnia and fathead minnow larvae were tested concurrently in each test period. Chemical water-quality parameters measured for each site-date
TABLE 3 Results of Ambient Toxicity Tests of Water from Six Sites on East Fork Poplar Creek
|
|
Site |
|||||
|
Water Quality |
22.8 |
21.9 |
20.5 |
18.2 |
13.8 |
10.9 |
|
Best for minnow growth |
2 |
1 |
3 |
1 |
2 |
1 |
|
Best for Ceriodaphnia |
1 |
1 |
0 |
1 |
4 |
1 |
|
Best for both speciesa |
0 |
1 |
0 |
0 |
2 |
0 |
|
Best for either species |
3 |
2 |
3 |
2 |
6 |
2 |
|
Worst for minnow growth |
1 |
3 |
2 |
0 |
0 |
2 |
|
Worst for Ceriodaphnia |
2 |
1 |
1 |
3 |
0 |
2 |
|
Worst for both speciesa |
0 |
1 |
0 |
0 |
0 |
1 |
|
Worst for either species |
3 |
3 |
3 |
3 |
0 |
3 |
|
a In all cases Ceriodaphnia dubia and Pimephales promelas were tested concurrently. NOTE: Numerals specifying sites refer to distances (km) upstream from the confluence of East Fork Poplar Creek with the Clinch River. |
||||||
combination included pH, alkalinity, conductivity, hardness, and total residual chlorine (TRC). First, 7-day means for each water-quality factor were computed. PCA then was used to identify two orthogonal water-quality axes (axis I, associated primarily with hardness, conductivity, and pH; and axis II, strongly associated with TRC). The two axes accounted for 60.5 and 17.6 percent, respectively, of the total variance in the chemical data. Multiple regression analysis was then used to test relationships between the results of the ambient toxicity tests and the two principal component factors. This analysis showed that the fathead minnow survival and growth did not correspond well to any combination of the measured chemical variables and that the Ceriodaphnia test results related strongly to axes I and II. Mean survival of Ceriodaphnia was related strongly to axis II (p < 0.001) and secondarily to axis I (p = 0.101), whereas mean reproduction of Ceriodaphnia had strong relationships to both axes (axis I, p = 0.011; axis II, p = 0.019). The results of the PCA-multiple regression analyses suggested that TRC was a biologically significant contaminant whose presence strongly influenced Ceriodaphnia test outcomes.
We were able to draw two more conclusions from the study using other supporting analyses. First, for ambient assessments of water quality in these streams, Ceriodaphnia tests detected toxic conditions better than fathead minnow tests. This conclusion was supported by examination of R2 changes in ANOVAs of the Ceriodaphnia and fathead minnow tests in response to data pruning by date, as described above. Second, we were able to show that ambient toxicity dynamics in the Oak Ridge National Laboratory streams were dominated by episodic events that sometimes caused acutely toxic conditions at "poor quality" sites. Together, the three conclusions focused subsequent remediation activities and shaped the strategy for more cost-effective monitoring at the Oak Ridge National Laboratory. We began frequent testing to assess episodic events, but using Ceriodaphnia only for reasons of sensitivity and cost; we documented long-term improvements in water quality by monitoring biological and chemical conditions at the poor quality sites; to reduce costs, we halted testing at nonreference sites that have shown no evidence of toxicity; and we continue to conduct special studies and use diagnostic testing to better understand the fate and ecological effects of low concentrations of TRC.
Logistic regression analysis was used to relate chemical conditions to Ceriodaphnia mortality patterns in water samples from East Fork Poplar Creek. When using 7-day static-renewal toxicity test methods to assess ambient water quality, the water in the test chambers is replaced daily with freshly collected water. This procedure generates both an interesting challenge and a strong potential bias. The challenge is this: How should one best relate a time-varying exposure regime (e.g., daily changes in conductivity, pH, TRC) to a single, biologically integrated measure of "response" (e.g., Ceriodaphnia reproduction, expressed as a 7-day mean)? The potential bias also relates to the problem of time. The physicochemical characteristics of a sample of stream water may not
be representative of in situ physicochemical conditions because some parameters (such as pH level) can vary naturally over daily cycles, and others (such as conductivity) may change strongly in response to waste-water discharges. These two issues were explored by using Ceriodaphnia tests to evaluate water-quality conditions in upper East Fork Poplar Creek, where TRC was suspected of causing or contributing to fish kills. Logistic regression was used to relate TRC data to toxicity test outcomes (Stewart et al., 1996).
We first analyzed the chemical data (daily measurements of pH, conductivity, alkalinity, hardness, and TRC) for 169 site and test-period combinations (4 sites were tested over a 50-month period). For each water-quality factor, we computed a 7-day mean and an estimate of daily variability, referred to as semirange. Semirange was defined as a parameter's 7-day maximum (transformed) value minus the 7-day mean. For toxicity assessments, one advantage of semirange is that it quantifies excursions above the mean but ignores excursions below the mean. (Toxicologically, pollutant concentrations above the mean are likely to be more significant than those below.) We then used stepwise logistic regression to explore relationships between the 7-day mean and 7-day semirange values for the water-quality factors and Ceriodaphnia mortality. Both the proportion of animals dying in each test and the pass-or-fail outcomes (using 60 percent survival as the pass-or-fail criterion [see Table 1]) were assessed.
The results of these analyses showed that 7-day mean TRC concentration and TRC semirange both strongly affected Ceriodaphnia mortality (p < 0.0001 for each factor). With these two factors included, the logistic regression model correctly predicted the outcome (mortality or survival, expressed as a proportion of the animals tested in each test) in 89.3 percent of the cases. The model's false positive rate (when the model predicted mortality, but no mortality occurred) was 20 percent, and the model's false negative rate (no mortality was predicted by the model but the animal died) was 7 percent. Distilling a test's outcome to a passor-fail status using the criterion of 60 percent survival was a satisfactory simplification: Both TRC mean and semirange values were significant as explanatory factors (p < 0.0001 in each case, with 91.7 percent of the cases being predicted correctly by the model), and the model's false positive rate and false negative rates were low (15.2 and 5.7 percent, respectively).
Figure 3 is a schematic showing the generalized flow for Ceriodaphnia toxicity test data used in the statistical analysis methods described in this paper. Various data-checking steps cited for use in the effluent data flow path (e.g., inspection of variance for homogeneity [Figure 2]) are also appropriate when analyzing ambient toxicity test data, but these are not shown in Figure 3 for convenience.
Diagnostic Testing and Ambient Toxicity Monitoring
The logistic regression study described above also demonstrated that diagnostic or ''experimental" toxicity testing should be integrated into any ambient
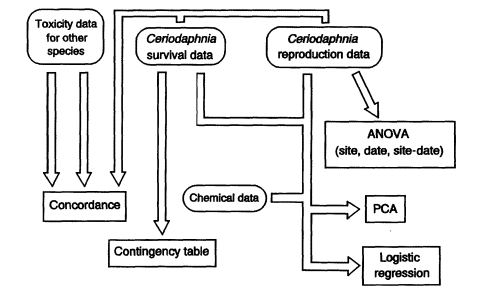
Figure 3
Generalized statistical analysis flow path for survival and reproduction data from Ceriodaphnia toxicity tests used for ambient water-quality monitoring (details provided in text).
toxicity monitoring program. Concurrent with the routine ambient toxicity monitoring tests for upper East Fork Poplar Creek, we conducted diagnostic toxicity tests to demonstrate that TRC (or related oxidants) accounted for the observed toxicity. In diagnostic testing, a specific treatment is imposed to alter water quality, and organisms' responses are compared statistically with those of the organisms in nontreated water to demonstrate causality. In the logistic regression study, diagnostic testing consisted of comparing responses of Ceriodaphnia in samples of dechlorinated water to nontreated water (daily renewal of water in both cases), with dechlorination using small quantities of sodium thiosulfate. Other treatments used in diagnostic ambient testing include adding metal-complexation agents (e.g., ethylenediaminetetraacetic acid); filtering to remove particulate matter; exposing the water to strong ultraviolet light to alter photosensitive chemicals or kill bacteria; aerating the water; adjusting the pH; and passing the water through a column of activated carbon. The results of the side-by-side tests of treated and nontreated water samples can be analyzed easily and effectively by ANOVA, with separate test periods serving as replicates. Examples of effective application of diagnostic experiments conducted to support ambient water-quality assessments are provided in studies by Kszos and Stewart (1992), Kszos et al. (1992), Nimmo et al. (1990), and Stewart et al. (1996).
Artifacts in Ambient Testing
Factors other than toxicants can affect fathead minnow survival and growth and Ceriodaphnia survival and reproduction in ambient waters. Growth of minnow larvae in laboratory tests, for example, is affected by concentrations of common salts, and survival of the larvae in ambient waters from relatively pristine streams can be low and variable due to the presence of pathogenic microorganisms (Kszos et al., 1997). Ceriodaphnia reproduction is commonly greater in ambient water than in diluted mineral-water controls, due to the nutritional benefits they derive from consuming naturally occurring particulate matter, but some naturally occurring algae can be toxic (Reinikainen et al., 1994). These situations make it inadvisable to compare the results of ambient tests only with diluted mineral water controls to determine if an ambient site is toxic or nontoxic. Comparison with an appropriate suite of reference sites is critical to derive the correct answer for the correct reasons. In ambient toxicity testing, and in biological monitoring generally, one must be constantly alert to the difference between biological importance and statistical significance (Cairns and Smith, 1994; Yoccoz, 1991).
Path Forward
New and potentially useful ambient assessment procedures are being developed at a rapid pace; innovations in biological monitoring occur more slowly; slower still is the rate at which field-validated bioassessment methodology is being incorporated and used in a regulatory framework (see, for example, Hart, 1994). Examples of rapid progress in bioassay development can be found in both the water- and the soil-assessment arenas. A 3-day laboratory test that uses snail feeding rate to evaluate water quality appears to be about as sensitive as a 7-day Ceriodaphnia test, at least for some kinds of contaminants (R. L. Hinzman, Environmental Sciences Division, Oak Ridge National Laboratory, unpublished data). Procedures for estimating the toxicity of sediments with laboratory tests using invertebrates are nearing readiness for regulatory use (American Society for Testing and Materials, 1991). Methods for laboratory tests designed to estimate the toxicity of soils are being revised, calibrated, and field validated (L. F. Wicker, Environmental Sciences Division, Oak Ridge National Laboratory, unpublished data).
The increasing use of ecological risk assessment methodology for regulatory purposes drives the need not only for faster and more cost-effective laboratory tests, but also for data that accurately reflect exposure regimes and reveal ecological effects in the field. In situ test procedures using caged or noncaged organisms are in various stages of development and validation for terrestrial (Callahan et al., 1991; Menzie et al., 1992) and aquatic environments (Napolitano et al., 1993). Aquatic (Graney et al., 1994) and terrestrial (Gunderson et al., 1997; Parmalee et al., 1993) mesocosm studies are key to the development of in situ test
methods that ultimately will be required for effective use of ecological risk-assessment methodology. Despite their limitations, simple laboratory tests, such as the Ceriodaphnia dubia and Pimephales promelas tests described in this paper, are likely to be relied on more and more. This is because the need for data that can be used for ecological risk assessments grows much faster than the rate at which regulatory agencies approve new methods for assessing the environment.
Conclusions
Standardized tests designed to estimate the toxicity of effluents to aquatic biota can, with minimal modification, also be used to assess ambient water-quality conditions in receiving streams. However, ambient tests should not be analyzed statistically in the same way as effluent tests. Site and test-period combinations, rather than effluent concentrations, serve as the principal unit of assessment for ambient toxicity test results. In addition, the results of ambient tests are in many cases more appropriately compared with the results of reference-site tests than with negative controls, which are commonly included with effluent tests. These considerations shape the strategy for cost-effective use of ambient toxicity testing. The value of ambient toxicity testing increases if the tests are used to support a broader-based, long-term biological monitoring program; conducted frequently with one sensitive species, rather than more often with two or more species; and accompanied by a diagnostic ("experimental") toxicity testing program. Data pruning by date can be used to help identify sites where water quality is suspect, and a representative suite of reference sites should be included in every ambient testing program to help place suspect sites into appropriate perspective. Specific linkages between ambient toxicity test results and chemical conditions at the test site are extremely desirable and can be revealed using methods such as PCA or logistic regression. The long-term prognosis is that in situ testing will replace the ambient toxicity testing procedures now in use. However, requirements for data that can be used in ecological risk assessments are likely to grow much faster than the rate of approval for in situ test methods for regulatory purposes. Thus, the next decade is likely to bring a marked increase in ambient testing with EPA-approved static-renewal laboratory procedures using organisms such as Ceriodaphnia and fathead minnow larvae.
Acknowledgments
This paper was improved through reviews and comments provided by T. L. Ashwood and T. L. Phipps and was made possible by technical contributions from members of the Biomonitoring Group, including L. A. Kszos, T. L. Phipps, L. F. Wicker, P. W. Braden, G. W. Morris, B. K. Beane, L. S. Ewald, J. R. Sumner, K. J. McAfee, and W. S. Session. Oak Ridge National Laboratory is managed for the U.S. Department of Energy by Lockheed Martin Energy Research Corp. un-
der contract DE-AC05-96OR22464. The Oak Ridge Y-12 Plant is managed for the U.S. Department of Energy by Lockheed Martin Energy Systems, Inc., under contract DE-AC05-84OR21400.
References
American Society for Testing and Materials. 1991. Standard Guide for Conducting Sediment Toxicity Tests with Freshwater Invertebrates. Philadelphia, Pa.: American Society for Testing and Materials.
Boston, H. L., W. R. Hill, and A. J. Stewart. 1993. Toxicity monitoring. Pp. 37-108 in Second Report on the Oak Ridge Y-12 Plant Biological Monitoring and Abatement Program for East Fork Poplar Creek, R. L. Hinzman, ed. Y/TS-888. Oak Ridge, Tenn.: Environmental Sciences Division, Oak Ridge National Laboratory.
Boston, H. L., W. R. Hill, L. A. Kszos, C. M. Pettway, and A. J. Stewart. 1994. Toxicity monitoring. Pp. 27-63 in Fourth Report on the Oak Ridge National Laboratory Biological Monitoring and Abatement Program for White Oak Creek and the Clinch River, J. M. Loar, ed. ORNL/TM11544. Oak Ridge, Tenn.: Environmental Sciences Division, Oak Ridge National Laboratory.
Cairns, J., Jr., and E. P. Smith. 1994. The statistical validity of biomonitoring data. Pp 49-68 in Biological Monitoring of Aquatic Systems, S. L. Loeb and A. Spacie, eds. Boca Raton, Fla.: Lewis Publishers.
Callahan, C. A., C. A. Menzie, D. E. Burmaster, D. C. Wilborn, and T. Ernst. 1991. On-site methods for assessing chemical impact on the soil environment using earthworms: A case study at the Baird & McGuire Superfund Site, Holbrook, Massachusetts. Environmental Toxicology and Chemistry 10:817-826.
Graney, R. L., D. H. Kennedy, and J. H. Rodgers, eds. 1994. Aquatic Mesocosm Studies in Ecological Risk Assessment. Boca Raton, Fla.: Lewis Publishers.
Gunderson, C. A., J. M. Kostuk, M. H. Gibbs, G. E. Napolitano, L. F. Wicker, J. E. Richmond, and A. J. Stewart. 1997. Multispecies toxicity assessment of compost produced in bioremediation of an explosives-contaminated sediment. Environmental Toxicology and Chemistry 16(12):2529-2537.
Hart, D. D. 1994. Building a stronger partnership between ecological research and biological monitoring. Journal of the North American Benthological Society 13:110-116.
Kooijman, S. A. L. 1996. An alternative for NOEC exists, but the standard model has to be abandoned first. Oikos 75:310-316.
Kszos, L. A., and A. J. Stewart. 1992. Artifacts in ambient toxicity testing. Paper AC92-020-005 in Proceedings of the Water Environment Federation, 65th Annual Conference and Exposition, New Orleans, La., September 20-24.
Kszos, L. A., A. J. Stewart, and P. A. Taylor. 1992. An evaluation of nickel toxicity to Ceriodaphnia dubia and Daphnia magna in a contaminated stream and in laboratory tests. Environmental Toxicology and Chemistry 11:1001-1012.
Kszos, L. A., A. J. Stewart, and J. R. Sumner. 1997. Evidence that variability in ambient fathead minnow short-term chronic tests is due to pathogenic infection. Environmental Toxicology and Chemistry 16:351-356.
Menzie, C. A., D. E. Burmaster, J. S. Freshman, and C. A. Callahan. 1992. Assessment of methods for estimating ecological risk in the terrestrial component: A case study at the Baird & McGuire Superfund Site in Holbrook, Massachusetts. Environmental Toxicology and Chemistry 11:245-260.
Mount, D. I., and T. J. Norberg. 1984. A seven-day life-cycle cladoceran toxicity test. Environmental Toxicology and Chemistry 3:425-434.
Napolitano, G. E., W. R. Hill, J. B. Guckert, A. J. Stewart, S. C. Nold, and D. C. White. 1993. Changes in periphyton fatty acid composition in chlorine-polluted streams. Journal of the North American Benthological Society 13:237-249.
Nimmo, D. R., M. H. Dodson, P. H. Davies, J. C. Greene, and M. A. Kerr. 1990. Three studies using Ceriodaphnia to detect nonpoint sources of metals from mine drainage. Journal of the Water Pollution Control Federation 62:7-15.
Norberg, T. J., and D. I. Mount. 1985. A new subchronic fathead minnow (Pimephales promelas) toxicity test. Environmental Toxicology and Chemistry 4:711-718.
Parmalee, R. W., R. S. Wentsel, C. T. Phillips, M. Simini, and R. T. Checkai. 1993. Soil microcosm for testing the effects of chemical pollutants on soil fauna communities and trophic structure. Environmental Toxicology and Chemistry 12:1477-1486.
Reinikainen, M., M. Ketol, and M. Walls. 1994. Effects of the concentrations of toxic Microcystis aeruginosa and an alternative food on the survival of Daphnia pulex. Limnology and Oceanography 39:424-432.
SAS Institute. 1985. SAS User's Guide: Statistics. Version 5. Cary, N.C.: SAS Institute.
Stewart, A. J. 1996. Ambient bioassays for assessing water-quality conditions in receiving streams. Ecotoxicology 5:377-393.
Stewart, A. J., and L. A. Kszos. 1996. Caution on using lithium (Li+) as a conservative tracer in hydrological studies. Limnology and Oceanography 41:190-191.
Stewart, A. J., and J. M. Loar. 1994. Spatial and temporal variation in biomonitoring data. Pp. 91-124 in Biological Monitoring of Aquatic Systems, S. Loeb and A. Spacie, eds. Boca Raton, Fla.: Lewis Publishers.
Stewart, A. J., W. R. Hill, K. D. Ham, S. W. Christensen, and J. J. Beauchamp. 1996. Chlorine dynamics and ambient toxicity in receiving streams. Ecological Applications 6:458-471.
Stewart, A. J., L. A. Kszos, B. C. Harvey, L. F. Wicker, G. J. Haynes, and R. D. Bailey. 1990. Ambient toxicity dynamics: Assessments using Ceriodaphnia dubia and fathead minnow (Pimephales promelas) larvae in short-term tests. Environmental Toxicology and Chemistry 9:367-379.
Taylor, P. A. 1993. An evaluation of the toxicity of various forms of chlorine to Ceriodaphnia dubia. Environmental Toxicology and Chemistry 12:925-930.
Weber, C. I., W. H. Peltier, T. J. Norberg-King, W. B. Horning II, F. A. Kessler, J. R. Menkedick, T. W. Neiheisel, P. A. Lewis, D. J. Klemm, Q. H. Pickering, E. L. Robinson, J. M. Lazorchak, L. J. Wymer, and R. W. Freyberg. 1989. Short-Term Methods for Estimating the Chronic Toxicity of Effluents and Receiving Waters to Freshwater Organisms, 2nd ed. EPA/600/4-89/001. Cincinnati, Ohio: U.S. Environmental Protection Agency.
Yoccoz, N. G. 1991. Use, overuse, and misuse of significance tests in evolutionary biology and ecology. Bulletin of the Ecological Society of America 72:106-111.


















