Life-Cycle Analysis: The Role of Evaluation and Strategy
Frank R. Field III and John R. Ehrenfeld
Life-cycle analysis (LCA) has become one of the most actively considered techniques for the study and analysis of strategies to meet environmental challenges. The strengths of LCAs derive from their roots in traditional engineering and process analysis. Also vital is the technique's recognition that the consequences of changes in technological undertakings may extend far beyond the immediate, or local, environment. A technological process or a change in process can produce a range of consequences whose impacts can only be perceived when this entire range is taken into consideration. The application of LCA promises to change the treatment of environmental considerations within the larger concerns of modern technological society. However, as the technique becomes more popular, it is becoming clear that some of the problems LCA is expected to solve lie outside its practical and conceptual boundaries.
Potential users of this technique span a wide spectrum of interests. Process and product developers view LCA as a way to incorporate environmental considerations into their design process, making it possible to anticipate and avoid potential pitfalls. Consumers and consumer interest groups see LCA as a way to better inform the customer of the relative environmental impact of alternative products, hoping to bring market pressures to bear on producers. Finally, regulators and policy makers see LCA as a tool to guide the development of environmental policy and also provide a mechanism to enforce legislative objectives.
The development of LCA arose largely from the need for tools that take account of the growing social importance of environmental objectives. The market, the principal way in which consumer interests are translated into technological action, currently does not supply consumers with environmentally relevant information. The complexity of the modern industrial economy makes it difficult
to know how any individual action affects the environment. LCA is being developed to produce a framework within which this information can be collected, refined, and acted on.
However, analysis of any kind is limited in its ability to resolve complex problems, particularly when an action has consequences that advance some objectives while hindering others. Under these conditions, the choice among alternatives must incorporate not only analytical elements, but strategic ones as well. LCA is well suited to supplying the former but not the latter.
Life-Cycle Analysis
The basic objective of LCA is to guide decision makers, whether consumers, industrialists, or government policy makers, in devising or selecting actions that will minimize environmental impacts while furthering other objectives. Decision makers must use this tool in concert with traditional criteria for selecting one action over another, including economic, engineering, and social goals.
The life-cycle paradigm requires the consideration not only of the immediate impacts of a product or process choice, but also of the products and processes that gave rise to that choice and of those that occur in response to it. This view reflects the notion that "industrial ecosystems," like natural ecosystems, are vast networks of interconnected activities. In such networks, the size of a particular change does not necessarily indicate the scope of its effect, and care must be taken to avoid changes that maximize local benefits at the expense of global effects.
LCA is a three-step process:
- inventory analysis, or the identification and quantification of energy and resource use and environmental releases to air, water, and land;
- impact analysis, or the technical qualitative and quantitative characterization and assessment of the consequences of resource use and environmental releases for the environment; and
- improvement analysis, or the evaluation and implementation of opportunities to reduce environmental burdens (Vigon et al., 1993).
The three stages of LCA reflect classical technical decision-making procedures. In each case, a control volume is identified. Resource flows into the control volume and waste emissions from the control volume are then measured. The next step is to determine the relationship between these resource and waste fluxes and the underlying scientific and technological principles. Finally, the problem is resolved based on the insight gained from these principles and the objectives of the analyst.
Much of the focus on LCA has been on how and why it is used. Organizations such as the Society of Environmental Toxicology and Chemistry and the
U.S. Environmental Protection Agency (EPA) have worked to develop a complete set of procedures to use in collecting and organizing the information that must be developed in the course of an LCA (Fava et al., 1990; Vigon et al., 1993). However, many observers remain uncertain about what to do with this information once it is collected. Expressed simply, LCA is a tool for enhancing positive environmental impacts.
Unfortunately, except in the simplest of situations, it is extremely difficult to determine how this general objective informs specific problems—a fact that increasing numbers of LCA practitioners recognize. This difficulty arises from several sources. The most apparent of these is the imperfect understanding of the relationship between releases to the environment and environmental damage, particularly when many such releases must be considered together. However, this limitation apparently has not inhibited the development and application of LCA methodology.
Improvement analysis has proved to be the most complicated aspect of LCA. Improvement analysis assumes that it is possible to discern the best action from a set of possible options. In simple cases, it may be possible to find an action that reduces all impacts on the environment. More often, the best course of action requires an assessment of the relative importance of each of a number of possible consequences. These relative importances reflect the strategic objectives that underlie the problem being considered rather than the results of any purely analytical evaluation. Because of this distinction, substantial hurdles must be overcome before LCA can be applied to broad questions of industrial and social policy.
Review of Valuation Concepts
This difficulty can be best understood by considering the general problem of valuation (see Goicoechea et al., 1982). Figure 1 depicts a hypothetical set of potential alternatives, each of which has (for the sake of illustration) only two characteristic environmental impacts, A and B. Assuming that only one alternative can be chosen, and that the objective is to reduce environmental impact, which alternative should be implemented?
It is easy to reject alternatives 2 and 3, because other choices exist (alternative 7, for example) that reduce impact A and impact B. Alternatives 2 and 3 are members of what is known as the dominated set of alternatives; they are clearly inferior to others. In environmental terms, rejection of the dominated alternatives is an expression of the so-called precautionary principle, which favors taking any action that unequivocally reduces all environmental impact. Similarly, an LCA that showed a facility operating at point 3 would lead to the implementation of an alternative (5 or 6) that reduces all impacts on the environment.
The difficulty arises when a choice must be made among alternatives on the lower edge of the frontier. Which one of these is the best way to operate? Decision analysis refers to these remaining points as the set of nondominated alterna-
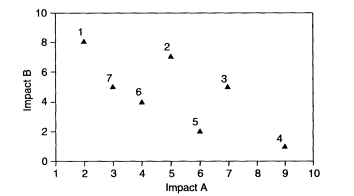
Figure 1
Hypothetical set of potential alternative technologies or procedures, each of which has only two characteristic environmental impacts, A and B. Decision analysis refers to the points 1, 4, 5, 6, and 7 as the set of nondominated alternatives. No member of the set is better than the others in all respects.
tives, meaning that no member of the set is better than the others in all respects. Rather, some are better in one or more aspect but worse in at least one other.
How best to select among members of the nondominated set of alternatives is one of the central questions of decision analysis and is frequently referred to as multiple-objective decision making. In multiple-objective decision making, there is no generally applicable rationale for selecting one alternative over the other; rather, the choice requires taking into account strategies and priorities. As Figure 1 shows, the only supportable reason for selecting alternative 6 over 5 is that reducing impact A is more important than reducing impact B.
In decision analysis, the simplest method for selecting from the nondominated set is to identify specific limits that either must be met or cannot be exceeded. When such constraints are imposed, the set of alternatives can be reduced, as shown in Figure 2. This approach mirrors the traditional command-and-control environmental regulatory model. However, it has important limitations when applied to environmental impact and LCA. The most obvious is that it is almost impossible to establish these limits for every potential impact. In addition, the figure illustrates a more subtle, and potentially more troubling, limitation. Note that alternative 7 is rejected in favor of alternative 6, even though the differences in impact B between the two are relatively small, whereas the differences in terms of A are relatively large. Is it really worthwhile to sacrifice the potential gains in terms of A that alternative 7 represents merely because it barely fails to meet the fixed limit on impact B?
The use of value functions overcomes this limitation of simple constraint-setting (or screening) methods of decision making. These functions represent
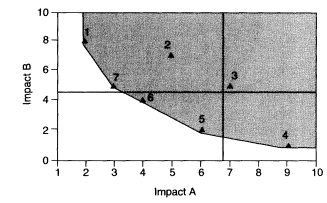
Figure 2
Hypothetical set as in Figure 1 with the addition of a line connecting the set of nondominated alternatives and vertical and horizontal lines denoting hypothetical maximum limits (e.g., regulatory limits) for impacts A and B.
preferences among the several attributes that form the basis for the decision (in this case, impacts A and B). The simplest form of a value function is represented in the top panel of Figure 3, the linear index. Essentially, this index estimates a measure of value by constructing a weighted average of the (two) criteria. The option yielding the best average value is selected. Alternatively, a nonlinear value function can also be constructed, as shown in the bottom panel. This value function can represent such observed preference behavior as saturation (i.e., attaining better levels of one attribute reduces the incremental value of further improvement) and variable rates of transformation among attributes.
The linear index method is directly analogous to the concept of monetization, the transformation of attributes into their dollar equivalents. (See, for example, the Swedish Environmental Priority Strategies (EPS) system [Steen and Ryding, 1992].) The straight line depicted in Figure 3 can then be thought of as a ''budget" for environmental damage. Alternatively, the nonlinear preference function methods directly represent the consumer economist's classical notion of cardinal utility, where the curved line represents a line of constant utility. The curved line in Figure 3 then represents all combinations of environmental damage from A and B that leave the observer equally well (or poorly) off.
As the figures demonstrate, both of these value functions establish that an alternative exists that is demonstrably the "best"; the point of tangency between the line or curve of constant value and the gray area is the alternative that yields the best combination of characteristics. Although establishing a best alternative in the real world requires considering a much larger set of attributes, the conceptual basis remains the same.
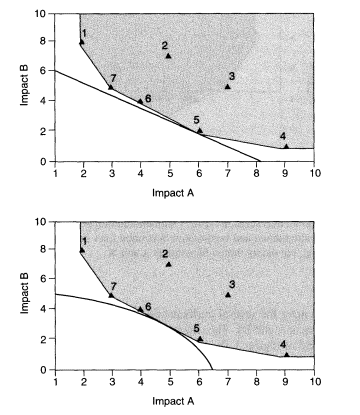
Figure 3
Hypothetical set as in Figure 2 with maximum-limit lines removed and lines added that represent alternative linear and nonlinear value functions. Each line connects points of equal value based on combinations of the two impacts.
Environmental Impact Assessment in Life-Cycle Analysis
This review of decision analysis suggests that users of LCA will face two clear-cut classes of problems in the final improvement-analysis stage of LCA where environmental impacts are assessed. In one class, the analyst will be confronted with the choice among several alternatives, one of which clearly dominates. This situation is analogous to choosing between an alternative that lies within the gray area in Figure 3 and another that lies on the lower edge of that area; that is, it is a choice between a nondominated and a dominated alternative. In this case, assuming the LCA treats the complete scope of environmental consequences, it will have revealed that one alternative has better environmental per-
formance in all aspects. For the rational decision maker facing this class of problem, LCA will have unquestionably made the choice easier.
The second class of problems, however, will be much more difficult to resolve. In this situation, the two possible alternatives both lie on the lower edge of the gray area; that is, the choice will be between two nondominated alternatives. The analyst therefore cannot resolve the problem without the application of some value function, which itself must represent the strategic interests of the community that the analyst is attempting to serve.
In these cases, establishing the relevant value functions will be a crucial element of the improvement analysis. Individuals and probably many firms can develop these functions using a variety of techniques and appropriately structuring the decision problem (Dyer and Forman, 1992; Keeney and Raiffa, 1976). However, substantial complexities are associated with a wider application.
The Swedish EPS system illustrates both the potential and the limitations of valuation methods when applied in such complex situations. This system, developed specifically with LCA in mind, employs monetization to establish the value of alternatives. Its application is currently being evaluated and endorsed by the Volvo Car Corp., among other companies. (For a complete treatment of this method, consult the references at the end of this paper.)
Linear Valuation: The Environmental Priority Strategies System
The EPS system is under development by the Swedish Environmental Research Institute, Chalmers Institute of Technology, and the Federation of Swedish Industries (Steen and Ryding, 1992). The system is designed as a tool for evaluating the ecological consequences of alternative activities or processes and ultimately for generating a value for the various changes to the environment induced by these activities.
The EPS system is specifically constructed to associate an environmental load with individual activities or processes, based on materials consumed or processed per unit. For example, EPS might associate X number of environmental load units (ELUs) per kilogram of steel produced and Y ELU per kilogram of steel components stamped. Thus, the environmental load of stamping a 5-kg automobile component, requiring 5.3 kg of steel, would be 5.3 X + 5 Y. This result could then be compared with the load associated with a different process or the use of a different material. The interesting questions are: How are these environmental loads established? and What do they mean?
Based on the environmental objectives of the Swedish Parliament, the EPS system relates all of the physical consequences of the processes under consideration to their impact on five environmental safeguard subjects: biodiversity, production (growth and reproduction of nonhuman organisms), human health, resources, and aesthetic values. Because a process may affect any one safeguard
subject in several forms, EPS allows for the individual consideration of each of these consequences, called unit effects. Two criteria are applied when establishing which impacts will become unit effects: How important the impact is on the sustainability of the environment; and is it possible to establish a quantitative value for that impact within traditional economic grounds. Examples of unit effects for human health include mortality due to increased frequency of cancer, mortality due to increased maximum temperatures, and decreases in food production (and hence increased incidence of starvation) due to global warming.
Once the individual unit effects are established, their values must be determined. This is accomplished by expressing each unit effect in terms of its economic worth and associated risk factors. Formally, the value of each unit effect is equal to the product of five factors, F1 through F5. F1 is a monetary measure of the total cost of avoiding the unit effect. The extent of the affected area (F2), how frequently the unit effect occurs in the affected area (F3), and the duration of the unit effect (F4) represent risk factors similar to those used in toxicological risk evaluations. F5 is a normalizing factor, constructed so that the product F1 x F5 equals the cost of avoiding the unit effect that would arise through the use or production of one kilogram of material. The product of all five factors yields the contribution of a particular unit effect to environmental load. Summing the values of each unit effect yields the environmental load index (ELI) in units of environmental load per unit of material consumed or processed (ELU per kilogram), as summarized in Figure 4. Because these unit effects were specified according to their relevance to the five safeguard subjects, the ELI represents the total environmental load (or impact) for all five safeguard subjects.
For example, consider Table 1, which illustrates how to estimate the ELI for the release of carbon monoxide (CO) to the air. The second and third columns of data demonstrate how the impact of two specific unit effects, nuisance and morbidity, are incorporated into the overall ELI for a CO release to air. Based on a variety of studies, the value of excess nuisance and morbidity are estimated at 102 and 105 ELU/person-year, respectively. (Note that according to the definition of Fl, these values are the estimated costs, in ELUs, of avoiding these unit effects.) Furthermore, the incidence of these impacts is estimated for the world urban population, assuming that hazardous levels of CO occur only 10 percent of the time, and that 10 and 0.1 percent, respectively, of the exposed population is affected at the nuisance or morbidity level. Finally, given that 1,600 million metric tons of CO are already being released, the incremental effect of one additional kilogram released is 1/1,600,000,000,000, the F5 term. These terms, F1-F5, are multiplied together and then summed over all unit effects to develop the ELI for CO release to the atmosphere, in ELUs per kilogram released. With this number, any life-cycle data that reveal the release of some amount of CO can be valued by multiplying that release by the ELI. The EPS system is designed to develop ELIs for all releases, as well as for all human activities that consume resources, so that the relative ELUs for any two life-cycle inventories can be computed and compared.
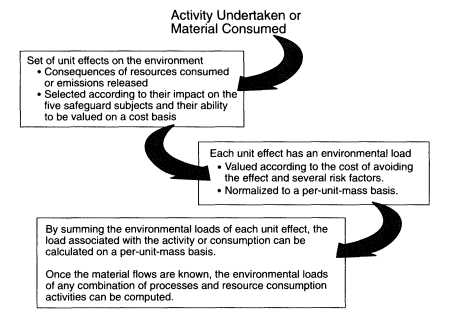
Figure 4
Flow chart summarizing the procedures used in the Environmental Priority Strategies (EPS) system. SOURCE: Steen and Ryding (1992).
Valuation Issues Raised by the Environmental Priority Strategies System
This formulation of valuation raises important questions of scientific feasibility. Indeed, it is debatable whether it is possible to characterize fully the unit effects of every process or activity that might be developed. However, the crucial valuation questions arise from two other aspects of this scheme: the nature of the economic measures used in calculating the cost of avoiding a unit effect and the assumption that the value of the total environmental impact of an action (the environmental load) is equal to the sum of each individual environmental load weighted by the size of each unit effect.
The first of these questions relates to the distinction between cost and worth. Although the theory of competitive markets argues that prices are an object's worth, the theory rests on assumptions that are difficult to support in the case of the environment. The first problem is that perfect markets assume that perfect information is available to all participants, which clearly is not the case. Furthermore, the theory of markets routinely discusses "consumer surplus," which can roughly be determined as the difference in the prevailing market price and the
TABLE 1 Calculation of Environmental Load Index (ELI) for 1 kg of CO Released to the Air
|
Unit Effect |
Nuisance |
Morbidity |
CO2 Effect |
Oxidant Effects |
|
Safeguard subject Impact measure |
Human health CO concentration |
Human health CO concentration |
All 5 CO2 equivalents |
All 5 Ethylene equivalents |
|
Fl, value |
100a |
100,000a |
0.08887b |
0.0005b |
|
F2, persons affected |
750,000,000c |
750,000,000c |
1 |
1 |
|
F3, frequency or intensity |
O.1d |
0.001d |
3e |
3e |
|
F4, duration |
0.01f |
0.01f |
1 |
1 |
|
F5, contribution to total effect |
6 x 10-13g |
6 x 10-13g |
1 |
1 |
|
ELI contribution |
0.000045 |
0.00045 |
0.266202 |
0.0015 |
|
ELI for 1 kg of CO released to the air |
|
0.27 |
||
|
a Fl values for the first two unit effects reflect the assessment that the value of "moderate nuisance" is 102 ELU/person-year and that of "painful morbidity and/or severe suffering" is 105 ELU/person-year. b Because CO has impacts similar to those of CO2 and ethylene, the ELIs for these two species are given in the last two columns of the F1 row. By definition, the ELI already aggregates the impact over all pertinent safeguard subjects. c The F2 value is the scope of the effect; in this case, an estimated one-third of the global urban population (~2,280 million) is exposed to excessive CO concentrations 1 percent of the time. d The F3 values represent World Health Organization estimates that 10 and 0.1 percent of those exposed to concentrations of CO above recommended levels are affected at the nuisance or morbidity level, respectively. e The magnitude of the impact of CO is estimated at three times the impact of CO2 and ethylene, so the F3 term is 3. Other terms are set to 1, because these other effects have already been captured in the ELIs of the equivalent chemicals f The F4 values represent estimates that critical levels of exposure to CO are experienced 1 percent of the time. g The F5 values represent the incremental effect of 1 kg of CO released. Because global human- caused releases of CO are estimated at 1,600 million metric tons/yr, the incremental impact of 1 kg released is 6.25 x 10-13. SOURCE: Steen and Ryding (1992). |
||||
higher price that some consumers would have been willing to pay (recall that demand curves slope downward). Finally, there is the critical question of how to establish these costs and prices when markets do not exist. Although litigators are prepared to place a value on wrongful death or pain and suffering during a civil suit, no markets exist for pain, clean air, or future well-being. Generally, most environmental attributes are external to markets; many of the classical examples of market externalities are based on environmental issues.
Where markets exist, EPS uses market prices to establish the costs of avoidance. Where market prices do not exist, EPS relies on two alternatives. If gov-
ernment funds are allocated to resolve specific problems (for example, to protect a particular species), these funds are normalized and extrapolated to obtain a cost figure; in this case, the value of maintaining biodiversity is established by normalizing the government's annual budget for species protection. If no funds have been allocated, then the method of contingent valuation is employed. This method (or set of methods) is based on direct inquiries of representative populations to determine their willingness to pay to avoid specific effects. As might be expected, this last approach to establishing the appropriate costs of avoidance is controversial because it is hard, both conceptually and practically, to design questions that demonstrably extract the correct measure of value.
The second of these valuation questions reflects the fact that the mathematical structure of the value function is a consequence of critical assumptions about the nature of the subject's preferences. The valuation used in the EPS system is an example of a linear, additive preference structure. Each unit effect is reduced to a monetary value, normalized for risk and exposure and for material quantity. Thereafter, the net impact of each increment in unit effect is the same, regardless of both how large the effect is and the size of any other unit effect. Although such value functions are simple to represent and employ (i.e., as linear combinations of linear functions), they are not the most accurate, general-purpose formulation of value functions for environmental impact. Although the appropriate form of the value function may be linear, EPS does not explicitly make this assumption. Rather, the linearity of the EPS valuation is based on the assumption that, because monetization reduces all effects to a common metric, the resulting metrics should be additive. In fact, most individuals do not even exhibit linear preferences for money, much less for more subjective attributes. (For example, most individuals would consider paying $0.50 to play a game offering a 50:50 chance of winning $1.00, while rejecting out of hand paying $5,000 for a 50:50 chance of winning $10,000.) In practice, preferences usually reflect nonlinearities both in individual effects and in substitution between effects.
A Third Limitation: Individuals Versus Groups
Viewing money as a measure of value and calculating linear additive preferences are not necessarily unworkable approaches when considering the development of value functions for the environment. Although difficult, it may be possible for someone to establish the dollar value that exactly offsets a particular unit effect. Similarly, linear additive preferences may be able to model the behavior of an individual over a restricted range. However, it is impossible to state that every individual in the affected population will agree to the same dollar value or the same summing of preferences for environmental considerations. If individuals cannot agree on the value or the structure of their preferences, then no single value function can be constructed to represent their wants.
Conceptually, value functions are based on the notion of individual prefer-
ence, reflecting strategic objectives. Value functions assume that, given two alternatives, the individual decision maker can say one of two things about them: one alternative is better than the other, or both alternatives are equally good.
The assumptions underlying the concept of value functions are particularly weak when considering the problem of establishing group preferences for environmental attributes. There are two reasons for this. First, to choose between two or more alternatives, the implications of the choice must be fully understood. Otherwise, the choice is meaningless and essentially random. When experts cannot establish the incremental effects of the potential changes in environmental release and resource consumption of two or more alternatives, it is virtually impossible to expect these experts, much less the public at large, to say that one is preferable to the other. Second, even if all the implications of each choice were characterized to the complete satisfaction of all members of the group, individuals still do not have a consistent set of objectives when confronted with environmental choices. For example, some might believe that preventing global warming is more important than reducing urban air pollution, whereas others might think that neither of these objectives is as important as maintaining and improving human health. This lack of a consistent set of priorities in the environmental area essentially eliminates the possibility of constructing a useful value function.
Although the EPS system is a commendable attempt at simplifying the enormous detail of inventory data, the system's developers have pointed out that it is based on their subjective value judgments, which are not necessarily supportable in all situations worldwide. The goals set out by the Society of Environmental Toxicology and Chemistry and the EPA for improvement analysis based on life-cycle inventories are laudable, but they can only be realized by some type of consensus on the value of avoiding environmental degradation.
This suggests that achieving the final stage of LCA will require the development of a basis for devising (and revising) this consensus. In the absence of a common strategic objective, it will be impossible to use LCA to designate ways to achieve environmental improvement beyond straightforward strategies for pollution prevention or the use of precautionary principles. A strategic consensus is required to trade off competing environmental, economic, and engineering goals.
Summary
LCA is a technique that has already shown great promise for improving our understanding of the wider implications and relationships that must be taken into consideration when incorporating environmental concerns into technical decision making. As these concepts diffuse into industrial and technical decision making, LCA will enable industry and government to find ways to both increase efficiency and reduce harm to the environment.
However, practitioners and proponents must guard against using LCA to de-
termine "best" modes of action when the consequences of the alternatives expose conflicting objectives and values within the group of decision makers. In these cases, no amount of analysis will directly resolve the conflict. Rather, the role of LCA should be to clearly articulate the consequences of each alternative and to provide a framework for the necessary negotiations.
References
Dyer, R. F., and E. H. Forman. 1992. Group decision support with the analytic hierarchy process. Decision Support Systems 8:99-124.
Fava, J. A., R. Denison, B. Jones, M. Curran, B. Vigon, S. Selke, and J. Barnum, eds. 1990. A Technical Framework for Life-Cycle Assessments: Workshop Report. Society for Environmental Toxicology and Chemistry, Foundation for Environmental Education. Smuggler's Notch, Vt., August 18-23, 1990.
Goicoechea, A., D. R. Hansen, and L. Duckstein. 1982. Multiobjective Decision Analysis with Engineering and Business Applications. New York: John Wiley & Sons.
Keeney, R. L., and H. Raiffa. 1976. Decisions with Multiple Objectives: Preferences and Value Tradeoffs. New York: John Wiley & Sons.
Steen, B., and S. O. Ryding. 1992. The EPS Enviro-Accounting Method: An Application of Environmental Accounting Principles for Evaluation and Valuation of Environmental Impact in Production Design. IVL Report B 1080. Göteborg, Sweden: Swedish Environmental Research Institute.
Vigon, B. W., D. A. Tolle, B. W. Cornaby, H. C. Lathan, C. L. Harrison, T. L. Boguski, R. G. Hunt, and J. D. Sellers. 1993. Life-Cycle Impact Assessment: Inventory Guidelines and Principles. EPA/600/R-95/245. Washington, D.C.: U.S. Environmental Protection Agency.













