Appendix F Regional Hydrogeology
Approaches To Studying Regional Aquifer Systems
In the broadest sense, a primary objective of studying a deep regional aquifer system is to improve understanding of the relevant processes and properties. Even after a given study has defined the properties of such a system, there will always remain much uncertainty. A unique definition of the system and its properties is simply not attainable, regardless of the amount of data collected. Data collection is very expensive in deep regional aquifer systems, and the costs of data collection and analysis must be weighed carefully against the benefits of additional data. There is no clear-cut point at which it can be determined objectively or scientifically that additional investments in data collection are either necessary or superfluous. Rather, a subjective assessment must be made on the basis of some type of consensus and in light of the significance of the problem, technical considerations, and economic constraints.
Although it is obvious that the properties of a regional aquifer must be defined with some accuracy in order to permit reliable predictions of ground-water flow and transport, it may be less clear that it is also necessary to define accurately the boundary conditions, recharge, and discharge in order to fully define and calibrate a model of the aquifer system. Studies of regional aquifer systems are most comprehensive when the study area extends to the natural geologic or hydrologic boundaries of the system and includes as much of the natural recharge and discharge areas of the system as possible. In reviewing the relevance of hydraulic analyses to contaminant transport problems, Reilly et al. (1987, p. 9) state that "although the details of the flow system in the immediate vicinity of the contaminant plume are of the utmost importance, an understanding of the regional ground-water flow system is required in order to understand the local system."
Because of the uncertainty and variability (heterogeneity) inherent in deep hydrogeologic systems, data collection in general, and drilling of new test wells in particular, often encounter unanticipated difficulties and frequently lead to some "surprises" in the definition or understanding of the properties of the system. Although experienced hydrogeologists expect this, such surprises unfortunately often lead to delays and tend to confound efforts to keep data collection and analysis to a strict, planned time line or budget.
Ground-Water Models
Ground-water simulation models help analysts improve their understanding of the subsurface system at the Waste Isolation Pilot Plant (WIPP) site faster than otherwise would be possible by integrating site-specific data with a theoretical understanding of the principles of flow and transport. The models offer a quantitative and objective means of testing hypotheses, evaluating the sensitivity of parameters, and guiding the data collection and experimentation process. Furthermore, if the models are based on reasonable and appropriate concepts, if they are adequately tested and calibrated, and if analysts have high confidence in their reliability, then the models can be used to predict how a particular system will respond to a particular stress or change in boundary conditions. However, even a well-calibrated model is still an approximation of the real system and incorporates many simplifying assumptions.
Sources of Error
In most model applications, conceptualization problems and uncertainty concerning the data are the most common sources of error. All three aspects of error are discussed below with reference to the performance assessment (PA) models for WIPP.
Conceptual Errors
Conceptual errors are derived from theoretical misconceptions about the basic processes, dimensionality, and/or boundary conditions that are incorporated in the model. Conceptual errors include neglecting relevant processes and representing inappropriate ones. Examples of such errors are applying a model based on Darcy's Law to materials or flow regimes for which Darcy's law is inappropriate, or using a two-dimensional model where significant flow or transport occurs in the third dimension.
That the PA models have a number of simplifying assumptions built into them is not, in itself, a problem, but rather reflects the very nature of models. Questions about ground-water models more typically center on whether the assumptions are too simple or too complex and whether they are appropriate for the system and problem at hand. However, there will never be a sure or precise way of measuring this. The reasonableness of the assumptions is perhaps best evaluated by a consensus of experts. If the conceptual models on which the PA models are based are, in fact, judged to be either too simple or inaccurate, then all of the complementary cumulative distribution functions (CCDFs) and risk assessments derived from the PA must be questioned.
The PA models start with the assumption that the primary release of contaminants under the human intrusion (HI) scenario is from leakage into the Culebra Dolomite. This assumption is part of the conceptual model. The risks and consequences of leakage into other formations have not been assessed or documented thoroughly. Release into the Culebra also is constrained by assumptions about the permeability of the material filling the borehole through which leakage occurs. However, in previous PA analyses, the assumed borehole permeability and assumed depths of impermeable plugs appear to be somewhat arbitrary.
Many of the concepts built into PA models may be based on preliminary judgments and assessments that are not well documented. For those ideas that may be critical but are based on minimal evidence, a range of alternative conceptual models should be evaluated in sufficient detail to document their consideration and the basis for their elimination. Examples of alternative conceptual models that should be evaluated further include (but are not limited to)
- contaminant leakage from a HI breach into formations shallower than the Culebra;
- flow and transport through the Culebra as part of a three-dimensional aquifer system;
- impact of changes in the flow field due to transient effects, climate change, or other factors; and
- internal "structure" of the Culebra, including the existence of vertical fracture zones and correlations between transmissivity and other parameters.
More detailed discussions of model testing, model calibration, predictive accuracy of models, and related issues are presented by Anderson and Woessner (1992), Bredehoeft and Konikow (1993), de Marsily et al. (1993), and Konikow and Bredehoeft (1993).
Numerical Errors
The partial differential equations describing ground–water flow and transport can be solved mathematically by using numerical methods. The continuous variables of the governing equations are replaced with discrete variables that are defined at grid blocks (or cells, elements, or nodes). Thus, the continuous differential equation that defines hydraulic head or solute concentration everywhere in the system is replaced by a finite number of algebraic equations that define the hydraulic head or concentration at specific points. This system of
algebraic equations generally is solved by using matrix techniques.
However, numerical methods yield only approximate (rather than exact) solutions to the governing equation (or equations); they require discretization of space and time. The variable internal properties, boundaries, and stresses of the system are approximated within the discretized format. Because numerical methods do not yield exact solutions, numerical errors will exist in the solution because of truncation errors, round-off errors, and numerical dispersion. As long as the sources of numerical errors are recognized and the magnitude of the error is controlled, the solution may be sufficiently accurate for use.
The solute-transport equation is in general more difficult to solve accurately using numerical methods than is the ground–water flow equation, largely because the mathematical properties of the transport equation vary depending on which terms in the equation are dominant in a particular situation. Thus, numerical errors often are negligible in solutions to the flow equation but can be significant in numerical solutions to the solute-transport equation.
Where solute transport is dominated by advective transport, as is common in many field problems, the transport equation approximates a hyperbolic type of equation (similar to those describing the propagation of a wave or of a shock front). In contrast, where a system is dominated by dispersive fluxes, such as might occur where fluid velocities are relatively low and aquifer dispersivities are relatively high, the transport equation becomes more parabolic in nature (similar to the transient ground–water flow equation).
In solving advection-dominated transport problems, in which a relatively sharp front (or steep concentration gradient) is moving through a system, it is numerically difficult to preserve the sharpness of the front. Obviously, if the width of the front is narrower than the node spacing, it is inherently impossible to calculate the correct values of concentration in the vicinity of the sharp front without using complex nonlinear mathematical functions or complex nonstandard numerical algorithms. However, even in situations where a front is less sharp, the numerical solution technique can calculate a greater dispersive flux than would occur by physical dispersion alone or would be indicated by an exact solution of the governing equation.
That part of the calculated dispersion introduced solely by the numerical solution algorithm is called numerical dispersion. The consequence of numerical dispersion is that the solute is artificially diluted, peak concentrations are lower than they should be, and the solute is distributed throughout a larger than actual area and volume of the aquifer. Although this alone may or may not represent a significant problem, the errors can in fact be magnified and accumulate if the model incorporates a representation of solute retardation processes in which rates or magnitudes are functions of the solute distribution and/or concentration gradients. Because the effectiveness of matrix diffusion and chemical retardation, for example, depends in part on the surface area of aquifer solids that are in contact with ground-water containing the solute (or contaminant), numerical dispersion may yield erroneously high rates of matrix diffusion and chemical retardation. Therefore, special care must be taken to assess and minimize numerical errors that artificially would add "numerical" spreading to the calculated spatial distribution of a contaminant.
Data Uncertainty
Data errors arise from uncertainties and inadequacies in the input data. A reasonable way to accommodate such uncertainty is to estimate the mean and the uncertainty in each relevant parameter on the basis of available data, and then use the simulation models to make predictions based on ranges of values of the parameters, rather than on single values. Outcomes from the deterministic models can then be presented and assessed in a probabilistic framework. In essence, this is the approach taken by the PA models.
The reliability of site-specific ground-water models typically requires that input data be based on field measurements of critical parameters at a scale appropriate to the size of the model. Unfortunately, very few field measurements are
available for the critical parameters describing the nature of fractures and retardation mechanisms in the Culebra.
Although the probabilistic approach is beneficial and appropriate, it must be cautioned that the results will be affected by assumptions about the statistical distributions and independence of parameters; that is, there is uncertainty in the estimates of uncertainty. The sensitivity of results to assumed frequency distributions should be evaluated.
In addition, the system behavior for some processes is governed essentially by the magnitude of nondimensional parameter groups (or ratios). The rationale for independently sampling the individual parameters comprising such a group is unclear and may result in unlikely parameter ratios.
Hydrologic Performance Assessment Models
Ground-Water Flow
In developing PA models for flow and transport through the Culebra Dolomite, estimates of recharge and transmissivity are keyed into the a priori assumptions that ground-water flow is two dimensional, steady state, and horizontal. In reality, the Culebra is one part of a three-dimensional flow system. Although flow may be predominantly horizontal, some vertical components of flow and transport undoubtedly exist, and they may significantly affect the flow, transport, travel times, and concentration distributions in the Culebra in areas downgradient from a potential release.
Fractures are the high-permeability avenues (or pathways) through which the fastest flow and transport of dissolved contaminants would occur. Fractures thus represent the most likely fatal flaw in site integrity if the HI scenario enables significant leakage of contaminants into the Culebra. In general, where vertical or near-vertical fractures exist, they
- tend to persist across formation boundaries,
- often yield some subtle but detectable expression or indication at the land surface, and
- tend to "channelize" ground-water flow.
Because the presence of a few high-permeability fractures will have a large effect on solute transport, additional efforts to characterize fracture properties are warranted.
Confidence in PA Analysis of Regional Ground-Water Flow
The existence and importance of heterogeneity in the Culebra Dolomite is well recognized. Modern, sophisticated, and complex geostatistical methods have been applied to analyze the statistical properties of the variability in transmissivity and to estimate values of transmissivity in areas where no measurements are available. Accomplished with the assistance and advice of a team of world-class experts, this is a state-of-the-art approach to estimating point values and spatially correlated trends in transmissivity based on existing data, as well as to assessing the reliability of these estimates.
In 1995, a new set of wells was drilled into the Culebra for the purpose of conducting multiwell tracer tests. The site (designated as H-19) was selected in part because it is in the area where the coupling of geostatistical methods and ground-water modeling indicates a relatively high transmissivity zone. If hydraulic testing at this new site confirms prior estimates, it would provide a basis for increased confidence in previous analyses. This new drilling site also would provide a control area in which to apply and test the effectiveness of high-resolution geophysical methods and topographic analyses, in order to better define fracture zones. The result of such analyses could then be correlated with the results of planned tracer tests.
Some concern remains about scale effects on permeability and transmissivity. For example, a comparison of transmissivity values for wells H-14, H-15, and H-17 that were estimated from single-well tests (Beauheim, 1987) with values for the same wells as calculated from data collected during a larger-scale pumping test at H-11 (Beauheim, 1989) shows that the latter are 20 to 60
times greater. Garven (1995) states that fractures in carbonate aquifers tend to increase the hydraulic conductivity at the regional level. He presents a curve indicating that at a regional scale of 1 km or greater, hydraulic conductivity may be a few orders of magnitude higher than estimated from borehole measurements at scales of less than 100 m.
This is relevant to WIPP studies and of some concern to the committee because the assumed transmissivity distributions are keyed to transmissivity values measured in boreholes (see LaVenue et al., 1995, for a detailed discussion of the methodology and its application to the WIPP site). These types of borehole measurements typically sense aquifer properties only in the immediate vicinity (perhaps a few meters) of the borehole. If some of those borehole measurements underestimate the larger-scale effective transmissivity in that area, the regional transmissivity values generated may be too low for purposes of large-scale transport predictions. Although the generated transmissivity fields are calibrated by using observed head measurements from both the assumed steady-state flow field and transient hydraulic tests at a few sites, the heads are less sensitive to transmissivity variations than are seepage velocities.
Geostatistical analysis does not explain why transmissivity varies the way it does. It does not answer the question of whether higher transmissivities are related to increases in fracture density (decrease in fracture spacing), increases in fracture aperture, increases in fracture length (and connectivity), changes in fracture orientation, increases in primary porosity, changes in the amount of evaporite minerals dissolved, and/or changes in mineralogy.
Some might ask whether it is important or necessary to understand the cause of these variations in order to predict ground–water flow and transport. Finding the answers to such questions is not merely an academic exercise; the answers are relevant to the PA models and analyses because whatever is causing the changes in transmissivity will most likely also affect the effective porosity and retardation processes. Developing a better understanding of the causes and controls of transmissivity variations may require improved geological and geophysical mapping of primary and secondary geological properties and characteristics of the Culebra dolomite, particularly fractures.
Franke et al. (1987, p. 2) state that "selection of the boundary surface and boundary conditions is probably the most critical step in conceptualizing and developing a model of a ground-water system." Neither the PA ground-water model of the Culebra nor any of the preceding deterministic models of the system extended to the natural boundaries of the regional aquifer. This makes it difficult to assess the reasonableness of the boundary conditions specified at the outer edges of the PA model, which encompasses only a small part of the entire regional system. It is similarly difficult to calibrate the flux through the Culebra and to distinguish between recharge-discharge in outcrop areas and recharge-discharge from leakage through confining beds. In addition to providing another example of a less than desirable level of understanding of the system of interest, this difficulty also casts doubt on the ability to evaluate and predict the impact of climate change because it is not known how a projected change in climate might interact with the aquifer system in general or with the Culebra in particular.
Future climate change may significantly affect the regional ground–water flow system. The PA assumes that the maximum amount of increased recharge to the Culebra can be represented by increasing assumed boundary heads in the model to the elevation of the land surface. However, because it is well known that heads in confined aquifers can be significantly higher than land surface, it is not clear that this assumption really represents a bounding case. If future climate change induces greater diffuse recharge to the water table, then the saturated thickness of the Dewey Lake Red Beds may increase significantly, resulting in greater transmissivity values and higher flow velocities. Since the recharge would likely retain a relatively low content of dissolved solids, use of the Dewey Lake as a drinking water source might increase significantly in the future. In such circumstances, the Dewey Lake Red Beds could
prove to be a greater long-term environmental risk than the Culebra.
Solute Transport
Solute-transport processes include advection, in which solutes move with the average seepage velocity of the flowing ground-water, and hydrodynamic dispersion, which has the net effect of causing the solute distribution to spread about the positions indicated by the mean seepage velocity. Of these two primary processes, advection is the most important to predict accurately, because it controls when the center of mass of a contaminant plume will arrive at the regulatory boundary. Any errors in the solution to the flow equation or in the estimates of effective porosity will affect advection.
The dispersion process in ground-water systems is still the subject of much active research. Although conventional theory holds that the dispersivity coefficients are generally an intrinsic property of the aquifer, in practice they are found to be dependent on and proportional to the scale of the measurement. Recent controlled field experiments and theoretical advances in the study of transport processes indicate that large-scale (macroscopic) dispersion results largely from spatial variations in velocity, caused by spatial variations in hydraulic conductivity and effective porosity (see Gelhar et al., 1992). In that sense, dispersion and advection are interrelated.
Experimental field studies of solute transport at sites that include a dense network of observation wells tend to show that contaminant plumes emanating from known point sources are narrower than expected and that actual dispersion is much less than anticipated by conventional theory (e.g., see Garabedian et al., 1991). The implication for a release of contaminants into the Culebra Dolomite under the HI scenario is that the resulting plume may be longer, narrower, and more sharply bounded than predicted with existing PA models. Overestimating dispersion would have the net effect of diluting the contaminant by spreading its mass through a larger volume of aquifer. In a homogeneous single-porosity medium for a nonreactive solute, this would have not net effect on the center of mass. However, in a heterogeneous system such as the Culebra, overestimating dispersion also forces too much solute into lower-velocity parts of the flow field. This will bias the results toward yielding lower releases during a given time period. Also, if the solute is subject to retardation, overestimating dispersion can lead to a bias of overestimating the magnitude of retardation, as discussed below.
Confidence in PA Analysis of Solute Transport
Because solute-transport processes could be critical to establishing a sufficiently low level of radionuclide releases at WIPP, achieving high confidence in the analyses is important. Although several tracer tests run in the field were valuable steps in this direction, they had to be run under forced-gradient conditions because of time and cost constraints. Running a long-term natural-gradient tracer test should be considered as well, because it would serve as an indicator of true long-term migration paths and velocities under conditions expected after a breach via the HI scenario. However, because such a test might require decades of monitoring, which could be done at very long intervals, it is not recommended that this type of test be performed prior to a compliance decision. Rather, it is suggested that its feasibility be evaluated for possible use as an operational and post-closure monitoring procedure.
Retardation Mechanisms
As solutes migrate through the aquifer, the apparent mean velocity of a particular solute may be retarded relative to the apparent velocity of the water because of several processes that may cause molecules or ions of that particular chemical species to be removed temporarily from the active flow field. Retardation processes thus provide another margin of confidence for the WIPP repository in that retardation will delay (but not prevent) the arrival of a contaminant at the regulatory boundary.
Matrix Diffusion and Physical Retardation
The PA models assume that solute transport through the Culebra Dolomite occurs through continuous sets of horizontal parallel fractures. However, some of the field tests have estimated parameter values for different types of fracture sets and distributions, such as orthogonal sets. The differences in conceptualization must not yield inconsistencies in the effective surface area of fractures per unit volume of aquifer between the field estimates and the PA models, because such inconsistencies might affect the calculated rates of matrix diffusion.
Overestimates of the amount of plume spreading can occur if the assumed dispersion coefficients are too large or if assumed patterns of heterogeneity artificially induce divergence of flow. These effects would be of minor consequence for transport of nonreactive solutes in a single-porosity system. However, if matrix diffusion is a simultaneous process, then the problem is more serious, since the net result would be too much retardation.
Inaccurate or imprecise initial conditions also can lead to significant artificial spreading of the contaminant plume. The HI scenario assumes that the contaminant is introduced into the Culebra by leakage from a borehole (or well) that has a diameter on the order of 0.3 m. In the 1992 PA model, that contaminant source is introduced as an initial condition at the finite-difference cell representing the well. Because that cell has dimensions of 125 m by 125 m, the initial width of the plume at the start of the simulation is perhaps several tens of times greater than it would actually be. The width of the plume then spreads out even more as it is advected and dispersed in a downgradient direction by the regional ground–water flow system.
If the initial width of the plume is much greater than it should be, it has the net effect of giving matrix diffusion an unrealistic "head start" and a growing "advantage" in retarding the movement of the contaminant plume by allowing the plume to be in contact with an erroneously large surface area of the matrix. In a fracture-dominated carbonate aquifer, it is possible that contaminant plumes can migrate long distances with very little lateral spreading, which would minimize any retardation induced by matrix diffusion.
Numerical dispersion also causes artificial plume spreading. The SECO transport code solves the transport equation by using a type of finite-difference scheme. When finite-difference methods are used to solve advection-dominated transport problems, some amount of numerical dispersion is likely to be induced in the solution. Because the numerical code has not been widely available for outside testing and evaluation, it is difficult to know how much numerical dispersion is present. However, any numerical dispersion will necessarily result in overestimates of matrix diffusion.
Confidence in PA Analysis of Matrix Diffusion
The PA models assume that matrix diffusion will be controlled by the intergranular properties of the matrix (including porosity and tortuosity), the free water diffusion coefficient for a particular constituent, and the concentration gradient. Tortuosity is a parameter reflecting the fact that the actual tortuous flow path that a fluid particle would travel through the liquid phase of a saturated porous medium is longer than the length of the porous medium sample. However, tortuosity has been estimated only indirectly in laboratory measurements on a limited number of Culebra samples (Kelley and Saulnier, 1990), where it is shown that the diffusion porosity is usually about two to eight times lower than the porosity measured by other standard methods on the same samples. It is unclear whether these laboratory measurements can be transferred to the field environment.
Field tests by the WIPP project to date have yielded somewhat ambiguous results regarding the occurrence and rates of matrix diffusion. If matrix diffusion must be relied upon to demonstrate compliance, further field studies are necessary to support the model assumptions. Field evidence is needed over moderate distance and time scales and could likely be obtained as part of a series of multiwell tracer tests. Sandia has proposed using single-well injection-recovery tracer tests to
demonstrate the existence of matrix diffusion. However, it is doubtful that such tests could provide either unambiguous results or meaningful measurements of the relevant parameters.
It is also possible that in the field, solute transfer between the fractures and the matrix may be hindered by some type of skin effect or discontinuity at the interface between a fracture and the matrix. Sharp et al. (1995) note that fracture skins are an important and integral part of natural, fractured rock systems and that skin permeabilities and mean pore diameters may be reduced by more than an order of magnitude relative to the matrix. They state that "an extreme case is where the fracture skins have zero permeability and porosity so that no interchange of fluids, colloids and solutes between the fracture and the matrix is possible." Analytical methods are available to interpret the results of tracer tests conducted in fractured aquifers having skin effects (see Moench, 1984; Sharp et al., 1995). The presence of a skin effect would render meaningless any projections of matrix diffusion rates based solely on the physical properties of the matrix. This possibility needs to be given further consideration.
Reactions and Chemical Retardation
As noted in Chapter 6, the appropriateness of predicting the transport of reactive solutes on the basis of a retardation factor (Rf) is questionable. Furthermore, if the use of a retardation factor represents a poor conceptual model, then it is doubtful that the theoretical difficulties can be overcome by simply evaluating a range of values for Rf. For example, if the governing reaction is chemical precipitation of a solid phase, rather than sorption, the species either is less likely to redissolve into the liquid phase in which transport occurs or will do so at a much slower rate. In this case, use of a retardation factor will probably indicate faster and further transport than might occur (but it will still depend on the precipitation rate).
Alternatively, too much retardation could be calculated if the governing process is indeed a type of sorption controlled by surface chemistry. For example, sorption is sometimes characterized by a Langmuir isotherm, which is one type of nonlinear isotherm (although it should not be inferred that a Langmuir isotherm would necessarily be applicable at the WIPP site). In such cases, retardation is greatest at very low concentrations, but at high concentrations the slope of the isotherm approaches zero and the medium will not adsorb additional solute (see Figure F.1). Thus, if sorption is actually governed by a Langmuir isotherm or a similar nonlinear isotherm, applying a retardation factor may lead to a calculation of too much retardation at the high end of the concentration range—the very part of the spectrum at which the greatest toxicity is likely to exist. This illustrates a major weakness of the linear Rf model: it places no upper limit on the amount of the chemical that can be sorbed. However, if it is known that the solute concentration will always remain relatively low, then even if the governing isotherm is nonlinear over the full range of possible concentrations, the sorption behavior within the range of expected conditions will not differ materially from that predicted by a linear isotherm model. If chemical retardation is to be relied on for compliance of WIPP, it must first be demonstrated that the use of a retardation factor is an appropriate representation of reaction processes in the Culebra for the solutes of interest over the transport scales anticipated.
Although most types of reactions tend to retard the transport of a reactive solute, the presence of colloids in the fluid may increase the mobility of solutes that otherwise are retarded or relatively immobile. For example, Ibaraki and Sudicky (1995) cite a case at a liquid waste disposal site at Los Alamos, New Mexico, where both plutonium and americium migrated more than 30 m. They report that predictions based on laboratory results that ignored the role of colloids severely underestimated the migration as just a few millimeters. Colloid-facilitated transport is an issue that warrants additional consideration to justify its exclusion from the PA evaluation.
Confidence in PA Analysis of Chemical Retardation
Not only is the concept of a retardation factor a theoretically weak one for predicting radionuclide transport through the Culebra, but the underlying parameter values for the equivalent Kd are highly uncertain, spatially variable, and based on minimal laboratory experiments that have questionable relevance to the large-scale field environment. Most of the available Kd values obtained by the WIPP project were determined from batch experiments on crushed or powdered samples of rock. There is little evidence that these Kd values are transferable to the field environment, in part because the effective surface areas for water-mineral interactions in crushed samples would be very different from those in situ. For example, Lienert et al. (1994) studied uranium transport in a sand and gravel aquifer and found that the in-situ Kd is much lower than most Kd values obtained from laboratory experiments.
Significant spatial variability in values of Kd may exist and, if so, is probably related to variations in mineralogy. However, in contrast to the consideration of spatial variability in transmissivity, no data are currently available to provide a basis for estimating the magnitude of such variability. A recently published review of transport of reactive contaminants in heterogeneous media concludes that ''the transport of reactive solutes appears to be influenced most greatly by subsurface heterogeneity and rate-limited mass transfer interactions" (Brusseau, 1994, p. 306). In discussing the application of theory and laboratory measurements to field-scale systems, the paper further concludes (p. 307): "Of course, true field-scale behavior can be obtained only by performing experiments in the field."
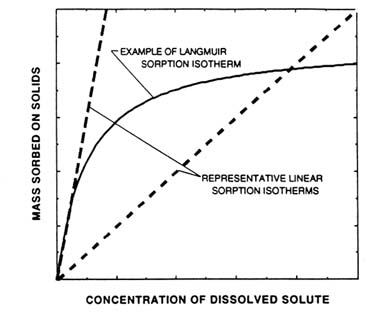
FIGURE F.1. Schematic comparison of representative linear isotherms, describing instantaneous reversible sorption-desorption reactions, with an example of a nonlinear Langmuir isotherm. The distribution coefficient Kd is equal to the slope of the linear isotherm and is directly proportional to the solute retardation factor Rf.
Source: Modified from Goode and Konikow (1989).









