4
Prevention of STDs
|
Highlights
|
Issues in Prevention
Americans have not done well in confronting issues associated with sexual behavior in general and with STDs in particular. Partially as a result of our failure to deal with these public health problems in a straightforward and effective manner, the prevalence of STDs is high, and the economic and health impact of STDs is enormous. Contrary to the misperceptions of some, use of available information and interventions could have a rapid and dramatic impact on the incidence and prevalence of STDs in the United States. Many effective and efficient behavioral and biomedical interventions are available. While there have not been rigorous assessments of the impact of many interventions on health outcomes, there is reason to believe that they could have a substantial impact on the risk of acquiring and spreading STDs if there were the resources and national will to implement some of these programs more widely (Hillis, Black, et al., 1995).
A Mathematical Model for Prevention
The rate of spread of communicable diseases in a population is determined by three factors: (1) the rate of exposure of susceptible persons to infected individuals; (2) the probability that an exposed, susceptible person will acquire the infection (i.e., the "efficiency of transmission"); and (3) the length of time that newly infected persons remain infected and are able to spread the infection to others. A simple transmission cycle for STDs is illustrated in Figure 4-1.
The transmission of STDs in a population can also be represented by the
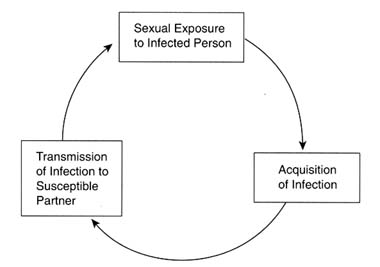
Figure 4-1
Basic transmission cycle for STDs.
mathematical model, R0 = ![]() cD (May and Anderson, 1987; Anderson, 1991). In this model, R0, the reproductive rate of infection, represents the average number of secondary cases of STDs that arise from a new case; c is the mean rate of sexual partner change within the population;
cD (May and Anderson, 1987; Anderson, 1991). In this model, R0, the reproductive rate of infection, represents the average number of secondary cases of STDs that arise from a new case; c is the mean rate of sexual partner change within the population; ![]() is the mean probability of transmission per exposure; and D is the mean duration of infectiousness of newly infected persons. Thus, interventions can prevent the spread of an STD within a population by reducing the rate of exposure to an STD; lowering the rate of partner change; reducing the efficiency of transmission; or shortening the duration of infectiousness for that STD. An extremely important conclusion from this model is that, for communicable diseases such as STDs, if R0 remains less than 1, the infection eventually disappears from the population. A sustained prevention program can drive the infection to extinction in the entire population, even when these interventions are provided only to individuals and social networks with the highest rates of transmission (Anderson, 1991).
is the mean probability of transmission per exposure; and D is the mean duration of infectiousness of newly infected persons. Thus, interventions can prevent the spread of an STD within a population by reducing the rate of exposure to an STD; lowering the rate of partner change; reducing the efficiency of transmission; or shortening the duration of infectiousness for that STD. An extremely important conclusion from this model is that, for communicable diseases such as STDs, if R0 remains less than 1, the infection eventually disappears from the population. A sustained prevention program can drive the infection to extinction in the entire population, even when these interventions are provided only to individuals and social networks with the highest rates of transmission (Anderson, 1991).
Anderson and May (1991) have highlighted differences in the epidemiology of communicable and noncommunicable diseases that have important implications for prevention of STDs. First, rates of partner change within the population and patterns of partner mixing greatly influence the spread of STDs. In essence, individuals with the highest rates of partner change, referred to as "core" groups or transmitters, disproportionately increase the rate of spread. Furthermore, mathematical models show that patterns of sex partner mixing and the characteristics of sexual networks are important determinants of the rate of spread of STDs. For example, if individuals with many partners tend to have sex with others who have
many partners ("assortative mixing"), infection spreads rapidly at first; and it spreads fastest within "dense" sexual networks with many sexual links over a short period of time (Morris, 1993). Thus, interventions should have the greatest impact if they reach, and are effective among, individuals who have many partners and in "dense" networks with "assortative mixing."
Primary Versus Secondary Prevention
For many infectious diseases, vaccines are a major method of prevention. It is important to recognize that early detection and curative treatment of individuals with communicable diseases provide not only secondary prevention at the individual level, but also primary prevention at the population level by preventing further transmission. Reduction in the duration of infectivity, particularly among those most likely to transmit the infection to others, lowers the reproductive rate of infection (R0). Thus, public health efforts to prevent the spread of communicable diseases need to include not only immunization programs but also early detection and curative treatment of communicable diseases, especially those for which vaccines are not available. For these diseases, behavioral interventions are also important.
Behavioral Versus Biomedical Approaches
Historically, STD programs have been based on a biomedical model that focused on the treatment of infected individuals and the development of biological and biomechanical interventions such as drugs, diagnostic tests, and barrier methods. Services have centered on the medical screening and treatment of individuals, coupled in some cases with partner notification. The system for delivering services typically has been composed of health professionals practicing in fixed clinical settings. Traditionally, STD prevention activities have involved episodic therapy driven by symptoms of disease and have provided limited clinical counseling or education to promote behavior change. In recent years, the approach to STD prevention has begun to change as a result of critiques by both affected communities and social and behavioral scientists (Fee and Krieger, 1993). Both biomedical and behavioral health disciplines have made important contributions to the knowledge base for STD prevention (Sparling and Aral, 1991). Because both behavioral and biomedical approaches to STD prevention are necessary, distinguishing between them is unimportant. Federal agencies recently have recognized the need to incorporate both behavioral and biomedical approaches in a more holistic approach.
Wasserheit (1994) examined six changes in patterns of STDs and described how physical and social environmental changes drive these disease patterns. She called for the development of STD prevention programs based on "an appreciation of the role of risk behaviors and macroenvironmental forces" using companion
clinic-based and community-based services. In another holistic approach to prevention, Stryker and colleagues (1994) identified several fundamental precedents that need to exist before effective HIV prevention is possible. These factors are: (a) sound policies that promote HIV risk reduction; (b) access to health and social services, including condoms, needles, syringes, and information; (c) interventions shown to motivate behavior change; (d) community-based organizations capable of reaching persons at risk; and (e) development and diffusion of technologies to interrupt HIV transmission. Similar conditions are probably necessary for the prevention of other STDs.
In terms of the mathematical model previously described, current technology can reduce ![]() , the mean probability of transmission per exposure, and D, the mean duration of infectiousness, to zero. This means that we have the technology and resources to interrupt transmission and greatly reduce many STDs in the United States. In this chapter, the committee describes the complex behavioral problems involved in reducing
, the mean probability of transmission per exposure, and D, the mean duration of infectiousness, to zero. This means that we have the technology and resources to interrupt transmission and greatly reduce many STDs in the United States. In this chapter, the committee describes the complex behavioral problems involved in reducing ![]() and c ("the effective mean rate of partner change") and in ensuring that individuals have access to, and make use of, the technologies that can reduce the efficiency of transmission and duration of infectiousness. The committee also evaluates the ability to effectively and efficiently screen for and treat STDs and describes available effective methods for preventing STDs. It should be noted that most of the behavioral interventions discussed in this chapter focus more on reducing efficiency of transmission than on reducing the rate of partner change. This is because many studies of behavioral interventions use consistent condom use as the primary behavioral outcome. In actuality, many behavioral interventions have multiple objectives that include reducing the rate of partner change. Examples of this are school-based interventions that seek to delay the onset of sexual intercourse and also promote condom use. Nevertheless, research on behavioral interventions to reduce the rate of partner change have been underemphasized. It should be noted that reducing the rate of partner change or the patterns of partner selection may affect the dynamics of how groups at differing risk for STDs subsequently interact in populations (Morris, 1996).
and c ("the effective mean rate of partner change") and in ensuring that individuals have access to, and make use of, the technologies that can reduce the efficiency of transmission and duration of infectiousness. The committee also evaluates the ability to effectively and efficiently screen for and treat STDs and describes available effective methods for preventing STDs. It should be noted that most of the behavioral interventions discussed in this chapter focus more on reducing efficiency of transmission than on reducing the rate of partner change. This is because many studies of behavioral interventions use consistent condom use as the primary behavioral outcome. In actuality, many behavioral interventions have multiple objectives that include reducing the rate of partner change. Examples of this are school-based interventions that seek to delay the onset of sexual intercourse and also promote condom use. Nevertheless, research on behavioral interventions to reduce the rate of partner change have been underemphasized. It should be noted that reducing the rate of partner change or the patterns of partner selection may affect the dynamics of how groups at differing risk for STDs subsequently interact in populations (Morris, 1996).
The question implicit in the subsequent sections is a perplexing and disturbing one: Why has the United States been unsuccessful in significantly reducing or eliminating a group of diseases that costs thousands of lives and billions of dollars annually in health care costs, despite the fact that effective tools are available?
Figure 4-2 depicts the levels of potential breakdown in steps required to prevent STDs. In regard to the third level (from the top of Figure 4-2), there is currently no way to influence the development of symptoms of STDs. All the other levels, however, represent a point for preventive interventions. Individual and population-level interventions are needed to (a) reduce individual risk behaviors and high population prevalence of STDs, both of which increase exposure to STDs; (b) promote safe practices and protective methods, such as condom use, necessary to reduce acquisition of an STD by those exposed; (c) educate the
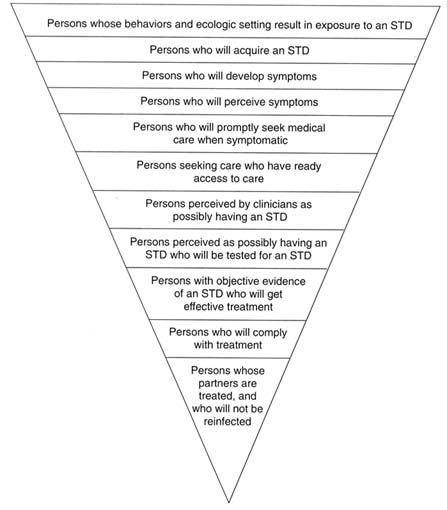
Figure 4-2
Schematic representation of the levels of potential breakdown in the steps required for preventing STDs. Each level, except for the third from the top, represents an important point for public health or clinical intervention. ADAPTED FROM: Waller HT, Piot MA. The use of an epidemiological model for estimating the effectiveness of tuberculosis control measures. Bull World Health Organ 1969;41:75-93. Waller HT, Piot MA. Use of an epidemiological model for estimating the effectiveness of tuberculosis control measures. Bull World Health Organ 1970;43:1-16. The model was also described in "Resource allocation model for public health planning-a case study of tuberculosis control," supplement to Vol. 84 of the Bull World Health Organ, 1973.
public, especially adolescents and young adults, to be aware of and recognize symptoms of STDs; (d) motivate prompt health-care-seeking behaviors for symptoms of STDs; (e) ensure access to health care for STDs; (f) train clinicians in risk assessment and diagnosis of STDs; (g) provide access to, and laboratory capabilities for, STD testing; (h) train clinicians how to treat STDs, including use of syndromic treatment when laboratory tests are unavailable or results are pending; (i) make single-dose therapies available for clinicians to dispense directly to patients to ensure compliance; and (j) ensure treatment of sex partners exposed to STDs. The following discussion describes interventions at each of the steps designed to reduce exposure to STDs, reduce transmission to those exposed, and reduce duration of infection.
Reducing Exposure and Transmission
STDs result from exposure to infectious organisms through sexual contact with an infected individual. Risk factors for exposure include the frequency and type of one's sexual behaviors, use or nonuse of contraceptive methods that provide protection against transmission of STDs, and the likelihood that one's partner is infected. The same behavior (e.g., unprotected intercourse with a new partner) will carry very different levels of risk of transmission, depending on the likelihood of STDs in the social network from which one's partner is chosen. For example, individuals may engage in apparently high-risk behaviors but avoid an STD if their sex partners are not infected.
An important strategy for reducing the rate of spread of STDs is to identify and treat infected individuals and their partners. However, it is necessary to supplement this approach with an understanding of how individual behaviors contribute to both exposure and transmission. This is especially important in the case of STDs for several reasons. First, medical treatment will not prevent transmission of some asymptomatic and incurable STDs, such as HIV infection and other viral STDs. For these diseases, initial exposure must be avoided to prevent infection. Second, reduction of STDs will be facilitated not only by secondary prevention through treatment of infected individuals but also by preventing initial infections. Therefore, prevention of most STDs requires modification of the behaviors that place individuals at risk.
In this section, the committee summarizes how individual factors influence exposure to and transmission of STDs. The committee then illustrates how individual factors affect condom use and summarizes behavioral and clinical methods for preventing exposure and reducing transmission of STDs.
Individual Factors
Many factors influence an individual's sexual behavior and risk for STDs. These factors include sexual and other behaviors, perception of risk, and personal
skills. There are also costs and obstacles associated with adopting behaviors that reduce individual risk of STDs. In this section, immediate factors that influence individual risk of STDs are summarized. It is important to note that these factors are influenced by the social, contextual factors described in Chapter 3, such as poverty and substance use.
Sexual and Other Behaviors
Aral (1994) recently reviewed the sexual and other behaviors that place individuals at greater risk of exposure to STDs. These behaviors are:
- Initiation of sexual intercourse at an early age. Persons who initiate intercourse at an early age may be at greater risk of STDs because of the longer time they are sexually active and the greater likelihood of risk factors for STDs such as nonvoluntary intercourse, greater number of partners, and less consistent use of condoms. In addition, adolescents are biologically more susceptible to STDs than adults.
- Greater number of partners. The greater the number of partners an individual has, the greater is the risk of exposure. This association may be due to the increased risk of exposure to an infected partner with increasing number of partners and the fact that having multiple partners may be associated with other risk factors such as high-risk partners and less consistent use of condoms.
- High-risk partners. Having sex with a partner who is likely to have had many partners increases the risk of an STD.
- Increased frequency of intercourse and certain sexual practices . The greater is the frequency of intercourse with an infected partner, the greater are the chances of transmission. Risk of HIV infection, hepatitis B virus infection, and other STDs is greater with anal intercourse than with vaginal or oral intercourse.
- Lack of circumcision of male partner. As discussed in Chapter 3, men who are not circumcised appear to have a greater risk of acquiring and transmitting certain STDs, such as HIV infection and chancroid, compared to men who are circumcised. Women with male partners who are circumcised are at reduced risk of exposure compared to those with uncircumcised partners.
- Use of vaginal douching. Women who douche are at higher risk for later complications of STDs, such as pelvic inflammatory disease, as discussed in Chapter 3.
- Lack of barrier contraceptive use. Consistent use of condoms and barrier contraceptives reduces the risk of STDs. As mentioned in Chapter 3 and Table 4-1, hormonal contraceptives may also affect risk of STDs.
Perception of Risk
Americans commonly underestimate their risk for STDs. In a 1993 survey
mentioned previously (EDK Associates, 1994), 84 percent of women surveyed were not concerned about acquiring an STD, including 72 percent of women from 18 through 24 years of age, and 78 percent of women reported having had ''many" sexual partners during their lifetime. Mays and Cochran (1988) reported on a study of African American college students who believed that African Americans were less likely to get AIDS than European Americans, even though the reverse is true. Of the sexually active women in the sample, almost a third had taken no actions to avoid STDs. Another nationwide survey of 1,000 persons in 1994 found that Americans underestimated their risk of STDs and were therefore not taking appropriate protective measures (EDK Associates, 1995). This survey found that 62 percent of men and 50 percent of women were at moderate to high risk for STDs (see Figure 4-3 for definitions of risk). Single and divorced men and women were most likely to be at high or moderate risk for STDs compared to married persons (Figure 4-3). Among those at high risk for STDs, 77 percent of women and 72 percent of men stated that they were not worried about getting an STD.
Perceived susceptibility has played a central role in most theories of health behavior (e.g., Wallston and Wallston, 1984; Weinstein, 1988). Perceiving one's personal susceptibility as low may arise from the experience of remaining STD- or HIV-free in the face of behavior that is known to be associated with a high risk of acquiring infection, such as engaging in anonymous unprotected sex with multiple partners over a prolonged period of time. Such perceptions may be reinforced by periodic negative testing. With consistent reinforcement of negative results in light of high-risk behavior, beliefs congruent with "genetic immunity" or "super invulnerability" may develop, leading to reduced motivation to adopt protective behaviors.
Knowledge is necessary but not sufficient to motivate action. Without knowledge, individuals may be unaware of risk or not know what actions to take to protect themselves against STDs. However, among those who do have sufficient knowledge, other factors will affect whether they take action. Thus, among populations with sufficient knowledge, knowledge itself is not related to the behavior (Morrison et al., 1994). Morrison and others (1994) studied adolescents who were incarcerated in the juvenile justice system. These adolescents, who reported engaging in high-risk sexual behaviors, had a good deal of knowledge regarding STDs and condoms, but this knowledge was not related to more positive attitudes toward use of condoms. Similarly, Wulfert and Wan (1993) found that college students with better knowledge about the HIV virus and how it is transmitted were no more likely to use condoms compared to those with less knowledge.
In virtually all behavioral theories regarding the reasons individuals either adopt or fail to adopt risk-avoidance strategies, reducing risk is viewed as a principal motivation of behavior (Cleary et al., 1986). Perceived risk is a critical component in the Health Belief Model (Becker and Maiman, 1975) and the Theory of Reasoned Action (Ajzen and Fishbein, 1980) and is reflected in outcome
TABLE 4-1 Effects of Contraceptives on STDs and Pregnancy
|
|
STDs |
|
|
|
Contraceptive Method |
Bacterial |
Viral (including HIV/AIDS) |
Pregnancy |
|
Condoms |
Protective (if used for STD/HIV prophylaxis) |
Protective (if used for STD/HIV prophylaxis) |
Protective |
|
Sterilization |
Not protective (except against salpingitis) |
Not protective |
Highly protective |
|
Spermicides with nonoxynol-9 |
Protective against cervical gonorrhea and chlamydial infection; associated with increased risk of urinary tract infections and altered vaginal floraa |
No proven protection in vivo |
Protective |
|
Diaphragms |
Protective against cervical infection; associated with increased risk of altered vaginal florab |
Insufficient data |
Protective |
|
Oral contraceptives |
Associated with increased cervical chlamydial infection; protective against symptomatic pelvic inflammatory disease |
Not protective; some studies suggest increased risk for acquisition of HIV;c others show no effectd |
Highly protective |
|
Implantable/injectable contraceptives |
Not protective |
Not protective; some studies suggest increase risk for acquisition of HIV infectiond,e |
Highly protective |
|
IUDs |
Associated with pelvic inflammatory disease in first month after insertion |
Not protective |
Protective |
|
Rhythm method |
Not protective |
Not protective |
Protective |
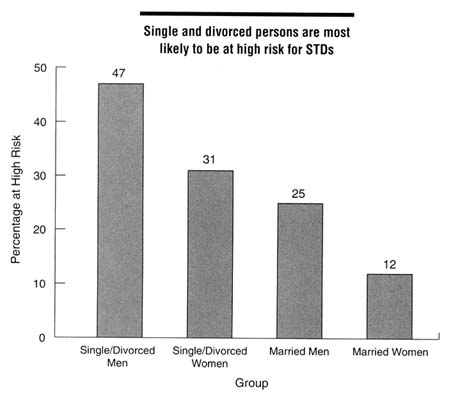
Figure 4-3
Proportion of persons at high risk for STDs by marital status and gender, 1994. High risk was defined as having at least two of the following: (a) six or more sex partners in lifetime, (b) partners who have had sex with six or more people or have no knowledge of their partners' sexual history, or (c) more than one sex partner in the past year. Moderate risk was defined as having one of these characteristics. SOURCE: EDK Associates, Inc. The ABCs of STDs. New York: EDK Associates, 1995.
expectancies in social learning theory (Bandura, 1977). All of these models predict that behavior change will be greater when individuals perceive that they are at risk of infection and that the behavior being recommended will reduce that risk. In addition to the reasons mentioned previously for why individuals fail to adopt protective behaviors, there are other explanations for why the association between perceived risk and protective behaviors is weak.
Link Between Perceived Risk and Protective Behaviors
Given the centrality of perceived risk to the theoretical models as well as to many intervention programs, it is surprising that the empirical evidence linking
perceived risk and health-protective behavior is weak. Confirming that risk perceptions directly lead to adoption of protective behavior is very difficult (Baldwin and Baldwin, 1988). Some studies have demonstrated a relationship between perceived risk of STDs and preventive behaviors (Janz and Becker, 1984; Joseph et al., 1987; Hingson et al., 1990; Weisman et al., 1991; Pendergrast et al., 1992; Stiffman et al., 1992) and number of sex partners (Catania et al., 1989), but others have failed to find such an association (Kegeles et al., 1989; Weisman et al., 1989; Shafer and Boyer, 1990; Cleary et al., 1991, 1995; Orr and Langefeld, 1993; Wulfert and Wan, 1993).
There are several possible explanations for why perception of risk has not been systematically linked to behaviors that reduce the risk of STDs. One is the difficulty of assessing risk adequately in such studies. Perceptions of risk involve perceptions of both the severity of the outcome, such as getting an STD, and the likelihood of its occurrence (Yates and Stone, 1992). Individuals are likely to differ in the extent to which they feel vulnerable to acquiring different STDs and in their views of the gravity of different STDs. Perceived risk usually has been assessed globally, but individuals are likely to have partner-specific perceptions of risk (Weisman et al., 1991; Pilkington et al., 1994; Ellen et al., 1996) and partner-specific patterns of condom use (Magura et al., 1994; Morris et al., 1995).
A second methodological reason why perceived risk has not been consistently linked with behavior may be that the temporal ordering of variables is hard to assess in cross-sectional studies. Individuals who perceive themselves at higher risk should be more likely to take protective action. However, if individuals are engaging in health-protective actions, their perception of risk may drop, and perceived risk would be negatively related to behavior. Longitudinal studies are needed to determine the temporal ordering of risk perceptions and change in risk behaviors.
Finally, there are substantive reasons why perceived risk may not be closely linked to behavior. Perceived risk of STDs may be necessary to motivate health-protective behavior or behavior change but may not be sufficient. There are other powerful factors that influence these behaviors. In addition to having knowledge, individuals need to be motivated to reduce risk behaviors. Behaviors that reduce the risk of STDs, such as reducing the number of sex partners and using a condom consistently, have substantial personal costs associated with them. Unless these costs are offset by a strong motivation to reduce risk or by other reasons to engage in these behaviors, it is unlikely that the person will take these actions.
Individuals may show different degrees of motivation based on their risk perception. For example, persons at relatively low risk for acquiring STDs or HIV infection may be easily stimulated to adopt behaviors that are self-protective, while high-risk individuals may be less able to control sexual impulses that lead to diminished self-protective strategies (Joseph et al., 1987) or such individuals perceive little actual benefit in changing behavior given other pressing life concerns.
An example of a barrier to protective behavior was seen early in the HIV epidemic, when men who were targeted for HIV risk-reduction behavior were asked to engage in behaviors, such as condom use, for which they had never been socialized. Using condoms was a new behavior for most men who had sex with men during the 1980s. The committee hypothesizes that a related barrier to adoption of condom use and reduction of unsafe sexual practices (e.g., anonymous partners) was the association of sexual behavior with self-identity. As the gay movement matured during the 1970s in the United States, a growing number of gay men equated their sexual practices with their own identity. Thus, admonitions to alter sexual behaviors were in direct conflict with the self-identities of gay men, and this conflict frustrated well-meaning attempts to alter behavior. However, this barrier is now diminishing with new generations of young Americans who have become socialized in the AIDS era.
Finally, most sexual risk-reduction efforts for STDs require mutual consent of at least two people. This requires communication about expectations, agreement on the value of engaging in protective strategies, and an understanding of sexual pleasure for each person. Communication regarding sexual behavior is problematic in the best of situations. Experience in the conduct of HIV prevention trials suggests that sexual negotiation and empowerment strategies may be perceived as meaning either that one's partner does not trust one or that there is a "hidden" reason why condom use is being added to an ongoing relationship. Neither of these perceptions builds trust or mutual respect, and these strategies may be extremely difficult to introduce into a stable relationship.
Personal Skills
An individual needs motivation, personal skills, and interpersonal resources to implement complicated behavior changes in the face of the types of barriers discussed above. These include interpersonal communication and negotiation skills and a sense of self-efficacy regarding accomplishment of the relevant behaviors (Bandura, 1990; Wulfert and Wan, 1993). For example, individuals who are able to communicate more readily about sex appear to be more effective in their use of condoms (Brien et al., 1994; Rickman et al., 1994; Shoop and Davidson, 1994).
The best evidence that having specific skills enhances STD-reducing behavior comes from evaluations of programs that provide training in specific behavioral skills. St. Lawrence and colleagues (1995) conducted a randomized trial of an educational program versus education with behavioral skills training. The latter intervention included problem-solving skills, assertion and refusal skills, and training in proper use of condoms. African American adolescents who were sexually active and who received the latter intervention increased condom use and had a lower frequency of unprotected intercourse compared to those who received only the educational program. In addition, adolescents who had not
begun sexual activity and who received the skills intervention were less likely to become sexually active in the next year compared to those who received only the educational program.
In addition to having specific skills, individuals having a greater sense of self-efficacy regarding their ability to enact the behaviors will be more likely to be effective (Bandura, 1990). Self-efficacy beliefs are important because they affect motivation to initiate behavior and to persevere if obstacles are encountered. Thus, men who feel that they can use condoms each time they have intercourse and women who feel that they will be able to get their partners to use a condom consistently should be more likely to implement the behaviors needed to achieve this goal (e.g., obtaining condoms, having them accessible at the time of intercourse, using them). Several studies have shown that greater self-efficacy and confidence in one's ability to use condoms predicts both a stronger intention to use condoms and more effective use of condoms (Marin et al., 1993; Schaalma et al., 1993; Wulfert and Wan, 1993; Mahoney et al., 1995; Rotheram-Borus et al., 1995).
An important determinant of self-efficacy is one's comfort level and acceptance of individual sexuality. Persons who have developed negative emotions regarding premarital sex, such as guilt and denial, are less likely to practice protective behaviors, such as use of contraceptives, compared to those who do not have such emotions (Herold and McNamee, 1982; Gerrard, 1987; Morrison and Shaklee, 1990; Gerrard et al., 1993). In addition, persons who are embarrassed about their sexual activity are less likely to use condoms consistently (Hingson et al., 1990; Koniak-Griffin et al., 1994).
Behavioral Methods
Behavioral interventions represent promising approaches to preventing STDs. While there are many reports of behavioral interventions to prevent STDs including HIV infection, most studies have not been conducted in a methodologically sound manner to determine their effectiveness in improving health outcomes (Oakley et al., 1995; Oakley, Fullerton, Holland, et al., 1995). Many studies, however, show that behavioral interventions can have a positive effect on self-reported sexual health behaviors. A meta-analysis of 12 controlled studies of risk-reduction interventions for HIV infection found that the mean weighted effect of such behavioral interventions on self-reported sexual behaviors was positive and statistically significant (Kalichman et al., 1996). In addition, two recent studies have demonstrated that certain feasible behavioral interventions are effective in reducing the risk of STDs (Kamb et al., 1996; Shain et al., 1996) and support a strong role for such interventions as part of a comprehensive approach to preventing STDs. An advantage of behavioral interventions is that they can be effective in preventing all STDs, in contrast to some biomedical interventions that are specific for only certain STDs.
A variety of strategies can lead to sustained behavior changes that reduce the risk of STDs. These intervention strategies include individually focused interventions relying heavily on one-on-one counseling that occurs independent of, or jointly with, STD testing; group- or community-based interventions (Kelly, 1994); and structural or "macro" level legislative solutions. A review of federally funded HIV prevention studies that evaluated the impact of individual- and community-based behavioral interventions found that most interventions had positive effects on knowledge of AIDS and sexual behavior such as increased rates of condom use (IOM, 1994). The intent of STD preventive interventions is to reduce the incidence of new STDs by assisting individuals in changing behaviors in ways that decrease risk of contracting STDs. Altering precursors of sexual decision making and actual sexual practices, such as increasing rates of condom use, reducing number of partners, or decreasing rates of unprotected sex, will ultimately reduce the number of new cases of STDs.
While reduced STD incidence and sexual behavior change are the primary endpoints in STD risk-reduction interventions, other endpoints also have merit. For example, several important studies in STD prevention have utilized changes in risk behavior intentions, condom use attitudes, and perceived vulnerability as principal outcome measures. Community-level interventions based on "stages of change" theoretical models (Prochaska and DiClemente, 1983) have defined success on the basis of shifting community attitudes towards greater readiness to enact a specific behavior change, stronger change intentions, or future resolve to engage in protective behavior. "Social marketing" approaches to condom promotion have included condom sales in the community as an indicator of programmatic success. Success needs to be judged independently for specific target populations and for desired behavioral and disease outcomes.
Among adolescents, delaying sexual intercourse or intermittent avoidance of sexual activity is effective in STD risk reduction (Kirby, 1980). Furthermore, it has been well documented (Gold et al., 1994; Ku et al., 1994) that it is easier to encourage consistent condom use in sexual relationships with nonprimary partners than in primary relationships. Thus, the context of behavioral change strategies needs to be specified.
The literature on the effectiveness of HIV prevention programs contains some findings applicable for developing other effective STD prevention programs. Holtgrave and others (1995) found that successful prevention programs that were able to avert, reduce, or modify HIV-risk-related behaviors or their determinants had the following characteristics:
- basis in real specific needs and community planning;
- culturally competent messages;
- clearly defined audience, objectives, and interventions;
- basis in behavioral and social science theory and research;
- quality monitoring and adherence to plans;
- use of evaluation findings and midcourse corrections; and
- sufficient resources.
The study's authors also concluded that some behaviorally based prevention programs are cost saving, and others are likely to be cost-effective relative to other health programs.
Theoretical Approaches to STD and HIV Risk Reduction
A number of theoretical approaches drawn from the social and behavioral sciences have been employed in developing STD prevention interventions (Cleary et al., 1986, 1995). These models were derived from efforts to promote change in nonsexual health-risk behaviors, such as smoking cessation, cardiovascular risk reduction, and cancer prevention. The dominant model guiding most STD prevention interventions has been social learning theory (also referred to as social cognitive or cognitive-behavioral theory), originally proposed by Bandura (1977). This approach postulates that specific skills are needed to alter risk behaviors. These skills can be imparted through modeling, rehearsal, or practice opportunities. Behavior change interventions have heavily focused on training participants in condom use skills, sexual assertiveness, safer sex negotiations and communication strategies, and self-management skills to deal with situations that might trigger vulnerability to high-risk sexual behavior (Kelly, 1994). Other theoretical approaches that are appropriately focused on the individual-level determinants of high-risk behavior and behavior change include the Theory of Reasoned Action (Ajzen and Fishbein, 1980) and the Precaution-Adoption Process (Weinstein, 1988).
At the community level, one approach that has been very popular over the past decade in STD prevention has been the "stages of change" formulation mentioned previously (Prochaska and DiClemente, 1983). This approach was originally developed to explain the process of changing health habits, primarily smoking, and postulates that people are at varying levels of readiness for change. Understanding the different levels of readiness for each person allows tailoring interventions that can successfully move the individual further along the continuum of change—towards action and then behavioral maintenance. While this approach has been widely discussed in the literature (Catania et al., 1990; O'Reilly and Higgins, 1991), there have been few empirical demonstrations of its utility in influencing behavior change at the community level.
Community-norm-change models that focus on influencing social or peer group norms regarding sexual behavior have proven particularly appropriate in studies of sexual risk practices of adolescents, heterosexual adults, and gay men. One approach for producing normative change at the community level is the "diffusion of innovation" model (Rogers, 1983) in which normative change attributable to advocacy by key, popular "opinion leaders" leads to accepted new
behavioral norms in the population. This strategy has been viewed as extremely successful in interventions focused on gay men. A second approach, "social marketing" (Andreasen, 1995), uses media campaigns to change attitudes towards condoms and improve their availability.
Individual-Focused Interventions
Intensive small-group risk-reduction interventions, largely guided by cognitive-behavioral theory, have been shown to be very effective in promoting self-protective behavior change (Kelly, 1994; Cleary et al., 1995). These studies have included randomized trials with gay men (Kelly et al., 1991), homeless and runaway adolescents (Rotheram-Borus et al., 1991), adolescents at risk for STDs (Jemmott et al., 1992; St. Lawrence et al., 1995), low-income and adult women of certain ethnic groups (Hobfoll et al., 1994; DiClemente and Wingood, 1995) and at-risk mentally ill men and women (Kalichman et al., 1994). These interventions have been delivered in small-group programs with 6 to 18 hours of contact time, allowing time to practice risk-reduction skills and review successes and problems encountered in enacting these behaviors. These interventions produced evidence of change in self-reported sexual risk behavior, usually on the order of 30 to 70 percent reduction in the frequency of unprotected sex from pre-intervention levels. While none of these studies incorporated STD incidence as a primary outcome measure, each study did utilize some method to validate self-reported behavioral changes. A limitation to these studies is that long-term maintenance of behavior change effects has not been examined.
Brief interventions focused on influencing knowledge and attitudes have been successful (Kalichman et al., 1994) but have had little impact on sexual behavior practices. Other strategies have focused on counseling and HIV testing as a method of increasing perceptions of vulnerability and promoting self-protection from STDs. Analyses of these strategies suggest that while these approaches have merit, the counseling, as practiced in field conditions, leaves much to be desired in meeting minimal criteria for being "successful" (Giesecke et al., 1991; Higgins et al., 1991).
Preliminary results of a major randomized, controlled trial evaluating the impact of enhanced prevention counseling for HIV and STD risk reduction strongly support individual-focused counseling (Kamb et al., 1996). Among public STD clinic patients, those who received a series of counseling sessions based on the Health Belief Model or the Theory of Reasoned Action were significantly more likely to adopt certain protective behaviors and less likely to acquire new STDs at six months of follow-up compared to those who received only educational messages.
In its latest report, the U.S. Preventive Services Task Force concluded that the ability of primary care clinicians to influence high-risk sexual behavior is limited, but that there is consistent evidence that Americans have changed their
behavior in response to information regarding STDs, including HIV infection, provided through a variety of clinical and other settings. Although the task force determined that the effectiveness of clinician counseling in the primary care setting is unproven, the group recommended that primary care clinicians counsel their adolescent and adult patients regarding measures to prevent STDs, and that such counseling should be tailored to the risk factors, needs, and abilities of each patient (U.S. Preventive Services Task Force, 1996). The CDC and several physician organizations have also recommended that primary care clinicians counsel their adolescent and adult patients regarding measures to prevent STDs (ACOG, 1992; AMA, 1993; CDC, 1993a; AAP, Committee on Adolescence, 1994; AAFP, 1994). Clinician counseling does not work in isolation and is a necessary component of appropriate clinical management of STDs. This is because clinician counseling takes advantage of opportunities to educate patients when they are most receptive to health messages and effectively reinforces messages from other sources (Bigelow et al., 1986).
Couple-based interventions to prevent high-risk sexual behaviors are also promising approaches to prevention. In this approach, both members in a relationship are the focus of an intervention. Perhaps the best evidence to support the effectiveness of such an approach is from HIV counseling studies among discordant couples.1 In one study, after multiple HIV testing and counseling sessions, condom use among discordant couples increased from 4 percent to 57 percent after one year of follow-up (Allen et al., 1992).
Community-Based Interventions
Community-based interventions to promote behavior change include interventions that target specific high-risk groups, such as female sex workers and adolescents, as well as interventions that attempt to change community norms, most commonly through mass media messages. A number of intervention trials involving high-risk groups such as gay men (Kelly et al., 1991, 1992), injection drug users and their sex partners, female sex workers, and youth in high-risk situations have been successful in improving knowledge and promoting behavior change (O'Reilly and Higgins, 1991; IOM, 1994). Some interventions have been modeled after the Diffusion of Innovation Theory and have successfully utilized peer opinion leaders and educators to change norms in a community by endorsing condoms and educating regarding their use (Kelly et al., 1991, 1992). For example, a multicity trial that recruited popular gay men to educate other gay men who frequented bars resulted in a dramatic decline in the frequency of unprotected intercourse after several months (Kelly et al., 1992). Studies in Tanzania show that community-based interventions to improve syndromic management of
STDs and health-care-seeking behavior significantly reduce HIV transmission and population incidence of urethritis and syphilis (Grosskurth et al., 1995a, b; Mwijarubi et al., 1996).
One major community-based intervention for disenfranchised groups that may be directly applicable to community-based STD prevention is the AIDS Community Demonstration Projects initiative (CDC, 1996a). These programs were initiated in 1989 to target populations at high risk of HIV infection in five cities, such as intravenous drug users and their sex partners, female sex workers, men who have sex with men, and youths in high-risk situations. The goal of these programs was to determine the efficacy of a specific community-based intervention among hard-to-reach populations, and one of the two main objectives was to increase consistent condom use among these populations.2 The intervention included distribution of printed materials that described ''role models" who successfully changed their behaviors and provided basic HIV and condom information. Peers and other community network members were used extensively to distribute materials. Preliminary data indicate that high rates of exposure to the intervention can be achieved within two years of the initiation of the program. In addition, for the three sexual behaviors examined, the mean stages of change-continuum value among persons who reported exposure to the intervention was greater than that among persons who did not report exposure to the intervention.3 Replications of successful interventions among high-risk groups are being undertaken in the United States and abroad, and the results will shed light on the long-term impact and applicability of these approaches to other communities at risk.
In January 1994, the CDC implemented its Prevention Marketing initiative for HIV and STD prevention (U.S. Conference of Mayors, 1994). This initiative was motivated by research on community interventions showing that they were most effective when designed and managed by the communities themselves. As part of this program, the CDC is contributing funds for pilot prevention-marketing interventions and is providing technical assistance to state and local health departments, community coalitions, and other partners. The initiative uses commercial marketing techniques, including mass media messages, and community involvement to promote healthy sexual behaviors. The social marketing approach adapted by the CDC includes the concepts of the right product, the right price, the right place, and the right promotion (DeJong, 1989).
Public health workers recognize that, in order for behavior change to occur, the community environment should not be a barrier but should be supportive of
such changes. In response to this issue, "enabling approaches" to prevention have recently gained attention (Tawil et al., 1995; O'Reilly and Piot, 1996). These interventions are intended to either remove barriers to adoption of protective behaviors or to erect barriers to risky behaviors. An example of how structural or environmental changes can significantly reduce risky sexual behaviors is the "100% Condom Program" that was implemented nationwide in Thailand by the Thai HIV/AIDS Prevention and Control Program in 1992, along with a mass media condom-promotion campaign and wide distribution of condoms to prevent the spread of HIV among sex workers (Rojanapithayakorn and Hanenberg, 1996). The program enforced universal use of condoms among sex workers through the use of sanctions against sex establishments where condoms were not being consistently used. This intervention was effective apparently because it supported desired behavior change and did not reduce the income of sex workers. An extensive evaluation of the program among Thai army male conscripts showed that the proportion of men who had sex with sex workers fell, the proportion who used condoms with sex workers increased, and the seroprevalence of HIV and the proportion with a history of an STD declined significantly after program implementation (Nelson et al., 1996). These data indicate that environmental interventions that adequately address structural or other barriers to behavior change are necessary for the adoption of healthy sexual behaviors.
School-Based Interventions
School is an obvious venue for providing information regarding STDs and for preventing the initiation of high-risk sexual behaviors among adolescents. More than half of teenagers surveyed in 1995 indicated that the school was their primary source of information (ASHA, 1996). As of mid-1994, 45 states and approximately 91 percent of school districts required schools to offer health education (Collins et al., 1995). Five states required a separate course devoted almost entirely to health topics in all elementary schools, 14 required such courses at the middle/junior high school level, and 28 required such courses in senior high school. A 1994 survey of state education agencies and teachers by the CDC showed that 28 of 43 states and the District of Columbia and 81 percent of school districts required teaching STD prevention in a required course (CDC, 1996b). In addition, 39 states plus the District of Columbia required HIV prevention education. As of September 1995, 22 states and the District of Columbia had legal mandates that required schools to provide both sexuality and STD/HIV education; an additional 15 states require schools to provide only STD/HIV education; and 13 states did not require schools to provide sexuality or STD/HIV education (NARAL Foundation, 1995). Many of the states that require education in STD/HIV mention education only for HIV/AIDS, not other STDs, in their laws. Although many states require schools to provide instruction in HIV or STD prevention, these legal mandates are often underfunded and restrictive in the content of
the instruction (NARAL Foundation, 1995). For example, in Louisiana, schools are required to teach that abstinence is the expected norm for students, but the law makes no mention of instruction regarding STD prevention. In addition, 19 states prohibit or restrict school health and education programs from making contraceptives, or in some cases information regarding contraceptives, available to students. The number of restrictive laws enacted or considered by states increased in 1995 (NARAL Foundation, 1995). Another important limitation of current school-based education is the lack of consistent STD-related education at lower grade levels.
The majority of health education teachers recently surveyed reported that they taught about sexual abstinence (76 percent); how to prevent STDs (75 percent); signs and symptoms of STDs (70 percent); and other topics related to risk factors for STDs (Collins et al., 1995). In the CDC survey mentioned previously, among teachers who taught in health education classes, 78 percent taught about sexual behaviors that transmit HIV (and other STDs), but only 37 percent taught about correct use of condoms (CDC, 1996b). The preparation of teachers who provide instruction on these topics is inconsistent. For example, while 86 percent of states and 33 percent of school districts that required instruction in STDs reported providing training on the topic (CDC, 1996b), only 16 percent of teachers surveyed reported receiving training on teaching STD prevention during the two years prior to the survey.
A 1989 survey of more than 4,200 seventh- through twelfth-grade teachers in specialties most likely to be responsible for sex education found that most teachers believed that information regarding HIV infection, other STDs, and pregnancy should be covered by the seventh and eighth grades at the latest (Forrest and Silverman, 1989). There was a gap between what the teachers think should be taught and what actually occurs. For example, almost all teachers believed that sex education information for students should include sexual decision-making and abstinence and birth control methods, but only 82 to 84 percent of teachers reported being in schools that provided instruction in these areas. Teachers cited (a) pressure from parents, the community, and school administration; (b) lack of appropriate teaching materials; and (c) lack of student interest as potential barriers to teaching sex education.
An IOM committee4 that is preparing a report on the role of comprehensive school health programs in the United States has come to the conclusion that health education does not commence at a sufficiently early age; the period prior to high school appears to be the most crucial for shaping attitudes and behaviors. By the time students reach high school, many are already engaging in risky behaviors or at least have formed accepting attitudes toward these behaviors. For
this reason, the committee believes that sequential, age-appropriate health education before high school is essential.
In many communities, there is considerable controversy regarding the role of "abstinence-based" (i.e., delaying intercourse until marriage) versus harm-reduction approaches (i.e., promoting use of condoms) to school-based education curriculum design. Some communities and school boards, in spite of predominant scientific evidence to the contrary, believe that harm-reduction approaches such as condom promotion encourage sexual intercourse among adolescents. Because of the controversial nature of school-based STD education programs, it has been strongly suggested that health departments and private organizations that desire to implement such programs work closely with school administrators, health educators, teachers, parents, and students throughout the planning and implementation process (Molbert et al., 1993).
It should be noted that although school-based programs will reach the overwhelming number of adolescents in the United States, as discussed in Chapter 3, a sizable number of adolescents are homeless, in detention facilities, or otherwise not attending school. These youths, who are at high risk for STDs because they are likely to be sexually active, have a history of being sexually abused, and use drugs and alcohol, present many challenges to prevention efforts. Information regarding the effectiveness of interventions to prevent STDs among youths who are not in school settings are limited (Rotheram-Borus et al., 1991).
Effectiveness of School-Based Programs. The quality of studies that have evaluated the effectiveness of school-based programs to reduce risky sexual behaviors varies greatly. Many studies that have evaluated the effectiveness of school-based programs in reducing risky sexual behaviors have used some type of experimental design, commonly randomization of students or schools to intervention and control groups to measure program effectiveness. Other evaluation methodologies include the use of data from national surveys of adolescent sexual behavior to relate past participation in health education programs to subsequent sexual health behaviors. Limitations of many of these studies include lack of appropriate control or comparison groups, insufficient sample size of students and resulting inadequate statistical power, variability of the time frame chosen for postintervention follow-up, and difficulty in accurately measuring health outcomes. For example, studies based on national surveys of adolescent sexual behavior are problematic because they rely on the recall of the respondent's past participation in health education activities. In addition, many specifics regarding the scope and quality of health education programs are not captured, thereby essentially grouping together programs of varying quality and scope. Because of ethical concerns and other problems associated with assessment of rates of STDs among students, it is not feasible to evaluate the direct impact of such programs on rates of STDs in most situations. Therefore, most studies evaluate effectiveness
on the basis of changes in self-reported risky sexual behaviors such as frequency of unprotected sexual intercourse.
The overwhelming proportion of peer-reviewed evaluations of the effectiveness of sex and AIDS and STD education programs have reported positive changes or no effect of programs on sexual health behaviors such as condom use and onset of sexual intercourse (Kirby et al., 1994). In a few studies based on national survey data, mixed outcomes (positive, negative, or no effect) have also been documented (Dawson, 1986; Marsiglio and Mott, 1986; Ku et al., 1993). Kirby and colleagues recently completed a comprehensive review of 23 studies of school-based sex and AIDS and STD education programs that were published in peer-reviewed journals and evaluated their impact on sexual behavior (Kirby et al., 1994) The authors found that some but not all programs were effective and that programs having the following six characteristics had a clear impact on behavior:
- narrowly focused on reducing sexual risk-taking behaviors that lead to HIV or other STDs or unintentional pregnancy;
- utilized social learning theories as a foundation for development;
- provided basic, accurate information about the risks of unprotected intercourse and methods of avoiding unprotected intercourse through experiential activities designed to personalize this information;
- included activities that address social or media influences on sexual behaviors;
- reinforced clear and appropriate values to strengthen individual values and group norms against unprotected sex; and
- provided modeling and practice in communication and negotiating skills.
The authors concluded that, contrary to the concerns of some individuals and groups, such educational programs do not increase sexual activity among students. Studies of specific programs found that programs that included instruction on contraception either delayed the onset of sexual intercourse or had no effect on onset. In addition, a previous IOM committee (IOM, 1995:233) evaluated 23 local programs, including school-based programs, related to unintended pregnancy and concluded that:
Sexuality education programs that provide information on both abstinence and contraceptive use neither encourage the onset of sexual intercourse nor increase the frequency of intercourse among adolescents. In fact, programs that provide both messages appear to be effective in delaying the onset of sexual intercourse and encouraging contraceptive use once sexual activity has begun, especially among younger adolescents.
A recent nationwide survey revealed that respondents wanted information on STDs from multiple sources and rated health care professionals and school-based
programs most frequently as being "very effective" sources of information on STDs (EDK Associates, 1995). Factors affecting the acceptance and effectiveness of school-based programs include community norms related to the appropriateness of the inclusion of certain topics in school curricula and the knowledge of teachers about, and attitudes towards, issues related to STDs. It is important to recognize that there is substantial heterogeneity in teacher and community attitudes towards how health curricula should deal with these topics. Competing demands on time and resources, political and religious attitudes, and beliefs about the effects of the teaching of such topics on children's attitudes and behavior vary tremendously. It is important to be aware of, and address when feasible, such factors that might inhibit the implementation of effective programs.
A significant barrier to implementation of effective school-based interventions is inadequate support for dissemination of such programs. To address this issue, the "Research to Classroom Project," sponsored by the Division of Adolescent and School Health, CDC, is the largest federal program to disseminate school-based curricula for reducing sexual risk behaviors. Under this program, the CDC identifies curricula that have been evaluated and shown to be effective in reducing specific risky behaviors and meet other selection criteria, and then provides resources, including training and technical assistance, to ensure that such curricula are disseminated on a national level.
Condom Availability in Schools. To address barriers to adolescent condom usage, approximately 431 schools in 50 school districts in 21 states have condom availability programs as part of HIV and STD prevention efforts, primarily in large urban public high schools (Kirby and Brown, 1996). Ninety-two percent of schools that made condoms available are high schools; these high schools represent only 2.2 percent of all public high schools in the United States (Kirby and Brown, 1996). The 50 school districts with condom availability programs represent only 0.3 percent of all U.S. high school districts. In 1994, there were a total of 9,573 middle schools, 20,059 high schools, and 14,881 school districts in the United States (U.S. Department of Education, National Center for Education Statistics, 1995). Massachusetts, New York State, and the District of Columbia are the only states or jurisdictions to recommend that their schools consider condom availability for students as part of a comprehensive HIV prevention program (NARAL Foundation, 1995). In addition, Los Angeles, New York City, and other cities have mandated condom availability in high schools as part of a comprehensive effort to prevent HIV infection (Kirby and Brown, 1996). In 1992, a survey of superintendents or their designees of 299 middle and high school districts found that only 8 percent of middle and high school students are in districts that have approved condom distribution programs (Leitman et al., 1993). Of schools with condom distribution programs in place, students were not given access to condoms before grade 9. Most districts with approved programs were located in the East and West and in areas with a large proportion of students
of lower socioeconomic status. Most schools with condom availability programs are located in Los Angeles and New York City because of these cities' mandates on condom availability. Condom availability programs have used a variety of mechanisms for distributing condoms in schools (Stryker et al., 1994; Advocates for Youth, 1995; Kirby and Brown, 1996). Many schools provide condoms through school health professionals, teachers, principals, or counselors. In only a small percentage of cases are condoms provided in bowls and baskets (5 percent) or through vending machines (3 percent) (Kirby and Brown, 1996). In 81 percent of schools with programs, some type of parental consent (active or passive) is required for student participation. Approximately half of schools that make condoms available require education and counseling before condoms are provided; students are commonly informed regarding use of condoms and that not having sex is the best protection against STDs. An analysis of utilization of condom availability programs showed that students in alternative schools, smaller schools, schools that made condoms available through bowls and baskets, and schools with health clinics obtained more condoms per person per year than did students in other schools (Kirby and Brown, 1996).
There are only limited data on the effectiveness of condom availability programs in schools to increase protective sexual behaviors and decrease STD rates, since these programs are relatively few and newly established (Kirby, 1993; Stryker et al., 1994). In addition, many condom availability programs were not designed to measure program effectiveness (Stryker et al., 1994). One study, however, estimated that an additional 6 to 13 percent of students would have had sexual intercourse without protection if their school had not provided contraceptives (Kirby et al., 1991). Preliminary data from the evaluation of the New York City program indicate that girls considered embarrassment and confidentiality concerns as main barriers to using the program (Guttmacher et al., 1995a). After implementation of condom availability programs in New York City high schools, 69 percent of parents surveyed supported condom availability for their children in school; 85 percent believed that providing condoms to students would either have no effect on, or would decrease the frequency of, sexual activity among the students; and 75 percent believed that providing condoms would result in students practicing safer sex (Guttmacher et al., 1995b).
There seems to be wide public support for school condom availability programs. A 1991 survey showed that 74 percent of adults surveyed favored condom availability in high school and 47 percent favored availability in junior high schools (The Roper Organization, 1991). Among Denver high school students, 85 percent believed that condoms should be provided in their school and 76 percent believed that having access to condoms would not affect the frequency of sexual activity among students (Fanburg et al., 1995). In New York City public high schools where passive parental permission is required for participation, fewer than 2 percent of parents have submitted written denials of participation for their children (Guttmacher et al., 1995b). Health care provider groups have
strongly endorsed condom availability for adolescents through schools (AAP, Committee on Adolescence, 1995; AMA, 1996).
Condom availability in schools is an emotionally and politically charged issue. Some of the other the major issues associated with condom availability programs are related to parental consent, funding of condom purchases, staffing and counseling, and legal liability. Opponents of condom availability in schools believe that providing or promoting condoms to adolescents hastens the onset of sexual intercourse, increases sexual activity, and violates parental autonomy in this area. There is no evidence, however, that condom availability or promotion programs increase sexual activity (Kirby, 1994). A study of three school-based clinics that provided contraceptives showed that students in these schools did not initiate sexual intercourse earlier or have intercourse more frequently compared to students in schools without such programs (Kirby et al., 1991). Another study of a high school condom availability program found that the benefit of the program in protecting a sexually active student against STDs and pregnancy was more than three times greater than the risk of encouraging a nonsexually active student to have intercourse (Wolk and Rosenbaum, 1995). In addition, a study of a community-based condom promotion and distribution program among Latino adolescents compared rates of sexual activity in the intervention city with a comparable city without such an intervention (Sellers et al., 1994). Researchers found that, compared to their counterparts in the control city, male adolescents in the intervention city were significantly less likely to initiate sexual intercourse, and female adolescents in the intervention city were significantly less likely to have multiple partners. There were no significant differences in the onset of sexual activity for female adolescents, multiple partnership among male adolescents, or the frequency of sex for male or female adolescents in the two cities.
The funding of condom availability programs can be as contentious as the programs themselves. Schools and local health departments are increasingly under budgetary constraints, and there are several concerns regarding the use of federal funds for these programs (Brindis, 1993). An examination of major condom availability programs in several cities demonstrates that a mix of funding sources, including public and private funds, is necessary to sustain these programs (Brindis, 1993; Stryker et al., 1994). A series of focus group discussions with school superintendents and board members in 1992 revealed that, although they may be supportive of condom availability programs under certain conditions, school officials were unlikely to be leaders in initiating condom availability programs (Greene, 1993).
School condom availability programs in Falmouth (Massachusetts), New York City, and Philadelphia have been challenged in the courts (Mahler, 1996). Program opponents have generally argued that such programs violate parental and religious rights. In January 1996, however, the U.S. Supreme Court declined to review Curtis v. School Committee of Falmouth. In this case, the Massachusetts Supreme Judicial Court upheld the school district's program that allowed
students in grades 7-12 access to condoms on request without a procedure for parents to refuse participation on behalf of their children (Mahler, 1996).
Mass Media Interventions
An important community-based approach to reducing STDs is to use mass media to disseminate information and promote specific behavior changes. There is compelling evidence that properly designed mass media campaigns can have beneficial effects on health behaviors. Flay (1987) reviewed 40 mass media programs focused on smoking and concluded that information and motivation programs generally produced positive changes in awareness, knowledge, and attitudes. Extensive national campaigns also produced meaningful behavior change. In many ways, changing knowledge and attitudes regarding smoking is less difficult than for STDs. Yet, because there is widespread lack of awareness and information regarding STDs, it is possible that national campaigns would have a greater impact on STDs compared to well-recognized issues such as smoking.
A recent review of HIV prevention mass media campaigns (Flora et al., 1995) concluded that, with the exception of campaigns in Australia and Britain, most of the campaigns that were intended to increase knowledge were successful (Appendix E). The results were mixed with respect to attitude change. Programs designed to change behaviors were largely successful. One prominent example is a Swiss multimedia campaign to promote condom use among adolescents and young adults that has significantly increased condom use among these groups (Wasserfallen et al., 1993). In addition, this campaign, which incorporated explicit messages regarding sexuality, did not result in increased sexual activity among young people. Authors of studies in Italy and Zaire have attributed reductions in HIV infection rates to mass media campaigns (Flora et al., 1995). As mentioned previously, perceived risk is an essential element in almost all models of behavioral risk reduction. The only studies to examine the impact of media campaigns on perceived risk were done in Brazil, France, and the Philippines, and the campaigns were deemed successful (Flora et al., 1995).
Other Methods
Effective interventions are available to prevent exposure to and reduce transmission of STDs. Biomedical methods, such as vaccines and antibiotic therapy, require education of, access to, and compliance among individuals. Similarly, condom use requires behavioral modification to utilize the intervention appropriately. Partner notification and treatment clearly has both behavioral and technical components. Thus, the technical expertise provides methods for intervening in the transmission of STDs, but utilizing the technology requires applying clinical and behavioral interventions concurrently.
Prophylaxis
An important method of preventing acquisition of an STD is to protect persons who have been exposed. Antimicrobial therapy is frequently administered to individuals exposed to bacterial infections. Currently, the only effective vaccine available for prevention of an STD is hepatitis B vaccine. Vaccines for herpes simplex virus are in clinical trials, and vaccines for other STDs are in various stages of development (NIH, 1996).
Although an effective vaccine against hepatitis B virus infection has been available for over a decade, the vaccine's impact has been small because the initial vaccination strategy of selective vaccination of persons with identifiable risk factors was not successful (CDC, 1991b). The Advisory Committee on Immunization Practice (ACIP) recommended in 1991 that hepatitis B vaccine become a routine childhood immunization to protect against later exposures in adolescence or adulthood (CDC, 1991b). Immunization of certain adults, including men who have sex with men and heterosexual persons at high risk for STDs, was also recommended. In 1994, the advisory committee further recommended vaccination of all 11-12-year-old children who had not been previously vaccinated as part of a routine adolescent immunization visit (CDC, 1995b). Current data on hepatitis B vaccination coverage of persons in high-risk groups, including sexually active adolescents and men who have sex with men, are limited, but vaccination coverage is considered to be low (CDC, 1996c; Frank Mahoney, CDC, Hepatitis Branch, personal communication, July 1996). In a recent study, only 3 percent of young men who have sex with men in the San Francisco area were adequately vaccinated against hepatitis B virus (CDC, 1996c). Reasons for inadequate vaccination of adolescents and men who have sex with men include lack of awareness among clinicians of groups at high risk for hepatitis B virus infection and lack of clinical opportunities to provide immunization, especially for adolescents (CDC, 1991b).
Hepatitis B vaccination of adolescents has been successfully implemented in school-based clinics, primary care clinics, and other clinical settings (CDC, 1994b; Kollar et al., 1994). Initiatives to administer hepatitis B vaccine to STD clinic patients show that such programs are feasible, although completion of all three vaccine doses is sometimes problematic (Moran et al., 1992; Lafferty et al., 1995). Since 1994, hepatitis B vaccine has been accessible free of charge under the Vaccines for Children program for children less than 19 years of age at high risk for hepatitis B virus infection, including adolescents seen in STD clinics and correctional facilities (CDC, 1994a). To be eligible for the program, children must be enrolled in Medicaid, have no health insurance, be an American Indian/Alaska Native, or have health insurance that does not cover hepatitis B immunization. Outside of limited federal demonstration projects, there are no major programs or public funds to increase vaccination of adults at high risk for sexually transmitted hepatitis B virus infection. Frequency of coverage for adult hepatitis
B immunization among private health plans is unclear but is considered to be low (Eric Mast, CDC, Hepatitis Branch, personal communication, October 1996).
A recent economic analysis of various immunization strategies to prevent hepatitis B showed that perinatal prevention (screening of pregnant women and prophylaxis of infants) and routine infant immunization would reduce the 4.8 percent lifetime risk of hepatitis B virus infection by at least 68 percent, compared with a 45 percent reduction of lifetime risk for adolescent vaccination (Margolis et al., 1995). The authors concluded that adolescent vaccination of those who were not currently immunized should be considered part of a national strategy against hepatitis B virus infection.
Condoms
With the exception of not having sexual intercourse with an infected partner, using a new latex condom during every act of sexual intercourse is currently the most effective method of preventing exposure to STDs (CDC, 1993b). When used correctly and consistently (during every act of intercourse), condoms are highly effectively against bacterial and viral STDs including HIV infection (Cates and Stone, 1992; Roper et al., 1993; Weller, 1993). Several studies that have followed ''discordant" partners show that consistent condom use significantly reduces the transmission of STDs including HIV infection (Laurian et al., 1989; European Study Group on Heterosexual Transmission of HIV, 1992).
Failure to use a condom correctly and consistently, rather than potential defects of the condom itself, is considered to be the major barrier to condom effectiveness (Cates and Stone, 1992; CDC, 1993b). Many incidents of condom breakage and leakage are associated with improper handling or inappropriate use of lubricants.
Data show that condom use has increased in the United States in the last few decades (DeBuono et al., 1990; Pleck et al., 1993; Peterson, 1995). Data from the National Survey of Family Growth show that, among women who had their first intercourse premaritally at 15-19 years of age, the proportion who used a condom at first intercourse rose from 28 percent during 1980-1982 to 55 percent during June 1988-November 1990 (Peterson, 1995). In addition, data from the CDC's Youth Risk Behavior Surveillance System show that, from 1990 through 1993, the proportion of high school students who reported using condoms at last sexual intercourse increased significantly from 46.2 percent to 52.8 percent (CDC, 1995a). Among unmarried sexually experienced women of reproductive age, approximately 30 percent reported using a condom for disease prevention every time or most times that they have intercourse (Anderson et al., 1996).
Although the first female condom was introduced in the 1920s, the polyurethane female condom has only recently been approved for use in the United States and represents an important alternative to the male condom (CDC, 1993b; IOM, 1996). A major advantage of the female condom is the greater control that
women have over its use compared to the male condom. Other advantages include insertion before intercourse, it protects a greater area of the vagina, and it is less likely to break than the male condom (Gollub and Stein, 1993). The female condom is an effective mechanical barrier to viruses including HIV (CDC, 1993b). The Food and Drug Administration has recently approved labeling for the female condom to reflect annual pregnancy protection failure rates of 21 percent for "typical use" (the product is used inconsistently or incorrectly) and 5 percent for "perfect use" (the product is used consistently and correctly every time).5 These data are consistent with results of a multisite study that found a six-month 2.6 percent unintended pregnancy rate (and no STDs) for U.S. women who used the female polyurethane condom consistently and correctly (Farr et al., 1994). Although a percentage of women in this study reported liking the female condom, there is insufficient experience with the female condom to determine its long-term acceptability (IOM, 1996). Potential disadvantages of the female condom include its relatively high costs, its appearance, and its acceptance by women (Gollub and Stein, 1993). The female condom represents one of the few female-controlled contraceptive methods that are effective against STDs. Many factors may influence individual behavior related to condom use. Understanding the impact of these individual factors is important in effectively promoting condom use as a measure to prevent STDs. Although studies on condom use behavior have increased in the last decade, many of the determinants of correct and consistent condom use have not been adequately examined (Roper et al., 1993).
Adolescence. Behavioral factors that influence condom use among adolescents include sufficient knowledge and skills, perceptions of condoms, ability to communicate with partners, and perception of condom use by peers (Brown et al., 1992; Orr and Langefeld, 1993; AAP, Committee on Adolescence, 1995). Other major factors that influence whether condoms are used by adolescents include access, availability, confidentiality, and cost (Kirby et al., 1994; AAP, Committee on Adolescence, 1995). Magura and others (1994) found that male adolescents of certain ethnic groups in the juvenile justice system were more likely to report using condoms if condoms were accessible. A sample of college males reported that not having condoms available was a major factor in their lack of condom use (Franzini and Sideman, 1994). The importance of ready access to condoms was underscored by another study that found that adolescents who carry condoms are almost three times more likely to use a condom during sexual
intercourse compared to other adolescents (Hingson et al., 1990). Embarrassment in obtaining and using condoms is also an important factor that may discourage their use (Hingson et al., 1990). In a sample of female adolescents who were pregnant or who already had a child, Koniak-Griffin and colleagues (1994) found that poor condom use was associated with greater embarrassment.
Age. Condom use among men declines with age. For example, data show that the rate of reported condom use at last intercourse steadily declined with increasing age from 39 percent of men 20-25 years old to 17 percent of men 35-39 years old in 1991 (Pleck et al., 1993). In 1992, 28 percent of adults 18-24 years of age surveyed reported using a condom at last intercourse compared to 19 percent of adults 30-34 years of age and 12 percent of adults 40-44 years of age (Laumann et al., 1994). These data may reflect the tendency to rely on contraceptive methods other than condoms as men grow older, establish long-term relationships, and depend more on female-controlled contraceptives such as oral contraceptives and sterilization (Landry and Camelo, 1994). Age also seems to be associated with the comfort level of persons in negotiating condom use with partners. For example, a national survey revealed that 69 percent of women 18-24 felt "very comfortable" in asking a new partner to use a condom compared to 55 percent of women 25-34 and 40 percent of women 35-44 years (EDK Associates, 1994).
Educational Level, Race, and Gender. Men with higher levels of education report higher rates of condom use compared to less educated men (Tanfer et al., 1993), but studies have failed to show that socioeconomic status is independently associated with condom use (Pleck et al., 1991; Ku et al., 1992). African American women are almost twice as likely to use condoms compared to women of other races (Anderson et al., 1996). In addition, African American men are more likely to have used condoms during their last episode of intercourse compared to either European American or Hispanic men (Laumann et al., 1994). The rate of condom use at first intercourse for African Americans, however, is lower than that for European American men independent of age at initial intercourse (Ku et al., 1993). Women generally report slightly lower rates of condom use at last intercourse compared to men. In 1992, 18 percent of men and 15 percent of women reported such use (Laumann et al., 1994).
Ability to Negotiate Use. Even if the individual has a condom, negotiating its use with one's partner may be difficult. Condom use may be particularly difficult in a romantic relationship. For a woman, asking a partner to use a condom (or for a man, using one himself) may convey a lack of trust in the partner. Women may fear that their partner will react angrily to the suggestion. Marin and colleagues (1993) found that Hispanic women's fear of an angry response by their partners to a request to use condoms predicted their reported use of condoms. In some cultures, suggestions about condom use may prompt male partners to view the
woman as "loose" (Mays and Cochran, 1988). Sexual communication between partners has been found to be an important determinant of condom use (Catania et al., 1992). In addition, studies have found that college students tended to use condoms in casual relationships, but when they became more committed and developed trust in the relationship, they stopped using them (Pilkington et al., 1994; Lear, 1995).
Perceptions of Condoms. Several studies show that persons who believe that condoms require interrupting the act of intercourse and that they reduce sexual pleasure are less likely to use condoms compared to those who did not have such beliefs (Wulfert and Wan, 1993; Norris and Ford, 1994; Ramos et al., 1995). In one study, adolescents who believed that condoms did not reduce sexual pleasure were more than three times as likely to use condoms compared to other adolescents (Hingson et al., 1990). In another study, men who felt that condoms would be uncomfortable or painful to use were less likely to intend to use them (Kegeles et al., 1989) Among unmarried women, favorable perceptions of the effectiveness of condoms strongly predict condom use (Anderson et al., 1996).
Competing Concerns. Concerns that compete with protective behaviors are important determinants of condom use. Disenfranchised and poor persons in particular may have more immediate survival concerns, such as obtaining money for food and shelter, that may hinder the implementation of protective health behaviors (Mays and Cochran, 1988; Donovan, 1996). In addition, if one or both partners wish to conceive, the desire for pregnancy may undermine conscientious use of condoms (Adler and Tschann, 1993). The impact of other contraceptive use on condom use is discussed in the following section.
Other Contraceptives and Dual Protection
Among sexually active women 15-44 years of age at risk of unintended pregnancy, 12 percent do not use a method of contraception (Peterson, 1995). As reflected in the high rates of unintended pregnancy in the United States, it is clear that many persons are not using contraceptives consistently or correctly (IOM, 1995). Among women who use contraception, the most common methods are female sterilization, oral contraceptives, and the condom. Barriers to contraceptive access include the cost of contraceptives, inadequate coverage of contraceptives by health insurance plans, and inadequate training and skills of some health care professionals in providing contraceptive services (IOM, 1995). These problems are particularly difficult for adolescents.
Women who rely on sterilization, oral contraceptives, or another method for protecting against pregnancy are less likely to use condoms compared to other women. For example, studies show that women who have been surgically sterilized are less likely to report condom use (CDC, 1992a, b). Women who used oral
contraceptives, had been pregnant, were surgically sterilized, wanted future births, or were older were less likely to use condoms for disease prevention than other women (Anderson et al., 1996; Santelli et al., 1996).
The effectiveness of various contraceptives against STDs (including HIV infection) and pregnancy is summarized in Table 4-1. Of the methods listed, condoms are the most protective method against STDs, including HIV infection, but are not the most effective pregnancy-prevention method. In contrast, surgical sterilization is most effective against pregnancy but confers no protection against STDs. Spermicides, such as nonoxynol-9, are effective against most STDs in vitro (Cates and Stone, 1992) and have been found to be partially effective against gonorrhea and chlamydial infection in clinical trials (Louv et al., 1988). Epidemiological and biological studies, however, have indicated that excessive use of nonoxynol-9 may irritate the vaginal lining, thus potentially facilitating HIV infection (Cates et al., 1992). There has been some debate about how women should be counseled regarding the relative effectiveness of condoms, diaphragms, and spermicides. Some believe that women should be counseled that both condoms and spermicides are effective against STDs (Rosenberg and Gollub, 1992; Stein, 1992). However, most believe that the effectiveness of spermicides against STDs other than gonorrhea and chlamydial infection is uncertain and that condoms should remain the primary recommended strategy for STDs including HIV infection (Cates et al., 1992). Hormonal contraceptives may actually increase the risk for cervical infections, but their effects on STD transmission and sequelae remain unclear (Cates and Stone, 1992). The IUD seems to increase the risk for STDs, especially around the time of insertion (Cates and Stone, 1992).
No single method of preventing STDs or pregnancy confers the maximum level of protection for both conditions (Cates and Stone, 1992). Use of dual protection—that is, one to protect against STDs and another to protect against pregnancy—is especially important for women. Women who use a contraceptive other than a condom are not fully protected against STDs. To obtain maximum protection against STDs and pregnancy, a condom (male or female) should be used with another effective contraceptive. There seems to be public interest in simultaneous protection against STDs and pregnancy, and dual use of contraceptives has increased (IOM, 1995). However, it is not clear how well the public understands the need for dual protection against STDs and pregnancy.
As mentioned in Chapters 2 and 3, women are more vulnerable to STDs than men. Additional contraceptive methods that are female-controlled and effective against all STDs need to be developed (Cates et al., 1992; Rosenberg and Gollub, 1992; Stein, 1992). In particular, topical microbicides that are effective against HIV and other STDs but do not impair a woman's ability to become pregnant would be an important female-controlled method for STD prevention (Elias and Heise, 1994). Another IOM committee has identified the development of chemical or physical barriers to conception and to transmission of STDs as a major priority in a research agenda focused on women (IOM, 1996). Currently, researchers
are attempting to develop methods of protection that are not harmful to beneficial microbes and the lining of the lower reproductive tract (unlike nonoxynol-9) but are active against pathogenic organisms (IOM, 1996).
Partner Notification and Treatment
Partner notification has been a component of STD programs in the United States for many years (Rothenberg and Potterat, 1990). Championed by Surgeon General Thomas Parran at the first National Conference on Venereal Disease Control in 1936, it became an integral component of efforts against syphilis in this country after penicillin became widely available in the 1940s (Brandt, 1985). STD patient interviews followed by partner notification were considered to be the cornerstones of the early federal efforts against syphilis implemented by the Venereal Disease Branch at the National Communicable Disease Center, now known as the CDC. Partner notification has continued to be supported through current federally funded STD programs.
Because the incubation period for early syphilis is long (an average of three weeks, but anywhere from 10 to 90 days from exposure to onset of symptoms), partner notification could break the "chain of transmission" not only by identifying "source" cases of illness and partners with clinical or serologic evidence of disease, but also by identifying and treating partners exposed to syphilis. By providing treatment to exposed but asymptomatic partners, a potential case could be prevented by treatment of "incubating'' syphilis.
When the syphilis model was expanded to include the referral of partners exposed to gonorrhea (Potterat et al., 1989; Alary et al., 1991; CDC, DSTD/HIVP, 1992) and chlamydial infection (Katz et al., 1988; Alary et al., 1991), the rationale for partner notification had to be modified, since the incubation periods are shorter for gonorrhea (usually a week or less) and chlamydial infection (one to two weeks). Therefore, therapy of partners with incubating infections was not possible; instead, emphasis was placed on locating asymptomatic infected female partners of symptomatic men and on providing early treatment to prevent complications (CDC, DSTD/HIVP, 1992).
Identification of partners exposed to treatable bacterial STDs makes intuitive sense as an STD prevention strategy. "Source" cases—those exposing others to an STD—require treatment to break the chain of transmission. Partners who have been exposed to an already infected and infectious individual are at greatest risk for developing STD infection themselves. Treatment of infected or exposed partners will not only cure or prevent the infection (as in the case of incubating syphilis) but will both prevent STD transmission to future partners and directly benefit the exposed individual by preventing complications of untreated infection. Partner notification followed by partner treatment, therefore, is considered to be a strategy that benefits the individual index patient, his or her partner, and the community as a whole.
Evaluation of STDs in men generally requires less time and less equipment and is easier to perform (a pelvic examination is not required) than in women. Nonetheless, for a number of reasons, clinicians, especially those who primarily treat women, often do not routinely examine and treat male sex partners of women found to have STDs. In some instances, clinicians do not counsel women regarding the importance of partner treatment. In other instances, women with STDs are given medications to give to their partners. This latter practice, although widespread, is of unproven benefit and is the subject of a recently initiated multi-center study conducted by the CDC. When utilized, this approach has several disadvantages for preventing STDs including the small but real risk of adverse drug reactions in unseen "patients," the inability to screen the partner for other STDs, and the lack of opportunity to examine and counsel the partner.
Techniques in Partner Notification. The method and intensity of partner outreach activities traditionally have varied according to the clinical setting. In dedicated public STD clinics, emphasis has been placed on the activities of trained program staff, commonly called "disease intervention specialists," to interview STD patients and identify names and the whereabouts of partners.6 The role of these "disease intervention specialists" will be discussed in detail in Chapter 5. Originally called "contact tracing" and now referred to as "provider referral,'' this method of partner notification relies on intensive interviews with patients about their sexual histories and partners, followed by active outreach by public health staff to identify and locate partners to ensure that they are examined and treated. Although labor intensive and costly, provider referral is still carried out within most public health programs for syphilis and selected other STDs (Rothenberg and Potterat, in press).
Any efforts by patients to notify their own partners about STD exposure without assistance from public health staff is called "patient referral." STD programs and staff have emphasized provider referral as the notification method of choice, especially for syphilis and to a lesser extent for other bacterial STDs identified in STD clinics, since the benefits of ensuring that partners receive preventive treatment have been thought to outweigh the substantial costs in staff time. Few efforts have been made to identify partners of individuals with other viral STDs such as herpes simplex or hepatitis B virus (Munday et al., 1983). The
cost of carrying out provider referral is significantly higher than that for patient referral (Oxman et al., 1994).
Partner notification performed for patients seen outside of the STD clinic setting has never been well developed or documented. Although disease intervention specialists make intensive efforts to identify partners of syphilis patients seen in public STD clinics and in private practice and to follow up on positive tests reported by laboratories, little effort is generally made to support partner notification for patients treated for gonorrhea or chlamydial infection in private health care settings such as physician offices and hospital emergency rooms (Toomey, 1990). Little is known about the practices of private providers regarding partner follow-up, and no systematic national efforts have been made to educate private sector providers regarding the importance of partner treatment as an essential component of STD-related care.
When the provider referral model was applied to HIV prevention and AIDS, other concerns about partner notification emerged (Potterat et al., 1989; Toomey and Cates, 1989; Giesecke et al., 1991; Bayer and Toomey, 1992; Rothenberg and Potterat, in press). The long asymptomatic incubation period for HIV infection makes partner follow-up difficult (Rutherford et al., 1991), and curative therapies are not available. Exposed partners who are identified and not yet infected can benefit substantially from risk-reduction counseling to change behavior, thereby potentially preventing future HIV infection among at-risk partners. HIV-infected persons benefit from early intervention since retroviral therapy and prophylaxis against opportunistic infections are beneficial when utilized appropriately.
Although confidentiality has been ensured with provider referral for STDs, concern about the scope and limits of confidentiality—as well as doubt about the relevance and potential efficacy of partner notification in preventing any STD—have emerged. As the debate regarding partner notification intensified, some public health leaders questioned the value of any provider referral activities (Bayer and Toomey, 1992).
Effectiveness of Partner Notification. Temporal trends suggest that partner notification contributed to the reduction of syphilis and congenital syphilis after the program was widely implemented in the 1950s (Baumgartner et al., 1962). In addition, published reports have documented the effectiveness of partner notification strategies in controlling focal outbreaks of gonorrhea and chancroid (Handsfield et al., 1982, 1989; Blackmore et al., 1985; Zenilman et al., 1988) and in targeting intervention for specific high-risk populations (Yorke et al., 1978; Phillips et al., 1980). In some countries, such as Sweden, partner notification for gonorrhea, syphilis, and chlamydial infection has been highly effective (Ramstedt et al., 1991). The effectiveness of partner notification strategies for STD prevention, however, has not been rigorously evaluated in terms of STD incidence or prevalence in the population at large or rates of reinfection among index patients.
Instead, STD programs emphasize "yields" from interviews and volume of activity as indirect programmatic indicators of efficacy (CDC, DSTD/HIVP, 1992; Rothenberg and Potterat, in press).
Recent studies suggest that provider referral for STDs, as it is currently performed by disease intervention specialists, is not working effectively. In many programs, fewer than one partner can be found per index patient, although index patients often report having many partners during the interview period (Gunn et al., 1995). A number of factors may contribute to the diminishing utility of provider referral as traditionally carried out in public STD clinics. Concerns about the safety of the interviewers working in high-crime communities, as well as concerns about the cultural sensitivity of the STD interviewers, continue to be raised by both supporters and critics of the process.
Crack cocaine use and the exchange of sex for drugs have emerged as major risk factors in recent epidemics of syphilis (Marx et al., 1991), other STDs (Schwarcz et al., 1992), and HIV infection (Edlin et al., 1994). The large number of often anonymous partners involved in sex-for-drug activities have reduced the efficacy of traditional patient interviewing to identify partners, to the point that many have questioned the continued utility of provider referral in these populations (Andrus et al., 1990; Oxman and Doyle, 1996). Implementing alternative case-finding methods (CDC, 1991a; Engelgau et al., 1995) and refocusing partner outreach toward communities and social networks (Klovdahl et al., 1994; Trotter et al., 1995; Gunn et al., 1995; Rothenberg and Narramore, 1996), rather than traditional partner identification, have been suggested as more effective strategies for reaching high-risk individuals for intervention and prevention activities (Rothenberg and Potterat, in press).
Research evidence concerning the effectiveness of partner notification is sparse at best. Oxman and others (1994) recently reviewed published studies in this area and found the following:
- simple forms of assistance for improving patient referral, such as telephone calls, can be effective;
- provider referral results in more partners being notified than does patient referral for HIV infection;
- evidence supporting provider referral as being more effective than patient referral for syphilis is weak;
- evidence is inconsistent regarding the effectiveness of health care professional referral compared with patient referral for gonorrhea and chlamydial infection; and
- there is only weak evidence to support the notion that trained interviewers are more effective than regular health care professionals at identifying partners, and there is no evidence that this slightly increased effectiveness has any practical importance for STD prevention.
Screening
Screening programs for many STDs are cost-effective and, sometimes, cost-saving (Handsfield et al., 1986; Arevalo and Washington, 1988; Trachtenberg et al., 1988; Randolph and Washington, 1990; Britton et al., 1992; Hillis, Nakashima, et al., 1995; Scholes et al., 1996). For example, using a decision model, Trachtenberg and colleagues (1988) estimated net savings of more than $60 million (in 1986 dollars) over the first five years of a California statewide chlamydial-screening program for asymptomatic women in family planning clinics. The CDC estimates that approximately $12 in costs associated with the complications of chlamydial and gonococcal infection could be saved for every $1 spent on early detection and treatment (CDC, DSTD/HIVP, 1995).
There are many examples of successful comprehensive screening programs. The Wisconsin chlamydial prevention program is a comprehensive program supported by state funding that includes public-private collaborations, screening in family planning and STD clinics, low-cost laboratory services, integrated information systems, and evaluation of program effectiveness (Addiss et al., 1994; Hillis, Nakashima, et al., 1995). In Wisconsin, substantial declines in the prevalence and incidence of chlamydial infections were observed statewide after the implementation of selective chlamydial screening in family planning clinics and universal screening in large STD clinics, in conjunction with other statewide interventions. Rates of positive laboratory tests for chlamydial, hospitalization for pelvic inflammatory disease, and ectopic pregnancy also declined. In addition, an Indianapolis chlamydial program that included screening demonstrated a 63 percent decrease in chlamydial infections among adolescent girls attending adolescent health clinics for the first time during the 8.75 years of the program (Katz et al., 1996).
The success of a CDC and Office of Population Affairs initiative begun in 1988 in Public Health Service Region X to reduce chlamydial rates led to the Preventive Health Amendments of 1992 that authorized federal funding for expansion of activities to prevent infertility associated with chlamydial and gonococcal infections. Appropriated funds of $12.2 million in fiscal year 1995 have allowed the CDC to screen and treat at least half of at-risk women and their sex partners using family planning and STD clinics in 4 of 10 regions; to initiate screening and treatment services in the other 6 regions; and to implement research and evaluation activities at 5 sites (CDC, Division of STD Prevention, unpublished data, 1996). The CDC estimates that $175 million per year, including $90 million in public funding, is needed to fully implement a national chlamydial prevention program to screen and treat all female adolescents and women between 15 and 34 years of age (CDC, DSTD/HIVP, 1995).
In the primary care setting, screening and treating women at increased risk for asymptomatic chlamydial infection significantly reduces the rate of subsequent pelvic inflammatory disease (Scholes et al., 1996). The U.S. Preventive
Services Task Force (1996) recently recommended a group of screening activities for primary care clinicians based on the age of the patient and risk category. A summary of the task force's recommendations related to STD screening and counseling is presented in Appendix F. These clinical guidelines were developed after an extensive review of data, studies, and expert opinions. It is important to note that the task force recommendations were based on evidence of prevention effectiveness rather than on cost-effectiveness or other considerations. Recognizing the limited amount of time available to primary care clinicians during patient visits, the task force only recommended interventions that were shown to be effective by peer-reviewed studies. The intent is that clinicians would choose from the specific recommended interventions and tailor them to the health needs of the individual patient. The task force evaluated and made specific recommendations for the following diseases and conditions related to sexual intercourse: hepatitis B virus infection, syphilis, gonorrhea, HIV infection, chlamydial infection, genital herpes, cervical cancer, and unintended pregnancy. Several medical professional societies, other organizations, and government agencies have also published guidelines regarding screening for STDs (U.S. Preventive Services Task Force, 1996). The recommendations of these organizations and agencies are very similar. For example, no major organizations recommend screening of the general population for chlamydial infection, genital herpes simplex virus, hepatitis B virus infection, or syphilis. The recommendations of these groups, however, often vary in the criteria recommended for selecting risk groups for screening.
Not all STD screening programs are cost-effective. State laws requiring premarital and prenatal screening in order to prevent syphilis transmission date back to the 1930s and 1940s (Brandt, 1985). As a result of data showing that only approximately 1 percent of syphilis infections were detected by premarital screening, many states have repealed their premarital testing requirements (Felman, 1981). As of 1996, however, 15 states still require premarital syphilis testing as a requirement for marriage licenses (CDC, Division of STD Prevention, unpublished data, 1996). The number of previously undetected cases of syphilis identified through premarital testing is extremely low (Felman, 1981; Haskell, 1984). In addition, studies show that premarital tests for syphilis or HIV infection are not cost-effective and have little public health impact (Haskell, 1984; Cleary et al., 1987; Peterson and White, 1990). In contrast, screening for syphilis during pregnancy has been shown to be cost-saving; the economic benefits of the national screening program in Norway were almost four times the program cost (Stray-Pederson, 1983).
Inadequate resources and other considerations may preclude implementation of widespread screening protocols or other intervention programs. In such situations, methods for identifying individuals or groups at particularly high risk are helpful in targeting interventions and maximizing effectiveness (Stergachis et al., 1993). For example, a study of public STD clinics in Dade County, Florida, found that it is possible to identify persons at highest risk for STDs using routinely
collected clinical data (Richert et al., 1993). Thirty-nine percent of those at highest risk for STDs were reinfected within a year compared to 7 percent of those at the lowest risk.
Reducing Duration of Infection
In addition to effective interventions designed to prevent exposure and reduce the efficiency of disease transmission, effective interventions to reduce the duration of infection are currently available. Reducing duration of STDs can be accomplished primarily by ensuring early diagnosis and treatment of infected persons and by reducing barriers to diagnostic and treatment services. Reducing the duration of STDs among infected individuals is an effective method of preventing STDs in the population because reducing duration will reduce the period of time that an individual is infectious and, consequently, reduce the number of partners exposed to infection. In addition, early detection and treatment prevents complications of STDs in infected individuals. This is illustrated by the trials in Tanzania demonstrating that early detection and treatment reduces active syphilis and symptomatic urethritis (Mwijarubi et al., 1996). In this section, the committee reviews the diagnostic tests available for STDs and the barriers to diagnosis and treatment.
Early Diagnosis and Treatment
Early, specific diagnosis and treatment of symptomatic and asymptomatic individuals will prevent further transmission of STDs to their partners. Currently available diagnostic and therapeutic technologies are adequate for containment or eradication of bacterial STDs in the United States. While improved diagnostic tests and more effective therapies would facilitate the task, the fact that countries such as Sweden have, for all practical purposes, eradicated endemic gonorrhea and syphilis indicates that bacterial STDs can be contained with current biomedical technologies. Diagnostic techniques are similarly effective for viral STDs; however, in general, curative therapeutic agents for viral STDs are not currently available.
Diagnostic Tests for STDs
Traditionally, diagnostic tests for STDs are used by clinicians to evaluate either persons who suspect they have an STD or sex partners of infected individuals. Appropriate diagnosis of an STD often requires multiple specific diagnostic tests because of the variety of STDs. Further complicating the diagnosis of STDs is the availability of several different diagnostic tests for each STD. No single test can be relied upon to provide timely (i.e., in less than 30 minutes) and accurate diagnosis of symptomatic individuals while also being utilized for accurate detection
of asymptomatic persons in the context of screening. Unfortunately, many clinicians fail to appreciate that no single laboratory test is optimal for use in all settings.
"Syndromic diagnosis," which utilizes the patient's history, results of physical examination, and rapid laboratory tests, can be utilized for the diagnosis of clinical syndromes. This allows appropriate treatment for infected individuals in a single visit. This approach is relatively inexpensive when compared to conducting specific laboratory testing. Unfortunately, syndromic diagnosis is not always specific even though, for many of the syndromes, only one or two STD pathogens are usually the cause. The major curable STD syndromes in adults include urethritis in males; vaginal discharge, cervicitis, and pelvic inflammatory disease in women; and genital ulcers in both men and women. In clinical practice in the United States, it is common to initiate syndromic treatment for urethritis in men and cervicitis and pelvic inflammatory disease in women (while results of laboratory testing are pending), using treatments effective against all of the common bacteria that can cause these syndromes. For genital ulcers and vaginal discharge, it is more common to perform rapid tests before initiating treatment. Since syndromic treatment, by definition, is used only for persons with symptoms or signs of a clinical syndrome, this approach is not useful in detecting mild or asymptomatic infection. It should also be noted that, like any diagnostic test, the predictive value and therefore diagnostic utility of syndromic diagnosis will vary with the prevalence of the disease being tested for in the population. In low-prevalence populations, construing all cervicitis or urethritis to represent an STD may result in a large number of false positive diagnoses, unnecessary treatment, and potential psychological distress.
Laboratory testing for specific causative infectious agents is necessary for the detection of minimally symptomatic and asymptomatic individuals. There are STDs, such as gonorrhea, for which the antimicrobial resistance patterns of the pathogen are important. The isolation of the pathogen permits a determination of sensitivity or resistance to appropriate antibiotics. In addition, laboratory isolation of the pathogen allows specific testing for epidemiological purposes to track the spread of infection in a population. Although analyses of antimicrobial resistance patterns for STDs are seldom used to guide individual treatment, they are essential to develop community-based treatment guidelines. Unfortunately, some specific laboratory tests are often not available at clinical sites other than dedicated STD clinics and, even when available, the test results are often not available during the initial patient visit. In addition, the expense of these tests may limit their availability and utility.
Specific laboratory tests often guide therapeutic decisions. Ideally, the test could distinguish between past and present infection. The adequacy of specimens collected and specimen transport conditions are important modifiers of test performance. For example, there may be nonpathogenic microorganisms present in some of the sites being sampled, and specimens must be managed to preserve the
integrity of the more labile organisms. For STDs, specimen collection procedures, such as a pelvic examination or obtaining a urethral swab, may be a disincentive for patients to seek testing or for providers to perform the test. Although diagnostic tests are available for each of the common STDs, they will not be appropriately utilized if the test is too expensive or limited in availability (Hitchcock et al., 1991).
Culturing
Culturing of the pathogen is a common laboratory test for specific diagnosis of many STDs. When available, organism-specific cultures are often the "gold standard" for etiologic diagnosis. However, recently available amplified nucleic acid detection tests, such as polymerase chain reaction (PCR) or ligase chain reaction (LCR), may soon displace culturing as these tests become more available and assessment of these tests is completed (Rumpianesi et al., 1996). The only bacterial STD that is very commonly diagnosed by culturing in North America is gonorrhea. The sensitivity of the culture technique is subject to conditions that affect pathogen viability, including transport time and conditions. The specificity is 100 percent with no false positive results except in cases of laboratory error. The medium for optimal culture diagnosis, however, may not be uniformly available. Currently, in the United States, nonamplified probe tests are probably performed almost as often as culture for the diagnosis of gonorrhea.
Microscopy
Results of microscopy are rapidly available and are of considerable importance in refining syndromic diagnoses. Sensitivity of this technique, however, varies with the pathogen suspected and the expertise of the microscopist. The preferred method for diagnosis of urethritis in men and vaginal discharge syndromes in women is the microscopic examination of materials. Because microscopy requires time, clinicians are discouraged from using it. Different stains and methodology are necessary for diagnosis of different STDs. Microscopic evaluation of Papanicolaou (Pap) stained smears of cervical specimens is a useful test for detection of malignant and premalignant cellular changes related to human papillomavirus infection.
Antibody Detection Tests
Currently, serological tests to detect antibodies against STDs are most often used for the diagnosis of syphilis, HIV infection, and viral hepatitis in North America. One of the advantages of serological testing is that multiple evaluations for different pathogens can be performed on a single serum specimen. The presence of antibody in a single serum, however, may not distinguish between previous
infection and existing infection. This is of particular importance if the disease has been appropriately treated in the past but the serological test remains positive. Potentially, serological testing can lead to false positive results if antibodies against an infection other than the one tested for produce a positive reaction in the assay. Serological tests are particularly useful for screening because they can be performed in large numbers by automation and by central laboratories that can process entire groups of sera at once.
Antigen Detection Tests
These tests use pathogen-specific antibodies to detect proteins, carbohydrates, or lipid-carbohydrates present on the surface of STD pathogens. They have been extensively used for the diagnosis of STDs such as hepatitis B virus infection, chlamydial infection, and genital herpes and are potentially very useful for syphilis. For example, a fluorescent antibody kit used fluorescein-labeled antichlamydia antibodies to stain specimens collected from the urethra or cervix and then visualize chlamydial organisms under a fluorescent microscope. An alternate approach is solid phase immunoassay and involves a variety of formats that have been widely used in STD diagnostics. These tests can be used to detect organisms than cannot be cultured (grown in the laboratory) or that are difficult to culture. Many have become relatively inexpensive, and some can be used for rapid diagnosis of STDs in the clinic. However, these tests, particularly the rapid tests, are generally less sensitive than culture tests (for the culturable organisms) or genomic detection tests, which are therefore beginning to replace the antigen detection tests and are described below.
Tests Based on Genetic Markers
There are two basic types of genetically based tests available. Nonamplified tests use a nucleic acid probe to detect the extremely small amount of an infectious organism's unique genetic sequence (nucleic acid) present in an infected person. In contrast, amplified tests first make many copies of an organism's genetic sequence, thereby magnifying the "signal" of the organism and enhancing the ease of detection.
Since the late 1980s, the availability of nonamplified nucleic acid detection tests has significantly increased the availability of diagnostic testing for chlamydial infection and gonorrhea in North America. Currently, most specific diagnoses of chlamydial infections are accomplished using these methods. Compared to culture, nucleic acid probe tests are more practical for STD diagnosis in many settings because they are less expensive and because specimens do not need to be handled and transported under ideal conditions. On the other hand, these tests are usually less sensitive than culturing, especially for patients with small infectious burdens, such as asymptomatic patients.
Nucleic acid amplification tests, such as PCR and LCR, are increasingly being utilized for diagnosis of many infections and will likely be considered the standard for diagnosis of STDs in the future. Chlamydial, gonorrhea, and HIV diagnostic tests from one or more manufacturers are currently approved by the Food and Drug Administration. Prototype tests for the diagnosis of syphilis, genital herpes, human papillomavirus, trichomonas, and most other sexually transmitted pathogens are in various stages of development. Because these assays amplify genetic material from infectious organisms, their specificity can approach 100 percent if the proper genetic sequences are selected for the test; their sensitivity is a function of the amplification process. In certain situations, such as when tests are performed soon after therapy, false positive results may be a problem. Nucleic acid amplification tests have been as sensitive as culture for several STDs, and the detection of some pathogens such as chlamydial and herpes virus has been improved by these tests. The causative pathogens of human papillomavirus and syphilis cannot be cultured but can be detected using these sensitive techniques. In addition, the sensitivity of these tests has enabled clinicians to use more easily collected specimens for diagnosis, such as simple urine and vaginal swabs, rather than specimens obtained by more invasive sampling techniques. Lastly, the tests are not dependent on the presence of viable organisms in the specimen; therefore, handling and transport of specimens are relatively easy.
Treatment for STDs
The diagnosis of an STD should lead to either curative and/or preventive therapy for the infected individual. Although ideal therapy does not exist for many infections, highly effective antimicrobial therapy is available for all bacterial STDs as well as those caused by protozoa and ectoparasites (CDC, 1993a). They are administered to eradicate infection and to prevent its complications. In contrast, drugs for viral STDs have largely been limited to alleviating symptoms because they cannot eradicate the organism. However, many viral STDs (e.g., HIV infection, genital herpes, hepatitis B virus infection) are increasingly being viewed as suppressible infections with new therapies. These treatments suppress viral replication and thereby reduce transmission and may be considered to be a viable approach for preventing STDs.
Utilization of antimicrobial drugs is guided by both syndromic and etiologic diagnoses. The STD Treatment Guidelines published by the CDC provide the current standards for therapy of STDs (CDC, 1993a). A significant barrier to appropriate treatment is failure to comply with a full course of medication. To address this problem, effective single-dose therapy for several STDs (e.g., chancroid, gonorrhea, syphilis, trichomoniasis) has been available for some time, and single-does therapy for chlamydial infection has recently become available. These single-dose regimens have been shown to be as effective as multiple-dose regimens
(CDC, 1993a; Thorpe et al., 1996; Zenilman, 1996). Some single-dose therapies, however, are substantially more expensive than standard multiple-dose medications.7
Various clinical encounters for potential health problems other than STDs can provide a valuable opportunity for clinicians to evaluate and, if appropriate, treat persons for STDs. In particular, persons seeking health services for unintended pregnancy, contraception, or potential HIV infection are also at high risk for STDs. In addition, such encounters provide ''teaching moments" where patients are more likely to be receptive to prevention messages (Bigelow et al., 1986). Thus, examples of underutilized opportunities to both prevent and treat STDs are clinical encounters for family planning services, evaluation of an unintended pregnancy, and encounters for HIV testing and counseling. Newer technologies, such as noninvasive diagnostic tests for STDs, would make the evaluation of patients in the above clinical venues much more practical.
Barriers to Diagnosis and Effective Treatment
Although many useful diagnostic tests and effective drugs for STDs are available, they have not been successfully used on a national basis. Several major barriers prevent early diagnosis and treatment of infected persons. These include inadequate access to health care, lack of health-care-seeking behavior, inadequate training of health care providers, inadequate financial and physical access to laboratory tests, and geographic factors.
Inadequate access to effective health care, as discussed in Chapter 3, is the major impediment to appropriate diagnosis and treatment of STDs, particularly because the young and certain ethnic and racial groups, who have the highest rates of STDs, are the least likely to have health insurance coverage. In the United States, diagnosis and treatment cannot occur without the direct assistance of a licensed health care provider. Factors that prevent persons from seeking health care for potential STDs, including lack of perception of risk, misinformation and lack of knowledge about STDs, and the social stigma of STDs, are mentioned in Chapter 3. Inadequate training of health care providers is a serious barrier to early diagnosis and treatment of STDs because it results in clinicians who are not aware of the scope of STDs and lack the clinical skills necessary for diagnosing and managing an STD. This issue is discussed further in Chapter 5. In addition, although newer laboratory tests hold much promise for improved screening and diagnosis, financial and physical accessibility to these tests presents a barrier to
clinician diagnosis. Expense is especially problematic in publicly sponsored facilities, and accessibility is also difficult in remote areas.
Geographic factors also present challenges to diagnosis and treatment of STDs. Specifically, some regions of the United States and rural areas have to overcome unique obstacles in ensuring access to STD-related services. For example, states along the national borders may have difficulty in identifying and reaching partners because of language and cultural barriers. These regions may also have difficulty in ensuring effective treatment of STDs as people seek care on both sides of the border. In rural areas, low population density makes it difficult to ensure convenient access to STD-related services and to maintain a ready group of health care professionals who are adequately trained and available to provide such services, especially during outbreak situations. In anticipation of sporadic demands for services, some health departments have organized provider networks.
Conclusions
There are many behavioral interventions that have been shown to change health risk behaviors, including sexual behavior. There also are biomedical interventions that are highly effective. If these interventions could be widely implemented in a comprehensive fashion, they would likely have a substantial impact on the prevention of STDs. The three primary goals of both individual- and population-based interventions are to prevent exposure to an STD, prevent acquisition of infection once exposed, and prevent transmission of the infection to others. Given the variety of factors that influence the risk for STDs, it is clear that a multifaceted approach to prevention that integrates both biomedical and behavioral interventions is needed.
Individual factors that increase risk of STDs, such as high-risk sexual behavior, misperception of risk, and lack of personal skills, need to be targeted on a national basis because of the high prevalence of these factors in the general population. Individual behavior, however, is clearly influenced by social factors such as inadequate access to health care. Many individual- and community-level behavioral interventions have been shown to be effective in changing risk behaviors for STDs. Promotion of condom use, in particular, will continue to be a central strategy for preventing STDs. Given the high rates of sexual activity among adolescents, school-based health programs deserve particular emphasis. Although not all school-based programs to reduce risky sexual behaviors have been effective, there is little evidence of adverse outcomes. Interventions that involve the mass media also can have beneficial effects on knowledge and health behavior, especially for adolescents. Clinical methods that are effective in preventing exposure and reducing transmission include prophylaxis and partner notification and treatment. Although treatment of sex partners of infected persons is critical to STD prevention, the traditional methods for identifying partners
need to be reevaluated and redesigned in light of the changing epidemiology and social context of STDs.
The duration of sexually transmitted infections and thus the period during which infected individuals are infectious to others can be reduced primarily by ensuring early diagnosis and treatment of infected persons through screening programs and by improving the clinical skills of health care providers. Appropriate use and interpretation of diagnostic tests and access to laboratory services are essential in ensuring accurate diagnosis and treatment. Barriers to early detection and treatment, such as inadequate access to health care and lack of health-care-seeking behavior, need to be addressed.
References
AAFP (American Academy of Family Physicians). Age charts for periodic health examination. Kansas City, MO: American Academy of Family Physicians, 1994 (reprint no. 510).
AAP (American Academy of Pediatrics), Committee on Adolescence. Sexually transmitted diseases. Pediatr 1994;94 (Pt. 1):568-72.
AAP, Committee on Adolescence. Condom availability for youth. Pediatr 1995;95:281-5.
ACOG (American College of Obstetricians and Gynecologists). Human immunodeficiency virus infection. Washington, D.C.: American College of Obstetricians and Gynecologists, 1992. [Technical Bulletin No. 169.]
Addiss DG, Vaughn ML, Hillis SD, Ludka D, Amsterdam L, Davis JP. History and features of the Wisconsin Chlamydia trachomatis control program. Fam Plann Perspect 1994;26:83-9.
Adler NE, Tschann, JM. Conscious and preconscious motivation of pregnancy among female adolescents. In: Lawson A, Rhode D, eds. The politics of pregnancy: adolescent sexuality and public policy. New Haven, CT: Yale University Press, 1993:144-58.
Advocates for Youth. Condom availability in schools: an integral component to comprehensive school health programs. Washington, D.C., 1995.
Ajzen I, Fishbein M. Understanding attitudes and predicting social behavior. Englewood, NJ: Prentice-Hall, 1980.
Alary M, Joly JR, Poulin C. Gonorrhea and chlamydial infection: comparison of contact tracing performed by physicians or by a specialized service. Can J Public Health 1991:82;132-4.
Allen S, Tice J, Van de Perre P, Serufilira A, Hudes E, Nsengumuremyi F, et al. Effect of serotesting with counselling on condom use and seroconversion among HIV discordant couples in Africa. British Med J 1992;304:1605-9.
AMA (American Medical Association). HIV blood test counseling. Physician guidelines. 2nd ed. Chicago: American Medical Association, 1993.
AMA. Policy compendium on reproductive health issues affecting adolescents. Gans Epner JE, ed. Chicago: American Medical Association, 1996.
ASHA (American Social Health Association). Teenagers know more than adults about STDs, but knowledge among both groups is low. STD News. A quarterly newsletter of the American Social Health Association. Winter 1996;3:1, 5.
Anderson JE, Brackhill R, Mosher WD. Condom use for disease prevention among unmarried U.S. women. Fam Plann Perspect 1996;28:25-8, 39.
Anderson RM. The transmission dynamics of sexually transmitted diseases: the behavioral component. In: Wasserheit JN, Aral SO, Holmes KK, Hitchcock PJ, eds. Research issues in human behavior and sexually transmitted diseases in the AIDS era. Washington, D.C.: American Society for Microbiology, 1991:38-60.
Anderson RM, May RM. Infectious diseases of humans: dynamics and control. Oxford, England: Oxford University Press, Inc., 1991.
Andreasen AR. Marketing social change. San Francisco: Jossey-Bass, 1995.
Andrus JK, Fleming DW, Harger DR, Chin MY, Bennet DV, Horan JM, et al. Partner notification: can it control epidemic syphilis [see comments]? Ann Intern Med 1990;112:539-43.
Aral SO. Sexual behavior in sexually transmitted disease research. An overview. Sex Transm Dis 1994;21(March-April Suppl):S59-S64.
Arevalo JA, Washington AE. Cost-effectiveness of perinatal screening and immunization for hepatitis B virus. JAMA 1988;259:365-9.
Baldwin JD, Baldwin JI. Factors affecting AIDS-related sexual risk-taking behavior among college students. J Sex Res 1988;25:181-96.
Bandura A. Social learning theory. Englewood, NJ:Prentice-Hall, 1977.
Bandura A. Perceived self-efficacy in the exercise of control over AIDS infection. Eval Program Plann 1990;13:9-17.
Baumgartner L, Curtis AC, Gray AL, Kuechle BE, Richman TL. The eradication of syphilis: a task force report. Washington, D.C.: Government Printing Office, 1962. [Public Health Service Publication No. 918.]
Bayer R, Toomey KE. HIV prevention and the two faces of partner notification [see comments]. Am J Public Health 1992;82:1158-64.
Becker MH, Maiman LA. Sociobehavioral determinants of compliance with health and medical care recommendations. Medical Care 1975;13:10-24.
Bigelow GE, Rand CS, Gross J, Burling TA, Gottlieb SH. Smoking cessation and relapse among cardiac patients . In: Tims FM, Leukefeld CG, eds. Relapse and recovery in drug abuse. NIDA Research Monograph No. 72, DHHS Publication No. (ADM) 86-1473. Washington D.C.: Government Printing Office, 1986.
Blackmore CA, Limpakarnjanarat K, Rigan-Perez JG, Albritton WL, Greenwood JR. An outbreak of chancroid in Orange County California: descriptive epidemiology and disease-control measures. J Infect Dis 1985;151:840-4.
Brandt AM. No magic bullet: a social history of venereal disease in the United States since 1880. New York: Oxford University Press, Inc., 1985.
Brien TM, Thombs DL, Mahoney CA, Wallnau L. Dimensions of self-efficacy among three distinct groups of condom users. J Am Coll Health 1994;42:167-74.
Brindis CD. Funding and policy options. In: Samuels SE, Smith MD, eds. Condoms in the schools. Menlo Park, CA: Henry J. Kaiser Family Foundation, 1993:37-61.
Britton TF, DeLisle S, Fine K. STDs and family planning clinics: a regional program for chlamydial control that works. Am J Gynecol Health 1992;6:80-7.
Brown LK, DiClemente RJ, Park T. Predictors of condom use in sexually active adolescents. J Adolesc Health 1992;13:651-7.
Catania JA, Coates TH, Kegeles S, Fullilove MT, Peterson J, Marin B, et al., Condom use in multiethnic neighborhoods of San Francisco: the population-based AMEN (AIDS in Multi-Ethnic Neighborhoods) Study. Am J Public Health 1992;82:284-7.
Catania JA, Dolcini MM, Coates TJ, Kegeles SM, Greenblatt RM, Puckett S, et al. Predictors of condom use and multiple-partnered sex among sexually-active adolescent women: implications for AIDS-related health interventions. J Sex Res 1989;26:514-24.
Catania JA, Kegeles SM, Coates TJ. Towards an understanding of risk behavior. An AIDS risk reduction model (ARRM). Health Educ Q 1990; 17:53-72.
Cates W Jr., Stewart FH, Trussell J. Commentary: the quest for women's prophylactic methods-hopes vs science. Am J Public Health 1992;82:1479-82.
Cates W Jr., Stone KM. Family planning, sexually transmitted diseases, and contraceptive choice: a literature update. Fam Plann Perspect 1992;24:75-84.
CDC (Centers for Disease Control and Prevention). Alternate case-finding methods in a crack-related syphilis epidemic—Philadelphia. MMWR 1991a;40:77-80.
CDC. Hepatitis B virus: a comprehensive strategy for eliminating transmission in the United States through universal childhood vaccination: recommendations of the Immunization Practices Advisory Committee (ACIP). MMWR 1991b;40(RR-13):1-20.
CDC. HIV-risk behaviors of sterilized and nonsterilized women in drug-treatment programs—Philadelphia, 1989-1991. MMWR 1992a;41:149-52.
CDC. Surgical sterilization among women and use of condoms—Baltimore, 1989-1990. MMWR 1992b;41:568-75.
CDC. 1993 Sexually transmitted diseases treatment guidelines. MMWR 1993a;42 (No. RR-14):56-66.
CDC. Update: barrier protection against HIV infection and other sexually transmitted diseases. MMWR 1993b;42:589-91, 597.
CDC. ACIP approves additional groups covered under the vaccines for children (VFC) program. [Memorandum to immunization program managers from Director, National Immunization Program, and Chief, Hepatitis Branch.] September 9, 1994a.
CDC. Hepatitis B vaccination of adolescents—California, Louisiana, and Oregon, 1992-1994. MMWR 1994b;43:605-9.
CDC. Trends in sexual risk behavior among high school students—United States, 1990, 1991, and 1993. MMWR 1995a;44:124-5, 131-2.
CDC. Update: recommendations to prevent hepatitis B virus transmission—United States. MMWR 1995b;44:574-5.
CDC. Community-level prevention of human immunodeficiency virus infection among high-risk populations: the AIDS Community Demonstration Projects. MMWR 1996a;45(RR-6).
CDC. School-based HIV-prevention education—United States, 1994. MMWR 1996b;45:760-5.
CDC. Undervaccination for hepatitis B among young men who have sex with men—San Francisco and Berkeley, California, 1992-1993. MMWR 1996c;45:215-7.
CDC, DSTD/HIVP (Division of STD/HIV Prevention). Approaches to partner notification and syphilis; partner notification and gonorrhea. Centers for Disease Control and Prevention. Internal working documents, 1992.
CDC, DSTD/HIVP. Plan for a national partnership to prevent STD-related infertility. Draft internal document, January 10, 1995.
Cleary PD, Barry MJ, Mayer KH, Brandt AM, Gostin L, Fineberg HV. Compulsory premarital screening for the human immunodeficiency virus: technical and public health considerations. JAMA 1987;258:1757-62.
Cleary PD, Rogers TF, Singer E, Avorn J, Van Devanter N, Perry S, et al. Health education about AIDS among seropositive blood donors. Health Educ Q 1986;13:317-29.
Cleary PD, Van Devanter N, Rogers TF, Singer E, Shipton-Levy R, Steilen M, et al. Behavior changes after notification of HIV infection. Am J Public Health 1991;81:1586-90.
Cleary PD, Van Devanter N, Steilen M, Stuart A, Shipton-Levy R, McMullen W, et al. A randomized trial of an education and support program for HIV-infected individuals. AIDS 1995;9:1271-8.
Collins JL, Small ML, Kann L, Collins Pateman B, Gold RS, Kolbe LJ. School health education. J School Health 1995;65:302-11.
Dawson DA. The effects of sex education on adolescent behavior. Fam Plann Perspect 1986;18:162-70.
DeBuono BA, Zinner SH, Daamen M, McCormack WM. Sexual behavior of college women in 1975, 1986, and 1989. N Engl J Med 1990;322:821-5.
DeJong W. Condom promotion: the need for social marketing program in America's inner cities. Am J Health Promot 1989;3:5-10.
DiClemente RJ, Wingood GM. A randomized controlled trial of an HIV sexual risk reduction intervention for young African American women. JAMA 1995;274:1271-6.
Donovan P. Taking family planning services to hard-to-reach populations. Fam Plann Perspect 1996;28:120-6.
EDK Associates. Women & sexually transmitted diseases: the dangers of denial. New York: EDK Associates, 1994.
EDK Associates. The ABCs of STDs. New York: EDK Associates, 1995.
Edlin BR, Irwin KL, Faruque S, McCoy CB, Work C, Serrano Y, et al. Intersecting epidemics-crack cocaine and HIV infection among inner-city young adults. The Multi-center Crack Cocaine and HIV Infection Study Team. N Engl J Med 1994;331:1422-7.
Elias CJ, Heise LL. Challenges for the development of female-controlled vaginal microbicides. AIDS 1994;8:1-9.
Ellen JM, Cahn S, Eyre SL, Boyer CB. Types and attributes of adolescent sexual partnerships and their association with condom use. J Adolesc Health 1996;18:417-21.
Engelgau MM, Woernle CH, Rolfs RT, Greenspan JR, O'Cain M, Gorsky, RD. Control of epidemic early syphilis: the results of an intervention campaign using social networks. Sex Transm Dis 1995;22:203-9.
European Study Group on Heterosexual Transmission of HIV. Comparison of female to male and male to female transmission of HIV in 563 stable couples. Br Med J 1992;304:809-13.
Fanburg JT, Kaplan DW, Naylor KE. Student opinions of condom distribution at a Denver, Colorado, high school. J Sch Health 1995;65:181-5.
Farr G, Gabelnick H, Sturgen K, Dorflinger L. Contraceptive efficacy and acceptability of the female condom. Am J Public Health 1994;84:1960-4.
Fee E, Krieger N. Understanding AIDS: historical interpretations and the limits of biomedical individualism. Am J Public Health 1993;83:1477-86.
Felman Y. Repeal of mandated premarital tests for syphilis: a survey of state health officers. Am J Public Health 1981;71:155-9.
Flay BR. Mass media and smoking cessation: a critical review. Am J Public Health 1987;77:153-60.
Flora JA, Miabach EW, Holtgrave D. Communication campaigns for HIV prevention: using mass media in the next decade. In: IOM. Assessing the social and behavioral science base for HIV/AIDs prevention and intervention. Background papers. Washington, D.C.: National Academy Press, 1995:129-54.
Forrest JD, Silverman J. What public school teachers teach about preventing pregnancy, AIDS and sexually transmitted diseases [see comments]. Fam Plann Perspect 1989;21:65-72.
Franzini LR, Sideman LM. Personality characteristics of condom users. J Sex Educ Ther 1994;20:110-8.
Gerrard M. Sex, sex guilt and contraceptive use revisited: the 1980s. J Pers Soc Psychol 1987;52:975-80.
Gerrard M, Gibbons FX, McCoy SB. Emotional inhibition of effective contraception. Anxiety, Stress, and Coping 1993;6:73-88.
Giesecke J, Ramstedt K, Granath F, Ripa T, Rado G, Westrell M. Efficacy of partner notification for HIV infection. Lancet 1991;33:1096-100.
Gold RS, Skinner MJ, Ross MW. Unprotected anal intercourse in HIV-infected and non-HIV-infected gay men. J Sex Res 1994; 3159-77.
Gollub EL, Stein ZA. Commentary: the new female condom—item 1 on a women's AIDS prevention agenda. Am J Public Health 1993;83:498-500.
Greene BZ. The view from schools: four focus groups. In: Samuels SE, Smith MD, eds. Condoms in the schools. Menlo Park, CA: Henry J. Kaiser Family Foundation, 1993:25-36.
Grosskurth H, Mosha F, Todd J, Mwijarubi E, Klokke A, Senkoro K, et al. Impact of improved treatment of sexually transmitted diseases on HIV infection in rural Tanzania: randomized controlled trial [see comments]. Lancet 1995a;346:530-6.
Grosskurth H, Mosha F, Todd J, Senkoro K, Newell J, Klokke A, et al. A community trial of the impact of improved STD treatment on the HIV epidemic in rural Tanzania: 2 baseline survey results. AIDS 1995b;9:927-34.
Gunn RA, Montes JM, Toomey KE, Rolfs RT, Greenspan JK, Spitters CE, et al. Syphilis in San Diego County 1983-1992: crack cocaine, prostitution, and the limitations of partner notification. Sex Transm Dis 1995;22:60-6.
Guttmacher S, Lieberman L, Hoi-Chang W, Ward D, Radosh A, Rafferty Y, Freudenberg N. Gender differences in attitudes and use of condom availability programs among sexually active students in New York City public high schools. J Am Med Women's Assoc 1995a;50:99-102.
Guttmacher S, Lieberman L, Ward D, Radosh A, Rafferty Y, Freudenberg N. Parents' attitudes and beliefs about HIV/AIDS prevention with condom availability in New York City public high schools. J Sch Health 1995b;65:101-6.
Handsfield HH, Jasman LL, Roberts PL, Hanson VW, Kothenbeutel RL, Stamm WE. Criteria for selective screening for Chlamydia trachomatis infection in women attending family planning clinics. JAMA 1986;255:1730-4.
Handsfield HH, Rice RJ, Roberts MC, Holmes KK. Localized outbreak of penicillinase-producing Neisseria gonorrhoea. Paradigm for introduction and spread of gonorrhoea in a community. JAMA 1989;261:2357-61.
Handsfield HH, Sandstrom EG, Knapp JS, Perine PL, Whittington, WL, Sayers DE, et al. Epidemiology of penicillinase-producing Neisseria gonorrhoea infections: analysis by auxotyping and serogrouping. N Engl J Med 1982;306:950-4.
Haskell RJ. A cost-benefit analysis of California's mandatory premarital screening program for syphilis. West J Med 1984;141:538-41.
Herold ES, McNamee JE. An explanatory model of contraceptive use among young single women. J Sex Res 1982;18:289-304.
Higgins DL, Galavotti C, O'Reilly KR, Schnell DJ, Moore M, Rugg DL, et al. Evidence for the effects of HIV antibody counseling and testing on risk behaviors. JAMA 1991;266:2419-29.
Hillis S, Black C, Newhall J, Walsh C, Groseclose SL. New opportunities for chlamydial prevention: applications of science to public health practice. Sex Transm Dis 1995;22:197-202.
Hillis SD, Nakashima A, Amsterdam L, Pfister J, Vaughn M, Addiss D, et al. The impact of a comprehensive chlamydial prevention program in Wisconsin. Fam Plann Perspect 1995;27:108-11.
Hingson RW, Strunin L, Berlin BM, Hereen T. Beliefs about AIDS, use of alcohol and drugs, and unprotected sex among Massachusetts adolescents. Am J Public Health 1990;80:295-9.
Hitchcock PJ, Wasserheit JN, Harris JR, Holmes KK. Sexually transmitted diseases in the AIDS era. Development of STD diagnostics for resource-limited settings is a global priority. Sex Transm Dis 1991;18:133-5.
Hobfoll SE, Jackson AP, Lavin J, Britton PJ, Shepherd JB. Reducing inner-city women's AIDS risk activities. Health Psychol 1994;13:397-403.
Holtgrave DR, Qualls NL, Curran JW, Valdiserri RO, Guinan ME, Parra WC. An overview of the effectiveness and efficiency of HIV prevention programs. Public Health Rep 1995;110:134-46.
IOM (Institute of Medicine). Understanding the determinants of HIV risk behavior. In: Auerbach JD, Wypijewska C, Brodie HKH, eds. AIDS and behavior. Washington, D.C.: National Academy Press, 1994:78-123.
IOM. Best intentions: unintended pregnancy and the well-being of children and families. Brown SS, Eisenberg L, eds. Washington, D.C.: National Academy Press, 1995.
IOM. Contraceptive research and development: looking to the future. Harrison PF, Rosenfield A, eds. Washington, D.C.: National Academy Press, 1996.
Janz NK, Becker MH. The health belief model: a decade later. Health Educ Q 1984;11:1-47.
Jemmott JB, Jemmott LS, Fong GT. Reductions in HIV risk-associated sexual behaviors among black male adolescents: effects of an AIDS prevention intervention . Am J Public Health 1992;82:392-77.
Joseph JG, Montgomery SB, Emmons CA, Kirscht JP, Kessler RC, Ostrow DG, et al. Perceived risk of AIDS: assessing the behavioral and psychosocial consequences in a cohort of gay men. J Appl Soc Psychol 1987;17:231-50.
Kalichman SC, Kelly JA, Johnson JR, Bulto M. Factors associated with risk for HIV infection among chronic mentally ill adults. Am J Psychiatry 1994;151:221-7.
Kalichman SC, Carey MP, Johnson BT. Prevention of sexually transmitted HIV infection: a meta-analytic review of the behavioral outcome literature. Ann Behav Change 1996;18:6-15.
Kamb ML, Douglas JM, Rhodes F, Bolan G, Zenilman J, Iatesta M, et al. A multi-center, randomized controlled trial evaluating HIV prevention counseling (Project RESPECT): Preliminary results. Eleventh International Conference on AIDS, July 7-12, 1996, Vancouver [abstract no. ThC 4380].
Katz BP, Blythe MJ, Van der Pol B, Jones RB. Declining prevalence of chlamydial infection among adolescent girls. Sex Transm Dis 1996;23:226-9.
Katz BP, Danos CS, Quinn TS, Caine V, Jones RB. Efficiency and cost-effectiveness of field followup for patients with Chlamydia trachomatis infection in a sexually transmitted diseases clinic. Sex Transm Dis 1988;15:11-6.
Kegeles SM, Adler NE, Irwin CD. Adolescents and condoms. Am J Dis Child 1989;143:911-5.
Kelly JA. Sexually transmitted disease prevention approaches that work. Interventions to reduce risk behavior among individuals, groups, and communities. Sex Transm Dis 1994;21[2 Suppl]:S73-S75.
Kelly JA, St. Lawrence JS, Diaz YE, Stevenson LY, Hauth AC, Grasfield TL, et al. HIV risk behaviors reduction following intervention with key opinion leaders of population: an experimental analysis. Am J Public Health 1991;81:168-71.
Kelly JA, St. Lawrence JS, Stevenson LY, Hauth AC, Kalichman SC, Diaz YE, et al. Community AIDS/HIV risk reduction: the effects of endorsements by popular people in three cities. Am J Public Health 1992;82:1483-9.
Kirby D. The effects of school sex education programs: a review of the literature. J Sch Health 1980;50:559-63.
Kirby D. Research and evaluation. In: Samuels SE, Smith MD, eds. Condoms in the schools. Menlo Park, CA: Henry J. Kaiser Family Foundation, 1993:89-109.
Kirby D. Sexuality and HIV education programs in schools. In: Garrison J, Smith MD, Besharov DJ, eds. Sexuality and American social policy: a seminar series. Sex education in the schools. Menlo Park, CA: Henry J. Kaiser Family Foundation, 1994;1-41.
Kirby DM, Brown NL. Condom availability programs in U.S. schools. Fam Plann Perspect 1996;28:196-202.
Kirby D, Short L, Collins J, Rugg D, Kolbe L, Howard M, et al. School-based programs to reduce sexual risk behaviors: a review of effectiveness. Public Health Rep 1994;109:339-60.
Kirby D, Waszak C, Ziegler J. Six school-based clinics: their reproductive health services and impact on sexual behavior. Fam Plann Perspect 1991;23:6-16.
Klovdahl AS, Potterat JJ, Woodhouse DE, Muth JB, Muth SQ, Darrow WW. Social networks and infectious disease: the Colorado Springs study. Soc Sci Med 1994;38:79-88.
Kollar LM, Rosenthal SL, Biro FM. Hepatitis B vaccine series compliance in adolescents. Pediatr Infect Dis J 1994;13:1006-8.
Koniak-Griffin D, Nyamathi A, Vasquez R, Russo AA. Risk-taking behaviors and AIDS knowledge: experiences and beliefs of minority adolescent mothers. Health Educ Res 1994;9:449-63.
Ku L, Sonenstein FL, Pleck JH. The association of AIDS education and sex education with sexual behavior and condom use among teenage men [published erratum appears in Fam Plann Perspect 1993 Jan-Feb;25:36]. Fam Plann Perspect 1992;24:100-6.
Ku L, Sonenstein FL, Pleck JH. Factors influencing first intercourse for young men. Public Health Rep 1993;108:680-94.
Ku L, Sonenstein FL, Pleck JH. The dynamics of young men's condom use during and across relationships. Fam Plann Perspect 1994;26:246-51.
Lafferty W. Ditmer D, Krekeler B, Stoner B, Tyrea T, Sucato G, et al. Feasibility of vaccinating high-risk adolescents for hepatitis B at STD clinic sites. Eleventh Meeting of the International Society for STD Research, New Orleans, August 27-30, 1995 [abstract no. 193].
Landry DJ, Camelo TM. Young unmarried men and women discuss men's role in contraceptive practice. Fam Plann Perspect 1994;26:222-7.
Laumann EO, Gagnon JH, Michael RT, Michaels S. The social organization of sexuality: sexual practices in the United States. Chicago, IL: University of Chicago Press, 1994.
Laurian Y, Peynet J, Verroust F. HIV infection in sexual partners of HIV seropositive patients with hemophilia . N Engl J Med 1989;320:183.
Lear D. Sexual communication in the age of AIDS; the construction of risk and trust among young adults. Soc Sci Med 1995; 41:1311-23.
Leitman R, Kramer E, Taylor H. A survey of condom programs. In: Samuels SE, Smith MD, eds. Condoms in the schools. Menlo Park, CA: Henry J. Kaiser Family Foundation, 1993:1-23.
Louv WC, Austin H, Alexander WJ, Stagno S, Cheeks J. A clinical trial of nonoxynol-9 as a prophylaxis for cervical Neisseria gonorrhoeae and Chlamydia trachomatis infections. J Infect Dis 1988;158:518-23.
Magura S, Shapiro JL, Kang S-Y. Condom use among criminally-involved adolescents. AIDS Care 1994;6:595-603.
Mahler K. Condom availability in the schools: lessons from the courtroom. Fam Plann Perspect 1996;28:75-7.
Mahoney CA, Thombs KL, Ford OJ. Health belief and self-efficacy models: their utility in explaining college student condom use. AIDS Educ Prev 1995;7:32-49.
Margolis HS, Coleman PJ, Brown RE, Mast EE, Sheingold SH, Arevalo JA. Prevention of hepatitis B virus transmission by immunization. An economic analysis of current recommendations. JAMA 1995;274:1201-8.
Marin BV, Gomez CA, Tschann JM. Condom use among Hispanic men with secondary female sexual partners. Public Health Rep 1993;108:742-50.
Marsiglio W, Mott F. The impact of sex education on sexual activity, contraceptive use and premarital pregnancy among American teenagers. Fam Plann Perspect 1986;18:151-62.
Marx R, Aral SO, Rolfs RT, Sterk CE, Kahn JG. Crack, sex, and STD. Sex Transm Dis 1991;18:92-101.
May RM, Anderson RM. Transmission dynamics of HIV infection. Nature 1987;326:137-42.
Mays VM, Cochran SD. Issues in the perception of AIDS risk and risk reduction activities by black and Hispanic/Latina women. Am Psychol 1988;43:949-57.
Molbert W, Boyer CB, Shafer MA. Implementing a school-based STD/HIV prevention intervention: collaboration between a university medical center and an urban school district. J Sch Health 1993;63:258-61.
Moran JS, Peterman TA, Weinstock HS, Bolan GA, Harden JW, Fleenor ME, et al. Hepatitis B vaccination trials in sexually transmitted disease clinics: implications for program development. Proceedings of the 26th National Immunization Conference, June 1992, St. Louis, MO:107-9.
Morris M. Epidemiology and social networks. Sociological Methods Res 1993;22:99-126.
Morris M, Pramualratana A, Podhisita C, Wawer MJ. The relational determinants of condom use with commercial sex partners in Thailand. AIDS 1995;9:507-15.
Morris M. Behavior change and non-homogeneous mixing. In: Isham V, Medley G, eds. Models for infectious human diseases. Cambridge, England: Cambridge University Press, 1996.
Morrison DM, Baker SA, Gillmore MR. Sexual risk behavior, knowledge, and condom use among adolescents in juvenile detention. J Youth Adolesc 1994;23:271-88.
Morrison DM, Shaklee H. Poor contraceptive use in the teenage years: situational and developmental interpretations. Adv Adolesc Mental Health 1990;4:51-69.
Munday PE, McDonald W, Murray-Sykes KM, Harris JR. Contact tracing in hepatitis B infection. Br J Vener Dis 1983;59:314-6.
Mwijarubi E, Grosskurth H, Mosha F, Mayaud P, Mugey K, Todd J, et al. Improved STD treatment significantly reduces prevalence of syphilis and symptomatic urethritis in rural Tanzania. Eleventh International Conference on AIDS, July 7-12, 1996, Vancouver [abstract LBC 6062].
NARAL (National Abortion Rights Action League) Foundation. Sexuality education in America: a state-by-state review, 1995. Rev. ed. Washington, D.C., September 1995.
Nelson KE, Celentano DD, Eiumtrakol S, Hoover DR, Beyrer C, Suprasert S, et al. Changes in sexual behavior and a decline in HIV infection among young men in Thailand. New Engl J Med 1996;335:297-303.
NIH (National Institutes of Health). The Jordan report: accelerated development of vaccines 1996. Bethesda, MD: National Institutes of Health, National Institute of Allergy and Infectious Diseases, Division of Microbiology and Infectious Diseases, 1996.
Norris AE, Ford K. Associations between condom experiences and beliefs, intentions, and use in a sample of urban, low-income, African-American and Hispanic youth. AIDS Educ Prev 1994;6:27-39.
Oakley A, Fullerton D, Holland J, Arnold S, France-Dawson M, Kelley P, et al. Sexual health education interventions for young people: a methodological review. Br Med J 1995;310:158-62.
Oakley A, Fullerton D, Holland J. Behavioral interventions for HIV/AID prevention. AIDS 1995;9:479-86.
O'Reilly KR, Higgins DL. AIDS Community Demonstration Projects for HIV prevention among hard-to-reach groups. Public Health Rep 1991;106:714-20.
O'Reilly KR, Piot P. International perspectives on individual and community approaches to the prevention of sexually transmitted disease and human immunodeficiency virus infection. J Infect Dis 1996;174(Suppl 2):S214-S222.
Orr DP, Langefeld CD. Factors associated with condom use by sexually active male adolescents at risk for sexually transmitted disease. Pediatr 1993;91:873-9.
Oxman AD, Scott EA, Sellors JW, Clarke JH, Millson ME, Rasooly I, et al. Partner notification for sexually transmitted diseases: an overview of the evidence. Can J Public Health 1994;85(1 Suppl):S41-7.
Oxman GL, Doyle L. A comparison of the case-finding effectiveness and average costs of screening and partner notification. Sex Transm Dis 1996;23:51-7.
Pendergrast RA, DuRant RH, Gaillard GL. Attitudinal and behavioral correlates of condom use in urban adolescent males. J Adolesc Health 1992;13:133-9.
Peterson LR, White CR. Premarital screening for antibodies to human immunodeficiency virus type 1 in the United States. The Premarital Screening Study Group. Am J Public Health 1990;80:1087-90.
Peterson LS. Contraceptive use in the United States: 1982-90. Advance data, No. 260. Hyattsville, MD: National Center for Health Statistics, February 14, 1995.
Phillips L, Potterat JJ, Rothenberg RB, Pratt C, King RD. Focused interviewing in gonorrhea control. Am J Public Health 1980;70:705-8.
Pilkington CJ, Kern W, Indest D. Is safer sex necessary with a "safe" partner? Condom use and romantic feelings. J Sex Res 1994;31:203-10.
Pleck JH, Sonenstein FL, Ku L. Changes in adolescent males' use of and attitudes toward condoms, 1988-1991. Fam Plann Perspect 1993;25:106-10, 17.
Pleck JH, Sonenstein FL, Ku LC. Adolescent males' condom use: relationships between perceived cost-benefits and consistency. J Marriage Fam 1991;53:733-46.
Potterat JJ, Spencer NE, Woodhouse DE, Muth JB. Partner notification in the control of human immunodeficiency virus infection. Am J Public Health 1989;79:874-6.
Prochaska JD, DiClemente CC. Stages and processes of self-change of smoking: toward an integrative model of change. J Consult Clin Psychol 1983;51:390-5.
Ramos R, Shain, RN, Johnson L. ''Men I mess with don't have anything to do with AIDS": Using ethno-theory to understand sexual risk perception. Sociological Q 1995;36:483-504.
Ramstedt K, Giescecke J, Forssman L, Granath L. Choice of sexual partner according to rate of partner change and social class of partners. Int J STD AIDS 1991;2:428-31.
Randolph AG, Washington AE. Screening for Chlamydia trachomatis in adolescent males: a cost-based decision analysis. Am J Public Health 1990;80:545-50.
Richert CA, Peterman TA, Zaidi AA, Ransom RL, Wroten JE, Witte JJ. A method for identifying persons at high risk for sexually transmitted infections: opportunity for targeting intervention. Am J Public Health 1993;83:520-4.
Rickman RL, Lodico M, DiClemente RJ, Morris R, Baker C, Huscroft S. Sexual communication is associated with condom use by sexually active incarcerated adolescents. J Adolesc Health 1994;15:383-8.
Rogers EE. Diffusion of innovations. New York: Free Press, 1983.
Rojanapithayakorn W, Hanenberg R. The 100% Condom Program in Thailand. AIDS 1996;10:1-7.
The Roper Organization. AIDS: public attitudes and education needs. 1991. [Poll conducted for Gay Men's Health Crisis, New York.]
Roper WL, Peterson HB, Curran JW. Commentary: condoms and HIV/STD prevention—clarifying the message. Am J Public Health 1993;83:501-3.
Rosenberg MJ, Gollub EL. Commentary: methods women can use that may prevent sexually transmitted diseases, including HIV. Am J Public Health 1992;82:1473-8.
Rothenberg R, Narramore J. The relevance of social network concepts to sexually-transmitted disease-control. Sex Transm Dis 1996;23:24-9.
Rothenberg RB, Potterat JJ. Strategies for management of sex partners. In: Holmes KK, Mårdh P-A, Sparling PF, Wiesner PJ, Cates W Jr., Lemon SM, et al., eds. Sexually transmitted diseases. 2nd ed. New York: McGraw Hill, Inc., 1990:1081-6.
Rothenberg RB, Potterat JJ. Partner notification for STD/HIV. In: Holmes KK, Sparling PF, Mårdh P-A, Lemon SM, Stamm WE, Piot P, et al., eds. Sexually transmitted diseases. 3rd ed. New York: McGraw Hill, Inc., in press.
Rotheram-Borus MJ, Koopman C, Haignere C, Davies M. Reducing HIV sexual risk behaviors among runaway adolescents. JAMA 1991;266:1237-41.
Rotheram-Borus MJ, Rosario M, Reid H, Koopman C. Predicting patterns of sexual acts among homosexual and bisexual youths. Am J Psychiatry 1995;152:588-95.
Rumpianesi F, Donati M, Negosanti M, D'Antuono A, La Placa M, Cevenini R. Detection of Chlamydia trachomatis by a ligase chain reaction amplification method. Sex Transm Dis 1996;23:177-80.
Rutherford GW, Woo JM, Neal DP, Rauch KJ, Geohegan C, McKinney KC, et al. Partner notification and the control of human immunodeficiency virus infection. Two years of experience in San Francisco. Sex Transm Dis 1991;18:107-10.
Santelli JS, Kouzis AC, Hoover DR, Polacsek M, Burwell LG, Celentano DD. Stage of behavior change for condom use: the influence of partner type, relationship and pregnancy factors. Fam Plann Perspect 1996;28:101-7.
Schaalma H, Kok G, Peters L. Determinants of consistent condom use by adolescents—the impact of experience of sexual intercourse. Health Educ Res 1993;8:255-69.
Scholes D, Stergachis A, Heidrich FE, Andrilla H, Holmes KK, Stamm WE. Prevention of pelvic inflammatory disease by screening for cervical chlamydial infection. New Engl J Med 1996;334:1362-6.
Schwarcz SK, Bolan GA, Fullilove M, McCright J, Fullilove R, Kohn R, et al. Crack cocaine and the exchange of sex for money or drugs. Risk factors for gonorrhea among black adolescents in San Francisco. Sex Transm Dis 1992;19:7-13.
Sellers DE, McGraw SA, McKinlay JB. Does the promotion and distribution of condoms increase teen sexual activity? Evidence from an HIV prevention program for Latino youth. Am J Public Health 1994;84:1952-8.
Shain R, Piper J, Newton E, Perdue S, Ramos R, Dimmitt J, et al. Preventing sexually transmitted disease among minority women: results of a controlled randomized trial at 12 months' follow-up. Eleventh International Conference on AIDS, July 7-12, 1996, Vancouver [abstract no. MoD 1773-MoD 1779].
Shafer MA, Boyer CB. Psychosocial and behavioral factors associated with risk of sexually transmitted diseases, including human immunodeficiency virus infection, among urban high school students. J Pediatr 1990;119:826-33.
Shoop DM, Davidson PM. AIDS and adolescents: the relation of parent and partner communication to adolescent condom use. J Adolesc 1994;17:137-48.
Sparling PF, Aral SO. The importance of an interdisciplinary approach to prevention of sexually transmitted diseases. In: Wasserheit JN, Aral SO, Holmes KK, Hitchcock PJ, eds. Research issues in human behavior and sexually transmitted diseases in the AIDS era. Washington, D.C.: American Society for Microbiology, 1991:1-8.
Stein ZA. Editorial: the double bind in science policy and the protection of women from HIV infection. Am J Public Health 1992;82:1471-2.
Stergachis A, Scholes D, Heidrich FE, Sherer DM, Holmes KK, Stamm WE. Selective screening for Chlamydia trachomatis infection in a primary care population of women. Am J Epidemiol 1993;138:143-53.
Stiffman AR, Earls F, Dore P, Cunningham R. Changes in acquired immunodeficiency syndrome-related risk behavior after adolescence: relationships to knowledge and experience concerning human immunodeficiency virus infection . Pediatr 1992;89:950-6.
St. Lawrence JS, Jefferson KW, Alleyne E, Brasfield TL. Comparison of education versus behavioral skills training interventions in lowering sexual HIV-risk behavior of substance-dependent adolescents. J Consult Clin Psychol 1995;63:154-7.
Stray-Pederson B. Economic evaluation of maternal screening to prevent congenital syphilis. Sex Transm Dis 1983:167-72.
Stryker J, Samuels SE, Smith M. Condom availability in schools: the need for improved program evaluations. Am J Public Health 1994;84:1901-6.
Tanfer K, Grady WR, Klepinger DH, Billy JOG. Condom use among US men, 1991. Fam Plann Perspect 1993;25:61-6.
Tawil O, Verster A, O'Reilly KR. Enabling approaches for HIV/AIDS prevention: can we modify the environment and minimize the risk? AIDS 1995;9:1299-306.
Thorpe EM, Stamm WE, Hook EW III, Gall SA, Jones RB, Henry K, et al. Chlamydial cervicitis and urethritis: single dose treatment compared with doxycycline for seven days in community based practices. Genitourin Med 1996;72:93-7.
Toomey KE. HIV infection: the dilemma of patient confidentiality [editorial]. Am Fam Physician 1990;42:955-6.
Toomey KE, Cates WC Jr. Partner notification for the prevention of HIV infection. AIDS 1989;3(1 Suppl):S57-S62.
Trachtenberg AI, Washington AE, Halldorson A. A cost-based decision analysis for chlamydial screening in California family planning clinics. Obstet Gynecol 1988;71:101-8.
Trotter RT 2d, Rothenberg RB, Coyle S. Drug abuse and HIV prevention research: expanding paradigms and network contributions to risk reduction. Connections 1995;18:29-45.
U.S. Conference of Mayors. CDC's Prevention Marketing initiative: a multi-level approach to HIV prevention. Washington, D.C.: U.S. Conference of Mayors, HIV Capsule Report, Issue 2, July 1994.
U.S. Department of Education, National Center for Education Statistics. Digest of education statistics 1995. Washington, D.C.: U.S. Department of Education, Office of Educational Research and Improvement, NCES 95-029, October 1995.
U.S. Preventive Services Task Force. Guide to clinical preventive services. 2nd ed. Washington, D.C.: U.S. Department of Health and Human Services, 1996.
Wallston BS, Wallston KA. Social psychological models of health behavior: an examination and integration. In: Baum A, Taylor SE, Singer JE, eds. Handbook of psychology and health, Vol. 4. Hillsdale, NJ: Erlbaum, 1984.
Wasserfallen F, Stutz ST, Summermater D, Hausermann M, Duboi-Arber F. Six years of promotion of condom use in the framework of the National Stop AIDS Campaign: experiences and results in Switzerland. Ninth International Conference on AIDS, June 6-11, 1993, Berlin [abstract no. WS-D27-3].
Wasserheit JN. Effect of changes in human ecology and behavior on patterns of sexually transmitted diseases, including human immunodeficiency virus infection. Proc Natl Acad Sci 1994;91:2430-5.
Weinstein ND. The precaution adoption process. Health Psychol 1988;7:355-86.
Weisman CS, Nathanson CA, Ensminger M, Teitelbaum MA, Robinson JC, Plichta S. AIDS knowledge, perceived risk and prevention among adolescent clients of a family planning clinic. Fam Plann Perspect 1989;21:213-7.
Weisman CS, Plichta S, Nathanson CA, Ensminger M, Robinson JC. Consistency of condom use for disease prevention among adolescent users of oral contraceptives. Fam Plann Perspect 1991;23:71-4.
Weller SC. A meta-analysis of condom effectiveness in reducing sexually transmitted HIV. Soc Sci Med 1993;36:1635-44.
Wolk LI, Rosenbaum R. The benefits of school-based condom availability—cross-sectional analysis of a comprehensive high school-based program. J Adolesc Health 1995;17:184-8.
Wulfert E, Wan CK. Condom use: a self-efficacy model. Health Psychology 1993;12:346-53.
Yates JF, Stone ER. The risk construct. In: Yates JF, ed. Risk-taking behavior. Chichester, NY: John Wiley & Sons, 1992:1-25.
Yorke JA, Hethcote HW, Nold A. Dynamics and control of the transmission of gonorrhea. J Am Vener Dis Assoc 1978;5:51-6.
Zenilman JM. Gonococcal susceptibility to antimicrobials in Baltimore, 1988-1994. What was the impact of ciprofloxcin as first-line therapy for gonorrhea? Sex Transm Dis 1996;23:213-8.
Zenilman JM, Bonner M, Sharp KL, Rabb JA, Alexander ER. Penicillinase-producing Neisseria gonorrhoeae in Dade County, Florida: evidence of core-group transmitters and the impact of illicit antibiotics. Sex Transm Dis 1988;15:45-50.

























































