APPENDIX E Using Decision Analysis in the Management of Contaminated Sediments1
John Toll,2 Spyros Pavlou, Dwayne Lee, Larry Zaragosa,3 and Peter Shelley
There are many ways to make decisions about how to manage contaminated sediments. Often the process is dictated by legal or political realities. In other cases, the process depends on the complexity of the decision. Simple decisions can be made almost instantaneously, whereas slightly more complicated problems may require a calculator or a detailed examination. Highly complex decisions, involving large amounts of data and considerable disagreement and uncertainty, may require more structured methods to account for all important factors. Computational or computer-based decision support is useful when the issue at hand is of substantial importance and uncertainty, when the situation is politically or emotionally volatile, and when the outcome must be acceptable to all parties. The management of contaminated sediments often falls into this category.
Cost-benefit analysis (addressed in Appendix D) is one tool for making complicated decisions, but it may not be sufficient in some cases. What is needed is a reliable tool for balancing the consideration of a variety of significant factors when the stakes are high and the issues are complex. Decision makers need to know how to use and communicate information about risks, costs, and benefits—information that may be controversial and difficult to evaluate, compare, or reconcile. This issue, identified earlier by the National Research Council (1989),
was assigned specifically as a task to be addressed in the present report. The need is becoming increasingly urgent as the number of remediation proposals grows and as costs and controversies multiply. To add to the burden, some of the committee's proposals for improving outcomes may introduce additional considerations that may initially complicate decision making.
One tool that may help resolve problems with many variables is decision analysis, a computational technique for predicting the outcomes of selected management approaches. Decision analysis provides a way to use both factual and subjective information to evaluate the relative merits of alternative courses of action. Decision analysis does not provide absolute solutions, but it can offer valuable insights. It can integrate the results of key management tasks (site characterization, risk assessment, technical feasibility studies, and economic assessment) into explicit models of the problem as it appears from the perspectives of different stakeholders. The modeling approach allows stakeholders to explore disagreements about subjective elements of the problem, thereby expediting problem solving. The process also formally accounts for uncertainties.
Although decision analysis involves complex computations, the general process can be described in simple terms. The process begins with the gathering of information about the problem and the selection of alternatives to be evaluated by the mathematical model The model evaluates and rates all possible outcomes to each alternative The model then identifies the alternative with the highest expected net benefit—that is, the strategy that offers the best odds for successful risk management although it cannot guarantee the best outcome.
Although decision analysis is not a new technique, it is only beginning to be used in managing contaminated sediments. Apparently, the first use of decision analysis in the management of contaminated sediment was in 1996 by Parametrix, Incorporated, in the case of the Asarco smelter site on Commencement Bay, Washington. Such applications may be particularly timely now because recent advances in computer hardware and software have made user-friendly, interactive analyses possible. Further impetus may be provided by the U.S Congress, which is considering requiring formal risk-based assessments and cost-benefit analyses of proposed federal environmental regulations with projected annual costs of $25 million or more.
This appendix examines how decision analytic techniques can be used to weigh economic, human health, and environmental risks and benefits in a balanced way. The first section provides a general introduction, including background on the unique benefits of decision analysis, the technical basis and merits of balancing risks, and the state of practice. The second part summarizes the practical benefits of decision analysis as demonstrated in a hypothetical test case developed by the committee using actual field data The test case, which involved choosing the best of three dredging and placement strategies for a hot spot contamination site, is described in detail in the third section.
PART I: BACKGROUND
It is important to distinguish decision analysis from the many other decision-making approaches that have emerged in recent years to improve the process of dispute or conflict resolution. The simplest method is to bring stakeholders together for a frank and constructive discussion. Other approaches include mediation, negotiated rule making, and collaborative problem solving. These approaches may be easier to explain to stakeholders and may, therefore, be approached with less skepticism than decision analysis, which is technical in design and involves complex computations. In some cases, they will be complementary to decision analysis. Each approach has a place in the arsenal of techniques that can be used to improve the prospects of making a politically acceptable and implementable decision. A detailed analysis of all the techniques is beyond the scope of this appendix, but the key aspects are summarized here.
Fostering a consensus on a management process among all interested or potential stakeholders is a separate discipline from decision analysis, and, whether carried out in the context of mediation, arbitration, or collaborative problem solving, it is more than simply going through the mechanics of communicating with all parties. The case studies reviewed by the committee (see Appendix C) underline the paramount importance of positive working relationships in fostering progress toward accommodating or resolving conflicts.
The literature on conflict resolution, in addition, stresses that the way threshold questions are handled is as central to success as the substantive outputs from the process itself. Threshold questions include who should be at the table, who should represent whom, how the interests of important stakeholders who fall to come forward will be determined, how to develop a common and constructive definition of the problem(s), and how to select a mutually acceptable decision-making process. There is a significant body of literature on dispute or conflict resolution. Carpenter and Kennedy (1988) provide lay readers with an extended discussion of the mechanics of a powerful dispute resolution program, many examples of public dispute resolution, and a detailed bibliography. Another resource of this type is Singer (1990).
Decision analysis, as defined and developed in the present report, is not intended to be and is not directly applicable as a dispute resolution technique. Increasingly, contaminated sediments are managed in complex, ever-changing social and political settings marked by the emergence of nontraditional stakeholders in addition to project proponents and regulatory agencies. Conflict is inevitable in this context regardless of the quality of the decision, and serious disagreements need to be addressed directly through appropriate conflict or dispute resolution. Federal agencies are authorized and encouraged to engage in alternative dispute resolution techniques by the Administrative Dispute Resolution Act of 1990 (P.L. 101-552). The U.S. Army Corps of Engineers (USACE) has developed
guidelines for using these techniques to resolve contract disputes but has not formalized their use in situations involving contaminated sediments. The Environmental Protection Agency (EPA) frequently uses formal dispute resolution techniques, both for developing regulations and for resolving disputes in specific Superfund projects.
Decision analysis is unique among the available techniques in terms of how it can improve the understanding and quality of decisions and choices. It is explicit and rigorous, and the analytical pathways are reproducible. Decision analysis has the particular virtue of integrating data and expertise from divergent sources into a single analysis, accommodating more variables and offering different perspectives than techniques such as cost-benefit analysis that evaluate single outcomes. Because of its strengths in handling multivariate problems and its capability to model various outcomes (so that the consequences of differing values or assumptions can be tested), decision analysis can be a powerful tool for conflict or dispute resolution in both public policy and project-specific settings. However, because the procedure is elaborate, stakeholders may need some time, as well as demonstrations, to gain confidence in the approach.
Risk Balancing
Uncertainties and disagreements concerning risks, costs, and benefits are impediments to effective decision making. Uncertainty can foster risk aversion and polarize already-divergent opinions. If the uncertainties are not explicit and available to the decision maker for analysis, then balanced decisions can be very difficult to make—and, perhaps, even more difficult to explain to the satisfaction of stakeholders. Decision analysis is a systematic approach that rigorously accounts for uncertainties and disagreements. If done well, decision analysis instills discipline in the overall problem-solving process, forces stakeholders to be explicit about their value assumptions, and provides disciplined consideration and interpretation of information about risks, costs, and benefits.
The merits of reliable risk balancing through decision analysis are fourfold. First, decision models can systematically work through calculations (arithmetic or logical) that are far too complex to perform manually in a timely and orderly way. Second, decision models can be used as records of how problems are formulated. The record can be communicated, examined, and critiqued so that the final model for a specific problem contains the collective insight of a variety of individuals, each of whom may have specialized knowledge and a different perspective. Third, the collective modeling effort and availability of a record may increase confidence and trust in decisions among those whose knowledge or concerns should be addressed in the decision-making process. The model can clarify the implications of uncertainties about factual information and disagreements about subjective aspects of the problem. The ultimate result can be a cooperative problem-solving environment, consensus building, and the expeditious
implementation of solutions. Finally, by accelerating the evolution of understanding, decision modeling can lead to faster and better solutions than would otherwise be possible. Formulations of the model can be run early in the decision-making process to test alternative assumptions and to evaluate the importance of various uncertainties.
State of Practice
Decision analysis was developed in the late 1960s and early 1970s (Raiffa, 1968; Keeney and Raiffa, 1976) and has been used to help solve policy, management, engineering, and medical diagnostic problems since the 1970s and is increasingly becoming a part of academic curricula in these fields (e.g., Howard and Matheson, 1984; Watson and Buede, 1987; Baird, 1989; Clemen, 1991). Recent advances in personal computers have spawned a new generation of powerful software packages that provide user-friendly, diagrammatic interfaces for building models of decision problems, graphics tools for analyzing modeling results, and rapid processing of computationally intensive problems. These developments have opened up new possibilities for applying decision analysis to a broad array of difficult problems, including environmental management problems. For example, decision modeling software enabled the committee to construct and display models as diagrams and spreadsheets, rather than as lines of computer code, and to display model output as useful graphs and diagrams (some of which are included in this appendix). These figures made it possible to perform valuable exploratory analyses of the problem in ways that would have been impractical without the software.
Few environmental management applications of decision analysis are well documented in the scientific or professional literature, although a number have been identified by the committee, particularly in the public sector. Decision analytic tools have been used successfully by a variety of federal agencies. An example is the development of National Ambient Air Quality Standards (NAAQS) by the EPA. Decision analysis was considered useful in that process because of the significant economic impacts of alternative standards and the complexity of evaluating the available scientific literature on the health effects of NAAQS (EPA, 1996). Development of the NAAQS for ozone, a primary motivation for pollution-control programs, such as vehicle inspection, was supported by the use of decision analytic methods for arraying the health impacts of alternative specifications.
Decision analytic methods also have proven useful for evaluating options for dumping of low-level radioactive wastes in the ocean. Information comparing different management choices has been valuable to the United States at international meetings such as the London Convention of 1972.
Some of the most significant efforts to use decision analytic techniques have been related to the environmental restoration of federal facilities. The costs of
cleaning up these sites are significant—hundreds of billions of dollars under some scenarios. Although decision analysis has proven useful for organizing information (U.S. Department of Energy, 1986), it has not been as successful for developing NAAQS, for example, for at least two reasons. First, the use of decision analytic techniques was an emerging concept at that time, and there was little precedent for its application to a wide range of problems. Second, it is not clear that the methodology (as applied at that time) adequately addressed the differences in values and uses of information desired by decision makers.
The U.S. Department of Energy (DOE) made another attempt to use decision analytic techniques for environmental waste management with its Response Allocation Resource System model. This model was designed to support setting priorities among projects to be funded by DOE's waste management division. The model was expected to provide insight concerning public risk, worker risks, environmental risks, and the costs of compliance with environmental statutes and to help set reasonable schedules and budgets. Several public meetings were held and scientific reviews conducted, but the project is, at this writing, still on hold.
Elsewhere in the public sector, Los Alamos and Sandia National Laboratories are using decision analysis to evaluate the costs, risks, and benefits of all their environmental, safety, and health action plans (D. Brooks, Arizona State University, personal communication to Marine Board staff, January 18, 1995). Decision analysis also has been used to analyze the societal risks, costs, and benefits of regional strategies to reduce ozone in Southern California. In addition, the Northwest Power Planning Council uses decision analysis in its activities, which require making multibillion dollar decisions based on forecasts of demand, costs, technologies, the political feasibility of particular alternatives, and environmental predictions that extend decades into the future (Northwest Power Planning Council, 1991).
There are few published examples of decision analysis in the private sector Chevron Corporation uses decision analysis to help integrate the quantitative analysis of environmental risks into its management decisions, and DuPont Environmental Treatment has used a decision analytical approach to find cost-effective, environmentally sound wastewater treatment methods (Horton, 1993). Details on projects like these are seldom available to the public.
As practical applications of decision analysis become more numerous in environmental decision making, the general concept is receiving attention in the literature as well, although the terminology varies. For example, the concept of decision analysis provides the underpinning of recent EPA guidance on data collection in support of environmental decision making (EPA, 1994). However, the term "decision analysis" is not used. The term is used in another conceptual guidance document, a recent Chemical Manufacturers Association report on the use of decision analysis for characterizing quantitative cancer risks (Silkien, 1990).
PART II: ASSESSMENT OF DECISION ANALYSIS
The committee's understanding of decision analysis and its potential benefits evolved over the course of the test case. The following is a summary of the test case and some important general insights from the project.
Test Case
The problem in the test case was to find a cost-effective dredging strategy for hot spot polychlorinated biphenyl (PCB) contamination in a harbor. Four types of information were needed to run the model: (1) the set of decision alternatives (dredging volumes), (2) performance constraints or standards of PCB concentration in the tissue of edible fish, (3) the set of important factors in the decision, and (4) a decision rule for selecting the best alternative. In the test case, the objective was to select the dredged volume that minimized the total cost while meeting health and environmental objectives. There were three options: low, intermediate, and high volumes. The solution was not obvious. The low dredged volume increased the risk of not meeting the constraints (expressed as PCB concentration in the tissue of fish), whereas the high dredged volume increased the cost. Therefore, the objective was to identify the alternative that represented the best balance of risks and costs.
The basic model for the test case defines the total cost of the decision about the volume of sediment to be dredged as the sum of two factors: (1) the costs of dredging and the placement of dredged material, and (2) the cost of resource damage caused by the contaminated sediment. The data input consisted of the three dredged volumes to be evaluated, and, for each volume, the probability of not meeting the target PCB level in fish tissue (i.e., the exceedance probability), the dredging and dredged material placement cost, and the resource damage cost. All of these variables are uncertain. Uncertainty probabilities were assigned to all possible values for each variable. Detailed descriptions of the procedures and mathematical calculations involved in running the test case model can be found in Part III (below).
The results indicated that the intermediate dredged volume was preferred. followed by the high dredged volume. However, the estimate for the latter was more reliable, perhaps making this choice attractive to a risk-averse decision maker. The results are sensitive to uncertainties in both dredged volume and fish tissue concentration, because these factors strongly affect dredging costs. Interestingly, however, the results are insensitive to changes in (or disagreements about) annual resource damage costs. This counterintuitive outcome, which is discussed further in Part III, suggests how decision analysis can be used to foster understanding and consensus. In this case, the model demonstrated that differing views on the value of an important and often controversial variable should not prevent stakeholders from agreeing on the key decision.
Model Simplicity
The test case demonstrated that a decision support model need not—and perhaps should not—be comprehensive in depth or breadth. The importance of simplicity becomes apparent in the model-building exercise. The uninitiated often notice immediately what is missing from a simplified model, but the desire to "model reality" precisely is a trap. The purpose of modeling is insight. Attempting to mimic complex reality is not the best way to gain insight because the model can never be complete; more can always be added, and in the process, modeling can become an end in itself. A simple model forces the modeler to be resourceful and to think about the problem.
Another benefit of simplicity is clarity of insight. If a model is conceptually complex, then, even if it is accurate, important insights may be buried among a number of irrelevant results. Computational complexity is not a problem; calculations can be made quickly with computers. But a computer cannot overcome a confused conceptualization. If the concept is inaccurate, then errors in results may be obscured. Therefore, the most useful decision models are designed to answer specific questions, not to solve broad problems. The best models are only as complex as necessary to answer the question. Formulating specific questions, and constructing decision models specifically to answer those questions, demands careful analysis and focused discussion about the broader management problem. The disciplined thinking required to distill a complex management problem into a concise decision model provides a wealth of insight that may not end up in the model but is available to the decision maker nonetheless. In addition, this type of model building reaches closure, so attention can be shifted from model building to analysis.
Paradoxically, then, the most effective modeling strategy for solving complex management problems is to build and analyze models of simpler decisions associated with the problem and then to use both direct insights from analyzing the model and indirect insights from formulating the model to make management decisions.
Consensus Building
The test case also suggested that decision analysis—assuming the concept is understood and accepted by all parties—could be useful in bringing stakeholders together to formulate and solve problems. Without explicit models, different groups are likely to formulate the problem differently. Unintentional conceptual variations can result in unnecessary misunderstandings and distrust, which may become major obstacles to decision making. Furthermore, implicit judgments can mask how various factors interact to affect the decision outcome. The value of explicit decision models is that they provide valuable insight into the factors that drive the outcome and value of a decision alternative and how these factors
interact. Decision models can assimilate expertise from a wide range of disciplines and individuals to provide a more informed analysis of the decision than an individual could manage alone. This is not to say that decision analysis can replace conventional consensus-building techniques, but it can be a valuable adjunct under certain circumstances.
Summary
Sound management of contaminated sediments can be hindered by conflicts and indecision related to the complexity, uncertainty, and volatility of the issues. To help overcome these barriers, reliable tools are needed for balancing and communicating information about risks, costs, and benefits. Decision analysis is such a tool. It can integrate multiple variables in an explicit, rigorous, and reproducible manner, and it can accommodate uncertainty. Decision analytic methods do not provide absolute solutions but they do provide insights that can be used to make balanced, well-informed decisions about the management of contaminated sediments. Decision analysis may also help foster consensus and communication among stakeholders.
There are clear advantages to collecting and analyzing relevant information in a format that can be understood and weighed by decision makers and other interested parties. Decision models can lay out the technical, scientific, and regulatory bases for decisions. In addition to fostering the sound management of contaminated sediments, decision analysis might also be used to improve government regulation. The models could help determine which regulations are controlling in a particular circumstance, thereby helping to focus the search for solutions. Even outcomes that were demonstrated to be infeasible in terms of regulatory compliance could be valuable for adjusting and, perhaps, streamlining requirements. As the federal government moves to tighten requirements for impact assessments, the use of powerful analytic tools, and the concomitant development of consistent methods of reporting data, may become increasingly attractive.
PART III: TEST CASE
The test case was developed to demonstrate the use of decision modeling and analysis in the management of contaminated sediments. Actual field data were used to ensure that the analysis was realistic. This section describes the test case in detail. The first section provides a conceptual overview of the mechanics of decision modeling. Readers unfamiliar with decision analysis or who are interested in its theoretical and conceptual underpinnings may find this information helpful. The second section describes the problem and the methodology, including the mathematical formulas used and the values chosen as parameters for the model. The third section summarizes the most important results of the decision modeling exercise.
Mechanics of Decision Modeling
Decision analysis is a computational technique for predicting the outcomes of specific candidate management approaches. Decision analysis does not provide absolute solutions but can offer valuable insights. When applied to situations involving contaminated sediments, decision analysis can be used to integrate key assessments (e.g., site characterization, risk assessment, technical feasibility studies, and economic assessment) into explicit ''decision models" that describe the management problem as it appears from the perspectives of different stakeholders. The modeling approach allows stakeholders to explore disagreements about subjective elements of the problem, thereby expediting problem solving. The process also formally accounts for uncertainties.
The first steps in decision modeling are gathering information about the decision problem and selecting a set of alternatives to be evaluated with the decision model. The committee used a computerized decision model, which evaluated all possible outcomes to each candidate strategy. The possible outcomes were then rated on a value scale, which provided a measure for identifying the "best" decision alternative based on the preferences encoded in the model. The value scale can simply rate the possible outcomes from best to worst (an ordinal scale) or can quantify each possible outcome (a cardinal scale) by, for example, assigning dollar values. The preferences encoded in the analysis can be those of the decision maker or some other stakeholder.
When the possible outcomes are rated on a cardinal scale, evaluation typically involves calculating the weighted average of the values of the possible outcomes to a given alternative; weighting is based on the probability of occurrence. The weighted average is called the expected value of the alternative. The alternatives are then ranked by their expected values, and the alternative with the highest expected value is recommended.
The term "utilities" is used to describe a particular set of values that represents a decision maker's preferences among outcomes. Assuming that a set of cardinal values assigned to possible outcomes represents these preferences accurately, the axioms for the expected utility criterion for decision making—which calls for selecting the outcome that provides, on average, the highest utility—may be found in utility theory, a general theory of decision making under uncertainty (Watson and Buede, 1987).
Modern utility theory, which originated with the publication of The Theory of Games and Economic Behavior (von Neumann and Morgenstern, 1944), provides a normative approach for making rational decisions under uncertainty. Watson and Buede (1987) cite Savage (1954) as the most comprehensive set of principles of the expected utility criterion for rational decision making. Baumol (1972) provides a mathematical proof demonstrating that, if one wishes to act in accordance with a set of five fairly innocuous behavioral postulates (which
constitute the axioms of utility theory),4 then one should always make decisions that maximize expected utility. In practice, utilities cannot be completely known, so an "expected value maximization" criterion is often used instead of expected utility maximization. In such cases, it is important that the ranking of alternatives provided by the model be checked against judgment and intuition.
Decision models calculate the expected value of the outcome for each decision alternative (i.e., the average of all the possible outcomes to the decision alternative) and identify the alternative with the greatest expected value (i.e., the alternative for which the average of all the possible outcomes rates highest on the value scale). The part of the model that rates the possible outcomes is called the value function.
The terms in the value function are the factors that are thought to exert a significant influence on the desirability of possible outcomes. In a decision about managing contaminated sediments, these factors include, for example, the costs of dredging, sediment placement, and natural resource damage. Each factor in a value function is estimated from field data, professional judgment, and models. The level of effort, method, and sources of information used to estimate the factors in the value function must be determined on a case-by-case basis, based on the availability and reliability of possible sources of information, the preferences of the decision maker, and the total level of effort to be spent on the decision.
In some cases, the decision maker may prefer something other than the recommended (maximum expected value) alternative. This would imply that the values used to describe preferences among outcomes differ to some degree from the decision maker's utilities on the outcomes. This might happen, for example, if the outcome of the recommended alternative is less certain than the outcome of another alternative with an acceptable expected value, or if the decision maker feels that an important factor is inadequately represented in the model. In these cases, the decision maker's preferences should override the results of the decision analysis (assuming the results are properly understood). It may be helpful for the decision maker to articulate the reasons for overriding the results to ensure understanding on the part of both the decision maker and others evaluating the decision.
The effectiveness of decision analysis depends on the skill of the analyst, the effort by the decision maker to use the model and understand its results, and the quality of the information put into the model. Sometimes modeling results are counterintuitive. These are the most important results because they provide unique opportunities to learn about the problem. Counterintuitive results that hold up to scrutiny become important insights. Some counterintuitive results will not hold up, in which case the decision maker can and should override the model's recommendation (and correct the model if it is to be used again).
Test Case Problem
The problem in the test case is to find a cost-effective dredging strategy for a PCB hot spot in a four-square-kilometer (km2) (roughly 1,000-acre) marine harbor.5 The average total PCB concentration in the sediments is estimated to be 360 micrograms per gram (µg/g of carbon (C). The primary source of PCB contamination is historical discharges, which have been controlled. The placement strategy for the materials to be dredged has been selected. The present analysis focuses on how much sediment should be dredged to minimize cost while meeting health and environmental objectives for the harbor. Clear, well-defined statements of purpose like these are essential to successful decision making, especially if decision analytic tools are used.
The harbor is home to a large commercial fishing port. Although the port remains active, the harbor itself, which was formerly a commercial fishery, has been closed to fishing because of PCB contamination. Winter flounder is used as an indicator species for PCB contamination because it is a bottom-dwelling fish caught by both commercial and recreational fishermen. Total resource damage costs associated with PCB contamination in the harbor have been estimated on the order of $100 million to $1 trillion (Clites et al., 1991).
The PCB contamination levels in the harbor sediments have been mapped. Localized concentrations range from background concentration (the value is unimportant for purposes of the demonstration) to 105 µg PCB/g C. This wide variation makes it difficult to assess the extent of dredging required to attain a target PCB concentration level. Sampling profiles suggest that half of the PCB sediment contamination is contained in the top meter of a five-acre hot spot. Sediment PCB data suggest that, after any amount of dredging has been completed, dredging the top meter of the next-most-contaminated five acres will remove approximately half of the remaining PCBs. In other words, dredging the most-contaminated 10 acres of sediment will remove an estimated three quarters of the total PCBs, dredging the most-contaminated 15 acres will remove about 88 percent, and so on (see Figure E-1). An error in the assumed relationship between dredged volume and PCB sediment concentration may affect the decision, as is discussed in the forthcoming analysis of the test case.
Overview of Model Development
Types of Information Needed to Run the Model
For the test case, the types of information needed to run the model are (1) the specific set of decision alternatives (in this case, dredging volumes) for which the
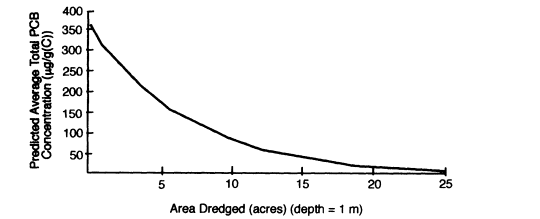
FIGURE E-1 Predicted average PCB concentration as a function of area dredged (to a depth of 1 meter), assuming sediments are dredged in order of decreasing PCB concentration.
model is to be run; (2) formal constraints on how well (at a minimum) the decision alternatives must perform (performance standards) or how much (at a maximum) must be done (stopping rules); (3) the set of important factors in the decision; and (4) a decision rule for selecting the best alternative.
Alternatives
The model has been constructed to evaluate three alternatives: low, intermediate, and maximum dredged volume. If the low or intermediate dredged volume is selected and it turns out, after dredging is completed, that the constraint (described in the forthcoming section) has not been met, then additional dredging will be done and the total volume dredged will equal the maximum (the third alternative). All three alternatives include a stopping rule, which states that dredged volume will not exceed the volume specified in the maximum dredged-volume alternative.
The first inputs into the decision model are the quantities of material to be dredged under the three alternatives (in cubic meters). It is assumed that the materials will be dredged in order of decreasing PCB concentration, according to existing maps of PCB concentrations in the harbor. Therefore, dredging locations need not be specified; they are implied in the assumption. Errors in PCB concentration maps contribute to the uncertainty about the accuracy of the assumed relationship (depicted in Figure E-1) between dredged volume and average PCB sediment concentration.
In the model's mathematical calculations, the best of the three alternatives is identified using the decision rule. Numerical values for the dredged-volume alternatives can be changed and the model run again, and the results can be compared
across model runs. The total number of alternatives considered can be as many or as few as the decision maker wishes. In general, for the sake of clarity, decision models should evaluate only a few alternatives per run; additional alternatives can be explored in reruns with modified values. This strategy is more computationally efficient than analyzing many decision alternatives in a single run. Small, repeated sessions also force the modeler and decision maker to interpret results at intermediate steps in the analysis, thereby encouraging insight into the decision.
Constraints
The Food and Drug Administration (FDA) action level (the value at which the FDA requires remedial action) for total PCB concentration in edible fish tissue (2 µg/g) is the benchmark for assessing whether health and environmental objectives have been met. The measurement end-point is the sample average total PCB concentration in edible tissues of fish (flounder in this case) taken from the harbor. The constraint on the dredged-volume decision is that enough PCB-contaminated sediments must be removed to reduce the average PCB body burden to 2 µg/g of total tissue weight.
Constraints that set minimum performance standards are not a fundamental requirement of decision models. The need for minimum performance standards is established by the details of the problem at hand. However, decision models for problems in which regulatory compliance is an issue—including virtually all problems involving the management of contaminated sediment—nearly always involve minimum performance standards, which are the regulatory criteria.
The stopping rule in the test case states that dredged volume will not exceed the volume specified in the maximum dredged-volume alternative. Sensitivity of the decision to this stopping rule is examined later in this appendix. It has been argued that stopping rules are an important element of the risk management framework (Clark, 1980). Stopping rules place a tangible burden of proof on those who claim a problem exists, thereby protecting the rights of those identified as responsible for the problem. Regardless of whether stopping rules are used in real situations, they are necessary in decision modeling because they put an upper limit on the costs associated with the decision alternatives.
Factors in the Decision
There are different ways to break out the important risks, costs, and benefits affecting the selection of a decision alternative. In this case, two factors were used: the cost of dredging and dredged material placement, and the cost of resource damage. The total cost of the dredged-volume decision is modeled as the sum of the two factors. Both depend on the amount of material dredged, and both are uncertain.
Both sets of costs rise if the amount of sediment dredged is too low to meet the flounder body burden constraint because the need to perform additional dredging increases the cost of dredging and dredged material placement, and the extended duration of PCB contamination drives up the cost of resource damage.
Dredging more than enough contaminated sediments to meet the constraint, however, also increases both sets of cost, because the unnecessarily high volume adds to dredging and placement costs. (Costs of resource damage do not change; once the flounder body burden constraint is met, the marginal reduction in the cost of resource damage remains zero as the volume dredged increases.)
In summary, a reduction in the volume of contaminated sediments dredged increases the risk of not meeting the constraint on allowable flounder PCB body burden, whereas an increase in the volume increases the cost of dredging. The test case does not take into account specific benefits that may differentiate the decision alternatives (e.g., the beneficial uses for the dredged materials, the benefits of deepening the harbor, or the health benefits of minimizing the volume of contaminated materials to be disposed). The objective is simply to identify the alternative that balances the costs of dredging, placement, and resource damage in the dredged-volume decision.
Decision Rule
The decision rule in the test case was to select the alternative that minimizes the expected total cost, where the total cost is the sum of the costs of dredging and placement and resource damage. The total cost associated with each decision is uncertain. The expected total cost of an alternative is the weighted average of the possible values for its total cost, where the weighting factors are the probabilities of occurrence of each possible value.6
The four elements just described constitute the basic structure of the decision model. The dredged-volume decision affects the probability of meeting (or not exceeding) the flounder body burden constraint. The decision also affects both dredging and placement costs and resource damage costs. Both of these cost factors also depend on whether the flounder body burden constraint is met. The total cost is the sum of the costs of dredging and dredged material placement and resource damage.
The following information is required to run the model: the decision alternatives (dredged volumes) to be evaluated; and, for each decision alternative, the probability of not meeting the flounder body burden constraint (the exceedance probability), the cost of dredging and dredged material placement, and the cost of resource damage.
Choosing Parameters for the Model
There are many ways to provide the specific information (parameters) required to use the model. The preferred method is to use actual data on cost factors
and exceedance probabilities—if they exist. If the data are available, then the decision is straightforward and decision modeling is unnecessary. If the data are not available or are unreliable, then there are two possible strategies:
- expand the model to predict the cost factors and exceedance probability, using whatever relevant information can be found and brought to bear on the problem
- try different values for the exceedance probability and cost factors to see whether the most cost-effective decision alternative changes (an approach known as a sensitivity analysis). If the decision outcome is insensitive to the changes in these values, then it is not necessary to quantify further the cost factors or exceedance probability.
In a typical decision analysis, establishing parameters for the model involves a combination of direct data, predictive models, and sensitivity analyses. The information usually comes from a variety of sources. For example, dredging and placement cost data might be provided by a team of engineers, resource damage cost estimates by resource economists and local residents, and exceedance probability by a PCB bioaccumulation model.
Test Case Decision Model
The dredge and placement decision model developed for the demonstration project is shown in Figure E-2. This is known as an influence diagram, which is similar to a decision tree but is expressed in compact notation. Each node in the model represents either a variable or a decision. Qualitative and quantitative information about the variable or decision is contained in each node. The nodes are all annotated so the user can check the data, models, and assumptions used to establish parameters of the decision model.
The diagram contains three types of nodes: decision nodes, shown in Figure E-2 as rectangular boxes with sharp corners; value nodes, shown as rectangular boxes with rounded corners; and chance nodes, shown as ovals. Each type of node is discussed below.
The rectangular node (dredged volume) is a decision node and contains a list of the alternatives to be evaluated. In this case, the model evaluates three decision alternatives: low, intermediate, and maximum dredged volume. The alternatives are quantified by the assignment of numerical values. For the baseline analysis, the dredged volumes were set at 25,000 cubic meters (m3), 35,000 m3, and 50,000 m3. The dredge depth was set at 1 meter.
Each value node (rounded rectangle) contains a set of values for the variable referred to in the node label; there is one value for each possible combination of influences. For example, the variable resource damage cost is influenced by two variables, annual resource damage cost and length of closure, each of which has
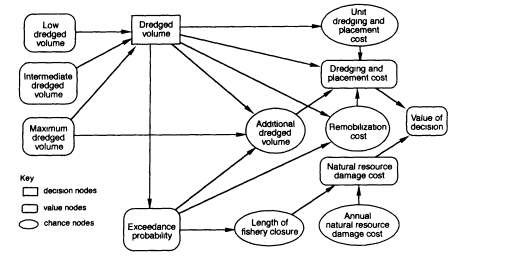
FIGURE E-2 Influence diagram of a test case Dredging and placement model for hot spot remediation at a commercial fishery.
a set of defined states. In this model, three states were defined for annual resource damage cost: low, intermediate, or high. Four states were defined for length of closure: none, four years, five years, or six years. Therefore, resource damage cost has 12 possible states, corresponding to all the possible combinations of annual resource damage cost and length of closure. A value is assigned to each of the 12 states. These values can be entered directly, or they can be calculated as a function of the influencing variables. In the test case, the 12 values of resource damage cost are calculated as the product of length of closure and annual resource damage cost.
A value node with no influences has a single state; for example the node low dredged volume has one state (i.e., one volume). The states in value nodes can be revised between model runs; for example, the value used for low dredged volume may be increased or decreased.
Each chance (oval) node contains a set of states and values. Unlike the value nodes, a chance node can have any number of states for each combination of influencing states. For example, the node additional dredged volume has two states, yes and no, for each decision alternative. This node must be in one of these states or the other, but its "correct" state is uncertain. Therefore, each state is assigned a probability. In the test case, the probability of the yes state is equal to the probability of exceeding the FDA action level for contaminant concentration in the edible tissue of fish at the site (the exceedance probability node), given the
state of the decision node (which might be set, for example, at the minimum dredged volume). The probability of the no state, therefore, is 1—exceedance probability (because, according to the axioms of probability theory, total probability always equals 1).
The model evaluates the three dredged-volume alternatives and identifies the lowest expected cost (maximum expected value) alternative. The value function (the rule for making the decision) is coded in the terminal node of the diagram, labeled value of decision. The value of each possible outcome to each alternative is calculated with the formula
value of outcome i =—(D&D cost + resource damage cost)outcome (1)
where D&D cost is the cost of dredging and placement of the contaminated sediments, and resource damage cost is the cost associated with the closure of a commercial fishery (the two factors affecting the decision in this analysis). The expected value (the average value) of each decision alternative is calculated with the formula
expected value of alternative j =S[—(D&D cost + resource damage (cost) outcome i X Pr(outcome i)] (2)
where nj is the number of possible outcomes to alternative j.
Figure E-2 shows the variables that directly and indirectly influence the values of D&D cost and resource damage cost. The analysis could be extended to include other factors, which do not have to be measured in monetary units. The only requirement is that there must be a rule (value function) for ranking the possible outcomes to each decision and for ranking the possible decisions. If the value of outcomes is not measured on a one-dimensional cardinal scale (e.g., dollars), then decision alternatives cannot be ranked by expected value.
Parameters in the Test Case
The previous section described the user interface for a rigorous mathematical model. This section provides details of the model, including the specific rules and data contained in the nodes, as applied to the test case.
D&D cost is a deterministic function of the total dredged volume (dredged volume + additional dredged volume), unit dredging and placement cost (unit D&D cost), and the cost of remobilizing dredging, placement, and support operations if the initial dredged volume is inadequate to meet the FDA action level (remobilization cost). The model defines dredging and placement cost as
D&D cost = unit D&D cost × (dredged volume + additional dredged volume) + remobilization cost (3)
There is significant uncertainty associated with unit D&D cost, as indicated by the use of a chance node to model this variable in Figure E-2. The unit cost may also vary with the dredging volume; that is, the values and probabilities assigned to the various states of unit D&D cost may be different for each of the three dredged-volume alternatives. For demonstration purposes, unit D&D cost was assigned a minimum value of $1,000/m3, a most likely value of $1,500/m3 and a maximum of $3,500/m3. This distribution was used for all three dredging volumes. Generally, the projects and studies from which cost data are obtained are documented in the annotation of each node, so that users of the model can critically evaluate the unit cost estimate. (The committee did not provide this information for the test case to protect the source of the data.)7
The definition of the variable additional dredged volume is very important because it provides a stopping rule for the dredged-volume decision. The following rules were used in defining this variable:
- After dredging the dredged volume (dredging depth = 1 m), contaminant partitioning in the dredged harbor will be allowed to reach a steady state, and a sampling protocol will be implemented to determine whether the contaminant concentration in edible fish tissue (as reflected in the test case by an age-adjusted sample mean from a random sample of flounder) exceeds the FDA action level.
- If the FDA action level is exceeded, then additional hot spots will be dredged (to a depth of 1 m), in order of decreasing level of contamination up to a total dredging volume of maximum dredged volume. Thus.
additional dredged volume = maximum dredged volume—dredged volume (4)
Of course, if the FDA action level is not exceeded, then additional dredged volume equals zero.
Based on these rules, the probability of having to do additional dredging is:
Pr(additional dredged volume > 0) = (a) exceedance probability if dredged volume is low or intermediate, or (b) 0 if dredged volume is the maximum (5)
The variable remoblization cost was estimated to be $15 million if remobilization is necessary (that is, if the FDA action level is exceeded after the initial dredging, and the initial dredged volume is less than the maximum dredged volume). This estimate was based on rough calculations of the projected cost of research and remediation for a hot spot contamination program; it is a weak link in the model but adequate for demonstration purposes. A more reliable estimate would be based on a combination of professional judgment and cost data.
Based on the rules for determining the need for additional dredging, the probability of incurring a remobilization cost is determined by the following formula:
Pr(remobilization cost > 0) = (a) exceedance probability if dredged volume is low or intermediate, or (b) 0 if dredged volume is the maximum (6)
Sediment contamination data and a contaminant bioaccumulation model were used to predict the probability of exceeding the FDA action level. The committee used a PCB bioaccumulation model developed by Connolly (1991), as modified by Dakins et al. (1994, 1996). As modified, this model provides age- and class-dependent probabilistic estimates of population mean contaminant concentration (TC) in flounder as a function of sediment contaminant concentration. This concentration, in turn, is assumed to be a function of dredged volume, using a model of the spatial distribution of sediment contaminant concentration at the site. Thus:
exceedance probability = Pr(TC ³ FDA action level) = f(dredged volume (7)
For the three dredged volumes selected (25,000 m3, 35,000 m3, and 50,000 m3), the exceedance probabilities calculated with the food web model are 0.48, 0.25, and ~0.001, respectively. A detailed presentation of the use of the bioaccumulation model to estimate exceedance probability as a function of volume of sediment dredged can be found in Dakins et al. (1994).
The second factor in the value function is resource damage cost, which represents the total economic impact of fishery closure. This factor was estimated as the product of two probabilistic variables, length of closure and annual resource damage cost. Length of closure represents the elapsed time (years) between the determination that initial dredging did not meet the FDA action level and the reopening of the fishery following additional dredging. The length of closure , if the FDA action level were exceeded, was estimated to be four to six years. Probabilities were assigned based on professional judgment (with five years the most likely length of closure, and the sum of the probabilities equal to one):
|
Length of Closure (years) |
Probability |
(8) |
|
0 |
1—exceedance probability |
|
|
4 |
0.25 x exceedance probability |
|
|
5 |
0.50 x exceedance probability |
|
|
6 |
0.25 x exceedance probability |
|
Variability in annual resource damage cost due to disagreements about risks, costs, and benefits is likely to exceed variability due to uncertainty because stakeholders can have widely divergent opinions about the value of this factor. Because it reflects opinions instead of facts, variability due to disagreement should be treated parametrically rather than probabilistically. That is, the model should be run repeatedly using different uncertainty distributions for annual resource damage cost, with each run representing a different opinion about this cost. For the test case, the committee used a distribution based loosely on a single economic analysis of the total impact of the closure of a commercial fishery (Clites et al., 1991):
|
Annual Resource Damage Cost |
Probability |
(9) |
|
$7 million |
0.1 |
|
|
$12 million |
0.8 |
|
|
$17 million |
0.1 |
|
Test Case Results
This section summarizes some of the key results of the decision modeling exercise. As noted earlier in this appendix, the most important results are insights that influence the direction of the analysis, rather than bottom-line recommendations. The use of decision modeling software8 allowed the committee to construct and display decision models as diagrams and spreadsheets, rather than as lines of computer code, and to display model output as graphs and diagrams. The software also made it possible to perform valuable exploratory analyses of the decision problem in ways that otherwise would have been impractical.
The set of parameter values given in the preceding section was used as the baseline for the dredged-volume decision model. All the nodes in the model were annotated with information about the data and assumptions used to develop the baseline. These values and assumptions were altered during the analysis to test
assumptions and explore the sensitivity of the results to various changes. The set of decision alternatives (the numbers of cubic meters in each alternative) was also changed to determine the optimal dredged volume for the baseline values.
Baseline Results
Figure E-3 show the results of the analysis for the three initial decision alternatives, using the baseline parameter values. The display is a simplified decision tree showing the expected value of each alternative. Using the criterion of highest expected value, the preferred alternative is the intermediate dredged volume (35,000 m3), with an expected value of-$96.25 million, followed by the alternative of immediately dredging the maximum dredged volume (50,000 m3), with an expected value of-$100 million.
Figure E-4 provides more information about these results—information that would not be readily visible without the graphic representations. The three curves are cumulative probability distribution functions for the values of the alternatives. The cumulative probability distribution functions for the maximum dredged volume is the steepest (most vertical) curve; the range of possible values along the horizontal axis (from $150 million to -$75 million) is much narrower than for the other two cumulative probability distribution functions. This narrow range
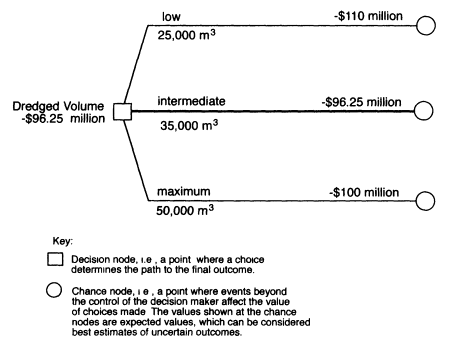
FIGURE E-3 Expected values of alternative dredged-volume decisions.
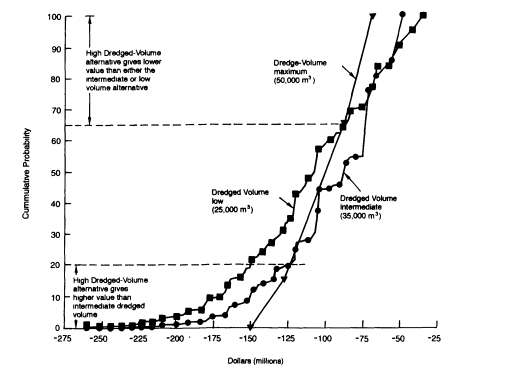
FIGURE E-4 Dredged-volume decision analysis.
means that the value of the maximum dredged-volume alternative is more certain than the values for the other two alternatives. (In this context, value is the negative of cost; a value of -$150 million is equivalent to a cost of +$150 million.)
The relatively low level of uncertainty associated with the maximum dredged-volume alternative makes sense because the low and intermediate dredged-volume alternatives involve more uncertainty about the remobilization and resource damage costs. The greater reliability (i.e., lower uncertainty) of the maximum dredged-volume scenario could persuade a risk-averse decision maker to select this alternative, despite its higher expected cost.
Another way of interpreting Figure E-4 is to note where the cumulative probability distribution functions intersect. The high and intermediate dredged-volume alternatives intersect at a cumulative probability level of approximately 20 percent (shown on the vertical axis), meaning that the model predicts about a 20 percent chance of the high dredged volume providing a better outcome than the intermediate dredged volume. However, the point where the high and low dredged-volume alternatives intersect predicts a 35 percent chance that the high dredged-volume alternative will have the worst outcome of the three alternatives considered.
This exercise indicates how decision modeling, and the visual display of the results, can foster understanding of the problem in ways that numerical formulas alone cannot.
Analysis of Alternative Scenarios
The values used as model parameters were changed to test assumptions and explore the sensitivity of the results. For example, the low uncertainty for the maximum dredged-volume alternative may hinge on the decision rule stating that the dredged volume will not exceed the defined maximum of 50,000 m3. On the other hand, the exceedance probability for a dredged volume of 50,000 m3 may be low enough that the uncertainty about this alternative is insensitive to the upper limit on the dredged volume. To test this assumption, the model was modified. The three decision alternatives remained the same, but the additional dredged volume required if the FDA action level were exceeded was defined as:
|
Additional Dredged Volume |
Probability |
(10) |
|
50,000 m3—dredged volume |
0.5 |
|
|
70,000 m3—dredged volume |
0.5 |
|
Figures E-5 and E-6 show the effect of the added uncertainty about the maximum dredged volume. Figure E-5 shows that the expected values of the low and intermediate dredged volumes have dropped compared to the baseline (shown in Figure E-3), whereas the value of the maximum dredged volume is essentially unchanged. By comparing Figure E-3 with Figure E-5, it can be seen that a 50 percent chance of having to dredge up to 70,000 m3 (see Equation 10) has essentially no effect on the outcome of the highest dredged-volume alternative. (The probability of exceeding the FDA action level is low [on the order of 0.001] if the initial decision is to dredge 50,000 m3.) On the other hand, the exceedance probabilities for the intermediate and low dredged-volume alternatives are sufficiently high that the added uncertainty about a possible penalty (assessed if the initial dredged volume is too low) drives down their expected values.
Another issue of interest to the committee was whether and how decision modeling could help resolve disagreements about values, such as the local economic impact of a sediment management decision. As an illustration, there might be significant disagreement in the test case about the annual resource damage cost of the closure of a fishery. For example, if a substitute existed for the damaged fishery, then one might argue that the resource damage should be set at the marginal cost of the closure, rather than the total cost. The impact of such disagreements on the decision outcome can be analyzed using a technique known as switchover, or policy region, analysis (Morgan and Henrion, 1990). In a switchover analysis, the model is run repeatedly, each time using a different
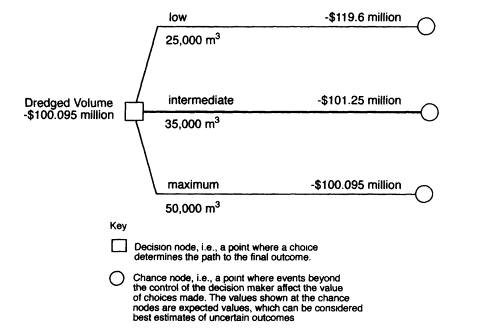
FIGURE E-5 Expected values of alternative dredged-volume decisions with modified model parameters.
estimate for the variable being analyzed. The computer determines the values at which the model's preference ''switches" from one alternative to another.
Figure E-7 shows the results of a switchover analysis for annual resource damage cost. The objective is to examine the sensitivity of the preferred decision alternative to uncertainty and/or disagreement about model parameter values. In this case, the value for this cost was varied from $0 to $20 million to determine the effect on the preferred decision (where the preferred decision is defined as having the highest expected value). All other model values and probabilities remained the same as in the baseline analysis.
The switchover analysis shows that the preferred decision (intermediate dredged volume) is insensitive to annual resource damage cost over a wide range of values (from $43,479 to $15 million). These limits were determined using the computer to perform repeated runs of the model. When the cost drops below $43,480, the low dredged volume becomes the preferred alternative (because the risk associated with the exceedance probability for this alternative diminishes). When annual resource damage cost exceeds $15 million, the maximum dredged volume becomes the preferred alternative (because as this cost rises, the risk associated with the exceedance probability for the intermediate dredged volume decision becomes unacceptably high).
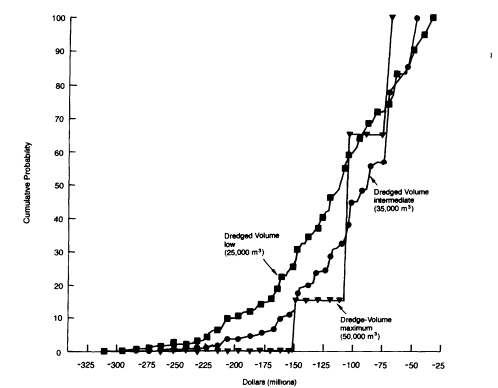
FIGURE E-6 Effect of modified model parameters on maximum dredged volume decision.
This is an enlightening exercise because it shows that disagreement about the economic impact of closure of the fishery does not have much impact on the decision, at least under the conditions and assumptions in the baseline model. If this conclusion held up over a range of variations to the model, then disputes concerning the actual value of resource damage could be set aside. And, if variability in cost estimates were due to disagreements (rather than uncertainties) about risks, costs, and benefits, then expensive analyses, which probably would not resolve the question anyway, could be avoided.
Summary of Results
The analysis of deciding how much sediment to dredge in the test case indicates that the low dredged-volume alternative probably can be eliminated from further consideration because it is consistently outperformed by the other two alternatives. The analysis also clarifies the issues involved in choosing between the intermediate and high dredged volumes. The high dredged volume would be
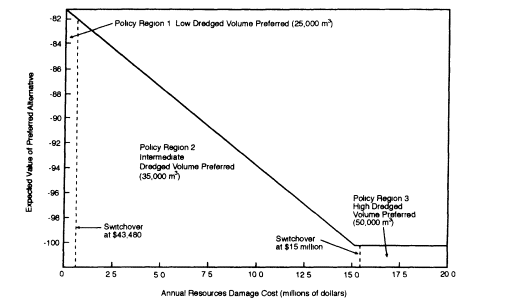
FIGURE E-7 Switchover analysis for the annual resource damage cost
preferred by a risk-averse decision maker because the outcome is more predictable than the intermediate dredged volume and the expected value is nearly as high.
Under the baseline scenario, the intermediate dredged volume is preferred, but the expected value is only $3.75 million (4 percent) higher than the value for the high dredged volume (as shown in Figure E-3), which has a more certain outcome. The range of possible costs for the high dredged-volume alternative is $75 million to $150 million, whereas the range of possible costs for the intermediate dredged-volume alternative is $50 million to $250 million (as shown in Figure E-4). The model predicts an approximately 20 percent chance of the high dredged volume providing a better outcome than the intermediate dredged volume. However, the model also predicts a 35 percent chance that the high dredged-volume alternative will have the worst outcome of the three alternatives.
If the model is altered slightly by increasing the uncertainty of the maximum dredged-volume alternative, then the high dredged-volume alternative becomes the model's preferred choice, demonstrating why a risk-averse decision maker might override the recommendation of the baseline analysis.
REFERENCES
Baumol, W.J. 1972. Economic Theory and Operations Analysis. Englewood Cliffs, New Jersey: Prentice-Hall.
Baird, B.F. 1989. Managerial Decisions Under Uncertainty: An Introduction to the Analysis of Decision Making. New York: John Wiley & Sons.
Carpenter, S.L., and W.J.D. Kennedy 1988. Managing Public Disputes A Practical Guide to Handling Conflicts and Reaching Agreements San Francisco, California: Jossey-Bass
Clark, W.C. 1980. Witches, Floods, and Wonder Drugs: Historical Perspectives on Risk Management in Societal Risk Assessment: How Safe is Safe Enough R.C. Schwing and W.A. Albers, eds. New York: Plenum Press.
Clemen, R.T. 1991. Making Hard Decisions: An Introduction to Decision Analysis . Boston: Kent Publishing Company.
Clites, A.H. , T.D. Fontaine, and J.R. Wells.1991. Distributed costs of environmental contamination Ecological Economics. 3:215-229.
Connolly, J.P. 1991. Application of a food chain model to polychlonnated biphenyl contamination of the lobster and winter flounder food chains in New Bedford Harbor Environmental Science and Technology. 25:760-770.
Dakins, M.E., J.E. Toll, and M.J. Small. 1994. Risk-based environmental remediation Decision framework and the role of uncertainty Environmental Toxicology and Chemistry. 13(12):1907-1915.
Dakins, M.E., J.E. Toll, M.J. Small, and K.P. Brand, 1996. Risk-based environmental remediation Bayesian Monte Carlo analysis and the expected value of sample information. Risk Analysis. 16(1):67-79
Environmental Protection Agency (EPA). 1994. Guidance for the Data Quality Objectives Process Final Report. EPA QA/G-4, Washington, D. C.: EPA Quality Assurance Management Staff September.
EPA. 1996. Review of National Ambient Air Quality Standards for Ozone: Assessment of Scientific and Technical Information: OAQPS Staff Paper. EPA 542/R-96-007. Office of Air Quality Planning and Standards Research Triangle Park, North Carolina: EPA.
Horton, C. 1993. To Build or Not to Build: Economic Assessment Model Helps Companies Decide Whether to Build Onsite Wastewater Treatment Facilities or Buy Services. Industrial Wastewater 1(2):39-43.
Howard, R.A., and J.E. Matheson, eds. 1984. The Principles and Applications of Decision Analysis. Menlo Park, California: Strategic Decision Group.
Keeney, R.L., and H. Raiffa. 1976. Decisions with Multiple Objectives. New York: John Wiley & Sons.
Morgan, M.G., and M. Hennon. 1990. Uncertainty: A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis. Cambridge, United Kingdom: Cambridge University Press.
National Research Council (NRC). 1989. Contaminated Marine Sediments-Assessment and Remediation. Washington, D.C.: National Academy Press.
Northwest Power Planning Council (NWPPC). 1991. 1991 Northwest Conservation and Electric Power Plan, vol. 2, part 2. Portland, Oregon: NWPPC.
Raiffa, H. 1968. Decision Analysis: Introductory Lectures on Choices Under Uncertainty. Reading, Massachusetts: Addison-Wesley.
Savage, L.J. 1954. The Foundation of Statistics. New York: Wiley & Sons.
Silkien, R.L. 1990. Decision Analysis and Quantitative Risk Characterization Information-Analysis Based Risk Characterization . Washington, D.C.: Chemical Manufacturers Association, Inc.
Singer, L.R. 1990. Settling Disputes Boulder, Colorado: Westview Press.
U.S. Department of Energy (DOE). 1986. A Multi-Attribute Utility Analysis of Sites Nominated for Characterization for the First Radioactive-Waste Repository-A Decision-Aiding Methodology. DOE/ RW-0074. Office of Civilian Radioactive Waste Management. Washington D.C.: DOE.
von Neumann, J., and O. Morgenstem. 1944. The Theory of Games and Economic Behavior Princeton. New Jersey: Princeton University Press.
Watson, S.R., and D.M. Buede. 1987. Decision Synthesis: The Principles and Practice of Decision Analysis. Cambridge, United Kingdom: Cambridge University Press.




























