APPENDIX C Explanation of Basic Stability
A ship or any other freely floating body displaces its own weight of the liquid it is in when afloat. This weight (w) acts downward through the center of gravity of the body (G) and is resisted by an upward buoyant force (equal to w), which acts through the center of buoyancy (B) (see Figure C-1). (B) is the geometric center of the submerged volume displaced by the ship. The metacenter (M) is the point through which all vertical forces are said to act.
The actual ''all up weight" of a ship and its contents is equal to the weight of water displaced by the hull; accordingly, this is referred to as its displacement. A vessel's displacement varies over a range of conditions from extreme lightship to a deep, heavy-loaded condition. The displacement alters as cargo or ballast is loaded or discharged or as fuel is consumed.
In stable ship, the centers of buoyancy and gravity strive at all times to remain vertically aligned. When a stable ship is caused to heel by an external force, such as wind, wave, or turning motion (not weight shift), the consequent change in underwater hull shape will result in (B) moving to one side while (G) does not move. The horizontal separation of (B) and (G) so caused is referred to as the righting lever, GZ (see Figure C-1), and the resulting righting moment, (w x GZ), will cause the vessel to oscillate from side to side as it attempts to realign (B) and (G).
The measure of a ship's initial stability, when upright or nearly upright, is indicated by the height of the metacenter (M) above (G), which is referred to as the metacenter height, GM, while the horizontal distance, GZ, more accurately indicates the measure of stability at angles of heel (OB:FO: "Theta") in excess of 5 degrees from the vertical. GZ is referred to as the measured of static stability.
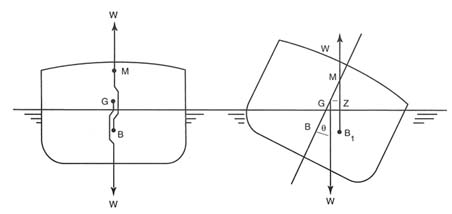
FIGURE C-1 Righting lever.
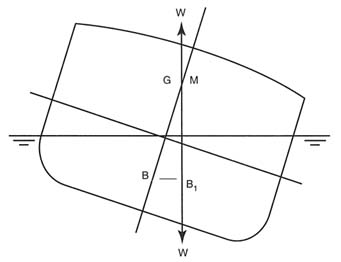
FIGURE C-2 Zero GM.
Should the ship's center of gravity (G) coincide with (M) and an external force be applied, the ship will assume an "angle of loll." The ship will maintain the assumed angle until a further force is applied. Should another external force be applied, the ship may assume an angle of loll to the other side or may worsen the existing loll condition if there is no righting lever, GZ, to correct the assumed heel angle. In this condition the ship is said to have zero or no GM (see Figure C-2).
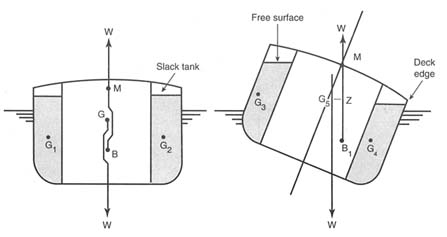
FIGURE C-3 Reduced GM with slack tanks (free surface effect).
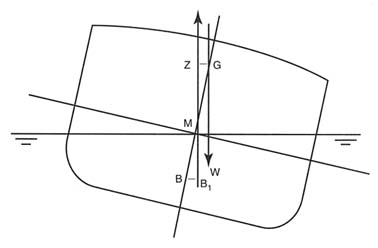
FIGURE C-4 Negative GM.
As shown in Figure C-1, when the vessel is upright, the center of buoyancy, (B), and the center of gravity of the ship, (G), remain in line and the ship is transversely stable, even with slack; that is, even with the ballast tanks partially full. However, if an external force is applied (because of wind, wave action, or the ship turning) and the ship is caused to heel, the center of gravity of the water in the ballast tanks (G1) and (G2) will move to positions (G3) and (G4), resulting
in the center of gravity of the ship moving from (G) to (G5) (see Figure C-3). This movement reduces the original righting lever, GZ, and the resultant height of the ship's GM. The ship therefore becomes less transversely stable.
Should the ship, for whatever reason, continue to heel, the position of (G5) will continue to move due to the movement of the center of gravity of the affected ballast tanks, thereby reducing the vessel's GM and the resulting GZ. If the deck edge becomes immersed, the center of buoyancy (B) will move inboard, the effect of which will again reduce GM and the resultant righting moment, GZ. The effect of this change will make the vessel become very "tender," and it will "flop" from side to side.
If more tanks are made slack or there is a cargo shift due to the excessive angle of heel, it is possible for (B) and (G5) to reverse positions. Should this occur, GZ will be converted from a righting lever into a coupled turning force, which could cause the ship to capsize. This condition is known as negative GM (see Figure C-4).




