Appendix C
Details of Aircraft-Pilot Coupling Examples
This appendix provides quantitative details of the APC examples discussed in summary form in the body of the report.
Essentially Linear Oscillatory Aircraft-Pilot Coupling Events
The simplest oscillatory APC events occur when both the effective aircraft and the pilot dynamics act as quasi-linear and time-stationary system elements. In terms of the pilot behavioral modes described in Chapter 5, the pilot dynamic behavior associated with the instability is initially compensatory but may change to synchronous as the oscillation becomes fully developed.
Figures C-1a and C-1b show the pitch attitude characteristics of an illustrative set of effective aircraft dynamics tested in flight and extensively analyzed.5,42 If it is assumed that the pilot operates in synchronous (pure gain) mode at the frequencies of interest, then data in Figures C-1a and C-1b correspond to the open-loop pilot-vehicle system (PVS) dynamics for pilot control using pitch attitude cues.
The key effective aircraft factors associated with susceptibility to an essentially linear PIO are properties that hinder the pilot's ability to close the PVS loop for various levels of pilot gain or to achieve adequate closed-loop performance. The first of these factors is illustrated by comparing Figures C-1a and C-1b. These are Bode plots and gain/phase (Nichols) diagrams of the open-loop dynamics of pilot-aircraft pitch attitude control systems.43 Figure C-1a shows that a pure-gain pilot operating on attitude cues can create stable loop closures using gains from zero to a value somewhat less than the value
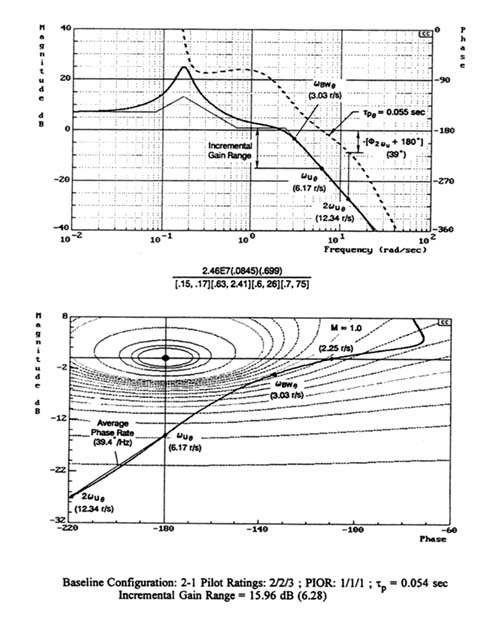
Figure C-1a Bode and Nichols diagrams for a synchronous PVS of an aircraft with low susceptibility to oscillatory APC events. Source: McRuer.42
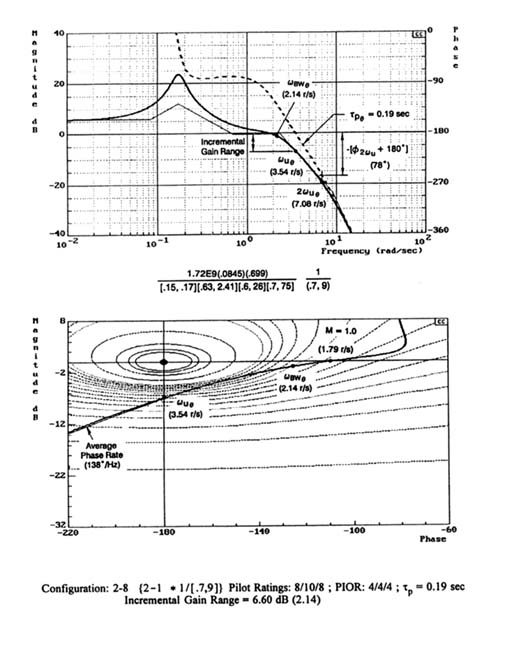
Figure C-1b Bode and Nichols diagrams for a synchronous PVS of an aircraft with high susceptibility to oscillatory APC events. Source: McRuer.42
corresponding to the neutral stability frequency, ωu (6.17 rad/sec), where the pilot-effective aircraft open-loop phase angle is -180 degrees. Within this entire range, the pilot can adjust gain as needed to achieve a desired level of closed-loop performance and control precision. Contrast this with the PVS attitude dynamics of Figure C-1b, where the maximum stable open-loop gain yields a neutral stability frequency of only 3.54 rad/sec. Because closed-loop system bandwidth and precision control (error performance) is proportional to the open-loop system gain, the attainable performance for the Figure C-1a system will be 1.75 times better than for the Figure C-1b system.
The analytically derived performance differences described above are reflected in the flight test experiments for these configurations.5 The Cooper-Harper Pilot Rating (CH PR) differences (2/2/3 versus 8/10/8) from the flight tests show that the flying qualities of the Figure C-1a aircraft are excellent while those of the Figure C-1b configuration are terrible. The PIO rating differences (1/1/1 versus 4/4/4) further indicate the high susceptibility of the latter aircraft to PIO, which was aptly demonstrated when several PIOs were encountered.5
The extent to which the pilot can adjust gain in tight closed-loop control circumstances is measured by the ''incremental gain adjustment range."42 This feature can be quantified in various ways. For instance it could be expressed as a frequency range—for example, from 0 to 3.54 rad/sec and from 0 to 6.17 rad/sec for the characteristics compared above. Or, when a suitable reference level exists, it could be expressed in terms of an incremental pilot gain. For those effective aircraft dynamics where a short period "shelf" exists (the horizontal asymptote starts at 1/Tθ2 = 0.7 rad/sec in Figures C-1a and C-1b and runs horizontally until it reaches the short-period, ωsp = 2.41 rad/sec), the amplitude ratio of the shelf asymptote can serve as a convenient and relevant reference gain level, as noted in the figures (relevant because, for the pilot to exert significant control over the effective short period dynamics of the effective aircraft, the minimum open-loop system gain crossover has to be somewhat greater than this value). An analysis of the several servere aircraft pilot coupling oscillations (Figure C-1b, for example) indicates that an available gain range from this kind of reference should be greater than a factor of 3 (9.5 dB) or so to avoid a high degree of susceptibility to essentially linear severe APC oscillations.5,42 In the example in Figure C-1b, it is only 6.6 dB. This same feature is implicitly reflected in indicators of K/s-like character, such as the Dropback criterion (see Chapter 6).
The inability to achieve adequate closed-loop system performance is also illustrated by Figures C-1a and C-1b when considered in the context of the associated pilot ratings. Achieving adequate performance with a linear system can be interpreted as attaining a specific open-loop system crossover frequency (ωc). In terms of the aircraft dynamics, the attainable crossover frequency without extensive pilot compensation is conveniently measured by the so-called
aircraft bandwidth (ωBW). In this situation, the aircraft bandwidth is the frequency at which the phase is - 135 degrees. The pilot ratings suggest that the ωBW = 3.03 rad/sec for the Figure C-1a aircraft is excellent, while the Figure C-1b system ωBW = 2.14 rad/sec is deficient.
The aircraft bandwidth can also be used as a basis for assessing the latitude available to the pilot in tightly closing the PVS loop. This basis contrasts the bandwidth frequency, as a nominal high-gain pilot-vehicle crossover frequency, with the maximum frequency available (ωu). The incremental frequency (Δω = ωu - ωBW) indicates the maximum increase in crossover frequency from the aircraft bandwidth that is available from an increase in pilot gain. As a dimensionless scalar measure, Dw/ ωBW does much the same thing. For the contrasting "good" (Figure C-1a) and "bad" (Figure C-1b) aircraft, respectively, these parameters are Δω = 3.14 rad/sec and 1.4 rad/sec and Δω/ωBW = 1.04 and 0.65. Thus the pilot has much greater latitude to increase the open-loop system bandwidth, thereby improving both performance and accuracy, with the good aircraft of Figure C-1a.
The aircraft bandwidth is an excellent absolute indicator of the capability of a PVS for precision closed-loop control. The flexibility and ease of making precision adjustments, assessed via various available gain range measures, as above, often have arbitrary reference levels. They are, therefore, useful for comparing specific related configurations, such as the two aircraft in these examples, but cannot easily be used to generalize across unrelated configurations. A more general way to assess this feature is to examine the rapidity of change in the aircraft phase in the region of extremely tight control near the limiting maximum available frequency (ωu). A convenient indicator for this purpose is available from many flying qualities studies. This is the "phase delay" (τpθ) which measures the rate of change of phase lag based on the instability frequency (see Chapter 6). For the data in Figure C-1a and C-1b, these are 0.054 see and 0.19 sec, respectively. In terms of all the criteria for flying qualities, the C-1a configuration is consistent with excellent Level 1, while the C-1b configuration is, at best, borderline PIO-prone.
All of the problems in the Figure C-1b system are direct consequences of the significantly greater high-frequency phase lag. Indeed, excessive lag is the most profoundly important single factor in essentially linear APC events because it limits both the attainable gain range and the attainable crossover frequency. The phase delay or some related quantity, such as average phase rate, and the aircraft bandwidth (ωBW) are excellent summary indicators of the properties of the effective controlled element dynamics in closed-loop control.
Some Nonlinear Characteristics That Can Lead To Flying Qualities Cliffs
Common Cliff Producers
Conceptually, the cliff metaphor evokes a picture of sudden large changes in aircraft motions associated with relatively slight changes in pilot activity. When cliff-like changes are caused only by an increase in the pilot's output amplitude, the pilot-aircraft system is not behaving like a linear system. Instead, there are significant nonlinearities in the dynamics of either the effective aircraft or the pilot.
In conventional mechanical/hydraulic manual primary flight control systems (FCSs), the principal nonlinearities are rate and position limits intrinsic to surface actuators and various preloads, thresholds, and detents. These latter features are introduced to offset frictional and other unfavorable effects, thereby improving the threshold properties of the cockpit manipulators. In other words, they are intended to make the primary mechanical control system feel more "linear." Thus, in a well designed mechanical system, the significant nonlinearities involved in tightly controlled closed-loop control are the rate and position of the surface actuator.
By contrast, fly-by-wire (FBW) FCSs offer a more extensive variety of possibilities for deliberate nonlinearities. These opportunities are often fully exploited, although not always with a comprehensive understanding and appreciation of the accompanying side effects, not the least of which can be an enhanced susceptibility to APC events. Some simple examples are described below.
Perhaps the two most common significant nonlinear characteristics within the effective aircraft are present in the FCS. These are command-path gain-shaping and rate limiting. Figure 2-2 (see Chapter 2) shows a simplified view of these nonlinearities in a FCS/aircraft ("effective aircraft") combination. Note that rate limiters can be present in several different locations. However, just as with the primary manual control systems of the past, one source of rate limiting illustrated in Figures 2-2 and 2-3 is in the fully-powered surface actuating subsystem. This limiting rate is still around, although it is sometimes "protected" from becoming active by pre-actuator rate limiters. In this example, a pre-actuation-loop rate limiter or a rate limiter intrinsic to the actuation system will have the same effect. Command-path gain-shaping and rate limiting are used in the two elementary examples below to illustrate the cliff-like APC potential that can be introduced.
Command-Path Gain-Shaping
Most modern FCSs incorporate gain-shaping in the pilot's command path. The shaping is usually shallow around neutral, with the gain (control gradients) adjusted to provide optimum pilot-aircraft closed-loop precision control. In Figure 2-4, this is the region |A| 8 a. For larger pilot-input amplitudes, the gradient(s) are increased at points along the gain curve (e.g., at A = a) until maximum deflection of the control effector is achieved by maximum pilot input. (It should be noted in passing that the abrupt change in slope at |A| = a is often made more smoothly and gradually.)
A typical PIO scenario involving this nonlinear feature might start with the PVS operating with high gain to achieve precision control around neutral. In terms of Figures 2-2 and 2-4 (see Chapter 2), the pilot's amplitude (A) for this condition does not exceed (a), although it can be arbitrarily close. To achieve a high degree of precision control, the pilot will be closing the loop with a relatively low gain margin. (Gain margin is the ratio of the open-loop system gain for instability to the operating point gain. In a typical PVS engaged in a high-gain tracking task, experimental data indicate that the gain margin will be nominally about 3/2 or 3.5 dB.45 In this case, an increase in the open-loop system gain, from either the pilot or the effective aircraft, of 50 per cent would result in neutral stability.)
If a large input or disturbance, or even greater task demands, result in a pilot output amplitude of |A| > a, the effective open-loop gain of the PVS will increase. If the increase is sufficient to consume the gain margin, then a PIO can occur. Figure C-2 shows the stability limits for a gain margin of 3/2 as a function of the gain-shaping slope ratio. The robust stability limit for any K2/K1 is given by the initial abscissa (i.e., ΔGM = 3/2 for a/A = 0). For values of the slope ratio K2/K1 > 1.5 there will be an input amplitude (A) that gives rise to an oscillatory instability once it is exceeded.
A typical moderate value of K2/K1 is about 3, although higher values do exist. For the high-gain PVS closure assumed here, an oscillation will occur for any pilot input amplitude over (4/3)a, or only a 33 per cent increase in the input amplitude beyond the slope break-upward point. Gains that are similarly sensitive to the pilot input have been indicted as a source of PIOs in the past, including the YF-22 case described in Chapter 2 and by James et al.36 Input-sensitive gains can act independently or in concert with various rate limiting features to cause an APC event.
Rate Limiting
Extensive control-surface rate limiting has been observed in almost all recorded severe oscillatory APC events. Detailed analyses of rate limiting
support the view that rate limiting exacerbates time lag effects.3,14,15,28,31,39 But how and when the additional time lags enter the closed-loop system have not been well documented in detailed experiments.
Although there is a consensus that rate limiting phenomena are important factors in fully developed, severe APC events encountered in operational situations, the transitional system behavior on the way to rate limiting and severe PVS oscillations has not been recorded in enough detail for a complete understanding. The possibility that rate limiting phenomena may be central initiating factors (triggers) in the development of some severe APC events has also not received enough attention. Yet it is easy to show that rate limiting features in FCSs can lead to unusual, potentially cliff-like situations.
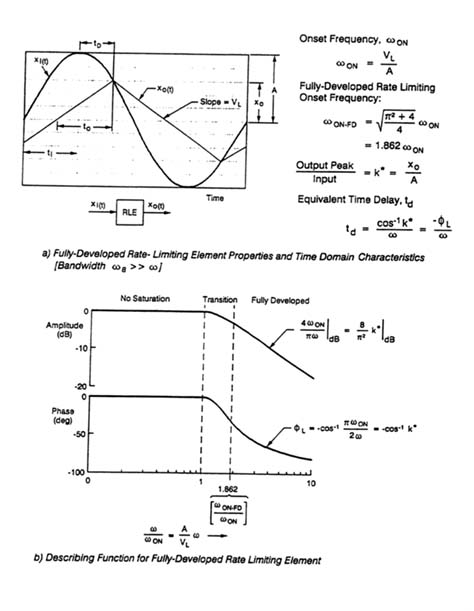
Some general aspects of rate limiting in actuation systems are described in the discussion of Figure 2-3 (see Chapter 2). When the input frequencies (PIO frequencies) are much smaller than the bandwidth of the actuation system, these rate limiting features can be generalized as properties of a "rate-limiting element." Actuator rate limiting characteristics that do not rely on this simplifying assumption have been developed.39 Both the time-domain and frequency-domain properties of a rate-limiting element are shown in Figure C-3.
Figure C-3a shows the output of the rate limiting element to a sinusoidal input as a triangular wave. This will occur when the system input amplitude (A) and input frequency (ω) create a maximum input-velocity command (ωA)
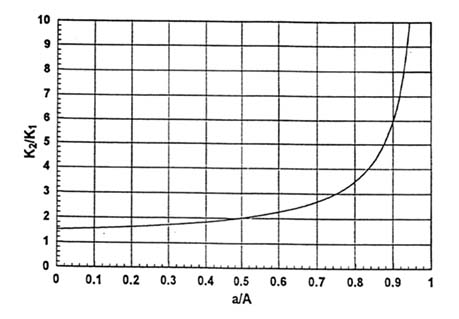
Figure C-2 Input amplitude-dependent stability boundaries as a function of command-path gain shaping ratio for a linear system gain margin ΔG M = 1.5.
large enough to keep the system essentially always on the rate limit. Figure C-3b gives a describing function for the amplitude ratio and phase angle as functions of a frequency ratio in which the normalizing frequency is the "onset frequency" (ωON). At the onset frequency, the input rate equals the rate limit (i.e., ωON A = VL, where A is the amplitude of the input position command and VL is the rate limit).
At normalized frequencies (ω/ωON) less than one, the amplitude ratio of the rate-limiting element is 1.0 and the phase lag is zero. Thus rate limiting, as expected, has no effect whatsoever in this range. At and slightly above the onset frequency, the amplitude ratio decreases somewhat, and a phase lag begins. This is the "transition" or "near saturation" zone (see Figure C-3b). Finally, when input amplitudes are large enough (or rate limits small enough) to pass the fully-developed onset frequency (ωON-FD = 1.862 ωON), the rate limiting becomes fully developed, introducing a significant phase lag into the PVS loop.14 This condition can lead to a cliff-like situation because the insertion of the phase lag occurs simultaneously with the increase in the magnitude of the pilot's command. At its most insidious, the phenomenon causes the sudden and dramatic onset of a substantial shift in the phase lag. This shift is equivalent to the sudden insertion of a significant added time delay into the loop.
A typical scenario might begin with a pilot who is well-adapted to an essentially linear closed-loop PVS that is operating at high gain to satisfy precision control purposes. The system is then confronted with task demands that call for just a bit more pilot control amplitude or gain. When the system is near the conditions for the onset of rate limiting, slight increases in either amplitude or gain (or both) are sufficient to enter the non-linear rate-limiting regions, with the concomitant introduction of a sudden substantial phase lag into the closed-loop system. (Recall the F-14 example described in Chapter 2.) In terms of the underlying physics of closed-loop systems, this is a classic example of jump resonance.28
To illustrate the general points about jump resonance and flying qualities cliffs caused by rate limiting in more quantitative detail, consider a closed-loop control task with effective aircraft dynamics that possesses nominally excellent flying qualities and to which the pilot is well-adapted. The PVS dynamics in the linear regime will be approximated by the crossover model of manual control theory. Assume that the effective vehicle dynamics include a rate-limited actuator operating in series with the pilot and that the effective aircraft in the linear regime possesses excellent flying qualities. When task demands require tight closed-loop performance, the pilot's gain and maximum amplitude are adjusted to satisfy the precision control requirements. Assume that these levels remain consistent with linear system operations, but with rate limit/pilot-input-amplitude values near the onset (or saturation) frequency. With an active,
attentive pilot, this baseline condition would exhibit a gain margin of about 3/2 and a phase margin of perhaps 25 degrees. In this essentially linear regime, the closed-loop system will perform well. It would be given Level 1 flying qualities assessments with good CH PRs and low PIO ratings and would exhibit no significant periodic oscillations.
Now increase the task demands so that the pilot's input amplitude is increased by 10 to 20 percent. This can be enough to push the system well past the onset frequency to a point where the phase margin is reduced from about 25 degrees to zero, resulting in a potentially severe PIO. With just a bit more input amplitude, the rate limiting can become fully active, introducing a much greater phase lag and a diverging closed-loop system oscillation.
To make this example even more specific, assume that the effective aircraft dynamics are consistent with excellent pilot ratings—say a CH PR of 2 or 3. For this to be so, the effective time delay (τ e in the crossover model—which accounts for both the pilot's lags and the higher-frequency dynamics of the effective aircraft) will be about 0.3 sec. In this crossover model case, the neutral stability frequency (ωu = π/2 τe) will be about 5 rad/sec, which is representative of the linear system.39,42 Taking the 25 degrees phase lag caused by rate limiting into account, the PIO frequency becomes about 3.5 rad/sec. This PIO frequency is 30 percent less than the neutral stability frequency of 5 rad/sec for the linear system. The sudden phase lag introduced by the phase deficit of 25 degrees can then, with the known PIO frequency, be equated to an equivalent incremental time lag of 0.12 sec. Thus, the frequency of the PIO is the same as would occur if an incremental delay of td = 0.12 sec was suddenly inserted into the system.
For the effective aircraft to have excellent flying qualities initially, the effective time delay of the aircraft alone would be about 0.1 sec or so, which would be more than doubled by virtue of the rate limiting effect. The total effective delay of 0.22 sec for the nonlinear system is also well above the value of about 0.19 sec associated with a high degree of PIO susceptibility for a linear system.
McRuer et al46 have provided a more detailed and precise analysis of these rate-limiting and gain-shaping effects. The examples above illustrate the importance of nonlinear concepts for identifying rate limiting and kindred features as potential sources of nonlinear, oscillatory, jump-resonance phenomena. The jump-resonance phenomenon is useful because it exhibits nonlinear features that correspond well with test pilot descriptions of nonlinear, cliff-like behavior when severe APC events occur (see Chapter 2).