Appendix B
Comparative Dosimetry
INTRODUCTION
In order to extrapolate the lung-cancer risk derived from the epidemiological analysis of the underground miner data to the general population, a number of steps are needed. The approach to dealing with smoking, gender, and age at exposure were discussed in chapter 3. In addition, it is necessary to account for the differences in exposure conditions between mines and homes, in breathing rates for different activities in mining and typical home behavior, and in respiratory physiology between men, women, children, and infants. These factors determine the relationships between exposure and dose and the possibility of differing relationships between exposure and dose for miners and for the general population needs to be considered in extrapolating a risk model from miners to the general population. The comparative dosimetry approach used by the committee follows that described by the Panel on Dosimetric Assumptions Affecting the Application of Radon Risk Estimates (NRC 1991) and the BEIR IV Committee (NRC 1988).
In chapters 2 and 3, the committee reviewed the biological and epidemiological data suggesting that lung-cancer risk varies directly with exposure to radon and its decay products It is now assumed that lung-cancer risks varies directly with the dose of alpha energy delivered to the appropriate cellular targets, and that the dose can be estimated from the exposure using a dosimetric model. A dosimetric model is employed to estimate the dose received by particular classes within the general population such as adult males (not miners), adult women, children, and infants as well as to adult male miners. The dosimetric
model takes into account the exposure conditions in homes and in mines as well as the relevant physiological characteristics of the population groups. The ratio of the dose of alpha energy per unit exposure for a particular population group (men, women, children, infant) as given by the radon concentration to the dose per unit radon concentration to the miners is given by K:
K = [Dosehome/Exposurehome]/[Dosemine/Exposuremine] (1)
The K-factor includes diverse environmental and physiological factors and the use of this double ratio greatly simplifies the risk assessment for indoor radon. This chapter addresses dosimetry of radon progeny in the lung and presents the calculated K-factor values by reviewing the information available on exposure conditions in homes and mines, presenting the dosimetric model used and then presenting the resulting distributions of K-factor values that were calculated.
EXPOSURE
Introduction
The formation and decay sequence for 222Rn was shown in Figure 1-1. Because 222Rn has an almost 4-day half-life, it has time to penetrate through the soil and building materials into the indoor environment where it decays into its progeny. There is some recent evidence that in spite of its short half-life, 55 seconds, 220Rn can also penetrate into structures in significant amounts. However, the data are limited and the extent of the thoron problem is quite uncertain as discussed in a subsequent section of this chapter.
The short-lived decay products, 218Po (Radium-A), 214Pb (Radium-B), 214Bi (Radium-C), and 214Po (Radium-C'), represent a rapid sequence of decays that result in two α-decays, two β-decays and several γ-emissions following the decay. To illustrate the behavior of the activity of the radioactive products of the radon decay, the activity of each of the short-lived isotopes is plotted as a function of time for initially pure 222Rn in Figure B-1. Because 222Rn has a longer half-life than either of the four short-lived products, the progeny reach the same activity (number of decays per unit time) as the radon. The mixture then decays with the 3.8 day half-life of the radon. Each 222Rn decay results in four progeny decays so that the total activity is then the sum of these individual decay-product concentrations. The activity is the product of the decay constant (In 2/half-life) times the number of radioactive atoms. Thus, the short-lived 218Po can have an activity equal to the 222Rn because a large decay constant times a small number of atoms becomes equal to a small decay constant times a large number of atoms.
If the products formed by the decay of the radon were to remain in the air, then there would also be equal activity concentrations of 218Po, 214Pb, and other progeny. The resulting mixture is said to be in secular equilibrium. As used in the monitoring of uranium mines, an equilibrium mixture of these decay products
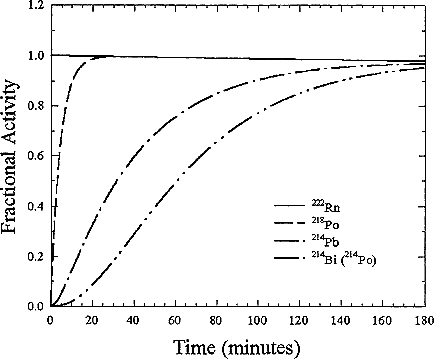
FIGURE B-1 Normalized in-growth of decay-product activities of an atmosphere initially containing only 222Rn.
at 3700 Bqm-3 (100 pCiL-1) is called a working level (WL). Thus, a 370 Bqm-3 (10 pCiL-1) equilibrium mixture represents 0.1 working level.
The cumulative exposure to such activity can be expressed as the amount of activity in WL multiplied by time of exposure. In occupational exposure assessments for miners, this cumulative exposure has historically been given in Working Level Months, WLM, where it is assumed there are 170 hours in a working month. The WLM is calculated as
where (WL)i is the average concentration of radon decay products during exposure interval expressed in WL and ti is the number of hours of the exposure. The cumulative exposure when spending all of the time in a house at a given decay product concentration is more than four times that for occupational exposure (8766 compared to 2000 hours worked on an annual basis).
More appropriately, the activity of the radon decay products is described by a quantity called the Potential Alpha Energy Concentration (PAEC). The total airborne potential alpha energy concentration, PAEC, is calculated as follows:
Cp(Jm-3) = (5.79C1 + 28.6C2 + 21.0C3) × 10-10 (3)
where Cp is the PAEC in Jm-3, and C1, C2, C3 are the activity concentrations of 218Po, 214Pb, and 214Bi in Bqm-3, respectively. This quantity incorporates the deposition of energy into the air. Exposure can be then expressed as the PAEC multiplied by the length of exposure in hours. This exposure is reported in the scientific units of Joule-hours per cubic meter (Jhm-3). Although much of the prior epidemiological studies on the radon risk as observed in underground miner populations have used exposure measured in WLM, these values can be easily converted into proper SI units by multiplying the original estimates of exposure in WLM by 3.5 × 10-3 Jhm-3 WLM-1.
In either homes or mines, decay products are lost from the air by attachment to environmental surfaces. In homes these surfaces include walls, floors, furniture, and the people in the room. The decay products also attach to airborne particles. The processes that control the airborne concentrations of the decay products are shown in Figure B-2. The attachment to the airborne particles maintains the radioactivity in the air since submicron particles typically remain suspended in the air over long times. The ratio of decay products to radon, termed the equilibrium factor, F, ranges from 0.2 to 0.8 with typical values of 0.35 to 0.4 (Hopke and others 1995).
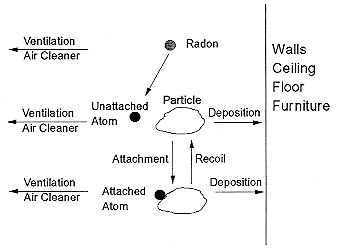
FIGURE B-2 Behavior of radon decay products in indoor air.
Another concept relating to the decay products is that of the ''unattached" fraction. Although it is now known that the decay-product atoms are ultrafine particles (0.5 to 2 nm in diameter), an operationally defined quantity called the "unattached" fraction has been used to describe this activity. However, there is no general agreement on a procedure for estimating its value. The "unattached" fraction should not be considered as single atoms of progeny; we now know that the unattached fraction actually comprises small clusters of molecules. These unattached decay products have much higher mobilities in the air than the attached activity and can more effectively deposit in the respiratory tract. Thus, the "unattached" fraction has been given emphasis in estimating the health effects of radon decay products. Typically most of the "unattached" activity is 218Po and the value of unattached fraction, fp, is usually in the range of 0.01 to 0.10 in indoor air, although it may be higher if the concentrations of particles in the air are very low. One does not actually measure unattached particle numbers but rather unattached decay-product activity in Bqm-3. Thus, the PAEC can be obtained directly from the unattached activity.
AIRBORNE PARTICLE PROPERTIES
The particles in indoor air are quite different in size from those that are typically encountered in the outdoor atmosphere. There are also many types of particle sources in a home such as open flames of a gas stove or candles, cooking, aerosol-spray products, and tobacco-smoking. In general, particles larger than 1 µm cannot penetrate into a house. A typical distribution of room air particles is shown in Figure B-3. The points are the average of 10 separate measurements. Particle sizes in typical room air are around 50 to 100 nanometers (nm). The size distributions for particles generated by gas stoves and by cigarette-smoking are shown in Figures B-4 and B-5. These distributions show that there are much higher particle concentrations when particle sources are operating. The high temperatures in the gas stove flame produces small particles with a peak in the distribution at about 20 nanometers while the lower temperatures in cigarette burning generates particles in the 100 to 300 nanometer (0.1 to 0.3 µm) range. The particle concentrations decrease over time because of surface deposition and ventilation. To obtain estimates of the activity-weighted size distributions, the number distributions are multiplied by the probability of attachment for the unattached radon decay product (Porstendörfer and others 1979).
Exposure in Normally Occupied Homes
Over the past decade, improvements in measurement technology have allowed the direct measurement of the activity-weighted size distribution of the radon decay products in normally occupied homes. Methods have been developed by which the entire radioactive aerosol size distribution can be
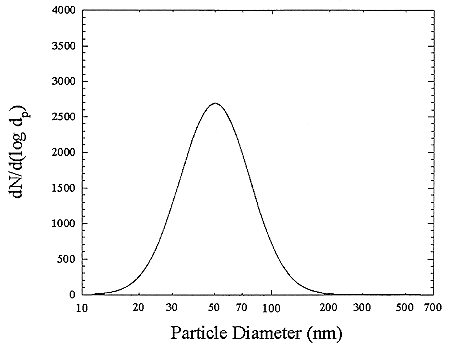
FIGURE B-3 Particle size distribution for room air. The curve is a fit to averages (points not shown). Each average derived from 10 separate measurements. Figure taken from Li and Hopke (1993).
deduced from the measured activity collected on or penetrating through a series of screens.
The first activity-size measurements in indoor and ambient air were made by Sinclair and others (1977) using a specially designed high-volume-flow diffusion battery. They observed bimodal distributions with activity mode diameters of 7.5 and 150 nm in indoor atmospheres and 30 and 500 nm outdoors in New York City. Similar results were reported by George and Breslin (1980). In Göttingen, West Germany, Becker and others (1984) only observed the larger mode using a modified impactor method with a minimum detectable size of 10 nm. More extensive measurements in New York City by the group at the Environmental Measurements Laboratory (EML) have been reported by Knutson and others (1984) using several different types of diffusion batteries as well as cascade impactors. They again observed modes around 10 nm and 130 nm in the PAEC-weighted size distribution measured with a low-volume screen diffusion battery. Four samples taken with a medium-volume (25 L min-1) screen diffusion battery showed a major mode at 80 to 110 nm and a minor mode containing 8 to 9% of
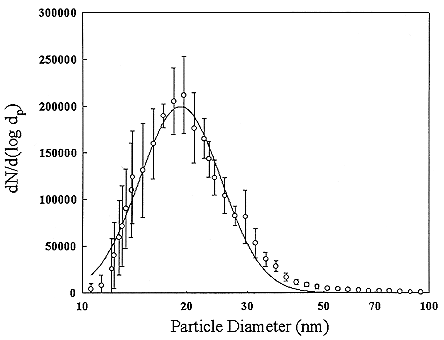
FIGURE B-4 Particle size distribution from a gas stove burner. Each point represents the average of 10 separate measurements. Figure taken from Li and Hopke (1993).
the PAEC with a diameter < 5 nm. Finally, the same group made measurements at Socorro, NM (George and others 1984). They report that the major mode was only slightly different from that found in New York. However, the minor mode was always < 5 nm, distinctly smaller than in the New York distributions.
One of the problems with the extension of screen diffusion batteries to smaller particle sizes is the substantial collection efficiency of the high mesh-number screens typically used in diffusion batteries designed to cover the range of particle size from 5 to 500 nm. At normally used flow rates, a single 635-mesh screen has greater than 90% efficiency for collecting 1 nm particles, the size of "unattached" 218Po having a diffusion coefficient of the order of 0.05 cm2s-1. A theory of screen penetration (Cheng and Yeh 1980; Cheng and others 1980; Yeh and others 1982) had been developed in the late 1970s and this theory was validated to 4 nm by Scheibel and Porstendörfer (1984). The limitations of high mesh-number screens were recognized and it then became possible to examine new types of diffusion battery designs that could be extended to smaller particle diameters.
Reineking and others (1985), Reineking and Porstendörfer (1986) and Reineking and others (1988) use the high-volume flow diffusion batteries de-
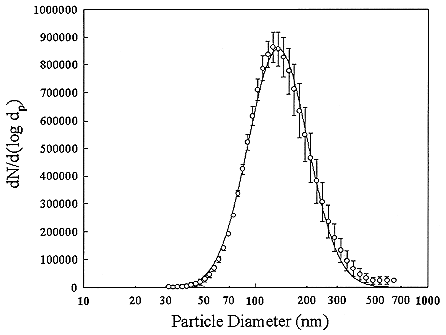
FIGURE B-5 Particle size distribution for sidestream cigarette smoke. Each point represents the average of 10 separate measurements. Figure taken from Li and Hopke (1993).
scribed in Reineking and Porstendörfer (1986) to obtain activity-size distributions. They obtained their size distributions by fitting lognormal distributions using an algorithm that searches the solution space for an acceptable fit (SIMPLEX). Size distributions of indoor air in rooms without and with the addition of particles from running an electric motor are presented in Figures B-6 and B-7.
Holub and Knutson (1987) report the development of low-flow diffusion batteries with low mesh number screens and extension of the EML batteries to smaller sizes. Tu and Knutson (1988a,b) have used the 25 L min-1 screen diffusion batteries to measure the 218Po-weighted size distributions in the presence of several specific aerosol sources. The results of these measurements are presented in Figures B-8 and B-9. The presence of a mode around 10 nm is again observed in curve 1 in Figure B-8. Only in curve 1 (no active aerosol sources) in Figure B-9 is a mode at 1 nm observed. In all of the other cases, the activity is attached to the aerosol present in the house. The attachment was confirmed by independently measuring the aerosol-size distributions using an electrical aerosol analyzer (Liu and Pui 1975) and the attachment coefficients recommended by Porstendörfer and others (1979). There was a high level of agreement between the measured and calculated activity-weighted size distributions.
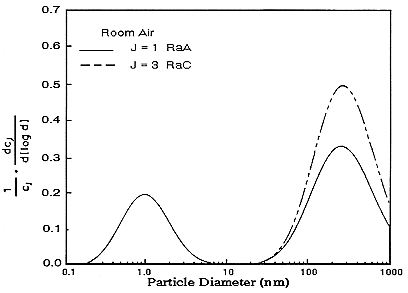
FIGURE B-6 Activity-weighted size distribution of the indoor aerosol in a closed room without active aerosol sources. Figure taken from Reineking and Portstendörfer (1986).
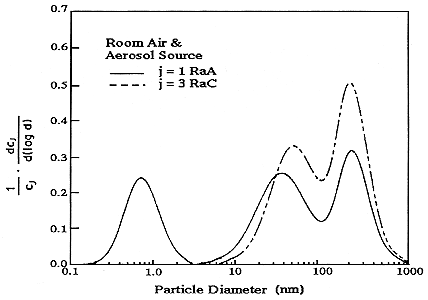
FIGURE B-7 Activity-weighted size distribution of the indoor aerosol in a closed room with an operating electric motor. Figure taken from Reineking and Porstendörfer (1986).
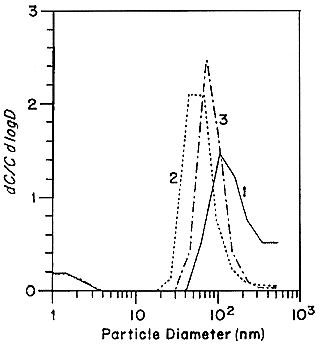
FIGURE B-8 218Po-weighted size distributions measured in house I. 1. Cooking (5 min.); 2. Frying food; 3. Cooking soap; 4. Cigarette smoldering. Figure taken from Tu and Knutson (1988a).
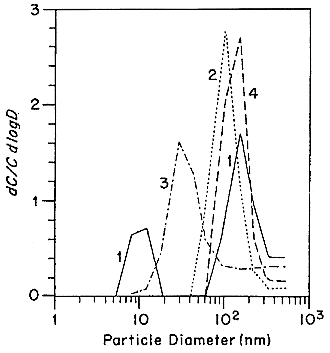
FIGURE B-9 218Po-weighted size distributions measured in house II after a kerosene heater was operated for: 1.0 min; 2.80 min; 3.20 min. Figure taken from Tu and Knutson (1988a).
Several other groups including the National Radiation Protection Board (NRPB) of the United Kingdom and the Australian Radiation Laboratory (ARL) have also developed these graded-screen diffusion batteries for activity-weighted size distribution measurements. Intercomparison experiments between the measurement methods have been performed (Hopke and others 1992). Generally good agreement was obtained.
Several automated systems to make use of this methodology have been developed. Strong (1988) used 6 sampling heads containing 0, 1, 3, 7 18, and 45 stainless steel, 400-mesh wire screens. He has measured the size distributions in several rooms in two houses at two times of the year. The size distributions observed in the kitchen are presented in Figure B-10.
These results are summarized in Table B-1. It should be noted that in the "kitchen" curve in Figure B-10, a trimodal distribution is observed; a true "unattached" fraction at 1 nm, a nuclei mode at 10 nm, and an accumulation mode at 100 to 130 nm. In the table, the "unattached" fractions presented are the integrated values from the size distributions. A problem of interpretation then arises regarding the "unattached'' fraction since Strong integrates the distribution up to > 10 nm to obtain the fraction that he attributes as being "unattached." For the distribution in a kitchen during cooking, the activity median diameter for the "unattached" fraction is given as 11 nm. This designation is a clear departure from the original purpose for defining an "unattached" fraction. The advent of these more sophisticated and sensitive measurement systems has necessitated either a more precise definition of the meaning of the "unattached" fraction or cessation of its use (Hopke 1992).
Subsequent to these original measurements, Strong (1989) modified his system by changing the screens to one 200-mesh screen and 1, 4, 14, and 45 400-
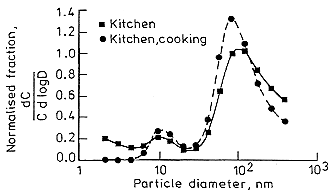
FIGURE B-10 PAEC size distributions measured in a rural house kitchen by Strong (1988).
TABLE B-1 Summary of activity size measurements made by Strong (1988) in row houses in the United Kingdom
|
Site |
Ambient Aerosol Median Diameter (nm) |
GSD |
N(cm-3) |
Attached AMD (nm) |
GSD |
fp (%) |
Unattached AMD (nm) |
|
Rural (summer) |
|||||||
|
Bedroom |
42 |
2.0 |
5000 |
130 |
2.4 |
17 |
2.0 |
|
Living Room |
30 |
2.0 |
5100 |
150 |
2.1 |
17 |
2.0 |
|
Kitchen |
33 |
1.7 |
11000 |
130 |
2.0 |
18 |
6.0 |
|
Kitchen (cooking) |
30 |
1.7 |
470000 |
110 |
1.9 |
11 |
11.0 |
|
Rural (winter) |
|||||||
|
Living Room |
32 |
1.7 |
4700 |
130 |
2.1 |
20 |
2.0 |
|
Urban (winter) |
|||||||
|
Living Room |
30 |
2.1 |
15000 |
110 |
2.1 |
20 |
3.5 |
|
Mean of all sites |
33 |
2.0 |
8200 |
130 |
2.1 |
18 |
3.1 |
mesh screens as well as the open channel. This modification provides a stage such that there is higher resolution for the smallest sized particles extending the range of the system to 0.5 nm. The effective resolution cut-off of the original battery was about 2 nm. With the new battery, tri-modal distributions are clearly observed (Figure B-11). Although these measurements were made in the living room, the kitchen is adjacent and cooking with a gas stove was being performed at the time of these measurements. These results show the need to measure the size distribution and determine the actual exposure of individuals to airborne radon-progeny activity in order to estimate doses.
A similar system has been developed at the Australian Radiation Laboratory by Solomon (1989). It is designed for measurements in the size range of 2 to 600 nm. The measurements have been extended to a smaller size range (0.5 to 100 nm) using a manual, serial single-screen array sampling at 1 to 6 L min-1 and to lower concentrations in the same size range using larger screens (9.5 cm diameter) and a 100 L min-1 flow rate. Dr. Solomon has examined both the Twomey (1975) and Expectation Maximization (Maher and Laird 1985) algorithms for deconvoluting the size distributions from the screen-penetration data. For both algorithms, he has developed a Monte Carlo method for determining the stability of the inferred size distributions. New input values for the concentrations found on each stage are chosen from a normal distributions using the measured radon decay-product activity as the mean value and the measured uncertainty as the standard deviation of the distribution. This process can be repeated a number of times to provide a measure of the precision and robustness of the estimated size distributions.
A semi-continuous automated system has been developed by Ramamurthi and Hopke (1991). This system has now been used extensively to measure the exposure in a series of 6 homes in the northeastern United States and southeastern Ontario, Canada (Hopke and others 1995). The locations and characteristics of these houses are presented in Table B-2. The results for several of these houses
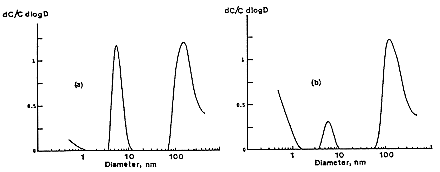
FIGURE B-11 Tri-model activity size distributions measured by Strong (1989) under conditions of a) F = 0.36, CN = 10,000 cm-3; b) F = 0.26, CN = 5000 cm-3.
TABLE B-2 Summary of the sampling campaigns and locations that provided activity-weighted size distribution in normally occupied homes
|
Location |
House ID |
Sampling Period |
No. of sample |
Smoker |
Heating System |
Stove |
|
Northfield, CT |
|
March-April, 1990 |
30 |
No |
Hot water baseboard, Oil-fired |
Gas pilot light |
|
Princeton, NJ |
31 |
November 1990 |
61 |
Yes |
Forced Air, Gas-Fired |
Gas pilot light |
|
Princeton, NJ |
31 |
February 1991 |
52 |
Yes |
Forced Air, Gas-Fired |
Gas pilot light |
|
Princeton, NJ |
41 |
April 1991 |
30 |
Yes |
Forced Air, Gas-Fired |
Gas without pilot light |
|
Arnprior, ON |
|
May to July 1991 |
208 |
No |
Electric baseboard |
Electric |
|
Parishville, NY |
|
February to March 1992 |
59 |
No |
Forced Air, Oil-Fired |
|
|
Princeton, NJ |
51 |
March 1992 |
46 |
No |
Forced Air, Gas-fired |
|
|
Princeton, NJ |
51 |
July 1992 |
21 |
No |
Forced Air, Gas-Fired |
|
|
Princeton, NJ |
51 |
March 1993 |
58 |
No |
Forced Air, Gas-Fired |
|
have been gathered in order to provide baseline data for a series of studies of the behavior of air cleaners; Northford, CT (Li and Hopke 1991), Arnprior, Ontario (Hopke and others 1993), and Parishville, NY (Hopke and others 1994). Preliminary results, including 2 Princeton, NJ houses and one week of the Arnprior data, have been reported by Wasiolek and others (1992). Three other houses have been studied, but the measurements were made in the basement and may not represent the living areas of these homes. In two other homes, measurements were made while they were unoccupied and particles were produced through various activities such as cooking, vacuuming, and smoking. However, these results are not representative of the activity-weighted size distributions produced in normally occupied homes. In all cases radon concentrations were also measured using standard continuous radon monitors.
The measurements in the houses were combined in order to estimate the distribution of exposures and resulting doses. There are differing numbers of measurements in these various houses, but in order to combine the data, it was assumed that all of the measurements come from a single distribution. The results for these measurements are presented as cumulative distribution functions. The distribution of the equilibrium factor, F, based on the complete set of results (565 samples) is presented in Figure B-12. Summary statistics for this distribution are presented in Table B-3. The geometric mean value of F is 0.374 and the geometric standard deviation is 1.57, while the arithmetic mean is 0.408 with an arithmetic standard deviation of 0. 159. Thus, the value of F in this sample of North American homes is lower than the previous estimate of 0.50 used by the Environmental Protection Agency in its risk estimates (USEPA 1992b) and is similar to the values measured in German homes by Reineking and Porstendörfer (1990).
Activity-weighted size distributions have been measured in 6 homes. In several cases, there was a person who lived in the home that smoked. The distributions of airborne radioactivity for each class of homes have been presented. In all of these cases, the activity-weighted size distributions are available so that doses can be calculated for each type of individual under consideration.
For a given radon concentration, and assuming other parameters to be constant, variation of F translates into a proportional variation in lung dose-rate. Wasiolek and others (1992) had earlier reported that the presence of a smoker in a home substantially affected the exposure and estimated dose. Thus, the size distributions were segregated into a non-smoking group (422 samples) and a smoking group (143 samples). The corresponding distributions for equilibrium factor for the non-smoking and smoking houses are given in Figures B-13 and B-14, respectively. The summary statistics for these distributions are also presented in Table B-3. These results will provide the basis for the activity-weighted size distributions that will be considered typical of exposure in normally occupied homes and used by the committee. For these measurements, the median dose is essentially the same in the homes with and without a smoker. This result is
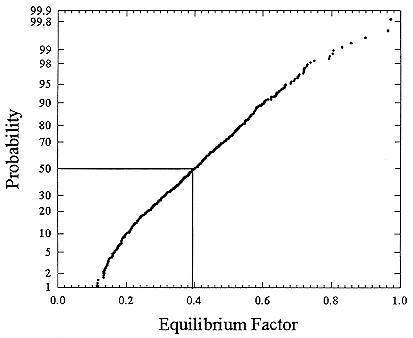
FIGURE B-12 Cumulative frequency distribution for equilibrium factor based on the complete set of 565 measurements in 6 homes (Hopke and others 1995).
caused by the compensating factors of particle size and concentration. With a smoker present, there is a higher particle concentration leading to higher F values. However, the activity is found in particle sizes around 200 to 300 nm that are not deposited in the respiratory tract at a high rate and thus produce low doses per unit exposure (as will be presented later in this chapter).
In the case of the separated distributions, the influence of the smoker on the exposure conditions can be observed in the values in this table. The equilibrium factor in the homes with smokers is higher than in the non-smoker homes, where the arithmetic mean value in the smoker homes is 0.481 and geometric mean is 0.469 while the non-smoker values are 0.383 and 0.346.
EXPOSURE IN MINES
Introduction
In the 1991 NRC report of the panel on Dosimetric Assumptions, an effort was made to estimate the aerosol characteristics that prevailed for the typical conditions that existed in mines. There are several major complicating factors in
TABLE B-3 Summary statistics for the measured or calculated distributions
|
|
Arithmetic Mean |
Arithmetic Standard Deviation |
Geometric Mean |
Geometric Standard Deviation |
|
All Houses Equilibrium Factor |
0.408 |
0.159 |
0.374 |
1.57 |
|
Dose Rate per Unit Exposure (nGy h-1/ Bqm-3) |
6.97 |
2.55 |
6.50 |
1.47 |
|
Houses With Smokers Present Equilibrium Factor |
0.481 |
0.108 |
0.469 |
1.24 |
|
Dose Rate per Unit Exposure (nGy h-1/ Bqm-3) |
6.77 |
1.45 |
6.62 |
1.24 |
|
Houses Without Smokers Present Equilibrium Factor |
0.383 |
0.166 |
0.346 |
1.61 |
|
Dose Rate per Unit Exposure (nGy h-1/ Bqm-3) |
7.04 |
2.83 |
6.346 |
1.54 |
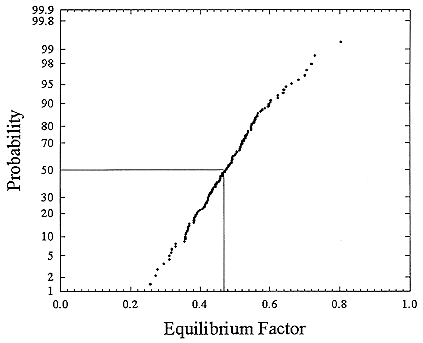
FIGURE B-13 Cumulative frequency distribution for equilibrium factor based on the set of measurements for houses with a smoker (Hopke and others 1995).
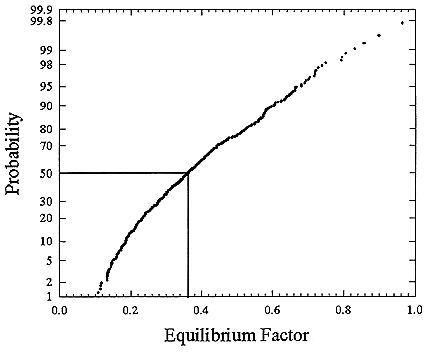
FIGURE B-14 Cumulative frequency distribution for equilibrium factor based on the set of measurements for houses without a smoker (Hopke and others 1995).
making the assessment of the activity-weighted size distributions. For example in the United States prior to 1961, there were no regulations of any kind with respect to the concentration of airborne activity and undoubtedly there were very high particle concentrations, particularly in the small mines if normal operations such as blasting and slushing were conducted. The history of ventilation in U.S. mines is outlined in Table B-4 (Also see workshop report in appendix E annex 2).
Early Mining Operations
There are only 2 reports of any measurements in the time period prior to 1962 (Simpson and others 1954; HASL 1960). In both of these reports, efforts were made to measure activity-size distributions using a Casella cascade impactor (May 1945). Simpson and others examined the airborne activity in the Beaver-lodge Mine. They found that essentially all of the activity was associated with particles less than 1 µm. When the dust concentrations were "high," there was more activity associated with larger particles. However, dust measurements were made with a konimeter. Particles in 5 cm3 of air which impacted on a glass slide
TABLE B-4 History of Work Practices in U.S. Minesa
which had been heated to 1000°F before and after acid treatment, were counted at a magnification of 150× against a dark field. Counts were made of particles less than 5 µm diameter with a lower level of visibility being 0.25 µm. The results were reported as particles per cubic centimeter (ppcc). It is clearly very difficult to relate these values to total airborne particulate mass and thereby define "high" dust concentrations.
Measurements were made by HASL (1960) in 3 mines in western Colorado. Again 81 to 97% of the activity was attached to particles less than 1 µm in aerodynamic diameter. There was no separation of particles by size below 1 µm and it is difficult to use these data to estimate the dose per unit radon concentration. There were no dust concentrations given in this report.
Later Measurements in Mines
There were a series of measurements made in 4 mines of the Grants Mineral Belt in New Mexico by George and others (1975, 1977). At the time, it was not possible to fully reconstruct the activity-weighted size distributions. However, subsequently Knutson and George (1992) have reanalyzed the data to obtain the full information from the original data. Typical distributions are shown in the next section. These results were chosen by the committee as the best representation of the aerosol conditions in typical working mines. Measurements were made in a variety of locations in the mines. Table B-5 presents a summary of the results of these measurements.
These data were grouped into 4 categories of work activities: slusher, stopes, drifts and haulageways, and machine shops as the representative regions within the mine. The hourly doses per unit radon concentration were calculated for each
TABLE B-5 Summary of the 1971 grants, NM mine measurements
|
Mine |
Date |
Description |
CNCa |
222Rn (kBqm-3) |
218Po |
214Pb |
214Bi |
F |
|
A |
06/22/71 |
Slushers Position 1 |
120,000 |
13.3 |
0.45 |
0.18 |
0.13 |
0.19 |
|
A |
06/22/71 |
Main Drift |
66,000 |
12.2 |
0.66 |
0.24 |
0.10 |
0.23 |
|
A |
06/23/71 |
Machine Shop |
140,000 |
4.1 |
0.57 |
0.23 |
0.12 |
0.22 |
|
A |
06/23/71 |
Slushers Position 2 |
110,000 |
10.0 |
0.34 |
0.13 |
0.05 |
0.12 |
|
A |
06/23/71 |
Main Drift |
93,000 |
6.3 |
0.63 |
0.18 |
0.06 |
0.18 |
|
B |
06/24/71 |
Stope 1 |
200,000 |
26.6 |
0.40 |
0.15 |
0.07 |
0.14 |
|
B |
06/24/71 |
Secondary Drift 2 |
210,000 |
44.4 |
0.27 |
0.05 |
0.01 |
0.06 |
|
C |
06/25/71 |
Machine Shop |
17,000 |
3.7 |
0.33 |
0.22 |
0.16 |
0.20 |
|
C |
06/25/71 |
Slushing Position |
17,000 |
4.8 |
0.38 |
0.12 |
0.12 |
0.15 |
|
C |
06/25/71 |
Main Drift 1 |
260,000 |
6.3 |
0.54 |
0.18 |
0.06 |
0.18 |
|
C |
06/28/71 |
Main Drift 2 |
400,000 |
14.1 |
0.49 |
0.21 |
0.18 |
0.23 |
|
C |
16/28/71 |
Stope 2 |
320,000 |
17.8 |
0.66 |
0.25 |
0.11 |
0.23 |
|
C |
06/28/71 |
Stope 3 |
100,000 |
20.7 |
0.41 |
0.14 |
0.06 |
0.14 |
|
D |
06/29/71 |
Stope 1 |
40,000 |
13.0 |
0.48 |
0.25 |
0.22 |
0.27 |
|
D |
06/29/71 |
Drift 1 |
12,000 |
17.4 |
0.32 |
0.18 |
0.17 |
0.19 |
|
D |
06/29/71 |
Drift 2 |
5,000 |
18.5 |
0.52 |
0.19 |
0.13 |
0.20 |
|
D |
06/29/71 |
Drift 3 |
15,000 |
19.6 |
0.20 |
0.14 |
0.14 |
0.15 |
|
D |
06/30/71 |
Stope 2 |
80,000 |
19.6 |
0.37 |
0.14 |
0.09 |
0.15 |
|
D |
06/30/71 |
Stope 3 |
70,000 |
16.7 |
0.67 |
0.27 |
0.17 |
0.27 |
|
D |
06/30/71 |
Stope 4 |
40,000 |
19.2 |
0.43 |
0.18 |
0.14 |
0.19 |
|
D |
07/01/71 |
Main Haulage 2 |
26,000 |
9.3 |
0.25 |
0.07 |
0.04 |
0.08 |
|
D |
07/01/71 |
Exause Draft |
70,000 |
22.2 |
0.50 |
0.17 |
0.10 |
0.18 |
|
D |
07/01/71 |
Near Shaft |
10,000 |
5.6 |
0.21 |
0.05 |
0.01 |
0.05 |
|
B |
06/24/71 |
Secondary Drift 1 |
25,000 |
5.9 |
0.40 |
0.06 |
0.02 |
0.06 |
|
C |
06/28/71 |
Stope 1 |
3,000 |
7.0 |
0.33 |
0.15 |
0.14 |
0.17 |
|
C |
06/28/71 |
Slusher Position 2 |
1,000,000 |
7.8 |
0.41 |
0.14 |
0.06 |
0.14 |
|
a CNC = condensation nuclei counted. |
||||||||
group based on their average activity-weighted size distributions. The dose per unit radon for the miner was then estimated using a distribution of time as 40% in the slushing position, 40% in stopes, 10% in drifts and haulageways, and 10% in machine shops. It is assumed that the exposure in drifts and haulageways was received in getting to and from the work locations while the machine shop time would also reflect lunchrooms and other places away from active mining areas.
Reference Size Distributions
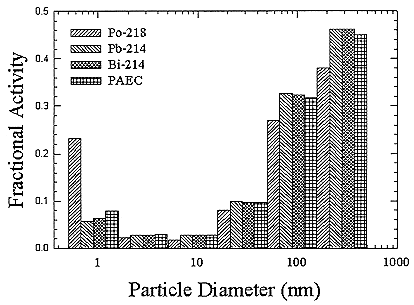
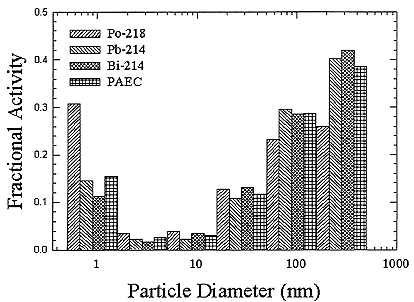
In order to estimate the dose in homes and in mines, activity-weighted size distributions are needed. The size-dependent dose conversion coefficients can then be multiplied by the activity at each particle size and summed to yield the total dose. The reference size distributions in homes were taken from those measured by Hopke and others (1995) which were described earlier in this chapter. The activity-weighted distributions at the median dose for the houses with and without a smoker present were chosen as the representative distributions for homes. Figures B-15 and B-16 show these distributions.
The mine size distributions were derived from the constructed size distributions of Knutson and George (1992) who provided their data to the committee for this purpose. The size distributions for the various positions in mines are shown in Figure B-17.
DOSE
Dosimetry
Dosimetry is defined as the measurement of the amount, type, rate, and distribution of radiation emitted from a source of ionizing radiation and the calculation of both spatial and temporal patterns of energy absorption in any material of interest as a result of ionizing radiation. For a general review, see NRC 1991. Instruments and techniques exist to measure fields of penetrating radiation such as x rays or gamma rays that are external to the body, and provide means for directly quantifying the amount of energy deposited per unit mass of material (air, tissue, water). These dose measurements can then be related to a person present in the radiation field and the radiation dose that he or she would receive. In the case of internally-deposited radionuclides, however, direct measurement of the energy absorbed from ionizing radiation emitted by the decaying radionuclide is rarely, if ever, possible. Therefore, one must rely on dosimetric models to obtain estimates of the spatial and temporal patterns of energy deposition in tissues and organs of the body. In the simplest case, when the radionuclide is uniformly distributed throughout the volume of a tissue of homogeneous composition and when the size of the tissue is large compared with the range of the particulate emissions of the radionuclide, then the dose rate within the tissue is
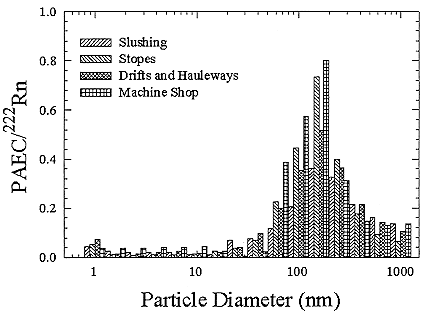
FIGURE B-17 Activity-weighted size distributions for the 4 types of locations in New Mexico mines.
also uniform and calculation of absorbed dose can proceed without complication. However, nonuniformities in the spatial and temporal distributions of the radionuclide, coupled with heterogeneous tissue composition, make the calculation of absorbed radiation dose complex and uncertain, as in the case of inhaled radon and radon progeny in the respiratory tract.
Biodosimetry
To adequately link radiation exposure to risk it is essential to understand the relationship between the radiation exposure and the effective radiation dose to respiratory tract cells. A number of mathematical models that relate exposure to dose have been developed and they will be discussed in the next section of this document. Many of these models, as shown in this chapter, depend on knowledge of a range of physical factors such as attached fraction, particle size, respiratory rate, and airway morphology. This section briefly reviews the use of biodosimetry as a means to provide an additional check on physical models to evaluate the relationships between exposure in Jhm-3 and dose in mGy in respiratory tract cells.
The biodosimetric approach has two major uses. First, to evaluate dose delivered to individuals in radiation accidents when no physical dosimetry is
present. This area has been and continues to be an important part of radiation protection. The major cell type used for these studies has been the blood lymphocyte because its response represents an average dose to the individual, blood lymphocytes are easy to obtain, these cells divide very slowly or not at all in vivo and can be stimulated to divide in vitro which makes them a useful integrator of radiation dose with time, and finally the dose-response relationship for these cells has been carefully developed for a number of different radiation types. A useful review of the state of the art for biodosimetry using blood lymphocytes has been published (Bender and others 1988).
The second use of biodosimetry is to validate models of dosimetry for cells at risk in organs or systems where it is difficult or impossible to have direct measures of dose to target cells or tissues (Brooks and others 1997). This area is currently being developed for the respiratory tract. The approach has been to develop an in vitro/in vivo experimental animal respiratory tract model cellular system to understand the relationships that exist between cytogenetic damage in different populations of respiratory tract cells and radiation dose. The damage in these cell types has been measured as cell-killing (Thomassen and others 1992), chromosome aberrations (Brooks and others 1990b), or as the frequency of micronuclei induced in binucleated cells (Khan and others 1994, 1995; Brooks and others 1997; Bao and others 1997). These studies have measured damage using five different cell types from the respiratory tract; nasal, tracheal, and deep-lung epithelial cells (Brooks and others 1992, 1997; Thomassen and others 1992), deep-lung macrophages (Johnson and Newton 1994; Bisson and others 1994), and deep-lung fibroblasts (Khan and others 1994, 1995).
To characterize the relationships which exist between exposure, dose and cytogenetic damage it was necessary to understand how both physical and biological variables impact the response of model systems to radiation exposure. The influence of physical parameters including; total dose, dose rate, radiation type, LET, and aerosol characteristics have been characterized in deep-lung fibroblasts on dose-response relationships. Biological factors can also influence the response per unit of exposure or dose. The biological factors including cell turnover, species, strain, sex, cell cycle, and cell type have to be considered in these studies. Both of these sets of factors make biological dosimetry difficult to apply without adequate background information on the system to be used.
Research on physical factors demonstrated that in lung fibroblasts over the range of doses studied the radiation exposure increased the frequency of micro-nuclei as a linear function of radiation dose for both high- and low-LET radiation (Brooks and others 1994; Bao and others 1997). To determine the influence of dose and estimate an RBE for radon-induced micronuclei, CHO cells or rat deep-lung fibroblasts were given acute in vitro exposure to 60Co or radon. The in vitro dose was calculated according to the methods of Hui and others (1993). The slopes of the dose-response relationships were compared and resulted in RBEs of from 10–12 following acute radiation exposure (Brooks and others 1994).
To determine how dose-rate influenced dose-response relationships, rats were exposed to graded doses of 60Co gamma rays for 4 or 67 hours and the frequency of micronuclei in deep-lung fibroblasts compared to that induced by acute exposure to 60Co (Brooks and others 1995). When these values were compared to those following acute in vivo exposures a dose-rate effectiveness factor of 6.1 was derived. Exposure of the animals to 60Co or inhalation of radon protracted over the same period of time (67 hrs) resulted in a linear increase in micronuclei as a function of dose. A comparison of the dose-response relationships for these exposure conditions resulted in an RBE of 65 for protracted exposures to radon vs low-LET gamma radiation (Brooks and others 1995).
In addition to physical factors, there are many biological factors that can influence observed dose and exposure response relationships. To extrapolate information from experimental animals to man it is essential to understand the dose-response relationships for in vivo and in vitro radiation exposure. When rat deep-lung fibroblasts were exposed either before or after isolation from the animal and the frequency of micronuclei determined, there were no differences observed in the slopes of the dose-response relationships (Khan and others 1994). Studies on the influence of cell proliferation on radon-induced micronuclei demonstrated that the sensitivity of proliferating and non-proliferating cells was not significantly different (Khan and others 1994). Studies on the induction of micronuclei in rat lung macrophages in vivo demonstrated that the maximum frequency of micronuclei was observed at 21 days after the radon inhalation. This is the time required in vivo for an optimum number of cells to undergo a single cell division and express the micronuclei induced by the radiation (Johnson and Newton 1994). The same length of time was used between exposure and scoring micronuclei for macrophages grown in vitro following exposure to alpha particles from 239Pu.
Understanding how between-species differences for the induction of early cytogenetic damage relates to species differences for cancer induction is essential for risk extrapolation. Research has been conducted in a range of different species and strains to determine if the sensitivity for early cytogenetic damage reflects cancer risk. Studies were conducted to evaluate the clastogenic potency of radon in Wistar rats, Syrian hamsters, and Chinese hamsters (Khan and others 1995) and two strains of mice (A/J and C57BL6J) (Groch and others 1997). These animals were selected because of their sensitivity to radiation and chemically induced lung-cancer. Rats are very sensitive to the induction of lung-cancer from radon while Syrian hamsters, and mice have been reported to be very resistant to radon-induced cancer (Cross 1994a,b). The two strains of mice are very different in their response to lung-cancer induced by ethyl carbamate. The A/J strain is very sensitive to chemically-induced lung-cancer and the C57B16J is resistant. Our studies demonstrated that the order of sensitivity between species for radon-induced micronuclei was mice>Chinese hamsters>Syrian hamster> rats. There was no significant difference between the two strains of mice in the
frequency of micronuclei induced by the radon inhalation or by ethyl carbamate injection. It was also determined that there was no influence of sex or strain of rats (Wistar vs Fischer 344) on 60Co-induced micronuclei in respiratory epithelial or fibroblast cells (Bao and others 1997) even though these two strains of rats show a marked difference in the frequency of 239Pu-induced lung-cancer (Sanders and Lundgren 1995). These data suggest that there is little relationship between radiation sensitivity for the induction of lung-cancer and micronuclei induction in respiratory-tract cells. There was on the other hand linear exposure- and dose-response relationships for the induction of micronuclei in all the animal species studied. This would support the concept that micronuclei are a very good indicator of dose but not a good indicator of cancer risk and extrapolation from dose or damage to risk should be done with caution.
It may be more important to understand the influence of cell type on cancer induction and genetic change than it is to understand how strain, sex, or species influences cancer risk. The basic assumption in using a relative risk model rather than the absolute risk model is that the induced cancer risk is related to the spontaneous cancer risk. The spontaneous cancer risk is very different in different organs and cells of the body. Studies related the initial radon-induced cellular damage to the cells at risk for radon-induced lung-cancer. In these studies the frequency of micronuclei was measured in the deep-lung fibroblasts, deep-lung epithelial cells, and in nasal and tracheal epithelial cells following exposure to either 60Co or radon inhalation. The 60Co studies were designed to maintain a constant dose to each cell type and determine if there was a difference in radiation sensitivity between cells (Bao and others 1997). The radon study would have both dose and response varied for each of the cell types being evaluated. It was determined that following exposure to 60Co the deep-lung fibroblasts and lung epithelial cells were from 2–3 times as sensitive for the induction of micronuclei as were the nasal or tracheal epithelial cells. The nose and trachea are much more resistant to radon-induced cancer than the deep-lung epithelial cells. When rats were exposed to radon and the frequency of micronuclei evaluated in all four cell types it was observed that the frequency of micronuclei in deep-lung epithelial cells (0.64 micronuclei/binucleated cell/WLM) was about 2–3 times as high as when fibroblasts were scored from the same animal (0.24 micronuclei/binucleated cell/WLM). This study demonstrated that even though these two tissues had similar sensitivity for the induction of micronuclei by low-LET radiation, they had different amounts of damage done by inhalation of radon. These observations suggest that the effective cellular dose (mGy) may be very different per WLM of exposure in the same animal.
By combining the data from the inhalation of radon in vivo and the dose-response relationship for micronuclei induced by radon exposure in vitro, it was possible to use micronuclei as a biodosimeter to convert exposure to dose in mGy (Khan and others 1994). Table B-6 shows the estimates of dose/exposure for a range of different tissues and cell types following inhalation of radon. Most of
TABLE B-6 Summary of biodosimetry
|
End Point |
Exposure (WLM) |
Dose (mGy) |
Exposure/Dose (mGy/WLM) |
|
Cell Survival (T.E.) |
Radon |
238Pu |
2.1 |
|
Chr. Abs (T.E.) |
Radon |
238Pu |
2.0–3.1 |
|
Micro (L.M.) |
Radon |
238Pu |
9.8 |
|
Micro (L.M.) |
Radon |
Gamma Rays |
0.75–2.5 |
|
Micro (D.L.E.) |
Radon |
Radon |
0.47–1.1 |
|
Micro (D.L.E.) |
Radon |
Calculation |
0.96–1.34 |
|
Micro (N.E.) |
Radon |
Calculation |
0.18–0.33 |
|
Micro (T.E.) |
Radon |
Calculation |
1.34–0.67 |
|
T.E. = Tracheal epithelial cells (Thomassen and others 1992, Brooks and others 1992, 1997) L.M. = Deep-lung macrophages (Johnson and others 1994, Bisson and others 1994) D.L.E. = Deep-lung epithelial cells (Brooks and others 1997) N.E. = Nasal epithelial cells (Brooks and others 1997) |
|||
the tissues had between 0.2–3.0 mGy/WLM. The major exception was for the deep-lung macrophages (Johnson and Newton 1994) where values of about 10 mGy/WLM were reported.
These studies indicate that careful characterization of model cell systems is necessary before they can be used in biological dosimetry. Following such characterization, it has been demonstrated that biological dosimetry may be useful in determining dose when physical dosimetry is not available and for evaluating the distribution of dose and damage in the respiratory tract following inhalation of radon or other environmental pollutants. Additional studies are needed to better determine how dose distribution relates to exposure parameters. This research points out some of the problems associated with using short-term tests to predict risk and demonstrates that many of these tests are better measures of dose and initial damage than risk. However, at this time it is clear that biodosimetry cannot be used to estimate the exposure or dose to either miners or people living in their homes. Thus, a dosimetric model will be needed to relate exposure to dose.
Dosimetric Models
Various models have been used to evaluate doses to the lungs from inhaled radon progeny (for example, Jacobi and Eisfeld 1980; Harley and Pasternack 1982; Hofmann 1982; NEA 1983; James 1988). These models divided the activity into two size categories: attached and unattached. In these models, a higher dose per unit exposure was assigned to the unattached fraction. However, the exact range of sizes that are assigned to this fraction in measurements by different investigators has varied widely (Ramamurthi and Hopke 1989). This imprecision in definition has necessitated more detailed assessments in which the dose conversion coefficients are calculated as continuous functions of particle size. The
1991 NRC report of the Panel on Dosimetric Assumption (NRC 1991) provides a detailed introduction to dosimetric models as well as a comprehensive evaluation of the conversion factors between exposure to PAEC and absorbed doses. The Panel's dosimetry model incorporated knowledge of model parameters of lung ventilation, aerosol deposition behavior, and anatomical descriptions of target cells as of 1990. This treatment was then further refined by the International Commission for Radiological Protection (ICRP 1994) based on subsequently developed information. Both of these dosimetry models consider the nuclei of secretory cells as well as those of basal cells as potentially sensitive targets in the respiratory tract. The ICRP's new respiratory tract deposition model also incorporates more accurate values for the filtration efficiency of the nasal passages (Swift and others 1992) than did the NRC model (NRC 1991). As described by James and others (1991) and James (1992), the new values for nasal filtration efficiency resulted in decreased doses to the bronchial tree from very small particles (below 3 nm) by a factor of around two in comparison with previous estimates. To use the newly adopted ICRP lung model to evaluate the equivalent lung dose as a function of the radon progeny activity-size distribution, the software code LUDEP (Jarvis and others 1993), which calculates regional lung deposition of activity per unit exposure, was extended to calculate tissue doses from the short-lived radon progeny as described by Birchall and James (1994). Subsequent to the committee's modeling and calculations, an additional model has been proposed by Harley and others (1996).
Respiratory Tract Deposition of Particles
Deposition is the process that determines what fraction of the inspired particles is caught in the respiratory tract and, thus, fails to exit with expired air. It is likely that all particles that touch a wet surface are deposited; thus, the site of contact is the site of initial deposition. Distinct physical mechanisms operate on inspired particles to move them toward respiratory tract surfaces. Major mechanisms are inertial forces, gravitational sedimentation, Brownian diffusion, interception, and electrostatic forces. The extent to which each mechanism contributes to the deposition of a specific particle depends on the particle's physical characteristics, the subject's breathing pattern, and the geometry of the respiratory tract. Radon progeny are unusual in that they tend to be smaller than most aerosols of concern to health, and thus, Brownian diffusion dominates.
Detailed treatments of particle deposition have been given by Brain and Valberg (1979), Lippmann and others (1980), Heyder and others (1982, 1986), Raabe (1982), Stuart (1984), and Agnew (1984). Comprehensive treatises on aerosol behavior are also available (Fuchs 1964; Davies 1967; Mercer 1981; Hinds 1982; Reist 1984).
The behavior of a particle in the respiratory system is largely determined by its size and density. Particles of varying shape and density may be compared by
their aerodynamic equivalent diameter (Dae). Aerodynamic diameter is the diameter of the unit density (1 g/cm3) sphere that has the same gravitational settling velocity as that of the particle in question. Aerodynamic diameter is proportional to the product of the geometric diameter and the square root of density.
Diffusional
Radon progeny undergo Brownian diffusion—a random motion caused by their collisions with gas molecules; this motion can lead to contact and deposition on respiratory surfaces. Diffusion is significant for particles with diameters of less than 1 µm; only then does their size approach the mean free path of gas molecules. Thus, this is probably the dominant mechanism for radon progeny deposition since most of the alpha activity resides on such small particles. Unlike inertial or gravitational displacement, diffusion is independent of particle density; however, it is affected by particle shape (Heyder and Scheuch 1983). For these particles, size is best expressed in terms of a thermodynamic equivalent diameter, Di, the diameter of a sphere that has the same diffusional displacement as that of the particle. The probability that a particle would be deposited by diffusion increases with an increase in the quotient (t/Dt)1/2, where t is the residence time and Dt is the particle diffusion coefficient. Deposition is only weakly dependent on the inspiratory flow rate. Diffusion, like sedimentation, is most important in the peripheral airways and alveoli, where dimensions are smaller. However, as particle size becomes very small, diffusion may become an important mechanism even in the upper airways.
Gravitational
Gravity accelerates falling bodies downward, and terminal settling velocity is reached when viscous resistive forces of the air are equal and opposite in direction to gravitational forces. Respirable particles reach this constant terminal sedimentation velocity in less that 0.2 ms. Then, particles can be removed if their settling causes them to strike airway walls or alveolar surfaces. The probability that a particle will deposit by gravitational settling is proportional to the product of the square of the aerodynamic diameter (Dae2) and the residence time. Thus, breathholding enhances deposition by sedimentation. Sedimentation is most important for particles larger than about 0.2 µm and within the peripheral airways and alveoli, where airflow rates are slow and residence times are long (Heyder and others 1986).
Inertia
Inertia is the tendency of a moving particle to resist changes in direction and speed. It is related to momentum—the product of the particle's mass and veloc-
ity. High linear velocities and abrupt changes in the direction of airflow occur in the nose and oropharynx and at central airway bifurcations. Inertia causes a particle entering bends at these sites to continue in its original direction instead of following the curvature of the airflow. If the particle has sufficient mass and velocity, it will cross airflow streamlines and impact on the airway wall. The probability that a particle will deposit by inertial impaction, therefore, increases with increasing product of Dae2 and respired flow rate. Generally, inertial impaction is an important deposition mechanism for particles with aerodynamic diameters larger than 2 µm. Thus, it is probably unimportant for radon progeny in indoor air. It can occur during both inspiration and expiration in the extrathoracic airways (oropharynx, nasopharynx, and larynx) and central airways.
As particle size decreases, inertia and sedimentation become less important, but diffusion becomes more important. For example, a 2-µm-unit-density spherical particle is displaced by diffusion (Brownian displacement) by only about 9 µm in 1 s. It is important to know that this displacement varies with the square root of time. It settles via gravity by about 125 µm in the same period. However, as the particle size drops to 0.2 µm, the diffusional displacement in 1 s increases to 37 µm whereas gravitational displacement drops to only 2.1 mm. At 0.02 µm, gravitational displacement is only 0.013 µm/s while diffusional displacement in 1 s has soared to 290 µm.
Anatomy of Respiratory System
The anatomy of the respiratory tract affects deposition through the diameters of the airways, the frequency and angles of branching, and the average distances to the alveolar walls. Furthermore, along with the inspiratory flow rate, airway anatomy specifies the local linear velocity of the airstream and the character of the flow. A significant change in the effective anatomy of the respiratory tract occurs when there is a switch between nose and mouth breathing. There are inter- and intraspecies differences in lung morphometry, even within the same individual, the dimensions of the respiratory tract vary with changing lung volume, with aging, and with pathological processes.
The human respiratory tract is pictured in Figure B-18. In order for the radon decay products to cause lung-cancer, they must enter the body through the nose or mouth, pass down the trachea and then reach the bronchial region. Here the airways split and become smaller. The smaller branches are called the bronchioles. They conduct the air to the alveolar region where the oxygen and carbon dioxide exchange takes place. The surface area of the lung increases greatly as the air moves down the airways to the alveolar region.
Particle deposition in the various portions of the respiratory tract varies with particle size, breathing rates, relative amounts of oral and nasal breathing, and the dimensions of the various regions of the respiratory system. The parameters listed in Table B-7 for the various populations to be modeled are then the input.
FIGURE B-18 Schematic diagram of the human respiratory tract. Adapted from Handbook of Air Pollution, USPHS 999-AP-44 (1968).
TABLE B-7Parameters used in the ICRP (1994) lung-deposition model
|
Functional Residual Capacity |
Tracheal Diameter |
|
Extrathoracic Dead Space |
First Bronchiolar Diameter |
|
Bronchial Dead Space |
Ventilation Rate (m3 h-1) |
|
Bronchiolar Dead Space |
Frequency |
|
Tidal Volume |
Volumetric flow rate |
|
Height |
Nasal/oral fraction |
Recently, the ICRP model has been incorporated into a computer program that includes the respiratory tract deposition model. The model is based on average dimensions of the parts of respiratory tract based on a number of measurements. Recent studies have measured the deposition of particles using physical models of the nose and mouth as well as the initial portions of the bronchial tree. Using magnetic imaging technology, images of the noses and mouths of various people can be obtained and from these images, models can be built. Measurements have been made on other input parameters that are needed for the mathematical lung model. The results of the calculation using the ICRP model for a typical male breathing through his nose with a breathing rate with a typical mix of sleeping, resting, and light exercise (0.779 m3h-1) are presented in Figure B-19.
The smallest-sized activity deposits efficiently by diffusion and is largely removed in the nose and mouth. Thus, the unattached fraction (particles around 1 nm), long considered as delivering a proportionally greater dose per unit exposure to lung cells, has limited penetration to the bronchi. However, if these smaller particles increase in size slightly by chemical or physical processes in the
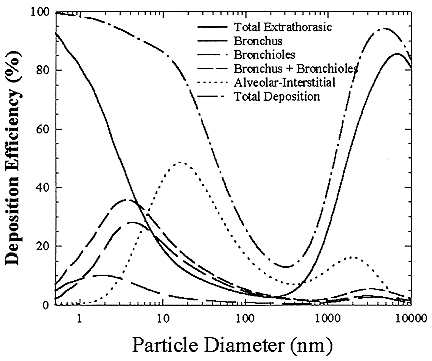
FIGURE B-19 Percent of particles of a specific size deposited in various parts of the human respiratory tract.
indoor air, they reach sizes around 5 nm. A 5 nm particle can effectively penetrate the nasal or oral passages, but still deposit in the bronchial region. Thus, the amount of radiation that reaches the lung tissue greatly increases in the 3 to 10 nm size range.
As the size continues to increase toward 100 nm, the effectiveness of the particle deposition decreases because the particle can move less effectively by diffusion. In the size range above 10 nm, most of the deposition occurs in the deep lung (alveolar region). In this region of the lung, there is a very large area so that the activity per unit surface area of the tissue is very small. For particle sizes above 500 nm, deposition starts to increase again because impaction can now help to deposit particles in the respiratory tract. For larger particles (> 2.5 µm) the deposition is mainly in the nose and mouth and very few of those particles reach the critical target cells of the lung where they could cause cancer. Thus, the size of the particle containing the radioactivity in both the home and the mines is very important in determining its effectiveness in delivering dose to the tissue.
The dose from radon progeny depends not only on the amount of aerosol deposited but also on the amount retained in the lungs over time. Retention is the amount of material present in the lungs at any time and equals deposition minus clearance. An equilibrium concentration is reached during continuous exposure to radon progeny when the rate of deposition equals the rate of clearance. The location where particles deposit in the lungs determines which mechanisms are used to clear them and how fast they are cleared. This influences the amount retained over time. Examples of the implications of particle characteristics on integrated retention were given by Brain and Valberg (1974) using a model developed by the Task Force on Lung Dynamics. They showed that the total amount as well as the distribution of retained dose among nose and pharynx, trachea and bronchi, and the pulmonary and lymphatic compartments were dramatically altered by particle size and solubility.
Particles that deposit on the ciliated airways are cleared primarily by the mucociliary escalator. Those particles that penetrate to and deposit in the peripheral, nonciliated lung can be cleared by many mechanisms, including translocation by alveolar macrophages, particle dissolution, or movement of free particles or particle-containing cells into the interstitium and/or the lymphatics. These pathways are relevant for materials that have a long biological half-life, such as silica, asbestos, or plutonium, but have little importance for radon progeny which are short-lived because of their short radioactive half-lives. The majority of the energy produced by alpha-particle emission is dissipated during the first hour following deposition. Thus, the movement of 222Rn progeny very soon after deposition is relevant to dosimetry. Reviews of clearance processes have been prepared by Kilburn (1977), Pavia (1984), and Schlesinger (1985).
The amount of particles retained within a specific lung region over time is a key determinant of dose. Mucous moves up the bronchial and bronchiolar regions and carries deposited material out of the lungs and into the gastrointestinal
tract. Because of the short half-lives of the radon decay products, and the integration of their resulting dose over regions of the respiratory tract (bronchus, bronchioles, etc.), the radon decay products generally decay and cause damage before they can be cleared as discussed in detail by ICRP 66 (1994). However, for the other important isotope of radon, 220Rn, the second decay product, 212Pb, has a half-life of about 11 hours so that much of the radioactive 212Pb can be cleared before it decays. Thus, the thoron decay products have been estimated to produce a lower dose for the same exposure as the 222Rn progeny. Consequently, they have received little consideration in previous risk estimations.
The assumption that the tracheobronchial region is completely cleared by a rapid process has been challenged by a number of investigators beginning with Davies (1980). The main evidence for slow clearance in humans comes from a series of experiments by Stahlhofen and coworkers (Stahlhofen and others 1980, 1986a,b, 1987a,b, 1990, 1994; Stahlhofen 1989; Scheuch 1991; Scheuch and others 1993). The results of these studies are discussed in detail in ICRP 66 (1994) which concludes that a slow-clearance phase should be included from a complete lung dose model. Thus, calculations based on the ICRP 66 model include a fraction of slow clearance of about 80%, based on the work of Stahlhofen and coworkers. It should be noted that the presence of a slow-clearance fraction may be controversial. A recent NCRP lung model report (NCRP 125) was not available for use in this BEIR VI study. The presence of a slow-cleared fraction would increase the effectiveness of the 220Rn decay products in delivering dose to the cells at risk in the bronchial epithelium. However, there are insufficient exposure data for either mines or homes to permit estimation of the potential contribution of 220Rn decay products to the risk.
Radon Progeny Dosimetry
The radioactive decay of inhaled short-lived radon progeny in the respiratory tract results in the deposition of alpha-energy in the cells of epithelial tissue. The dosimetric quantity measuring the radiation energy absorbed in tissue is the absorbed dose, D, expressed in grays (Gy).
Deposition of radon progeny in the respiratory tract causes alpha irradiation of several epithelial tissues; in the nasal passages, the bronchi, the bronchioles, and the alveolated part of the lungs (NRC 1991). Each of these tissues is potentially at risk for carcinogenesis (ICRP 1994). However, because the majority of lung-cancers have been observed only in the bronchial and bronchiolar regions of the lung (Saccomanno and others 1996), only the dose to the bronchial and bronchiolar regions will be considered in the calculation of the dose per unit exposure.
Dose Calculation
The conversion coefficients between airborne radon-progeny concentration
and the equivalent dose-rate to the lungs as a whole, calculated as functions of monodisperse particle size, that are given by ICRP's lung dosimetry model are presented in Figures B-20(a) through B-20(c), for 218Po, 214Pb, and 214Bi, respectively. A breathing rate of 0.779 m3 h-1 is assumed to represent the average breathing rate of a reference subject (adult male) over the 7000 h yr-1 assumed to be spent indoors at home (ICRP 1994a). This average breathing rate is estimated as 55% of time sleeping (0.45 m3 h-1), 15% sitting (0.54 m3 h-1), and 30% light exercise (1.5 m3 h-1). These dose conversion coefficients will be the basis for comparing the effects of exposure received from radon progeny arising from different exposure scenarios.
Comparative Dosimetry
The objective of the comparative dosimetry is to calculate the differences in dose that are deposited in the respiratory tract between males working underground and males under more normal conditions as given above, women, children at the age of 10, and infants at the age of 1. The principal differences in the deposited doses for the same exposure conditions will be due to differences in the lung deposition. According to ICRP (1994), the depth and distribution of cells at risk are identical for all ages and both genders. Thus, the lung-deposition module of LUDEP was used to calculate particle deposition as a function of particle size for a series of different input parameters characterizing the different subpopulations of interest. The values for these parameters have been taken from ICRP (1994) and are presented in Tables B-8, B-9, and B-10. The results of the deposition modeling are the total particle deposition as a function of size summed over bronchial and bronchiolar regions of the lung for infants (1 year), children (10 years), men, and women in domestic environments. These values will be ratioed to the deposition in males at occupational breathing rates. The miner breathing rate value was chosen to be 1.25 m3 h-1, a value in agreement with the average value of 1.28 ± 0.26 m3 h-1 derived by Ruzer and others (1995) from measurements of underground metal miners in Tadjikistan. These values are substantially lower than the 1.8 m3 h-1 that had been used in the 1991 Dosimetry Panel Report (NRC 1991). ICRP (1994) suggests 1.69 m3 h-1 for heavy work. However, unpublished data from the South African Chamber of Mines Research Organization reported by ICRP (1994) estimated a mean value of around 1.3 m3 h-1. From the ratio of deposition and the dose-conversion coefficients calculated using the dose model described above, dose-conversion coefficients could be calculated for each type of individual (man, woman, child, and infant).
K-FACTOR CALCULATION
To calculate the K factor, the typical dose rates to a member of the general population for each of the 2 exposure conditions (smoking/non-smoking environ-
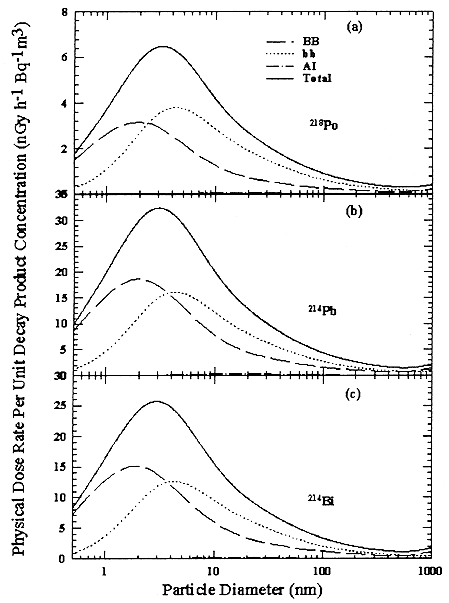
FIGURE B-20 Physical Lung Dose Conversion Factor between airborne concentration of the short-lived radon progeny (in Bqm-3 and dose rate (in nGy h-1), as a function of carrier particle diameter (in nm). The overall equivalent dose rate to the lungs as a whole is shown, together with the contributions from dose received by the bronchial region (BB), the bronchiolar region (bb), and the alveolar-interstitial region (A—I); (a) for 218Po, (b) 214Pb, and (c) 214Bi
TABLE B-8 Respiratory reference values for a general Caucasian population at various levels of activity (taken from ICRP 1994)
|
Population Subgroup |
Sleeping |
Sitting |
Light Activity |
Heavy Activity |
||||||||
|
|
VTa |
Bb |
fRc |
VT |
B |
fR |
VT |
B |
fR |
VT |
B |
fR |
|
|
(dm) |
(m3 h-1) |
(min-1) |
(dm) |
(m3 h-1) |
(min-1) |
(dm) |
(m3 h-1) |
(min-1) |
(dm) |
(m3 h-1) |
(min-1) |
|
Infant, 1 yr |
0.074 |
0.15 |
34 |
0.102 |
0.22 |
36 |
0.127 |
0.35 |
46 |
N/A |
N/A |
N/A |
|
Child, 10 yr |
0.304 |
0.31 |
17 |
0.333 |
0.38 |
19 |
0.583 |
1.12 |
32 |
0.841d |
0.667e |
2.22 |
|
|
|
|
|
|
|
|
|
|
|
1.84 |
44 |
36 |
|
Female adult |
0.444 |
0.32 |
12 |
0.464 |
0.39 |
14 |
0.992 |
1.25 |
21 |
1.364 |
2.70 |
33 |
|
Male adult |
0.625 |
0.45 |
12 |
0.750 |
0.54 |
12 |
1.250 |
1.50 |
20 |
1.923 |
3.00 |
26 |
|
a Tidal Volume. b Ventilation Rate. c Respiration Frequency. d Male. e Female. |
||||||||||||
TABLE B-9 Relative distribution of time in various activities for the time spent indoors at home (taken from ICRP 1994 and LUDEP default settings from Jarvis and others 1993)
|
Population Subgroup |
Sleeping |
Sitting Light |
Activity |
Heavy Activity |
|
Infant, 1 yr |
58.33% |
12.50% |
25.00% |
— |
|
Child, 10 yr |
41.67% |
12.28% |
30.56% |
— |
|
Female adult |
55.00% |
15.00% |
30.00% |
— |
|
Male adult |
55.00% |
15.00% |
30.00% |
— |
|
Miner adult |
0.00% |
31.30% |
68.80% |
— |
TABLE B-10 Morphometric, physiologic, and lung volumes for children and adults (taken from ICRP 1994)
|
|
Infant, 1 yr |
Child, 10 yr |
Adult Male |
Adult Female |
|
Height (cm) |
75 |
138 |
176 |
163 |
|
Weight (kg) |
10 |
33 |
73 |
60 |
|
TLCa (mL) |
|
|
|
|
|
Mean |
548 |
2869 |
6982 |
4968 |
|
Standard Deviation |
61.5 |
— |
700 |
600 |
|
FRCb (mL) |
|
|
|
|
|
Mean |
244 |
1484 |
3301 |
2681 |
|
Standard Deviation |
26 |
311 |
600 |
500 |
|
VCc (mL) |
|
|
|
|
|
Mean |
377 |
2326 |
5018 |
3551 |
|
Standard Deviation |
47 |
— |
560 |
420 |
|
VDd (mL) |
|
|
|
|
|
Mean |
20 |
78 |
146 |
124 |
|
Standard Deviation |
— |
14.9 |
22.5 |
21.0 |
|
Anatomical Dead Space (mL) |
|
|
|
|
|
VBBe |
6.81 |
25.10 |
50.00 |
40.08 |
|
Vbbf |
4.70 |
26.45 |
47.06 |
40.19 |
|
VETg |
8.73 |
26.49 |
48.75 |
44.18 |
|
Smallest Bronchiole (cm) |
0.1068 |
0.1429 |
0.1651 |
0.1587 |
|
Largest Bronchus (cm) |
0.7502 |
1.3114 |
1.6500 |
1.5342 |
|
a Total lung capacity. b Functional residual capacity: volume of air that remains in the lungs after exhalation. c Vital capacity: maximum volume of air breathed in during inspiration. d Total anatomical dead space: the volume in which no gas exchange occurs. e Bronchial dead space volume. f Bronchiolar dead space volume. g Extrathoracic dead space volume. |
||||
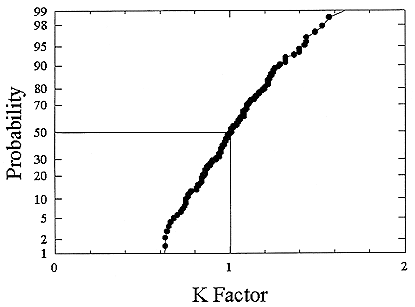
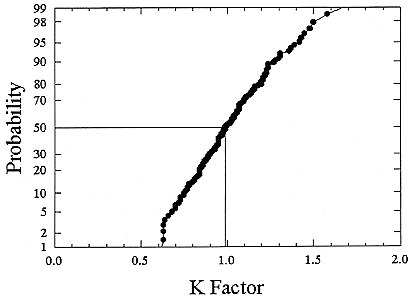
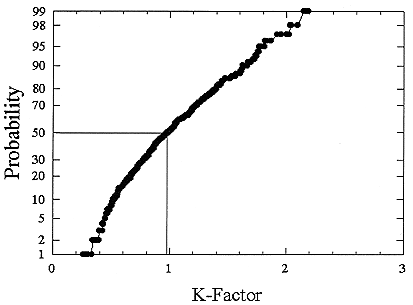
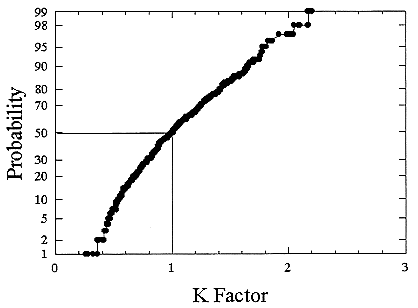
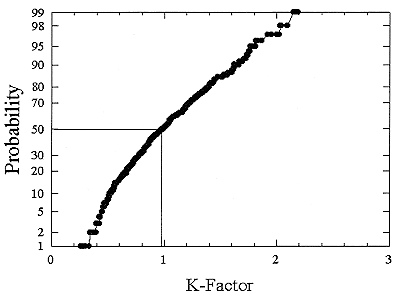
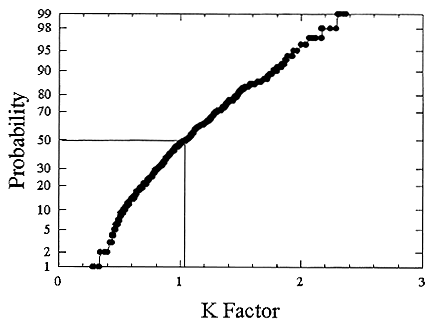
ments) were calculated from activity concentrations associated with the activity-weighted size distributions for the home environment and the dose-conversion coefficient. This physical dose-rate per unit radon concentration is then divided by the estimated average dose to a miner based on the exposure results presented above. The miner dose-rate per unit radon concentration is 7.0 nGy h-1/(Bqm-3). The dose-rates per unit radon are calculated for men, women, children, and infants based on the activity-weighted size distributions measured. Each value of the dose per unit radon concentration in homes is divided by the dose per unit radon concentration in mines to yield a series of K values. The distributions for the K values for houses with a smoker are presented in Figures B-21 to B-24. The distributions for the K values for homes without a smoker are shown in Figures B-25 to B-28.
The median values for the K factor for the various classes of individual in the 2 exposure scenarios (smoker and non-smoker) are given in Table B-11. It can be seen that all of these values are near to 1 so that the dose per unit exposure per unit 222Rn concentration are essentially the same in mines and homes. The measurements in homes (Hopke and others 1995) showed that the median dose per unit radon was relatively insensitive to the aerosol conditions in the homes.
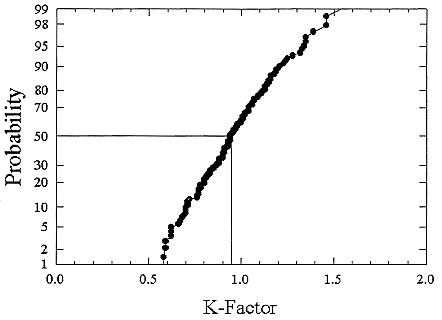
FIGURE B-21 Cumulative frequency distribution for the K factor for adult males based on the set of measurements in smoker homes.
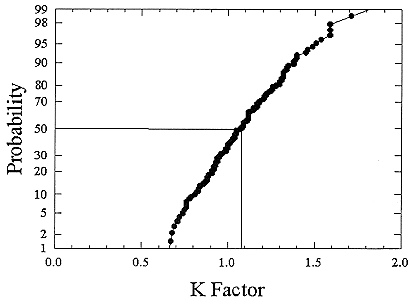
FIGURE B-24 Cumulative frequency distribution for the K factor for 1 year old infants based on the set of measurements in smoker homes.
In the case of the homes with a smoker, there is increased radon-progeny activity per unit radon gas concentration as shown by the increased equilibrium factor, but because the activity tends to be carried by larger particles, it is less effective in delivering dose to the respiratory tract. In the case of the non-smoker homes, the number of the larger particles is smaller and the amount of airborne progeny activity per unit radon gas concentration is also less, but because it tends to be carried by smaller particles, the average dose rate per unit activity concentration is higher.
The previous NRC analyses of lung dosimetry in mines and homes (NRC 1991) found K factor values around 0.75 for males and females and somewhat higher for children and infants. In that earlier NRC report, a sensitivity analysis was performed to ascertain the effects of changes in input parameters to the dosimetric model on the resulting K values. The dosimetric model used here is very similar to that used in that report and a new sensitivity analysis was not undertaken.
In that analysis, it was found that changes in the breathing rate had the largest effects on the dosimetry. Although breathing rate has some effect on the amount and the location of activity deposition in the lungs, the largest effect of changing the breathing rate is the resulting change in the total volume of air inhaled and thus the total amount of PAEC inhaled. The median K factor in the new calculation has increased from previously calculated values to close to 1. This change
TABLE B-11 Values of the K Factor
|
Subject Type |
Home with a Smoker |
Home without a Smoker |
|
Male |
0.94 |
0.95 |
|
Female |
1.0 |
1.00 |
|
Child |
0.99 |
0.98 |
|
Infant |
1.08 |
1.05 |
primarily reflects a reduction of the miner breathing rate from the 1.8 m3 h-1 to 1.25 m3 h-1 in this present study. A comparison of the inputs to the dosimetric modeling that was used to derive the K factor is presented in Table B-12. As discussed above, the major difference between the 2 results was the change in breathing rates based on Ruzer and others (1995) and the South African Miner Data quoted by ICRP (ICRP 1994). In this analysis, the committee was able to utilize the more extensive set of the measurement in homes by Hopke and others (1995) and the more complete reconstruction of the activity-weighted size distributions in mines provided by Knutson and George (1992) and George (1993). For the earlier study, the growth of particles when respirated into the high humidity of the lungs was estimated to be a factor of 2. In the intervening time, a number of measurements on room air and a variety of materials (Li and Hopke 1993, 1994; Dua and others 1995; Dua and Hopke 1996) have suggested that this growth factor is quite reasonable for typical room air and since much of aerosol in the ventilation air in the mine is ambient aerosol, particularly in the size range below 1 µm where the attached activity is typically observed, this factor of 2 is also quite reasonable for mines as well.
THORON
There are 2 other naturally occurring isotopes of radon, 220Rn and 219Rn, commonly referred to as thoron and acton. 220Rn is a decay product of 232Th and 219Rn is a decay product of 235U. 219Rn has a half-life of 3.6 s and thus, it is not transported far after its formation to produce measurable exposure even to miners. However, even with a half-life of 55.6 s, 220Rn can be found present in the atmosphere (Schery 1992). Thoron undergoes a-decay through short-lived 216Po (0.15 s) which also undergoes a-decays to 212Pb with a half-life of 10.64 h. The decay chain, including half-lives and the energies of the emitted radiation, is outlined in Table B-13.
Homes
There have only been limited measurements of 220Rn and its decay products in indoor air. In the measurement of 220Rn there can be substantial variation
TABLE B-12 Comparison of input parametersa to comparative dose modeling
|
Parameter |
1991 Dose Panel |
BEIR VI |
|
Respiratory Physiology |
ICRP66 Defaultsb |
ICRP66 Defaults |
|
Breathing Rates (Miners) |
1.80 m3 h-1 |
1.25 m3 h-1 |
|
Extrathoracic Deposition of Ultrafine Activity |
~50% for ''unattached" (Breslin and others 1969) |
~85% for 1 nm (Swift and others 1992) |
|
Breathing Rates (Domestic) |
ICRP66 Defaultsb |
ICRP66 Defaults |
|
Exposure Conditions in Mines |
Limited size distributions (Cooper and others 1973) |
30 distributions recalculated from 1970 data (Knutson and George 1992) |
|
Exposure Conditions in Homes |
Measurements with created exposure scenarios (Li and Hopke 1991) |
565 measurements in normally occupied homes (Hopke and others 1995) |
|
Hygroscopic Growth |
Estimated factor of 2 |
Factor of 2 based on series of published measurements (Li and Hopke 1993, 1994; Dua and others 1995; Dua and Hopke 1996) |
|
a Parameters are listed in tables B-8 through B-10 earlier in this appendix. b Although ICRP officially adopted the parameter values after the 1991 NRC report was issued, the parameter values were the same. |
||
TABLE B-13 Properties of the 220Rn decay chain
|
|
Type of Radiation |
Half-Life |
Radiation Energies (Move) |
|
Radon-220 (Th) |
α |
55.6s |
6.2883 |
|
Polonium-216 (ThA) |
α |
0.15s |
6.7785 |
|
Lead-212 (ThB) |
β |
10.64h |
0.331, 0.569 |
|
|
γ |
|
0.23863, 0.30009 |
|
Bismuth-212 (ThC) |
β (64%) |
60.6m |
0.67, 0.93, 1.55, 2.27 |
|
|
γ |
|
0.7272 |
|
|
α (36%) |
6.051, 6.090 |
|
|
Polonium (ThD) |
a |
0.298 ms |
8.7844 |
|
Thallium-208 (ThC') |
b |
3.053 min |
1.796, 1.28, 1.52 |
|
|
g |
|
2.6146, 0.5831, 0.5107 |
|
Lead-208 |
— |
Stable |
|
across the volume of a room because of the short half-life. Consequently, it is difficult to define representative values of 220Rn. Thus, most of the available measurements have been made of the 220Rn progeny rather than 220Rn. The available data for the ratio of PAEC arising from 220Rn decay products to that from 222Rn are summarized in Table B-14. Rannou (1987) has examined the variation of the PAEC(220Rn) as the PAEC(222Rn) changes and found that
PAEC(220Rn) = PAEC (222Rn)0.4 (4)
so that the exposure from the 222Rn progeny increases more rapidly than the 220Rn decay products. Thus, for dwellings with high 222Rn concentrations, it appears
TABLE B-14 Approximate ratio of PAEC for 220Rn progeny to 222Rn progeny at various locations (Schery 1990)
|
Location |
PAEC (222Rn) PAEC (220Rn) |
|
Italy (Latium), 50 dwellings |
1.3 |
|
Canada (Elliot Lake), 90 dwellings |
0.3 |
|
Hungary, 22 dwellings |
0.5 |
|
Norway, 22 dwellings |
0.5 |
|
Germany (western), 150 dwellings |
0.8 |
|
Germany (southwestern), 95 dwellings |
0.5 |
|
France (Finistere), 219 dwellings |
0.3 |
|
United States (20 states), 68 measurements |
0.6 |
|
United States (Colorado), 12 indoor locations (Martz and others 1990) |
0.3 |
|
Hong Kong, 10 indoor sites |
0.8 |
that the 220Rn progeny will not be an important additional source of exposure and dose.
In the measurements of the activity-weighted size distributions described above, the system used to make the activity measurements included a-spectroscopy so that 220Rn progeny could have been observed. Such activities were not observed and thus, for these homes, only 222Rn decay products provided exposure and dose.
Steinhäusler (1996) has recently reviewed the information available regarding thoron exposure and dose. He concludes that the extent of information on 220Rn and its decay products is analogous to the state of affairs for 222Rn before the large-scale national radon surveys of the past 15 years. Few health studies have been conducted on the possible health effects of inhaling thoron decay products. Among residents in high-background areas of Brazil, China, and India, statistically significant increases have been observed for chromosome aberrations. The study in China found no increase in lung-cancer for thoron exposure at a mean concentration of 168 Bqm-3 (Wei and others 1993).
Mines
Exposure measurements for 222Rn based on gross-counting methods can be affected by the presence of 220Rn decay products. For most of the mines which employed the workers used in the epidemiological studies, measurements are not available to determine the presence or absence of 220Rn progeny. For the mines in the Colorado Plateau and the Grants Mineral Belt of New Mexico, negligible concentrations of 220Rn decay products have been found. There are substantial concentrations of 220Rn decay products in the mines of the Elliot Lake, Ontario (DSMA Atcon 1985), where the PAEC arising from 222Rn and 220Rn were approximately equal. Corkill and Dory (1984) made a retrospective study of exposure in the fluorspar mines of Newfoundland. However, they do not mention 220Rn or its decay products. A similar lack of information exists for the other mining environments. Bigu (1985) has examined theoretical models for estimating the PAEC levels arising from the presence of both radon isotopes. The relative amounts of the radon isotopes and their progeny can be estimated based on the weight ratio of 238U to 232Th. For the Ontario uranium mines, this ratio is assumed to be 1. Results were then calculated based on a number of models that had been previously developed to predict the airborne activity concentrations. Bigu found that a substantial number of the measurements fall outside of the theoretical bounds and there are substantial differences among the results calculated by the various available models. Thus, more sophisticated models will need to be developed to permit adequate estimation of the exposure to 220Rn progeny. Thus, it is not possible to assess the uncertainty from a concentration of 220Rn progeny to lung dose in the miner-based risk estimates.
Steinhäusler (1996) also summarized the information available on occupa-
tionally exposed individuals (iron and rare-earth miners, workers in Th-processing plants and the monazite industry totaling 1557 persons). Increases in respiratory diseases, pancreatic cancer, and chromosome aberrations were found to be statistically significant. Among niobium miners in a Th-rich area, an increase in lung-cancer rates (observed/expected lung-cancer cases = 11.3) was found (Solli and others 1985). Among approximately 53,000 European and Japanese patients treated with thorium oxide injections, an increase in lifetime excess cancer risks for liver and bone cancer as well as leukemia has been observed. However, there were no excess lung-cancers. To reduce the uncertainties concerning the effects of 220Rn decay products, we will need to better characterize dosimetry of thoron progeny and obtain more data on exposures.
CONCLUSIONS
In this chapter we have reviewed the basis for the dosimetric extrapolation of risk from miners to the general population, taking into account differences in the aerosol characteristics, breathing rates, and the respiratory physiology of the various segments of the population (women, children, infants, as well as men). The constants have changed from the values of about 0.70 to 0.75 reported by the NAS Dosimetry Panel (NRC 1991) to values very close to 1. The differences in input parameters between the calculations are summarized in Table B-13. The primary cause of the shift in K value is attributable to the reduction in the miner breathing rate based on measurements of actual miners in Tajikistan and South Africa. The risks for infants are slightly higher than for miners, but for the other groups, the risks per unit exposure are essentially identical in homes and mines. This value around 1 is reasonable given the compensatory factors of particle concentration raising the airborne concentrations, but in sizes that are only weakly deposited in the lung. Thus, the doses per unit radon concentration are essentially the same although in each case, specific unusual aerosol conditions could substantially increase the dose per unit exposure.