Appendix E
Exposures of Miners to Radon Progeny
INTRODUCTION
The epidemiologic studies of underground miners have become the principal basis for estimating the quantitative risk of lung-cancer associated with exposure to radon progeny. As a result, there has been persistent concern about the extent of error in estimates of the exposures of the underground miners to radon progeny and of any resulting bias in risk estimates. The exposures of the underground miners have been estimated on the basis of incomplete information and ad hoc procedures have been used to complete gaps in the measurement data.
The BEIR IV committee recognized the potential for measurement error to affect risk estimates and consequently, the BEIR IV report provided extensive descriptions of the approaches used to estimate exposures in the four cohorts that served as the basis for the risk model. Since publication of the BEIR IV report, there has been increasing methodologic research on measurement error and its consequences, and on methods for adjusting for bias resulting from measurement error (Thomas and others 1993). The number of cohorts used to develop the BEIR-VI risk model has been increased from the four used by BEIR IV to 11, bringing a need to understand the varying approaches followed to assess exposures among the cohorts. Additionally, exposures have been re-estimated for several studies, giving insights into the potential magnitude of error in the studies.
The presence of errors in the exposure estimates for the miners has been widely recognized. Some investigators have addressed the problem by carrying out subgroup analyses. Risk patterns for miners considered as having the ''better"
exposure data were compared to risk patterns for miners with the "poorer" exposure data. Criteria for the identification of subgroups having better quality exposure data were based on surrogate indicators, such as calendar year of first employment, calendar year of follow-up, age at first employment, or exposure rate. Another approach was to limit analyses to miners with the more extensive measurement data. In more recent years, some mining companies have developed individual estimates of exposure, using increasingly extensive radon progeny measurement data and detailed information on exposure-time and work location. This era of improved exposure assessment temporally corresponds to the lower radon progeny levels in modern mines and corresponding lower total exposure values (Jhm-3 or WLM), compared with earlier years. In addition, relatively few miners started working after the improved exposure assessment procedures were put in place. Thus, information on risks to these more contemporary miners is still limited.
For a truly linear exposure-response relationship, it is widely recognized that misspecification of exposures tends to reduce the gradient of the trend, and to induce curvilinearity, from below. However, it is less well-recognized that misspecification of exposure does not always bias the exposure-response towards the null (Dosemeci and others 1990), although with the error patterns that prevail among the miner data sets, error would be unlikely to steepen the exposure-response relationship. With multiple exposure variables subject to error, for example, exposure to radon progeny, exposure to arsenic-containing dusts and cigarette-smoking, correlations among the variables could lead to either positive or negative bias in the radon progeny exposure-response relationship.
Interpretation of analyses of the miner data is further complicated by the relationships among radon progeny level, calendar year, and degree of error. High radon progeny levels generally occurred in the earliest years of operations of the mines and the high levels tended to occur during an era with limited numbers of measurements, incomplete coverage of work areas, and measurements of radon rather than radon progeny. In addition, work histories were usually less accurate in the early years of mining operations. Moreover, improvements in ventilation and reduction of radon levels were generally carried out over an extended period of time. Any attempt in analysis to designate specific years as "good" versus "bad" with regard to data quality is of necessity a substantial oversimplification.
Exposure estimation required work history information on time spent underground, which in most of the studies was obtained from company employment or medical history records. Thus, errors in the estimation of radon progeny exposure depended on the completeness and accuracy of these data. Exposure estimation was further compromised in some studies by lack of information on exposures that occurred outside the recorded work periods, and prior or subsequent to employment in the study mines. For example, some miners in the Colorado
cohort were reported to mine on weekends, although the specific details on the amount of extra time and the exposed miners were lacking.
The impact of measurement error on radiation risk estimates was explored in the study of atomic-bomb survivors (Jablon 1971). Analyses were also conducted by Pierce and others (1990) using the Lifespan Study data. The intent was to adjust the linear dose-response estimate to account for random error in the dose estimates. The investigators assumed that errors in dose estimates were proportional to dose, and therefore worked on the logarithm scale for dose. Using a lognormal error distribution and a plausible estimate of error of about 30%, the authors found that the adjusted dose-response estimate was about 5 to 15% greater than if account was not taken of exposure error.
This appendix brings together information on exposure estimates made for the miners in the epidemiologic studies and related work on error in these estimates. One annex to the chapter describes the basis for the exposure estimates in each of the studies. An additional annex provides the proceedings of a workshop convened by the committee on exposure estimates; valuable insights were gained from participants who were extremely knowledgeable on the history of the U.S. and Canadian uranium mining industries and consequently the BEIR VI committee has included the proceedings in its report.
ESTIMATION OF EXPOSURES OF MINERS TO RADON PROGENY
Published descriptions of the mines that are the basis of the epidemiologic studies indicate that the sources of radon included the ore being mined, air flowing into the areas where miners were working, and radon-containing water in the mines (NRC 1988; Lubin and others 1994a). Under the circumstances of mine operation, it is likely that concentrations of radon and progeny varied spatially and temporally within a particular mine, although little data have been published that document such variation. In the New Mexico mines, for example, information presented at the committee's workshop on dosimetry documented extensive variation in concentrations of radon progeny across various locations within mines in Ambrosia Lake, New Mexico (Table E-1). Thus, exposure estimates for individual miners would be ideally based on either a personal dosimeter, as used for low-LET occupational exposures, or on detailed information on concentrations at all locations in mines where participants in the studies received exposure (SENES 1989). For the participants, information would be needed on the locations where time was spent, the duration of time spent in the locations, and the concentrations in the locations when the miners were present. A miner might have spent time in a number of different locations during a typical working day including the stope (the area where mining actually takes place), the haulage way leading to the stope, and perhaps a separate lunch area. Personal dosimeters for radon progeny have not been developed until recently and their usage has been
TABLE E-1 Measurement data for individual mines in New Mexico
|
Mine |
Dates |
Location |
Working Level (WL) |
|
A |
5/5–13/60 |
Room 6-1, SE Area |
6.8 |
|
|
|
Room 9-1, SE Area |
15.2 |
|
|
|
Station |
10.0 |
|
|
|
Room 9-1, SE Area |
5.0a |
|
|
|
Room 6-1, SE Area |
4.6a |
|
|
|
Room 8-1, SE Area |
6.7a |
|
|
|
1 Left-15, NW Area |
0.1a |
|
|
|
Station |
2.4a |
|
|
8/5/60 |
Station |
20.2 |
|
|
|
13 West |
3.9 |
|
|
8/10–11/60 |
Station |
10.6 |
|
|
|
11 West, N End |
0.9 |
|
|
|
11 West, N End |
1.1 |
|
|
|
Shaft Collar |
15.0 |
|
|
|
Station |
9.6a |
|
|
|
Shaft Collar |
10.8a |
|
B |
2/19/60 |
Near old magazine |
37.0 |
|
|
|
Slusher station |
25.0 |
|
|
|
Ventilation course |
16.0 |
|
|
|
Station |
20.0 |
|
|
9/29/60 |
Breakthrough to drift |
26.0 |
|
|
|
Breakthrough to drift |
27.0 |
|
|
|
Drift |
1.5 |
|
|
|
Top of fresh air incline |
2.0 |
|
|
|
Station |
23.5 |
|
|
6/15–16/61 |
Shop |
0.5 |
|
|
|
Station |
0.4 |
|
|
|
South area |
10.5 |
|
|
|
Drift |
10.3 |
|
|
|
South area |
9.0a |
|
|
|
Drift |
6.2a |
|
|
|
Station |
3.4a |
|
a Measured after intervention. |
|||
limited, and detailed information on concentrations within mines and time spent in various locations has not been available to most of the epidemiologic studies.
In the epidemiologic studies, these ideal approaches have been replaced by various, pragmatically determined strategies for exposure estimation that draw on measurements made for regulatory and research purposes and extend the measurements using interpolation and extrapolation to complete gaps for mines in particular years. Additionally, missing information for mines in the earliest years of some of the studies was completed by either expert judgment or by re-creation of operating conditions. The numbers of measurements made also varies widely across the different studies included in the pooled analysis and
within studies the numbers of measurements tend to be greater in the later years of operation of the mines, when the exposures were generally lowest.
A pilot case-control study of lead-210 levels in the skull and lung-cancer risk in the Chinese tin miners points to the promise of this technique for exposure estimation. In this study, exposures are estimated for 19 miners with lung-cancer and 141 age-matched controls. Lead-210 levels were measured in the skull and lung-cancer risk was estimated in relationship to lead-210 level estimated for the time of last radon exposure. There was a gradient of risk with exposure. This technique is also applied in an exploratory fashion with former uranium miners in New Mexico (Lauer and others 1993).
PREVIOUS WORK ON ERRORS IN EXPOSURE ESTIMATES IN STUDIES OF MINERS
Cohort Study of Colorado Plateau Uranium Miners
Epidemiologists conducting research on lung-cancer in radon-exposed miners have long been aware of the potential for measurement error. The study of Colorado Plateau uranium miners conducted by the U.S. Public Health Service involved approximately 4,000 men, both whites and Native Americans, who worked in thousands of mines scattered across remote regions of four states. Measurements were not made regularly in all of the mines and no measurements were made in some of the mines. Consequently, the investigators based exposures on the actual measurements and on interpolated and extrapolated concentrations and on "guesstimates". For mines with missing data, concentrations were imputed from other mines in a hierarchy that began at the level of mining district and moved to the state level (see description in this chapter).
A descriptive evaluation of the consequences of using this approach was published in Joint Monograph No. 1 of the National Institute for Occupational Safety and Health and the National Institute for Environmental Health Sciences (Lundin and others 1971). The coefficient of variation was provided by year and by average concentration value (Jm-3 or WL) for the small number of mines with at least five or more samples in a particular year. The coefficient of variation tended to be less than 100 percent and not to vary over time.
To assess error associated with their interpolation procedure for completing gaps in measurements of radon progeny concentrations, the investigators used data for the mines having the longest period of continuous radon progeny measurements to compare estimated with actual values. Comparisons were made for mines during three periods, 1952–1954, 1956–1960, and 1960–1968. Lundin and others (1971) compared actual values to estimates based on averaging adjacent years. This analysis showed that the error was greatest for the earliest time period; because of the general trend of declining progeny concen-
trations, backward projection tended to underestimate and forward projection to overestimate.
A further analysis was directed at the imputation of missing values based on mining locality. Four of the largest uranium mining areas were selected for this analysis. Individual mines were omitted from the calculation of the average for the locality and the average for the locality was compared to the actual measurements. The differences tended to be large for the earliest years and declined substantially by 1968. The direction of bias tended to be positive; the investigators reported that during the four years considered, 55 to 70 percent of the estimates exceeded mine averages based on measurements.
This report also examined the potential for distortion of the results by errors in exposure assessment. Standardized mortality ratios (SMR) for lung-cancer deaths for miners who had 25% or more of their cumulative exposure based on measurement data (called exposures of the "highest quality", 1,325 miners including 20 lung-cancer cases, from a total of 3,325 miners and 70 lung-cancer cases) were compared with SMRs for miners with and without previous hardrock mining experience, which was used as a surrogate for previous radon progeny exposure. While this analysis of previous hardrock mining experience does not directly address exposure error and the quality of the exposure estimates, exposures for miners with previous mining are likely estimated with substantial error. Results of the comparison of the highest quality data and mines with and without previous hardrock experience are displayed in Figure E-1. In this informal analysis, there was no difference in the exposure-response for the high quality exposure data and either those with or without previous hardrock mining experience.
The 1987 National Institute for Occupational Safety and Health document, A Recommended Standard for Occupational Exposure to Radon Progeny in Underground Mines (NIOSH 1987), includes a systematic attempt to quantify the errors associated with the exposure (Jhm-3 or WLM) estimates for participants in the Colorado Plateau Study. Following the approach of Joint Monograph No. 1 (Lundin and others 1971), four sources of error were identified: 1) actual measurements; 2) interpolation or extrapolation in time; 3) geographic area estimation; and 4) estimates for years prior to 1950 when measurements were largely unavailable. The estimated coefficients of variation for each of these sources of error were 1.13, 1.21, 1.49, and 1.86, respectively. A pooled estimate of 1.37 was calculated as a weighted average. Using this figure, an average coefficient of variation of 0.97 was estimated for the cumulative exposure received by the miners. The report comments that if these errors are lognormally distributed then there would be minimal bias in the preferred power function model for the exposure-response relationship of lung-cancer risk with exposure to radon progeny. The possible effects of systematic errors were not considered.
At a 1994 BEIR VI committee workshop, Dr. Duncan Thomas presented preliminary results from an analysis of exposure errors using a method for inferring annual dose rates directly from miners' exposure histories, allowing for gaps
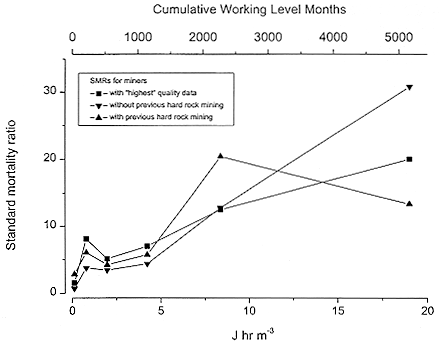
FIGURE E-1 Standardized mortality ratios for Colorado Plateau uranium miners study by cumulative radon progeny exposure and quality of exposure data (Lundin and others 1971).
in exposure. Data from the 1987 follow-up of the Colorado miners were used. Unlike the Colorado data set used in the committee's analysis of pooled miner data, Thomas did not limit exposures to < 11.20 Jhm-3 (< 3,200 WLM). Several assumptions were made that represented a simplified characterization of the true error structure (Table E-2).
Thomas considered the effects of exposure error on curvilinearity, and the modification of the exposure-response relationship by time since exposure and exposure rate. Table E-3 shows that there was significant curvilinearity in the exposure-response trend if no adjustment was made for exposure errors ![]()
![]() . With adjustment for error, the deviation from the linear exposure-response model was not significant
. With adjustment for error, the deviation from the linear exposure-response model was not significant ![]() . For the linear model and the linear-exponential model, the magnitude of the exposure-response trend increased when adjustment was made for exposure errors. Further, the estimate of ß for the linear model with error adjustment was about the same magnitude as the unadjusted linear-exponential model, suggesting that the curvilinearity was largely the result of exposure errors.
. For the linear model and the linear-exponential model, the magnitude of the exposure-response trend increased when adjustment was made for exposure errors. Further, the estimate of ß for the linear model with error adjustment was about the same magnitude as the unadjusted linear-exponential model, suggesting that the curvilinearity was largely the result of exposure errors.
TABLE E-2 Assumptions made by D. Thomas in analysis of exposure errors in the Colorado Plateau uranium miners study presented to the committee
|
• Classical error model applied to annual exposure rates • True exposure rate in WLM/yr (x) has a Weibull distribution • Observed exposure rate z=xu, where the error distribution (u) is lognormal with mean 0 and standard deviation: |
|
- CV = 1.00 before 1960, 0.50 after 1960 (large error) - CV = 0.50 before 1960, 0.25 after 1960 (small error) |
|
• True exposure x integrates over time to produce cumulative exposure X. • Relative risk (RR) models: |
|
- Curvilinearity: - Time since exposurea: - Exposure-rate: Model 1: Model 2b: |
|
ax5–9, x10–19, and x20+ denote true exposures accumulated 5–9, 10–19, and 20 years and more prior to age at risk. b |
The consequences of adjusting for exposure error on the effects of time since exposure and exposure rate were also considered by Thomas. Results indicated that adjustment for errors had little effect on the pattern of risk with time since exposure, but adjustment for errors reduced the effects of exposure rate (Tables E-4 and E-5).
The analyses suggested that exposure errors were likely to have had their greatest influence on the modeling of the inverse exposure-rate effect. However, the precise magnitude of the influence of the adjustment for errors was uncertain, due to limitations of the analysis. For example, exposure rates were inferred, rather than computed directly from mine records and measurement data, and the assumption that errors were independent across individuals can be questioned, since the same concentration value Jhm-3 (WL) would often be given for all
TABLE E-3 Parameter estimates and change in deviance for modeling curvilinearity in the exposure-response for the Colorado data.a Adjusted estimates account for error in exposures. Presented to the committee by D. Thomas
|
|
ßx100 |
a |
Change in deviance |
|
Unadjusted |
0.40 |
|
— |
|
|
0.69 |
-0.011 |
5.2 |
|
Adjustedb |
0.73 |
|
— |
|
|
1.08 |
-0.012 |
1.9 |
|
a Model of the form: RR = 1 + ßxe-ax where x is cumulative exposure in WLM. b Assumed error: CV=1.00 before 1960 and CV=0.50 after 1960. |
|||
TABLE E-4 Parameter estimates and change in deviance for modeling time since exposure in the exposure-response for the Colorado data.a Adjusted estimates account for error in exposures. Presented to the committee by D. Thomas
|
|
β×100 |
θ2 |
θ3 |
Change in deviance |
|
Unadjusted |
1.26 |
0.65 |
0.13 |
19.2 |
|
Adjustedb |
1.92 |
0.80 |
0.15 |
23.8 |
|
a Model of the form: RR = 1 + β(X5–9 + θ2X10–19 + θ3X20+) where X5–9, X10–19, and X20+ are cumulative WLM exposures 5–9, 10–19, and 20 years and more prior to age at risk. b Assumed error: CV = 1.00 before 1960 and CV = 0.50 after 1960. |
||||
workers in a particular mine and workers' movements among mines or among companies were not independent. Finally, in his presentation Thomas indicated that the Weibull distribution provided a poor fit to the exposure rate data.
Cohort Study of New Mexico Uranium Miners
Samet and others (1986b) addressed several issues in the estimation of exposures for the New Mexico uranium miners. For selected years, relatively large numbers of measurements had been made in the large mines of Ambrosia Lake. During several day visits to the mines, the mine inspectors sometimes made over 100 measurements. Samet and colleagues addressed the most appropriate parameter for summarizing the measurements. In New Mexico, the inspectors from the state calculated a person-weighted index, termed the "Total Mine Index" which weighted the measurements by the approximate number of workers associated with the measurement by the inspector. Using the Total Mine Index as the standard for comparison in a regression analysis, Samet and colleagues compared the performance of the arithmetic mean and various trimmed means and the median in estimating the Total Mine Index. The arithmetic mean was found to be
TABLE E-5 Parameter estimates and change in deviance for modeling the effect of exposure rate on the exposure-response for the Colorado data.a Adjusted estimates account for error in exposures. Presented to the committee by D. Thomas
|
|
β×100 |
α |
Change in deviance |
|
Unadjusted |
0.40 |
|
— |
|
|
1.89 |
-0.35 |
8.0 |
|
Adjustedb |
0.73 |
|
— |
|
|
1.06 |
-0.21 |
2.0 |
|
a Model of the form: b Assumed error: CV = 1.00 before 1960 and CV = 0.50 after 1960. |
|||
an unbiased predictor of the Total Mine Index, suggesting that measurements had been made in approximate proportion to the distribution of the exposed miners within the mine. The median was lower than the mean and the Total Mine Index, as anticipated for the skewed distribution of the measurements.
Cohort Study Of Czechoslovakian Uranium Miners
Estimation of the "true" exposures for all miners in the epidemiologic studies is not currently feasible. However, improving the overall quality of study data reduces the effects of errors. Recent analysis of the study of Czech uranium miners (sometimes referred to as the West Bohemian uranium miners) have resulted in two rather different estimates of the ERR/exposure. An analysis by Tomásek and others (1994a) estimated the ERR/exposure in WLM as 0.0064 (95 percent CI 0.004, 0.011), while in the pooled analysis of 11 cohorts, Lubin and others (1994a) estimated the ERR/exposure in WLM for the Czech study as 0.0034 (95 percent CI 0.002,0.006). The former estimate was based on using male Czechoslovakian lung-cancer mortality rates as an external referent population, while the latter estimated was based on an internal referent population (Tomásek and Darby 1995).
Tomásek and Darby (1995) showed that methodologic differences did not explain the different estimates of ERR/exposure, but that the principal difference in the two estimates was the result of improvements in two aspects of data quality. First, follow-up information was re-examined, using additional sources, such as pension offices, and local inquiries. These efforts resulted in an increase in the number of deaths and a reduction in the number of miners who were lost to follow-up. Following the reevaluation, the number of lung-cancer deaths increased from 661 to 705. However, the added number of lung-cancer deaths had minimal impact on the ERR/exposure estimate (Tomásek and Darby 1995). Second, exposures for all miners were re-assessed, correcting arithmetic and transcription errors and, for some men, accounted for exposures at other uranium mines which previously had not been included. Revised exposures were recomputed for each miners for each month of employment.
Improving the exposure data nearly doubled the estimate of ERR/exposure. It should be noted that the Czech data, along with the Colorado data, exhibited curvilinearity in the exposure-response in the pooled miner analysis. Unlike the Colorado data (see below), the exposure-response relationship in the Czech data continued to exhibit significant curvilinearity after the exposure reassessment (Tomásek and Darby 1995).
Cohort Study of Beaverlodge Uranium Miners
Exposures have also been recalculated for the Beaverlodge, Canada, cohort of uranium miners for those included in a case-control study of lung-cancer,
smoking, and radon-progeny exposure (L'Abbe and others 1991). The new exposures replaced the median by the arithmetic mean for the assignment of values to mines and company records were used to place the participants in more specific areas within mines rather than simply using mine-wide averages (Howe and Stager 1996). The new exposure estimates were higher than the previous ones: 0.28 Jhm-3 (81.3 WLM) versus 0. 18 Jhm-3 (50.6 WLM). The new and old values were moderately correlated (r = 0.66). There were few major changes in individual estimates.
The estimated excess relative risks were calculated for the cohort study and the case-control study with original exposure estimates and for the case-control study with the new exposure estimates. The values of ERR/exposure were 0.01/100 Jhm-3 (2.63/100 WLM) for the cohort study, 0.01/100 Jhm-3 (2.70/100 WLM) for the case-control study with the original exposure estimates, and 1/100 Jhm-3 (3.25/100 WLM) for the case-control study with the new exposure estimates. The authors attributed the increase in the estimate of excess relative risk with the new estimates to reduction in measurement error which more than compensated for the increase in average exposure.
General Assessments Of Exposure Error In Miner Studies
In 1989 the effects of exposure error were considered for the Czechoslovakia, Colorado, Ontario, Sweden, Beaverlodge, and Port Radium studies in a study conducted by SENES Consultants Limited in Canada (SENES 1989). This report described several sources of uncertainty in the miner studies and was one of the earliest efforts to address the consequences of error analytically. The focus was on adjusting the exposure-response parameter for the excess RR model and for the absolute excess risk model. The approach was limited, because the authors did not have access to data on individual miners and utilized only published RRs within categories of exposure (Jhm-3 or WLM). No attempt could be made to evaluate patterns of error for different mining periods within a study. For the excess RR model, the authors estimated that the most likely range for the ERR/ exposure parameter for this group of studies was 0.009 to 0.00005 per Jhm-3 (0.005 to 0.015 per WLM).
In the pooled analysis, Lubin and others (1994a) considered the impact of errors in exposure only in the most general way and only within the context of the modification of the exposure-response relationship by exposure rate and exposure duration. Exposure error was considered greatest in the earliest years of mining, years in which exposure rates were at their highest. Exposure error would therefore have tended to attenuate the effects of high exposures, and potentially induced an observed inverse exposure-rate pattern.
To assess the contribution of exposure error to the inverse exposure-rate effect, the authors analyzed RR patterns within categories of several variables which were considered as indicators of the magnitude of exposure error, for
example, year of first exposure, attained age, years since last exposure, and total cumulative exposure. Figure E-2 shows the result of one of these analyses. Observed RRs, adjusted for cumulative exposure (Jhm-3 or WLM) and other factors, are plotted by categories of calendar year of first exposure from the pooled analysis of 11 underground miner studies (Lubin and others 1994a). Also, shown are loglinear models fit to the observed RRs. The overall levels of the RRs were affected by the small numbers of lung-cancer cases in the referent category <0.1 WL (6, 5 and 8 cases in the <1945, 1945–54, and = 1955 year of first exposure categories, respectively), but the figure shows a similar pattern of declining RRs with WL, suggesting that it was unlikely that the inverse exposure-rate effects were entirely the result of exposure errors.
In a report to the Canadian Atomic Energy Control Board, Howe and Armstrong presented a sensitivity analysis of the potential impact of measurement error on risk of lung-cancer using hypothetical data, but based on the pooled analysis of 11 cohorts of underground miners (Howe and Armstrong 1994). The
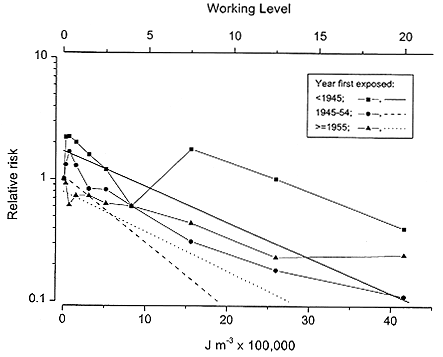
FIGURE E-2 Relative risks by categories of exposure rate and fitted trends by calendar year first exposure for data from analysis of underground miner studies (Lubin and others 1994a). Relative risks adjusted for attained age, cohort, ethnicity, and cumulative exposure.
error structure was assumed a combination of Berkson and classical errors, with no systematic error in exposures. The measurement errors were assumed to have a Berkson component, that is errors arising from the assignment of an overall mine or area mean to a group of miners. Bias in risk estimates occurs because the true mine or area mean for the group of miners was unknown and must be estimated from measurement samples. The estimation of the area mean exposure rate introduced a classical error structure, that is, error was independent of the true exposure (Howe and Armstrong 1994).
In the analysis, exposure-time in working months was assumed as known without error. While some error in individual employment records was inevitable, the assumption was considered a reasonable approximation, particularly in comparison with the amount of error introduced by exposure rate. There was additional uncertainty about the amount of time miners spent at their underground work sites and in travel ways, but again this source of error was considered of less consequence for biasing risk modeling (Howe and Armstrong 1994).
The authors presented results from two simulation studies. One simulation, which closely mimicked average data in actual studies, generated matched case-control data with mean numbers of cases from 300 to 835, and equal numbers of controls. Exposure rate was assumed lognormally distributed with geometric mean 5.0 WL and standard deviation (of log WL) of 0.5. 1.0, and 2.0. Three schemes for the number of measurements per year were used: (1) one measurement per year for all years of the study; (2) one measurement per year increasing linearly to 100 measurements per year over the years of the study; and (3) 100 measurements per year in all years. For true data generated using a simple linear excess RR model, RR = 1 + ß(WLM)(WL)a with true ß equal to 0.010 and true a = 0.00, bias in the estimate of ß was minimal under measurement schemes 2 and 3 (Table E-6). For these schemes, there was some attenuation of the exposure-response relationship only with a standard deviation of log (WL) of 2.0. With schemes 2 and 3, a significant exposure rate effect was induced only with the extreme standard deviation. In contrast, with a single measurement per year, there was induced curvilinearity when the standard deviation was 1.0 or greater.
Due to computational limitations, a second simulation using simplified cohort data was carried out, in which exposure did not overlap follow-up. The simulation assumed that all exposure was accumulated by age 30 years, and that follow-up started at age 35. Subgroups of the cohort were given exposure rates 1, ... , 20 WL and follow-up continued for 20–50 years. In each simulated data set, there was 14,000 subjects and cumulative exposure ranged from 0.35 to 7.00 Jhm-3 (100 to 2,000 WLM). True RR again followed the simple linear excess RR model, with true ß = 0.010. The same three standard deviations for log (WL) and three schemes for measurements per year were used. Again, attenuation of the exposure-response was observed, particularly with the scheme of one WL measurement per year.
TABLE E-6 Effect of measurement error in exposure on the excess relative risk estimate in a linear excess relative risk model,a based on computer simulation of case-control data with parameters ß = 1.00 and a = 0.00. Table adapted from Howe and Armstrong (1994)
|
WL measurement schemeb |
Standard deviation of log(WL) |
Median (ß) |
Median (a) |
|
1–1 |
0.5 |
0.90 |
-0.075 |
|
|
1.0 |
0.70 |
-0.41 |
|
|
2.0 |
0.26 |
-0.79 |
|
1–100 |
0.5 |
1.10 |
0.021 |
|
|
1.0 |
1.10 |
-0.07 |
|
|
2.0 |
0.54 |
-0.32 |
|
100–100 |
0.5 |
1.01 |
0.026 |
|
|
1.0 |
1.00 |
0.019 |
|
|
2.0 |
0.77 |
-0.22 |
|
a Data simulated under the model: RR = 1+ß(WLM)(WL)a b Measurement schemes for WL: 1–1: one measurement per year for all (25) exposure years; 1–100: one measurement per year increasing linearly to 100 measurements per year over exposure years; 100–100:100 measurements per year in exposure years. |
|||
Simulations also addressed the effect of measurement error on estimating the effects of time since exposure, age at risk, and exposure rate. With 100 measurements per year (scheme 3), there was little effect on the patterns of risk with any of these factors, although as previously observed, there was some bias in the main risk effect of exposure. With scheme 3, there was some induced bias when the standard deviation of the error was large 2.0. With measurement scheme 2, some bias was induced, but only in the extreme category (=25 years since exposure, =65 years of age, or exposure rate =15 WL). With a single measurement per year (scheme 1), there was marked bias.
Howe and Armstrong identified two key elements for assessing the effects of measurement error: variation of the true exposure rate, that is, the degree that the true exposure rate for individuals differed from the true mean exposure rate; and the number of measurements used to estimate the true mean exposure rate.
The authors concluded that ''measurement error leads to (a) reduction in the main effects coefficient, that is, that for cumulative exposure; (b) increasing downward bias in risk estimates with increasing time since exposure; (c) increasing downward bias in risk estimates with increasing age at risk and (d) increasing downward bias with increasing exposure rate." They further conclude that "biases are likely to be negligible if estimates are based on 100 or more samples per year and if the standard deviation of log(exposure rate) has a value of 1.0 or less." And "these conditions are met for the majority of the miners' cohort studies, and
hence, although there may well be a contribution by measurement error to these apparent effects within some of the studies, overall it appears that measurement error of itself does not account for the existence of these effects."
SUMMARY
There was marked variation among the cohorts in the approaches used to estimate exposures and in the extent of data available (see Annex to this chapter). All exposure estimates are subject to measurement error. Within cohorts, the degree of measurement error likely depends on the calendar years during which exposures were incurred; across cohorts, there is likely a varying impact of measurement error. Some work has addressed the consequences of error, both in individual cohorts and more generally. These analyses show that error would generally blunt exposure-response relationships. Time-dependent errors pose an additional constraint in interpreting time-dependence of effect, such as the inverse dose-rate effect. The substantial variation in methods for exposure assessment among the cohorts undoubtedly contributes to the heterogeneity of risk estimates from the individual studies.















