Massive Data Sets in Navy Problems
J.L. Solka, W.L. Poston, and D.J. Marchette
Naval Surface Warfare Center
E.J. Wegman
George Mason University
I. Abstract
There are many problems of interest to the U. S. Navy that, by their very nature, fall within the realm of massive data sets. Our working definition of this regime is somewhat fuzzy although there is general agreement among our group of researchers that such data sets are characterized by large cardinality (>106), high dimensionality (>5), or some combination of moderate levels of these two which leads to an overall large level of complexity. We discuss some of the difficulties that we have encountered working on massive data set problems. These problems help point the way to new needed research initiatives. As will be seen from our discussions one of our applications of interest is characterized by both huge cardinality and large dimensionality while the other is characterized by huge cardinality in conjunction with moderate dimensionality. This application is complicated by the need to ultimately field the system on components of minimal computational capabilities.
II. Introduction
We chose to limit the focus of this paper to two application areas. The first application area involves the classification of acoustic signals arising from military vehicles. Each of these acoustic signals takes the form of (possibly multiple) time series of varying duration. Some of the vehicles whose acoustic signatures we may desire to classify include helicopters, tanks, and armored personal carriers. In Figures la and b we provide an example plot of signals collected from two different rotary wing vehicle sources. These signals are variable in length and can range anywhere from tens of thousands of measurements to billions of measurements depending on the sampling rate and data collection interval. Part of our research with these signals involves the identification of advantageous feature sets and the development of classifiers which utilize them. As will be discussed below this process in itself is fraught with associated massive data set problems. An additional layer of difficulty comes from the fact that we are interested in ultimately
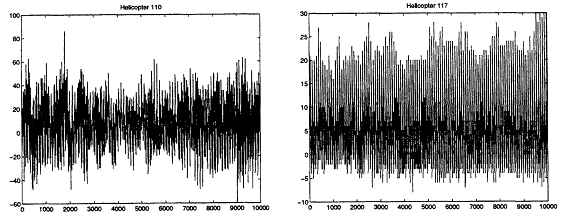
Figure 1
Time series plots for two helicopter models.

Figure 2
Grayscale images of a tank and mammogram.
fielding an instrument which will be capable of classifying acoustic signatures under battlefield conditions in as near to a real-time manner as possible. This burden places severe restrictions on the complexity and robustness of the system that is ultimately fielded.
Our second application focuses on the automatic segmentation of images into regions of homogeneous content, with an ultimate goal of classifying the different regions. Our research has focused on a wide variety of image modalities and desired classification systems. They include the detection of combat vehicles in natural terrain (Solka, Priebe, and Rogers, 1992), the detection of man-made regions in aerial images (Priebe, Solka, and Rogers, 1993 and Hayes et al., 1995), and the characterization of mammographic parenchymal patterns (Priebe et al., 1995). In Figure 2, we provide representative vehicular and mammographic images. The homogeneity criterion in this case is based on functionality of the region. For example, we wish to
have the capability to identify a given region as containing a tank or a bush, normal parenchymal tissue or tumor. This problem is more difficult then the previous one with regard to the size of the data sets, the spatial correlation of the extracted features, and the dimensionality of the extracted features.
In the following sections we discuss at length the specific difficulties that we have encountered analyzing the data sets associated with these two applications. There are associated problems with both the exploratory data analysis of potential features, the development of density estimates of these features, and the ultimate testing and fielding of classification systems based on these features. After presenting these problems, we next suggest a course of potential research initiatives which will help alleviate these difficulties. This is followed by a brief summary of our main points.
III. Discussions
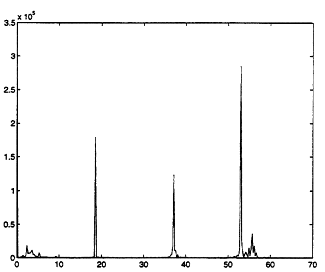
We first discuss the simpler of these problems. In the acoustic signal processing application, one is initially concerned with identifying features in the signals that will be useful in distinguishing the various classes. Fourier-based features have been useful in our work with rotary wing vehicles because the acoustic signals that we have studied to date have been relatively stationary in their frequency content. Depending on the type of signal which one is interested in classifying, one typically keeps a small number of the strongest frequency components. We currently employ a harmogramic hypothesis testing procedure to decide which and how many of the spectral components are significant (Poston, Holland, and Nichols, 1992). For some of our work this has led to two significant spectral components. In the case of rotary wing aircraft, these components correspond to the main and tail rotor frequencies (see Figure 3). Given a signal for each class of interest one extracts these features from each signal based on overlapping windows. In our application this easily leads to approximately 106 points residing in R2 for each of 5 classes.
However, once we extend the problem to the classification of moving ground vehicles, these simple features are no longer adequate. In fact, it is not surprising that the periodograms from moving ground vehicles exhibit nonstationary characteristics. In Figure 4, we present a periodogram for one of the vehicle types. This problem requires that one must perform exploratory data analysis on the possible tilings of regions of the time-frequency plane in order to discover their utility as classification features. This increases the dimensionality of our problem from 2 to between 16 and 100 depending on our tiling granularity. So we are faced with the task of performing dimensionality reduction using millions of observations in tens of dimensions. Even if one utilizes automated techniques such as projection pursuit for the determination of the needed projection, there can be problems with long projection search times and overplotting in the lower-dimensional projected views.
In order to cast the classification problem within a hypothesis testing framework, probability density estimates are built for each of the classes. Performing quality probability density estimation in a moderately low dimensional space (<4) using millions of features can be difficult. Many density estimation procedures are analogous to clustering and as shown by Wegman (1995), clustering procedures are computationally costly. With an ultimate cost of between O(n3/2) and O(n2) depending on the nature of the algorithm, extremely long execution times can be expected for the analysis of these large data sets.
These probability density estimators are ultimately deployed as part of the fielded system. In addition it is desirable for the system to have some limited capability to either refine the existing estimates for a given class or to add in an estimate of a new class's probability density function as part of its field operation. Although we have developed and do utilize schemes for density estimation that are recursive in nature (Priebe and Marchette, 1991 and Priebe, 1994), given a new signal of limited duration one may need to have stored the features for a period of time in order to obtain a good maximum likelihood density estimate for the signal features. In addition the nature of this problem dictates our interest in density estimation and dimensionality reduction procedures in the presence of partial classification information.
The second problem is much more daunting in extent. To begin with it is not uncommon to deal with images that are on the order of 4,000 × 4,000 pixels in size, with anywhere from 1 to 7 spectral bands per pixel. Typical data sets can range from tens to thousands of images. Unlike some industrial applications where there is tight control on the background and possible content of the image, these images can have a very wide range of subjects. A typical example is to detect and identify the ground vehicles within an image. The range of possible backgrounds is enormous: desert, farmlands, forest, jungle, and city streets. Each background will require different kinds of processing to eliminate clutter. Further, one is often forced to determine the background from the image without a priori knowledge (for example, for an automated system on a satellite).
In order to solve this problem, features must be computed from the image. These are then used for the classification task. Typically the problem is partitioned into sub-problems. For example, one might first determine the environment (forest, desert, etc.). This would then dictate the types of algorithms to be used for the detection of regions of interest (ROI), the detection of objects, and finally the classification of the objects into the desired categories. Each of these problems will require (potentially) different features to be extracted and processed.
Given the nature of the image classification problem there are many different types of features that can be extracted at each pixel or within each region of the image. Even if one limits their attention to ''low level'' features (for ROI detection, for example), it is very easy to find 30 features of interest, each of which must be computed for each pixel or small region of pixels. Assuming 20 images are used to identify good combinations of features for classification this still leads to roughly 9.6 billion observations in R30. This may have to be repeated for each different environment or class of potential targets. At this level of complexity even the most rudimentary exploratory data analysis (EDA) tasks are inadequate.
The curse of dimensionality (Scott, 1992) often requires a projection to a lower dimensional space before density estimation or other classification techniques can be performed but this still reduces the complexity of the problem only by an order of magnitude. The added complexity from the selection of appropriate projections more than makes up for this reduction. Rampant problems with overplotting and slow plotting times are the norm for this kind of data, making interactive EDA extremely difficult. Again, Wegman (1995) suggests that direct visualization of data sets over about 106 data points is virtually impossible. In fact, the unwieldy nature of these images makes it difficult for human operators to obtain ground truth on them. In addition, one often produces a number of "interesting" projections or other derived data associated with a given set of features. It becomes a very difficult task, just in the data structures area, to keep track of all of this associated data.
Even if one first segments the image into regions and extracts features based on regions rather than individual pixels, there are still serious problems. One still must deal with the entire image in order to do the segmentation and so the original requirement to deal with approximately 16 million pixels per image still holds. In addition, different features may require different segmentation algorithms and so the apparent reduction in number of feature vectors is easily matched by an increase in computational complexity.
Once a "best" combination of features is found, one must build probability density estimates for each of the classes in the image. In this case the huge data sets that are associated with each class can lead to extremely slow convergence of recursive density estimation procedures. This phenomena has been observed by us in the case of likelihood maximization of over determined mixture models under the Expectation Maximization (EM) algorithm (Solka, 1995). In these cases careful monitoring of the parameter estimation process is essential (Solka, Poston, Wegman 1995). If one attempts to mitigate this problem through the use of iterative procedures one is faced with the overhead associated with the storage of all of the observations.
The problem becomes more pronounced when one realizes that 20 images is by no means sufficient for validation of the algorithms. Many hundreds or thousands of images must be processed in order to get good estimates of performance. These images are then typically used as part of a leave-one-image-out cross validation procedure. Furthermore, these numbers may increase dramatically as the number of target types increases.
A final problem, alluded to above, is that often truth values are known only for a very small subset of the images. Imagine trying to build a system to detect Scud missiles in Iraq. This obviously would require images of these missiles in the terrain in which they were likely to be deployed. However, in order to obtain these images one must either be lucky, spend a lot of time examining images, or already have a method for finding Scud missiles in Iraq. While it is sometimes possible to use images of similar targets, or construct mock targets, there is always the danger of building a system which finds mock targets (as opposed to real ones). As a result of this problem, detection and classification algorithms must be able to handle partially categorized and uncategorized data.
Fielded systems that will be utilized to build classifiers "on the fly" are required to deal with hundreds or thousands of images even in the training phase of the procedure. After an initialization phase these classifiers will be expected to continue to update their density estimates for the existing "target" classes and also build new estimates for any new target classes that might appear. As we discussed with regard to the acoustic signal processing work the use of recursive estimation procedures becomes essential.
IV. Proposed Needs
Given this daunting list of problems what are some of the possible solutions? We will discuss our "wish list" of solutions in the order into which we decompose the classification problem. First we will discuss the needs of feature extraction, followed by exploratory data analysis, then density estimation, and finally classification. We hope that these observations will help point the way to some fruitful research areas.
First and foremost the problems associated with the design of classification systems must be managed by some sort of database management system. There has been some recent press by such developers as StatSci regarding database utilities which will be included in their new releases. There are also some packages provided by third party developers such as DBMS COPY. These packages are aimed at providing a seamless interface between statistical analysis software and database management systems. That being said, there are yet fundamental research issues associated with the seamless integration of statistical software and database management systems. There are numerous types of information that occur routinely in the classification process that these systems could be used to manage. We have focused on situations in which ele-
ments of the database may be multispectral images. How, for example, can one index and browse such multispectral image databases? Low resolution, thumbnail sketches, for example, may essentially obscure or eliminate texture which often is the very feature for which we may be browsing. To our knowledge, no database management system has proven to be adequate for the problems addressed above, especially those inherent in managing a large image library with associated features and class models.
More to the point, statisticians as a group tend not to think in terms of massive data files. The implication of this is that flat file structures tend to be adequate for the purposes of most small scale data and statistical analysis. There is no perceived need to understand more complex database structures and how to exploit these structures for analysis purposes. Very few academic statistics programs would even consider a course in data structures and databases as a legitimate course for an advanced degree program. One interesting consequence of this is the newfound interest in the computer science community for the discipline they now call data mining. While principally focused on exploratory analysis of massive financial transaction databases, tools that involve not only statistical and graphical methods, but also neural network and artificial intelligence methods are being developed and commercialized with little input from the statistics community. Two URLs which give some insight into the commercial knowledge discovery and data mining community are http://info.get.com/~kdd/ and http://www.ibi.com/. In short, we believe that a fundamental cultural shift among statistical researchers is needed.
Next we turn our attention to the EDA portion of the task. Some of the needs here include techniques for dimensionality reduction in the presence of partial classification information and recursive dimensionality reduction procedures. Since the dimensionality reduction technique ultimately is part of any fielded system, it seems that recursive techniques for updating these transformations based on newly collected observations are needed. Techniques to deal with the problem of overplotting are also required. Density estimation has been suggested by Scott (1992) as a technique to improve on the overplotting problem. The inclusion of binning procedures such as the hexagonal procedure of Carr et al. (1992) as part of the existing statistical analysis packages would be helpful. Another approach to this problem is the use of sampling techniques to thin the data before plotting. These techniques have the requirement of efficient methods for outlier identification (Poston et. al., 1995 and Poston, 1995). Techniques for the visual assessment of clusters in higher dimensional space are also needed. We have previously developed a system for the visualization of data structures in higher dimensions based on parallel coordinates (Wegman, 1990), but much work remains to be done on this and new approaches to higher dimensional cluster visualization.
There remain many technical issues associated with probability density estimation for massive data sets in moderately high-dimensional spaces. Efficient procedures for estimating these densities and performing cluster analysis on them are needed. These procedures must be highly efficient in order to combat the large cardinality of these data sets. Further study into recur-
sive estimation procedures is needed. Recursive or some sort of hybrid iterative/recursive procedure becomes essential when the data sets become too massive for full storage. Continued study into overdetermined mixtures models is needed. In particular additional work into the visualization of these models and the derivation of their theoretical properties is needed.
Last we turn our attention to some needs in the area of discriminant analysis. Image classification procedures based on the use of Markov random field models continues to be a fruitful area of research. In addition research into the use of pseudo-metrics such as Kullback Leibler for comparisons of probability density functions as an alternative to the standard likelihood ratio hypothesis testing deserves continued research. Finally procedures that attempt to combine some of the modem density estimation techniques with the Markov random field approach have merit. On very large images, Markov random field techniques may be inappropriate due to computation time. Fast versions of these techniques need to be developed.
V. Conclusions
We have examined some of the problems that we have encountered in building systems which perform automatic classification on acoustic signals and images. The design of these systems is a multifaceted problem that spawns a large number of associated massive data set subproblems. We have not only indicated some of the problems that we have encountered but we have also pointed the way to fruitful problems whose solutions are required to produce the tools which researchers in this area need.
A final point is the use of video over single images, which is becoming more important as the technology advances. The use of video not only vastly decreases the time allowed to process each image (or frame) but also greatly increases the number of images. With image frame rates of 30 fps and higher this gives a potential new meaning to the word massive data set. Since these images are highly correlated in time and space, this raises potentially a whole new conceptual framework. We conceive, for example, an animation or movie as a sequence of two dimensional images. Alternatively we could conceive of an animation or movie as a function f(x, y, t) which lives in R4. This change of perspective raises the need for filtering, processing, and analysis techniques for three dimensional "images" as opposed to the two dimensional images we have been primarily discussing here. Of course, at each "voxel" location it is possible to have a vector-valued function (e.g. a multispectral vector). But this discussion raises many new issues, and is beyond the scope of this paper.
VI. Acknowledgments
The authors (ILS, WLP and DIM) would like to acknowledge the support of the NSWCDD Independent Research Program through the Office of Naval Research. In addition, the work of EJW was supported by the Army Research Office under contract number DAAH04-94-G-0267, by the
Office of Naval Research under contract number N00014-92-J-1303.
VII. References
Carr, D.B., Olsen, A.R. and White, D. (1992), "Hexagon mosaic maps for display of univariate and bivariate geographical data," Cartography and Geographic Information Systems, 19(4), 228-236 and 271.
Poston, W.L., Holland, O.T., and Nichols, K.R. (1992) "Enhanced Harmogram Analysis Techniques for Extraction of Principal Frequency Components," TR-92/313
Poston, W.L., Wegrnan, E.J., Priebe, C.E., and Solka, J.L. (1995) "A recursive deterministic method for robust estimation of multivariate location and shape," accepted pending revision to the Journal of Computational and Graphical Statistics.
Poston, W.L. (1995) Optimal Subset Selection Methods, Ph.D. Dissertation, George Mason University: Fairfax, VA.
Priebe, C.E., (1994), "Adaptive Mixtures," Journal of the American Statistical Association, 89, 796-806.
Priebe, C.E., Solka, J.L., Lorey, R.A., Rogers, G.W., Poston, W.L., Kallergi, M., Qian, W., Clarke, L.P., and Clark, R.A. (1994), "The application of fractal analysis to mammographic tissue classification," Cancer Letters, 77, 183-189.
Priebe, C. E., Solka, J. L., and Rogers, G. W. (1993), "Discriminant analysis in aerial images using fractal based features," Adaptive and Learning Systems II, F. A. Sadjadi, Ed., Proc. SPIE 1962, 196-208.
Priebe, C.E. and Marchette, D.J. (1991) "Adaptive mixtures: recursive nonparametric pattern recognition," Pattern Recognition, 24(12), pp. 1196-1209.
Scott, D. W. (1992), Multivariate Density Estimation, John Wiley and Sons: New York.
Solka, J.L., Poston, W.L., and Wegman, E.J. (1995) "A visualization technique for studying the iterative estimation of mixture densities," Journal of Computational and Graphical Statistics, 4(3), 180-198.
Solka, J.L. (1995) Matching Model Information Content to Data Information , Ph.D. Dissertation, George Mason University: Fairfax, VA.
Solka, J. L., Priebe, C. E., and Rogers, G. W. (1992), "An initial assessment of discriminant sur-
face complexity for power law features," Simulation, 58(5), 311-318.
Wegman, E.J. (1990) "Hyperdimensional data analysis using parallel coordinates," Journal of the American Statistical Association, 85, 664-675.
Wegman, E.J. (1995) "Huge data sets and the frontiers of computational feasibility," to appear Journal of Computational and Graphical Statistics , December, 1995.