Information Retrieval: Finding Needles in Massive Haystacks
Susan T. Dumais
Bellcore
1.0 Information Retrieval: the Promise and Problems
This paper describes some statistical challenges we encountered in designing computer systems to help people retrieve information from online textual databases. I will describe in detail the use of a particular high-dimensional vector representation for this task. Lewis (this volume) describes more general statistical issues that arise in a variety of information retrieval and filtering applications. To get a feel for the size of information retrieval and filtering problems, consider the following example. In 1989, the Associated Press News-wire transmitted 266 megabytes of ascii text representing 84,930 articles containing 197,608 unique words. A term-by-document matrix describing this collection has 17.7 billion cells. Luckily the matrix is sparse, but we still have large p (197,000 variables) and large n (85,000 observations). And, this is just one year's worth of short articles from one source
The promise of the information age is that we will have tremendous amounts of information readily available at our fingertips. Indeed the World Wide Web (WWW) has made terabytes of information available at the click of a mouse. The reality is that it is surprisingly difficult to find what you want when you want it! Librarians have long been aware of this problem. End users of online catalogs or the WWW, like all of us, are rediscovering this with alarming regularity.
Why is it so difficult to find information online? A large part of the problem is that information retrieval tools provide access to textual data whose meaning is difficult to model. There is no simple relational database model for textual information. Text objects are typically represented by the words they contain or the words that have been assigned to them and there are hundreds of thousands such terms. Most text retrieval systems are word based. That is, they depend on matching words in users' queries with words in database objects. Word matching methods are quite efficient from a computer science point of view, but not very effective from the end users' perspective because of the common vocabulary mismatch or verbal disagreement problem (Bates, 1986; Furnas et al., 1987).
One aspect of this problem (that we all know too well) is that most queries retrieve irrelevant information. It is not unusual to find that 50% of the information retrieved in response to a query is irrelevant. Because a single word often has more than one meaning (polysemy), irrelevant materials will be retrieved. A query about "chip", for example, will
return articles about semiconductors, food of various kinds, small pieces of wood or stone, golf and tennis shots, poker games, people named Chip, etc.
The other side of the problem is that we miss relevant information (and this is much harder to know about!). In controlled experimental tests, searches routinely miss 50-80% of the known relevant materials. There is tremendous diversity in the words that people use to describe the same idea or concept (synonymy). We have found that the probability that two people assign the same main content descriptor to an object is 10-20%, depending some on the task (Furnas et al., 1987). If an author uses one word to describe an idea and a searcher another word to describe the same idea, relevant material will be missed. Even a simple concrete object like a "viewgraph" is also called a "transparency", "overhead", "slide", "foil", and so on.
Another way to think about these retrieval problems is that word-matching methods treat words as if they are uncorrelated or independent. A query about "automobiles" is no more likely to retrieve an article about "cars" than one "elephants" if neither article contains precisely the word automobile. This property is clearly untrue of human memory and seems undesirable in online information retrieval systems (see also Caid et al., 1995). A concrete example will help illustrate the problem.
2.0 A Small Example
A textual database can be represented by means of a term-by-document matrix. The database in this example consists of the titles of 9 Bellcore Technical Memoranda. There are two classes of documents -5 about human-computer interaction and 4 about graph theory.
Title Database:
|
c1: Human machine interface for Lab ABC computer applications |
|
c2: A survey of user opinion of computer system response time |
|
c3: The EPS user interface management system |
|
c4: System and human system engineering testing of EPS |
|
c5: Relation of user-perceived response time to error measurement |
|
m1: The generation of random, binary, unordered trees |
|
m2: The intersection graph of paths in trees |
|
m3: Graph minors IV: Widths of trees and well-quasi-ordering |
|
m4: Graph minors: A survey |
The term-by-document matrix corresponding to this database is shown in Table 1 for terms occurring in more than one document. The individual cell entries represent the frequency with which a term occurs in a document. In many information retrieval applications these frequencies are transformed to reflect the ability of words to discriminate among documents. Terms that are very discriminating are given high weights and undiscriminating terms are given low weights. Note also the large number of 0 entries in the matrix-most words do not occur in most documents, and most documents do not contain most words
Table 1
Sample Term-by-Document Matrix (12 terms × 9 documents)
|
|
C1 |
C2 |
C3 |
C4 |
C5 |
M1 |
M2 |
M3 |
M4 |
|
human |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
interface |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
computer |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
user |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
system |
0 |
1 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
|
response |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
time |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
EPS |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
survey |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
trees |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
graph |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
minors |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Consider a user query about "human computer interaction." Using the oldest and still most common Boolean retrieval method, users specify the relationships among query terms using the logical operators AND, OR and NOT, and documents matching the request are returned. More flexible matching methods which allow for graded measures of similarity between queries and documents are becoming more popular. Vector retrieval, for example, works by creating a query vector and computing its cosine or dot product similarity to the document vectors (Salton and McGill, 1983; van Rijsbergen, 1979). The query vector for the query "human computer interaction" is shown in the table below.
Table 2.
Query vector for "human computer interaction", and matching documents
|
Query |
|
C1 |
C2 |
C3 |
C4 |
C5 |
M1 |
M2 |
M3 |
M4 |
|
1 |
human |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
interface |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
computer |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
user |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
system |
0 |
1 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
|
0 |
response |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
time |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
EPS |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
survey |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
trees |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
graph |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
minors |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
This query retrieves three documents about human-computer interaction (C1, C2 and C4) which could be ranked by similarity score. But, it also misses two other relevant documents (C3 and C5) because the authors wrote about users and systems rather than humans and computers. Even the more flexible vector methods are still word-based and plagued by the problem of verbal disagreement.
A number of methods have been proposed to overcome this kind of retrieval failure including: restricted indexing vocabularies, enhancing user queries using thesauri, and various AI knowledge representations. These methods are not generally effective and can be time-consuming. The remainder of the paper will focus on a powerful and automatic statistical method, Latent Semantic Indexing, that we have used to uncover useful relationships among terms and documents and to improve retrieval.
3.0 Latent Semantic Indexing (LSI)
Details of the of the LSI method are presented in Deerwester et al. (1990) and will only be summarized here. We begin by viewing the observed term-by-document matrix as an unreliable estimate of the words that could have been associated with each document. We assume that there is some underlying or latent structure in the matrix that is partially obscured by variability in word usage. There will be structure in this matrix in so far as rows (terms) or columns (documents) are not independent. It is quite clear by looking at the matrix that the non-zero entries cluster in the upper left and lower fight comers of the matrix. Unlike word-matching methods which assume that terms are independent, LSI capitalizes on the fact that they are not.
We then use a reduced or truncated Singular Value Decomposition (SVD ) to model the structure in the matrix (Stewart, 1973). SVD is closely related to Eigen Decomposition, Factor Analysis, Principle Components Analysis, and Linear Neural Nets. We use the truncated SVD to approximate the term-by-document matrix using a smaller number of statistically derived orthogonal indexing dimensions. Roughly speaking, these dimensions can be thought of as artificial concepts representing the extracted common meaning components of many different terms and documents. We use this reduced representation rather than surface level word overlap for retrieval. Queries are represented as vectors in the reduced space and compared to document vectors.
An important consequence of the dimension reduction is that words can no longer be independent; words which are used in many of the same contexts will have similar coordinates in the reduced space. It is then possible for user queries to retrieve relevant documents even when they share no words in common. In the example from Section 2, a two-dimensional representation nicely separates the human-computer interaction documents from the graph theory documents. The test query now retrieves all five relevant documents and none of the graph theory documents.
In several tests, LSI provided 30% improvements in retrieval effectiveness compared with the comparable word matching methods (Deerwester et al., 1990; Dumais, 1991). In most applications, we keep k~100-400 dimensions in the reduced representation. This is a large number of dimensions compared with most factor analytic applications! However, there are many fewer dimensions than unique words (often by several orders of magnitude) thus providing the desired retrieval benefits. Unlike many factor analytic applications, we make no attempt to rotate or interpret the underlying dimensions. For information retrieval we simply want to represent terms, documents, and queries in a way that avoids the unreliability, ambiguity and redundancy of individual terms as descriptors.
A graphical representation of the SVD is shown below in Figure 1. The rectangular term-by-document matrix, X, is decomposed into the product of three matrices-X = T0 S0 D0', such that T0 and D0 have orthonormal columns, S0 is diagonal, and r is the rank of X. This is the singular value decomposition of X. T0 and D0 are the matrices of left and right singular vectors and S0 is the diagonal matrix of singular values which by convention are ordered by decreasing magnitude.
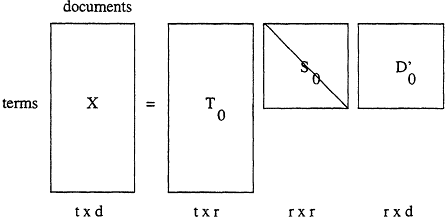
Figure 1.
Graphical representation of the SVD of a term-by-document matrix.
Recall that we do not want to reconstruct the term-by-document matrix exactly. Rather, we want an approximation that captures the major associational structure but at the same time ignores surface level variability in word choice. The SVD allows a simple strategy for an optimal approximate fit. If the singular values of S0 are ordered by size, the first k largest may be kept and the remainder set to zero. The product of the resulting matrices is a matrix ![]() which is only approximately equal to X, and is of rank k (Figure 2).
which is only approximately equal to X, and is of rank k (Figure 2).
The matrix ![]() is the best rank-k approximation to X in the least squares sense. It is this reduced model that we use to approximate the data in the term-by-document matrix.
is the best rank-k approximation to X in the least squares sense. It is this reduced model that we use to approximate the data in the term-by-document matrix.
We can think of LSI retrieval as word matching using an improved estimate of the term-document associations using ![]() , or as exploring similarity neighborhoods in the reduced k-dimensional space. It is the latter representation that we work with-each term and each document is represented as a vector in k-space. To process a query, we first place a query vector in k-space and then look for nearby documents (or terms).
, or as exploring similarity neighborhoods in the reduced k-dimensional space. It is the latter representation that we work with-each term and each document is represented as a vector in k-space. To process a query, we first place a query vector in k-space and then look for nearby documents (or terms).
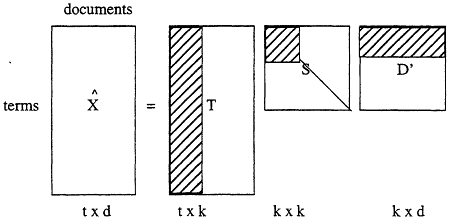
Figure 2.
Graphical representation of the reduced or truncated SVD
4.0 Using LSI For Information Retrieval
We have used LSI on many text collections (Deerwester, 1990; Dumais, 1991; Dumais, 1995). Table 3 summarizes the characteristics of some of these collections.
Table 3.
Example Information Retrieval data sets
|
database |
ndocs |
nterms (>1 doc) |
non-zeros |
density |
cpu for svd; k=100 |
|
MED |
1033 |
5831 |
52012 |
.86% |
2 mins |
|
TM |
6535 |
16637 |
327244 |
.30% |
10 mins |
|
ENCY |
30473 |
75714 |
3071994 |
.13% |
60 mins |
|
TREC-sample |
68559 |
87457 |
13962041 |
.23% |
2 hrs |
|
TREC |
742331 |
512251 |
81901331 |
.02% |
—— |
Consider the MED collection, for example. This collection contains 1033 abstracts of medical articles and is a popular test collection in the information retrieval research community. Each abstract is automatically analyzed into words resulting in 5831 terms which occur in more than one document. This generates a 1033 × 5831 matrix. Note that the matrix is very sparse-fewer than 1% of the cells contain non-zero values. The cell entries are typically transformed using a term weighting scheme. Word-matching methods would use this matrix. For LSI, we then compute the truncated SVD of the matrix keeping the k largest singular values and the corresponding left and fight singular vectors. For a set of 30 test queries, LSI (with k=100) is 30% better than the comparable word-matching method (i.e., using the raw matrix with no dimension reduction) in retrieving relevant documents and omitting irrelevant ones.
The most time consuming operation in the LSI analysis is the computation of the truncated SVD. However, this is a one time cost that is incurred when the collection is indexed and
not for every user query. Using sparse-iterative Lanczos code (Berry, 1992) we can compute the SVD for k=100 in the MED example in 2 seconds on a standard Sun Sparc 10 workstation.
The computational complexity of the SVD increases rapidly as the number of terms and documents increases, as can be seen from Table 3. Complexity also increases as the number of dimensions in the truncated representation increases. Increasing k from 100 to 300 increases the CPU times by a factor of 9-10 compared with the values shown in Table 3. We find that we need this many dimensions for large heterogeneous collections. So, for a database of 68k articles with 14 million non-zero matrix entries, the initial SVD takes about 20 hours for k=300. We are quite pleased that we can compute these SVDs with no numerical or convergence problems on standard workstations. However, we would still like to analyze larger problems more quickly.
The largest SVD we can currently compute is about 100,000 documents. For larger problems we run into memory limits and usually compute the SVD for a sample of documents. This is represented in the last two rows of Table 3. The TREC data sets are being developed as part of a NIST/ARPA Workshop on information retrieval evaluation using larger databases than had previously been available for such purposes (see Harman, 1995). The last row (TREC) describes the collection used for the adhoc retrieval task. This collection of 750k documents contains about 3 gigabytes of ascii text from diverse sources like the APNews wire, Wall Street Journal, Ziff-Davis Computer Select, Federal Register, etc. We cannot compute the SVD for this matrix and have had to subsample (the next to last row, TREC-sample). Retrieval performance is quite good even though the reduced LSI space is based on a sample of less than 10% of the database (Dumais, 1995). We would like to evaluate how much we loose by doing so but cannot given current methods on standard hardware. While these collections are large enough to provide viable test suites for novel indexing and retrieval methods, they are still far smaller than those handled by commercial information providers like Dialog, Mead or Westlaw.
5.0 Some Open Statistical Issues
Choosing the number of dimensions. In choosing the number of dimensions to keep in the truncated SVD, we have to date been guided by how reasonable the matches look. Keeping too few dimensions fails to capture important distinctions among objects; keeping more dimensions than needed introduces the noise of surface level variability in word choice. For information retrieval applications, the singular values decrease slowly and we have never seen a sharp elbow in the curve to suggest a likely stopping value. Luckily, there is a range of values for which retrieval performance is quite reasonable. For some test collections we have examined retrieval performance as a function of number of dimensions. Retrieval performance increases rapidly as we move from only a few factors up to a peak and then decreases slowly as the number of factors approaches the number of terms at which point we are back at word-matching performance. There is a reasonable range of values around the peak for which retrieval performance is well above word matching levels.
Size and speed of SVD. As noted above, we would like to be able to compute large analyses faster. Since the algorithm we use is iterative the time depends some on the structure of the matrix. In practice, the complexity appears to be O(4*z + 3.5*k), where z is the number of non-zeros in the matrix and k is the number of dimensions in the truncated representation. In the previous section, we described how we analyze large collections by computing the SVD of only a small random sample of items. The remaining items are "folded in" to the existing space. This is quite efficient computationally, but in doing so we eventually loose representational accuracy, especially for rapidly changing collections.
Updating the SVD. An alternative to folding in (and to recomputing the SVD) is to update the existing SVD as new documents or terms are added. We have made some progress on methods for updating the SVD (Berry et al., 1995), but there is still a good deal of work to be done in this area. This is particularly difficult when a new term or document influences the values in other rows or columns-e.g., when global term weights are computed or when lengths are normalized.
Finding near neighbors in high dimensional spaces. Responding to a query involves finding the document vectors which are nearest the query vector. We have no efficient methods for doing so and typically resort to brute force, matching the query to all documents and sorting them in decreasing order of similarity to the query. Methods like kd-trees do not work well in several hundred dimensions. Unlike the SVD which is computed once, these query processing costs are seen on every query. On the positive side, it is trivial to parallelize the matching of the query to the document vectors by putting subsets of the documents on different processors.
Other models of associative structure. We chose a dimensional model as a compromise between representational richness and computational tractability. Other models like nonlinear neural nets or overlapping clusters may better capture the underlying semantic structure (although it is not at all clear what the appropriate model is from a psychological or linguistic point of view) but were computationally intractable. Clustering time, for example, is often quadratic in the number of documents and thus prohibitively slow for large collections. Few researchers even consider overlapping clustering methods because of their computational complexity. For many information retrieval applications (especially those that involve substantial end user interaction), approximate solutions with much better time constants might be quite useful (e.g., Cutting et al., 1992).
6.0 Conclusions
Information retrieval and filtering applications involve tremendous amounts of data that are difficult to model using formal logics such as relational databases. Simple statistical approaches have been widely applied to these problems for moderate-sized databases with promising results. The statistical approaches range from parameter estimation to unsupervised analysis of structure (of the kind described in this paper) to supervised learning for filtering applications. (See also Lewis, this volume.) Methods for handling more complex models and for extending the simple models to massive data sets are needed for a wide variety of real world information access and management applications.
7.0 References
Bates, M.J. Subject access in online catalogs: A design model. Journal of the American Society for Information Science, 1986, 37(6), 357-376.
Berry, M. W. Large scale singular value computations. International Journal of Supercomputer Applications, 1992, 6, 13-49.
Berry, M. W. and Dumais, S. T. Using linear algebra for intelligent information retrieval. SIAM: Review, 1995.
Berry, M. W., Dumais, S. T. and O'Brien, G. W. The computational complexity of alternative updating approaches for an SVD-encoded indexing scheme. In Proceedings of the Seventh SIAM Conference on Parallel Processing for Scientific Computing, 1995.
Caid, W. R, Dumais, S. T. and Gallant, S. I. Learned vector space models for information retrieval. Information Processing and Management , 1995, 31(3), 419-429.
Cutting, D. R., Karger, D. R., Pederson, J. O. and Tukey, J. W. Scatter/Gather: A cluster-based approach to browsing large document collections. In Proceedings of ACM: SIGIR'92, 318-329.
Deerwester, S., Dumais, S. T., Landauer, T. K., Furnas, G. W. and Harshman, R. A. Indexing by latent semantic analysis. Journal of the Society for Information Science, 1990, 41(6), 391-407.
Dumais, S. T. Improving the retrieval of information from external sources. Behavior Research Methods, Instruments and Computers, 1991, 23(2), 229-236.
Dumais, S. T. Using LSI for information filtering: TREC-3 experiments. In: D. Harman (Ed.), Overview of the Third Text REtrieval Conference (TREC3). National Institute of Standards and Technology Special Publication 500-225, 1995, pp.219-230.
Furnas, G. W., Landauer, T. K., Gomez, L. M. and Dumais, S.T. The vocabulary problem in human-system communication. Communications of the A CM, 1987, 30(11), 964-971.
Lewis, D. Information retrieval and the statistics of large data sets , [this volume].
D. Harman (Ed.), Overview of the Third Text REtrieval Conference (TREC3). National Institute of Standards and Technology Special Publication 500-225, 1995.
Salton, G. and McGill, M.J. Introduction to Modem Information Retrieval . McGraw-Hill, 1983.
Stewart, G. W. Introduction to Matrix Computations. Academic Press, 1973
van Rijsbergen, C.J. Information retrieval. Buttersworth, London, 1979










