Analyzing Telephone Network Data
Allen A. McIntosh*
Bellcore
Abstract
As our reliance on computer networks grows, it becomes increasingly important that we understand the behavior of the traffic that they carry. Because of the speeds and sizes involved, working with traffic collected from a computer network usually means working with large datasets. In this paper, I will describe our experience with traffic collected from the Common Channel Signaling (CCS) Network. I will briefly describe the data and how they are collected and discuss similarities with and differences from other large datasets. Next, I will describe our analysis tools and outline the reasons that they have been found useful. Finally, I will discuss the challenges facing us as we strive for a better understanding of more data from faster networks. While my emphasis in this paper is on the CCS Network, it has been my experience that both the problems and the solutions generalize to data from other networks.
As our reliance on computer networks grows, it becomes increasingly important that we understand the behavior of all aspects of the traffic that they carry. One such network, used by millions of people every day, is the Common Channel Signaling (CCS) Network. The CCS Network is a packet-switched network that carries signaling information for the telephone network. It carries messages for a number of applications, including messages to start and stop calls, to determine the routing of toll free (area code 800) calls and to verify telephone credit card usage. Network failures, while rare, can affect hundreds of thousands of telephone subscribers. As a result, telephone companies are very interested in the health of their portion of the CCS Network. At Bellcore, we help network providers keep their part of the CCS Network running smoothly by testing vendor equipment and by monitoring live networks. To test equipment, we build small test networks and subject them to extreme stress and catastrophic failure, such as might be caused by a fire at a switch or a backhoe cutting a cable during a mass call-in. We usually collect all the
traffic on the test network, though selective collection may be used if a test involves subjecting the network to a heavy load. To monitor live networks, we collect all the traffic from a small subnetwork. Collecting all the data from a network provider's live network would require monitoring several thousand communication links, and is beyond the capacity of our monitoring equipment.
In North America, a protocol called Signaling System Number 7 (SS7, ANSI (1987)) governs the format of data carried by the CCS Network. 1 The major components of the CCS network are telephone switches (SSP's), database servers (SCP's), and SS7 packet switches (STP's). STP's are responsible for routing traffic, while SSP's and SCP's can only send and receive. STP's are deployed in pairs for redundancy. Each SSP and SCP is connected to at least one pair of STP's. The (digital) communications links between nodes run at a maximum speed of 56000 bits per second. When extra communications capacity is required, parallel links are used. 56000 bits per second is relatively slow, but there are many links in a CCS network, and many seconds in a day. Anyone trying to collect and analyze SS7 data from a CCS network soon must deal with large datasets.
To date, our main data-collection tool for both live and test networks has been a Network Services Test System (NSTS). The NSTS is about the size of a household washing machine. Each NSTS can monitor 16 bi-directional communication links, and store a maximum of 128 megabytes of data. This represents two to four million SS7 messages, which can be anywhere from one hour of SS7 traffic to and from a large access tandem to approximately four days of traffic to and from a small end office. We usually collect data by placing one NSTS at each STP of a pair. Thus, our datasets from Live networks are usually 256 megabytes in size. Datasets from test networks tend to be smaller, depending on the length of the test. Along with every message that it saves, the NSTS saves a header containing a millisecond timestamp, the number of the link that carried the message, and some other status information. The timestamps are synchronized with a central time source, and so are comparable between monitoring sites.
Our SS7 datasets have many of the "standard" features of the large datasets discussed in this volume. Inhomogeneity and non-stationarity in time are the rule. For example, Figure 1 shows the call arrival process on a communication link to a small switch from 22:45 Wednesday to 14:15 Sunday. There are 31,500 points in this plot, joined by line segments. Each point represents the number of calls received during a ten second interval, expressed in units of calls per second. Evidently there is a time-of-day effect, and the effect is different on the weekend. This dataset is
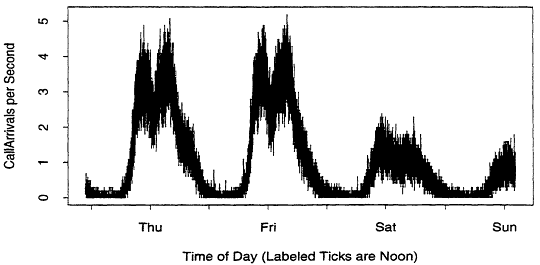
Figure 1:
Call Arrival Process
discussed in more detail in Duffy et al. (1993). They show that the call arrival process in Figure 1 is well described by a time-inhomogeneous Poisson process. The overall packet arrival process shows signs of long range dependence, and is not well modeled by a time-inhomogeneous Poisson process. Plots such as this also suggest that it is virtually impossible to find a stationary busy hour, the typical engineering period in traditional telephone networks.
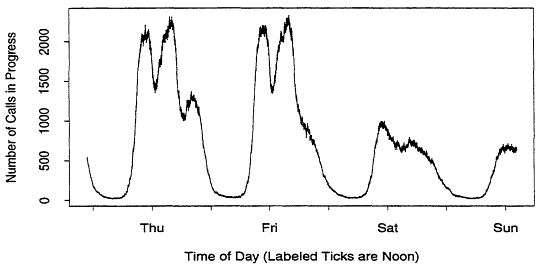
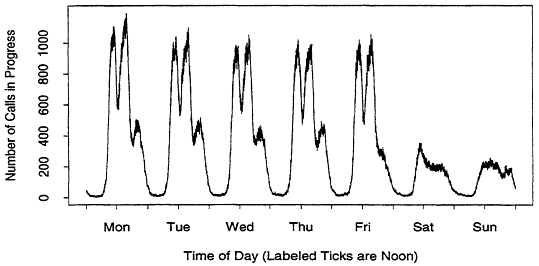
The inhomogeneity can be subtle. For example, Figure 2 illustrates the number of calls in progress for the same switch as a function of time. Since most telephone calls are short, one would expect Figures 1 and 2 to be similar. However, Figure 2 contains an extra peak on Thursday evening which is not present in Figure 1. This suggests that evening calls (from residential customers) tend to be longer than daytime calls (from business customers).2 Similar signs are visible Friday and Saturday evenings, but they are not as pronounced. Figure 3 is a plot of the number of calls in progress over a one week period, taken from a different dataset. Now we can see that Monday through Thursday evenings are similar, and the remaining evenings are very different. This abundance of features is typical of our data.
Some other features of our SS7 data make analysis more difficult. First, there are many different kinds of message, and most of them have variable length. This makes it difficult to use conventional database tools, which usually insist on fixed length records. Second, SS7 messages are binary, and several fields may be packed
into a single byte to save space. This renders them unsuitable for processing by most statistical packages and other commonly used tools (UNIX utilities such as awk and perl, in our case) which are ASCII-based. In a pilot study, we tried converting our data to an ASCII representation and processing it in this form. This resulted in a tenfold increase in the size of our data. The ASCII tools that we used for processing, being very general, were not very efficient to begin with, and the data bloat exacerbated the problem.
In the end, we decided to keep our data in the original binary file format written by NSTS. We wrote a suite of tools (described below) to process the data in this format. We still needed tools to produce ASCII output, but these were usually used in the final steps of an analysis.
In designing our data processing tools, we followed an old and well tested paradigm. Kernighan and Plauger (1976) wrote:
A surprising number of programs have one input, one output, and perform a useful transformation on data as it passes through. ... A careful selection of filters that work together can be a tool-kit for quite complicated processing.
Because our network datasets are sequential over time, it is natural to view them as sequences of messages. Our tools for analyzing binary SS7 data are thus message filters. Conceptually, they read one or more binary files one message at a time, perform some operation on each message, and write some or all of the messages out again. Some filters translate to ASCII instead of writing in binary. Our filters perform a number of functions, including
- subsetting. Huber (1996) mentions the importance of building subsets, an observation we share. Most of the subsetting operations on our SS7 data are performed by one filter program. This filter appears (usually multiple times) in any analysis I do. Its user interface is easily the most complex of any of our message filters. There are more than two dozen different fields that can be referenced. We have built a GUI (graphical user interface) to make this filter easier to use. Fortunately, the complexity of the external interface is not matched by either internal complexity or long running times.
- sampling.
- content and protocol checking. We can check for malformed SS7 messages, and can do some checking of the protocol for managing calls.
- sort/merge. The raw data files produced by NSTS need to be sorted into time order, and sorted files from multiple NSTS's need to be merged.
- call assembly. It takes several messages to set up and tear down a call. They appear at different times and may appear on different links. [The best analogy I can think of is to imagine point-of-sale data for a store where keystrokes for odd numbered keys are recorded on one tape and keystrokes for even numbered keys are recorded on another tape.] Significant processing is required to gather these together if one wants to analyze calls rather than packets.
- checking for wiring errors. We learned the hard way that this was necessary.
- drawing plots of link load in PostScript3
- counting, by message type, priority, destination, and so on.
- translating to ASCII, with varying levels of detail
It is instructive to examine how Figures 2 and 3 were produced. The data gathered by NSTS were stored on disk in time sorted order. To produce the plots, the data were run through the following filters, in sequence:
- A filter to trim off end effects that arise because the two NSTS's do not start and stop simultaneously.
- A filter to select only messages related to call setup and termination.
- A filter to organize messages into groups where each group contains the messages from a single telephone call.
- A filter to print out (in ASCII) the timestamps of the start and end of every call, along with a +1 (start) and a -1 (end).
- An ASCII sort filter, since the output of the previous step is no longer in time sorted order.
- A filter to do a cumulative sum of the result of the previous step and print out the value of the sum at a reasonable number of equally spaced times. The output from this step was handed to plotting software.
The filters in steps one through four are message filters, and the filters in steps five and six are ASCII filters.
Aside from the soundness of the underlying concept, there are a number of reasons why this approach succeeded. First, the message filters we have written are
efficient. A filter that copies every message individually takes 77 seconds elapsed time to read a 256 Megabyte file on my workstation. A standard system I/O utility takes 73 seconds for the same task. The bottleneck in both tasks is the I/O bandwidth. Most simple filters are I/O bound like this. An exploratory analysis can thus proceed by saving only a few key intermediate results (perhaps from steps requiring more extensive processing), and repeating other intermediate operations when required.
Second, we have made message filters easy to write. To build a simple filter, it is only necessary to write a C++ function that examines a message and returns a value indicating whether it is to be output or discarded. Argument processing, a ''Standard I/O" library, and a support library are provided for the more adventurous. I was both amused and disturbed that in some ways this puts us where we were over 20 years ago with the analysis of small and medium-sized datasets, namely writing one-of-a-kind programs with the help of a large subroutine library. Fortunately, programming tools have improved over the last 20 years, and the one-of-a-kind programs can be connected together.
Third, message filters are easily connected to perform complex processing tasks. This is easily done by combining filter programs, as in the example above. It is also easy to manipulate filters as objects in C++ code when considerations of convenience or efficiency dictate. Filters are implemented as C++ classes derived from a single base class. The interface inherited from the base class is small, and defaults are provided for all functionality. Support is also provided for lists of filters, and for simple Boolean operations like inversion and disjunction.
The analyses we perform on our data are intended for a wide audience whose members have different needs and very different views of the network. They include:
- Network planners, who are interested in traffic trends over months or years. The network nodes themselves provide gross traffic data. Network monitoring can provide more detail, such as traffic counts for source-destination pairs.
- Network operations personnel, who are interested in anomalies such as might be found in a set of daily source-destination pair counts. (See Duffy et al. (1993) Section 3.3)
- Traffic engineers, who are interested in building models for traffic. The intent here is to evaluate buffer management policies and other issues affected by the randomness of traffic. Data can help validate models, though there are some pitfalls, as we shall see.
- Analysts interested in anomalies in subscriber calling patterns.
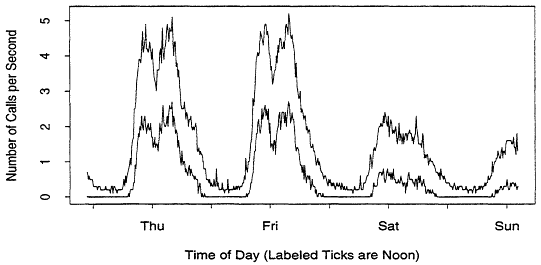
Figure 4:
Figure 1 With Data Reduction
- Testers, who are interested in protocol errors, and do not care about the data from the 99.99% of the time that the test network worked correctly.
To satisfy these needs, we must provide tools to explore both trends and exceptions in our data at differing levels of detail. Our filter building blocks allow us to design software tools to fit each application. Because the applications share a common infrastructure, the programming effort required is not large.
A 256 megabyte dataset contains the details of more telephone calls than there are pixels on my workstation screen, and nearly as many messages as there are dots on an 8.5 by 11 piece of paper at 300 dots per inch. Good visualization tools must therefore be able to avoid burying important details in a blob of ink. Even drawing the blob can be prohibitively expensive. For example, Figure I contains 31,500 line segments, and seems to take forever to draw on an X terminal running over a modem. Figure 4 plots the same data as Figure 1, but reduces it by plotting the minimum and maximum 10 second load in each 10 minute period. Peaks and valleys have been preserved, thus preserving the overall appearance of the plot, but the number of points plotted has been reduced by a factor of 30.
On the other hand, smoothing to reduce data is not a good idea, as Figure 5 illustrates. The upper and lower jagged lines are respectively the maximum and minimum 5-second loads in each one minute period. The smooth line in the middle misses the main feature of the plot completely.
To date, we have not had much opportunity for in-depth modeling of our data. The efforts described in Duffy et al. (1993) and Duffy et al. (1994) barely scratch the
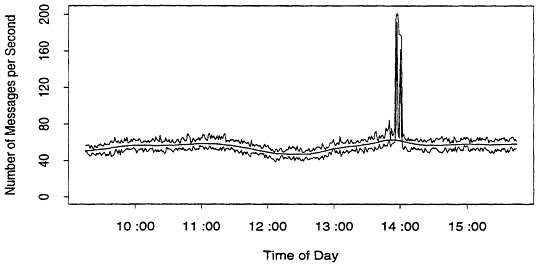
Figure 5:
The Dangers of Oversmoothing
surface. The complexity of Figure 3 suggests that building a comprehensive model is a daunting task. Traditional techniques can be inappropriate for even simple models. For example, a 256 megabyte file contains roughly six million messages. In a certain context, one can view these as Bernoulli trials with p = 0.5. Since adherence to the Bernoulli model is not perfect, a sample this size is more than sufficient to reject the hypothesis that p = 0.5 in favor of p = 0.5 + ![]() (and indeed in favor of something that is not Bernoulli at all). Unfortunately, the hypothesis tests don't answer the real question: does it matter?
(and indeed in favor of something that is not Bernoulli at all). Unfortunately, the hypothesis tests don't answer the real question: does it matter?
There are some classes of analysis, such as resampling methods, that are more practical with large datasets. An adequate model for a large dataset may be so complex that one would be better off resampling. Are there adequate tools for doing this? One potential pitfall that comes to mind immediately: a 32 bit random number generator may not provide enough bits to sample individual records.
The strategy described here has worked well for our 256 megabyte datasets. We have a proven set of tools that enable us to do flexible, efficient analyses. However, there are monsters in our future! We are testing a second generation of SS7 data collection equipment that can store roughly 55 gigabytes of data from 96 (bidirectional) communication links at a single STP site without manual intervention. This is roughly a week of data from a medium-sized Local Access and Transport Area (LATA). If someone is available to change tapes periodically, the amount of data that can be collected is unlimited.
We are still trying to come to grips with datasets of this size. Just reading 55
gigabytes of data off tape and putting it onto a disk takes two and a half days. Storing the data on disk is problematic, because my workstation doesn't allow files bigger than two gigabytes. It is likely that some sort of parallelism will be required for both storage and processing. Splitting the data across the right dimension is a difficult problem. The wrong choice can force an analysis to be serial rather than parallel, and it is not clear that the same choice cam work for all questions of interest.
A parallel effort at Bellcore has involved the collection and analysis of Ethernet traffic (Leland et al. (1994), Willinger et al. (1995), Leland et al. (1995)). Datasets here have been larger, in part because of the higher transmission speed involved, but there has been significantly less detail available because only the IP headers were saved.
We are now turning our attention to traffic on emerging networks, such as ATM and Frame Relay. These networks are used to carry data from other protocols (IP, SS7). As a consequence, we expect to encounter many of the challenges, and the opportunities, that were present in our SS7 and Ethernet datasets.
Acknowledgements
Diane Duffy, Kevin Fowler, Deborah Swayne, Walter Willinger and many others contributed to the work described here. The opinions axe mine.
References
ANSI (1987). American National Standard for Telecommunications-Signalling System Number 7. American National Standards Institute, Inc., New York. Standards T1.110-114.
Duffy, D. E., McIntosh, A. A., Rosenstein, M., and Willinger, W. (1993). Analyzing Telecommunications Traffic Data from Working Common Channel Signaling Subnetworks. In Tarter, M. E. and Lock, M. D., editors, Computing Science and Statistics: Proceedings of the 25th Symposium on the Interface, pages 156-165. Interface Foundation of North America.
Duffy, D. E., McIntosh, A. A., Rosenstein, M., and Willinger, W. (1994). Statistical Analysis of CCSN/SS7 Traffic Data from Working CCS Subnetworks. IEEE Journal on Selected Areas in Communications, 12(3):544-551.
Huber, P. J. (1996). Need to get the title of this article. In Kettenring, J. and Pregibon, D., editors, Massive Data Sets, pages 111-999.
Kernighan, B. W. and Plauger, P. L. (1976). Software Tools. Addison-Wesley, Reading, Mass.
Leland, W. E., Taqqu, M. S., Willinger, W., and Wilson, D. V. (1994). On the Self-Similar Nature of Ethernet Traffic (Extended version). IEEE/ACM Transactions on Networking, 2:1-15.
Leland, W. E., Taqqu, M. S., Willinger, W., and Wilson, D. V. (1995). Self-Similarity in High-Speed Packet Traffic: Analysis and Modeling of Ethernet Traffic Measurements. Statistical Science, 10:67-85.
Willinger, W., Taqqu, M. S., Sherman, R., and Wilson, D. V. (1995). Self-Similarity Through High-Variability: Statistical Analysis of Ethernet LAN Traffic at the Source Level. Computer Communications Review, 25:100-113. Proceedings of the ACM/SIGCOMM'95, Boston, August 1995.