Massive Data Assimilation/Fusion in Atmospheric Models and Analysis: Statistical, Physical, and Computational Challenges
Gad Levy
Oregon State University
Carlton Pu
Oregon Graduate Institute of Science and Technology
Paul D. Sampson
University of Washington
Abstract
The goals and procedures of the most data intensive operations in atmospheric sciences-data assimilation and fusion-are introduced. We explore specific problems which result due to the expansion in observing systems from conventional to satellite borne and the corresponding transition from small, medium, and large data sets to massive data sets. The satellite data, their volumes, heterogeneity, and structure are described in two specific examples. We illustrated that the atmospheric data assimilation procedure and the satellite data pose unique problems that do not exist in other applications and are not easily addressed by existing methods and tools. Existing solutions are presented and their performance with massive data sets is critically evaluated. We conclude that since the problems are interdisciplinary, a comprehensive solution must be interdisciplinary as well. We note that components of such a solution already exist in statistics, atmospheric, and computational sciences, but that in isolation they often fail to scale up to the massive data challenge. The prospects of synthesizing an interdisciplinary solution which will scale up to the massive data challenge are thus promising.
1 Introduction
The purpose of data assimilation is to combine atmospheric measurements and observations with our knowledge of atmospheric behavior in physical atmospheric models, thus producing a best estimate of the current state of the atmosphere. The similar but distinct purpose of data fusion is to extract the best information from a multitude of heterogeneous data sources, thus devising an optimal exploitation of the synergy of these data. The resulting analyses (a.k.a. 'initialization fields') have great diagnostic value, and are the basis for
model prediction. This procedure of analysis and model initialization has seen an exponential growth in the volume of observational geophysical data. The main purpose of this paper is to (1) critically evaluate how existing methods and tools scale up to the massive data challenge: and (2) explore new ideas/methods/tools appropriate for massive data sets problems in atmospheric science. Our interest and focus is in the joint exploration of the different facets of what we consider some of the weakest components of current data assimilation/fusion schemes in atmospheric and climate models as they attempt to process massive data sets. We firmly believe that since the problems are interdisciplinary, a comprehensive solution must bring together statisticians, atmospheric and computational scientists to explore general methodology towards the design of an efficient, truly open (i.e., standard interface), widely available system to answer this challenge. Recognizing that the greatest proliferation in data volume is due to satellite data, we discuss two specific problems that arise in the analysis of such data.
In a perfect assimilation scheme, the processing must allow merging of satellite and conventional data, interpolated in time and space, and for model validation, error estimation and error update. Even if the input and output data formats are compatible, and the physical model is reasonably well understood, the integration is hampered by several factors. These roadblocks include: the different assumptions made by each of the model components about the important physics and dynamics, error margins and covariance structure, uncertainty, inconsistent and missing data, different observing patterns of different sensors, and aliasing (Zeng and Levy, 1995).
The Earth Observing System and other satellites are expected to down-load massive amounts of data, and the proliferation of climate and General Circulation Models (GCM) will also make the integrated models more complex (e.g., review by Levy, 1992). Inconsistency and error limits in both the data and the modeling should be carefully studied. Since much of the data are new, methods must be developed which deal with the roadblocks just noted, and the transformation of the (mostly indirect) measured signal into a geophysical parameter.
The problems mentioned above are exacerbated by the fact that very little interdisciplinary communication between experts in the relevant complementary fields takes place. As a consequence, solutions developed in one field may not be applied to problems encountered in a different discipline, efforts are duplicated, wheels re-invented, and data are inefficiently processed. The Sequoia 2000 project (Stonebraker et al., 1993) is an example of successful collaboration between global change researchers and computer scientists working on databases. Their team includes computer scientists at UC Berkeley, atmospheric scientists at UCLA, and oceanographers at UC Santa Barbara. Data collected and processed include effects of ozone depletion on ocean organisms and Landsat Thematic Mapper data. However, much of the data management and statistical methodology in meteorology are still being developed 'in house' and are carried out by atmospheric scientists rather than in collaborative efforts. Meanwhile, many statisticians do not use available and powerful physical constraints and models and are thus faced with the formidable task of fitting to data statistical models of perhaps unmanageable dimensionality.
As a preamble, we describe in the next section the satellite data: volumes, heterogeneity, and structure, along with some special problems such data pose. We then describe some existing methods and tools in section three and critically evaluate their performance with massive data sets. We conclude with some thoughts and ideas of how methods can be
improved and developed to scale up to the massive data sets challenge.
2 The Satellite Data
In atmospheric studies, as in many other fields of science, researchers are increasingly relying upon on the availability of global data sets to support their investigations. Problems arise when the data volumes are huge and the data are imprecise or undersampled in space and time as is often the case with satellite sampling. Numerical weather prediction models have traditionally accepted observations at given time intervals (synoptic times) from a network of reporting stations, rawindsondes, island stations, buoys, weather ships, ships of opportunity, aircrafts and airports, treating the state variables in a gridded fashion. This has set the norm for the acceptable data format in these studies, dictating the need for most observations to be eventually brought to 'level 3' (gridded) form. It has also contributed to the development of the statistical and meteorological field known as objective analysis. However, volumes and sampling patterns of satellite data often lead to bottlenecks and to the failure of traditional objective analysis schemes in properly processing asynoptic satellite data to level 3 geophysical records as the examples in the next paragraphs demonstrate.
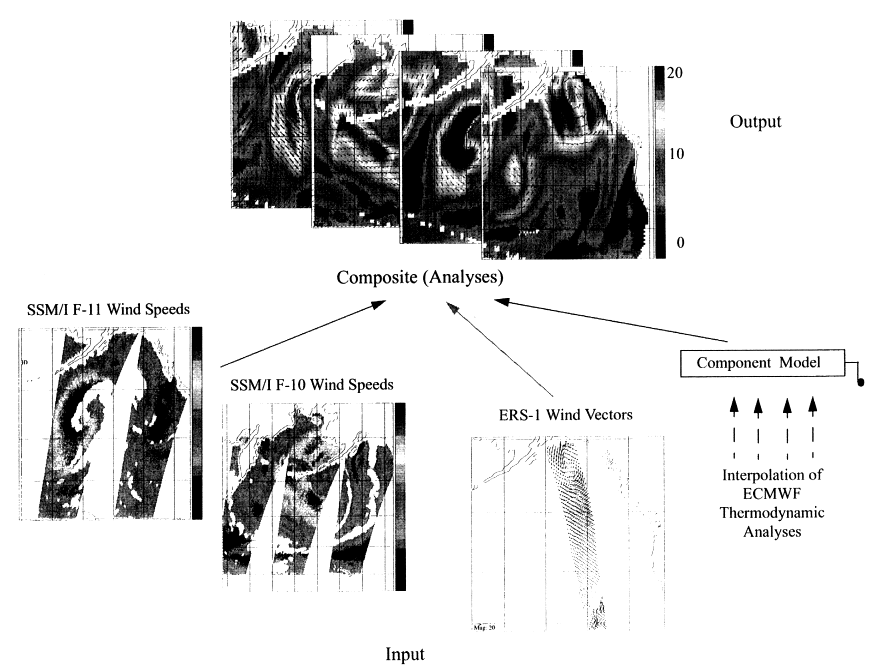
Figure 1 presents a small (storm-size) scale schematic illustration of data structure, volume, and heterogeneity. In it, data from three different satellite instruments (two wind speed products from different channels of the Special Sensor Microwave Imager (SSM/I) on the Defense Meteorological Satellite Program (DMSP) space craft, and one wind vector product from the Active Microwave Instrument (AMI) on board the first European Remote Sensing (ERS1) satellite) are combined with the European Centre for Medium-Range Weather Forecasts (ECMWF) model thermodynamic output to create composite analysis fields (upper panels). Each of the data products has been sampled at different times and locations and has already undergone some quality control and data reduction procedures. The compositing procedure of eighteen looks at a single storm such as the one illustrated in fig. 1 required the reduction of approximately 3 Gb of input data to 290 Mb in the final product. Operational weather prediction centers need to process similar products four times daily, globally, at 20 vertical levels, and with additional conventional and satellite data. The imperative of having fast algorithms and fast data flow is clear in this example.
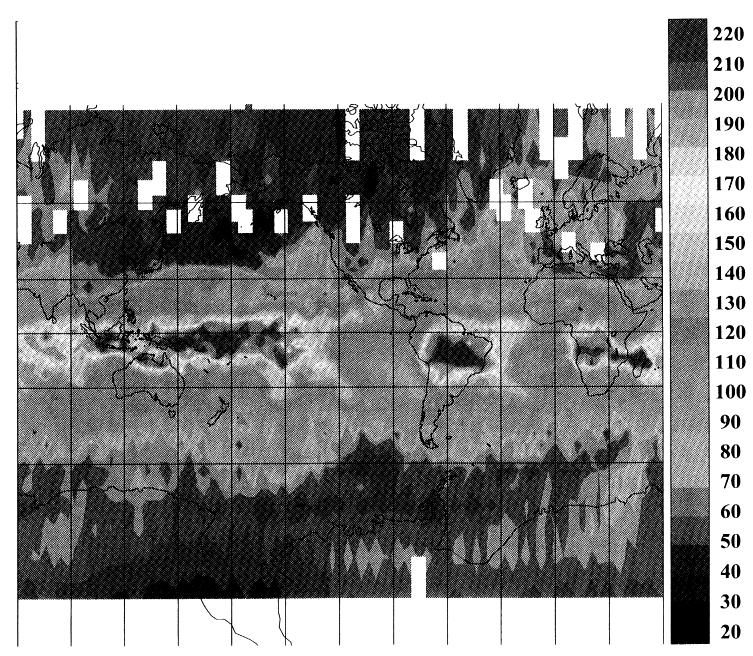
The monthly mean (climate scale level 3 product) stratospheric water vapor from the Microwave Limb Sounder (MLS) on board the Upper Atmosphere Research Satellite (UARS) for January 1992 is shown in Figure 2. Spatial structure which is related to the satellite orbital tracks is apparent in this figure. Careful inspection of the maps provided by Halpern et al. (1994) reveals similar structures in the ERS1/AMI monthly and annual mean for 1992, as well as in the Pathfinder SSM/I monthly mean wind speeds maps. The corresponding monthly means created from the ECMWF daily synoptic maps (also presented in Halpern et al., 1994) do not show this structure. These observations strongly imply that the structure is caused by the sampling rather than by an instrument error. Zeng and Levy (1995, hereafter, ZL95) designed an experiment to confirm that the structure is indeed a result of the satellite sampling. The ECMWF surface wind analyses were sampled with the ERS1 temporal-spatial sampling pattern to form a simulated data set which exhibited the same structure as in figure 2. In their experiment, the application of a bicubic spline filter to the monthly
mean simulated data resulted in a field that was usually free of the structure. However, large biases of up to 3 m s-1 remain in several areas, and there was no significant reduction in the variance added to the control set by the aliasing (spatial structure) caused by the satellite sampling in these areas. The scatter plot of the smoothed field versus the control set presented by ZL95 demonstrates that the smoothed field has less variance but is still seriously biased from the control set (0.5 m s-1 globally). Problems with spectral analysis of both the simulated and simulated-smoothed fields were also reported by ZL95.
The examples above underscore two serious problems with the analysis and assimilation of satellite data in atmospheric studies. The first example demonstrates the special need for the construction of efficient, inexpensive, maintainable, and modular software tools for application in synoptic scale atmospheric models. The second example and the analysis in ZL95, clearly show how irregular sampling and undersampling at higher frequencies by polar-orbiting satellite instruments can lead to aliasing at scales which are of interest to climate studies requiring monthly means. It was pointed out by Halpern (1988) and Ramage (1984) that an error of 0.5 m s-1 in surface wind in the tropics may lead to an uncertainty of about 12 W m-2 in surface heat flux. This amount of uncertainty was associated with a 4K increase in global sea surface temperature in model sensitivity tests reported by Randall et al. (1992).
3 Existing Methods and Tools: Prospects and Limitations
In this section we critically evaluate some disciplinary and interdisciplinary methods that we have experimented with while trying to address the specific needs described in section two. We also discuss potential improvement and available products that may make these methods scale up to massive data.
Part of the special needs demonstrated by the first example in the previous section is for efficient data storage and retrieval tools. The main goal of database researchers in the Sequoia 2000 project is to provide an efficient storage and retrieval mechanism for the scientific data being collected, characterized by massive size (100 Terabytes in four sites), complex data types as mentioned above, and sophisticated searching for scientific research. The project has been quite successful in the creation of software for the management of tertiary storage (tapes and cartridges), since the amount of data still exceeds the current economic capacity of magnetic disks.
However, the Sequoia 2000 benchmark, created as a model for testing and evaluating databases for Earth Science users, does not address the critical issues mentioned previously in this paper. Concretely, the Sequoia 2000 benchmark consists primarily of four kinds of data: raster data, point data, polygon data, and directed graph data. While these benchmarks are very useful, they do not touch data assimilation problems that are the real bottleneck in the system.
In general, the lack of attention to data assimilation has been the situation with computer vendors as well. Many vendors currently offer Hierarchical Storage Managers capable of storing and handling petabytes of data, typically using a combination of magnetic disks, optical juke boxes, and tapes/cartridges managed by robots. The system software knows
how to handle and process bits, possibly arranged in columns as in relational database management systems, but the handling of missing data and irregularly taken samples is beyond the state of art of current systems software.
More recently, new object-relational database management systems such as Illustra have created support for new access methods particularly suitable for special applications such as Earth Sciences. However, these new access methods are still concerned primarily with bit movement and comparisons. Most commercial databases and software, including Illustra, simply assume that data are consistent and clean. In fact, discussions on data assimilation are absent from almost all of Sequoia 2000 papers on data management, including Stonebraker et al. (1993). This is another manifestation of the difficulties of cross-fertilization among disciplines.
As noted above, most database management systems provide support only for precise data, though in the physical world data are often imprecise. In these cases, the scientist is left with the unpleasant decision of whether to ignore the imprecise information altogether and store some approximation to the precise value, or to forgo the use of a standard database management system and manage the data directly. The latter is the decision most commonly taken. However, with ever increasing volumes of data and with real time processing demands (e.g., first example in section 2), such a decision can no longer be afforded. In many of the situations where precise data are not available, information much more useful than ''value unknown'' or "predicate is possibly true" is available, even though imprecise. One of the most common and useful forms of information available to a scientist is the ability to bound the amount of imprecision and estimate the error associated with the data. We think that it could prove valuable if the database management system were able to represent and store values with bounded error, along with error covariance information, thus supporting the direct manipulation of imprecise data in a consistent and useful manner according to physical models. In this context, the most immediate problems we need to address are: (1) can we represent imprecise and error information, (2) can we develop a data model for imprecise information, and (3) is it feasible to manipulate imprecise data in a consistent manner? The value representation will be designed explicitly to deal with imprecise data with known error bounds. Our preliminary (disciplinary) work includes an algebra for interval relations that uses methods from interval arithmetic as operators (Barga and Pu, 1993). Algorithms designed for Epsilon Serializability (Pu and Leff, 1991) provide us with the means for bounding the amount of the imprecision introduced into the data.
In atmospheric modeling, generally a forecast is combined with data in a manner that takes account of correlation structure between the various sources of data. Certain kinds of errors or imprecision have a complicated correlation structure. Putting an interval about such numbers and propagating these intervals by interval methods do not capture common kinds of error structure that occur in meteorological observational data bases. Similarly, the often non-linear physical model operations require different methods of propagating imprecision. Although interval methods are applicable in other sciences, more sophisticated error handling must be included to be useful in atmospheric modeling. We are interested in utilizing error covariance information and testing the feasibility of building software tools that facilitate such integration. A toolkit approach is necessary to lower the cost of incorporating these error handling techniques into atmospheric models, so the model prediction produced can achieve a quality inaccessible to naive models.
It is clear from the previous section that the spatial-temporal sampling requires new methods for the interpolation and extrapolation of the gridded data in a manner that will provide accurate estimates in gap areas and times. Most applications of spatial estimation (i.e., objective analysis) have used models for the spatial-temporal covariance structure that are (1) separable in time and space—i.e., that factor into separate models for the spatial and temporal correlation structure, and (2) stationary in time and space. Some do accommodate nonstationarity in the mean, but do not accurately reflect nonstationarity (heterogeneity) in the spatial covariance structure. There is little reason to expect spatial covariance structures to be homogeneous over the spatial scales of interest in our application. In our attempts to perform analyses based primarily on scatterometer data (e.g., Levy and Brown, 1991: Levy, 1994) we have experimented with common methods of interpolation and extrapolation of the original data. Most (e.g., the B-spline interpolation and smoothing in section 2) are incapable of handling the unique satellite nonsynoptic sampling pattern even on the much larger (monthly) scale (e.g., the second example in section 2).
ZL95 have designed a three-dimensional spatial-temporal interpolator. It makes use of both the temporal and spatial sampling pattern of the satellite, substituting temporal information where spatial information is missing, and vice versa. Since there are usually non-missing values around a missing value when both the time and space dimensions are considered, a missing value at a point in space and time can be estimated as a linear (weighted) combination of the N non-missing values found within a prescribed space and time 'neighborhood'.
There are several shortcomings to the ZL interpolator which need to be addressed if it is to be generalized. Since the interpolator does not use any spatial or temporal correlation structure information the weights it employs may be sub-optimal. Establishing a systematic approach to determine the optimal weight function for specific satellite instruments or study goals would make the interpolator more robust. Unfortunately, since only simulated data were used in ZL95, there was no control set to verify the results in an absolute sense or to test whether the interpolator weights are optimal for the true field. The ECMWF field (control set) in ZL95 does not contain high frequency oscillations with temporal scale shorter than the 6-hour ECMWF analysis interval or spatial scale smaller than the grid spacing, which may appear in real satellite data. The rest of this section outlines ideas for methods that may address these shortcomings and scale up to the massive satellite data.
Sampson and Guttorp, 1992 (hereafter SG92) developed a modeling and estimation procedure for heterogeneous spatial correlation that utilizes the fact that much environmental monitoring data are taken over time at fixed monitoring sites, and thus provide a sequence of replicates from which to compute spatial covariances. Their technique uses multidimensional scaling to transform the geographic coordinates into a space where the correlation structure is isotropic and homogeneous so standard correlation estimation techniques apply. When these methods are applied to polar orbiting satellite data rather than to reporting stations one is faced again with the unique problem related to the sampling frequency: waiting for the satellite to return to the same spatial location may result in an irrelevantly long temporal lag. Additionally, with massive data and increased resolution, the dimensionality of the problem gets to be unmanageably large. Therefore the adaptation of the SG92 model to the massive satellite data sets requires different data processing and estimation procedures. We propose to start by simultaneously reducing the data into representative summaries and
modeling the space-time correlation error structure. One can then directly carry out the space-time estimation. Relying on good physical models ensures that the statistical model is now needed merely to describe an error field which is usually much smaller in magnitude than the observed or predicted field. This approach derives from an analysis and modeling of temporal autocorrelation functions and space-time cross-correlation functions bound by strong physical constraints. It incorporates statistical error information into the ZL95 idea of proper data reduction and substituting temporal information for missing spatial information, while relaxing some of the assumptions implicit in the ZL method (e.g., stationarity, isotropy).
4 Summary and Concluding Remarks
The greatest proliferation in data volumes in atmospheric studies is due to satellite data. The importance of these data for monitoring the earth atmosphere and climate cannot be underestimated. However, the unique perspective from space that polar orbiting satellites have is accompanied by massiveness of data and a unique sampling pattern which pose special problems to the traditional data assimilation and management procedures. For most applications these data need to be transformed into 'level 3' (gridded) form. We have presented two specific examples of two different processes to illustrate the problems and special needs involved in properly generating the level 3 data. Without devising proper tools for error assessment and correction, many of the level 3 global data sets may lead to serious misinterpretation of the observations which can be further propagated into atmospheric models.
We have identified some disciplinary partial solutions, along with their limitations. New object-relational database management systems offer some needed support for new access methods and for the management and storage of massive data sets, but do not handle imprecise data. Interval methods attempt to handle imprecise data but do not propagate observational error information properly. The ZL95 method properly interpolates and reduces data on some scales, but may be sub-optimal for some sensors. It is scale dependent, and does not incorporate statistical error information. The SG92 estimation technique handles heterogeneous spatial correlation for small and medium data sets, but does not scale up to massive data sets as its dimensionality increases unmanageably with increased data volume and resolution.
A comprehensive solution is possible by a synergistic combination of the partial disciplinary solutions. We have outlined an idea for a general methodology to incorporate the statistical error structure information with the physical and dynamical constraints and with proper data reduction into representative summaries. A better statistical, physical, and numerical understanding of the error structure and growth may then lead to software solutions that will properly propagate imprecision.
Acknowledgments
The authors are grateful to Suzanne Dickinson for generating the figures and commenting on the manuscript. This work was jointly supported by the Divisions of Mathematical Sciences and Atmospheric Sciences at the National Science Foundation under grant DMS-9418904.
References
[1] Barga R., and C. Pu. Accessing Imprecise Data: An Interval Approach . IEEE Data Engineering Bulletin, 16, 12-15, 1993.
[2] Halpern, D., On the accuracy of monthly mean wind speeds over the equatorial Pacific J. Atmos. Oceanic Technol., 5, 362-367, 1988.
[3] Halpern, D., O. Brown, M. Freilich, and F. Wentz, An atlas of monthly mean distributions of SSMI surface wind speed, ARGOS buoy drift. AVHRR/2 sea surface temperature. AMI surface wind components, and ECMWF surface wind components during 1992. JPL Publi, 94-4, 143 pp., 1994.
[4] Levy, G., Southern hemisphere low level wind circulation statistics from the Seasat scatterometer. Ann. Geophys., 12, 65-79, 1994.
[5] Levy, G., Trends in satellite remote sensing of the Planetary Boundary Layer, 1993. (Review chapter), in Trends in Atmospheric Sci., 1 (1992), 337-347. Research Trends Pub.
[6] Levy, G., and R. A. Brown, Southern hemisphere synoptic weather from a satellite scatterometer. Mon. Weather Rev., 119, 2803-2813, 1991.
[7] Pu C., and A. Leff, Replica control in distributed systems: An asynchronous approach. In Proceedings of the 1991 ACM SIGMOD International Conference on Management of Data, 377-386, Denver, May 1991.
[8] Ramage, C.S., Can shipboard measurements reveal secular changes in tropical air-sea heat flux? J. Clim. Appl. Meteorol., 23, 187-193, 1984.
[9] Randall, D.A., et al., Intercomparison and interpretation of surface energy fluxes in atmospheric general circulation models. J. Geophys. Res., 97, 3711-3724, 1992
[10] Sampson P.D., and P. Guttorp, Nonparametric estimation of nonstationary spatial covariance structure. Journal of the American Statistical Association 87, 108-119, 1992.
[11] Stonebraker, M., Frew, J., Gardels, K., and J. Meredith, The Sequoia 2000 Storage Benchmark, in Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, Washington, D.C., 1993.
[12] Zeng L. and G. Levy, Space and time aliasing structure in mean polar-orbiting satellite data. Journal of Geophysical Research, Atmospheres, 100, D3, pp 5133-5142, 1995.