This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.
Earthquake prediction: The interaction of public policy and science
LUCILE M.JONES
U.S. Geological Survey, Pasadena, CA 91106
ABSTRACT Earthquake prediction research has searched for both informational phenomena, those that provide information about earthquake hazards useful to the public, and causal phenomena, causally related to the physical processes governing failure on a fault, to improve our understanding of those processes. Neither informational nor causal phenomena are a subset of the other. I propose a classification of potential earthquake predictors of informational, causal, and predictive phenomena, where predictors are causal phenomena that provide more accurate assessments of the earthquake hazard than can be gotten from assuming a random distribution. Achieving higher, more accurate probabilities than a random distribution requires much more information about the precursor than just that it is causally related to the earthquake.
Research in earthquake prediction has two potentially compatible but distinctly different objectives: (i) phenomena that provide us information about the future earthquake hazard useful to those who live in earthquake-prone regions and (ii) phenomena causally related to the physical processes governing failure on a fault that will improve our understanding of those processes. Both are important and laudable goals of any research project, but they are distinct. We can call these informational phenomena and causal precursors.
It is obvious that not all causal precursors are informational. We investigate phenomena related to the earthquake process long before we have enough information to tell the public about a significant change in the earthquake hazard. In addition, however, not all informational phenomena are causal. We use the geologically and seismologically determined rates of past earthquake occurrence to assess the earthquake hazard in a socially useful way without knowing anything about the failure processes active on a fault. What, if anything, lies at the intersection of these two groups is perhaps the greatest goal of earthquake prediction (Fig. 1).
Much of the early research in earthquake prediction in the 1970s was directed toward causal earthquake precursors. The laboratory research showing dilatancy and strain softening preceding rock failure encouraged many to believe that precursors arising from these processes could be measured in the field (e.g., refs. 1 and 2). When field measurements did not live up to this expectation, research in the 1980s began to shift toward nonprecursory processes, earthquake rates, and earthquake forecasting (e.g., ref. 7). In the last few years, as the informational capacity of rate analyses has been more fully explored, interest is beginning to return to possibly causal precursors. However, our approach to the research and our communication with the public now rests on a different foundation. The public has become accustomed to earthquake probabilities and processes further information within this context.
In this new environment, I believe we must clarify the difference between informational phenomena and causal precursors and where, if anywhere, they overlap. To do so, I propose a grouping similar to the meteorological categories of climate and weather. If climate is what one expects and weather is what one gets, then earthquake climate is the hazard we expect from the known aggregate rates of earthquake occurrence, and earthquake weather would be the prediction of earthquakes from phenomena related to the failure of one particular patch of a fault. Nonprecursory informational phenomena are a type of climate, causal precursors are weather phenomena, and predictive precursors are weather phenomena that predict earthquakes with a probability greater than expected from the climate. In this paper, I will classify proposed earthquake precursors into these three categories. Causal precursors, informational phenomena, and predictive precursors should all continue to be the focus of scientific study, but only the latter two should be the basis for public policy.
Classifications
Nonprecursory information predicts the earthquakes expected from the previously recorded rates of earthquakes. Because these estimates are based on rates, they include no implied time to the mainshock. We use an arbitrary time to express the probabilities, but the probability is flat with time, except when the rate itself varies with time, as in an aftershock sequence. Nonprecursory information does not require assumptions about the earthquake failure process such as stress state (i.e., earthquakes happen when the stress goes up) or in any way relate to the failure process of any particular event.
Causal precursors, in contrast, are deterministic and in some way causally related to the occurrence of one particular earthquake. Just as in weather where a hurricane must travel to shore before the rain and winds begin, the search for precursors assumes that something must happen before the earthquake can begin. Even if the temporal relationship to the mainshock is not understood, precursors assume that a temporal relationship exists.
Predictive precursors assume a causal relationship with the mainshock and provide information about the earthquake hazard better than achievable by assuming a random distribution of earthquakes. Because these are precursors, these imply a defined time for the mainshock. To achieve predictive precursors, we must know much more about the phenomenon than simply that it exists.
We can classify phenomena related to the earthquake process into these three categories by considering the temporal distribution and the assumptions behind the analysis of that
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
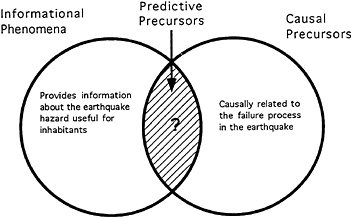
FIG. 1. Classification of earthquake-related phenomena.
phenomenon. Nonpredictive information is derived from rates and assumes a random distribution about that rate. Causal precursors assume some connection and understanding about the failure process. To be a predictive precursor, a phenomenon not only must be related to one particular earthquake sequence but also must demonstrably provide more information about the time of that sequence than achieved by assuming a random distribution.
Let us consider some examples to clarify these differences. Determining that southern California averages two earthquakes above M5 every year and, thus, that the annual probability of such an event is 80% is clearly useful, but nonprecursory, information. On the other hand, if we were to record a large, deep strain event on a fault 2 days before an earthquake on that fault we would clearly call it a causal precursor. However, it would not be a predictive precursor because recording a slip event does not guarantee an earthquake will then occur, and we do not know how much the occurrence of that slip event increases the probability of an earthquake. The only time we have clearly recorded such an event in California (3), it was not followed by an earthquake. To be able to use a strain event as a predictive precursor, we would need to complete the difficult process of determining how often strain events precede mainshocks and how often they occur without mainshocks. Merely knowing that they are causally related to an earthquake does not allow us to make a useful prediction.
Long-Term Phenomena
Long-term earthquake prediction or earthquake forecasting has extensively used earthquake rates for nonprecursory information. The most widespread application has been the use of magnitude-frequency distributions from the seismologic record to estimate the rate of earthquakes and the probability of future occurrence (4). This technique provides the standard estimate of the earthquake hazard in most regions of the United States (5). Such an analysis assumes only that the rate of earthquakes in the reporting period does not vary significantly from the long-term rate (a sufficient time being an important requirement) and does not require any assumptions about the processes leading to one particular event.
It is also possible to estimate the rate of earthquakes from geologic and geodetic information. The recurrence intervals on individual faults, derived from slip rates and estimates of probable slip per event, can be summed over many faults to estimate the earthquake rate (6–8). These analyses assume only that the slip released in earthquakes, averaged over many events, will eventually equal the total slip represented by the geologic or geodetic record. Use of a seismic rate assumes nothing about the process leading to the occurrence of a particular event.
A common extension of this approach is the use of conditional probabilities to include information about the time of the last earthquake in the probabilities (9–11). This practice assumes that the earthquake is more likely at a given time and that the distribution of event intervals can be expressed with some distribution such as a Weibull or normal distribution. This treatment implies an assumption about the physics underlying the earthquake failure process—that a critical level of some parameter such as stress or strain is necessary to trigger failure. Thus, while long-term rates are nonprecursory, conditional probabilities assume causality—a physical connection between two succeeding characteristic events on a fault.
For conditional probabilities to be predictive precursors (i.e., they provide more information than available from a random distribution), we must demonstrate that their success rate is better than that achieved from a random distribution. The slow recurrence of earthquakes precludes a definitive assessment, but what data we have do not yet support this hypothesis. The largest scale application of conditional probabilities is the earthquake hazard map prepared for world-wide plate boundaries by McCann et al. (12). Kagan and Jackson (13) have argued that the decade of earthquakes since the issuance of that map does not support the hypothesis that conditional probabilities provide more accurate information than the random distribution.
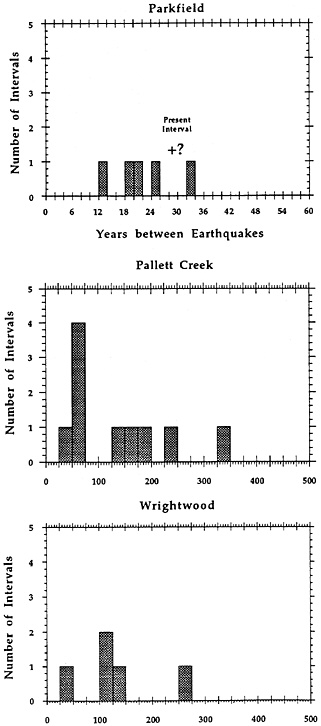
Another way to test the conditional probability approach is to look at the few places where we have enough earthquake intervals to test the periodicity hypothesis. Three sites on the San Andreas fault in California—Pallet Creek (14), Wrightwood (15), and Parkfield (16)—have relatively accurate dates for more than four events. The earthquake intervals at those sites (Fig. 2) do not support the hypothesis that one event interval is significantly more likely than any others. We must therefore conclude that a conditional probability that assumes that an earthquake is more likely at a particular time compared to the last earthquake on that fault is a deterministic approach that has not yet been shown to produce more accurate probabilities than a random distribution.
Intermediate-Term Phenomena
Research in phenomena related to earthquakes in the intermediate term (months to a few years) generally assumes a causal relationship with the mainshock. Phenomena such as changes in the pattern of seismic energy release (19), seismic quiescence (20), and changes in coda-Q (21) have all assumed a causal connection to a process thought necessary to produce the earthquake (such as accumulation of stress). These phenomena would thus all be classified as causal precursors and because of the limited number of cases, we have not yet demonstrated that any of these precursors is predictive.
Research into intermediate-term variations in rates of seismic activity falls into a gray region. Changes in the rates of earthquakes over years and decades have been shown to be statistically significant (22) but without agreement as to the cause of the changes. Some have interpreted decreases in the rate to be precursory to large earthquakes (20). Because a decreased rate would imply a decreased probability of a large earthquake on a purely Poissonian basis, this approach is clearly deterministically causal. However, rates of seismicity have also increased, and these changes have been treated in both a deterministic and Poissonian analysis.
One of the oldest deterministic analyses of earthquake rates is the seismic cycle hypothesis (23–25). This hypothesis assumes that an increase in seismicity is a precursory response to the buildup of stress needed for a major earthquake and deterministically predicts a major earthquake because of an increased rate. Such an approach is clearly causal and has not been tested for its success against a
random distribution. How to test against random distribution is also the question raised by the other approach to intermediate-term rate changes, which is to say that with an unknown cause behind the rate change, we still know that the rate has changed and the new rate should be the basis for a random assessment. This is philosophically noncausal but requires a consistent approach to the questions of when is a rate change real or fluctuation and how to approximate the real rate at any instant.
Short-Term Phenomena
Short-term earthquake prediction has been attempted through analysis of foreshocks and of nonseismic potential precursors. To assume that phenomena such as ground water changes, strain rates, and geoelectrical phenomena are related to the occurrence of earthquakes clearly requires some causality. They are usually thought to be related to an acceleration of strain premonitory to failure of the mainshock. From lack of sufficient data, they have not yet been tested for success compared to random occurrence.
The use of potential foreshocks to assess the earthquake hazard is sometimes causal and sometimes not. At first, it would appear that the use of foreshocks must be causal because we often assume we are looking at a special relationship between foreshock and mainshock. However, in practice, the use of foreshocks in making public assessments has often been based on simple rates.
Earthquakes cluster and the occurrence of one earthquake increases the rate of other earthquakes in that region as described by Omori’s Law (26). This rate decreases with time. A random distribution about this time-variant rate predicts the probability of aftershocks in the sequence (27). Although an assumption of relationship is implicit in defining a cluster in which to assess the rate, this process does not require assumptions about what is causing the earthquake to happen. This procedure has been used to make statements to the public about the possibility of damaging aftershocks in California (28).
The same equations have been used to assess the probability that an earthquake is a foreshock by allowing the magnitude of the “aftershock” to be greater than the mainshock. Using average California values for the parameters in the equations, this approach predicts a rate of foreshocks before mainshocks comparable to that actually seen in California (6%). Thus this use of foreshocks is essentially noncausal because it assesses the consequences of a rate without looking at what is the physical connection between a foreshock and its mainshock. Public statements about these rates include an arbitrary time window. A 72-hr window is often used as a practical choice to incorporate most of the hazard in the time-variant rate.
Foreshocks would be precursory to a particular event if a foreshock discriminant could be recognized. If we found some characteristic of foreshocks that differentiated them from other earthquakes, we would be looking at information about the failure process. However, no discriminant for foreshocks has yet been recognized.
One other use of foreshocks that is precursory in principle is the use of fault-specific foreshock probabilities (29, 30). In this scheme, the probability that an earthquake near a major fault may be a foreshock to the characteristic mainshock for that fault is calculated by assuming that foreshocks are part of the mainshock process and that the rates of foreshock occurrence are a function of the mainshock rates and not the background seismicity. Even though this system includes no recognizable difference between foreshocks and background seismicity, it assumes a theoretical difference. In a sense, the foreshock discriminant is the location of the earthquake near a major fault.
Whether these fault-specific foreshock probabilities are predictive precursors has still not been completely tested. Although much of the data used in determining these probabilities are available, such as rate of background seismicity, a fundamental quantity, the rate at which foreshocks precede mainshocks is not well defined. Because this quantity so strongly controls the answers, I do not feel that we can a priori assume that correct mathematics means a correct answer. We need to compare the probabilities calculated with this system with the actual occurrences of earthquakes to determine if these foreshocks are truly precursory or demonstrate convincingly that we know the rate at which foreshocks precede mainshocks. An analysis of all foreshocks recorded worldwide might provide enough information, but the data to do this have not yet been collected.
Discussion
The last few decades of research in earthquake prediction have increased our understanding of the earthquake process and led to several methods for producing useful estimates of the seismic hazard (Table 1). However, as yet we have found no phenomena that can provide us information about the timing of a particular earthquake any better than we could achieve through assuming a random distribution of events (Fig. 3).
Because the public is driven by an emotional need for earthquake prediction only partially connected to practical need, scientists have an even greater responsibility to communicate carefully their findings in earthquake prediction. By this, I do not mean keeping quiet about results. After every major earthquake, a rumor spreads that scientists know the time of another earthquake but are keeping quiet to avoid panic. Our only defense against this rumor is to make sure that it is never true. Our obligation is to communicate our results in the clearest possible way, including when possible a statistical assessment of their validity. When such is not possible, we should clearly acknowledge this and not expect these results to be the basis of public policy.
Research should be separate from public policy, and the criteria for public use of earthquake information should be independent of the criteria for scientific study. I propose that public policy should be based only on informational phenomena and, when they become available, predictive precursors. By this I mean that probabilities for public use, both short-term warnings and long-term forecasts for land-use planning, should be derived only from historical, geodetic, or geologic rates of activity and precursors that have been demonstrated to provide more accurate information than the rates alone. We cannot justify expenditures if we have not demonstrated that our assessment is better than random. This approach to public policy is independent of scientific research where we must continue the research into causal precursors both for our understanding of the physics of earthquakes and for any future hope of obtaining a predictive precursor.
At this time, no precursors have been proven to be predictive. Two different classes of models of how earthquakes occur that are currently in vogue imply quite different predictions about whether predictive precursors will ever be achievable. These two classes are failure models and triggering models. Failure models assume that a fault is pushed to failure and a critical level of some parameter is needed before failure can occur. Combined with laboratory findings of strain softening (31), these models suggest that changes in seismicity or strain could be signs of precursory deformation that leads to failure of the fault and thus that predictive precursors are an attainable goal. Triggering models (17, 32) assume a much more chaotic system, where potential triggers such as small earthquakes or strain events could occur regularly but only trigger
Table 1. Phenomena used in earthquake hazards and prediction
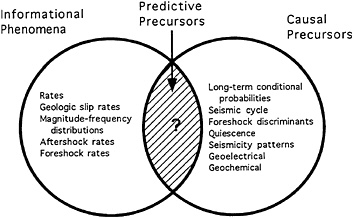
FIG. 3. The holy grail of earthquake prediction: predictive precursors.
a large earthquake some of the time, when the system is unstable. This model suggests that even though potential triggers are observed, assessing the probability of a major event will be difficult because we cannot discriminate between the potential and actual triggers.
The two models imply quite different temporal relationships of the precursor or trigger to the earthquake. A causal failure model, especially when drawing on accelerated creep as a mechanism, implies a distinct time to failure and thus a probability function for the earthquake as shown in Fig. 4A. It implies a deterministic relationship with the probability function expressing our uncertainty in our knowledge of the relationship. A triggering model would have a probability function expressing the likelihood that that event would actually be able to trigger the mainshock. Drawing on the evidence of aftershocks, we often assume that the potential for triggering decreases quickly with time as shown in Fig. 4B.
Either model requires much more data to make precursors or triggers useful to the public. The Agnew and Jones (29) analysis of foreshocks can be applied to all potential earthquake precursors and demonstrates the data needed to quantify the risk from a precursor. The probability that an earthquake that is either a foreshock (F) or a background earth-
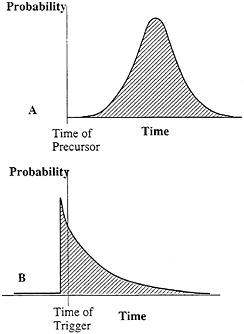
FIG. 4. The temporal distribution of probability associated with failure models of earthquake occurrence (A), and triggering models of earthquake occurrence (B).
quake (B) and we cannot tell which will be followed by a characteristic earthquake (C) is then the ratio of the number of foreshocks to the total number of events or
[1]
Assuming the rate of foreshocks is the rate at which foreshocks precede mainshocks [P(F|C)] times the mainshock rate, P(F) =P(F|C)*P(C), then
[2]
Thus, the probability of a characteristic earthquake on the fault after a potential foreshock is a function of the rate of background earthquakes [P(B)], the rate of mainshocks [P(C)], and the rate at which foreshoeks preceded mainshocks [P(F|C)]. For other precursors, the probability of an earthquake after the phenomenon has occurred depends on the long-term probability of the mainshock, the false alarm rate of the phenomenon, and the rate at which that phenomenon precedes the mainshock. Collecting the data to determine the last two quantities will require much effort beyond demonstrating a correlation with the mainshock.
Conclusions
Phenomena related to earthquake prediction can be broken into three classes: (i) phenomena that provide information about the earthquake hazard useful to the public, (ii) precursors that are causally related to the failure process of a particular earthquake, and (iii) the intersection of these two classes, predictive precursors that are causally related to a particular earthquake and provide probabilities of earthquake occurrence greater than achievable from a random distribution. In the long term, probabilities derived from geologic rates and historic catalogs are predictors, while conditional probabilities are precursors. Aftershock and foreshock probabilities derived from time-decaying rates are predictors, whereas all other investigated phenomena are precursors. At this time, no phenomenon has been shown to do better than random, and we have no predictive precursors so far. The data necessary to prove a better than random success are much greater than that needed to show a causal relationship to an earthquake.
1. Aggerwal, Y.P., Sykes, L.R., Simpson, D.W. & Richards, P.G. (1973) J. Geophys. Res. 80, 718–732.
2. Anderson, D.L. & Whitcomb, J. (1975) J. Geophys. Res. 80, 1497–1503.
3. Linde, A.T. & Johnston, M.J.S. (1994) Trans. Am. Geophys. Union 75, 446 (abstr.).
4. Allen, C.R., Amand, P.S., Richter, C.F. & Nordquist, J.M. (1965) Bull. Seismol. Soc. Am. 55, 753–797.
5. Algermissen, S.T., Perkins, D.M., Thenhaus, P.C., Hanson, S.L. & Bender, B.L. (1982) U.S. Geol. Surv. Open-File Rep. 82–1033.
6. Wesnousky, S.G., Seholz, C.H., Shimazaki, K. & Matsuda, T. (1984) Bull. Seismol. Soc. Am. 74, 687–708.
7. Wesnousky, S.G. (1986) J. Geophys. Res. 91, 12587–12632.
8. Ward, S.N. (1994) Bull. Seismol. Soc. Am. 84, 1293–1309.
9. Sykes, L.R. & Nishenko, S.P. (1984) J. Geophys. Res. 89, 5905–5928.
10. Working Group on California Earthquake Probabilities (1988) U.S. Geol. Surv. Open-File Rep. 88–398.
11. Working Group on California Earthquake Probabilities (1990) U.S. Geol. Surv. Circ. 1053.
12. McCann, W.R., Nishenko, S.P., Sykes, L.R. & Krause, J. (1979) Pure Appl. Geophys. 117, 1082–1147.
13. Kagan, Y.Y. & Jackson, D.D. (1991) J. Geophys. Res. 96, 21419–21431.
14. Sieh, K.E., Stuiver, M. & Brillinger, D. (1989) J. Geophys. Res. 94, 603–624.
15. Fumal, T.E., Pezzopane, S.K., Weldon, R.J. II & Schwartz, D.P. (1993) Science 259, 199–203.
16. Bakun, W.H. & McEvilly, T.V. (1984) J. Geophys. Res. 89, 3051–3058.
17. Heaton, T.H. (1990) Phys. Earth Planet. Inter. 64, 1–20.
18. Biasi, G. & Weldon, R., II (1996) J. Geophys. Res. 100, in press.
19. Keilis-Borok, V. I., Knopoff, L., Rotwain, I.M. & Allen, C.R. (1988) Nature (London) 335, 690–694.
20. Wyss, M. & Habermann, R.E. (1988) Pure Appl. Geophys. 126, 333–356.
21. Aki, K. (1985) Earthquake Predict. Res. 3, 219–230.
22. Reasenberg, P.A. & Matthews, M.V. (1988) Pure Appl. Geophys. 126, 373–406.
23. Fedotov, S.A. (1965) Trans. Inst. Fiz. Zemli Akad. Nauk SSSR 36, 66–93.
24. Ellsworth, W.L., Lindh, A.G., Prescott, W.H. & Herd, D.G. (1981) in Earthquake Prediction: An International Review: Maurice Ewing Series, eds. Simpson, D.W. & Richards, P.G. (Am. Geophys. Union, Washington, DC), Vol. 4, 126–140.
25. Mogi, K. (1985) Earthquake Prediction (Academic, Tokyo).
26. Utsu, T. (1961) Geophys. Mag. 30, 521–605.
27. Reasenberg, P.A. & Jones, L.M. (1989) Science 243, 1173–1176.
28. Reasenberg, P.A. & Jones, L.M. (1994) Science 265, 1251–1252.
29. Agnew, D.C. & Jones, L.M. (1991) J. Geophys. Res. 96, 11959– 11971.
30. Jones, L.M., Sieh, K.E., Agnew, D.C., Allen, C.R., Bilham, R., Ghilarducci, M., Hager, B., Hauksson, E., Hudnut, K., Jackson, D. & Sylvester, A. (1991) U.S. Geol. Surv. Open-File Rep. 91–32.
31. Dieterich, J.H. (1979) J. Geophys. Res. 84, 2169–2175.
32. Brune, J., Brown, S. & Johnson, P. (1993) Tectonophysics 218, 1–3, 59–67.





