This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.
A selective phenomenology of the seismicity of Southern California
L.KNOPOFF
Institute of Geophysics and Planetary Physics and Department of Physics, University of California, Los Angeles, CA 90024–1567
ABSTRACT Predictions of earthquakes that are based on observations of precursory seismicity cannot depend on the average properties of the seismicity, such as the Gutenberg-Richter (G-R) distribution. Instead it must depend on the fluctuations in seismicity. We summarize the observational data of the fluctuations of seismicity in space, in time, and in a coupled space-time regime over the past 60 yr in Southern California, to provide a basis for determining whether these fluctuations are correlated with the times and locations of future strong earthquakes in an appropriate time- and space-scale. The simple extrapolation of the G-R distribution must lead to an overestimate of the risk due to large earthquakes. There may be two classes of earthquakes: the small earthquakes that satisfy the G-R law and the larger and large ones. Most observations of fluctuations of seismicity are of the rate of occurrence of smaller earthquakes. Large earthquakes are observed to be preceded by significant quiescence on the faults on which they occur and by an intensification of activity at distance. It is likely that the fluctuations are due to the nature of fractures on individual faults of the network of faults. There are significant inhomogeneities on these faults, which we assume will have an important influence on the nature of self-organization of seismicity. The principal source of the inhomogeneity on the large scale is the influence of geometry—i.e., of the nonplanarity of faults and the system of faults.
The Magnitude-Frequency Law
Assume that our goal is the prediction of large earthquakes in a region as well studied as Southern California. Large earthquakes in Southern California occur so rarely that statistically based predictions of large earthquakes are not possible. We therefore try to limit the broad range of possible extrapolation scenarios that can be constructed from meager geological or geophysical observations with physics-based models. Before one can discuss efforts to model the physics of earthquakes, and especially of large earthquakes, one must appreciate the relevant phenomenology which must perforce form the targets of modeling efforts.
The extraordinary simplicity and universality of the familiar Gutenberg-Richter (G-R) power-law relation for the frequency of occurrence of earthquakes with a given energy has been a magnet for the statistical physics community, especially since power law relations also characterize the properties of magnetism, melting, etc., near critical points. The scale-independence of an empirical power law implies that the underlying physics is also to be found in scale-independent processes, and this course has been followed with much visibility and success in the model of self-organized criticality (1–8) and its application to the development of power-law relations for earthquakes.
The G-R power-law relation for earthquakes—the distribution of the number of earthquakes with seismic energy radiated greater than E,
Ncum~E−b/β[1]
where b is the usual coefficient in the magnitude-frequency relation and is a number close to 1 for any region world wide (9, 10), and β is the coefficient in the radiated energy vs. magnitude relation, which has been measured to be 1.5 (11, 12), and has been calculated to be 3/2 for all but the largest earthquakes (13).
While the arguments for self-similarity are persuasive, there are even more persuasive arguments that the power-law relation cannot be extended to the largest energies and that large earthquakes obey different statistics and, hence, are subject to a different set of physical interrelationships than are small ones. Expression 1 cannot be extended indefinitely to infinite energies; otherwise the exponent b/β≈2/3 would imply that an infinite amount of energy be available from the motion of tectonic plates for the generation of earthquakes (14). Thus, there must be a cutoff or rolloff to the distribution at its large energy end. It follows that the occurrence of large earthquakes must take place under a different set of rules than the small ones. Thus, while the system is undoubtedly self-organizing, it is not self-organizing to a critical state.
There is also a power-law seismic moment-frequency relation with a similar exponent (15, 16). In the moment-frequency form, Eq. 1 describes the distribution of the product of the integrated final slip in the earthquake over the area of the rupture surface. Although the moment is written in energy units, it should not be considered to be anything other than a measure of slip, and thus this distribution is a constraint on the slip. By an argument similar to the above, we can show that the integrated slip rate on all earthquakes in the region cannot exceed the slip rate between the tectonic plates. Thus the moment distribution, too, must have a rolloff or cutoff.
It has been expressed frequently that the G-R law provides a basis for estimating seismic risk by extrapolating the statistics of small earthquakes to estimate the probability of occurrence of large ones (see ref. 17, for example). From the argument above, an extrapolation of this type can seriously overestimate the frequency of occurrence of large earthquakes. If the real distribution has a cutoff, its extrapolation may provide a finite estimate of the probability of occurrence of very large earthquakes that may never occur.
Because the G-R power-law distribution cannot be appropriate for large earthquakes, the properties of models of
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
Abbreviations: G-R, Gutenberg-Richter; SAF, San Andreas fault.
seismicity on isolated faults that describe self-organization leading to a critical point may be irrelevant to our task. Because our concern is with the problems of large earthquakes, we try to understand why large earthquakes, and possibly others as well, fail to follow the power-law relation. We describe the phenomenological basis for developing an understanding of the physical processes that lead to the occurrence of large earthquakes.
We take as the basis for most of our discussions of phenomenology, observations of earthquakes in Southern California, which are the most extensive local data base we have, and thus the most studied of any history of instrumental seismicity. The magnitude-frequency relations for Southern California are reasonably well-established for the 60 yr of the Southern California catalog. The magnitude distribution of earthquakes in the Southern California catalog with aftershocks removed not only shows that the expected log-linearity for small magnitudes extends, most remarkably, up to the largest earthquakes (Fig. 1), excluding aftershocks. The 60-yr distribution of Fig. 1 does not show any hint of a deviation from linearity of the log-frequency vs. magnitude relation around M=6.4 that has been proposed by a number of authors (13, 18–22) to correspond to a transition between two-dimensional and one-dimensional fracture shapes in a seismogenic zone of finite thickness. Despite the reasonableness of the proposal that it is the thickness of the seismogenic zone, which is of the order of 15 km in Southern California, that provides this characteristic dimension, contrary to recent assertions (21), the sharp cutoff to the distribution near M=7.5 and the absence of a rolloff at smaller magnitudes does not support the simplistic proposal. A similar conclusion has been reached from a study of the energy-frequency distribution (23).
Excluding aftershocks, the statistics of the smallest earthquakes, which are by inspection the most numerous, is Poissonian (24); this does not imply that the less frequent stronger earthquakes are also randomly occurring events.
Large Earthquakes
Despite the presence of a cutoff to the distribution in Fig. 1 for the most recent 60 yr, we know that earthquakes with magnitudes greater than M=7.5 occur in Southern California on a longer time scale, as for example the great Fort Tejon earthquake of 1857 on the San Andreas fault (SAF) in this region. Ten prehistoric earthquakes with large slips, and hence presumably with large magnitudes, have been identified by geochronometric methods between 671±13 A.D. and 1857;
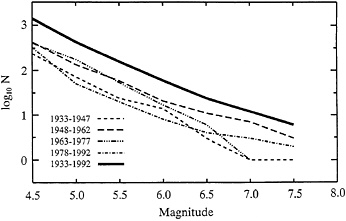
FIG. 1. Number of earthquakes in Southern California as a function of magnitude for the interval 1935–1994 in intervals of 0.5 magnitude units (upper curve). Lower curves are the subdivision into 15-yr intervals. Aftershocks have been removed from the distributions (from ref. 42).
the interval times range from roughly 50 to 330 yr, with a mean of about 135 yr (25, 26).
Because the form of the distribution of large earthquakes cannot depend on the power-law statistics of small earthquakes and appears to depend on events that have not happened within the time span of the catalog, we have no seismographic information to bear on this point. We approach the problem of the distribution of large earthquakes from a different point of view. Because the fracture length and the energy released in a large earthquake are roughly related, we assume that the distribution of fracture lengths also has a cutoff or rolloff. If it has a rolloff, then there is a finite probability that a fracture will occur whose length will extend completely across a region as large as Southern California. It has been argued that the fractures in the largest earthquakes are confined by relatively fixed barriers to the extension of growth (27) that may be associated with fault geometry. In this model, these characteristic fault segments have characteristic slips in large earthquakes. But a process of repeated slip between strong barriers must ultimately accumulate stress at the barrier edges, and the barriers in this model must ultimately break as well; under the constraint of a long-term average uniform slip rate at every point in a plate boundary, barriers cannot remain unbroken forever. Thus the stresses at the barriers must ultimately relax, either by fractures in even stronger earthquakes or by some (generalized) viscous relaxation. If the process is viscous, then the relationship between the time constants for stress relaxation and for loading the system becomes important. In most modeling exercises, the restricted view is taken that viscous stress relaxation is extremely slow and, hence, that even long-term stress relaxation can take place by brittle fracture.
If one barrier must ultimately break, does it follow that sooner or later all barriers within a given region must break in the same earthquake, if only we wait long enough? It is sufficient to apply this question to the faults that support the largest of the earthquakes, which are those that occur on the SAF. Hence our question really refers to earthquakes that have not happened in the catalog interval of the most recent 60 yr. If earthquakes on the SAF are stopped according to the same processes as the smaller earthquakes—namely, because of encounters with strong barriers with low stored prestress, then, since all points on an individual plate boundary such as the SAF must sooner or later break, sooner or later two adjacent barriers may reach a nearly threshold state at about the same time—i.e., their prestresses must be close to their strengths at the same time. If this is the case, then, on the model that a stress at the edge of a crack is scaled by the length of the crack, one barrier must surely be triggered into fracture by a rupture on an adjacent barrier and, hence, a superearthquake will be developed.
But this model is valid under the assumption that the earth is homogeneous. The barrier property of the characteristic earthquake model argues for a weaker region of the faults in the reaches between barriers and, hence, that the appropriate scaling distance for redistribution of stress is the size of the nucleation zone of these greatest earthquakes—i.e., the barrier dimension, rather than the length of the crack. Observational support for this point of view is to be found in the self-healing pulses observed in the dynamics of the rupture process described by Heaton (28). We argue in a companion paper (29) that a smaller scaling length is sufficient to prevent an earthquake from tearing through several barriers, if the barriers are widely spaced compared to the scaling distance for the size of the fluctuations in stress outside the edge of the crack and for a sufficiently large ratio between the fracture strengths of the barriers and the relatively smoother segments between them. The scaling distance is the size of the nucleation zone or it is the size of the self-healing pulse, and these two sizes may be the same (30).
Because the largest earthquakes do not fit the G-R distribution and are most likely limited in fracture length by barriers, the characteristic earthquake model is probably appropriate for their description. There is very likely a sharp cutoff to the distribution of earthquake sizes. If it were not for information derived from the spatial distributions of smaller earthquakes, we would be inclined to suppose that it would not be appropriate to describe smaller earthquakes by the characteristic earthquake model because the smaller events are dominated by the G-R distribution, and hence these events may be strongly influenced by the processes of self-organization. But to be able to draw a clearer opinion, we must describe the spatial distributions of earthquakes in Southern California.
Spatial Fluctuations
The epicenters of the earthquakes that define the G-R law for Southern California are widely distributed over the entire area (Fig. 2). If the G-R law and other features of the seismicity are properties of earthquakes in two dimensions, is it appropriate to try to simulate these features by modeling faulting in one dimension, as has been the vogue in recent years? If we are successful in simulating seismicity on a single fault, can these simulations be related to seismicity in two dimensions?
With regard to the G-R law, there is no convincing evidence that the hypocenters of small earthquakes, other than aftershocks, have a well-defined geometrical relationship to the mapped faults, or to buried faults for that matter. The seismicity on a number of mapped faults, including the SAF, is essentially nil over the 60-yr interval, an observation not inconsistent with the proposal above that the earthquakes on the faults that support large earthquakes have different statistical properties than the earthquakes on fault structures that support small ones. In the case of the SAF, there is an extraordinary absence of activity on the segment of the SAF that ruptured in the 1857 earthquake, down to magnitudes less than 3 (31). The Salton segment of the southernmost part of the SAF is also dormant (31, 32). Indeed, “no large earthquake (M≥7.0) has been documented in the historic record (since 1749) for the SAF south of Cajon Pass” (32). These observations imply, as already indicated, that efforts to synthesize a power-law distribution on a single major fault such as the SAF are inappropriate. An important feature of the seismicity in Southern California is that the major part of the SAF and other faults on which large earthquakes can occur are quiet at the
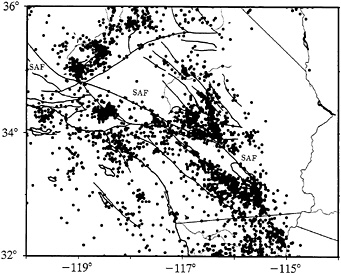
FIG. 2. Epicenters of earthquakes in Southern California with magnitudes greater than 3.5 in the inclusive interval 1935–1994. Aftershocks have not been deleted. Most of the clusters of epicenters are due to aftershocks of large earthquakes. The SAF is indicated.
present time and that very likely they will only slip in great earthquakes (33–35).
Not only are the earthquakes that define the G-R distribution widely distributed in two dimensions but also the epicenters of the largest earthquakes of the past 80 yr with magnitudes near the cutoff in the instrumental distribution at M=7.5 are also widely distributed two-dimensionally over Southern California, and all are located on faults other than the SAF. The 23 earthquakes with Mw≥6.4 since 1915 fall into two mutually exclusive categories: To the north and west of a line extending between the epicenters of the 1933 Long Beach and the 1993 Landers earthquakes, all of the focal mechanisms of the eight earthquakes are not strike-slip; while to the south and east of this line, all of the 15 earthquakes including the Long Beach and the Landers earthquakes have strike-slip focal mechanisms (36); most of the earthquakes in the southeastern region are located on the San Jacinto fault and its prolongation. The horizontal component of the slip on the nonstrike slip earthquakes in the northern part of the region is parallel to the plate motions. But since these earthquakes lie off the plate boundary, sooner or later the locked section of the SAF must also tear in a great earthquake with a component of slip parallel to the plate motions.
We have no way of knowing whether the absence of activity on the SAF, except for the largest earthquakes, is a condition that is likely to persist. The punctuation of activity on the SAF by relatively more frequent large earthquakes off the fault may be a steady process. Although it is possible that there might be a shift in style of seismicity from one that favors exclusivity of large earthquakes to one that favors a broad distribution of sizes on the SAF, some numerical simulations of seismicity on single faults with configurations of fracture thresholds that have been designed to favor the characteristic earthquake model have exhibited abrupt changes in size of earthquakes by factors that are much smaller than the range demanded by these speculations.
Large earthquakes on neighboring faults produce significant fluctuations in stress on the SAF and vice versa and influence the mode of self-organization under the conditions of stress redistribution. Simulations on a model of a single fault with spatially variable strengths, especially designed to simulate the influence on seismicity of strong barriers, lead to the strongest earthquake events that have a great regularity (37, 38). The large variability in the interearthquake times of the strongest earthquakes (26) on the SAF has, however, been modeled in a restricted sense by the study of seismicity on a pair of interacting faults; these have variations in the time intervals between large earthquakes by as much as the factor of 6 observed. While the demonstration of large variable interearthquake times through a model of a pair of interacting faults is not an adequate representation of interactive fault coupling on a model of the network of faults in Southern California, it is a genuine indication that simulations on single fault models are observed to be inadequate vehicles for the study of seismicity in a region with as complex a fault geometry as that of Southern California. Thus the modeling of fractures on the major units of the fault system must take into account coupling between the members of a two-dimensional web of faults through interactive stress transfer.
The modeling of seismicity on a network of faults as numerous as those in Southern California may not be a tractable problem, even with extraordinarily large computing resources. Although the time scale for the largest earthquakes on the SAF which is of the order of 135 years, with a variation that spans a factor of 6 [modeled with a truncated exponential distribution (29)], the time scale for the recurrence of earthquakes on the other faults of this region may be much longer. Sieh (39) has found that the last preceding earthquake on much of the fault complex that ruptured in the 1992 Landers (M=7.3) event took place 6000 to 9000 yr before the present.
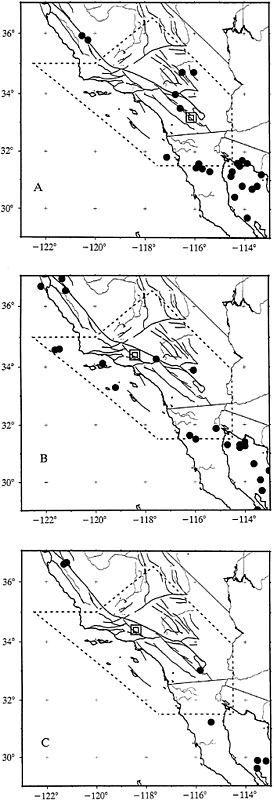
FIG. 3. (A) Epicenters of earthquakes in Southern California with magnitudes between 5.1 and 6.3 from January 1, 1965, to April 9, 1968, which is the date of the Borrego Mountain (M=6.5) earthquake; the epicenter of the (M=6.5) earthquake is indicated by the double square. (B) Same as A for the interval April 9, 1968, to February 9, 1971; the latter is the date of the San Fernando (M=6.6) earthquake. The epicenter of the San Fernando earthquake is shown by the double square. (C) Same as B for the 2 yr after the San Fernando earthquake, February 9, 1971, to February 8, 1973 (from ref. 42).
Assume the time scales for large earthquakes on faults other than the SAF are of the order of only 2000 yr. Assume, for the sake of argument, that M=7 earthquakes occur 10 times as frequently as M=8 earthquakes, using a factor taken from a convention that we have already argued against. Assume all of the M=7 earthquakes do not take place on the SAF and all of the M=8 events do take place on it. If we scale the rates of recurrence of individual earthquakes on the two classes of faults by a factor of 20, being the ratio between 2000 yr and 100 yr, we find that there are roughly 200 times as many fault segments that support M=7 earthquakes as the SAF, which supports M=8 earthquakes. We conclude that the SAF ruptures much more frequently than any other fault in the network, at least among the panoply of faults that support strong earthquakes, but that there are many such fault segments. The probability of a strong earthquake occurring on any specific fault other than the SAF is finite but small; the probability of occurrence of a strong earthquake with magnitude M=7 is significantly higher than that of an earthquake with M=8. The modeling demands are stupendous, especially in view of the fact that mapping has not yet identified most of the faults that support strong earthquakes of the Northridge or Landers types, in a network that we estimate to include as many as several hundred faults. A statistical model of rupture on a large network in two dimensions will be needed.
Small Earthquakes: “The G-R or Characteristic Earthquake Distribution, Which Is It?”
The title of this section reproduces the title of a paper by Wesnousky (40). We have proposed that the largest earthquakes are ruptures that take place on massively inhomogeneous faults. We return to the issue whether the smaller earthquakes, which fit the G-R distribution, belong to a distinct class of events from that of large ones, with an independent set of statistical rules, or whether there is a more complicated interaction. We offer the following speculations.
Consider the following extreme model. Aftershocks of individual strong earthquakes fit the Omori law in its simplest form n~t−p with p≈1. The aftershocks also fit the G-R distribution well with the usual exponent. Formally there is a small but finite probability of having an aftershock a very long time after a strong earthquake because of the infinite tail of the function. On this model, small earthquakes near New Madrid, MO, and Charleston, SC, today might be aftershocks of the earthquakes of 1811–1812 and 1886. If this is the case, the risk of strong earthquakes is small in the foreseeable future in these areas since aftershocks are windows to the past, rather than to the future. The rate of occurrence of the number of aftershocks in these regions appears to be more or less constant at the present time because of the long interval since these strong parents. Up to the present time, shocks in the vicinity of the Kern County, CA, earthquake of 1952 and the San Fernando earthquake of 1971 appear to be consistent with the Omori law, even 40+ yr after the Kern County event. In our description of the G-R distribution (Fig. 1), we have excluded aftershocks on a nominal basis through the use of a formula that looks for satellite earthquakes within a specified time and space window after a strong event in the catalog. If the Omori
and G-R laws hold for a long time after the parent, then how many earthquakes in the Southern California catalog are in reality aftershocks of strong events that took place before the start of the catalog? If the Omori law is taken literally, then are all of the earthquakes that constitute the observations of the G-R distribution today aftershocks of past strong events(?). Since aftershocks depend on the existence of a mechanism for providing for a time delay between the main, strong shock and the aftershock, any model that purports to describe seismicity in a region such as Southern California and uses the G-R law as a paradigm must include a mechanism for time delays—i.e., some nonelastic stress transfer. Under this assumption, the G-R law does not tell us anything about future seismicity since aftershocks only refer to the past history of strong shocks.
However, today there are no significant aftershocks of the 1857 earthquake on the SAF. Thus at least for SAF earthquakes, the Omori law does not have an infinite tail, and there is a temporal cutoff for aftershocks. We speculate that the map of Southern California seismicity, which is dominated by the smallest earthquakes (Fig. 2), shows that some faults can produce long-term and others only short-term aftershocks. It is likely that we should not assume that all earthquakes in Southern California can be modeled under the same set of physical rules. Thus, we conclude that the relationship between the present-day small earthquakes that define the G-R law and future large earthquakes on the major faults is ill-defined; there exists the possibility that there is no relationship between present small and future large earthquakes.
Assume that the smaller earthquakes do not take place on the same fault structures as the larger ones. Then, except in unusual circumstances, the two populations of small and large earthquakes have independent distributions; we can assume that the smaller events fit the G-R law, and the larger ones have their own distribution, whatever that may be. If large mapped faults, or faults that are large enough to be mapped, are reserved for big earthquakes, then where do the small ones take place? The process zones at the tips of cracks are regions of highly deformed and/or broken material. As a fault grows, it must certainly grow through its own process zone. Thus we expect that the entire length of all faults must be surrounded by a zone of weakened material. Under an increasing tectonic stress, this zone will slip in small earthquakes. Irregular slip in large earthquakes on the nearby fault surface could cause fluctuations in stress that could trigger aftershocks in the adjoining process zone; aftershocks can thus occur along the entire length of a large earthquake, both in the process zone nearby and in the process zone beyond the ends of the crack by the more conventional mechanism of stress intensification. Thus small earthquakes with rupture lengths that are most frequently, but not necessarily, less than the thickness of the process zone occur in an elongated three-dimensional zone astride the fault. Hence, the distribution of small earthquakes on this model is characterized by the distribution of sizes of contacts where slips might take place in a three-dimensional space and might have different focal mechanisms, as well as different spatial locations, than the larger earthquakes, consistent with our conjecture.
If small and large earthquakes have different temporal distributions, why does the projection of the distribution for small earthquakes in Southern California extend almost perfectly into the magnitude range of the largest earthquakes in the past 60 yr, only to be truncated by an abrupt cutoff (Fig. 1)? Suppose that we divide Southern California into smaller seismic zones that each includes at least one fault that supports large earthquakes. Assume each zone will have its own G-R law for small earthquakes and that the exponent is the same for each. But the cutoff (or rolloff) will depend on the properties of the dominant fault in the zone, and especially its length, and we can expect that it will be different for each region. The sum of the seismicity distributions over all zones will give the seismicity for all of Southern California; the spatially cumulative distribution will have the usual power-law relation for small earthquakes with the usual exponent; but the rolloff for the spatial sum distribution will reflect the distribution of cutoffs (or rolloffs) for the zones. Because the summation seismicity has a sharp cutoff (Fig. 1), then either the distributions for each of the zones must have the same cutoff, which seems very unlikely, or the distributions at the large magnitude ends must vary widely, with some of the zones having a rate for large earthquakes that is greater than the extrapolation of the seismicity from the simple power-law relation, and some less than it. Thus the properties of the large earthquakes differ significantly from the G-R law for small earthquakes in each zone, and hence the small and large earthquakes interact differently. On the last model, the sharp cutoff in Fig. 1 is a coincidence.
Of course, there is always the argument that the distribution in Fig. 1 is based only on two earthquakes in the magnitude range 7.25−7.75 and, hence, the uncertainties are so large that the apparent sharp cutoff is a statistical fluctuation itself. In either case, one cannot say much about the validity of extending the G-R curve out to the largest magnitudes.
Space-Time Fluctuations
We have argued that the G-R law, which describes small earthquakes, excluding aftershocks, over a 60-yr period in Southern California, cannot be used directly to predict large earthquakes. However if the distribution is temporally variable or it is not Poissonian, fluctuations in the magnitude-frequency law might give possible indications of forthcoming large earthquakes. Fluctuations are indeed found on a time scale of 15 yr, in the magnitude range of 4.8–6.2 approximately, that are significant at the 2σ level (Fig. 1). Jones has also identified that there was a significant increase in the rate of occurrence of earthquakes with M≥5 in Southern California by a factor of two over the interval 1986–1992 in comparison with the rate over the 40 yr preceding 1986 (41). On the time scale of the order of 1–10 yr, there is an increase in the rate of occurrence of earthquakes with magnitudes greater than 5.1 before all of the strongest earthquakes in California with magnitudes M≥ 6.8 (42). It is doubtful whether these fluctuations in seismicity might be useful for earthquake prediction on the above time scale, because their space scale is so large, being of the order of the size of Southern California. No detailed exploration has been made as yet to see if similar fluctuations are to be found for smaller magnitudes, at shorter distances, and over shorter time intervals before strong earthquakes with magnitudes less than 6.8.
We have listed above nonuniform properties of earthquake occurrence that includes observations that (i) the rate of occurrence of the strongest earthquakes differs from the extrapolations of the G-R law for small earthquakes, (ii) there is long-term spatial quiescence at all magnitudes on the faults that support the largest earthquakes, (iii) there are fluctuations in the interval times between the strongest earthquakes on the SAF, and (iv) there are temporal fluctuations of intermediate-magnitude seismicity. We mention briefly the phenomenology of fluctuations that are coupled in space and in time. Kanamori (43) has given an excellent review of space-time-coupled fluctuations: quiescence or reduced activity has been identified prior to 41 very strong earthquakes worldwide out of a list of 52 earthquakes, over a time scale of a few months to as much as 30 yr, and over distance scales that are usually of the order of the dimensions of the fracture of the strong earthquake. Wyss and Habermann (44) have identified 17 cases of earthquakes that preceded by seismic quiescence on time scales of the order of 1 to 6 yr and distance scales of the order of the size of the fracture length in the strong earthquake. These examples include several earthquakes in Southern California.
Of particular interest is the case history of quiescence before both the Landers and the Big Bear earthquakes (45). A 75% to 100% reduction in the seismicity of small earthquakes took place within a space of dimensions of 10–20 km adjoining or astride the faults and extending for 4.5 yr and 1.6 yr before these earthquakes.
In a small number of cases of Japanese earthquakes, a contemporaneous local reduction and a distant increase of seismicity have been noted (46). Knopoff et al. (42) have described an increase in intermediate-magnitude seismicity to distances of the order of several hundred km before all 11 documentable earthquakes with magnitudes ≥6.8 in California over a time scale of the order of 1–10 yr as noted; the increase in activity ceases abruptly after selected strong earthquakes. Although stress redistributions are expected on the scale size of the fractures, these latter observations (42) are notable in two respects: (i) The precursory episode of increase of distant earthquakes terminates abruptly, (ii) The distances spanned by the precursor earthquakes is much larger than the classical scale size of the fracture in the strong earthquakes, thereby implying a much larger range of interactions than possible from standard elastic models of fracture. An example of remote prior increase in activity and subsequent rapid extinction associated with the smaller San Fernando earthquake (M=6.6) of 1971 is shown in Fig. 3. The epicenters of earthquakes with magnitudes between 4.7 and 6.3 between 1965 and the date of the earthquake in 1972 are shown in two 3-yr stages; a remarkable decrease in the number of such earthquakes in the following two years is seen to extend over distances from the epicenter of the San Fernando earthquake, which are at least an order of magnitude larger than the size of its fracture dimensions (42). There does not appear to be any change in the level of activity before and after the Borrego Mountain earthquake (M=6.5) 3 yr earlier.
In most cases, the anomalous precursory seismicity is widespread in two dimensions, and arguments for or against intermediate-term clustering in space and time, as well as any attempt to understand the mechanism for such clustering, must depend on the construction of a model of regional faulting that consists of a two-dimensional network of faults.
Stress Fluctuations and the Fracture Process
If the self-organization of seismicity is a response to the redistribution of stress by earthquake fractures, the final stress field after a fracture represents an initial state for the next fracture on the same fault segment and in its neighborhood; the stress field depends as well on the increase of stress by the tectonic load and the changes due to subsequent fractures in the neighborhood. Thus, the conditions of the fracture in the dynamic episode of “fast time” is a strong determinant of the times and locations of future earthquake events. The details of the rupture in an individual fracture depend on a number of parameters that include the friction on the fault, the degree of spatial inhomogeneity of the fracture threshold, and the aforementioned spatial distribution of prestress. Some information that bears on these points can be inferred from observations of earthquake occurrence. We cite a part of the list.
(i) From the focal mechanisms of small earthquakes in the neighborhood, we learn that the stress field along large parts of the extent of the SAF is oriented so that the principal compressional stress is normal to the fault (47). This orientation is a rotation from the expectation for an elastic continuum in which the component of the stress field on the SAF should be a shear field parallel to the tectonic load stress. This observation implies that much of the fault has a low fracture strength or coefficient of static friction, and, hence, that the strength of much of the SAF has not been restored to a fully healed value after the most recent major rupture.
(ii) The stress drops in Southern California earthquakes are highly variable quantities, ranging by a factor of from 300 to 400, from values less than 1 bar to more than 300 bars, as determined from the ratio between the seismic energy radiated and the seismic moment Es/Mo, this ratio itself being proportional to the ratio σ/μ of the stress drop to the shear modulus, for a homogeneous earth and fracture model. On the high side, a value of about 300 bars has been reported for the Landers earthquake (48). Low values are found for small earthquakes on the San Jacinto fault (49). This quantity has been tabulated for almost 500 earthquakes worldwide (49–53), including 22 in Southern California, and for these, the ratio Es/Mo is also highly variable. Kanamori et al. (50) propose that the faults in Southern California that undergo more frequent rupture, such as the SAF and the San Jacinto fault, tend to have much lower stress drops than do the faults that support less frequent events, implying that the healing process is gradual. On this interpretation, only small amounts of stress are stored in the fault zone in the time interval between SAF and San Jacinto fault earthquakes, over the time scale of repetition, and is a result that is not inconsistent with the observation of Zoback et al. (47) (see above).
(iii) Bullard (54) suggested that the frictional heat developed in great earthquakes should be enough to melt rocks in the vicinity of major earthquake faults in some tens of millions of years (and hence that earthquakes should no longer occur on old fault structures), and hence one ought to see an elevated heat flow along the major faults of the world. Measurements of heat flow along the SAF and several other major faults of Southern California indicate that the heat flow along the faults is not greatly elevated over the regional average (55–58), suggesting that the friction during sliding is low. There are at least two explanations: either the faults have been weakened significantly by the dynamics of the rupture event itself, or they have been weak for some time both before and during the ruptures (56).
In the first case, which is the proposal that the fault is weakened due to the dynamics of the event in fast time, melting during sliding was proposed early, but this model can be rejected because it implies high friction and a high level of residual heat. Brune et al. (59) have proposed that the heat flow paradox can be explained by assuming that a dynamical mode of slip on the fault exists that involves interface separation of fault contacts that has a traveling wave property in the wake of the rupture front, thereby reducing the sliding friction. It is not known if this model can be successful if the fault has strong inhomogeneity; the nature of the propagation of interface waves of separation in the presence of inhomogeneities of stress drop has not been studied.
The second alternative asks whether an inhomogeneous distribution of strength thresholds, frictions, and stress drops along the fault can be consistent with the heat flow paradox, as well as with seismological observations. In Kanamori’s (43) asperity model, most of the deformational energy released in an earthquake is accumulated at a localized high strength node or asperity before the earthquake. The asperity is bounded by zones of very low strength; slip generated at the asperity then spreads easily through the region of low strength. In this model the average stress drop can be small because the regions of low stress drop can be large; the fracture length is large, being the sum of the lengths of the adjoining regions and the central asperity; thus the ratio of energy to moment can be low. High heat will be generated only in the zones of high stress drop, which are the asperities, and the heat flow has an average over the fault that is constrained by the friction on the low-friction patches that adjoin the site of nucleation.
Support for a model of inhomogeneous fracture is to be found in the following observations:
(iv) Heaton (28) has observed self-healing pulses of slip in large earthquakes; these are propagating patches of slip that
imply a reduction in the scale length of fracture, as indicated above; the best-documented example of self-healing patches of slip is the inversion for the slip in the Landers earthquake (60). It can be shown that self-healing slip pulses of constant duration require a critical scaling dimension for their generation. Cochard and Madariaga (30) have argued persuasively that the critical scale size is given by the dimensions of a nucleation zone, which we equate with an asperity. In this model, the pulse generated at the asperity breaks into a region of lower stress drop, wherein its velocity of growth attenuates, slip begins to diminish, and ultimately a velocity-dependent friction that is intrinsic to the healing process causes ultimate cessation of motion.
(v) The earthquakes studied by Heaton (28, 60) show significant irregularities of the slip distributions in the rupture plane, which indicate the presence of significant inhomogeneity of stress drop and/or fracture threshold in the plane. The slip at the surface in the Landers earthquake of 1992 has been studied in detail in the field (60–62) and over the entire plane by inversion of the seismic signal (60, 63, 64). Of particular interest is the presence of time delays of about 1–3 sec between termination of rupture on one strand of the fault and initiation of rupture on a neighboring strand (60, 63, 64). These time delays between rupture of successive strands of the large fracture can be accounted for by inhomogeneity of the fracture threshold or the stress drop, or both, as well as by a slip-weakening in slow time, over the time interval of the time delay, of the strength in the high-stress drop barriers.
Summary
We summarize these observations on the seismicity of Southern California as follows. Not all faults in Southern California behave in the same way statistically. For example, the SAF today supports large earthquakes only and does not support small ones. Hence an effort to apply a universal model that yields the G-R statistical law is doomed to failure.
The G-R law is valid for small earthquakes but not for large ones. The G-R law is a manifestation of seismicity over the entire area of Southern California. Thus efforts to model the power-law character through a process of self-organization on a single fault is misdirected. The power law is probably a manifestation of the distribution of little faults and/or aftershocks in two dimensions—i.e., it is a manifestation of the geometry of faulting in Southern California.
Although we do not know what the distribution for large earthquakes is, the distribution for large earthquakes on faults other than the SAF is likely to show large spatial fluctuations. Large earthquakes on the SAF occur more frequently than large earthquakes on any other major fault in Southern California; the SAF is the most rapidly slipping element of the fault network but may be slipping under conditions of low average stress drop—i.e., a small energy-to-moment ratio.
The temporal distribution of earthquakes must be dependent on the limitations of fracture size. What stops the growth of a fracture is the encounter of a growing crack with a barrier region, which is a zone of large stress drop. If the large stress drops are localized, the earthquake ruptures are confined, and the characteristic earthquake model is appropriate. Localization is possible where significant changes in the geometry of faulting are encountered, such as at sites of step-overs (echeloning) or bifurcations (fault junctions). Under the constraint of uniform average rate of moment release, strong barrier sites must themselves break or the stresses at these sites must relax. Not only is geometry on a network of faults likely to be important for the modeling enterprise, but also the geometry of individual faults is going to lead to fluctuations in strength, in rapidity of restoration of strength (suturing) after a big earthquake. These geometrical fluctuations are likely to lead to nonuniformity of slip. Temporal fluctuations in seismicity imply the importance of time-dependent stress transmission processes, such as those associated with creep. Probably the most alluring proposal for intermediate-term earthquake prediction is the idea that local quiescence of small earthquakes develops near the site of a future strong earthquake and that intermediate magnitude activity increases at distance from the future earthquake. The most likely candidate for modeling the fluctuations in stress drops and fracture thresholds is an asperity model for individual earthquakes and a barrier model that accounts for the complexity of the fault network.
This research was supported by a grant from the Southern California Earthquake Center. This paper is publication number 4621 of the Institute of Geophysics and Planetary Physics, University of California, Los Angeles, and is publication number 322 of the Southern California Earthquake Center.
1. Bak, P. & Tang, C. (1989) J. Geophys. Res. 94, 15635–15637.
2. Nakanishi, H. (1990) Phys. Rev. A 41, 7086–7089.
3. Nakanishi, H. (1991) Phys. Rev. A 43, 6613–6621.
4. Christensen, K. & Olami, Z. (1992) J. Geophys. Res. 97, 8729– 8735.
5. Christensen, K. & Olami, Z. (1992) Phys. Rev. A 46, 1829–1838.
6. Christensen, K., Olami, Z. & Bak, P. (1992) Phys. Rev. Lett. 68, 2417–2420.
7. Olami, Z., Feder, H.J.S. & Christensen, K. (1992) Phys. Rev. Lett. 68, 1244–1247.
8. Olami, Z. & Christensen, K. (1992) Phys. Rev. A 46, 1720–1723.
9. Gutenberg, B. & Richter, C.F. (1944) Bull. Seismol Soc. Am. 34, 185–188.
10. Gutenberg, B. & Richter, C.F. (1954) Seismicity of the Earth (Princeton Univ. Press, Princeton, NJ).
11. Gutenberg, B. & Richter, C.F. (1956) Ann. Geofis. 9, 1–15.
12. Gutenberg, B. (1956) Q.J.Geol. Soc. London 112, 1–14.
13. Kanamori, H. & Anderson, D.L. (1975) Bull. Seismol. Soc. Am. 65, 1073–1095.
14. Knopoff, L. & Kagan, Y. (1977) J. Geophys. Res. 82, 5647–5657.
15. Kanamori, H. (1977) J. Geophys. Res. 82, 2981–2987.
16. Hanks, T.C. & Kanamori, H. (1979) J. Geophys. Res. 84, 2348– 2350.
17. Turcotte, D.L. (1990) Global Planet. Change 3, 301–308.
18. Rundle, J.B. (1989) J. Geophys. Res. 94, 12337–12342.
19. Romanowicz, B. (1992) Geophys. Res. Lett. 19, 481–484.
20. Romanowicz, B. & Rundle, J.B. (1993) Bull. Seismol. Soc. Am. 83, 1294–1297.
21. Pacheco, J.F., Scholz, C.H. & Sykes, L.R. (1992) Nature (London) 355, 71–73.
22. Okal, R. & Romanowicz, B.A. (1994) Phys. Earth Planet. Inter. 87, 55–76.
23. Sornette, D., Knopoff, L., Kagan, Y. & Vanneste, C. (1996) J. Geophys. Res., in press.
24. Gardner, J.K. & Knopoff, L. (1974) Bull. Seismol. Soc. Am. 64, 1363–1367.
25. Sieh, K.E. (1978) J. Geophys. Res. 83, 3907–3939.
26. Sieh, K., Stuiver, M. & Brillinger, D. (1989) J. Geophys. Res. 94, 603–623.
27. Schwartz, D.P. & Coppersmith, K.J. (1984) J. Geophys. Res. 89, 5681–5698.
28. Heaton, T.H. (1990) Phys. Earth Planet. Inter. 64, 1–20.
29. Knopoff, L. (1996) Proc. Natl. Acad. Sci. USA 93, 3830–3837.
30. Cochard, A. & Madariaga, R. (1994) Pure Appl Geophys. 142, 419–445.
31. Sieh, K.E. & Williams, P.L. (1990) J. Geophys. Res. 95, 6629– 6645.
32. Jones, L.M. (1988) J. Geophys. Res. 93, 8869–8891.
33. Raleigh, C.B., Sieh, K.E., Sykes, L.R. & Anderson, D.L. (1982) Science 217, 1097–1104.
34. Lindh, A.G. (1983) U.S. Geol. Survey Open File Rep. 83–63.
35. Sykes, L.R. & Nishenko, S.P. (1984) J. Geophys. Res. 89, 5905–5927.
36. Press, F. & Allen, C.R. (1995) J. Geophys. Res. 100, 6421–6430.
37. Knopoff, L. (1993) Proc. Am. Philos. Soc. 137, 339–349.
38. Knopoff, L. & Ni, X.X. (1995) in Impact, Waves and Fracture, eds. Batra, R.C., Mal, A.K. & MacSiphigh, G.P. (Am. Soc. Mech. Eng., New York), pp. 175–187.
39. Sieh, K. (1996) Proc. Natl. Acad. Sci. USA 93, 3764–3776.
40. Wesnousky, S.G. (1994) Bull. Seismol. Soc. Am. 84, 1960–1970.
41. Jones, L.M. (1994) Bull. Seismol. Soc. Am. 84, 892–899.
42. Knopoff, L., Levshina, T., Keilis-Borok, V.I. & Mattoni, C. (1995) J. Geophys. Res. 101, 5779–5796.
43. Kanamori, H. (1981) Earthquake Prediction: An International Review, eds. Simpson, D.W. & Richards, P.G. (Am. Geophys. Union, Washington, DC), pp. 1–19.
44. Wyss, M. & Habermann, R. (1988) Pure Appl. Geophys. 126, 319–332.
45. Wiemer, S. & Wyss, M. (1994) Bull. Seismol. Soc. Am. 84, 900–916.
46. Mogi, K. (1969) Bull. Earthquake Res. Inst., Tokyo Univ. 47, 395–417.
47. Zoback, M.D., Zoback, M.L., Mount, V., Eaton, J., Healy, J., et al. (1987) Science 238, 1105–1111.
48. Kanamori, H., Thio, H.-K., Dreger, D., Hauksson, E. & Heaton, T. (1992) Geophys. Res. Lett. 19, 2267–2270.
49. Kanamori, H., Mori, J., Hauksson, E., Heaton, T.H. & Hutton, L.K. (1993) Bull. Seismol. Soc. Am. 83, 330–346.
50. Vassiliou, M.S. & Kanamori, H. (1982) Bull. Seismol. Soc. Am. 72, 371–388.
51. Kikuchi, M. & Fukao, Y. (1988) Bull. Seismol. Soc. Am. 78, 1707–1724.
52. Houston, H. (1992) Geophys. Res. Lett. 17, 1413–1417.
53. Choy, G.L. & Boatwright, J.L. (1995) J. Geophys. Res. 100, 18205–18228.
54. Bullard, E.C. (1954) in The Earth as a Planet, ed. Kuiper, G.P. (Univ. of Chicago Press, Chicago, IL), pp. 57–137.
55. Henyey, T.L. & Wasserburg, G.J. (1971) J. Geophys. Res. 76, 7924–7946.
56. Lachenbruch, A.H. & Sass, J.H. (1980) J. Geophys. Res. 97, 6185–6222.
57. Lachenbruch, A.H. & Sass, J.H. (1988) Geophys. Res. Lett. 15, 981–984.
58. Lachenbruch, A.H. & Sass, J.H. (1992) J. Geophys. Res. 97, 4995–5015.
59. Brune, J.N., Brown, S. & Johnson, P.A. (1993) Tectonophysics 218, 59–67.
60. Wald, D.J. & Heaton, T.H. (1994) Bull. Seismol. Soc. Am. 84, 668–691.
61. Sieh, K., Jones, L., Hauksson, E., Hudnut, K., Eberhart-Phillips, D., Heaton, T., Hough, S., Hutton, K., Kanamori, H., Lilje, A., Lindval, S., McGill, S.F., Mori, J., Rubin, C., Spotila, J.A., Stock, J., Thio, H., Treiman, J., Wernicke, B. & Zachariasen, J. (1993) Science 260, 171–176.
62. Spotila, J.A. & Sieh, K. (1995) J. Geophys. Res. 100, 543–559.
63. Campillo, M. & Archuleta, R.J. (1993) Geophys. Res. Lett. 20, 647–650.
64. Cohee, B.P. & Beroza, G.C. (1994) Bull Seismol. Soc. Am. 84, 692–712.








