This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.
Implications of fault constitutive properties for earthquake prediction
JAMES H.DIETERICHAND BRIAN KILGORE
United States Geological Survey, Menlo Park, CA 94025
ABSTRACT The rate- and state-dependent constitutive formulation for fault slip characterizes an exceptional variety of materials over a wide range of sliding conditions. This formulation provides a unified representation of diverse sliding phenomena including slip weakening over a characteristic sliding distance Dc, apparent fracture energy at a rupture front, time-dependent healing after rapid slip, and various other transient and slip rate effects. Laboratory observations and theoretical models both indicate that earthquake nucleation is accompanied by long intervals of accelerating slip. Strains from the nucleation process on buried faults generally could not be detected if laboratory values of Dcapply to faults in nature. However, scaling of Dcis presently an open question and the possibility exists that measurable premonitory creep may precede some earthquakes. Earthquake activity is modeled as a sequence of earthquake nucleation events. In this model, earthquake clustering arises from sensitivity of nucleation times to the stress changes induced by prior earthquakes. The model gives the characteristic Omori aftershock decay law and assigns physical interpretation to aftershock parameters. The seismicity formulation predicts large changes of earthquake probabilities result from stress changes. Two mechanisms for foreshocks are proposed that describe observed frequency of occurrence of foreshock-mainshock pairs by time and magnitude. With the first mechanism, foreshocks represent a manifestation of earthquake clustering in which the stress change at the time of the foreshock increases the probability of earthquakes at all magnitudes including the eventual main shock. With the second model, accelerating fault slip on the mainshock nucleation zone triggers foreshocks.
The occurrence of earthquake faulting indicates catastrophic loss of fault strength during an earthquake and the repetition of earthquakes requires constitutive mechanisms for restoration of strength after each earthquake. A variety of constitutive formulations for fault slip have been used for investigation of earthquake processes. Some models just prescribe an idealized constitutive law to accomplish the gross characteristic of repeated fault instability and healing while others are based, to various degrees, on detailed experimental observations of fault properties and are capable of representing additional slip phenomena.
This paper first reviews the experimental evidence for, and characteristics of, the rate- and state-dependent constitutive formulation for fault slip. This formulation provides a generalized representation of fault friction that unifies observations of diverse sliding phenomena and the rather disparate features of most simplified constitutive representations. Some implications of these constitutive properties, relevant to earthquake prediction, are then examined. These include characteristics of the earthquake nucleation process, possibility of detecting precursors related to nucleation, changes of earthquake probabilities after changes of stress state such as those caused by a prior earthquake, and models of foreshock occurrence.
Rate- and State-Dependent Friction
Constitutive laws with slip-rate and state dependence represent a variety sliding phenomena observed in an exceptionally diverse range of natural and synthetic materials (1–7). Fig. 1 illustrates the response of several materials to imposed steps of sliding speed that we have examined (7). The top curve gives the predicted response from the rate- and state-dependent constitutive formulation. In each material, a step change of sliding speed, under conditions of constant normal stress, results in immediate jumps in frictional resistance followed by displacement-dependent decay and stabilization at a new steady-state sliding friction. In rocks, this frictional behavior has been documented for bare surfaces and simulated fault surfaces separated by a layer of gouge under the range of conditions accessible in laboratory experiments. This includes wet and dry conditions, the range of temperatures and pressures characteristic of crustal earthquakes, and sliding rates from mm/year to mm/s (1–9).
Several similar, essentially equivalent, formulations of rate-and state-dependent fault strength have been employed. The Ruina (3) approximation of the Dieterich (1) formulation for sliding resistance is in general use and may be written as
[1]
where τ and σ are shear and effective normal stress, respectively; μ0, A, and B are experimentally determined constants; ![]() is sliding speed; θ is a state variable; and
is sliding speed; θ is a state variable; and ![]() * and θ* are normalizing constants. μ0 is the nominal coefficient of friction that has values near 0.6. For silicates at room temperature, A and B generally have values of 0.005 to 0.015. To bound the sliding resistance as
* and θ* are normalizing constants. μ0 is the nominal coefficient of friction that has values near 0.6. For silicates at room temperature, A and B generally have values of 0.005 to 0.015. To bound the sliding resistance as ![]() or θ approach zero, constants are often summed with the logarithmic terms of Eq. 1. The state variable θ has the dimensions of time and is interpreted to be the age of the load supporting contacts across the fault surface. State evolves with time, displacement, and normal stress
or θ approach zero, constants are often summed with the logarithmic terms of Eq. 1. The state variable θ has the dimensions of time and is interpreted to be the age of the load supporting contacts across the fault surface. State evolves with time, displacement, and normal stress
[2]
where Dc is a characteristic sliding distance for evolution of state and a is a constant (6). Laboratory measurements of Dc vary from 2 to 100 μm and Dc is found to increase with with surface roughness, gouge particle size, and gouge thickness (1–10). Values of α fall in the range 0.25−0.50 for bare surfaces of Westerly granite (7). Alternative evolution laws are also in use (3). Each has the property that θ evolves over the char-
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
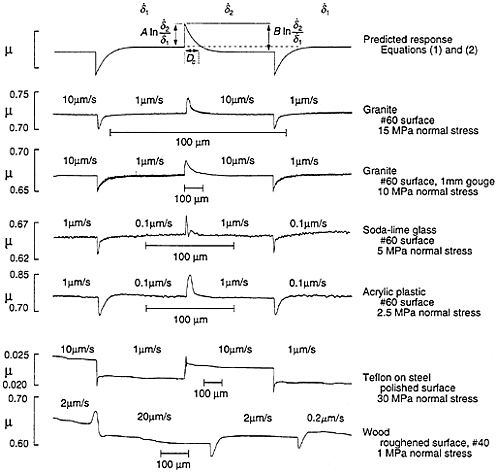
FIG. 1. Effect of velocity steps on coefficient of friction μ in various materials, from Dieterich and Kilgore (7). The top curve gives the response predicted by the rate- and state-dependent constitutive formulation.
acteristic slip, Dc and seeks the steady-state value ![]() Under conditions of stationary contact, Eq. 2 has the property that θ increases with the time of stationary contact. This results in strengthening of surfaces by the logarithm of time, which is also observed in experiments (1, 7, 11). At constant normal stress, θ increases whenever
Under conditions of stationary contact, Eq. 2 has the property that θ increases with the time of stationary contact. This results in strengthening of surfaces by the logarithm of time, which is also observed in experiments (1, 7, 11). At constant normal stress, θ increases whenever ![]() , which provides for the recovery of frictional strength after unstable slip events.
, which provides for the recovery of frictional strength after unstable slip events.
It is beyond the scope of this brief review to discuss the physical mechanisms that give rise to the rate- and state-dependent behavior. Observations of micromechanical processes for bare surfaces are described by Dieterich and Kilgore (7). Controlling mechanisms for gouge layers are somewhat more problematic (10, 12).
Relationship to Other Constitutive Characterizations
A variety of other fault constitutive formulations have been employed in analyses of earthquake processes. These include velocity-weakening laws, displacement weakening at the onset of slip, apparent fracture energy at a rupture front, and the rudimental concept of a static and sliding friction. Each of these representations can be described as an approximate limiting-case characterization of the rate- and state-dependent formulation.
The dependence of steady-state fault strength on sliding speed is obtained from Eq. 1 by taking dθ/dt=0 in evolution law (2). Under conditions of constant normal stress, the steady-state condition is ![]() , which gives from Eq. 1,
, which gives from Eq. 1,
[3]
where the definition ![]() has been used. If the transient evolution effects observed when sliding speed changes (Fig. 1) are ignored, Eq. 3 represents a constitutive law for decreasing strength with increasing slip speed (velocity weakening) provided B>A (Fig. 2A).
has been used. If the transient evolution effects observed when sliding speed changes (Fig. 1) are ignored, Eq. 3 represents a constitutive law for decreasing strength with increasing slip speed (velocity weakening) provided B>A (Fig. 2A).
Fig. 2b illustrates the sliding resistance as a function of slip displacement of a fault that was previously stationary and then is constrained to slip at a constant sliding speed. Because slip speed is constant, only the evolution of the state variable governs the displacement-weakening behavior. From Eq. 2, the evolution of state at constant slip speed is
[4]
where θ0 is state at ![]() , and σ and
, and σ and ![]() are held constant. Substitution of Eq. 4 for θ in Eq. 1 yields displacement weakening from the peak strength τp to the steady-state strength τss (Fig. 2b). The change of resistance from τp to τss is governed by the evolution of state from θ0 to the steady-state value
are held constant. Substitution of Eq. 4 for θ in Eq. 1 yields displacement weakening from the peak strength τp to the steady-state strength τss (Fig. 2b). The change of resistance from τp to τss is governed by the evolution of state from θ0 to the steady-state value ![]() ,
,
[5]
which gives from Eq. 3
[6]
Slip weakening comparable to that of Fig. 2b has been documented at the front of dynamically propagating slip instabilities where the slip speed is approximately constant (13, 14). The apparent fracture energy at a rupture front is defined
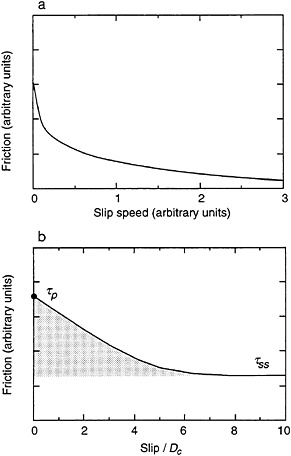
FIG. 2. Limiting case responses of the rate- and state-dependent constitutive formulation, (a) Effect of sliding speed on steady-state friction. The minimum slip speed is 0.001. (b) Displacement weakening from peak friction at the onset of slip to steady-state friction at constant slip speed. The shaded area gives the apparent fracture energy for the onset of slip.
by the shaded area in Fig. 2b. Finally, if all rate and evolution effects are ignored, τp and τss define simple static and sliding friction parameters sometimes used in modeling of earthquake processes.
Each of these alternate characterizations has some appeal because their use often permits simplified analytical methods to be employed and experimental evidence can be cited in support of their use. However, none of the simpler forms is able to represent the full range of phenomena represented by the rate- and state-dependent formulation and observed in laboratory experiments. We emphasize that unconstrained sliding histories will violate the particular conditions required for the experimental observation of the isolated properties illustrated in Fig. 2. Therefore, use of these more idealized constitutive formulations can yield theoretical solutions for sliding behaviors that are fundamentally different from the actual phenomena.
Unstable Fault Slip
The rate- and state-dependent constitutive formulation has been employed in modeling of various fault slip phenomena including stable creep, earthquake slip, and earthquake afterslip (15–18). Characteristics of sliding instabilities in systems consisting of a single slider connected to a loading point through a spring of stiffness K have been extensively analyzed and applied to analysis of laboratory fault experiments (1–6, 19–21). For an instability to occur, those studies establish that the system stiffness must be less than the critical value
[7]
where ξ depends on loading conditions and constitutive parameters. For stiffnesses K<Kc, unstable slip (stick-slip) will ensue, K>Kc results in stable slip, and at K=Kc the system is neutrally stable. If shear and normal stresses are coupled through a spring inclined at an angle to the sliding surface
[8]
where μss=τss/σ and ϕ is the angle between the spring and the sliding surface [taken as positive if an increase of shear stress results in an decrease of normal stress (21)]. Eq. 8 applies to instabilities that arise from perturbations of steady-state slip. When ϕ=0, normal stress remains constant during slip. If ϕ<−cot−1μss, slider lock-up or instability will occur independent of specific constitutive properties.
Conditions for sliding instabilities on a fault patch embedded in an elastic medium are obtained by combining the spring and slider results with elasticity solutions for displacement along a crack (22). This yields
[9]
where Lc is the minimum patch half-length for unstable fault slip, G is the shear modulus (Poisson’s ratio taken to be 0.25), and η is a factor with values near 1 that depends upon the geometry of the slip patch and assumptions relating to slip or stress conditions on the patch. Lc defines a lower bound for the dimensions of the earthquake source.
The relationship for Lc has been verified by laboratory experiments that employ a biaxial apparatus that accommodates samples with simulated faults 2 m long. See Okubo and Dieterich (13), for description of the apparatus. Fig. 3 illustrates an example of a confined slip event in which the region of slip is approximately equal to Lc. For the conditions of the experiments (σ=5 MPa), measured constitutive parameters (ξ=0.4B=0.004, Dc=2 μm), and assumed model parameters (G=15,000 MPa, η=0.67), Lc is estimated to be 75 cm. The observed region of slip for the event shown in Fig. 3 is 60–90 cm long. We have observed numerous confined slip events by using this apparatus. In all cases, the length of the zone of unstable slip is never less than the predicted Lc, within the uncertainty of the observations and model parameters. The unstable slip event shown in Fig. 3 also illustrates an interval of stable slip prior to the instability, which is characteristic of unstable fault slip in the laboratory. This topic is taken up in the following section.
Earthquake Nucleation
The process leading to the localized initiation of unstable earthquake fault slip is sometimes referred to as earthquake nucleation (22–24). This subject is relevant to earthquake prediction because the nucleation process may be accompanied by detectable precursors and because nucleation determines the time and place of origin of earthquakes. Also, it is shown below that the sensitivity of the nucleation times to stress changes may result in significant changes of earthquake probabilities after relatively small stress perturbations, such as occur in the vicinity of prior earthquakes.
Numerical models of nucleation on faults with rate- and state-dependent properties indicate that the initiation of unstable slip is preceded by a long interval of accelerating slip that spontaneously localizes to a subsection of the fault where stresses, relative to τss, are highest (24). Fig. 4 illustrates
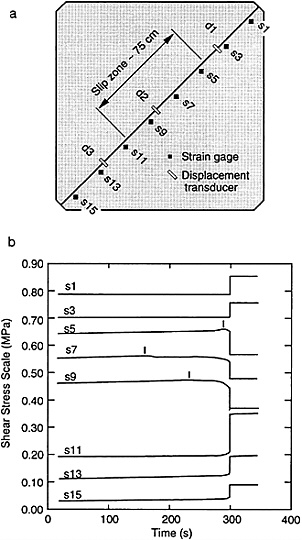
FIG. 3. Confined unstable slip in a large scale biaxial experiment. (a) Diagram of sample and location of transducers, (b) Strain gage records as a function of time and position. An unstable slip event occurs within the central section of the fault and results in a stress drop at gages s5, s7, and s9. The short vertical lines indicate the approximate onset of premonitory slip.
features of the nucleation processes for a fault model with heterogeneous initial stress. Nucleation is characterized by development of a zone accelerating slip of length Lc as given by Eq. 9 with ξ≈0.4B. In simulations where slip is forced to begin over a region L>Lc, the region of most active slip contracts to Lc as the time of instability approaches.
The acceleration of slip speed as a function of time for a fault patch of fixed length L>Lc and τ>τss is found to be
[10]
[11]
where
[12]
K is the effective stiffness of the patch, and τ is the externally applied rate of shear stress increase (24). ![]() is the slip speed
is the slip speed
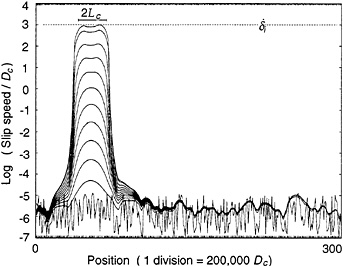
FIG. 4. Numerical model of accelerating slip leading to instability on a fault with 300 fault elements and randomized initial shear stress from Dieterich (24) showing slip speeds at successive times in the calculation. The interval between time steps decreases as slip speed increases. Every 50th step is shown. ![]() is the assumed slip speed at initiation of unstable slip. Lc is the characteristic length from Eq. 9.
is the assumed slip speed at initiation of unstable slip. Lc is the characteristic length from Eq. 9.
at time t=0 and is fixed by τ and θ. Slip speeds for the case ![]() approach the asymptote formed by the
approach the asymptote formed by the ![]() case as the slip speeds become large compared to the stressing rate. Once the shear stress on the nucleation zone exceeds the steady-state friction, τss, external stressing of the fault is no longer needed to drive the acceleration of slip to instability (i.e., the nucleation process is self-driven). The time to reach instability from the initial speed
case as the slip speeds become large compared to the stressing rate. Once the shear stress on the nucleation zone exceeds the steady-state friction, τss, external stressing of the fault is no longer needed to drive the acceleration of slip to instability (i.e., the nucleation process is self-driven). The time to reach instability from the initial speed ![]() is obtained directly from Eq. 10 and 11 by solving for t when
is obtained directly from Eq. 10 and 11 by solving for t when ![]() is set to an assumed speed at the initiation of seismic slip.
is set to an assumed speed at the initiation of seismic slip.
The solutions for the time to instability are plotted in Fig. 5 and compared with laboratory observations of premonitory slip. We obtained the observations by using the previously described large-scale biaxial apparatus. Measurement of premonitory slip at ![]() was accomplished by slowly loading the fault until premonitory creep was detected. Then the hydraulic supply used to increase stress was closed off (in
was accomplished by slowly loading the fault until premonitory creep was detected. Then the hydraulic supply used to increase stress was closed off (in ![]() the absence of fault slip) and continuing self-driven accelerating slip was observed that culminated in a slip instability. These data are preliminary but appear to show good agreement with the model predictions. Additional experiments are under way to obtain data at lower stressing rates and longer intervals of premonitory creep.
the absence of fault slip) and continuing self-driven accelerating slip was observed that culminated in a slip instability. These data are preliminary but appear to show good agreement with the model predictions. Additional experiments are under way to obtain data at lower stressing rates and longer intervals of premonitory creep.
When applied to faults in nature, tectonic stressing rates and values of θ appropriate to earthquake recurrence intervals give, from Eqs. 10 and 11, an interval of accelerating slip prior to earthquakes on the order of a year or more. We hasten to point out, however, that for most of this time, the slip speeds would be extremely small and most likely could not be detected for buried fault sources. However, near the end of the nucleation process the higher slip speeds may become detectable if the dimensions of the nucleation zone Lc is sufficiently large. Hence, the scaling of the nucleation process (size of zone and amount of premonitory displacements) bears directly on the question of the detectability of the precursory slip. Assuming a circular zone of accelerating slip with radius Lc, the moment of premonitory creep in the interval t1 to t2 may be derived from the nucleation solution of Eq. 11, giving
[13]
where t1 and t2 are the times remaining to instability (t1>t2) and ∆δ is the slip in the time interval. This result assumes ξ=
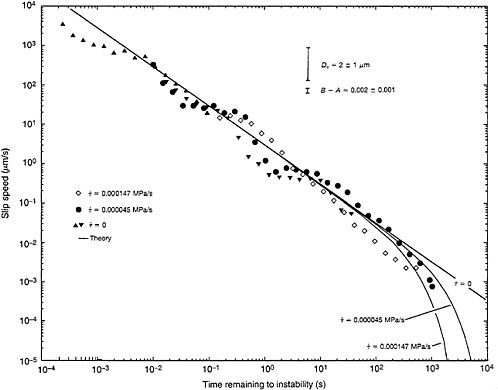
FIG. 5. Comparison of theory and laboratory observations of the time remaining to instability and speed of premonitory slip. Experimental data were obtained at the indicated stressing rates using the large biaxial apparatus employed for the experiment of Fig. 3. The curves give the solutions of Eqs. 10 and 11 at the stressing conditions of the experiments. The error bars indicate the sensitivity of the solutions to the uncertainties in constitutive the parameters Dc and (B−A).
0.4B and ![]() and corrects a typographical error in the relationship given in ref. 24. Note the scaling by
and corrects a typographical error in the relationship given in ref. 24. Note the scaling by ![]() . Generally, strains from the nucleation process on buried faults could not be detected if laboratory values of Dc apply to faults in nature. For example, using Dc=10−4 m, which is the upper limit of the of the laboratory observations, with G=20,000 MPa, A =0.006, B=0.01, σ=50 MPa, and η=1, the expected radius of the nucleation zone is 10 m and the moment of premonitory slip is only 2×103 Nm for the interval t1=10,000 s before instability to t2=10 s.
. Generally, strains from the nucleation process on buried faults could not be detected if laboratory values of Dc apply to faults in nature. For example, using Dc=10−4 m, which is the upper limit of the of the laboratory observations, with G=20,000 MPa, A =0.006, B=0.01, σ=50 MPa, and η=1, the expected radius of the nucleation zone is 10 m and the moment of premonitory slip is only 2×103 Nm for the interval t1=10,000 s before instability to t2=10 s.
However, the scaling of Dc to faults in nature remains an open question. In the laboratory, Dc increases with surface roughness and gouge particle size, and possibly gouge thickness. Compared to natural faults, laboratory experiments employ exceptionally smooth faults with thin zones of fine gouge. It appears somewhat plausible, therefore, that portions of natural faults may have much greater values of Dc, which could be sufficient to result in detectable premonitory slip for some earthquakes. The existence of very small earthquakes with source dimensions of 10 m or less (25) argues for very small nucleation sources for those events that would be extremely difficult to detect. Hence, it is also plausible that all earthquakes originate from small nucleation zones that would generally escape detection.
Some independent evidence pertaining to scaling of the nucleation process is provided by high-resolution near-source observations of earthquakes that indicate that strong ground motions of earthquakes are frequently preceded by an emergent interval of weak seismic radiation (26, 27). This interval has been designated as a seismic nucleation phase and it appears to be localized to a small region of a fault. In one interpretation of Ellsworth and Beroza (27), the seismic nucleation phase is proposed to represent the transition from accelerating quasi-static fault slip to fully dynamic rupture propagation. In addition they find that the source dimensions, displacements, and duration of the seismic nucleation process appear to scale by the moment of the earthquake. If the seismic nucleation phase represents the transition from stable accelerating slip to dynamic rupture propagation, the dimensions of the quasi-static nucleation process may also scale by the moment of the eventual earthquake.
Effect of Stress Changes on Seismic Activity
It is evident from laboratory observations and the rate- and state-dependent formulation that small changes of shear stress or normal stress will result in large changes in slip speed. Because the time to nucleate an earthquake depends on slip speed (Eqs. 10 and 11 and Fig. 5), earthquake rates and probabilities may be very sensitive to stress changes. This effect can be evaluated by treating seismicity as a population of nucleation events in which the distribution of initial conditions (slip speeds) over the population of nucleation sources and stressing history control the timing of earthquakes (28). This approach yields
[14]
where rate R is the rate of earthquake production for some magnitude interval, r is a constant steady-state background rate at the reference shear stressing rate  , and γ is a state variable that depends on the stressing history. Evolution of γ is given by
, and γ is a state variable that depends on the stressing history. Evolution of γ is given by
[15]
where σ is the effective normal stress. For positive shear stressing rates with ![]() , Eq. 15 has the property that γ seeks the steady-state value,
, Eq. 15 has the property that γ seeks the steady-state value, ![]() , with the characteristic relaxation time of
, with the characteristic relaxation time of ![]() .
.
A step change of stress followed by constant stressing at rate ![]() gives
gives
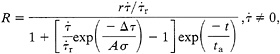
[16]
where ∆τ is the stress step, t=0 at the time of the step, and ta is the characteristic relaxation time ![]() . At times t<ta, this solution has the form of Omori’s aftershock decay law. At t> ta, earthquake rates return to a constant background. It is proposed (28) that aftershocks and other forms of earthquake clustering that obey an Omori aftershock decay law arise from stress perturbations of previous earthquakes that change the subsequent rate of earthquake activity as given by Eq. 16. This model assigns physical interpretation to the Omori aftershock parameters and earthquake data appear to support a model prediction that aftershock duration ta is proportional to mainshock recurrence time. Additionally, observed spatial and temporal clustering of earthquake pairs can be quantitatively described by this model and arise as a consequence of the spatial dependence of stress changes caused by the first event of the pair.
. At times t<ta, this solution has the form of Omori’s aftershock decay law. At t> ta, earthquake rates return to a constant background. It is proposed (28) that aftershocks and other forms of earthquake clustering that obey an Omori aftershock decay law arise from stress perturbations of previous earthquakes that change the subsequent rate of earthquake activity as given by Eq. 16. This model assigns physical interpretation to the Omori aftershock parameters and earthquake data appear to support a model prediction that aftershock duration ta is proportional to mainshock recurrence time. Additionally, observed spatial and temporal clustering of earthquake pairs can be quantitatively described by this model and arise as a consequence of the spatial dependence of stress changes caused by the first event of the pair.
Because of the proposed sensitivity of earthquake rates to stress changes, there will be a corresponding sensitivity in the probability of earthquakes to stress history. To illustrate this, we assume a Poisson model of earthquake occurrence (nonuniform in time) for probability of one or more earthquakes of magnitude ≥M in the time interval t
[17]
By using the rate Eq. 14, this gives
[18]
Assuming the frequency distribution of earthquake magnitudes remains constant, the effect of stress changes on earthquake probability at different magnitude thresholds may be expressed through the background earthquake rate r≥M by using the familiar Gutenberg-Richter frequency distribution of earthquake magnitudes
[19]
where ∆t is the time interval used to define the background rate. Fig. 6 shows an examples of the predicted effect of stress changes on the probability of earthquake occurrence. This result indicates that large changes in earthquake probabilities can arise from the stress changes that commonly occur in the earth’s crust.
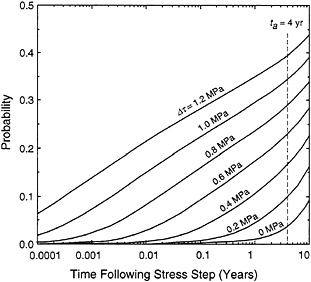
FIG. 6. Effect of stress change on earthquake probability over cumulative time after the stress step. Parameters employed for calculation of this example are based on representative values obtained from modeling of aftershocks by Dieterich (28) (A=0.01, σ=10 MPa, ta=4 years, and ![]() MPa/year). The background earthquake rate is 0.01 events per year before the stress change.
MPa/year). The background earthquake rate is 0.01 events per year before the stress change.
Foreshocks
Faults with rate- and state-dependent properties appear capable of generating foreshocks by two mechanisms, designated here as model 1 and model 2. Model 1 assumes mainshocks are, in essence, aftershocks to prior earthquakes that are smaller than the aftershock. The process is described by the aftershock Eq. 16 combined with the stress change around the foreshock source. With this model, aftershocks are presumed to obey the Gutenberg-Richter frequency distribution of earthquake magnitudes. Hence, there is a finite chance, determined by the frequency distribution of earthquake magnitudes, that any aftershock will exceed the magnitude of the mainshock. Because aftershocks rates decay with time, the likelihood of a new mainshock also decays after every earthquake.
Model 2 assumes foreshocks are driven by the strain changes of the mainshock nucleation process. In particular, the accelerating slip of the mainshock nucleation, Eq. 10, perturbs the stressing rate at a foreshock nucleation source as given by
[20]
where ![]() , σ is assumed constant, the factor C depends position and distance relative to the fault patch that is nucleating the mainshock, and t is the time remaining to the mainshock. In areas of positive C, this accelerating stressing rate results in increasing probability of foreshocks as the time of the mainshock approaches. For this model to operate, the stress change caused by the mainshock nucleation must be large compared to the tectonic stressing rate
, σ is assumed constant, the factor C depends position and distance relative to the fault patch that is nucleating the mainshock, and t is the time remaining to the mainshock. In areas of positive C, this accelerating stressing rate results in increasing probability of foreshocks as the time of the mainshock approaches. For this model to operate, the stress change caused by the mainshock nucleation must be large compared to the tectonic stressing rate ![]() at the sites of the foreshocks. This implies the dimensions of the mainshock nucleation zone are much greater than the foreshock nucleation sources so that (i) mainshock nucleation is able to drive the foreshock nucleation and (ii) the region of stress perturbation is of sufficient size to yield an appropriate probability of triggering a foreshock.
at the sites of the foreshocks. This implies the dimensions of the mainshock nucleation zone are much greater than the foreshock nucleation sources so that (i) mainshock nucleation is able to drive the foreshock nucleation and (ii) the region of stress perturbation is of sufficient size to yield an appropriate probability of triggering a foreshock.
Fig. 7 compares predictions of the two models with the data of Jones (29) for foreshock-mainshock pairs as a function of the time interval between each foreshock-mainshock pair. To implement model 1, the spatial distribution of the stress change caused by slip in an earthquake (the potential foreshock) is substituted for ∆τ in Eq. 16, and the net change of earthquake
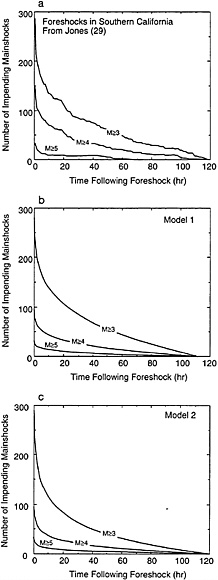
FIG. 7. Number of main shocks yet to occur and elapsed time from the foreshock for foreshock-mainshock pairs in southern California. (a) Data of Jones (29). Data set consisted of 4811 earthquakes M≥3 with 287 foreshock-main shock pairs, (b) Results for foreshock model 1. (c) Results for foreshock model 2.
rates, integrated around the source, are obtained by using the approach of Dieterich (28). A circular source with stress drop ∆τe is assumed. Parameters needed to compute the expected rate of foreshock-mainshock pairs include the background rate r at the magnitude threshold employed for compilation of the foreshock data; the b slope for the frequency distributions of earthquake magnitudes, which is used to obtain expected rates at higher magnitudes; the normalized earthquake stress drop (∆τe/Aσ), which scales the magnitude of the spatially dependent stress changes around the potential foreshock source; and the characteristic time ta appearing in Eq. 16. The computation assumes the stressing rate before each possible foreshock equals the stress rate after the event (i.e., ![]() ). The results for model 1 are shown in Fig. 7b and employ rM≥3=93.4/year, which is the observed rate of all events M≥3 in the catalog used by Jones (29). The stress drop term was fixed at (∆τe/Aσ) =40, based on the observed relation between aftershock duration and mainshock recurrence intervals in California (28). Values of b and
). The results for model 1 are shown in Fig. 7b and employ rM≥3=93.4/year, which is the observed rate of all events M≥3 in the catalog used by Jones (29). The stress drop term was fixed at (∆τe/Aσ) =40, based on the observed relation between aftershock duration and mainshock recurrence intervals in California (28). Values of b and ![]() were adjusted to scale the solution to the data. This yielded a characteristic time of ta= 5.2 years, which is consistent with the aftershock durations of 1–10 years previously obtained for California earthquakes (28). The b slope of −0.5 is significantly less than b=0.75 reported by Jones (29).
were adjusted to scale the solution to the data. This yielded a characteristic time of ta= 5.2 years, which is consistent with the aftershock durations of 1–10 years previously obtained for California earthquakes (28). The b slope of −0.5 is significantly less than b=0.75 reported by Jones (29).
The calculation for model 2 (Fig. 7c) is based on tracking the evolution of γ for the stressing history prescribed by the premonitory creep Eq. 20. From the time series for γ, the change of the rate of activity was then obtained from Eq. 14. Because of uncertainties relating to scaling of the nucleation zone sizes by magnitudes of foreshocks and mainshocks, no attempt was made to define the spatial and dependence of factor C, which appears in Eq. 20. Instead, a constant value of C=9300 was obtained by scaling the model results to the observations. Somewhat arbitrarily, H was assigned a value of 10. Other parameters in model 2 were identical to those used for model 1.
Discussion
The rate- and state-dependent constitutive formulation encompasses characteristics of rather disparate simplified constitutive formulations and it describes laboratory observations of fault healing and history dependence that are not represented in other formulations. Several features of the earthquake nucleation process arising as a consequence of this constitutive formulation may be relevant to earthquake prediction. These include scaling relations for the amount of premonitory slip during earthquake nucleation, its duration, and the dimensions of the nucleation zone; sensitivity of the nucleation process to stress perturbations that may lead to large probability changes for earthquake occurrence; and physical models of foreshocks.
The long-term quasi-static nucleation process inferred from this constitutive model is very different from predictions obtained from the other, more idealized, constitutive formulations. Faults with displacement-independent slip rate weakening and faults with a simple peak strength and sliding friction do not have a quasi-static nucleation phase or minimum dimension for initiation of unstable slip. Earthquake nucleation for faults assumed to have displacement weakening but velocity-independent constitutive properties (30) consists of an unstable increase in the size of the slipping region once a critical length has been reached. In contrast the rate- and state-dependent model for a sliding instability can occur under conditions of constant stiffness (i.e., instability on a patch of fixed size). In the laboratory instability shown in Fig. 3, notice the region of premonitory slip coincides with the region of instability, indicating that slip instability can occur without a lengthening of the slip region. This type of instability is incompatible with the displacement-weakening model of earthquake nucleation. An important characteristic of nucleation on faults with rate- and state-dependent properties is the long interval of self-driven accelerating slip and its sensitivity to stress perturbations.
The properties that establish the basis for the rate- and state-dependent formulation have been widely investigated in the laboratory. Because strain rates and time scales of earthquake processes are largely beyond the range of laboratory investigations, the results presented here remain somewhat
speculative. However, agreement of the rate- and state-dependent model for seismic activity with observations of aftershocks and earthquake clustering (28) lends support to the use of the formulation over the time-scale aftershock phenomena (months to years). This includes apparent confirmation of a predicted independence of aftershock duration ta on earthquake magnitude and an inverse dependence of ta on stressing rate. Alternative mechanisms for aftershocks and clustering, based on viscoelastic stress transfer or diffusion processes that alter fault stress, lead to characteristic aftershock times that are insensitive to stressing rates but depend on a characteristic length of the mainshock disturbance.
Both foreshock models provide comparable fits to the data. Model 1 is more specific than model 2, and the parameters used for the model 1 computation appear consistent with other results. The value (∆τe/Aσ)=40 is based on the aftershock analysis of Dieterich (28). Assuming a typical laboratory value of A=0.001 and earthquake stress drop ∆τe=4 MPa, this gives σ=10 MPa. In turn, these values and ![]() years give a stressing rate
years give a stressing rate ![]() MPa/year. Model 2 is nonspecific and demonstrates only that the shape of the predicted temporal decay of foreshock-mainshock pairs is consistent with the data. The large value of the stress coupling parameter, C=9300, indicates strong coupling between slip during mainshock nucleation and stresses at regions of foreshock nucleation. This suggests the model 2 mechanism can work only if foreshocks nucleate at the edges of the mainshock nucleation zone or perhaps as small patches embedded within the slipping region for mainshock nucleation.
MPa/year. Model 2 is nonspecific and demonstrates only that the shape of the predicted temporal decay of foreshock-mainshock pairs is consistent with the data. The large value of the stress coupling parameter, C=9300, indicates strong coupling between slip during mainshock nucleation and stresses at regions of foreshock nucleation. This suggests the model 2 mechanism can work only if foreshocks nucleate at the edges of the mainshock nucleation zone or perhaps as small patches embedded within the slipping region for mainshock nucleation.
1. Dieterich, J.H. (1979) J. Geophys. Res. 84, 2161–2168.
2. Dieterich, J.H. (1981) Mechanical Behavior of Crustal Rocks, Geophysical Monograph 24, eds. Carter, N.L., Friedman, M., Logan, J.M. & Stearns, D.W. (Am. Geophys. Union, Washington, DC), pp. 103–120.
3. Ruina, A.L. (1983) J. Geophys. Res. 88, 10359–10370.
4. Weeks, J.D. & Tullis, T.E. (1985) J. Geophys. Res. 90, 7821–7826.
5. Tullis, T.E. & Weeks, J.D. (1986) Pure Appl. Geophys. 124, 383–414.
6. Linker, M.F. & Dieterich, J.H. (1992) J. Geophys. Res. 97, 4923–4940.
7. Dieterich, J.H. & Kilgore, B.D. (1994) PureAppl. Geophys. 143, 283–302.
8. Blanpied, M.L., Lockner, D.A. & Byerlee, J.D. (1991) Geophys. Res. Lett. 18, 609–612.
9. Kilgore, B.D., Blanpied, M.L. & Dieterich, J.H. (1993) Geophys. Res. Lett. 20, 903–906.
10. Marone, C. & Kilgore, B. (1993) Nature (London) 362, 618–621.
11. Beeler, N.M., Tullis, T.E. & Weeks, J.D. (1994) Geophys. Res. Lett. 21, 1987–1990.
12. Sammis, C.G. & Biegel, R.L. (1989) Pure & Appl. Geophys. 131, 253–271.
13. Okubo, P.G. & Dieterich, J.H. (1984) J. Geophys. Res. 89, 5817–5827.
14. Ohnaka, M., Kuwahara, Y., Yamamoto, K. & Hirasawa, T. (1986) Earthquake Source Mechanics, Vol. 6, Geophysical Monograph 37, eds. Das, S., Boatwright, J. & Scholz, C.H. (Am. Geophys. Union, Washington, DC), pp. 13–24.
15. Tse, S.T. & Rice, J.R. (1986) J. Geophys. Res. 91, 9452–9472.
16. Stuart, W.D. (1988) Pure Appl. Geophys. 126, 619–641.
17. Marone, C.C., Scholz, C.H. & Bilham, R. (1991) J. Geophys. Res. 91, 8441–8452.
18. Rice, J.R. (1993) J. Geophys. Res. 98, 9885–9907.
19. Rice, J.R. & Ruina, A.L. (1983) J. Appl Mech. 50, 343–349.
20. Gu, Y. & Wong, T.-F. (1991) J. Geophys. Res. 96, 21677–21691.
21. Dieterich, J.H. & Linker, M.F. (1992) Geophys. Res. Lett. 19, 1691–1694.
22. Dieterich, J.H. (1986) Earthquake Source Mechanics, Vol. 6, Geophysical Monograph 37, eds. Das, S., Boatwright, J. & Scholz, C.H. (Am. Geophys. Union, Washington, DC), pp. 37–47.
23. Ohnaka, Y. (1992) Tectonophysics 211, 149–178.
24. Dieterich, J.H. (1992) Tectonophysics 211, 115–134.
25. Abercrombie, R. & Leary, P. (1993) Geophys. Res. Lett. 20, 1511–1514.
26. Iio, Y. (1992) Geophys. Res. Lett. 19, 477–480.
27. Ellsworth, W.L. & Beroza, G.C. (1995) Nature (London) 268, 851–855.
28. Dieterich, J.H. (1994) J. Geophys. Res. 99, 2601–2618.
29. Jones, L.M. (1985) Bull. Seismol. Soc. Am. 75, 1669–1679.
30. Shibazaki, B. & Matsu’ura, M. (1992) Geophys. Res. Lett. 19, 1189–1192.








