(NAS Colloquium) Earthquake Prediction: The Scientific Challenge (1996)

This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.

MITIYASU OHNAKA

Earthquake Research Institute, University of Tokyo, Bunkyo-ku, Tokyo 113, Japan

ABSTRACT Based on the recent high-resolution laboratory experiments on propagating shear rupture, the constitutive law that governs shear rupture processes is discussed in view of the physical principles and constraints, and a specific constitutive law is proposed for shear rupture. It is demonstrated that nonuniform distributions of the constitutive law parameters on the fault are necessary for creating the nucleation process, which consists of two phases: (i) a stable, quasistatic phase, and (ii) the subsequent accelerating phase. Physical models of the breakdown zone and the nucleation zone are presented for shear rupture in the brittle regime. The constitutive law for shear rupture explicitly includes a scaling parameter D_cthat enables one to give a common interpretation to both small scale rupture in the laboratory and large scale rupture as earthquake source in the Earth. Both the breakdown zone size X_cand the nucleation zone size L are prescribed and scaled by D_c, which in turn is prescribed by a characteristic length λ_crepresenting geometrical irregularities of the fault. The models presented here make it possible to understand the earthquake generation process from nucleation to unstable, dynamic rupture propagation in terms of physics. Since the nucleation process itself is an immediate earthquake precursor, deep understanding of the nucleation process in terms of physics is crucial for the short-term (or immediate) earthquake prediction.

The mechanical instability that gives rise to a dynamically propagating shear rupture is caused by frictional slip failure on a preexisting fault or shear fracture of intact materials. As will be discussed later, frictional slip instability and shear fracture instability of intact rock are the two extreme cases of shear rupture. Therefore, if there is a constitutive law that governs the shear rupture, both frictional slip failure and shear fracture of intact materials should be treated unifyingly and quantitatively in terms of the single constitutive law. The shear rupture can proceed stably and quasistatically at a slow speed even in the brittle regime or, alternatively, propagate unstably and dynamically at a fast speed close to sonic velocities. These two extreme phases are part of the rupture process, so that both phases should also be treated unifyingly and quantitatively by the single constitutive law. These must be kept in mind when we discuss what type and form are the most appropriate and physically reasonable for the constitutive law of earthquake shear rupture.

The stability or instability of the rupture process once the rupture has occurred is governed by how progressively the local strength in the breakdown zone behind the rupture front degrades with ongoing local slip displacement. The transient response of the shear traction to the local slip displacement in the breakdown zone is a key to the quantitative analysis of the stability or instability of the rupture. The breakdown zone is defined as the zone behind the tip of a propagating rupture over which the shear strength degrades with ongoing slip to a residual friction stress level. Careful and well prepared, high-resolution laboratory experiments (1–3) have made it possible to reveal the transient response of the shear stress to the local slip displacement in the breakdown zone, and a specific form of the constitutive law for shear rupture can be determined from these experimental observations so as to meet the physical principles and constraints established.

We first wish to discuss what type and form are the most appropriate and physically reasonable as the constitutive law for shear rupture and to present a specific constitutive law for shear rupture and a model of the breakdown zone based on a series of our high-resolution laboratory experiments on local breakdown near the propagating front during shear rupture along a fault of weak junction in a large rock sample (1–3). We then present a model of earthquake rupture nucleation, which is also based on intrinsic properties of the local breakdown during shear rupture nucleation revealed in the recent high-resolution laboratory experiments. The shear rupture nucleation is defined here as the transition process (or zone) where shear rupture grows with a slow speed from the point where the shear rupture nucleus is formed to the critical point beyond which the rupture front propagates at a speed close to sonic velocities. Data obtained from the high-resolution laboratory experiments enable one to discuss how unstable, dynamic shear rupture is nucleated in the brittle regime and its mechanical conditions in terms of the constitutive law for shear rupture in the framework of fracture mechanics. The breakdown zone and the nucleation zone will be modeled physically in terms of the constitutive law parameters, and it will be shown how well and physically reasonably the breakdown zone and the nucleation zone are scaled in terms of one of the constitutive law parameters, which in turn strongly depends on a characteristic length representing geometrical irregularities of the rupturing fault. Finally, we discuss the earthquake nucleation and immediate precursors associated with the nucleation.

Basic Principles. The surface of a solid, even when best-prepared, is made up of asperities. When two surfaces of solid materials are pressed in contact, they do not touch over the entire area A_a (apparent area of contact), but they get in contact only at a number of asperities. The sum of the areas of all the asperity contacts constitutes the real area of contact A_r(<A_a). The atomic interaction between the surfaces takes place at these really contacting portions (atom-to-atom contact); however, the powerful interatomic forces are of very short range, of the order of a

few Angstroms. Solid surfaces in general form adsorbed films, such as molecules of water vapor and/or oxygen. The thickness of these films may be of the order of a few molecularly thick layers (4). The presence of adsorbed films between the mating solid surfaces interrupts the surface’s atom-to-atom interaction at the contacting portions. This is the reason why frictional strength is in general much lower than fracture strength.

However, adhesion or cohesion occurs at the contact areas where the adsorbed films have been broken up during the normal load application or during sliding. In this case, the shearing strength of these adhesive (or cohesive) junctions is the prime cause of frictional resistance (5). For rocks containing typical, hard silicate minerals such as quartz, feldspar, and pyroxene, the penetration of hard asperities into the films on the opposing surface easily occurs during the normal load application or during sliding, and the asperities at the contacting portions fail by brittle fracture, rather than by plastic shear (6). In this case, frictional strength is primarily due to brittle fracture of these asperities.

Let the sum of the solid-solid contact (film-broken) areas be denoted by A₁, which is a fraction of the sum of the whole junction areas A_r, and the rest of the junction (solid-film-solid contact) areas by A₂=A_r−A₁. When two surfaces are pressed together by a normal load N, the total frictional force F is

[1]

where μ₁ and μ₂ are the frictional coefficients for the solid-solid contact and solid-film-solid contact portions, respectively (7). Average frictional coefficient μ between the surfaces is given by

[2]

The frictional coefficient μ₁ represents the shearing strength of the solid material and μ₂ represents the shearing strength of the adsorbed or intervening films. It has been found that μ₁ is much greater than unity, but μ₂ is less than unity; for instance, it has been estimated for Solenhofen limestone that μ₁=4–18, and μ₂=0.3 (7).

We have from Eq. 2 that μ=μ₂ if A₁=0, and that μ=μ₁ if A₂=0. When A₁=0, μ has a minimum value, so that frictional strength is very low in this case. In contrast, at a higher normal load, larger deformation of the asperities that are in contact causes more asperities to get in contact, which results in larger A_r and A₁. At a sufficiently high normal load at elevated temperature, the entire area A_a of fault surface may get into real, cohesive contact (A₁=A_r=A_a), and in this case the shear frictional resistance comes equal to (but never exceeds) the shear strength of intact rock. In other words, the shear strength of intact rock can be regarded as the upper limit of frictional strength. This shows that frictional slip instability on a preexisting fault (of a case where A₁=0) and shear fracture instability of intact rock are the two extreme cases of shear rupture, and therefore both instabilities should be treated unifyingly and quantitatively in terms of a single constitutive law for shear rupture. Indeed, there is considerable circumferential evidence that earthquake rupture instability that occurs in the Earth’s crust is a mixed process between what is called frictional slip and fresh fracture of initially intact rock.

The two extreme phases, that is, (i) stable, quasistatic rupture growth, and (ii) unstable, dynamic fast-speed rupture propagation, should also be treated unifyingly and quantitatively by the single constitutive law, because both phases are part of the rupture process. It has been demonstrated that unstable, dynamic rupture processes are neither time nor rate dependent (8) and that strong motion source parameters such as slip acceleration for dynamically propagating shear rupture are well explained by a slip-dependent constitutive law in quantitative terms (3), as will be discussed later. These show that the time or rate effect is of secondary significance to the constitutive law for shear rupture and that the constitutive law for shear rupture should primarily be slip dependent.

Shear rupture is essentially an inhomogeneous and nonlinear process where local concentration of deformation in a potential thin zone of imminent rupture results in the bond separation in the zone during slip, forming the macroscopic rupture surfaces and releasing the accumulated stress (and strain energy). In other words, shear rupture is the process where the shear strength eventually degrades to a residual stress level with ongoing slip displacement on the rupturing surfaces (Fig. 1A), and the zone behind the rupture front over which the shear strength degrades to the residual stress level is referred to as the breakdown zone (cf. Fig. 1B). The slip-weakening property in the breakdown zone is intrinsic to shear rupture of any type, any phase, and any size scale. That is to say, even if shear rupture occurs along the preexisting fault of weak zone with a finite thickness, which may be made up of gouge particles, or even if shear fracture is of intact material, essentially common is the slip-weakening property in the breakdown zone. This property is also common, despite vast differences in the size scale. Thus, if there is a constitutive law applicable for shear rupture of any type, any phase, and any size scale, the law should primarily be slip dependent.

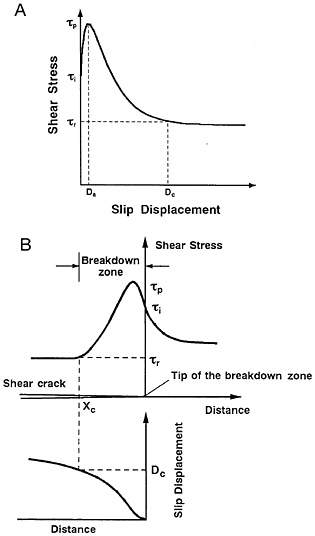
FIG. 1. (A) A constitutive relation for shear rupture. (B) A physical model of the breakdown zone near the propagating tip of shear rupture in the brittle regime, derived from the constitutive relation shown in A. τ_i is the initial shear stress on the verge of slip, τ_p is the peak shear stress, τ_r is the residual friction stress, D_a is the slip displacement at which the peak stress is attained, D_c is the critical slip displacement, and X_c is the breakdown zone size.

The shear rupture process is greatly affected by geometrical irregularities of the rupturing surfaces, and hence it is size-scale dependent. Accordingly, the constitutive law for shear rupture should include a scaling parameter explicitly. Fault surfaces in general have fractal roughnesses; however, they exhibit self-similarity only over finite bandwidths (9, 10), and a different fractal dimension can be calculated for each band bounded by upper and lower corner wavelengths (9). If this is the case, the corner wavelength λ_c separating the neighboring two bands is a characteristic length representing geometrical irregularities of the fault. The corner wavelength in the 10- to 10⁻⁶-m band is particularly important because the breakdown process that occurs near the tip of propagating rupture is virtually governed by such a characteristic length scale. We will find later that λ_c plays a key role in scaling the rupture size.

In view of all the above facts, and given that the parameters prescribing the constitutive law depend on ambient conditions and the slip velocity (or slip rate), the law may be expressed as follows (11):

[3]

In this expression, the shear traction τ on the fault surfaces is a function of the slip displacement D, the slip velocity Ḋ on the fault, the effective normal stress (defined by , where σ_n is the normal stress across the fault, and P is the pore water pressure), ambient temperature T, λ_c, and the chemical effect CE of pore water pressure; however, it has been assumed that τ depends primarily on D, with the dependence of τ on the other parameters being of secondary significance. The specific functional form of Eq. 3 must be determined by careful and well prepared laboratory experiments so as to meet the physical principles and constraints established.

Experimental Basis. To reveal local breakdown processes near the propagating tip of a shear rupture along the fault in rock of the brittle regime, and to get information on what specific functional form well represents the constitutive law for shear rupture, a number of high-resolution laboratory experiments (1–3, 12) have been performed on propagating shear rupture (mode II) along a preexisting fault. Fig. 2A shows an example of a fault surface three-dimensional profile for a granite sample used in the experiments, measured with a diamond stylus profilometer, and Fig. 2B shows a log-log plot of the power spectral density calculated for the surface profile against wavelength. The fault surface prepared in the laboratory is fractal at wavelengths shorter than the corner wavelength λ_c (cf. Fig. 2B), which is prescribed by the grit sizes used for lapping in the laboratory (13, 14). The corner wavelength is a good indicator of surface roughness (14).

The careful, high-resolution laboratory experiments (1–3) have revealed intrinsic properties of the breakdown zone behind the front of a propagating shear rupture (mode II) and a specific constitutive relation for the shear rupture. The observed relation between the local shear stress and slip displacement (see figure 2A of ref. 3) is particularly important, since it represents a self-consistent constitutive relation for shear rupture. The relation demonstrates that the shear strength degrades transitionally, from its peak value (or the breakdown strength) to a residual friction stress level with ongoing slip (slip-weakening). It has been established that the slip-weakening relation during the dynamic breakdown process does not depend on the slip velocity (2, 3, 8).

The high-resolution experiments (1, 3) further revealed that the shear strength in the breakdown zone initially increases with ongoing slip (slip-strengthening) before the peak shear strength is attained (see figure 4 of ref. 3) (1, 3). That the slip displacement D_a at which the peak shear strength τ_p is attained becomes larger on rougher fault surfaces has been confirmed by more recent laboratory experiments (unpublished data).

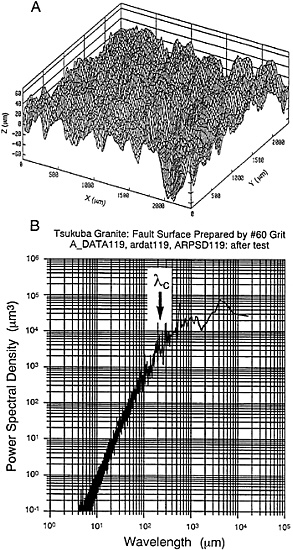
FIG. 2. (A) A three-dimensional fault surface profile measured with a stylus profilometer. (B) A log-log plot of the power spectral density calculated for the fault surface against wavelength. λ_c indicates the corner wavelength.

The property that the slip-strengthening precedes the slip-weakening plays an essential role in giving rise to bounded slip acceleration near an unstably and dynamically propagating tip of the rupture zone (3, 15), and therefore this constitutive property must be incorporated into a physical model from which earthquake strong motion source parameters such as the peak slip acceleration can be treated rigorously in quantitative terms (3). Note that the shear stress has its peak value not at the crack tip but near the inner crack tip in the brittle regime (cf. Fig. 1B), because the peak shear stress is attained at a small but nonzero value of slip displacement (3).

Why does the slip-strengthening occur prior to the slip-weakening? The real area of asperity junctions between mating surfaces in general increases with ongoing slip before the peak frictional resistance or the steady-state friction is reached, and this results in an increase in the fault strength with ongoing slip (7, 16, 17). This phenomenon is referred to as the slip (or displacement) hardening or strengthening (7). An increase in the area of the junctions with ongoing slip is attained, for instance, when the number of asperities penetrated into the

opposing surface increases with ongoing slip. Biegel et al. (16) found that the rate and extent of slip-strengthening depend on the surface’s roughness and the applied normal load; that is, the rate of slip-strengthening is higher for rougher surfaces, and the greater rate of slip-hardening at higher normal loads.

Fig. 1A conceptually summarizes the observed constitutive relation for shear rupture. In the figure, τ_i denotes the initial strength on the verge of slip, τ_p the peak shear strength, τ_r the residual friction stress, D_a the slip at which the peak shear strength is attained, and D_c the critical slip displacement, which is defined as the slip displacement required for the shear strength to degrade to τ_r. The constitutive property for shear rupture is prescribed and characterized by these five parameters. In particular, the following three parameters, τ_p, ∆τ_b, and D_c, are most crucial, because they virtually determine the constitutive property for shear rupture. Here, ∆τ_b is the breakdown stress drop, which is defined as the difference between τ_p and τ_r. These constitutive parameters depend on fault zone properties, ambient conditions, and the applied strain rate (or slip rate). For instance, τ_p and ∆τ_b are affected by , T, Ḋ, mechanical properties of the fault zone, and chemical effect of pore water, while D_c depends on λ_c representing geometrical irregularities of the fault, mechanical properties of the fault zone, , and T (18).

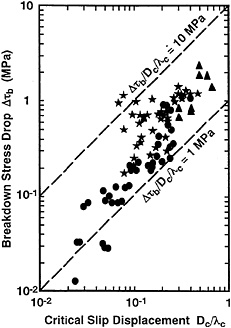
Fig. 3 shows a relation between ∆τ_b and D_c/λ_c for frictional slip failure (stick-slip) that occurred on a preexisting fault in granite samples (18), indicating that there is a positive correlation between ∆τ_b, and D_c/λ_c, which in general may be represented as

[4]

where ∆τ_b0 and M are constants. Fig. 3 suggests that the exponent M can approximately be regarded as unity. We will find later that relation 4 plays a significant role in scaling the size of shear rupture. Kuwahara et al. (14) demonstrated that the critical slip displacement D_c increases proportionally with λ_c at a constant normal stress σ_n. Taking this into consideration, Ohnaka (18) has concluded that D_c is related to λ_c by

FIG. 3. An observed relation between the breakdown stress drop ∆τ_b, and the critical slip displacement D_c normalized to the corner wavelength λ_c.

where m(σ_n) is a numerical parameter, which is an increasing function of σ_n. This is consistent with the observed result shown in Fig. 3, because ∆τ_b increases with increasing σ_n.

A Slip-Dependent Constitutive Equation. Ohnaka and Yamashita (3), based on the high-resolution laboratory experiments, proposed a specific, slip-dependent constitutive equation for shear rupture to quantitatively describe the observed breakdown process near the dynamically propagating front of shear rupture. The observed entire phases from slip-strengthening to slip-weakening can well be represented by the proposed equation. As will be discussed later, if we consider that the parameters prescribing the constitutive equation are a function of position τ on the fault, the shear traction τ on the fault near the tip of the breakdown zone is a function of not only D, but also r, and hence the constitutive equation proposed by Ohnaka and Yamashita (3) may be rewritten as follows (11):

[6]

where d=D/D_a, and S=∆τ_b/τ_p. Eq. 6 has been chosen to conform to the constitutive relation observed in the laboratory (3). We find from Eq. 6 that the constitutive equation at a position r on the fault is completely prescribed if the parameters τ_i, τ_p, ∆τ_b, D_a, and D_c are given, because the parameters A and B in Eq. 6 are determined uniquely from the following two relations (11):

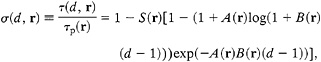
[7]

and

[8]

where χ is a given parameter of small fraction (say, χ=0.01−0.2).

As mentioned above, the physically reasonable constitutive equation for shear rupture should result in the nonsingularity of not only the stresses but also the slip acceleration at or near the unstably and dynamically propagating tip of the rupture zone, because the unbounded acceleration is physically unreasonable. In fact, the bounded acceleration is crucial when strong motion source parameters, such as the peak slip acceleration, are discussed from a physical viewpoint. Ida (15) has shown theoretically that the acceleration can be bounded at the propagation tip if the shear traction is a suitable function of the slip displacement. Since the functional form Eq. 6 has been determined on an experimental basis so as to quantitatively describe the dynamic breakdown process for shear rupture instabilities, Eq. 6 not only gives the bounded slip acceleration and stresses at or near a dynamically propagating crack tip during shear rupture but also explains relations between strong motion source parameters quantitatively. This will be discussed briefly below but is more fully described in an earlier paper (3).

For simplicity, we here assume a two-dimensional shear crack whose tip is moving at a constant speed V in an unbounded elastic medium, and τ_r=0 over the entire crack plane. We further assume that the constitutive equation is a function of slip displacement D alone. Under these assumptions, the slip velocity and acceleration are given as (3)

[9]

[10]

where the rupture has been assumed to propagate in the positive x direction. In the above equations, C(V) is a known function of V, μ is the rigidity, and ϕ′ and ϕ″ are the dimensionless slip velocity and slip acceleration, respectively. Γ is a dimensionless quantity defined by (3)

[11]

Γ is related to the shear fracture energy G_c by (3)

[12]

which shows that G_c is prescribed by ∆τ_b and D_c alone, since Γ can virtually be regarded as constant for the present model (3).

The dimensionless slip velocity ϕ′ and slip acceleration ϕ″ have been calculated numerically, and it has been found that the calculated results agree well with experimental results in the laboratory (3). One specific example derived theoretically from the present model is

[13]

where is the maximum slip acceleration, Ḋ_max the maximum slip velocity, and the cutoff frequency of the power spectral density of the slip acceleration versus time record observed at a position near the fault. The cutoff frequency is equal to the reciprocal of the breakdown time T_c, defined as the time required for the crack tip to break down. The theoretical relation 13 agrees quantitatively with the experimental results (3).

It is thus concluded that the slip-dependent constitutive Eq. 6 not only does not give rise to unrealistic singularities of slip acceleration and stresses at or near the rupture front but also can quantitatively explain experimental data on an unstably, dynamically propagating shear rupture. This provides a physical constraint to be imposed on the constitutive law for shear rupture.

When we assume that the shear traction τ on the fault in the breakdown zone is a function of the slip displacement D, and that its specific relation is given as shown in Fig. 1A, spatial distributions of the shear stress and slip displacement near the tip of the breakdown zone can be calculated theoretically, as illustrated in Fig. 1B (3). This breakdown zone model (Fig. 1) is scale independent, so that it is applicable to shear rupture of any scale. However, some of the model parameters are scale dependent; this will be discussed below.

In tensile fracture, the relative displacement to open a crack is perpendicular to the macroscopic fracture plane, and hence the size of the cohesive zone is not affected by geometric irregularities of the fracturing surfaces. By contrast, in shear rupture, the relative displacement is on the rupturing plane, and hence the rupturing surfaces are in mutual contact and interactive throughout the breakdown process. This shows that the size of the breakdown zone is affected by geometrical irregularities of rupturing surfaces and that the critical slip displacement is necessarily size-scale dependent, as demonstrated by the laboratory experiments. For instance, the large amount of slip displacement is required for an asperity of large size to break down. Accordingly, D_c is a fundamental parameter for scaling the shear rupture size, and at the same time it is a crucial parameter for prescribing the slip-dependent constitutive law. It is essentially important that the constitutive law for shear rupture includes a scaling parameter D_c explicitly. In fact, the vast difference in size and time scales between the laboratory and field rupture events is successfully scaled in terms of D_c, as will be discussed below, and the breakdown zone model (Fig. 1) based on the slip-dependent constitutive law in the framework of fracture mechanics enables one to give a common interpretation to both small scale rupture in the laboratory and large scale rupture as earthquake source in the Earth (1, 3, 12, 19).

The breakdown zone size X_c is directly related to D_c by (3)

[14]

where

[15]

for the present slip-weakening model. Here, ξ is a numerical parameter, and k has a value ranging from 1.4 to 2.7, assuming that τ_i/∆τ_b=0.5−0.8, and that V/V_s=0.1−0.5 (V_s, shear wave velocity). This indicates that D_c/X_c has the same order of magnitude of ∆τ_b/μ. Since the stress parameters τ_p, τ_r, and, consequently, ∆τ_b(=τ_p−τ_r) in the vicinity of the tip of propagating rupture are independent of the size scale (1, 12), X_c and G_c are necessarily size-scale dependent (1) (for G_c see Eq. 12), because D_c is size-scale dependent. As will be discussed later, if the breakdown of larger λ_c results in the fault rupture of larger size, both D_c and X_c necessarily increase with an increase in the geometric scale. It is obvious from Eq. 14, however, that the ratio of D_c to X_c is independent of the size scale, because ∆τ_b is size-scale independent.

Laboratory data on stick-slip show that ∆τ_b/μ has a value ranging from 10⁻⁵ to 10⁻³ according to different normal stresses; however, ∆τ_b/μ does not exceed the order of magnitude of 10⁻³ even if the applied normal stress is high enough (1). This is because frictional strength on the precut fault can never exceed the shear strength of intact rock even at sufficiently high normal stresses, and because ∆τ_b/μ for intact rock takes a constant value of the order of 10−³ despite the variation of normal stress over wide ranges (1). It thus follows from Eq. 14 that D_c/X_c is of the order of 10⁻³ or less. This agrees with values of D_c/X_c estimated by Papageorgiou and Aki (20) for earthquakes of moderate-to-large sizes with different fault lengths ranging from 20 to 300 km.

The earthquake source strong motion can be represented by such parameters as, , and . From Eqs. 9 and 10, we have

[16]

[17]

The cutoff frequency at the source is similarly expressed for the present model as (3)

[18]

These relations show that and are proportional to the reciprocal of D_c, while Ḋ_max is independent of D_c. Since D_c is size-scale dependent (but V and ∆τ_b are size-scale independent), both and are size-scale dependent, while Ḋ_max is size-scale independent (1, 12). We can thus conclude that D_c, which is one of the constitutive law parameters, plays a fundamental role in scaling the physical quantities dependent on the size scale.

The high-resolution laboratory experiments on rock in the brittle regime (2, 12) have shown that an intrinsic part of dynamic rupture is the nucleation process, which consists of two phases; (i) an initial quasistatic phase, and (ii) the subsequent accelerating phase. Fig. 4 shows a plot of the rupture

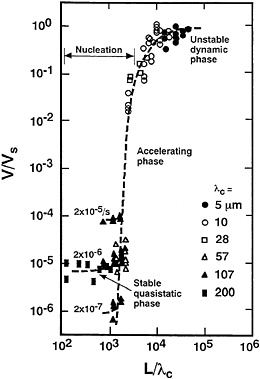
FIG. 4. A log-log plot of the rupture growth rate V normalized to the shear wave velocity V_s against the growth length L normalized to λ_c. Numerals attached to the curves indicate the applied strain rate. Data are from ref. 20 in addition to our recent unpublished data.

velocity V normalized to the shear wave velocity V_s against the rupture growth length L normalized to the corner wavelength λ_c. This shows how shear rupture grows from stable, quasistatic phase, to subsequent accelerating phase, and eventually to unstable, fast-speed dynamic phase. The rupture speed depends on the applied slip rate (or strain rate) in the stable, quasistatic phase, whereas it no longer depends on the applied slip rate in the accelerating phase. Fig. 4 indicates that to reach the rupture velocity of, say, V=0.1V_s, the rupture needs to grow up to the critical length of L=4×10³λ_c.

Fig. 5 shows an example of data on rupture nucleation of quasistatic phase that occurred along a preexisting fault of λ_c =200 μm (very rough fault surface), of which surface three-dimensional profile has been shown in Fig. 2A. In Fig. 5A, the rupture initiation time t normalized to λ_c/V_s is plotted against position X, normalized to λ_c, on the fault, where the origin of t has been set arbitrarily. In this experiment, a series of strain gage sensors were mounted at every 2.5-cm interval along the fault at positions 5 mm from the fault surface to monitor local shear strains, and the corresponding shear stresses were obtained from the shear strains multiplied by the rigidity (2×10⁴ MPa) of the granite sample used. A constant strain rate of 2 ×10⁻⁶ was applied during this particular experiment. We notice from the figure that the rupture began to nucleate at position Ch.4 for this event, and that it proceeded bidirectionally at approximate speeds of 1–4 cm/s.

One can see from Fig. 5A how progressively the nucleation has developed with time. In Fig. 5B, local fault strength τ_p is plotted against X/λ_c, showing how nonuniformly the fault strength is distributed on the fault. It is found from Fig. 5 that the rupture growth is prohibited by local barriers of the strength; that is, high strength barriers inhibit rupture from spreading at a high speed. It should be noted that the size of the breakdown zone (hatched portion in Fig. 5A) increases roughly linearly with time during the stable, quasistatic phase of nucleation.

After the zone size of the stable, quasistatic nucleation has exceeded a certain length, the rupture begins to extend at an accelerating speed (Fig. 4), and at the same time the break

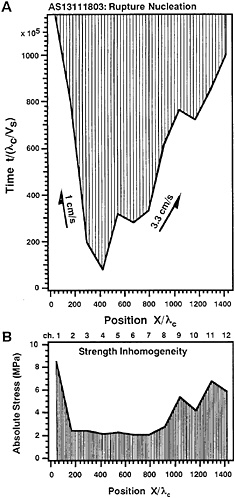
FIG. 5. (A) Space-time view of the nucleation for the fault of λ_c= 200 μm. Time t and position X are normalized to λ_c/V_s and λ_c, respectively. (B) Plot of the local shear strength τ_p against position X/λ_c on the same fault.

down zone develops at the same rate. Fig. 6 shows how dynamically at accelerating speeds the breakdown zone (hatched portion) develops with the rupture growth during the later phase of the nucleation process. By contrast, the size of the breakdown zone is almost constant in the zone of dynamic, fast-speed rupture propagation (Fig. 6). Fig. 6 was obtained from data on slip failure (stick-slip) on the precut fault of λ_c =10 μm (smooth fault surface) (2). Note that λ_c of the fault surfaces for the data shown in Fig. 5 is 20 times larger than λ_c for that shown in Fig. 6, and that both the breakdown zone size

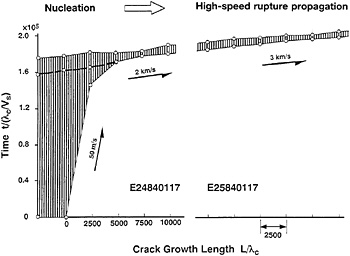
FIG. 6. Space-time view of the transition process from the nucleation to dynamic fast-speed rupture propagation for the fault of λ_c=10 μm.

X_c and the nucleation zone size L are much larger for the fault with λ_c=200 μm than with λ_c=10 μm. Figs. 4, 5, and 6 show that both X_c and L can successfully be scaled in terms of λ_c. This will be discussed later from a theoretical viewpoint.

Here I discuss the conditions under which the shear rupture nucleates and under which the transition from stable, quasistatic phase to unstable, fast-speed phase occurs. This has been studied experimentally in the framework of fracture mechanics (2, 12). Fig. 7 shows how the constitutive law parameters ∆τ_b, D_c, and (τ_p −τ_i)/∆τ_b vary along the fault in the nucleation zone. For comparison, the variations of these parameters in the zone of fast speed rupture propagation are also shown in Fig. 7. Each symbol connected by thin lines in Fig. 7 represents data for one rupture event. The fluctuation of individual data points in Fig. 7 may partly be due to experimental errors, but it mostly reflects inhomogeneities on the fault. We find from Fig. 7 that spatial

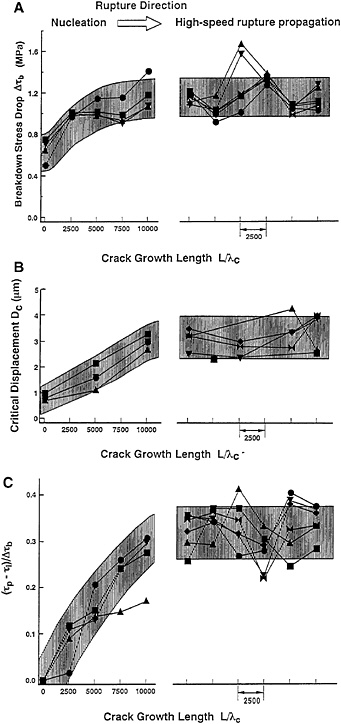
FIG. 7. Plot of ∆τ_b(A), D_c(B), and (τ_p−τ_i)/∆τ_b(C) against rupture growth length L/λ_c during the transition process from nucleation to dynamic rupture propagation for the fault of λ_c=10μm.

distributions of ∆τ_b, D_c, and (τ_p−τ_i)/∆τ_b on the fault in the nucleation zone distinctly differ from those in the zone of dynamic, fast-speed rupture propagation. In the nucleation zone, ∆τ_b, D_c, and (τ_p−τ_i)/∆τ_b have minimum values at the initiation point of nucleation, and they increase with rupture growth without exception. By contrast, ∆τ_b, D_c, and (τ_p−τ_i)/∆τ_b do not systematically vary in the zone of high-speed dynamic rupture propagation. This shows that nonuniform distributions of the constitutive law parameters on the fault, which may be regarded as a function of position on the fault, are crucial for creating the nucleation.

The energy required for the rupture front to further grow (shear fracture energy) is given by Eq. 12, and hence an increase in the magnitudes of ∆τ_b and D_c brings about increasing resistance to rupture growth. Accordingly, the above results may be paraphrased as follows: the resistance to rupture growth increases with rupture extension in the nucleation zone.

The above experimental findings have been confirmed and clarified by a number of theoretical studies (17, 21). In particular, a recent theoretical study and numerical simulation by B. Shibazaki and M. Matsu’ura (personal communication), based on a slip-dependent constitutive law, and taking the experimental results shown in Fig. 7A and B into consideration, have successfully explained the transition process from the nucleation to high-speed rupture propagation revealed in the high-resolution laboratory experiments in quantitative terms. This leads to the conclusion that nonuniform distributions of the constitutive law parameters on the fault are necessary and sufficient conditions for creating the nucleation in the brittle regime.

It has been shown that the shear rupture nucleation does occur in the brittle regime when the constitutive law parameters are distributed nonuniformly on the fault and that the size of the nucleation zone increases proportionally with λ_c. This indicates that λ_c is a crucial parameter (pertinent to geometrical irregularities of the fault) for scaling the nucleation zone size, which is discussed below from a theoretical viewpoint.

Consider a shear rupture nucleation model shown in Fig. 8, in which it is assumed that the critical size L_c of the nucleation zone is attained at a critical time t_c, when the rupture begins to propagate bidirectionally at a constant velocity V. For this particular model, the following relation holds

at the critical time t_c. From Eq. 14,

[20]

If ∆τ_b is assumed to be constant, Eqs. 19 and 20 show that both X_c and L_c are directly proportional to D_c. The assumption that ∆τ_b is constant may be justified for rough discussion purposes.

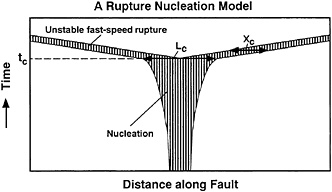
FIG. 8. Model of rupture nucleation. Hatched portion indicates breakdown zone where slip-weakening proceeds. X_c is the breakdown zone size, and L_c is the critical size of the nucleation zone. It has been assumed in this model that the rupture begins to propagate bidirectionally at a constant velocity at time t_c.

Laboratory data (Fig. 3) show, however, that both ∆τ_b and D_c are an increasing function of σ_n, so that the assumption of ∆τ_b being constant is not justified for more rigorous discussion. From Eqs. 4, 5, and 20,

[21]

which shows that X_c is directly proportional to λ_c, and that X_c is independent of σ_n if M=1. If M≠1, X_c depends not only on λ_c, but also on σ_n. However, the dependence of {m(σ_n)}^1−M on σ_n is modest, so that X_c is practically prescribed by λ_c alone. One can thus conclude from Eqs. 19 and 21 that X_c and L_c are virtually prescribed and scaled by λ_c alone. If it is tentatively assumed that the critical size of the nucleation zone is attained at a value in the V/V_s range 0.1–0.5, and that τ_i/∆τ_b=0.5−0.8, then L_c=(4.9−9.7)×10³λ_c from Eqs. 19 and 21 by considering that μ=2×10⁴ MPa for the granite sample used, and assuming that M=1 and ∆τ_b0=3 MPa (see Fig. 3). This theoretical estimate agrees with the experimental result (Fig. 4).

During the nucleation, the energy is exclusively consumed in and around the zone of nucleation, since the nucleation is the process (or zone) in which slip failure deformation is concentrated and accelerated. Accordingly, dynamic instabilities of small to microscopic scales (microseismicity or acoustic emission) are induced and activated during the nucleation process, when the rupture growth resistance on the fault varies on small to microscopic scales. This has been demonstrated by recent laboratory experiments (unpublished data). It has also been found that seismic b values decrease as the nucleation proceeds (unpublished data). These observations suggest that microcrack interactions in the fault zone play a crucial role in the nucleation process.

We have seen that geometrical and/or mechanical inhomogeneities play a crucial role in the shear rupture nucleation process. Such inhomogeneities prevail in the brittle seismogenic layer in the Earth’s crust. The seismogenic layer contains a large number of preexisting faults of microscopic to macroscopic scales, and therefore the seismogenic layer is inherently inhomogeneous. In addition, a preexisting fault itself in the Earth’s crust exhibits geometrical irregularities and mechanical inhomogeneities of various scales on the fault surfaces and in the fault zones. This strongly suggests that earthquake dynamic rupture is necessarily preceded by a quasistatic to quasidynamic nucleation process. However, whether or not a sizable zone of the nucleation appears prior to earthquake dynamic instability depends on how nonuniformly the constitutive law parameters prevail on the fault in the lithosphere (18).

The shear rupture nucleation model presented in this paper (see also ref. 18) can explain why and how short-term (or immediate) precursors are intrinsically related to the earthquake nucleation that proceeds quasistatically to quasidynamically prior to the mainshock dynamic rupture and how essential it is in carrying immediate foreshocks that the rupture growth resistance is distributed nonuniformly on a local to small scale in the fault zone in the brittle regime. The model shows that immediate foreshock activity is a part of the mainshock earthquake nucleation (18, 22). This provides a physical explanation for observations commonly made for decades that immediate foreshocks are concentrated in the vicinity of the epicenter of the pending mainshock. Whether or not immediate foreshocks occur during the mainshock nucleation depends on how the rupture growth resistance varies on a local to small scale in the nucleation zone (18, 22).

During the nucleation, local shear stresses decrease gradually in the breakdown zone, and at the same time the corresponding premonitory slip also proceeds in the zone, since the shear strength degrades with ongoing slip in the nucleation zone. Premonitory stress (or strain) changes are also observed outside (but adjacent to) the nucleation zone; that is, local shear stresses on the remaining unslipped parts adjacent to the nucleation zone increase with time because the unslipped segments must bear extra stress loads that have been sustained by the slipped parts. These gradual, accelerating changes in both local stress and slip are inevitable precursors that occur locally in or adjacent to the zone of the rupture nucleation. However, no such precursory slip and stress degradation necessarily occurs in a region distant from the nucleation zone, and the precursory deformation and stress changes can locally be confined in (or adjacent to) the zone of the nucleation. This suggests that the key to the short-term (or immediate) earthquake prediction is to identify where the nucleation occurs on the fault that has the potential to cause a major earthquake.

If the critical size of the nucleation zone for a real major earthquake is small enough, it may be meaningless to regard the nucleation process as an effective tool for the immediate prediction. In this sense, it is important to know how large is the critical size of the nucleation zone for a real major earthquake. The critical size of the nucleation zone has recently been estimated for a number of major earthquakes (B.Shibazaki and M.Matsu’ura, personal communication; see also refs. 22 and 23), showing that L_c for major earthquakes with M=7.0−7.7 is 5−10 km.

For a given L_c of 5–10 km, λ_c=0.5−2 m from Eqs. 19 and 21. This estimate suggests that for earthquakes of M=7.0−7.7, the breakdown process behind the tip of propagating rupture is virtually governed by a characteristic length of the order of 1 m, which is 10⁴–10⁵ times greater than λ_c for shear rupture in the laboratory.

I am deeply grateful to Professor L.Knopoff and the other organizers for inviting me to present this paper and for their courtesy during the Colloquium.

1. Ohnaka, M., Kuwahara, Y. & Yamamoto, K. (1987) Tectonophysics 144, 109–125.

2. Ohnaka, M. & Kuwahara, Y. (1990) Tectonophysics 175, 197–220.

3. Ohnaka, M. & Yamashita, T. (1989) J. Geophys. Res. 94, 4089–4104.

4. Rabinowicz, E. (1965) Friction and Wear of Materials (Wiley, New York).

5. Bowden, F.B. & Tabor, D. (1954) The Friction and Lubrication of Solids (Clarendon, Oxford).

6. Byerlee, J.D. (1967) J. Appl Phys. 38, 2928–2934.

7. Ohnaka, M. (1975) J. Phys. Earth 23, 87–112.

8. Okubo, P.G. & Dieterich, J.H. (1986) Geophys. Monogr. Am. Geophys. Union 37, 25–35.

9. Aviles, C.A., Scholz, C.H. & Boatwright, J. (1987) J. Geophys. Res. 92, 331–344.

10. Okubo, P.G. & Aki, K. (1987) J. Geophys. Res. 92, 345–355.

11. Ohnaka, M. (1995) in Theory of Earthquake Premonitory and Fracture Processes, ed. Teisseyre, R. (Polish Sci. Publ., Warsaw, Poland).

12. Ohnaka, M. (1990) Can. J. Phys. 68, 1071–1083.

13. Brown, S.R. & Scholz, C.H. (1985) J. Geophys. Res. 90, 12575–12582.

14. Kuwahara, Y., Ohnaka, M., Yamamoto, K. & Hirasawa, T. (1985) Annual Meet. Seis. Soc. Japan Progr. Abstr. 2, 110.

15. Ida, Y. (1973) Bull. Seis. Soc. Am. 63, 959–968.

16. Biegel, R.L., Wang, W., Scholz, C.H. & Boitnott, G.N. (1992) J. Geophys. Res. 97, 8951–8964.

17. Matsu’ura, M., Kataoka, H. & Shibazaki, B. (1992) Tectonophysics 211, 135–148.

18. Ohnaka, M. (1992) Tectonophysics 211, 149–178.

19. Shibazaki, B. & Matsu’ura, M. (1995) J. Geophys. Res., SUBMITTED.

20. Papageorgiou, A.S. & Aki, K. (1983) Bull. Seis. Soc. Am. 73, 953–978.

21. Kuwahara, Y., Ohnaka, M., Yamamoto, K. & Hirasawa, T. (1986) Annual Meet. Seis. Soc. Japan Progr. Abstr. 2, 233.

22. Yamashita, T. & Ohnaka, M. (1991) J. Geophys. Res. 96, 8351–8367.

23. Ohnaka, M., Yoshida, S. & Shen, L.-F. (1994) Workshop on Earthquake Source Modeling and Fault Mechanics, IASPEI General Assembly, Wellington, New Zealand.

24. Ohnaka, M. (1993) J. Phys. Earth 41, 45–56.

25. Ellsworth, W.L. & Beroza, G.C. (1995) Science, in press.