This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.
Rock friction and its implications for earthquake prediction examined via models of Parkfield earthquakes
(constitutive laws/numerical models)
TERRY E.TULLIS
Department of Geological Sciences, Brown University, Providence, RI 02912–1846
ABSTRACT The friction of rocks in the laboratory is a function of time, velocity of sliding, and displacement. Although the processes responsible for these dependencies are unknown, constitutive equations have been developed that do a reasonable job of describing the laboratory behavior. These constitutive laws have been used to create a model of earthquakes at Parkfield, CA, by using boundary conditions appropriate for the section of the fault that slips in magnitude 6 earthquakes every 20–30 years. The behavior of this model prior to the earthquakes is investigated to determine whether or not the model earthquakes could be predicted in the real world by using realistic instruments and instrument locations. Premonitory slip does occur in the model, but it is relatively restricted in time and space and detecting it from the surface may be difficult. The magnitude of the strain rate at the earth’s surface due to this accelerating slip seems lower than the detectability limit of instruments in the presence of earth noise. Although not specifically modeled, microseismicity related to the accelerating creep and to creep events in the model should be detectable. In fact the logarithm of the moment rate on the hypocentral cell of the fault due to slip increases linearly with minus the logarithm of the time to the earthquake. This could conceivably be used to determine when the earthquake was going to occur. An unresolved question is whether this pattern of accelerating slip could be recognized from the microseismicity, given the discrete nature of seismic events. Nevertheless, the model results suggest that the most likely solution to earthquake prediction is to look for a pattern of acceleration in microseismicity and thereby identify the microearthquakes as foreshocks.
Frictional sliding of rocks on laboratory scale faults or on faults in the earth are similar. Both systems involve an interaction between the frictional response of the rocks in the fault zone and the elastically distorted surroundings that can either be unstable or stable.
It is not the coefficient of friction of rocks, but the way the coefficient of friction depends on time, sliding velocity, and displacement that is important to whether sliding will be stable or unstable. These relatively small effects are more subtle and experimentally difficult to measure, but they are of primary importance in determining whether a fault will slide by creep or by catastrophic earthquakes. There are other factors such as changes in pore fluid pressures that may also play a role in earthquake generation, but some kind of dependence on velocity and sliding displacement is probably needed to allow a sustained runaway instability. In this paper I will explore the implications of the observed time, velocity, and displacement dependence of rock friction in the laboratory for the possible behavior of natural faults, recognizing that this may represent only part of the story. This approach has the advantage that it is clear from work already done that the laboratory-derived constitutive laws offer at least one likely explanation for many phenomena involved in earthquakes (1–11).
This success, combined with the fact that accelerating slip precedes unstable sliding in the laboratory, leads one to investigate the relevance of rock friction data for predicting earthquakes. One, debatably encouraging, fact is that there is general agreement between observations from the earth and predictions from the modeling on the small size of any premonitory signals. The fact that at least small signals may exist suggests that it might eventually be possible to detect them.
Review of Rock Friction Behavior
Observed Behavior. Generalities. Static friction increases with the time of being static and there is an associated tendency for dynamic friction to decrease with increasing slip velocity. In addition, when the velocity is changed, the transition to the new frictional resistance requires sliding some distance. These features are illustrated in Fig. 1. Two competing effects are seen in the behavior shown in Fig. 1, the evolution effect and the direct effect.
Evolution effect. The most important single aspect of rock friction in terms of application to earthquakes is that surfaces in stationary contact increase in strength with time. This effect is known as the evolution effect. It is demonstrated by the slide-hold-slide test, in which sliding is stopped for some period of time after having attained a steady-state frictional resistance at constant velocity. When sliding is resumed, the resistance climbs to a peak value larger than the steady-state value prior to the hold, subsequently decaying to the original steady-state value. As shown in Fig. 2, there is a nearly linear relationship between the magnitude of the peak value and the logarithm of the hold time (12, 13). This phenomenon is responsible for the restrengthening of surfaces between slip episodes, without which repeated unstable slip is impossible, and for a tendency for frictional resistance to be lower at higher sliding velocities. This potential for decreasing strength with increasing velocity is the aspect of rock friction that allows for runaway instabilities (14, 15).
After abrupt changes in velocity the frictional resistance evolves to a new steady-state resistance over a characteristic slip distance (thus the term “evolution effect”). This has been interpreted (16–18) as the slip required to destroy all the contacts established at one velocity and to create a new set of contacts having an average age appropriate to the new velocity.
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
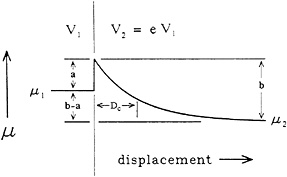
FIG. 1. Response of friction to an abrupt increase in sliding velocity. The parameters a, b, and Dc are those in Eqs. 1a, 1b, and 1c. The behavior given by the equations for a sudden velocity change is illustrated graphically. The magnitude of the direct effect is measured by a and of the evolution effect is measured by b.
However, a complete understanding of what occurs at the contacting asperities does not yet exist.
The other effect seen in all friction experiments is an initial increase in the resistance to sliding that occurs when the velocity of sliding is abruptly increased (Fig. 1). This is termed the direct effect because the change of resistance occurs instantaneously and in the same sense as the change in velocity.
Stability of sliding. The absolute value of frictional resistance is unimportant for controlling the stability of sliding. However, the time, velocity, and displacement dependence of friction interact with the elastic stiffness of the surroundings to produce either stable or unstable sliding. The stability has been analyzed by using the constitutive laws described in the following section (14, 16, 17, 19–24).
The stability of sliding is ultimately controlled by an interaction between the stiffness of the loading system and the dependence of frictional resistance on displacement. In systems for which the frictional behavior is as illustrated in Figs. 1 and 2, the dependence of frictional resistance on displacement is itself a function of how friction depends on velocity (15, pp. 566–569). If the frictional resistance decreases with increasing velocity, a behavior termed velocity weakening, then unstable sliding is possible. This unstable sliding generally is not possible for a velocity strengthening material, one in which the resistance increases with slip speed. This generality must be modified if the resistance does not show a monotonic change after the direct peak (26).
Predictability of unstable sliding. The onset of an unstable sliding event in the laboratory is typically preceded by some nonlinearity in the loading curve and by accelerating slip. Whether this is a universal feature of all laboratory experiments is not known, since detecting this behavior may require high precision measurement of the stress and perhaps measurement of the displacement using a transducer mounted
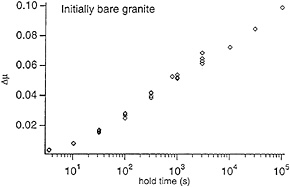
FIG. 2. Increase of static friction as a function of the time period of holding static.
inside the pressure vessel immediately adjacent to the sample. In Fig. 3 is shown a typical sequence of stick slip events measured with internal stress and displacement transducers in our rotary shear apparatus (26). At first glance (Fig. 3A), the events look as if they occur without warning, but successively closer examinations (Fig. 3 B-D) show that there is accelerating slip and an associated nonlinearity in the stress-time curve that foretells each unstable event. There is no reason to believe that this precursory accelerating slip should not occur in the earth. The real question is whether it will be large enough to be usefully detected and so provide the basis for a short-term earthquake prediction. In order to answer this we need to learn how to extrapolate the laboratory results to the earth. The constitutive laws discussed in a following section form the present basis for doing this.
Constitutive Laws. Empirical constitutive laws have been used by many workers to fit the frictional behavior described (e.g., refs. 13, 17, 26–38). Although a variety of functions have been presented, two laws are most commonly used, and even these can be cast in slightly different ways. The form used in ref. 13 is convenient because the state variable has dimensions of time in both laws. Both laws represent friction as a function of velocity and a state variable by the same equation:
μ=μ0+a ln(V/V0)+b ln(θV0/Dc). [1a]
The direct effect is contained in the term a ln(V/V*) and the evolution effect in the term b ln(θDc/V*). The nature of the evolution is what differs in the two laws. In the law termed the slip law, because slip is required for evolution, the state variable evolves according to:
dθ/dt=(θV/Dc) ln(θV/Dc). [1b]
In the law termed the slowness law, because the evolution depends on the slowness (inverse of velocity) or on time, the evolution is given by:
dθ/dt=1−θV/Dc. [1c]
Neither of these two commonly used laws fits all aspects of experiments data (39), and a better law is needed. Both laws do a reasonable job of fitting data until one looks carefully at the details. If the processes that cause the observed behavior can be understood, then the correct form of this law may be found, and we can have more confidence in extrapolating its behavior outside the range of existing laboratory data.
Lack of Data and Constitutive Laws for Dynamic Slip Under Realistic Conditions. No laboratory experiments combine the large displacement, high slip rate, high normal stress, and presence of pressurized pore fluids that characterize dynamic earthquake slip. Most experiments involving high slip velocity (e.g., refs. 40–42) have been done at low total displacement and low normal stress, without the presence of pore fluids. These failings mean that processes that may occur during dynamic slip in earthquakes have not been explored experimentally. Chief among these are shear heating and associated possible melting or increase in pore fluid pressures. Some experiments at low normal stress at relatively high velocity and large total displacement have produced shear melting (43–45). Experiments on foam rubber suggest the importance of reduction of normal stress during dynamic slip (46).
Thus, although we have considerable data that may be relevant to the accelerating slip that occurs prior to an earthquake, we have no experimental data that is really useful for characterizing the velocity or displacement dependence of frictional resistance that might cause self-healing slip pulses (47–49), the lack of a heat flow anomaly in area of faults that typically slip in seismic events (50–52), or other evidence for the absolute and relative weakness of major faults (53–55).
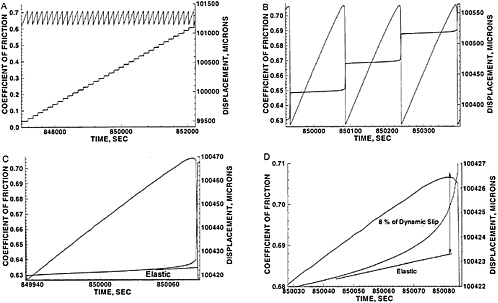
FIG. 3. Four successively closer looks (A-D) at the behavior of stick slip events found in the laboratory, showing that some premonitory slip occurs. The jagged line is the friction and the one that increases in steps is the displacement. The data is for a bare quartzite sample that slid at 25 MPa normal stress at 1 μm/s.
Implications of Instability Model of Parkfield Earthquakes for Earthquake Prediction
A three-dimensional model of magnitude ≈6 earthquakes on the San Andreas fault at Parkfield, CA, has been developed, by using the laboratory-based constitutive behavior described above (3, 4). This model takes the boundary conditions relevant to the Parkfield section of the San Andreas fault, and by using constitutive parameters consistent with laboratory experiments, generates a spontaneous sequence of characteristic earthquakes. The magnitude and spatial and temporal extent of any premonitory creep in this model can be studied to see whether it could be detected and form the basis for a prediction of the earthquake. Although differences will exist between the model and real Parkfield earthquakes, the model has the advantage of forming a concrete example of the implications of the laboratory results. Its success can in part be evaluated when the next Parkfield earthquake occurs.
Description of the Model. More details of the model can be found in ref. 4. The fault is assumed to be vertical and planar and shows only strike slip motion. To the south of the Parkfield section, the fault is assumed to be locked at the surface down to a depth of 9 km as a result of the reduction in stress after the great 1857 Fort Tejon earthquake. The fault is assumed to be creeping at 35 mm/year at the surface to the northwest of the Parkfield section along the central creeping section of the San Andreas. This boundary condition of 35 mm/year is also applied at depth under the Parkfield section and under the locked 1857 section (Fig. 4A). In the Parkfield section itself to a depth of 39 km and to 45 km northwest of Middle Mountain (the north end of the Parkfield section) the behavior of the fault is a computed result of the boundary conditions, the constitutive properties, and the initial conditions.
The constitutive properties of the fault have been assigned in several different ways in the model examples studied in ref. 4. The properties used in the present paper are taken from the behavior of granite (26–29) and serpentine (30–33) and are designated L1 in ref. 4. In the Parkfield section itself, the fault is considered to have the properties of granite, which is velocity-strengthening at the surface, velocity-weakening from a depth of 1.8–8.2 km, and velocity-strengthening below that. To the north of the Parkfield section, the material is assumed to act like serpentine at low velocity; namely, it is velocity-strengthening and shows only the direct effect. Because serpentine is velocity strengthening and is weak (30–33), its presence on the San Andreas fault in the creeping section could simultaneously explain the lack of significant earthquakes there and the low absolute and relative strength of this part of the fault (53–55). A smooth transition over 6 km along strike occurs between the granite-like and the serpentine-like sections.
The slip on the fault causes changes in strain on the surface of the earth where it is possible to make measurements in the real world. Since detection of these changes in strain is one of the more likely ways that the slip at depth might be detected, calculation of these changes has been done for this model. Because the rate of slip on the fault best characterizes any particular stage in the model earthquake, the associated rate of strain at the earth’s surface has been calculated and displayed.
The detailed behavior of the model is affected by the size of the cells on the fault plane used to approximate a more continuous distribution of slip. A larger number of smaller cells does a better job of approximating the behavior of a continuum (5), but it uses considerably more computer time. Because of this time constraint, the behavior has been studied most extensively for a model in which the smallest cells are squares, 1.0 km on a side. A few examples of the behavior when the smallest cells are 1080 m, 360 m, and 120 m on a side have been briefly studied, but this work is still in progress. Preliminary results are shown comparing the behavior as the cell size is decreased. Because larger cells are more compliant than smaller ones, cells are more able to slip independently from their neighbors when they are larger. The discreteness intro-

FIG. 4. Behavior at selected times in the model with the smallest grid size h=1 km. In A the boundary condition of 35 mm/year is applied over the brown area and the behavior is calculated over the grey area with the grid. In the interseismic period (B), the Parkfield patch is essentially locked and the rest of the fault is slipping at 35 mm/year. A rapid creep event (D) would represent a false alarm. At other times (C and E-H), the only unusual behavior is that a variety of cells at the north end of the Parkfield section are creeping rapidly, due to the boundary condition of slip extending to the surface in the north. Finally, within an hour of the earthquake (I-K), the pattern of strain rate on the earth’s surface is developed, but the magnitudes are too small to detect. The earthquake (L) in this model does not deal properly with the dynamics of rupture.
duced by oversized cells introduces a spatial and temporal heterogeneity that in a crude way proxies for the heterogeneity that variations in rock type and geometric irregularities on the fault may cause in the real world. As models are studied with smaller grid sizes, it will be possible to introduce heterogeneities in material properties that can represent real world variations in a more controlled way. The cell size used (5) should be substantially less than h*=2GDc/[π(B−A)m], where G is the shear modulus (30 GPa) and (B−A)m is the maximum value of B−A, where B−A=σn(b−a). For the parameter values used here [model L1 of ref. 4], (B−A)m is 0.575 MPa and Dc is 13 mm, giving h*=431 m. Our cell sizes h of 1080, 360, and 120 m represent h/h* of 2.51, 0.84, and 0.28.
Behavior of the Model. In the model the velocity weakening part of the Parkfield segment slips very slowly in the interseismic period. Its northwest end is eaten into by episodic creep events until one of them, at a depth where the velocity weakening is the greatest, accelerates to a slip velocity of 1 m/s, the definition used for dynamic rupture, and becomes the hypocenter. Representative typical images from an earthquake cycle are shown in Fig. 4 B-L. A complete set of such images exists in a video showing the behavior of the model in more detail.
Results of a preliminary examination of the effect of cell size on the behavior of the model is shown in Fig. 5. In this figure, models with three sizes for the smallest cells are shown, all for 0.1 s before the earthquake to show the final stage of acceleration of the eventual hypocentral cell. The general location of the hypocentral cell is similar in these models. However, this is a complex issue, since the model tends to move the hypocenter to nearby slightly larger cells and so successive models were run in each case to find a distribution of cells so that the hypocenter occurred within the smallest cells.
From the point of view of earthquake prediction, it is the pattern in space and time of the accelerating slip leading up to the main shock that might be used to predict it.
Slip in the model at velocities higher than the 35 mm/year boundary condition might be expected to correspond to increased microearthquake activity. The coarseness of the grid precludes explicit modeling of small earthquakes. It is reasonable to imagine that the more rapid the slip event, the more numerous the small earthquakes or the larger their size, since these more rapid creep events correspond to larger moment rates. Thus the spatial and temporal variation in moment rate in the model might be expected to be detected in the earth by changes in seismicity. The model predicts that foreshocks should occur and that they are more numerous as the mainshock approaches. The model also shows what might be considered to be false alarms, for example, a rapid creep event at 2.8 years prior to the mainshock (Fig. 4D) that can be regarded as a foreshock.
Some of the creep events that occur in the few years prior to the mainshock are large enough that they are reflected in the pattern of strain rate on the earth’s surface. This is invariably true for the creep event that accelerates to become the mainshock, and it is true for the larger of the “foreshocks.”
Predictability of the Model Earthquake. The premonitory increases in slip in the hypocentral region that precede the main shock are expected to correspond in the earth to increases in microseismicity and in foreshocks that could be
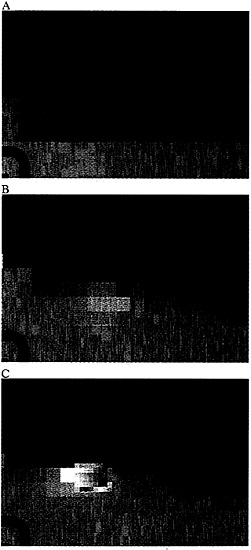
FIG. 5. Details of the models with successively smaller grid sizes at 0.1 s before the earthquake. (A) The smallest grid size is 1080 m; h/h* =2.5. (B)h=360m; h/h*=0.83. (C)h=120 m; h/h*=0.28. Finally, in C, the grid size is small enough that the cells begin to behave as a group rather than individually.
detected seismically and to increases in strain and strain rate that might or might not be detectable at the earth’s surface. There might also be changes in other parameters such as electric and magnetic fields (56). The question is whether or not these various changes could be used to predict the earthquake.
Strain at earth’s surface. Whether the pattern of strain rate on the Earth’s surface can be used to detect that the main shock is coming is still debatable. Clearly the pattern itself develops soon enough prior to the mainshock in the 1-km grid size example shown in Fig. 4 to be useful if it could be observed, although it only gives a few hours warning. However, the magnitude of the increase in strain rate is not large. A few hours prior to the mainshock the maximum strain rates are only 5×10−15 s−1. Given that one might want to detect this in perhaps an hour, a strain of 2×10−11 would have to be detectable. Given the noise spectrum for strain (57–59), strains of ≈10−9 are detectable at that period, suggesting that the increase in strain rate is about two orders of magnitude below the detectable level. Similarly at 1 s before the mainshock the maximum strain rates are 2×10−11 s−1, requiring a detectability of better than 10−11 at a 1-s period. This is about an order of magnitude below the detectability limit at a 1-s period. Fig. 6 shows plots of the maximum strain rates observed on the Earth’s surface in the model versus logarithm of time before the earthquake, together with an estimate of the detectability limit for sampling at appropriate rates for that period. This is analogous to the plots shown in ref. 2 for the two-dimensional earthquake model of ref. 1. As expected (2), the signals for the three-dimensional model are lower than for the two-dimensional model. The difference is large enough that whereas the two-dimensional model strain rates might have been detectable, the three-dimensional ones seem too small. Note that in the model for which h/h* is the smallest, a large number of creep events occur that might be observed. However, it is important to note that the duration of these creep events is very small and so the fact that they seem to rise above the detectability limit is misleading since the time axis is time before the eventual earthquake, not the time before the particular creep event. On the other hand, as discussed below, these events could be associated with microseismicity and so be detected on seismometers.
Note that the detectability arguments just presented correspond to one’s ability to detect the pattern of the rate of strain at any instant prior to the mainshock, without regard for prior history. If a pattern of strain develops that is consistently growing in the same area over some interval of time (4), then that pattern might be detected, even if it could not be with only a brief measurement. Thus, based on the analysis done to date, it is too early to be sure whether or not the strain at the earth’s surface might be useful in predicting the earthquake.
Microseismicity. It is also an open question as to whether the expected increase in slip rate could be detected from increases in microseismicity. In the model, there is an increase in the moment release in the vicinity of the hypocenter in the few years late in the seismic cycle prior to the earthquake. As far as we know, even if much of this increase in slip occurred aseismically, it should be accompanied by an increase in microseismicity. This should be detectable seismically and might serve to give a general intermediate-term prediction of the earthquake. The question is whether or not such an increase could be used for a short-term earthquake prediction. If it were to occur as smoothly as in the model, it might be quite useful for such a prediction. However, if it occurs primarily through discrete earthquakes of magnitude 3 to 5, then it may be difficult to discern enough details of the pattern of accelerating activity to allow a short-term prediction.
There is one tantalizing result from this model in terms of providing a path to intermediate- and short-term earthquake prediction. In the 2.8 years after the foreshock (Fig. 4D), the logarithm of the rate of moment increase on the eventual hypocentral cell increases essentially linearly with logarithm of time to the mainshock (Fig. 7). Thus if there was some way to follow this increased rate of moment release seismically (for example, by monitoring microseismicity), then the data would “point” to the eventual time of the mainshock with increased precision as the time of the mainshock approached. In principal, such monitoring could also be done with a borehole strain meter in a deep borehole if one knew where to place it. Such a linear increase on a log-log plot is exactly the form that K.Aki (personal communication) suggested would make an ideal earthquake prediction. The linear change of moment rate on this log-log plot has a slope of approximately minus one in terms of logarithm of time to the earthquake. Thus, over the
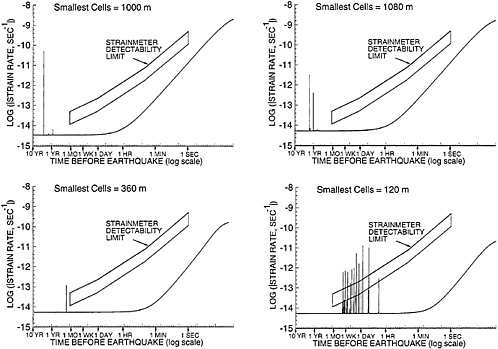
FIG. 6. Strain rate as a function of time prior to the earthquake with four grid sizes. These are calculated for the point on the earth’s surface where the strain rate is the highest. In all cases the strain rate is smaller than can be detected in the time interval available, given the behavior of sensitive borehole instruments installed in the earth.
essentially linear portion of this curve the moment rate and the time to the earthquake are inversely proportional.
The way the linear increase in moment rate versus time to the earthquake on a log-log plot (Fig. 7) might be used to predict the time of the earthquake is shown in Fig. 8. In practice one would not know the actual time of the earthquake to make a plot similar to that in Fig. 7. However, if the logarithm of the moment rate data were plotted versus the logarithm of various possible times until the earthquake, then only if the correct time is used will the plot remain linear. As shown in Fig. 8, the moment rate will either climb too rapidly as the time is approached if too long a time is used, or it will not climb rapidly enough if too short a time is used. The departure from linearity on the log-log plot becomes more apparent as the time approaches that of the earthquake. As shown in Fig. 8, it allows making increasingly more accurate time predictions as the earthquake approaches. In general, for the ideal model behavior, the departure from linearity resulting from choosing an erroneous time becomes evident at a time before the earthquake that is 1–3 times longer than the error in the time chosen. Thus, in Fig. 8, the departure from linearity by making an error in the time of the earthquake of 1 day is very evident 2 days before the earthquake but cannot be seen 1 week before it. The same can be seen for longer and shorter times.
Whether this behavior of the ideal model could be useful for earthquake prediction is not clear. The question is whether the signal (the logarithm of the moment rate) can be detected with sufficient accuracy. There are two possible problems. The moment rate might be too low to observe even with down-hole seismometers, and the discreteness of the microseismic events might preclude seeing any underlying pattern in the moment rate. In the model, at a time 2 days before the actual earthquake the difference between the moment rate for a correct guess and for a guess late by 1 day is only a factor of 2 in moment rate. Whether this could be distinguished given the discretization of seismic moment rate is questionable. One way to get some idea of what the moment rates are and how they compare with what one can observe is to note that in Fig. 7 the moment rate on the hypocentral cell reaches 35 mm/year corresponding to the average slip rate on the fault in the
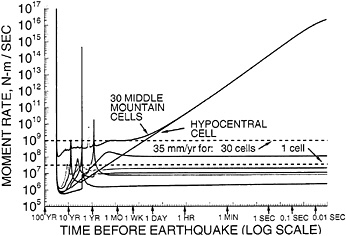
FIG. 7. Linear increase on a log-log plot of the moment rate on the hypocentral cell for the model with 1-km cell sizes. This corresponds to a reciprocal relationship between the moment rate and the time until the earthquake. The moment rates on a variety of other cells are also illustrated. They peak at various times corresponding to creep events that occur on only one cell. The moment rate for 30 1-km cells under Middle Mountain is also shown, as is the moment rate corresponding to 1 and to 30 cells slipping at 35 mm/year.
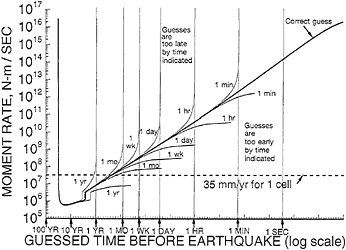
FIG. 8. Estimation of the time of the earthquake by plotting the moment rate versus a variety of possible times to the earthquake and seeing which time gave the most linear plot.
creeping section at 2.5 months before the mainshock. Whether this is a detectable rate for a 1-km square patch on the fault with a sampling time of a few weeks depends on the sensitivity of the seismic system. It might be detectable by using the down-hole seismic array around Middle Mountain at Parkfield. By a day before the earthquake, the moment rate on the hypocentral cell increases by a factor of 60 over the rate corresponding to 35 mm/year, but the available sampling time to detect this is much smaller. If this increase in moment rate occurs only via a few discrete earthquakes, then the increasing moment rate may not be clearly seen as part of a gradually accelerating signal. These earthquakes would be foreshocks, but the pattern might not be clear enough for them to be recognized as such.
Thus the problems of predicting the model earthquake seem similar to the problems of predicting real earthquakes, even if preceded by foreshocks. Namely, how does one discriminate a pattern of increasing moment rate preceding the eventual mainshock when that increasing moment rate is strongly discretized. Some kind of temporaral averaging of the moment rate may be a solution, but the accelerating pattern could be lost in the averaging.
Conclusions. The behavior of the model Parkfield earthquakes discussed here is based on laboratory determinations of rock friction constitutive laws. The model earthquakes show premonitory slip prior to the eventual mainshock, but the spatial and temporal extent of it is relatively small. Like prediction of real earthquakes, the prediction of these model earthquakes is not an easy task. It is encouraging for the usefulness of the models that they are similar in many ways to the behavior of real faults. However, even if in principle one could predict the model earthquakes, this may be impossible in a realistic field setting. This is due to one’s inability to place instruments close enough to the accelerating part of the fault to detect the motions and to recognize an accelerating slip pattern when it occurs via discrete events.
The mainshock grows out of accelerating local creep and failure as the stress reaches sufficiently high levels, just as in the laboratory experiments. The modeling suggests that monitoring microseismicity may be the most sensitive way to detect the growing failure.
Much of the modeling on which this work is based was done in collaboration with William Stuart and I am grateful for his generosity in sharing his computer programs and his insight. My work was supported by U.S. Geological Survey Grants 1434–93-G-2278 and 1434–94-G-2422 and by National Science Foundation Grants EAR-88–16791, 9206649, 9220005, and 9317038.
1. Tse, S.T. & Rice, J.R. (1986) J. Geophys. Res. 91, 9452–9472.
2. Lorenzetti, E.A. & Tullis, T.E. (1989) J. Geophys. Res. 94, 12,343–12,361.
3. Stuart, W.D. & Tullis, T.E. (1992) Eos Trans. AGU 73, Fall Meeting Abs. Supp., 406–407.
4. Stuart, W.D. & Tullis, T.E. (1995) J. Geophys. Res. 100, 24,079–24,099.
5. Rice, J.R. (1993) J. Geophys. Res. 98, 9885–9907.
6. Beroza, G.C. & Jordan, T.H. (1990) J. Geophys. Res. 95, 2485–2510.
7. Jordan, T.A., Ihmlé, P.F. & Marone, C.J. (1993) Eos, Trans. AGU 74, Spring Meeting Abs., Supp., 292.
8. Dieterich, J.H. (1994) J. Geophys. Res. 99, 2601–2618.
9. Dieterich, J.H. (1992) Tectonophysics 211, 115–134.
10. Marone, C., Vidale, J.E., Ellsworth, W.L. (1995) Geophys. Res. Lett., 22, 3095–3098.
11. Vidale, J.E., Ellsworth, W., Cole, A. & Marone, C. (1994) Nature (London) 368, 624–646.
12. Dieterich, J.H. (1972) J. Geophys. Res. 77, 3690–3697.
13. Beeler, N.M., Tullis, T.E. & Weeks, J.D. (1994) Geophys. Res. Lett. 21, 1987–1990.
14. Rice, J.R. & Ruina, A.L. (1983) Trans ASME, J. Appl. Mech. 50, 343–349.
15. Tullis, T.E. (1988) Pure Appl. Geophys. 126, 555–588.
16. Dieterich, J.H. (1978) Pure Appl. Geophys. 116, 790–806.
17. Dieterich, J.H. (1979) J. Geophys. Res. 84, 2161–2168.
18. Dieterich, J.H. & Kilgore, B.D. (1994) Pure Appl. Geophys. 143, 283–302.
19. Gu, J.C., Rice, J.R., Ruina, A.L. & Tse, S. (1984) J. Mech. Phys. Solids 32, 167–196.
20. Rice, J.R. & Gu, J.C. (1983) Pure Appl. Geophys. 121, 187–219.
21. Blanpied, M.L. & Tullis, T.E. (1986) Pure Appl. Geophys. 124, 43–73.
22. Gu, Y. & Wong, T.-f. (1991) J. Geophys. Res. 96, 21,677–21,691.
23. Gu, Y. & Wong, T.-f. (1992) Rock Mechanics Proceedings of the 33rd U.S. Symposium, (A.A.Balkema, Rotterdam), pp. 151–158.
24. Gu, Y. & Wong, T.-f. (1994) AGU Geophys. Monogr. Ser. 83, 15–35.
25. Weeks, J.D. & Tullis, T.E. (1985) J. Geophys. Res. 90, 7821–7826.
26. Tullis, T.E. & Weeks, J.D. (1986) Pure Appl. Geophys. 124, 10–42.
27. Blanpied, M.L., Lockner, D.A. & Byerlee, J.D. (1995) J. Geophys. Res. 100, 13,045–13,064.
28. Beeler, N.M., Tullis, T.E., Blanpied, M.L. & Weeks, J.D. (1996) J. Geophys. Res. 101, in press.
29. Blanpied, M.L., Lockner, D.A. & Byerlee, J.D. (1991) Geophys. Res. Lett. 18, 609–612.
30. Reinen, L.A., Weeks, J.D. & Tullis, T.E. (1991) Geophys. Res. Lett. 18, 1921–1924.
31. Reinen, L.A., Tullis, T.E. & Weeks, J.D. (1992) Geophys. Res. Lett. 19, 1535–1538.
32. Reinen, L.A., Weeks, J.D. & Tullis, T.E. (1994) Pure Appl. Geophys. 143, 318–358.
33. Reinen, L.A. (1993) Ph.D. thesis (Brown Univ., Providence, RI).
34. Dieterich, J.H. (1981) AGU Geophys. Monogr. Ser. 24, 103–120.
35. Ruina, A.L. (1983) J. Geophys. Res. 88, 10359–10370.
36. Linker, M.F. & Dieterich, J.H. (1992) J. Geophys. Res. 97, 4923–4940.
37. Chester, F.M. (1994) J. Geophys. Res. 99, 7247–7261.
38. Marone, C., Raleigh, C.B. & Scholz, C.H. (1990) J. Geophys. Res. 95, 7007–7025.
39. Tullis, T.E., Beeler, N.M. & Weeks, J.O. (1993) Eos Trans. AGU, 74, Spring Meeting Abs. Supp., 296.
40. Okubo, P.G. & Dieterich, J.H. (1984) J. Geophys. Res. 89, 5815–5827.
41. Okubo, P.G. & Dieterich, J.H. (1986) AGU Geophys. Monogr. Ser. 37, 25–35.
42. Ohnaka, M. (1986) AGU Geophys. Monogr. Ser. 37, 13–24.
43. Spray, J.G. (1987) J. Struct. Geol. 9, 49–60.
44. Spray, J.G. (1988) Contrib. Mineral. Petrol. 99, 464–475.
45. Shimamoto, T. (1994) J. Tectonic Res. Group Japan 39, 103–114.
46. Brune, J., Brown, S. & Johnson, P. (1992) Tectonophysics 218, 59–67.
47. Heaton, T.H. (1990) Phys. Earth Planet. Inter. 64, 1–20.
48. Beeler, N.M. & Tullis, T.E. (1996) Bull. Seismol. Soc. Am., in press.
49. Perrin, G., Rice, J.R. & Zheng, G. (1994) J. Mech. Phys. Solids, 43, 1461–1495.
50. Brune, J.N., Henyey, T.L. & Roy, R.F. (1969) J. Geophys. Res. 74, 3821–3827.
51. Lachenbruch, A.H. & Sass, J.H. (1973) Proceedings of the Conference on Tectonic Problems of the San Andreas Fault System, eds. Kovach, R.L. & Nur, A. (Stanford Univ. Press, Palo Alto, CA), pp. 192–205.
52. Lachenbruch, A.H. & Sass, J.H. (1980) J. Geophys. Res. 85, 6185–6222.
53. Hickman, S.H. (1991) Rev. Geophys. Suppl. 759–775.
54. Zoback, M.D., Zoback, M.L., Mount, V.S., Suppe, J., Eaton, J.P., Healy, J.H., Oppenheimer, D., Reasenberg, P., Jones, L., Raleigh, C.B., Wong, L.G., Scotti, O. & Wentworth, C. (1987) Science 238, 1105–1111.
55. Rice, J.R. (1992) Fault Mechanics and Transport Properties of Rocks, Academic Press, London, 476–503.
56. Stuart, W.D., Banks, P.O., Sasai, Y. & Liu, S.-W. (1995) J. Geophys. Res. 100, 101–110.
57. Agnew, D.C. (1986) Rev. Geophys. 24, 579–624.
58. Johnston, M.J.S., Borcherdt, R.d. & Linde, A.T. (1986) J. Geophys. Res. 91, 11,497–11,502.
59. Wyatt, F.K. (1988) J. Geophys. Res. 93, 7923–7242.









