This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.
Slip complexity in earthquake fault models
(physics of earthquakes/seismic complexity/earthquake statistics/fault mechanics)
JAMES R.RICE AND YEHUDA BEN-ZION
Department of Earth and Planetary Sciences and Division of Applied Sciences, Harvard University, Cambridge, MA 02138
ABSTRACT We summarize studies of earthquake fault models that give rise to slip complexities like those in natural earthquakes. For models of smooth faults between elastically deformable continua, it is critical that the friction laws involve a characteristic distance for slip weakening or evolution of surface state. That results in a finite nucleation size, or coherent slip patch size, h*. Models of smooth faults, using numerical cell size properly small compared to h*, show periodic response or complex and apparently chaotic histories of large events but have not been found to show small event complexity like the self-similar (power law) Gutenberg-Richter frequency-size statistics. This conclusion is supported in the present paper by fully inertial elastodynamic modeling of earthquake sequences. In contrast, some models of locally heterogeneous faults with quasi-independent fault segments, represented approximately by simulations with cell size larger than h* so that the model becomes “inherently discrete,” do show small event complexity of the Gutenberg-Richter type. Models based on classical friction laws without a weakening length scale or for which the numerical procedure imposes an abrupt strength drop at the onset of slip have h*=0 and hence always fall into the inherently discrete class. We suggest that the small-event complexity that some such models show will not survive regularization of the constitutive description, by inclusion of an appropriate length scale leading to a finite h*, and a corresponding reduction of numerical grid size.
Earthquakes show aperiodic recurrence with generally irregular slip during large events and pronounced “asperities” (local areas of high moment release) in the slip distribution. Small to moderate events on a single large fault segment tend to have a power law frequency-size (F-S) distribution of the Gutenberg-Richter (G-R) type, although such distribution rarely extends to the largest events on an identifiable fault segment (1) and generally underestimates seismic risk. Amid this disorder there is, at least at Parkfield, fairly regular recurrence of microearthquakes over small patches (2), and while those patches generate more than half of the microearthquakes, they occupy only a small portion of fault area, about 1 km2 collectively. The starting of an earthquake is complex, with a nucleation zone of low initial rate of moment release relative to the main shock, before rapid dynamic breakout, plausibly estimated to occupy rupture areas with dimensions ranging from under 50 m to 5 km, sizes that tend to scale with the final size of the earthquake (3) and are much larger than a nucleation size h* based on fault constitutive laws. Also, seismic radiation is usually enriched in high-frequency content in a way suggesting phase incoherence during the earthquake slip process.
Our focus in the present report is on the following question: What features of theoretical earthquake fault models give rise to such complexities? We consider the class of models that incorporate laboratory-derived fault constitutive laws, implemented within continuum mechanics, in settings that meet primary thermal, geologic, and geodetic constraints, as in earlier studies by Tse and Rice (4), Rice (5), and Ben-Zion and Rice (6).
The issues involving slip complexity may have implications for another problem in earthquake theory, namely, the overall stress levels at which faulting occurs. Some, if not all, major faults slip under low overall driving stress compared to strength estimated by assuming friction coefficient f in the typical lab-based range f=0.6 to 0.8 at the onset of slip and assuming normal stress σn comparable to the overburden and hydrostatic pore pressure p. In the case of the San Andreas fault, there is an absence of heat flow, suggesting that the average stress acting during slip is far less than the strength as estimated above, and probably less than 10–20 MPa. Also, the steep inclination of the principal compressive direction to the fault trace and existence of thrust structures in the adjacent crust suggest that more stress is being sustained on faults in the adjacent crust than on the San Andreas fault. However, arguments for irrelevance of lab friction results to the earth must be tempered by evidence from borehole studies that in situ stresses in active areas are generally in agreement with expectations from the lab/range (7).
In trying to understand earthquake complexities, we pose the following questions: (i) Can slip complexity like that in natural events be generated by the nonlinear dynamics of stressing and rupture on an essentially smooth fault, (ii) is, instead, the heterogeneity of fault zones in the form of geometric disorder (step-overs, branching) and perhaps other strong property variations (lithological contrasts, pressurized compartments) central to the process, or (iii) is something else responsible?
The first possibility, that complexity is generated by nonlinear dynamics on a smooth fault, did not emerge in the first modeling of slip histories on faults between elastic crustal plates with laboratory-derived friction laws (4, 8). It was, however, raised as a serious possibility in three important papers in 1989, one by Horowitz and Ruina (9) on faults with lab-based friction between deformable elastic continua, another by Carlson and Langer (10) on the dynamics of Burridge-Knopoff (B-K) arrays of spring-connected blocks with classical velocity-weakening friction laws, and a third by Bak
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
Abbreviations: F-S, frequency-size; G-R, Gutenberg-Richter; B-K, Burridge-Knopoff; 2D and 3D, two and three dimensional, respectively.
and Tang (11) on a simple cellular-automata model of failure at a critical stress and stress shedding to neighboring cells.
Rice (5) suggested that some of the above models [not including the work of Horowitz and Ruina (9)] showed aspects of slip complexity as an artifact of their use of simplified constitutive laws, which are not fully compatible with continuum elastic models, as we discuss below. It was also suggested that such models produce results that depend on the cell size (or in the B-K context block spacing) h of the numerical scheme and should not properly be regarded as models of smooth faults. Instead, they may be taken as approximate models of strongly disordered faults with a fundamental scale of heterogeneity equal to h. Such an interpretation has been expanded upon by Ben-Zion and Rice (6, 12) whose results are summarized subsequently. The conclusion reached was that some of the modeling introduced as showing complexity through the first route, dynamics on a smooth fault, may have a surer physical interpretation as examples of the second route to complexity, strong heterogeneity. This conclusion has, however, been contested (13, 14) and we return to it below.
It has been a concern in evaluating the first possibility, (i) that previous studies (5, 6) from this group used a quasidynamic approximation, that we explain shortly, rather than fully solving the equations of elastodynamics, and that earlier studies (4) used similar quasistatic analyses. The question was whether the conclusions (5, 6, 12) reached on complexity would change if there was full inclusion of inertial dynamics. Indeed, Carlson and Langer (10) suggested that the complexity of slip history predicted for their B-K array was linked to inertial dynamic effects, which were fully included (within the lumped mass and one-dimensional fault model approximations) in their simulations. As we remark below, however, we think there is evidence that features of their classical constitutive description, and also of their numerical solution algorithms [abrupt strength drop “σ” imposed at onset of slip, a feature repeated in Shaw (13) and Myers et al. (14)], which are not fully suitable for representation of slip on a smooth fault, may have a dominant role in giving the small-event complexity of the G-R type that they found. Cochard and Madariaga (15, 16) have also argued, from elastodynamic studies of repeated antiplane slip ruptures on an isolated fault segment in an elastic continuum, that inertial effects are critical to the complexity they observe. However, they seem to require a restricted class of constitutive assumptions to find such complexity and the small event distribution they show is not of G-R type (16).
We have recently developed the methodology to use full elastodynamics in some of our modeling of repeated earthquakes and present some results that support previous conclusions (5, 6, 12) from this laboratory; we have found no evidence that inclusion of fully inertial elastodynamics brings small event complexity of G-R type to our smooth fault models.
Smooth Fault Modeling
To understand the response of a smooth fault, we have studied slip-rupture sequences along a smooth vertical strike-slip fault in an elastic half-space. The basic model for this, from Rice (5) and subsequent studies (6, 17, 18), is shown in Fig. 1. The fault is driven below a depth of 24 km at rate Vp1(=35 mm/year in cases shown here), and the slip history is calculated in the shallower zone. The modeling includes laboratory-constrained temperature, and hence depth, variability of friction properties, based on experiments on granite gouge under hydrothermal conditions by Blanpied et al. (19). The laboratory data were adapted (5) for a depth-variable model of frictional properties of the crust by using a San Andreas fault geotherm, thus making the friction properties, denoted a and b subsequently, functions of depth z in the crust. The depth variation of the friction properties implies a transition from potentially
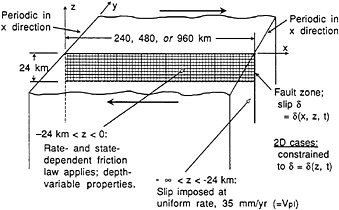
FIG. 1. Vertical strike-slip fault in elastic half space (5).
unstable velocity-weakening behavior, b>a, to inherently stable velocity strengthening, b<a, at an ≈14-km depth, and this serves to confine unstable slip to a roughly 15-km seismogenic depth. Over the 4.0- to 13.5-km depth, a=0.015 and b=0.019 in the model (5).
The friction model incorporates the observed displacement-dependent features of friction as in rate- and state-dependent frictional constitutive laws. Such assures that numerical fault models have a well-defined limit with refinement of the computational grid (5); the same is not necessarily the case with modeling based on classical friction laws without gradual displacement-dependent features of strength transition. In the two-dimensional (2D) versions of the modeling, slip δ varies just with depth z, δ=δ(z, t). In three-dimensional (3D) versions, it varies with depth and distance x along strike, δ= δ(x, z, t), with the slip distribution being repeated periodically along strike with wavelengths ranging from 240 to 960 km. Here δ(x, z, t)=ux(x, 0+, z, t)−ux(x, 0−, z, t), where (ux, uy, uz) is the displacement vector and we disallow discontinuities in uy and uz.
Our procedure for fully elastodynamic analysis is based on the spectral method of Perrin et al. (20), who use it for 2D studies of spontaneous antiplane rupture with rate- and state-dependent constitutive laws. The formulation has been extended (21) to spontaneous rupture in 3D, with slip or crack opening varying with position x, z on a plane and with time, but implemented thus far only for problems of tensile cracks. Thus all of our fully dynamic earthquake simulations to date are of 2D type, δ=δ(z, t).
The shear stress τ(x, z, t), corresponding to the tensor stress component τyx(x, 0, z, t) on the fault, has an elastodynamic representation in the form
τ(x, z, t)=τ°(x, z)+ϕ[δ(x′, z′, t′)−Vp1t′; x, z, t] −μV(x, z, t)/2cs,
where τo(x, z) is an initial value, μ is shear modulus, V=∂δ/∂t, cs is shear wave speed, and ϕ represents a quantity at x, z, t, which is a linear functional of its first argument, δ(x', z', t')−Vp1t′, over all x′, z′, t′ values within the “wave cone” influencing x, z, t. The functional ϕ can be written as an integral over that wave cone, as in several sources on elastodynamics (22, 23, 24, 25), and such is the usual starting point for related boundary integral formulations. We represent both ϕ and δ−Vp1t, in the form of Fourier series in x and z and use expressions from elastodynamics for how the time-dependent Fourier coefficients for ϕ are given as convolutions over prior time of those for δ−Vp1t .
The route to handling entire earthquake cycles elastodynamically begins with the recognition (20) that
![]()
Here ϕs is the functional of its first argument, which represents the static elastic stress at x, z, t associated with the slip distribution δ(x′, z′, t)−Vp1t. It is a functional over all x′, z′ at which the first argument is nonzero and has a simple representation in the spectral formulation. The residual elastodynamic effects, representing the actual wave mediation of stress transfers along the fault, are left in the functional ϕd, which is negligible at long times after a variation in slip. In developing our numerical method for repeated earthquakes, we have devised [see Zheng, et al. (44)] rational procedures for dealing with the related convolution integrals in such a manner that they make negligible contribution during most of the history but are active when the nature of response demands. This allows us to treat accurately, within a single computational procedure, long nearly quasistatic intervals of order 100 years interspersed with intervals of a few seconds duration during which inertial and wave effects become significant. Further details on the numerical procedures are given in the Appendix. The quasi-dynamic approximation (5, 6) amounts to setting ϕd=0, so that stress transfers along the fault are calculated by static elasticity (i.e., using ϕs only) but the radiation damping term −μV/2cs is retained so that solutions continue to exist during unstable slip episodes when the purely static elasticity equations do not have solutions.
The elastodynamic relation above shows how the histories of τ and V should be related if the equations of elasticity are to be satisfied in the regions of Earth adjoining the fault. We must also assure that their histories are related to one another by the constitutive law for the fault, phrased in terms of the friction coefficient f appearing in τ=f (σn−p), where σn is normal stress and p is pore pressure. We have studied several variations of the constitutive description in obtaining the results summarized here. Rice (5) used the Ruina-Dieterich “slip” version of the friction law (20, 26), a form where state can evolve only during slip and, hence, in which there is no restrengthening during truly stationary contact. Ignoring any high- or low-speed and short- or long-time truncations of the logarithmic terms, this law has the form
f=fo+a ln(V/Vo)+b ln(V0θ/L), dθ/dt=−(Vθ/L)ln(Vθ/L).
We take fo=0.6 and Vo=35 mm/year. The equation for dθ/dt may be more familiar when we write Ψ for ln(Voθ/L) and then realize that dΨ/dt=−(V/L)[Ψ+ln(V/Vo)] is implied. Alternatively, a Dieterich-Ruina “ageing” or “slowness” version of the friction law (20, 26) is sometimes used. This version includes restrengthening in truly stationary contact; it adopts the same equation as above for f in terms of V and θ but writes
dθ/dt=1−Vθ/L.
Rice (17) found that these two laws sometimes differ significantly in the complexity of slip histories predicted, with the former leading to periodically repeated events in the attempted simulations but the latter allowing apparently chaotic slip sequences of moderate and large events.
While it does not always seem to be necessary for well defined solutions to exist, we regularize the equation for f near V=0 by regrouping to identify an expression for exp(f/a) and reinterpret that as 2 sinh(f/a), and we replace V by |V| in the equation for dθ/dt; generally, |f|≫a and V>0. Note that both laws give θ=L/V in steady-state sliding so that the “steady-state” friction at slips much larger than L, at constant rate V, is
f=fss≡fo+(a−b)ln(V/Vo).
The class of rate- and state-dependent constitutive laws discussed, like for the simpler slip-weakening laws that they generalize so as to include velocity and ageing-time dependence of strength, involve a characteristic slip distance L. There is a nucleation size (5) h* associated with L; h* may also be called a coherent slip patch size in that it represents the size scale over which the slip on a surface between elastically deforming continua must remain relatively correlated. For the laws above (5),
h*=(2/π){μ/[(σn−p)(−Vdfss/dV)]}L =(2/π){μ/[(σn−p)(b−a)]}L.
The term in curly brackets may be of order 104 to 105 at slip rates important for nucleation. Proper numerical solution of the system of governing equations then requires that the cell size (or FFT sample point spacing) h satisfies h≪h*, and solutions of the discretized numerical system are qualitatively different (5, 6), in a way suggestive of small event G-R complexity, when we do not meet this condition. To keep h≪h* in our smooth fault models, but yet keep the number of numerical cells in a range allowing computational tractability with current computers, we must choose values of L that are large compared to lab values of 5–100 μm.
An option used in some runs is to allow a multimechanism type of response in which friction is competitive with creep (27, 28). The version we use assumes that deformation in the fault zone can include both slip on frictional surfaces and more distributed “creep” deformation, writing V=Vcreep+Vfriction, with both processes taking place under the same τ. The friction part, Vfriction, satisfies laws like those above, and to represent hot dislocation creep, we write Vcreep=cτ3, where c is negligible in the shallow cold crust but increases rapidly with temperature T and hence with depth in the fault zone. This feature does not seem to impact our conclusions on complexity and is not further discussed. Also, in the present work, the distributions of σn, p, and T with depth z are fixed. In a wider class of models including hydraulic and thermomechanical coupling of the fault to its surroundings (18, 29, 30), p and T are variable.
Some Simulation Results and Implications for Complexity
We find that all smooth fault models as thus far examined in our simulations fail to produce complex slip sequences like those of realistic G-R F-S statistics of earthquakes, at least for events with a maximum rupture dimension that is comparable to or less than the seismogenic depth. Rather, the responses involve sequences of large earthquakes, and sometimes mixtures of moderate and large events, repeating either periodically or chaotically. The models do not simulate the multitude of small- and intermediate-size earthquakes occurring in na
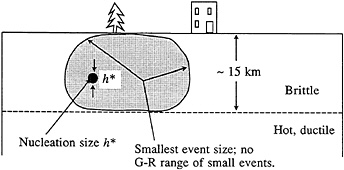
FIG. 2. Generic response for smooth fault models; to complexify with a G-R range of small events, we must stop the ruptures that, in smooth models, burst from nucleation size h* to a size limited by overall seismogenic zone dimensions.
ture, with ruptures smaller than the seismogenic thickness of the crust and some range of G-R scaling. This is shown schematically in Fig. 2: Rupture begins as gradually accelerating quasistatic slip that breaks away dynamically when the size of the slipping region becomes comparable to h*. The resulting rupture is not readily stopped on a smooth fault surface; its minimum dimension seems usually to be set by characteristic distances marking the brittle thickness of the crust. Most commonly in our basic model this is an ≈15-km thickness. In some models with extreme variation in effective normal stress (6), to represent large local variations in pore pressures, the size of crustal ruptures can be set by dimensions of such pressurized zones.
To see examples, consider the following 3D results (hence with the quasidynamic procedures): When using the Ruina-Dieterich “slip” version of the friction law and a 240-km repeat distance along strike, it was found (5) that each large earthquake tended to break the entire length of the model, so there were only great events. Recent studies (17) with the slip version confirm that result; indeed, there is a remarkable resistance to break-up into smaller events even when the periodic repeat distance along strike is increased to 960 km (calculations are barely feasible for much longer sizes). This is shown in Fig. 3 where we plot the depth-averaged slip
as a function of distance x along strike at 5-year intervals. The large separations between curves correspond to earthquakes, the smaller separations occur because the interval over which the depth average is done includes deep parts of the fault that creep continuously.
In contrast, a very different response occurs (17) when the Dieterich-Ruina ageing, or slowness, version is used, which includes restrengthening in truly stationary contact. Then, as seen in Fig. 4 for a simulation with 480-km repeat distance along strike, complex aperiodic earthquake sequences with a broad F-S distribution for large events do result. However, it is important to note that such occurs just for the population of large earthquakes, whose rupture length along strike is at least somewhat greater than the seismogenic depth (i.e., ruptures longer than 20–25 km). This limitation of complexity to large events is more clearly seen in Fig. 5 where we show slip δ(x=
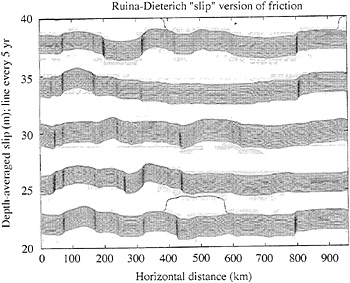
FIG. 3. Results for Ruina-Dieterich slip version of friction law, with h=1.5 km and h*/h=2: Depth-averaged slip ![]() versus distance x along strike, shown at 5-year intervals. The repeated distance in the model of Fig. 1 is 960 km.
versus distance x along strike, shown at 5-year intervals. The repeated distance in the model of Fig. 1 is 960 km.

FIG. 4. Results for Dieterich-Ruina slowness, or ageing, version of friction law, with h=0.75 km and h*/h=3: Depth-averaged slip ![]()
![]() versus distance x along strike, shown at 5-year intervals. The repeat distance in the model of Fig. 1 is 480 km. Note paucity of events with along-strike distance shorter than about 20 to 25 km.
versus distance x along strike, shown at 5-year intervals. The repeat distance in the model of Fig. 1 is 480 km. Note paucity of events with along-strike distance shorter than about 20 to 25 km.
0, z, t) versus z every 5 years at a particular place along strike, x=0. There are essentially no events with sizes between the nucleation size and seismogenic dimensions, and hence this model also fails to produce the multitude of small and intermediate events that makes up a G-R distribution, although it does show a complex history of large events. The simulations for Figs. 3–5 are based on the standard (5) a and b distributions with depth, but the amplitude of the distributions is varied by 0%, ±5%, or ±10% in different sectors along strike to enhance any potential tendencies for heterogeneous slip.
We think the large event complexity in the model using the ageing friction law may reflect saturation of the growth of stress concentration at a rupture front, with increase of rupture dimension, for events larger than the seismogenic thickness. We do not yet know why the same fails to stop ruptures and complexify with the slip law. Also, it cannot be concluded that only the ageing version gives disordered large event response, since Horowitz and Ruina (9) sometimes found a disordered chaotic slip history (but, so far as can be seen from their results, nothing corresponding to “small” events) with the slip version.
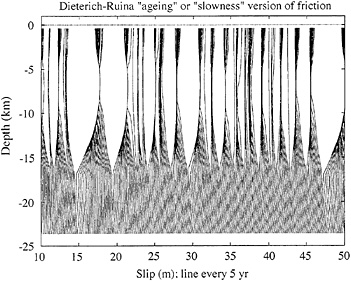
FIG. 5. Results for a model as in Fig. 4: Slip δ(x=0, z, t) versus depth z, shown at 5-year intervals, at x=0.
Fig. 6 shows slip δ(z, t) as a function of depth and time during an event encountered in a fully elastodynamic 2D simulation with the slip version of the constitutive law. Accelerating slip begins under quasistatic conditions over a zone that grows to size comparable to the nucleation size h* before rupture breaks out into a dynamic event. The rupture history is complex, with a first propagation upward to the Earth’s surface and then, a few seconds later, a propagation downward toward the base of the seismogenic zone that induces a step of further slip in the shallow crust. Fig. 7 shows slip versus depth every 5 years for a long fully elastodynamic simulation using the same law. For this case, as with all other fully dynamic 2D simulations done so far, with both the slip law and the slowness or ageing law, the long-term response is one of quasi-periodic large events.
While our elastodynamic studies have not shown a broad distribution of event sizes, Cochard and Madariaga (15, 16) found, for repetitive failures on an isolated fault segment, that some greater degree of complexity could arise in certain ranges of constitutive parameters. They assumed an ad hoc combination of slip-weakening and velocity-weakening friction, the latter regularized by a Dieterich-like state variable and involving linear decrease of steady-state strength with velocity to zero at a certain rate. Their results show ruptures extending over essentially all the segment when −dτss/dV is small or moderate in size compared to the radiation-damping coefficient μ/2cs. But when the weakening is stronger, such that −dτss/dV becomes comparable to μ/2cs, they find a broad, but not power-law-like (16), distribution of event sizes. Previous experience (25, 31) suggests that when −dτss/dV in their particular form of constitutive representation is large or small compared to μ/2cs, there will be only large events, so the complexity seems to require some parameter tuning. The results indicate that laws which gave complexity also showed partial stress drop and self-healing of slip during rupture (31), which can lock-in strong heterogeneities of stress and affect nucleation and arrest of subsequent events. Such does not occur in our work based on the Dieterich-Ruina logarithmic laws, which become relatively insensitive to changes in velocity at the high slip rates and thus give rupture propagation that is more in the mode of a classical enlarging shear crack. Studies of self-healing pulses (20, 32), of the type advocated by Heaton (33), concluded that a significant velocity weakening at slip rates toward the lower end of the range experienced during the dynamic event is critical to allowing the fault surfaces to relock
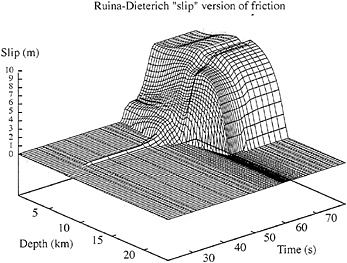
FIG. 6. Slip δ(z, t) during a dynamic event in a 2D fully elastodynamic simulation in a model based on the Ruina-Dieterich slip law, with h=0.375 km and h*/h=4: Accelerating slip begins under quasistatic conditions over a zone that grows to size comparable to the nucleaiion size h* before rupture breaks out into a dynamic event.
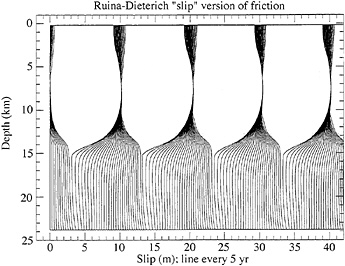
FIG. 7. Slip δ(z, t) versus depth z at 5-year intervals in a 2D fully elastodynamic simulation for a model in Fig. 6.
and produce a short-duration slip. (Such constitutive response is not the only route to short slip duration, which can apparently also be induced by strong fault heterogeneity, and also when slip is confined to a limited depth range.)
Unfortunately, the present experimental basis for the constitutive laws covers only the range of slip rates between, roughly, 10−7 and 1 mm/s, as is appropriate for earthquake nucleation. Their logarithmic form may ultimately derive from an Arrhenius activated rate process at the asperity contacts (27), but it may be conjectured that different physical mechanisms prevail at contacts during seismic instabilities, during which average slip rates (33) are on the order of 1 m/s and maximum slip rates near the rupture front might be as large as 100 m/s. In that range, the dynamics of rapid stress fluctuations from sliding on a rough surface, related tendencies for openings of the rupture surfaces, profuse microcracking, and perhaps some sort of fluidization of finely comminuted fault materials may result in very different velocity dependence, possibly with a dramatic weakening. Strong velocity weakening at high rates is also of interest as a possible mechanism, among others, allowing fault operation at low overall driving stresses.
A common feature of smooth fault models is that the growing stress concentration at a rupture tip is so strong that ruptures become unstoppable, at least until the growth of stress concentration with rupture size saturates at seismogenic dimensions. To complexify for small events, we must stop ruptures, and some possibilities for doing so may be as follows:
-
Self-organization of the stress distribution on a smooth fault, with extremely strong stress fluctuations over scales extending down to (at least nearly) h*. This is, of course, what we have been looking for in our smooth fault studies. They have not yet shown this mechanism and it may not exist or, at best, may exist only for special cases or tuned laws.
-
Heterogeneities within the fault system, which may be geometric (bends and offsets) or material (lithological contrasts and pressurized compartments). We lack good models of their effect, other than the simplified procedure of using oversized cells in the computations (6, 12), i.e., breaking the requirement h≪h* and instead choosing h>h*, as discussed below.
-
Bifurcation of rupture path and possible arrest. The elastodynamic stress field at a rupture tip distorts as speed accelerates toward the limiting speed (Rayleigh speed for in-plane slip and shear wave speed for antiplane slip), so that far less shear stress is resolved onto the main fault plane than on subfaults oriented at an angle to that plane (34), but their effect on rupture dynamics is yet to be studied. They may cause
-
the rupture path to bifurcate into unproductive directions for continued propagation, and hence arrest, or may just lead to intermittent propagation. Recent finite-element simulations of tensile failure (35), in a special formulation that allowed fractures to develop along all sufficiently stressed element boundaries, gave a reasonable description of analogous nonplanar rupture bifurcations in rapid failures, and effects of off-plane stressing are seen in recent antiplane strain lattice simulations (36).
Strongly Heterogeneous Faults and Inherently Discrete Models
In contrast to the generic response summarized above for smooth faults, we showed (6, 12) that models which incorporate approximately geometric fault zone disorder can produce slip histories with features that are indeed comparable to observed response, specifically with small event complexity like that of a G-R distribution. Those models represent disorder in a way that, as yet, has no rigorous mapping from any postulated geometric pattern of step-overs and bends along a fault. They do so by using oversized cells in the computational grid, i.e., they have h>h* rather than meeting h≪h*. Such models act as “inherently discrete” systems, in that cells of their computational grid are capable of failing independently of one another and thus may represent, approximately, strongly heterogeneous quasi-independent fault segments.
Several works have been presented as models of smooth faults that give complexity, not only for large events as in the cases discussed above, but also for model analogs of the small and intermediate events that make up typical G-R distributions. These include simulations based on the one-dimensional B-K model (10, 13), and for a 2D elastic plate that is elastically coupled to a substrate (14). It seems significant that all those models adopted constitutive laws (e.g., pure velocity weakening without a slip length L for state transition) and/or numerical procedures (specifically, imposition of an abrupt strength drop σ at the start of slip) that render the nucleation size h*=0. This is also true of a study (13) that introduced a second gradient of slip velocity term into the expression for friction to assure that the system had, in some sense, a continuum limit with reduction of cell size (or block spacing) h. All of those cases have h*=0 and hence necessarily fall into the inherently discrete class h>h*. Thus a sound interpretation of their results may be as actually representing locally heterogeneous fault systems. This seems at present the best candidate for explanation of why their response is so strikingly different from smooth fault models we have examined with h≪h*.
Ben-Zion and Rice (6, 12) studied inherently discrete fault systems in a 3D elastic matrix. This was done by allowing the fault zones to consist of quasi-independent oversized cells (h>h*=0), with stress dropping in each single cell failure to a lower level than that required to continue slip there as part of a multicell event, while using long-range stress transfer function appropriate for dislocations in a 3D elastic half-space. Different levels of fault zone disorder were represented approximately by various distributions of stress drops on failing segments (cells). The results from those works are summarized here as follows: Such models with a single size scale of disorder (i.e., cell size h) generate G-R-like scaling only over rupture area range h2 to ≈200h2 (≈2 magnitude units). The increase of stress concentration with rupture size in an elastic solid makes larger events statistically unstoppable [assuming (200h2)½ < seismogenic thickness]. These conclusions are similar to those of Fukao and Furumoto (37). Stronger potential bariers at larger scales are needed to extend the scaling range. A wide range of size scales of barriers, as for immature fault zones with high density and variability of offsets (1), leads to a broad region of power-law F-S statistics and random or clustered temporal recurrence of large events. A narrow range of size scales, as for mature highly slipped fault zones, leads to quasi-periodic recurrence and characteristic large events, a response generally compatible with the seismic gap hypothesis. Our discrete fault models with 3D elastic stress transfers generate, typically, discontinuous rupture areas. This feature, while being commonly observed in the field, is outside the scope of the cellular-automata and block-spring simulations with the simplified nearest-neighbor interactions. We have also noted, in our simulations with rate- and state-dependent friction, that models with oversized cells develop zones of initially slower moment release in earthquake nucleation that span several cells, before an abrupt break out, and hence those zones are much larger than h*; this has some consistency with the observations of Ellsworth and Beroza (3). Also, repeating small earthquakes are generated in such models, perhaps similar to what Nadeau et al. (2) found at Parkfield.
Other factors favoring control of fault zone response by geometric and/or property disorder including the following: The Wesnousky (1) correlations show that, among fault zones capable of significant earthquakes, small-event seismic productivity is greatest for geometrically disordered fault zones with many step-overs, and least for smooth highly slipped faults with few step-overs. There is also known to be enriched high frequency radiation from propagating ruptures, and an accepted picture for that involves the assumption of incoherent subevents as may be expected on a strongly heterogeneous fault. Also, the only existing quantitative laboratory-based theory of aftershocks and seismicity rate changes (38) is tacitly founded on a model that assumes that such seismicity occurs on quasi-independent fault segments. Short-duration slip pulses are also an expected consequence of strong fault heterogeneity, although other explanations are possible as remarked earlier.
The above discussion raises a dilemma from the standpoint of rigorous modeling. The models with oversized cells are at present an ad hoc representation of fault heterogeneity, stumbled upon inadvertently in some cases, and there is no accepted way of mapping distributions of geometric or material disorder into such a model. Yet the predictions of those models make it evident that there is much to recommend them. It is important therefore that studies of strongly inhomogeneous fault systems be done within the ground rules for rigorous modeling now understood (e.g., with h≪h*), to try to establish a sound basis for simpler representations such as the inherently discrete models. There are formidable difficulties in such a work: The calculations demand very fine grids (h must be small compared to scale lengths of each inhomogeneous feature) and, more fundamentally, in some cases it is not yet clear how to rigorously address the problems. An example of the latter is provided by a step-over on the fault surface. This is amenable to modeling, with effort, if we regard the step-over as two disconnected faults in elastic surroundings (39), but if we wish to consider distributed fracturing in the jog at the stepover, the problem moves beyond what present techniques can reliably handle.
Conclusions
The reported studies are part of an attempt to understand stressing, seismicity, and rupture characteristics associated with earthquakes on the basis of physical models of faulting processes. These combine basic mechanics with lab-based rheological laws for fault zones. A critical feature of those laws, particularly for modeling rupture on smooth surfaces in a deformable continuum, is that there is a characteristic sliding distance L for slip weakening or for alteration of contact population along the frictional surface. Associated with that L and scaling with it (but many orders of magnitude larger), there is a nucleation size, or coherent slip patch size, h*.
A summary of what we find from smooth fault models, analyzed with constitutive laws giving finite h*, and with cell
size h≪h* to properly represent the underlying continuum model, is as follows:
-
Dynamic events burst from the nucleation size h* to much larger size.
-
Some friction laws (e.g., the Ruina-Dieterich slip law) generally lead to rupture of the entire length of the brittle zone. Other laws [e.g., Dieterich-Ruina slowness law; also, a law formulated by Cochard (15, 16)] allow ruptures of only portions of the brittle thickness, as part of complex periodic or chaotic event sequences. However, even for such irregular sequences, the event sizes are generally much greater than h* and the distribution is not of the G-R type.
-
The growth of elastic stress concentration with rupture size leads to such strong stresses at the rupture tip that slip events become unstoppable, at least until the growth of stress concentration saturates at seismogenic dimensions. There is no small event complexity and, indeed, no small events.
-
While previous work reaching similar conclusions (5, 6) has been questioned on the grounds that it approximated the elastodynamic effects during rupture propagation, we have now been able to simulate the entire earthquake cycle in a rigorous elastodynamic framework, at least for our 2D models, and the conclusions are unchanged.
To complexify for small events, we must stop ruptures. The possibility of doing so by self-organization of the stress distribution on a smooth fault, with extremely strong stress fluctuations over scales extending down to (at least nearly) h* , has not been supported by our results. Thus we argue that some other mechanism is acting and the primary candidates are geometric and/or material heterogeneities within the fault system. At present we lack good and tractable mechanical models of their effect, other than models following the simplified procedure of using oversized cells in the computations.
A summary of our results based on such inherently discrete fault models (i.e., models with cell size h>h*) is as follows:
-
The numerical formulation no longer has an unambiguous correspondence to an underlying continuum problem, which may not be well posed in cases with h*=0.
-
Results show complex event sequences.
-
Some G-R-like range of small events seems to be generic.
-
Cells can fail independently of one another, which seems critical to the small event complexity and is why the class of models may be called “inherently discrete.”
-
Models of an inherently discrete fault in a 3D elastic solid (6, 12), with various brittle property distributions representing approximately different levels of fault zone disorder, show a variety of phenomena compatible with observations. These include G-R F-S distribution of small events, enhanced frequency of large events resembling the characteristic earthquake distribution for models with a narrow range of size scales, extended range of power-law F-S statistics for models with a wide range of size scales, noncontiguous rupture areas, and repeating small events near locked zones.
Models based on classical friction laws with L=0, or which adopt solution algorithms with imposition of abrupt strength drops, have nucleation size h*=0, so they are automatically in the inherently discrete class. Thus solutions based on those models may exhibit qualitative features, relating to small event complexity, which will not survive the regularization of choosing a friction law with the laboratory-based feature L>0, and appropriately reducing h below the then finite h*. Such models based on classical friction laws are best interpreted not as models for failure on an essentially smooth and homogeneous fault, as they have sometimes been intended, but rather as somewhat ad hoc models of heterogeneous faults, with an underlying fundamental scale of disorder corresponding to the cell size (or block spacing).
All simple fault models of the type discussed have no interaction between slip and alteration of fault-normal stress σn near the rupture tip. Such could result from roughness of fault surfaces, so that normal motions and consequent alterations of σn accompany sliding (40, 41). They could also result even on a smooth planar fault because nonlinear continuum constitutive properties, or heterogeneity of property distributions, outside the fault cause slip to induce an alteration in σn (e.g., a generic nonlinear continuum effect is that simple shear deformation alters the normal stress, and contrast even in linear material properties across the fault generates head waves (42, 43) leading to oscillatory variations of σn). Significant slip-induced reduction of σn is one mechanism for fault operation at low overall driving stress. Other possibilities are (i) that fault strength is low due to unusually weak materials or because pore pressure is elevated well above hydrostatic or (ii) that fault strength, at least at the onset of slip, is high but toughness is low because strength decreases significantly during rupture, due to strong velocity weakening and/or strong slip weakening (e.g., as consequence of shear heating of a fluid-infiltrated fault). Mechanisms of the low-toughness class could be important if, indeed, the stress field can self-organize into strong locked-in variations of stress (on the basis of our work here, that would have to happen with the help of some strong geometric of material property disorder), such that the peaks of stress left by prior events could serve as future nucleation sites while the overall stress is still low.
We thank A.Cochard, L.Knopoff, J.S.Langer, J.Morrissey, C.R.Myers, A.Needleman, B.E.Shaw, and G.Zheng for discussions. The studies were supported by the U.S. Geological Survey under Grant NEHRP 1434–94-G-2450 and the National Science Foundation Southern California Earthquake Center under Subcontract PO 621911 from the University of Southern California.
Appendix: Further Notes on Elastodynamic Methodology
We explain the methodology in connection with the 2D case. The slip distribution is taken in the form of the truncated Fourier series
where N is even and λ is the periodic repeat distance in the depth direction. We know (20) how to choose ϕ if such slip is imposed between adjoining half-spaces, and we do so in this work. Thus, to choose λ, let Hc be the crustal depth, i.e., the 24-km depth of Fig. 1. To meet the stress-free condition at the Earth’s surface, and also about some large depth z=−Hm in the mantle (we have taken Hm=2Hc or 4Hc), the slip distribution between the half-spaces must have mirror symmetry about z=0 and −Hm. The distribution of δ(z, t)−Vp1t over −Hm<z<0 (it vanishes for −Hm<z<−Hc) is thus extended with mirror symmetry to the domain 0<z<+Hm and replicated periodically with λ=2Hm. This is equivalent to representing the slip in a cosine series with terms cos(mπ z/Hm). Then the functional
can be represented in a similar series,
where each coefficient F(k, t) is given in terms of the corresponding coefficient D(k, t) by (20)
The first term within the curly brackets corresponds to ϕs and the second, with the convolution integral, corresponds to ϕd.
We deal with stress and displacement at values of x, z corresponding to FFT sample points, and these values are constrained to be related to one another to meet the constitutive law. In the 3D spectral implementation, δ(x, z, t) is expanded as a Fourier series in z and x, with vertical period 2Hm and mirror symmetries as above, and with horizontal period along strike as noted in Fig. 1. Other formulations (4–6, 8, 12, 25) have been based on a cellular basis set for the slip distribution, making it spatially uniform within rectangular cells and enforcing the constitutive law in terms of the stresses at cell centers.
The mirror symmetry condition of the spectral formulation causes the shear-free conditions τzx(x, y, 0, t)=τzy(x, y, 0, t) =0 to be met exactly at the Earth’s surface, and also at z= −Hm. However, the symmetry condition replaces the condition of vanishing normal stress, τzz(x, y, 0, t)=0, at the surface with vanishing displacement, uz(x, y, 0, t)=0. One condition implies the other in the 2D cases but not in 3D. A number of 3D trial runs with the quasidynamic procedures, comparing spectral results with uz=0 to those for the cellular slip basis in a formulation meeting τzz=0, have shown no qualitative differences for results with the different boundary conditions. That may be less so with full elastodynamics since the former case disallows Rayleigh waves on z=0.
The fully elastodynamic results so far available on modeling repeated sequences of earthquakes have used coarse meshes of 64 or 128 FFT sample points through the 24-km thickness. These are zero-padded below 24 km and repeated as images above the earth’s surface such that the total number of FFT points is 4 or 8 times greater than the basic 64 or 128 points for Hm=2Hc or Hm=4Hc, respectively. The studies of repeated earthquakes have been done on SPARC10 workstations, whereas the basic spectral elastodynamic methodology (20, 21) was also implemented on the massively parallel Connection Machine 5 (CM5, available with up to 512 processors). We anticipate that the version of the fully elastodynamic program with ϕs extracted and ϕd truncated, to deal with long earthquake histories, can be similarly implemented on the CM5 and extended to 3D fault modeling.
1. Wesnousky, S.G. (1994) Bull. Seismol. Soc. Am. 84, 1940–1959.
2. Nadeau, R.M., Foxall, W. & McEvilly, T.V. (1995) Science 267, 503–507.
3. Ellsworth, W.L. & Beroza, G.C. (1995) Science 268, 851–855.
4. Tse, S.T. & Rice, J.R. (1986) J. Geophys. Res. 91, 9452–9472.
5. Rice, J.R. (1993) J. Geophys. Res. 98, 9885–9907.
6. Ben-Zion, Y. & Rice, J.R. (1995) J. Geophys. Res. 100, 12959– 12983.
7. Zoback, M.D., Apel, R., Baumgartner, J., Brudy, M., Emmermann, R., Engeser. B., Fuchs, K., Kessels, W., Rischmuller, H., Rummel, F. & Vernik, L. (1993) Nature (London) 365, 633–635.
8. Stuart, W.D. (1988) Pure Appl Geophys. 126, 619–641.
9. Horowitz, F.G. & Ruina, A. (1989) J. Geophys. Res. 94, 10279– 10298.
10. Carlson, J.M. & Langer, J.S. (1989) Phys. Rev. A 40, 6470–6484.
11. Bak, P. & Tang, C. (1989) J. Geophys. Res. 94, 15635–15637.
12. Ben-Zion, Y. & Rice, J.R. (1993) J. Geophys. Res. 98, 14109– 14131.
13. Shaw, B.E. (1994) Geophys. Res. Lett. 21, 1983–1986.
14. Myers, C.R., Shaw, B.E. & Langer, J.S. (1994) “Slip complexity in a crustal plane model of an earthquake fault”, preprint, Report 94–98, NSF Institute for Theoretical Physics (Santa Barbara, CA).
15. Cochard, A. & Madariaga, R. (1994) EOS Trans. Am. Geophys. Union 75, Suppl. 44, 461 (abstr.).
16. Cochard, A., (1995) Ph.D. thesis (University of Paris).
17. Rice, J.R. (1994) EOS Trans. Am. Geophys. Union 75, Suppl. 44, 441 (abstr.).
18. Rice, J.R. (1994) EOS Trans. Am. Geophys. Union 75, Suppl. 44, 426 (abstr.).
19. Blanpied, M.L., Lockner, D.A. & Byerlee, J.D. (1991) Geophys. Res. Lett. 18, 609–612.
20. Perrin, G., Rice, J.R. & Zheng, G. (1995) J. Mech. Phys. Solids 43, 1461–1495.
21. Geubelle, P. & Rice, J.R. (1995) J. Mech. Phys. Solids 43, 1791–1824.
22. Das, S. (1980) Geophys. J.R.Astron. Soc. 62, 591–604.
23. Andrews, D.J. (1985) Bull. Seismol. Soc. Am. 75, 1–21.
24. Das, S. & Kostrov, B.V. (1987) J. Appl. Mech. 54, 99–104.
25. Cochard, A. & Madariaga, R. (1994) Pure Appl. Geophys. 142, 419–445.
26. Beeler, N., Tullis, T.E. & Weeks, J.D. (1994) Geophys. Res. Lett. 21, 1987–1990.
27. Chester, F.M. & Higgs, N. (1992) J. Geophys. Res. 97, 1859–1870.
28. Reinen, L.A., Tullis, T.E. & Weeks, J.D. (1992) Geophys. Res. Lett. 19, 1535–1538.
29. Sleep, N.H. & Blanpied, M.L. (1992) Nature (London) 359, 687–692.
30. Segall, P. & Rice, J.R. (1995) J. Geophys. Res. 100, 22155–22171.
31. Madariaga, R. & Cochard, A. (1994) Ann. Geofis. 37, 1349–1375.
32. Beeler, N.M. & Tullis, T.E. (1995) Bull Seismol. Soc. Am., in press.
33. Heaton, T.H. (1990) Phys. Earth Planet. Inter. 64, 1–20.
34. Rice, J.R. (1980) in Physics of the Earth’s Interior, eds, Dziewonski, A.M. & Boschi, E. (North-Holland, Amsterdam), pp. 555– 649.
35. Xu, X.P. & Needleman, A. (1994) J. Mech. Phys. Solids 42, 1397–1434.
36. Marder, M. & Gross, S. (1995) J. Mech. Phys. Solids 43, 1–48.
37. Fukao, Y. & Furumoto, M. (1985) Phys. Earth Planet. Inter. 37, 149–168.
38. Dieterich, J. (1994) J. Geophys. Res. 99, 2601–2618.
39. Harris, R. & Day, S.M. (1993) J. Geophys. Res. 98, 4461–4472.
40. Lomnitz-Adler, J. (1991) J. Geophys. Res. 96, 6121–6131.
41. Brune, J.N., Brown, S. & Johnson, P.A. (1993) Tectonophysics 218, 59–67.
42. Ben-Zion, Y. (1990) Geophys. J. Int. 101, 507–528.
43. Ben-Zion, Y. & Malin, P. (1991) Science 251, 1592–1594.
44. Zheng, G., Ben-Zion, Y., Rice, J.R. & Morrissey, J. (1995) EOS Trans. Am. Geophys. Union 76, Suppl. 46, 405 (abstr.).








