This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA
Dynamic friction and the origin of the complexity of earthquake sources
RAÚL MADARIAGA* AND ALAIN COCHARD
Département de Sismologie, Centre National de la Recherche Scientifique Unite Associée 195, Institut de Physique du Globe de Paris et Université Paris 7, case 89, 4 Place Jussieu, 75252 Paris Cedex 05, France
ABSTRACT We study a simple antiplane fault of finite length embedded in a homogeneous isotropic elastic solid to understand the origin of seismic source heterogeneity in the presence of nonlinear rate- and state-dependent friction. All the mechanical properties of the medium and friction are assumed homogeneous. Friction includes a characteristic length that is longer than the grid size so that our models have a well-defined continuum limit. Starting from a heterogeneous initial stress distribution, we apply a slowly increasing uniform stress load far from the fault and we simulate the seismicity for a few 1000 events. The style of seismicity produced by this model is determined by a control parameter associated with the degree of rate dependence of friction. For classical friction models with rate-independent friction, no complexity appears and seismicity is perfectly periodic. For weakly rate-dependent friction, large ruptures are still periodic, but small seismicity becomes increasingly nonstationary. When friction is highly rate-dependent, seismicity becomes nonperiodic and ruptures of all sizes occur inside the fault. Highly rate-dependent friction destabilizes the healing process producing premature healing of slip and partial stress drop. Partial stress drop produces large variations in the state of stress that in turn produce earthquakes of different sizes. Similar results have been found by other authors using the Burridge and Knopoff model. We conjecture that all models in which static stress drop is only a fraction of the dynamic stress drop produce stress heterogeneity.
A fundamental problem for understanding seismicity and the nature of large earthquakes is the origin of stress and slip complexity on seismic faults. Although seismicity has been carefully studied, the dynamics of the observed complexity of seismic sources is poorly understood although it is generally considered to be mainly due to fault segmentation. Initial work on seismic source dynamics (1–3) was derived from models of mode I fracture. In mode I, residual stress after opening a crack is obviously zero. This assumption had the virtue of simplifying the solution of the crack problems and allowed us to calculate radiation (4) and compare it with empirical models of radiation (5). At the end of the 1970s, the first models of complexity (asperities and barriers) were proposed but their relation to seismicity was not explored (6–8). A fundamental question that was left unanswered in these models was how do asperities arise on a fault loaded by very slow tectonic forces? According to current models, asperities are due to preseismic slip and foreshocks that concentrate stresses on locked areas of the fault; so that it is not enough to consider individual events, but the complete seismicity of the fault before a large event has to be studied in detail. To do this we have to specify the state of stress before and after an earthquake. In most of the previous work on earthquake dynamics as reviewed by Kostrov and Das (9), it was invariably assumed that residual stress after any event was uniform and equal to zero. This is very unlikely as we have attempted to show in our recent work (10, 11).
The question of the origin of complexity was posed from a completely different point of view by research on self-organized criticality (12), and on the artificial seismicity of the box and spring model of Burridge and Knopoff (13–18). These studies suggested that stress and slip would become spontaneously heterogeneous because of nonlinear instabilities in the mechanical model of a frictional fault. These results led to an interesting controversy because quasi-static models studied by Rice using the experimentally derived friction laws by Dieterich (19, 20) and Ruina (21) did not give rise to any significant heterogeneity. Rice and coworkers (22, 23) suggested that heterogeneity may be due to the lack of a continuum limit of some of these models.
Without waiting for the clarification of nature of heterogeneity of problems for the Burridge and Knopoff models, we started a study of a simple antiplane fault model (10, 11) where the only change with respect to Kostrov’s original formulation (3) was that the friction law was assumed to be rate dependent, as suggested by Carlson and Langer (14). In the present paper, we present results for a simple fault with rate-dependent friction that has been regularized at small scales by using a slip-weakening zone (24). We will demonstrate that depending on the value of a single parameter that measures the rate dependence of friction, we either produce complexity or suppress it. We are of course quite aware that our fault models are very crude and lack many complexities of actual faults; yet some of them have a large number of the features observed in actual seismicity including slip and stress complexity, events of many different sizes, variable recurrence times, etc.
Definition of the Model
Let us consider, as in Fig. 1, a two-dimensional antiplane crack of length 2L embedded in a linear elastic medium of elastic constant μ and mass density ρ. The elastic medium is subject to a slowly increasing uniform shear stress σyz(x, y, t)=Te(t), due to slow plate motion or intraplate deformation. As the external stress, Te(t), increases with time, the frictional resistance to slip between the walls of the fault is eventually overcome, and slip occurs. The amount of slip and the history of slip on the fault depends on the nonlinear friction law that relates shear stress transmitted across the fault T(x, 0, t), to slip D(x, 0, t), slip velocity V(x, 0, t)=Ḋ(x, 0, t), and possibly to certain state variables θi(x, 0, t). The exact nature of this
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely t indicate this fact.
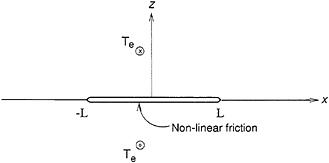
FIG. 1. Simple model of an antiplane fault in a homogeneous linear elastic medium. The fault extends from −L to L and is clamped at the ends by unbreakable barriers. The fault is driven by a slowly increasing homogeneous shear stress field. The only possible source of heterogeneity in this problem is the nonlinear frictional interaction between the walls of the fault.
friction law will be discussed after we set up the elastodynamical problem.
We have assumed antiplane slip, so that the only component of displacement that we consider is u=uy and the relevant traction component across the fault is T=−σyz. Thus, u satisfies the wave equation
[1]
where β is the shear wave speed. By using the symmetry about the fault plane z=0, we find the appropriate boundary conditions for the solution of the problem in the upper half-space (z>0):
u(x, 0+, t)=0 on -∞ <x<−ℓ1(t) and ℓ2(t)<x<∞ [2]
outside the slipping part of the fault delimited by ℓ1(t) and ℓ2(t),
T(x, 0+, t)=Te(t)+T(D, V, θ) on −ℓ1(t)<x<ℓ2(t) [3]
inside the fault. T(D, V, θ) is the friction law. This problem is then a typical crack problem with mixed boundary conditions, which consists in finding the slip D(x, 0, t)=2u(x, 0+, t) on the fault.
In spite of the apparent simplicity of this crack problem, in most cases it is intractable by analytical methods because of the mixed boundary conditions (Eqs. 2 and 3). As discussed (25), finite differences are too inaccurate because of high frequency dispersion, so that we adopted a boundary integral equation method that we believe is the most appropriate for solving this kind of crack problem (26, 27). The appropriate boundary integral equation (10) is
[4]
where S is the space-time convolution integral
[5]
with ![]() . The convolution over space has a Cauchy-like singularity at ξ=x. The convolution over time, on the other hand, is regular because K(x, t) → 0 when x → 0. The details of the numerical method used to solve this problem and its implementation in a CM5 parallel computer have been discussed (10). Thus it is sufficient to say that Eq. 4 is a nonlinear algebraic equation for the simultaneous solution of D, V, T, and θ.
. The convolution over space has a Cauchy-like singularity at ξ=x. The convolution over time, on the other hand, is regular because K(x, t) → 0 when x → 0. The details of the numerical method used to solve this problem and its implementation in a CM5 parallel computer have been discussed (10). Thus it is sufficient to say that Eq. 4 is a nonlinear algebraic equation for the simultaneous solution of D, V, T, and θ.
Let us remark that the fault is assumed to be clamped at the ends by unbreakable barriers. This boundary condition is different from the periodic conditions used by Carlson and Langer (14). To apply periodic boundary conditions, we would have to change the Green functions used to derive Eq. 4.
Friction Law
The nature of the solution of Eq. 4 is completely determined by the friction law T(D, V, θ). Extensive work on rock friction has been discussed by Dieterich (28) and does not need to be repeated here. Experimental evidence (20, 21, 29) shows that friction laws at low slip rates should at least include three elements: (i) direct stress change for rapid increases in slip velocity, (ii) an intrinsic time constant for the response to abrupt changes in velocity, and (iii) velocity weakening at steady-state slip.
At present we are unable to introduce such laws in our numerical method because they were proposed for very low values of slip velocity, so that the solution of the boundary integral equation problem would have to take into account slip rates varying over more than six orders of magnitude (i.e., from μm/s for fault creep up to m/s for seismic slip). Since the time step for the solution of Eq. 4 is controlled by the faster time scales present in it, the slow evolution of the fault in the interseismic period would have to be computed at the time steps appropriate for the dynamic regime, which is several orders of magnitude less than those that are actually needed. Equations of this type are called stiff and require special techniques for their solution as shown by Tse and Rice (30) for a spring-loaded massive slider. A possible method to increase the time steps during the interseismic period would be to modify Eq. 4 at low speeds by using its quasi-static approximation as proposed by Perrin et al. (31), but we have not implemented this option yet.
Because of the difficulties discussed in the previous paragraph, we have used a simplified friction law. The most sweeping assumption is that the fault is perfectly locked during the inter-seismic period so that successive events can be treated independently. In the Dieterich-Ruina rate- and state-dependent laws, slip occurs at all times no matter how small the total stress. In the period when the fault is locked, we assume that there is no slip on the fault, so that stress increases steadily during the continuous load Te(t). When the total stress on a certain point of the fault reaches a threshold Tu, slip begins and we immediately switch to the dynamic equation (Eq. 4).
The particular friction law assumed in our computations is
T(D, V, θ)=Tu(1−D/U0) for D<U0
T(D, V, θ)=0 for D>U0 and θ>θ0[6]
T(D, V, θ)=Tsp(1−θ/θ0) for D>U0 and θ<θ0,
to which we add the following evolution equation for θ
[7]
where D is slip measured from the beginning of the current slip episode, θ is a state variable, and V is instantaneous slip velocity. At steady state, θ is equal to the slip rate, so that θ differs from slip rate V only during fast rate changes. The first-order evolution equation for θ introduces a relaxation time scale τ0 and a corresponding relaxation length Dc=βτ0. These are the small scale parameters needed to regularize the fault model at small scales and avoid the intrinsic discreteness of our previous models (10). The dependence of friction on slip and steady-state slip rate (θ) is better appreciated in Fig. 2. As slip begins, there is a slip-weakening process that simulates
energy dissipation near the rupture front. U0 controls the minimum size of a fault patch before it becomes unstable. As shown by Dieterich (32) and Ohnaka (33), this is an observable feature of realistic friction laws. In the state- and rate-dependent laws, slip-weakening is produced by the direct change of stress due to rapid increases in slip rate. Dynamic simulations of simple crack models by Okubo (34) showed that rate- and state-dependent laws behave in a very similar way to slip-weakening models near the rupture front.
The other main feature of the friction law described in Fig. 2 is slip rate weakening at low slip rates. This is a more controversial feature that has been included in the rate- and state-dependent friction laws in the form of a logarithmic decrease of friction with increasing velocity. In the present study, we assume a linearly decreasing dynamic friction as a function of increasing steady-state slip rate to simulate the simpler frictional models used by Carlson and Langer (14). They assumed that friction was a simple function of slip rate only:
[8]
so that stress increased as the slip rate decreased. Rate dependence may destabilize healing depending on the value of Tsp (11). For small Tsp, the friction law is not very different from the usual rate-independent friction. For large values of Tsp, the destabilizing effect is more pronounced and spontaneous heterogeneity develops for large values of this parameter.
That friction decreases with slip rate seems to be a well documented feature of many frictions including those of Dieterich (19, 20) and Ruina (21). In these friction laws, steady-state frictional stress is proportional to a logarithm of steady-state slip rate of the form Tss(Vss)=−a log(Vss), so that frictional stress decreases more mildly as a function of slip rate than in the model of Carlson and Langer (14).
Fig. 2 also shows the trajectory of a point on the fault in the slip-steady-state-slip-rate space. As slip begins, stress slowly decreases transferring load to neighboring points on the fault. Simultaneously slip velocity increases rapidly because any stress relaxation is initially compensated by increases in slip velocity. The time scale of this rapid velocity increase is controlled by the relaxation time τ0 and the slip-weakening time U0/vR, where vR is the rupture front speed. In our computations, these two time scales are of the same order as they are also in the slip- and rate-dependent models. After this brief time, the fault slips freely at high slip rates. Slip rate becomes determinant for the fate of the fault only when the slip rate is less than the threshold V0 (which corresponds to θ0). At that point, stress increases as slip rate decreases, further driving the local point on the fault toward locking. This locking process is a highly nonlinear feature of the friction law that is entirely due to local conditions on the fault and is completely
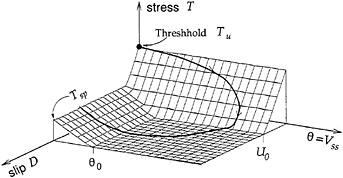
FIG. 2. Main features of the friction law assumed in this paper. Friction is represented as a function of slip (D) and state variable (θ). Transient slip rate may be different from θ in the course of rapid changes in slip rate.
independent of the propagation of stopping phases or other signals along the fault.
Simulation of Seismicity on a Finite Fault
Let us now study the seismicity on the fault model that we have just described. In the following simulations, all parameters will be rendered nondimensional by the following choices: stress is scaled by μ, the rigidity. We choose Tu/μ=1 as the peak traction resistance on the fault. We scale length by the unit step ∆x used to discretize the fault. The total fault length L/∆x= 511 in most of the simulations presented here. Time is scaled as t×β/∆x, slip scales are scaled as D×μ/(2Tu×∆x), and slip rate is scaled as V×μ/(β×2Tu). The shortest nondimensional time scale admissible in our computations was 0.5 so that the Courant parameter of our numerical solutions is also h=0.5. We could have used the maximum stable value h=1, but we prefer to stay on the safer side. All the other parameters appear in the friction law and were adopted as follows: U0=10, τ0=3, θ0=1, and Tsp will be varied as explained later. Let us remark that when Tsp=0, we get the classical Coulomb friction law with initial slip-weakening. Computations using this law were extensively studied by Andrews (26) and produce perfectly repeatable earthquake sequences in our computations. For Tsp=1, the final stress is equal to the peak stress on the fault as assumed in the original work by Carlson and Langer (14). In this case, events can be artificially triggered by relaxing a point on the fault. We consider these two values as extreme models of slip rate sensitivity of friction. As we will show later, a transition in the behavior of the fault occurs around Tsp=0.6.
Let us emphasize that in all our calculations the material parameters μ, β, Tu, τ0, θ0, and U0 are considered to be uniform along the fault. The presence or lack of heterogeneity of stress and slip will be entirely due to the nonlinear features of the friction law (Eq. 6).
The slip-weakening parameter U0 determines the shortest scale in our problem. Let us define the total length of an event ℓ as the total number of fault elements involved in the rupture. In our simulations, events occur at scales ℓ shorter and longer than U0. Only the larger events are considered as seismic events; small events, such that ℓ<U0, never develop the fast rates typical of seismic events and friction never drops to 0 as allowed by the friction law of Fig. 2. These events would disappear if we could include fault creep in our model.
Simulation of a Relatively Smooth Fault (Tsp=0.4). Let us consider first a model that is just below the critical value of partial stress drop. In Fig. 3, we show the velocity and stress field for a typical large event in this model. Because of limited resolution, we have decimated the output so that Fig. 3 (and also Fig. 4) presents only 1 line in 10. Although the slip velocity field does not resemble the classical self-similar crack models of Burridge (1) or Madariaga (4) much, slip continues for a long time after the passage of the rupture front. A weak stopping phase is clearly observed traveling across the fault, so that that slip duration is controlled by the total length of the slip zone. An interesting feature of the slip velocity field is the variation of velocity intensity near the rupture front. After a period of growth, the velocity peak decreases temporarily near the center of the fault. This is quite different from models with constant stress drop in which velocity intensity grows like the square root of distance from the nucleation point. This is a clear manifestation of incipient complexity. The stress field shows a clear decrease after the passage of the rupture front although several slip events leave a trace inside the fault. At the end of the rupture process, stress drops to a value close to 0.2 and is rather uniform. After reloading of the fault by the slow external stress field, the next event in the series will occur under a mildly complex stress distribution that is not enough

FIG. 3. Slip velocity and stress fields as a function of position and time for a typical large event when the control parameter Tsp=0.4 is less than critical.
to excite the small scale fluctuations that are observed in the rougher models.
Simulation of a Rough Fault (Tsp=0.8). Let us look now at a typical event for a model in which Tsp is higher than the critical value. As shown in Fig. 4, the velocity field has completely changed compared to that of Fig. 3. Rupture occurs now in the form of several successive narrow slip velocity pulses. Each of these narrow pulses propagates at a rather constant velocity, increasing slip velocity rapidly and then freezing spontaneously behind the rupture front. Because these pulses do not completely relax the stress on the fault, other pulses may be triggered in their trail, producing complex rupture sequences. We observe also that velocity intensity changes rapidly as rupture develops. Whenever the velocity intensity decreases below a certain level determined by the velocity-weakening properties of friction, rupture stops. The stress field is also completely different from that of the previous case. After the passage of each of the rupture episodes, stress recovers immediately behind the rupture front, and the fault remains in a state of complex stress. The stress distribution has reached a steady state that maintains complexities of all scales. These results suggest we have reached a critically self-organized state (12).
Properties of the Seismicity for Different Values of Tsp. Fig. 5 compares the history of seismicity on the two previous fault models. As already discussed above, these plots contain two families of events: small events that occur repeatedly at the same place and that are smaller than 10 grid points, the minimum “seismic” event size. Since the total size of the fault is 511 grids, we have a practical range of less than two orders of magnitude in size. This is clearly not enough to define properties like spectral distribution of heterogeneities but is enough to get a qualitative feeling for the properties of the “seismicity” of our models. As it is easily observed in Fig. 5, there is a substantial difference between the seismicity for the
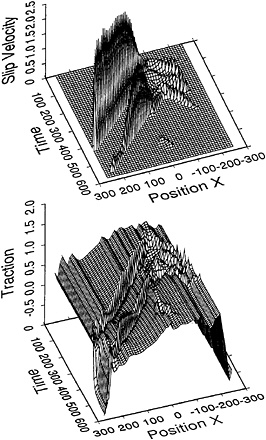
FIG. 4. Slip velocity and stress fields as a function of position and time for a typical large event when the control parameter Tsp=0.8 is larger than critical.
model with Tsp=0.4 and the model for Tsp=0.8. For Tsp=0.4, all large events rupture the entire fault, so that they all have very similar seismic moment. Although they have the same length, large events are not identical and they occur at irregular intervals. The distribution of stress on the fault changes substantially from event to event, but the stress distribution is not complex enough to produce self-organized criticality.
For the larger value of Tsp, the seismicity changes qualitatively: events of all sizes occur with variable lengths and seismic moments. Seismicity is now disorganized in space and time: large events continue to occur at a mean rate determined by the loading rate of the system, but interseismic intervals vary widely. Also, seismic events are much more frequent in this model because seismic events release less stress than in the previous case. Each event in this complex fault model is unique. Stress drop varies substantially along the fault and the slip function is very complex as is clearly shown by the stress and slip velocity distributions shown in Fig. 4.
Finally, let us look at the scaling law for these two types of models. The scaling law for the model with Tsp=0.4 is trivial and does not need to be plotted because all seismic events rupture the whole fault. Apart from a small variation in average stress drop and slip from event to event, the seismic moment of all the large events is the same and is completely determined by the rate at which the fault is loaded. The seismicity in this case is typically slip-predictable. For the more complex model with Tsp=0.8, the scaling law is shown in Fig. 6 where we also plot two lines corresponding to the moment-length relation for different values of stress drop. Clearly, although the spread of lengths is not very large due to the computer limitations already cited above [although, for this figure, L/∆x=1023 instead of 511], the seismic moment for these events is proportional to ℓ2, as expected for two dimensions. Thus in the case of complex seismicity, the seismicity
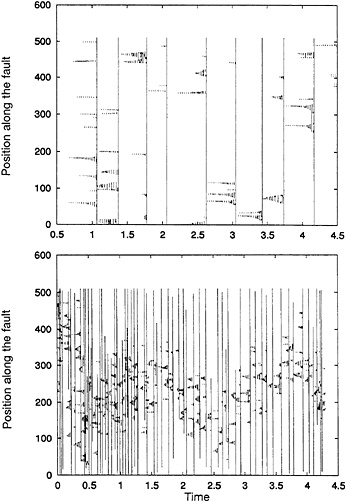
FIG. 5. Seismicity as a function of time for two models of seismicity in the presence of a velocity-weakening friction law. (Upper) The control parameter is less than critical (Tsp=0.4). Only large events crossing the whole fault occur. (Lower) The control parameter is supercritical (Tsp=0.8). Events of all sizes occur more frequently with different rupture lengths and a wide spread of seismic moments.
spontaneously satisfies the scaling law. Somehow, in our simulations, the length of every event is automatically chosen so that the scaling law is satisfied. We did not initially expect this result, but in retrospect it is not difficult to understand. In our model, there are only two physical length scales: the minimum event size controlled by the slip-weakening zone and
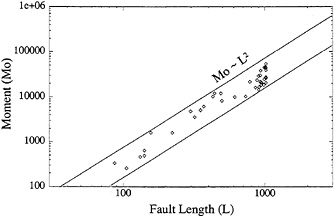
FIG. 6. Scaling law of seismic-like events for the supercritical model (Tsp=0.8) of Fig. 4. Events of different sizes with variable rupture lengths ℓ occur. These events satisfy a scaling law where the moment is proportional to ℓ2. Diagonal lines represent models of equal stress drop.
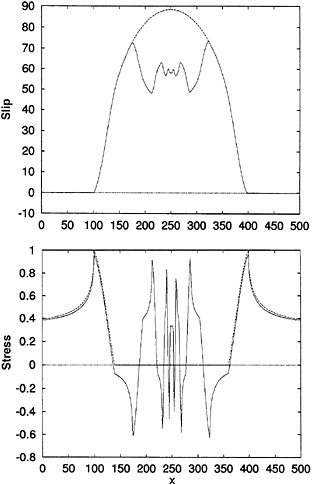
FIG. 7. Stress and slip for a simple and a somewhat complex slip distribution. For the elliptical distribution shown with a broken line, stress drop is constant. For the variable slip model shown with a continuous line, stress is highly variable. Stress on a fault is roughly speaking proportional to the slip gradient so that it can have large variations for very small changes in slip. Complexity will develop whenever these variations in stress are compatible with the friction law. Partial stress drop seems to be a condition that favors the development of heterogeneity.
the total fault length L. The later should of course not appear in the scaling law for events that do not rupture the entire fault. Thus, the scaling properties of events larger than the minimum size should depend only on the minimum event size and on their own fault length. Our results suggest that the minimum rupture size does not influence the behavior of the fault. This is an encouraging result that indicates that our previous computations using a nonregularized friction law (10) were not affected by the lack of a small cut-off size.
The Origin of Complexity. For rate-independent friction (Tsp=0), static and dynamic stress drops are almost the same. Actually, for antiplane faults, static stress drop overshoots the dynamic stress drop by ≈24%. For higher values of Tsp, the fault locks prematurely so that static stress drop becomes less than the dynamic one and varies significantly from point to point. This lateral variation develops because slip arrest occurs locally, not in response to waves propagating inside the fault. Because of this early healing, the final slip at neighboring points on the fault may be quite variable. Since—roughly speaking—stress changes on the fault are related to the gradient of slip, even small variations of slip can produce strong heterogeneities in the static stress field after the event. Let us illustrate this by considering a simple fault with uniform stress drop. Slip in this case has an elliptical distribution tapered near the edges by the slip-weakening distribution of stress. This slip distribution and its corresponding stress change are shown in
Fig. 7 by the broken lines. Let us add to this distribution some heterogeneity and look at the slip and stress distribution, as shown in Fig. 7 with the solid lines. We observe that a modest change of the slip distribution produces large variations in the residual stress pattern. Since stress can only change inside a limited range (0 < T < Tu), these lateral variations put some fault elements closer to rupture than others. As a consequence, the future seismicity of the fault is completely determined by these heterogeneities in the residual stress field. Thus the mechanism that generates complexity in our model is clearly identified, although we do not know what is the bifurcation value for the control parameter Tsp. We propose that the key to the creation of heterogeneity in our models is partial stress drop. This is not at all a new concept in seismology; Brune (5) proposed from observational arguments that most earthquakes presented partial stress drop and suggested that the dynamic stress drop (Tu in our case) was much larger than the static stress drop. The main difference between our results and the suggestion by Brune (5) is that he considered a model where partial stress drop was uniform along the fault, while in our models a partial stress drop triggers strong lateral variations of the static stress drop.
Conclusions
We have demonstrated that, for certain highly rate-dependent friction laws, a simple antiplane fault embedded in a homogeneous medium can spontaneously become complex. This complexity has several interesting features:
-
Premature locking of the fault, so that slip duration at any point of the fault is independent of the total size of the fault. Premature healing produces partial stress drop, so that stress heterogeneity may be simply due to the extreme sensitivity of fault stress to very small changes in the slip distribution.
-
Self-healing slip pulses are spontaneously generated for large values of Tsp. These pulses were proposed by Heaton (35) and they were explained in our previous work (10).
-
Stress heterogeneity and partial stress drop are manifestations of the same underlying instability. Partial stress drop occurs for all friction models that have a strong rate-dependent friction. Partial stress drop disorganizes the fault for the simple reason that stress drop of neighboring points will be highly variable.
-
Slip gradient (dislocation density) and stress heterogeneity appear when small scale modes of slip on the fault can express themselves. For full stress drop models like rate-independent friction laws, these small scale modes are suppressed by the requirement that the stress drop be fixed, uniform, and determined only by constitutive parameters. In that case, only material heterogeneity can produce complexity.
-
Seismic events (i.e., events whose length is greater than the length of the slip-weakening zone) follow an ℓ2 scaling law in which seismic moment scales like the product of partial stress drop and the square of the length of the zone that actually slipped during the event. Thus, the regularization length that is included in our slip-weakening model has no influence on the properties of large seismic events. We find that the size of the slip pulse that traverses the fault determines the actual final size of the rupture. If the slip pulse is large, it simply reaches further along the fault.
-
Seismic-like events in our simulations are both periodic and simple for small values of the control parameter Tsp. For values larger than a critical value situated around Tsp=0.6, we observe events of all sizes and a much higher rate of seismicity.
In conclusion, we have shown that a rate-dependent friction can spontaneously produce heterogeneity for large values of a control parameter. This limit corresponds to that of the friction law used by Carlson and Langer (14) in their study of the Burridge and Knopoff model. At the other extreme, the rate-independent friction suppresses these instabilities for the very simple reason that partial stress drop is eliminated from the outset. It is very likely that both material heterogeneities and dynamically generated complexity play a role in determining the observed complexity of faulting and seismic events. Given the little knowledge that we currently have about the friction laws at high slip rates, we firmly believe that heterogeneity should be explored without preconceived assumptions about which of material and dynamically generated heterogeneity dominates in the earth.
J.P.Vilotte provided many useful and timely discussions. This work was initiated with support from the European Union under Contract N ERBSC1 from the “Science” Program.
1. Burridge, R. (1969) Philos. Trans. R. Soc. London A 265, 353–381.
2. Kostrov, B.V. (1964) J. Appl Math. Mech. 28, 1077–1087.
3. Kostrov, B.V. (1966) J. Appl. Math. Mech. 30, 1241–1248.
4. Madariaga, R. (1976) Bull. Seismol. Soc. Am. 66, 639–666.
5. Brune, J.N. (1970) J. Geophys. Res. 75, 4997–5009.
6. Das, S. & Aki, K. (1977) J. Geophys. Res. 82, 5658–5670.
7. Kanamori, H. & Stewart, G.S. (1978) J. Geophys. Res. 83, 3427–3434.
8. Madariaga, R. (1979) J. Geophys. Res. 84, 2243–2250.
9. Kostrov, B.V. & Das, S. (1982) Bull. Seismol. Soc. Am. 72, 679–703.
10. Cochard, A. & Madariaga, R. (1994) Pure Appl. Geophys. 142, 419–445.
11. Madariaga, R. & Cochard, A. (1994) Ann. Geof. 37, 1349–1375.
12. Bak, P., Tang, C. & Wiesenfeld, K. (1988) Phys. Rev. A 38, 364–374.
13. Burridge, R. & Knopoff, L. (1967) Bull. Seismol. Soc. Am. 57, 341–371.
14. Carlson, J.M. & Langer, J.S. (1989) Phys. Rev. Lett. 62, 2632– 2635.
15. Carlson, J.M., Langer, J.S., Shaw, B.E. & Tang, C. (1991) Phys. Rev. A, 44, 884–897.
16. Shaw, B.E., Carlson, J.M. & Langer, J.S. (1992) J. Geophys. Res. 97, 479–488.
17. Myers, C.R. & Langer, J.S. (1993) Phys. Rev. E 47, 3048–3056.
18. Schmittbuhl, J., Vilotte, J.-P. & Roux, S. (1993) Europhys. Lett. 21 (3), 375–380.
19. Dieterich, J.H. (1978) Pure Appl. Geophys. 116, 790–806.
20. Dieterich, J.H. (1979) J. Geophys. Res. 84, 2161–2168.
21. Ruina, A. (1983) J. Geophys. Res. 88, 10359–10370.
22. Rice, J.R. (1993) J. Geophys. Res. 98, 9885–9907.
23. Rice, J.R., Ben-Zion, Y. & Kirn, K.-S. (1994) J. Mech. Phys. Solids 42, 813–843.
24. Ida, Y. (1972) J. Geophys. Res. 77, 3796–3805.
25. Virieux, J. & Madariaga, R. (1982) Bull. Seismol. Soc. Am. 72, 345–368.
26. Andrews, D.J. (1985) Bull. Seismol. Soc. Am. 75, 1–21.
27. Koller, M.G., Bonnet, M. & Madariaga, R. (1992) Wave Motion 16, 339–366.
28. Dieterich, J.H. (1994) J. Geophys. Res. 99, 2601–2618.
29. Scholz, C.H. (1990) The Mechanics of Earthquakes and Faulting (Cambridge Univ. Press, Cambridge, U.K.).
30. Tse, S.T. & Rice, J.R. (1986) J. Geophys. Res. 91 (B9), 9452– 9472.
31. Perrin, G.O., Rice, J.R. & Zheng, G. (1995) J. Mech. Phys. Solids 43, 1461–1495.
32. Dieterich, J.H. (1992) Tectonophysics 211, 115–134.
33. Ohnaka, M. (1992) Tectonophysics 211, 149–178.
34. Okubo, P.G. (1989) J. Geophys. Res. 94, 12321–12335.
35. Heaton, T.H. (1990) Phys. Earth Planet. Inter. 64, 1–20.






