This paper was presented at a colloquium entitled “Earthquake Prediction: The Scientific Challenge,” organized by Leon Knopoff (Chair), Keiiti Aki, Clarence R.Allen, James R.Rice, and Lynn R.Sykes, held February 10 and 11, 1995, at the National Academy of Sciences in Irvine, CA.
The organization of seismicity on fault networks
L.KNOPOFF
Department of Physics and Institute of Geophysics and Planetary Physics, University of California, Los Angeles, CA 90024–1567
ABSTRACT Although models of homogeneous faults develop seismicity that has a Gutenberg-Richter distribution, this is only a transient state that is followed by events that are strongly influenced by the nature of the boundaries. Models with geometrical inhomogeneities of fracture thresholds can limit the sizes of earthquakes but now favor the characteristic earthquake model for large earthquakes. The character of the seismicity is extremely sensitive to distributions of inhomogeneities, suggesting that statistical rules for large earthquakes in one region may not be applicable to large earthquakes in another region. Model simulations on simple networks of faults with inhomogeneities of threshold develop episodes of lacunarity on all members of the network. There is no validity to the popular assumption that the average rate of slip on individual faults is a constant. Intermediate term precursory activity such as local quiescence and increases in intermediate-magnitude activity at long range are simulated well by the assumption that strong weakening of faults by injection of fluids and weakening of asperities on inhomogeneous models of fault networks is the dominant process; the heat flow paradox, the orientation of the stress field, and the low average stress drop in some earthquakes are understood in terms of the asperity model of inhomogeneous faulting.
Homogeneous Faults
Our interest is in the prediction of large earthquakes since these are of the greatest societal concern. If large earthquakes are periodic, the problem is trivial. Since large earthquakes at the same site are not periodic (1, 2), we must inquire into the causes of the dispersion of interval times and especially to see if patterning is likely to develop. If patterns of seismicity emerge, then these can be used as templates for studies of likelihood of occurrence of strong earthquakes that take into account the small amount of information that is currently available concerning these events.
The physical causes of nonperiodicity of earthquakes must be rooted in interactions, since the absence of interactions would imply that the events earthquakes are simple relaxation oscillators. The only serious model for interactions that has been proposed is the redistribution of elastic stress by fractures. Thus, efforts to simulate evolutionary seismicity have focused on the development of fractures in an environment of fluctuations of the elastic stress field produced by earlier fractures: The stress field locally is lowered by fractures that occur when certain thresholds are reached, is restored by tectonic plate motions in the interval between earthquakes, and can be increased or decreased by the occurrence of fractures nearby and by stress relaxation from nonelastic processes. Do identifiable patterns of fractures arise under these conditions of fluctuating stresses?
Many of the simulation studies to date have taken as their paradigm the Gutenberg-Richter (G-R) power-law distributions of earthquake energies and moments and have attempted to do so by understanding the self-organization of fractures on a single, uniform earthquake fault. While these studies give insights into the process of self-organization of a complex system of small and large events, they are inappropriate to study the organization of large earthquakes on several accounts. First, the G-R law is appropriate only for small earthquakes and cannot be applicable to the description of large earthquakes (3). Second, the small earthquakes of Southern California do not take place on the plate boundary which is the San Andreas fault (SAF), or on some of the other major faults of Southern California but rather take place on a complex two-dimensional network of secondary and higher order faults (3). A third point concerns the current scale of computing of the simulations: Since the computational lattice size must correspond to events larger than the largest possible earthquakes, then the smallest plausible earthquake that is simulated well on the present-day lattice models corresponds to a magnitude 5 earthquake roughly. These smallest model earthquakes are close to the upper limit of applicability of the G-R law (3), and smaller earthquakes are not well modeled computationally today.
Large earthquakes are so rare in any given region, that we are unable to provide an appropriate statistical paradigm for their study. One goal of simulation studies must be the development of paradigms that are physically plausible.
Before discussing recent progress toward our goal of studying simulated seismicity on a network of faults (3), we first summarize some of the relevant results in the modeling of seismicity on a single fault as a preliminary step toward the more difficult problem. The focus on simulations of the power-law part of the distribution has led a number of authors to suggest that a scale-independent physics regulates the self-organization. The simplest scale-independent fault model is a homogeneous one, in which it is assumed that the structure of a given seismic region does not play an important part in the earthquake process at any scale, and that the seismicity is dominated by the mechanics of the self-organization due to the stress redistribution on a homogeneous landscape of structure (4–11). The total stress on the fault in scalar one- and two-dimensional (antiplane) elastostatic fractures does not decrease with time; thus, ultimately the stress in the system must exceed the fracture strength everywhere and a fracture must occur that is larger than any given size. If we require that the largest earthquakes be of finite length and that their growth stops by the same mechanism as the smaller ones, then these quasistatic models must ultimately develop a fracture whose length is greater than the largest that is geophysically possible.
Thus, an event must develop that is equal to the size of any finite computational lattice; at this point, the fracture interacts with the boundaries, and the system is no longer homogeneous: the evolutionary development of fractures is subsequently influenced by the interaction with the boundaries, by the
Abbreviations: G-R, Gutenberg-Richter; SAF, San Andreas fault; B-K, Burridge-Knopoff; 1D, one-dimensional.
inappropriate modeling of the transfer of stress from the fault regions outside it into the lattice segment. A throughgoing or lattice-wide fracture is not stopped by the same mechanism as that which stops the smaller fractures whose spans lie wholly within the lattice. There are thus two arguments against the applicability of homogeneous lattice models of self-organization: first, it is not possible to prevent the “runaway” or lattice-wide event, which is not stopped by the same mechanism as the smaller earthquakes, and second, there is no mechanism for discriminating between small and large earthquakes, as demanded by the finiteness of the energy budget for earthquakes (3). The same arguments apply against the development of scaling on an otherwise homogeneous system in the tensor (in-plane) case as well.
The dynamics of the fracture process represents an escape from the tyranny of the resolute increase of stress. A redistribution argument based on conservation laws no longer applies in this case, since the stresses are no longer solutions to Laplace’s equation but are solutions to the elastic wave equation. The loss of energy in elastic wave radiation reduces the amount of energy available to promote further slip. However, dynamics does not provide an escape from the failure of a homogeneous system to develop an internally derived scale size that separates large from small fractures; absence of scaling is a powerful argument that self-organization of dynamic fractures on a single homogeneous fault must also lead to the abyss of the lattice-wide event.
We illustrate these remarks by a consideration of the self-organization of dynamic fractures on a single homogeneous fault model with periodic edge conditions through the vehicle of the Burridge-Knopoff (B-K) (12) spring-block model in one dimension. We do not elaborate on the dynamic B-K model, which has been discussed in detail elsewhere, except to remark that, in order that changes in the stress due to fracture be redistributed via elastic wave transmission, we guarantee that the (supersonic) dispersion, due to the local influence of the transverse springs in some dynamic versions of this model (13, 14), is moderated by fine-tuning a radiation damping term (15) that is equivalent to introducing a local viscosity as a frictional damping of the slip (12). It can be shown that the tunable radiation term merely represents a scaling of the size of the fracture with respect to the lattice spacing. Laboratory measurements of the nature of sliding friction in the range of slip velocities that occur in earthquakes have not been made: in our model, we do not invoke a velocity-dependent sliding friction; instead, the strength of the bonds at the crack edges drops instantly to the dynamic friction at the instant that the critical threshold stress is reached (15). Although the B-K models do not generate redistributed stresses that are scaled by the crack length, nevertheless these B-K models with critical radiation damping generate slip pulses whose ranges are of the order of a(l/k)1/2 where a is the lattice spacing and l and k are the transverse and longitudinal spring constants and hence appropriate to simulations of self-healing pulses (16) in large earthquakes wherein slip is concentrated mainly near the growing edge of a crack. This model is more appropriate to the modeling of large earthquakes than small ones.
For arbitrary initial conditions on the homogeneous one-dimensional (1D) dynamic B-K fault model, the system quickly organizes itself into fractures with a power-law distribution of sizes (17). The events with power-law distribution of fracture sizes is only a transient state. Power-law transiency in the self-organization of other nonlinear systems has also been identified recently (18). Ultimately, a runaway event takes place that spans the entire lattice and hence has an infinite length on the periodic lattice. After the first runaway, subsequent seismicity displays only periodic runaways to the exclusion of smaller events, but this is a consequence of the smoothness of the stress after each runaway; other scenarios after the first runaway are possible, but they too lead to further runaways, and so on indefinitely.
In the transient state, the power-law distribution for the sequence of seismicity is not Poissonian but is rather a distribution that is dominated by (almost) periodic localized clusters. There is an intense clustering of repetitive events of almost the same size at the same locations, at almost equal time intervals (Fig. 1). These persistent clusters disappear after some time and others appear elsewhere. Such persistence is due to the smoothness of the stress across the extent of a fracture in this model (19). If the stress is smooth after fracture, the restoration of stress by the external loading mechanism brings the extent of a previous fracture to the uniform critical threshold at the same time, and hence local recurrence dominates this phase. Because of the nearest-neighbor property of the 1D B-K model, any changes in the stress can only take place at the edges of the fractures. Thus, the length of a fracture differs from its immediate predecessor only at its edges, and hence the persistence of a cluster is approximately scaled by the length of the fractures. The power-law distribution that results from this model describes the number of clusters of a given length weighted by the number of repetitions within the cluster. Thus, the spatial localization is evanescent, and the pattern has an overriding imprint of a periodicity imposed by the coupling of the smoothness of the postfracture stress and the homogeneity of the threshold fracture strength. The probability that any point along this fault will experience a large earthquake is the same for all points along the fault over the long term; over the long term, there can be no spatial localization.
A rolloff that is observed in the distribution (17) does not define a characteristic length; the scale size that is implied is an artifact of the fact that the count is terminated at the time of the first lattice-wide event; events that are slightly less than lattice-wide in size are undercounted compared with expectations for a larger lattice. The magnitude that corresponds to the rolloff corresponds to the parameter that mimics the seismic radiation; the larger the energy loss in the parameterized radiation, the longer the time to inevitable runaway.
Even if long-range forces are taken into account, the self-organization of fractures on a homogeneous landscape must ultimately develop a dynamic crack that is larger than any given size. A similar conclusion is reached if one introduces a weakening of strength into continuum quasistatic models with long-range redistribution of stress (20).
The Influence of Geometry
We turn to inhomogeneous faults or fault zones as systems with intrinsic scale sizes to explore the differences between large
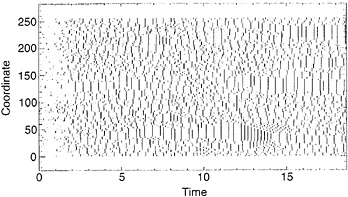
FIG. 1. Portion of the slip history of the transient phase on a homogeneous 1D B-K model with periodic end conditions. Vertical strokes define the linear extent of a fracture; fractures with greater length release more energy. Evanescent persistent clusters can be identified. After a long time, this pattern is replaced by lattice-wide periodic fractures. [Reproduced with permission from ref. 17 (copyright 1994, American Institute of Physics).]
and small earthquakes. We assume that the inhomogeneities on faults mirror the nonplanarity of geometry. The simplistic view of the physics of the resting or sliding of a single block on an inclined plane and the simplistic mathematics of planar fractures have obliged us to parameterize friction on a plane; in both cases, the complexity of the interface between the block and plane is ignored because it is physically or mathematically convenient to do so. The usual models of the development of fractures on planar fault surfaces with parameterized friction, including the continuum models of Kostrov (21), Burridge and Halliday (22), and successors, as well as the discrete nearest-neighbor models of B-K type (19), have relatively smooth distributions of stress after fracture; on the other hand, real earthquake fractures have very irregular poststress distributions, in view of the large numbers of aftershocks that occur close to the rupture surface.
There are several scales of nonplanar geometric features: (i) topographic irregularities on fault surfaces and the presence of fault gouge that are the cause of friction on faults; (ii) larger-scale geometrical fluctuations of faults such as bends, stepovers, bifurcations, etc., of faults; (iii) the dendritic nature of the network of secondary faults associated with plate boundaries and a possibly tegular character of the space between elements of the network; and (iv) the influence of the curvature of the earth and the distances between triple junctions of the tectonic plates. We have no contribution to make to this discussion on the influence of this last item on the organization of earthquakes worldwide.
While there is much to be said concerning the dynamics of friction at the smallest scales, limitations of space do not allow for a full discussion of recent efforts at modeling the dynamics of sliding of blocks with irregular contacts (23–25) or of the development of a fluid dynamics and deformation mechanics of granular materials (26–31).
We concentrate attention on the issue of larger scale irregularities in fault geometry. The two problems of the irregularity on the small and the large scales differ by virtue of the size of the dimensions of the irregularities scaled by the size of the slip. On the large scale, the dimensions of the irregularities are large compared with the slips, which are a number of meters in the largest earthquakes. The offset between the two more or less parallel sections of the SAF in Southern California is about 100 km. Whereas there is strike-slip motion on the parallel sections, the link between them, such as the connection between the two parallel sections of the SAF, must have some thrust component of motion. The continuum mechanics, especially from the viewpoint of iterative seismicity, is difficult and has not yet been worked out.
We make the assumption that there is a correspondence between irregularities in the large-scale fault geometry and spatial fluctuations in the fracture strength on a planar model; in other words, we make the usual, unjustifiable assumption about planarity. While we do not know the precise nature of these relationships, for the purpose of modeling assume that the fracture threshold is high where a fault has a relatively complex geometry (see list above) and that the threshold will be low when the fault is relatively straight and parallel to the regional shear stress, because it should be relatively more difficult to prolong propagation of a fracture that arrives at a region of complex fault geometry; King (32, 33) has presented persuasive arguments why the strength of these regions of complex geometries cannot persist and that stresses stored in them due to repeated fractures that stop there or nearby should relax on the long time scale. We do not consider these issues of long-term stress relaxation in this paper. We apply these considerations of inhomogeneity to the B-K model and preserve other properties of the B-K model including the homogeneity of the elastic parameters and the periodicity of the boundary conditions. As in the case of a homogeneous distribution of thresholds of fracture strengths, this system also rapidly enters upon an apparently steady state condition (15, 34), although it is hardly stationary on a short or intermediate time scale. Despite the seeming stochastic character of the space-time patterns in an example of large, correlated spatial fluctuations of fracture strength along the fault (Fig. 2) with a fractal distribution, there is a large-scale imprint of systematic pattern development, if not one of multidimensional chaos, not unlike the large-scale spatial localization with small-scale irregularity that appears in other nonlinear systems. In the example, the small fractures occur relatively frequently where the fracture thresholds are low. Large events are located where fracture strengths are large, with longer time intervals between events. Because of the correlations between fracture strengths in the model, a region of large fracture strength can store large amounts of potential energy that will be released in large earthquakes; sites with large fracture stresses require a greater time for restoration of the stress to the fracture threshold from plate tectonic sources than do those with small thresholds. The larger events have greater stress drops than do the small ones in these models with fractal distributions of thresholds, a result that is not wholly consistent with observation, thus suggesting that this fractal barrier model is inappropriate for the description of large earthquakes. In order that these cracks grow dynamically, they must deliver enough stress at their edges to overcome the local difference between the strength and the prestress. A region with a large, increasing change of strength will usually represent a barrier to crack growth. There is an anisotropy: fractures entering a region of increasing friction will have decreasing rates of growth and may stop; a crack leaving the same region but growing in the opposite direction will speed up; events that initiate in regions of high strength and high stress drop will occasionally extend into regions of low stress drop but the reverse is less likely.
Does a system with spatially varying thresholds develop runaways? The extent of the fracture is defined by its encounter with a barrier—i.e., a site with a sufficiently large difference between fracture threshold and prestress. Whether a given fracture breaks through a barrier or is stopped by it depends on the amount of stress available at the crack tip. In quasistatic models, the stress at the crack tip is proportional to the product of the average stress drop and the instantaneous length of the slipping region. Thus, a runaway must sooner or later occur on a quasistatic model because the longer a crack, the greater the size of the barrier that the crack can break through. But if dynamic slip is localized near the edge of a crack, the stress at the edge of a slipping patch of a dynamic crack is scaled by the size of the patch, which may or may not be the final length of the crack. From an elementary theory, except for reasonable dimensionless factors, the scale size of a dynamic crack is
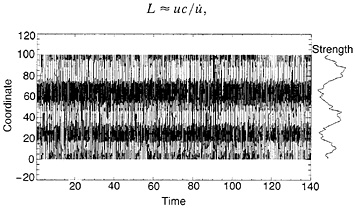
FIG. 2. Portion of the slip history on an inhomogeneous 1D B-K model with periodic end conditions. The fractal distribution of fracture thresholds is shown on the right. Where fracture strengths are low, small earthquakes occur frequently.
where u is the mean slip, ú is the mean slip velocity, and c is the speed of the edge of the crack, which we take to be the shear wave velocity. For the largest earthquakes such as Landers or San Francisco, the scale size is of the order of 15 km, a distance that is more appropriate to the thickness of the seismogenic zone than is the length of the crack, by factors of 5 and 30 in the two cases. Thus, the stress at one edge of the largest earthquakes does not depend on the conditions at the remote, opposite edge but depends instead on some local property. We remark in passing that the range of aftershocks beyond the edge of an earthquake fracture can be expected to be scaled by L (35), which is more appropriately 15 km than the total length of the fracture. Conversely, the relatively short range of aftershocks in great earthquakes implies the presence of a moving patch of slip as the mode of rupture and is a condition observed for a number of earthquakes (16). If the scale size of rupture is independent of the length of the rupture in the largest earthquakes, then the stress at the edge does not increase with increasing length of rupture, and hence a sufficiently strong barrier will stop crack growth. If there are several such barriers in a region, then the breaking of one of these will not cause the others to fail. Hence, there will be no runaway in this case. Because of the nearest-neighbor coupling of stresses in the B-K model and the short range of stress interactions on the ruptured segment, this model is not likely to develop runaways in the presence of a nonuniform distribution of fracture strengths. Since large fluctuations in fracture thresholds serve to prevent runaways, and vanishingly small ones do not, we expect that there should be a transition between the cases of small fluctuations in barrier strengths, which allow for runaways, and those of large fluctuations, which allow for localization.
The distribution of earthquakes that is found on these inhomogeneous models is very sensitive to the distribution of fracture thresholds. A spiky distribution of fracture strengths, intended to simulate a sparse distribution of barriers on a single fault, leads to a very different display of space-time seismicity, from the preceding case (Fig. 3). In the example, the ratio of threshold fracture strengths in the spikes to that of the broad and almost flat valleys between them is very large. The space-time patterns show much greater regularity than in the preceding example. However, the notable interruptions from one seemingly stable pattern to another equally seemingly stable pattern, occur at times that are episodic and not apparently predictable, even on a deterministic model such as this one. These instabilities are triggered by the breaking of the strong barriers that form the borders to the deep, broad valleys of low strength, in contrast to models with infinite barriers at the edge of the lattice. Even the site with the greatest strength must break because of the constraint that the long-term average slip velocity be uniform at all lattice sites. The barrier earthquakes are usually strong, since these are the sites of large storage of deformational potential energy. The opening of the barrier gates transfers a large stress from one low strength valley to another and changes the stress distribution in the adjoining valley, thereby triggering a new mode of repetitive fractures in the valley. We suppose that in models with inhomogeneous thresholds the relaxation of the stresses in the barriers are important events, whether the thresholds are spiky or not. To assume that barriers are unbreakable with infinite thresholds leads to evolutionary histories that are not reliable.
In some cases, the valley with low fluctuations appears to be smooth and fractures are throughgoing from one barrier spike to the next barrier spike. But if the valley is sufficiently long, seismicity in the valleys breaks up into shorter fracture segments; these cases would appear to be consistent with a long model with homogeneous fracture strengths as described above (17). The factors that determine whether the seismicity in the valleys will be of one type or the other are the ratio between the fracture strengths of the peaks and valleys, which determines the strength of the stress impulse that is sent into a valley from a rupture at a peak, and the ratio between the length of the valley and the scale size for the B-K Green’s function a(l/k)1/2, which determines how far into the valley the stress impulse can travel.
In the models of this section, we have found it possible to generate a series of large or barrier events that belong to a different class than small or valley events. Some of the valleys break only in long fractures, while others break in a broad distribution of events having the G-R distribution, which is schematically a pattern not unlike seismicity in Southern California, although there are significant differences. The models are sensitive to the choice of geometry, but generally these models favor the characteristic earthquake model for large events on some of the faults of the system and the statistical model for smaller events on other faults of the system. The large events are stopped by significant barriers associated with major geometrical features of long faults. In these models, the smaller events are dominated by processes of self-organization on relatively smooth faults, since we have not allowed for their occurrence on individual faultlets that are not directly linked to major faults nearby.
By the arguments above, I have tried to suggest that the G-R law is not a characteristic of faults that support large earthquakes. If this is the case, what is the structure that supports the G-R law? Although the scale independence implied by the G-R law may arise due to self-organization on the scale independent, homogeneous system, this system has the defects already enumerated, that it does not develop localization, it does not provide for a discrimination between small and large earthquakes, and it does not prevent runaways. An orthogonal point of view is that the G-R distribution is a consequence of the geometry of the fault network, as are the properties of the largest earthquakes. On the geometrical model, we suppose that the power law distribution of earthquake sizes is due to seismicity on a myriad of isolated and noninteractive faults having a power-law distribution of sizes and strewn over the entire space. The failure of the SAF and several of the other faults to observe the regularity of the G-R law suggests therefore that the faults that support large earthquakes have different physical properties and geometry than do the smaller ones, a conclusion already suggested by the phenomenology. If the G-R law is an image of a power-law distribution of sizes of small faults or fracture surfaces, why is the G-R distribution universal? One possible answer is to propose that the formation of the fault surfaces of small dimension that support small earthquakes is linked to the process of slip on the larger, irregular faults, which may induce the formation of these secondary fractures. Under this model, the universality of the G-R law is a consequence of the universality of the fracture process of a three-dimensional structure under the influence
of a hierarchy of fractures of various sizes. Such a model has been proposed by Turcotte (36, 37) to explain the distribution of fragments in granular assemblages and in the present context can be assumed to describe the evolution of a fault network, whether dendritic or not, under some process of aggregation, such as diffusion-limited aggregation, in the process of development of regional fault structure.
Two Coupled Faults
The model of Fig. 3 favors characteristic earthquakes that are dominated by intervals of local periodicity, interrupted by episodic instabilities. The periodicity is, of course, not appropriate to the seismicity of Southern California. We consider whether the regularity of the large events is modified by exploring models of seismicity on a network or web of faults. In the discussion in this section, we describe only the interactions between two parallel faults. There is still much to be done before we can simulate a region as complex as Southern California.
Consider, as a simple model of fault interaction, the problem of two 1D scalar B-K fault models, coupled so that a fracture event on one fault reduces the stress on the other (Fig. 4); hence, both faults cannot tear in the same earthquake. This coupled system may be considered to be a skeletal model of the interaction between the San Jacinto fault (SJF) and the SAF in the southern part of the Southern California region, if we exclude the influence of all other faults in the region. We endow each model fault with its own set of fracture thresholds. The dissipation on each fault is tuned to the transverse spring constant.
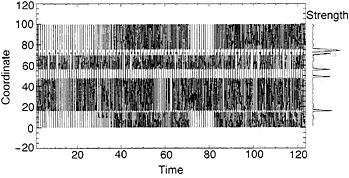
We consider a distribution of thresholds on each fault that is intended to simulate several strong barriers that are separated by valleys with low threshold strength (Fig. 5). The barriers are staggered on the two faults; the valleys on the upper fault have slightly lower thresholds than on the lower fault and have rather higher thresholds at the barriers. Seismicity is notably different from the single fault model of Figs. 2 and 3, especially in the development of notable episodes of local quiescence on the faults. The principal difference from the case of a spiky distribution of thresholds on a single fault (Fig. 3) is the disappearance of local periodicity. The history is much less predictable.
The seismicity on the two faults is almost Babinet complementary: where one set of sites is active, the sites on the parallel fault are usually inactive (Fig. 5). (Quiescence does not disappear if the angular distribution of redistributed stresses at the ends of the fractures are taken into account.) The complementary quiescence and activity are-due to the differences in fracture thresholds between the two faults: The fault that is the stronger of the pair at a given coordinate will in general be locked against slip, and fractures will take place on the weaker of the pair and its neighboring elements because of the correlations in fracture thresholds. Due to the coupling, stress on the stronger element of a pair does not build up because of the unloading when its weaker sibling ruptures. These results suggest that the dormancy of the SAF is complementary to the activity on the SJF but that at some time in the future, activity and quiescence will interchange between the two.
Because of the inexorable motion of the driving blocks, locked segments on the two faults cannot remain in the locked state indefinitely; the (diagonal) region between two locked segments on opposing faults stores increasingly more potential energy as tectonic motion continues, and this region must eventually lose its energy by fractures at one or the other of the locked segments. When one of the two locked segments breaks, it induces an extended episode of quiescence on weak segments on the companion fault. Around time 1720, activity on the upper fault is almost totally absent over the entire length but only temporarily so. Activity on the lower fault is similarly
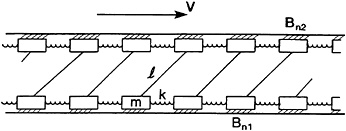
FIG. 4. Two 1D B-K model faults, coupled so that a fracture on one fault lowers the stress on the other. The two anvils have constant relative velocity. During sliding of any particle, there is a friction proportional to slip velocity with coefficient 2(ml)1/2, where m is the mass of any particle and l is the constant of the transverse coupling springs.
absent over much of its length around time 1960, again only temporarily.
Because the barrier locations are staggered between the two faults, the zones of quiescence are found to alternate spatially from one fault to the other, from region of strength to region of strength. It is notable that the extended absence of activity at the barrier on the upper fault at coordinate 200 between times 1300 and 1800 is matched by relatively frequent ruptures of the barrier at coordinate 175 on the lower fault. At about time 1800, activity on barrier upper 200 resumes and activity at barrier lower 175 ceases until time 2000.
Although the sum of the slip rates at a given coordinate is a constant for the entire region, the slip rates on the individual faults are not constant over time at a given coordinate. The slip rates can change abruptly; some active faults may become dormant, only to resume their activity later. These results are inconsistent with contemporary models that estimate seismic risk using the assumption that the present slip rate on a single fault of system is likely to be unchanged in the future (38).
The largest events occur where the barriers break and successive events at a given barrier release about the same amount of energy. Slip in the greatest earthquakes at a given site is not simply periodic: the interval times show significant variation. A cumulative distribution of the interval times is fit well by a truncated exponential distribution (Fig. 6): there are no interval times less than a certain critical value; the upper end of the distribution is terminated by the values for the extended lacunae, which are evidently inconsistent with the exponential distribution.
A comparison between the numerical distribution for intervals between large events on the model and the intervals between great earthquakes on the more northerly SAF measured at Pallett Creek (1, 2) suggests that the distribution at the latter site may also be truncated; it cannot be confirmed that the decay is exponential because of the small number of data. Lacunae are not be expected here since there are no long faults parallel to the SAF in this region to absorb the strain. It is likely that the fluctuations in interval times at Pallett Creek are due to interactions with large earthquake events in the neighborhood that generate stress transfer among ruptures on a more complex network of faults.
Without detailed information about the stress and strength distributions on the network, which is evidently not now possible for the faults of Southern California, we have no way at present to predict either the onset of lacunarity where appropriate or the interval time to the next great earthquake. It is doubtful that the time series of seismicity can be considered to be stationary if the effects of localization due to barriers are taken into account appropriately.
Intermediate Time Scale
Thus far, we have considered models with a time scale of seismic events that is set by the ratio between the elastic stress
drop at a lattice site and the stress loading rate. This time scale is appropriate to the long time scale of earthquake recurrence, which is of the order of 100 years in the case of the SAF and longer in the case of the other faults in its neighborhood. On the shorter time scale of intermediate-term precursory processes, let us say on a time scale of 1–10 years, we wish to identify clustering of smaller earthquakes before larger ones, a problem not adequately described by the above models. We modify the above models in two ways. First, we ask whether there is any physical mechanism that is competitive with brittle fracture to load or unload a fault on this time scale or shorter. In this section, we consider the diffusion of water in and out of fault zones and the nonelastic processes of slip weakening prior to fracture, which are mechanisms that are indeed important on the intermediate time scale; identification of precursory patterns of activity that make use of models of self-organization that are based on simple brittle-fracture processes only (39–41) must be modified to take the important influences of fluids and slip weakening into account. Second, we must be able to compute in detail over shorter time intervals, and hence we must forego the opportunity to study long-term evolutionary seismicity; here we describe computational schemes that explore precursors before each strong earthquake individually.
Because the normal stress on faults increases with depth below the earth’s surface, brittle fracture on faults becomes increasingly difficult even at shallow depths in the crust; without the agency of water to reduce strength, faults would become locked, and yielding would not be localized on discrete fault surfaces. Hubbert and Rubey (42) proposed that the introduction of water into a fault would lower the friction and permit sliding to take place. Sibson (43–47) has described how water can be introduced into a fault zone from below the seismogenic zone before a large earthquake and how it can be removed after a large earthquake; removal allows for reestablishment of friction and hence for renewal of the earthquake process.
The introduction of fluids into a fault zone not only lowers the normal stress on the fault zone but also causes the normal stress on nearby faultlets to increase—i.e., as the walls of a major fault are pushed apart, other nearby faults should be squeezed together. Thus, activity of small earthquakes in the neighborhood of a fluidizing or fluidized fault should decrease—i.e., quiescence should be initiated. But why does not a fluidized fault rupture immediately upon lowering of the normal stress? To allow for a time delay between the onset of quiescence and occurrence of a strong earthquake, we assume that the fault is inhomogeneous and that while parts of it are fluidized, other parts remain locked in frictional contact; this is the asperity model of earthquakes.
In the barrier model (48) of the preceding sections, the growth of elastic fractures may stop at regions of low ratio of stress drop to strength. In the asperity model (49), a central, strong brittle zone or asperity is surrounded by a weak zone such as a crack that has a low shear strength or low friction because of the continuing presence of fluids, a structure that is inherently inhomogeneous. On a 1D fault, the asperity separates two disconnected, fluid-filled cracks. In the asperity model, unstable sliding is prevented by the asperity sutures; large scale sliding takes place when the asperities break. This model is not unlike the “bed-of-nails” model (50) proposed to understand porous flows in rocks at low pressures and the “fiber bundle model” (51, 52) designed to understand failure of braided cables or ropes. Neither of the latter statistical models have the correlations implicit in the present context; the issues in the present case involve the spatiotemporal development of conditions for occurrence of large earthquakes due to self-organization of the stress field.
An instability due to a decrease of friction with an increase of slip or slip rate for rocks close to their breaking point has been known for some time (53) and is a property of most solid materials. The instability associated with a lessening of strength as the critical state of fracture approaches has been studied more recently in experiments on stress corrosion, subcritical crack growth, and slip-weakening (54–59) and has been used in studies of self-organization on extended single faults (60–63). The presence of water vastly accelerates the rate of weakening of strength of fault materials and especially so at elevated temperatures because the weakening follows an activation process; it is the accelerated weakening that makes this process competitive in the intermediate time scale.
We combine the slip-weakening physics with the asperity model. We first consider a planar 1D array of fluid-filled preexisting cracks, separated by asperities (64). The crack lengths and the asperity widths are random variables, which we choose to have power law distributions. The cracks are subjected to an in-plane shear (mode II) stress. We solve the problem of the stress field in the complete long-range formulation. Cracks develop accelerated growth at their tips under the influence of the external shear stress, thereby causing the width of the asperities at their edges to decrease; cracks grow only along their own fault lines. The velocity of growth is a very strong function of the stress intensity factor at the crack tip, which we specify as vtip ~ eσ or vtip ~ σn with n large (54–55). As the crack lengths increase, and as the widths of asperities at the edges of cracks decrease, the stress intensity factor at crack tips increases, and hence the velocities of the tips increase. When the velocity of the tip of a crack approaches the S-wave velocity, the crack begins to radiate seismic energy (60, 61) and, in the quasistatic approximation we use, the asperity disappears at this instant and an earthquake event occurs. The stress is now redistributed to the ends of the new crack, which has linear dimensions equal to the sum of the lengths of the two cracks and the now-vanished asperity; the suddenly increased stress intensity factors at the tips may cause further asperities to be consumed. For a finite array, in most cases only a few foreshocks, and in most cases no foreshocks, precede a strong event that releases prestress energy accumulated in the nucleation volume of the asperities; the large event transfers stress to great distance, being the extent of the fluidized zone. A homologous distribution of the few foreshocks over many simulations is in agreement with the inverse Omori law observed, also homologously, in large earthquakes worldwide (65, 66). It is to be expected that faults that are fluidized over much of their length, except for asperity contacts, should have normal stresses that are perpendicular to the fault structures, as observed (67), except at the asperities. This inhomogeneous model of faulting has bearing on the problem of the heat flow paradox. Lachenbruch and Sass (68) have remarked that the (average) stress drop in strong earthquakes is low (69) and that the heat flow across the SAF is not much above background (70, 71); these features combine to suggest that the fault is weak, a result inconsistent with field and laboratory measurements on whole rocks. There has been some discussion of the possibility of reducing the friction to very low values through a process of interface separation during the dynamics of rupture on relatively homogeneous materials (72); the asperity model suggests that the friction is low over much of the inhomogeneous fault before the rupture was initiated.
Consider now a network of faults (73). Suppose that fluids are introduced from below the seismogenic zone into the network when the region is at a sufficiently high state of stress. Let the width of the fluidized band of faults be small compared with their length. Seismic activity develops over the entire region in a series of local events of intermediate magnitude on individual faults of the network by the mechanism above. At a later time, a large earthquake having low average stress drop and great length develops on one of the faults. The large event not only extinguishes activity on its own fault but also lowers the stress on nearby faults and thus extinguishes activity on
them as well; activity on the entire region now ceases. If the fault network is studded with occasional asperity contacts in the fluidized state, the redistribution of stress may take on a filamentary geometry, as observed in experiments on granular assemblages, the grains having mainly free surfaces and only occasional bridging contacts (74–76).
If, however, an asperity having a dimension of let us say a few tens of kilometers does not break completely through, then a high stress drop earthquake will occur; because of failure to connect to the fluidized regions, these events will not cause significant changes in activity at distances of the order of several hundred kilometers. The agency of extended regions of fluid penetration into fault networks may help to understand the observations of an increase in intermediate-magnitude activity on a time scale of several years before a strong earthquake and its subsequent, rapid extinction on a distance scale of many times the classical dimension of rupture of a large earthquake that has been recently noted as part of the phenomenology of strong earthquakes in California (77). Reactivation takes place on the tectonic time scale.
If the faults of the network are somewhat farther apart in comparison with the length of the zone of activation, faults at intermediate distance may become reactivated after an episode of quiescence by the stress corrosion mechanism (73); the stress-corrosion reactivation time scale is much shorter than the tectonic reactivation time scale on an individual fault zone. Reactivation on a time scale of decades is consistent with some patterns of seismicity in Japan and is consistent with a greater width of the fault network in Japan than in California.
Summary
Because of scale independence, homogeneous fault models develop power-law distributions of seismicity that reproduce well the G-R distribution for small events. Unfortunately, the seismicity is only a transient state; for any finite fault, sooner or later seismicity interacts with inhomogeneities at the boundaries that leave an imprint on future seismicity that is characteristic of the nature of the boundaries. We have therefore
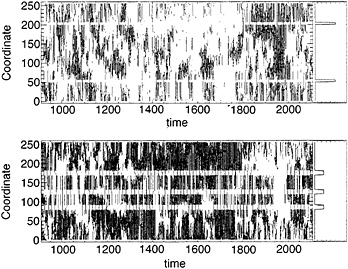
FIG. 5. Distribution of seismicity for a part of the time sequence for two faults coupled as in Fig. 4. The distribution of fracture thresholds is shown on the right. Periodic end conditions on both faults. Seismicity is largely complementary, with quiescence on one fault matched by activity on the other at the same coordinate and time. Around time 1600, the fault with stronger barriers becomes quiet over almost its entire length, which is matched by activity over almost the entire length of the other. Around time 1920, the pattern is almost completely reversed. Noteworthy is the interval from times 1300 to 1800, when the barrier at coordinate 200 on the upper fault does not tear; after time 1800, it tears frequently.
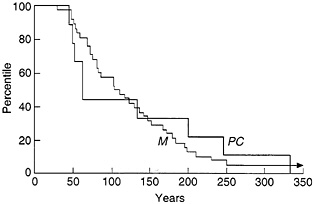
FIG. 6. Cumulative distribution of interval times for fractures of the strong barrier at coordinate 200 on the upper fault of the model (M), compared with the distribution of interval times for great earthquakes at Pallett Creek (PC). The model curve is well fit by a truncated exponential distribution except for the instabilities at the lacunae, such as that between times 1300 and 1800 (see Fig. 5). Time scales of the two curves have been adjusted to have a common median.
considered inhomogeneous fault models, with geometrical fluctuations of fracture strengths, to guarantee that large events are localized and do not interact with boundaries and to guarantee that large earthquakes will not obey the power-law distribution. Inhomogeneous fault models favor the characteristic earthquake model for large events—namely, those that are limited by the strongest inhomogeneities—while the smaller earthquakes may continue to be described by power-law distributions. However, we find that the character of the seismicity is extremely sensitive to the geometrical distributions of inhomogeneities of fracture thresholds.
Most models of the seismicity of the largest events on single inhomogeneous faults show little dispersion of interval times. To generate significant dispersion of interval times, we have explored the nature of seismicity on a pair of parallel faults, whose stress redistribution patterns influence the occurrence of earthquakes on one another. Model simulations show that the instabilities of seismicity on a single fault have a different character in the coupled cases; seismicity now displays complementarity behavior as well as episodes of lacunarity. The distribution of interval times for the strongest earthquakes is a truncated exponential. We conclude that the popular assumption that the average rate of slip on individual faults is a constant is not likely to be valid.
Intermediate-term precursory activity in Southern California is simulated well by an asperity model that assumes that faults are fluidized and hence are weak over much of their length. Accelerated weakening of strength, coupled with the infusion of fluids from below the seismogenic zone, can account for local precursory quiescence for an increase of intermediate-magnitude activity at long range and the abrupt extinction of the latter by the occurrence of strong earthquakes with low average stress drop; the range of interaction can be many times the dimensions of the zone of brittle fracture in a large earthquake. The model of a fluidized fault network, sutured by occasional asperities, can explain the heat flow paradox, the orientation of the stress field near the SAF, and the low average stress drop in some strong earthquakes.
This research was supported by a grant from the Southern California Earthquake Center. This paper is publication no. 4622 of the Institute of Geophysics and Planetary Physics, University of California, Los Angeles, and is publication no. 323 of the Southern California Earthquake Center.
1. Sieh, K.E. (1978) J. Geophys. Res. 83, 3907–3939.
2. Sieh, K., Stuiver, M. & Brillinger, D. (1989) J. Geophys. Res. 94, 603–623.
3. Knopoff, L. (1996) Proc. Natl. Acad. Sci. USA, 3756–3763.
4. Bak, P. & Tang, C. (1989) J. Geophys. Res. 94, 15635–15637.
5. Nakanishi, H. (1990) Phys. Rev. A 41, 7086–7089.
6. Nakanishi, H. (1991) Phys. Rev. A 43, 6613–6621.
7. Christensen, K. & Olami, Z. (1992) J. Geophys. Res. 97, 8729–8735.
8. Christensen, K. & Olami, Z. (1992) Phys. Rev. A 46, 1829–1838.
9. Christensen, K., Olami, Z. & Bak, P. (1992) Phys. Rev. Lett. 68, 2417–2420.
10. Olami, Z., Feder, H.J.S. & Christensen, K. (1992) Phys. Rev. Lett. 68, 1244–1247.
11. Olami, Z. & Christensen, K. (1992) Phys. Rev. A 46, 1720–1723.
12. Burridge, R. & Knopoff, L. (1967) Bull. Seismol. Soc. Am. 57, 341–371.
13. Carlson, J. & Langer, J.S. (1989) Phys. Rev. Lett. 62, 2632–2635.
14. Carlson, J.M. & Langer, J.S. (1989) Phys. Rev. A 40, 6470–6484.
15. Knopoff, L., Landoni, J.A. & Abinante, M.S. (1992) Phys. Rev. A 46, 7445–7449.
16. Heaton, T.H. (1990) Phys. Earth Planet. Inter. 64, 1–20.
17. Xu, H.J. & Knopoff, L. (1994) Phys. Rev. E 50, 3577–3581.
18. Wacker, A., Bose, S. & Sehöll, E. (1995) Europhys. Lett. 31, 257–262.
19. Abinante, M.S. & Knopoff, L. (1995) Phys. Rev. E 52, 5675–5678.
20. Rice, J.R. (1993) J. Geophys. Res. 98, 9885–9907.
21. Kostrov, B.V. (1996) J. Appl. Math. Mech. 30, 1241–1248.
22. Burridge, R. & Halliday, G.S. (1971) Geophys. J.R.Astron. Soc. 25, 261–283.
23. Lomnitz-Adler, J. (1991) J. Geophys. Res. 96, 6121–6131.
24. Pisarenko, D. & Mora, P. (1994) Pure Appl. Geophys. 142, 447–466.
25. Knopoff, L. & Ni, X.X. (1995) in Impact, Waves and Fracture, eds. Batra, R.C., Mal, A.K. & MacSiphigh, G.P. (Am. Soc. Mech. Engrs., New York), pp. 175–187.
26. Scott, D.R., Marone, C.J. & Sammis, C.G. (1994) J. Geophys. Res. 99, 7231–7246.
27. Chester, F.M. (1994) J. Geophys. Res. 99, 7247–7261.
28. Herrmann, H.J. (1992) Physica A 191, 263–276.
29. Knight, J.B., Jaeger, H.M. & Nagel, S.R. (1993) Phys. Rev. Lett. 70, 3728–3731.
30. Ehrichs, E.E., Jaeger, H.M., Karczmar, G.S., Knight, J.B., Kuperman, V.Y. & Nagel, S.R. (1995) Science 267, 1632–1634.
31. Tillemans, H.-J. & Herrmann, H.J. (1995) Physica A 217, 261–288.
32. King, G. (1986) Pure Appl. Geophys. 124, 567–585.
33. King, G. & Nabelek, J. (1985) Science 228, 984–987.
34. Knopoff, L. (1993) Proc. Am. Philos. Soc. 137, 339–349.
35. Chen, Y.-T. & Knopoff, L. (1986) Geophys. J.R. Astron. Soc. 87, 1005–1024.
36. Turcotte, D.L. (1986) J. Geophys. Res. 91, 1921–1926.
37. Turcotte, D.L. (1992) Fractals and Chaos in Geology and Geophysics (Cambridge Univ. Press, Cambridge, U.K.).
38. Working Group on California Earthquake Probabilities (1995) Bull. Seismol. Soc. Am. 85, 379–439.
39. Kossobokov, V.G. & Carlson, J.M. (1995) J. Geophys. Res. 100, 6431–6441.
40. Pepke, S.L., Carlson, J.M. & Shaw, B.E. (1994) J. Geophys. Res. 99, 6769–6788.
41. Shaw, B.E., Carlson, J.M. & Langer, J.S. (1992) J. Geophys. Res. 97, 479–488.
42. Hubbert, M.K. & Rubey, W.W. (1959) Bull. Geol Soc. Am. 70, 115–205.
43. Sibson, R.H. (1981) in Earthquake Prediction: An International Review, eds. Simpson, D.W. & Richards, P.G. (Am. Geophys. Union, Washington, DC), pp. 593–603.
44. Sibson, R.H., Moore, J. McM. & Rankin, A.H. (1975) J. Geol Soc. London 131, 652–659.
45. Sibson, R.H. (1992) Earth-Science Rev. 32, 141–144.
46. Sibson, R.H. (1992) Tectonophysics 211, 283–293.
47. Sibson, R.H. (1994) Geol. Soc. Spec. Publ. 78, 69–84.
48. Aki, K. (1979) J. Geophys. Res. 84, 6140–6148.
49. Kanamori, H. (1981) in Earthquake Prediction: An International Review, eds. Simpson, D.W. & Richards, P.G. (Am. Geophys. Union, Washington, DC), pp. 1–19.
50. Gangi, A.F. (1978) Int. J.Rock Mech. Min. Sciences Geomech. Abstr. 15, 249–257.
51. Newman, W.I. & Gabrielov, A.M. (1991) Int. J.Fract. 50, 1–14.
52. Newman, W.I., Gabrielov, A.M., Durand, T.A., Phoenix, S.L. & Turcotte, D.L. (1994) Physica D 77, 200–216.
53. Griggs, D.T. (1940) Bull. Geol. Soc. Am. 51, 1001–1022.
54. Atkinson, B.K. (1982) J. Struct. Geol. 4, 41–56.
55. Atkinson, B.K. (1984) J. Geophys. Res. 89, 4077–4114.
56. Dieterich, J.H. (1978) Pure Appl. Geophys. 116, 790–806.
57. Dieterich, J.H. (1979) J. Geophys. Res. 84, 2161–2168.
58. Dieterich, J.H. (1981) Geophys. Monogr. Am. Geophys. Union 24, 103–120.
59. Ruina, A. (1983) J. Geophys. Res. 88, 19359–10370.
60. Cao, T. & Aki, K. (1984) Pure Appl. Geophys. 122, 10–24.
61. Cao, T. & Aki, K. (1986) Pure Appl. Geophys. 124, 487–513.
62. Dieterich, J.H. (1986) Geophys. Monogr. Am. Geophys. Union 37, 37–47.
63. Dieterich, J.H. (1988) Pure Appl. Geophys. 126, 589–617.
64. Yamashita, T. & Knopoff, L. (1989) Geophys. J.R.Astron. Soc. 96, 389–399.
65. Kagan, Y.Y. & Knopoff, L. (1978) Geophys. J.R.Astron. Soc. 55, 67–86.
66. Jones, L.M. & Molnar, P. (1979) J. Geophys. Res. 84, 3596–3608.
67. Zoback, M.D., Zoback, M.L., Mount, V., Eaton, J., Healy, J. et al. (1987) Science 238, 1105–1111.
68. Lachenbruch, A.H. & Sass, J.H. (1992) J. Geophys. Res. 97, 4995–5015.
69. Kanamori, H. & Anderson, D.L. (1975) Bull. Seismol. Soc. Am. 65, 1073–1095.
70. Brune, J.N., Henyey, T.L. & Roy, R.F. (1969) J. Geophys. Res. 74, 3821–3827.
71. Lachenbruch, A.H. & Sass, J.H. (1980) J. Geophys. Res. 85, 6185–6222.
72. Brune, J.N., Brown, S. & Johnson, P.A. (1993) Tectonophysics 218, 59–67.
73. Yamashita, T. & Knopoff, L. (1992) J. Geophys. Res. 97, 19873–19879.
74. Dantu, P. (1967) Ann. Ponts Chausées 4, 144.
75. Travers, T., Ammi, M., Bideau, D., Gervois, A., Messager, J.C. & Troadec, J.P. (1987) Europhys. Lett. 4, 329–332.
76. Liu, C.-h., Nagel, S.R., Schecter, D.A., Coppersmith, S.N., Majumdar, S., Narayan, O. & Witten, T.A. (1995) Science 269, 513–515.
77. Knopoff, L., Levshina, T., Keilis-Borok, V.I. & Mattoni, C. (1996) J. Geophys. Res. 101, 5779–5796.
78. Yamashita, T. (1995) J. Geophys. Res. 100, 8339–8350.