Geometric incompatibility in a fault system
ANDREI GABRIELOV*†, VLADIMIR KEILIS-BOROK*, AND DAVID D.JACKSON‡
*International Institute of Earthquake Prediction Theory and Mathematical Geophysics, Russian Academy of Sciences, Warshavskoye sh.79, k.2. Moscow 113556, Russia; †Departments of Mathematics and Earth and Atmospheric Sciences, Purdue University, West Lafayette, IN 47907–1395; and ‡Institute of Geophysics and Planetary Physics, University of California, Los Angeles, 405 Hilgard Avenue, Los Angeles, CA 90024–1567
Contributed by Vladimir Keilis-Borok, August 7, 1995
ABSTRACT Interdependence between geometry of a fault system, its kinematics, and seismicity is investigated. Quantitative measure is introduced for inconsistency between a fixed configuration of faults and the slip rates on each fault. This measure, named geometric incompatibility (G), depicts summarily the instability near the fault junctions: their divergence or convergence (“unlocking” or “locking up”) and accumulation of stress and deformations. Accordingly, the changes in G are connected with dynamics of seismicity. Apart from geometric incompatibility, we consider deviation ![]() from well-known Saint Venant condition of kinematic compatibility. This deviation depicts summarily unaccounted stress and strain accumulation in the region and/or internal inconsistencies in a reconstruction of block- and fault system (its geometry and movements). The estimates of G and
from well-known Saint Venant condition of kinematic compatibility. This deviation depicts summarily unaccounted stress and strain accumulation in the region and/or internal inconsistencies in a reconstruction of block- and fault system (its geometry and movements). The estimates of G and ![]() provide a useful tool for bringing together the data on different types of movement in a fault system. An analog of Stokes formula is found that allows determination of the total values of G and
provide a useful tool for bringing together the data on different types of movement in a fault system. An analog of Stokes formula is found that allows determination of the total values of G and ![]() in a region from the data on its boundary. The phenomenon of geometric incompatibility implies that nucleation of strong earthquakes is to large extent controlled by processes near fault junctions. The junctions that have been locked up may act as transient asperities, and unlocked junctions may act as transient weakest links. Tentative estimates of
in a region from the data on its boundary. The phenomenon of geometric incompatibility implies that nucleation of strong earthquakes is to large extent controlled by processes near fault junctions. The junctions that have been locked up may act as transient asperities, and unlocked junctions may act as transient weakest links. Tentative estimates of ![]() and G are made for each end of the Big Bend of the San Andreas fault system in Southern California. Recent strong earthquakes Landers (1992, M=7.3) and Northridge (1994, M=6.7) both reduced
and G are made for each end of the Big Bend of the San Andreas fault system in Southern California. Recent strong earthquakes Landers (1992, M=7.3) and Northridge (1994, M=6.7) both reduced ![]() but had opposite impact on G: Landers unlocked the area, whereas Northridge locked it up again.
but had opposite impact on G: Landers unlocked the area, whereas Northridge locked it up again.
The geometry of a fault system imposes certain limitations on the movements within it; a wide class of movements would require a change of geometry. A simple illustration of such limitations is the intersection (“junction”) of strike-slip faults (Fig. 1A). If their movement could follow the arrows, the corners A and C would penetrate each other as shown in Fig. 1B. Obviously, this is not possible, so that the movement along the faults has to be accommodated by additional fracturing and/or deformation, changing fault geometry near the junction point.
The concept of such phenomena was first introduced by McKenzie and Morgan (1). They considered subduction zones, mid-ocean ridges, and transform faults under a formulated condition in which triple junctions of the plate boundaries were “stable”—that is, “could retain their geometry as the plates moved”; this was expressed as a relation between the rates of relative plate movement at each plate boundary. Systematic description of 125 possible types of triple junctions is given in ref. 2.
If the stability condition were not satisfied, the plate movements would lead to stress accumulation around the junction and formation of new faults of a smaller scale (3, 4). Generally speaking, this situation will not prevent the accumulation of stress but only redistribute it among newly formed fault junctions. King (3) suggested that such redistribution will lead to generation of new faults of progressively smaller and smaller scale, so that a hierarchical system of faults is formed around the initial junction. This conclusion is in good accordance with neotectonic data on specific structures that are formed around the junctions of active faults (5). These structures, called “morphostructural nodes” or “knots,” are wider than the intersecting fault zones. They are characterized by particularly intensive fracturing and contrasting neotectonic movements with a mosaic pattern of structure and topography resulting. Their formalized definition is described in ref. 6. It was demonstrated in a series of studies (e.g., refs. 7, 8) that epicenters of strong earthquakes are situated only within some of the nodes, identified by pattern recognition.
In this paper we introduce a quantitative measure of incompatibility between the geometry and kinematics of a fault system. We call this measure “geometric incompatibility.”
Let us outline basic definitions. Consider a system of blocks separated by faults. At each intersection of the faults (fault junction) the slip rates on faults at the junction point should satisfy the condition of Eq. 1
[1]
which is a discrete analogue of a well-known Saint Venant compatibility condition in continuum mechanics. Here the sum is taken over all faults entering the junction. This condition ensures that the relative movements on the faults can be realized through the absolute movements of the volumes (blocks) separated by the faults. The value of ![]() computed from observations may differ from zero because of observational errors or because some deformations are not allowed for. Accordingly, we call
computed from observations may differ from zero because of observational errors or because some deformations are not allowed for. Accordingly, we call ![]() the Saint Venant incompatibility.
the Saint Venant incompatibility.
However, the Saint Venant condition is not sufficient to ensure that faults movements are possible without a change in the fault system geometry around the junction. For example, if the rate of movement along each fault in Fig. 1a is the same for both sides of the junction point, the Saint Venant condition is satisfied. Nevertheless, the movement requires a geometric change; otherwise the junction point would split into a parallelogram (Fig. 1b). After a time interval t the (oriented) area of this unrealizable parallelogram would be ![]() . In general case, a junction point would split into a polygon with area
. In general case, a junction point would split into a polygon with area
S(t)=Gt2/2. [2]
The coefficient G is our measure of geometric incompatibility. It depends on all the slip rates ![]() at the junction point. In our example,
at the junction point. In our example, ![]() . Note that in this case G is negative because the corners A and C overlap. In such cases, compression concentrates at the junction, locking it up. Fig. 2 shows an example of a junction with all corners diverging; then G is positive, and the junction is unlocked by tension.
. Note that in this case G is negative because the corners A and C overlap. In such cases, compression concentrates at the junction, locking it up. Fig. 2 shows an example of a junction with all corners diverging; then G is positive, and the junction is unlocked by tension.
Below we derive the formulas for geometric incompatibility in a fault system with many junctions. In such a system, Saint Venant and geometric incompatibilities depend also on rota
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
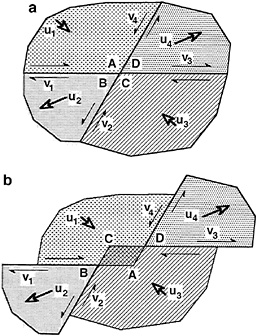
FIG. 1. Example of geometric incompatibility near fault junction. 1, Faults; 2, horizontal component of absolute movement of a block, ![]() ; 3, horizontal component of slip rate on a fault,
; 3, horizontal component of slip rate on a fault, ![]() ; A, B, C, and D, corners of the blocks; a, initial position of the blocks; b, extrapolation of initial movement. Corners A and C are converging and would overlap; this indicates that the movement cannot be realized without the change of the fault geometry.
; A, B, C, and D, corners of the blocks; a, initial position of the blocks; b, extrapolation of initial movement. Corners A and C are converging and would overlap; this indicates that the movement cannot be realized without the change of the fault geometry.
tion and deformation of blocks separated by the faults. Both measures of incompatibility have the following useful property, reminiscent of the Stokes formula: To estimate their values in a whole region, it is sufficient to know only the movements on the faults that cross the boundary of this region.
Analytical expressions for G are derived below first for a single junction and then for a system of faults with many junctions within a given contour. The expressions for a single junction are the same for rotating and nonrotating blocks. For a fault system with many junctions these expressions are
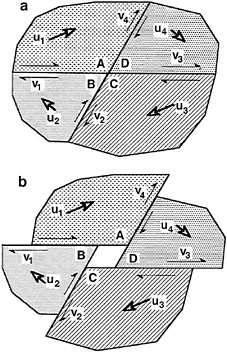
FIG. 2. Example of geometric incompatibility. Notations are the same as in Fig. 1. Geometric incompatibility leads to divergence of the block corners.
different for deformable/rotating blocks; we consider this case in the Appendix.
Geometric Incompatibility for a Single Junction
Consider n fault segments with a common junction point; a fault crossing this point is regarded as two segments. We choose some segment as the first one, and assign the numbers from 2 to n to the other segments counterclockwise. The n blocks separated by these faults meet at the junction. We number them in such a way that the ith fault separates the blocks i and i+1.
Let ![]() be the rate of movement of the ith block at the junction point, and
be the rate of movement of the ith block at the junction point, and ![]() the rate of relative movement on the ith fault. We always set
the rate of relative movement on the ith fault. We always set ![]() and
and ![]() Because we consider only horizontal components of the movements, the vectors
Because we consider only horizontal components of the movements, the vectors ![]() and
and ![]() are two-dimensional. For two such vectors,
are two-dimensional. For two such vectors, ![]() and
and ![]() , we define the cross-product
, we define the cross-product ![]() . After a time period t the junction, which we place at the origin, becomes, due to block movement, a polygon with the vertices
. After a time period t the junction, which we place at the origin, becomes, due to block movement, a polygon with the vertices ![]() . Computing the (oriented) area of this polygon, we obtain the following expression for the geometric incompatibility G defined in ref. 2:
. Computing the (oriented) area of this polygon, we obtain the following expression for the geometric incompatibility G defined in ref. 2:
[3]
We easily verify that this sum does not change when we add a common vector to all the rate vectors ![]() . Replacing
. Replacing ![]() by
by ![]()
![]() and substituting
and substituting ![]() , we can rewrite G in terms of the relative movement rates
, we can rewrite G in terms of the relative movement rates ![]() :
:
[4]
This formula depends on the arbitrary choice of the first segment. However, it will lead to the same values of G, for any choice, if ![]() if the observed values of satisfy
if the observed values of satisfy ![]() the Saint Venant condition Eq. 1. If this condition is not satisfied— e.g., due to observational errors or block deformation, we have to satisfy it by modification of
the Saint Venant condition Eq. 1. If this condition is not satisfied— e.g., due to observational errors or block deformation, we have to satisfy it by modification of ![]() . This can be done in a nonunique way. In the absence of additional information we simply subtract from each of
. This can be done in a nonunique way. In the absence of additional information we simply subtract from each of ![]() a fraction of
a fraction of ![]() proportional to the absolute value of vi:
proportional to the absolute value of vi:
[5]
The following properties of G may be of interest: (i) The value of G does not change when all slip rates reverse directions, (ii) For intersections of strike-slip faults, a negative sign of G indicates the tendency of the blocks to “penetrate” each other at the junction (Fig. 1), so that the movement along one fault locks up another fault. On the contrary, if G were positive, the movement on one fault unlocks another one (Fig. 2).
Geometric Incompatibility for a System of Faults with Multiple Junctions
We consider here the case of rigid nonrotating blocks, which is analytically simpler than the general case and can be of independent interest. Generalization for the case of deformable and/or rotating blocks is given in the Appendix.
Suppose we have a map with a system of blocks divided by faults. Consider on this map a simply connected region D surrounded by a boundary L. Because the blocks do not rotate, the rates of block movement are the same at all points of a block, and the rates of relative fault movements are the same between fault junctions.
As before, we number the blocks crossing the boundary L of the region D counterclockwise, and number the faults crossing
L in such a way that the ith fault separates the blocks i and i +1. Let be ![]() the rate of movement of the ith block crossed by L, and be
the rate of movement of the ith block crossed by L, and be ![]() the slip rate along the ith fault crossing L. These rates do not change when we deform the boundary L of the region, as long as it does not cross any fault junctions and no intersection points of L with faults appear or disappear.
the slip rate along the ith fault crossing L. These rates do not change when we deform the boundary L of the region, as long as it does not cross any fault junctions and no intersection points of L with faults appear or disappear.
The Saint Venant condition is again expressed by Eq. 1 with the new definition of the sequence ![]() .
.
Let us define now geometric incompatibility G. Consider the contour L drawn at a time moment t0. At a time t>t0, this contour will be deformed into a contour Lt. For example, if L is the external boundary in Figs. 1A and 2A then Lt is the boundary in Figs. 1B and 2B. Generally, Lt is defined as follows. The segments of L within blocks move together with blocks. Each crossing of L with a fault splits into two points. To form a closed contour Lt, we connect these points by a segment of a straight line. Let S(t) be the area of the region bounded by Lt. We define the geometric incomp atibility as
[6]
It can be shown that (i) G can be computed from slip rates ![]() by the same formula (Eq. 4) as for a single junction, but with the new meaning of
by the same formula (Eq. 4) as for a single junction, but with the new meaning of ![]() , and (ii) the value G for the region D equals the sum of the values G for all fault junctions that exist inside D at the time moment t0.
, and (ii) the value G for the region D equals the sum of the values G for all fault junctions that exist inside D at the time moment t0.
Application to Southern California Fault Junctions
To illustrate the method suggested here, we considered a schematic representation of two nodes with multiple fault junctions around the ends of the Big Bend segment of the San Andreas fault. Only a few major faults out of the much more complicated fault system are allowed for in our analysis. Such a fault may actually represent a set of faults with a common dominant orientation. With the data available, we could only get an insight into the range of the values of geometric incompatibility.
We used the slip rate data from comprehensive summaries (9) and (10).
The values of  and G were computed from formulas (Eq. 1) and (Eq. 4), which do not allow for rotation, little known so far, or for blocks deformation.
and G were computed from formulas (Eq. 1) and (Eq. 4), which do not allow for rotation, little known so far, or for blocks deformation.
Fig. 3 shows a simplified scheme of the Big Bend, after (ref. 9, Fig. 3). We analyze separately two nodes of the Big Bend shown in Fig. 3 by dashed ellipses.
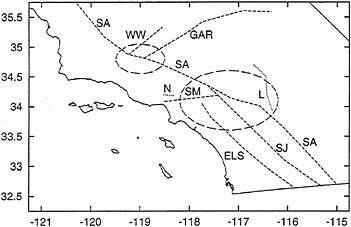
North-West Node. This area encompasses the junction of San Andreas and Garlock faults. One of the two strongest earthquakes of this century in Southern California (Kern County, M=7.5, 1952) occurred on the adjacent White Wolf fault. Ironically, it is sometimes not regarded as a major fault, probably due to the small slip rate, which is 2 mm/yr.
The slip rate vectors are given in Table 1. The values of ![]() and G are given in the first two lines of Table 2. Line 1 corresponds to the case when only the San Andreas and Garlock faults are considered. The Saint Venant incompatibility lies within 12% of the slip rate on the San Andreas fault. We can reduce
and G are given in the first two lines of Table 2. Line 1 corresponds to the case when only the San Andreas and Garlock faults are considered. The Saint Venant incompatibility lies within 12% of the slip rate on the San Andreas fault. We can reduce ![]() by taking into account the White Wolf fault (line 2 in Table 2). The value of G does not change much. Its negative sign indicates that this node is “locked up”.
by taking into account the White Wolf fault (line 2 in Table 2). The value of G does not change much. Its negative sign indicates that this node is “locked up”.
South-East Node. This area encompasses the branching of the San Andreas fault into at least three faults: San Andreas proper, San Jacinto, and Elsinore. The San Andreas fault is joined here from the west by a complicated series of bilateral thrusts represented in Fig. 3 by the Sierra Madre fault. The slip rate vectors are given in Table 1. The values of ![]() and G are given in lines 3–6 of Table 2.
and G are given in lines 3–6 of Table 2.
Line 3 corresponds to four major faults only, after ref. 9. We see that ![]() is rather large, of the same order of magnitude as slip values on some faults. To reduce
is rather large, of the same order of magnitude as slip values on some faults. To reduce ![]() , we take into account 3 mm/yr horizontal shortening across the Sierra Madre fault, and change the slip rate on the Mojave segment of San Andreas fault from 34 to 30 mm/yr, as suggested in ref. 10, table 5. The results are given in line 4 in Table 2. We see that only the lateral component of
, we take into account 3 mm/yr horizontal shortening across the Sierra Madre fault, and change the slip rate on the Mojave segment of San Andreas fault from 34 to 30 mm/yr, as suggested in ref. 10, table 5. The results are given in line 4 in Table 2. We see that only the lateral component of ![]() is noticeably reduced by these changes.
is noticeably reduced by these changes.
Finally, we can reduce ![]() to acceptable limits by increasing the slip rate on Sierra Madre fault from 3 to 8 mm/yr, which is within the difference between estimates by different authors (see ref. 10); the results are given in line 5 of Table 2. We see that this junction is also locked up by geometric incompatibility.
to acceptable limits by increasing the slip rate on Sierra Madre fault from 3 to 8 mm/yr, which is within the difference between estimates by different authors (see ref. 10); the results are given in line 5 of Table 2. We see that this junction is also locked up by geometric incompatibility.
Note that G cannot be reduced to zero in such a configuration of faults without reversing the movement on some faults or introducing new faults.
Impact of Strong Earthquakes. Qualitatively, an earthquake is equivalent to additional slip rate directed as the slip vector in the earthquake source. Let us discuss now how the values of ![]() and G may be influenced by two strongest recent earthquakes in this region, Landers (1992, M=7.3) and Northridge
and G may be influenced by two strongest recent earthquakes in this region, Landers (1992, M=7.3) and Northridge
Table 1. Slip rates along the faults in the Big Bend junctions
|
|
|
Slip rate, mm/yr |
|
|
Fault name |
Azimuth |
Tangent |
Normal |
|
North-West node |
|||
|
San Andreas N |
318 |
34 |
0 |
|
San Andreas S |
118 |
34 |
0 |
|
Garlock |
57 |
−10 |
0 |
|
White Wolf |
55 |
0 |
−2 |
|
South-East node |
|||
|
San Andreas N |
|||
|
After ref. 9 |
298 |
34 |
0 |
|
After ref. 10 |
298 |
30 |
0 |
|
Elsinore |
125 |
5 |
0 |
|
San Jacinto |
132 |
10 |
0 |
|
San Andreas S |
133 |
19 |
0 |
|
Sierra Madre |
|||
|
After ref. 10 |
270 |
0 |
−3 |
|
Modified |
270 |
0 |
−8* |
|
“Landers” |
0 |
5 |
0 |
|
Data are taken from ref. 10 unless otherwise indicated. Tangent component is positive for right-lateral strike-slip; the normal component is positive for extension. *Closer to the upper estimate indicated in ref. 10. |
|||
Table 2. Saint Venant ![]() and geometric (G) incompatibilities in the Big Bend junctions
and geometric (G) incompatibilities in the Big Bend junctions
|
No. |
|
|
G, mm2/yr2 |
|
North-West end of Big Bend |
|||
|
1 |
−1.1 |
3.9 |
−326.7 |
|
2 |
0.0 |
2.2 |
−324.3 |
|
South-East end of Big Bend |
|||
|
3 |
−4.6 |
−6.6 |
−22.4 |
|
4 |
−1.1 |
−5.4 |
−106.9 |
|
5 |
−1.1 |
−0.4 |
−234.1 |
|
6 |
−1.1 |
−0.4 |
30.0 |
(1994, M=6.7). The corresponding fault breaks are indicated on Fig. 3 by dotted lines.
To analyze the impact of the Landers earthquake, we included in our computation 5 mm/yr of right-lateral slip along the meridional part of its fault break. The rest of the parameters were the same as for line 4 of Table 2. The results are shown in line 6. Comparing these lines, we see that the Landers earthquake leads to a reduction of both incompatibilities and, because G becomes positive, unlocks the junction.
At the same time, this earthquake created a new junction and therefore new incompatibility on the bend of its own fault break.
The Northridge earthquake occurred on a bilateral thrust fault in the above-mentioned compression zone represented in our scheme (Fig. 3) by the Sierra Madre fault. The Landers earthquake, although more complicated, started as a submeridional right-lateral strike-slip. Though different in mechanism and location, both earthquakes reduce ![]() similarly. However, their contribution to G is opposite.
similarly. However, their contribution to G is opposite.
The Northridge earthquake is equivalent to an increase of the thrust rate on Sierra Madre fault. Comparing lines 4 and 5 in Table 2, we see that, due to such an increase, the meridional component of ![]() would be reduced. However, |G| becomes larger, so that this earthquake locks up the region.
would be reduced. However, |G| becomes larger, so that this earthquake locks up the region.
Coarse quantitative estimates can be done as suggested in ref. 11. Consider a fault with length L and width H. An earthquake on this fault causes a fault break of length l and width h and an average slip vector ![]() . We spread this slip over the whole fault and over the recurrence time T. The additional slip rate on the fault is roughly estimated as
. We spread this slip over the whole fault and over the recurrence time T. The additional slip rate on the fault is roughly estimated as
Because this relation is very coarse, we can use, at the best, only the orders of magnitude for all parameters involved, taking the values indicated in ref. 10.
Assuming l≈102 km, h≈101 km, d≈103 mm, L≈102 km, H≈101 km, T≈102−103 yr, we get for additional slip rate an estimate ve≈100−101 mm/yr. Comparing these numbers with numerical experiments in Table 1, we see that the contribution of strong earthquakes to geometric and kinematic incompatibilities is indeed essential. For example, Landers earthquake alone could well unlock the region completely, reversing the sign of G.
Discussion
(i) This work is a continuation of the quest for integral parameters that control the dynamics of seismicity. Geometric G and kinematic ![]() incompatibilities in an active fault system seem to be highly relevant for this purpose, representing the tendency of a system to stress and strain accumulation and fracturing. This interconnection may determine some of the features of seismicity, regardless of the physical processes involved.
incompatibilities in an active fault system seem to be highly relevant for this purpose, representing the tendency of a system to stress and strain accumulation and fracturing. This interconnection may determine some of the features of seismicity, regardless of the physical processes involved.
Geometric incompatibility seems to be the only known parameter that gives a comprehensive description of fault junctions.
The analogs of the Stokes formula established here allow one to estimate G and ![]() in a complicated area from observations on its boundary, thus reducing the requirements for observations.
in a complicated area from observations on its boundary, thus reducing the requirements for observations.
(ii) Because geometric incompatibility depicts the locking up or unlocking of the fault junctions, it may be one of the major factors controlling nucleation (triggering) of strong earthquakes. It is generally accepted that earthquakes occur when the stress exceeds the static friction (strength). Traditionally, such triggering is assigned to “strong” fault segments. Actually, this condition will be first reached rather near a fault junction where both factors are more favorable: The strength may be much smaller due to intense fracturing. And the stress itself may rise faster due to geometric incompatibility.
This conjecture is in accordance with the well-confirmed conclusion that epicenters of strong earthquakes—that is, their nucleation areas, are, as a rule, confined to the vicinity of fault junctions (7, 8).
(iii) Existing observations allow, at best, only coarse estimates of G and ![]() . Still, they provide important insight into how different faults and earthquakes may affect the general equilibrium of a region. In particular, the impact of a strong earthquake cannot be neglected: it is comparable with the role of long-term (“geodetic”) movements and, moreover, it may reverse the geometric incompatibility, locking the junction up or unlocking it. A junction that is locked up may act as a transient asperity until it is broken by a strong earthquake or unlocked by subsequent impacts. A junction that is unlocked may act as a “weakest link” in the earthquake triggering or, alternatively, as a relaxation barrier.
. Still, they provide important insight into how different faults and earthquakes may affect the general equilibrium of a region. In particular, the impact of a strong earthquake cannot be neglected: it is comparable with the role of long-term (“geodetic”) movements and, moreover, it may reverse the geometric incompatibility, locking the junction up or unlocking it. A junction that is locked up may act as a transient asperity until it is broken by a strong earthquake or unlocked by subsequent impacts. A junction that is unlocked may act as a “weakest link” in the earthquake triggering or, alternatively, as a relaxation barrier.
In this way, geometric incompatibility and, therefore, seismicity may migrate within a fault system.
(iv) Simplifications in our analysis may be summarized as follows: we considered rigid blocks and horizontal movements; in computations possible rotation, being unknown, was not allowed for. When more data are available, these simplifications may have to be removed.
(v) Summing up, geometric incompatibility deserves attention as an important integral characteristic of the tectonic development of fault systems. In particular, it may be one of the parameters that controls the dynamics of seismicity.
Appendix: Incompatibilities for Deformable and Rotating Blocks
For a system of deformable blocks, the Saint Venant compatibility condition, in the integral form, can be written as follows (ref. 12, see also ref. 13). Let ![]() be displacement rate vector. Its components ui(x) are smooth functions within each block, with discontinuities at the block boundaries. Let L be a closed contour crossing the block boundaries at the points x1,…,xn counterclockwise, and let x0 be a fixed reference point. For v =1,…, n, let
be displacement rate vector. Its components ui(x) are smooth functions within each block, with discontinuities at the block boundaries. Let L be a closed contour crossing the block boundaries at the points x1,…,xn counterclockwise, and let x0 be a fixed reference point. For v =1,…, n, let ![]() and
and ![]() be the rate of movement
be the rate of movement ![]() (xv) in the blocks that contain the contour L before and after it crosses the block boundary at xv, and let
(xv) in the blocks that contain the contour L before and after it crosses the block boundary at xv, and let ![]() be the rate of relative movement of the two blocks at xv. Then
be the rate of relative movement of the two blocks at xv. Then
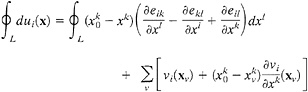
[A1]
should be zero, for all i. Here ![]() is the strain tensor.
is the strain tensor.
Linearization of ![]() (x) defines affine operators
(x) defines affine operators
[A2]
For x=xv, let ![]() be the operators corresponding to
be the operators corresponding to ![]() . The operator
. The operator ![]() , linearization of the relative rate of movement of two blocks at xv, does not depend on the rate of movement of the coordinate system. Expression in brackets in A1 can be rewritten as the ith component of the vector Σv Vv(x0).
, linearization of the relative rate of movement of two blocks at xv, does not depend on the rate of movement of the coordinate system. Expression in brackets in A1 can be rewritten as the ith component of the vector Σv Vv(x0).
When the blocks are rigid, the integral in A1 vanishes, and the Saint Venant compatibility condition is satisfied if and only if the affine operator
[A3]
is zero. This is an element of the Lie algebra
of the orthogonal affine group. This operator is a natural generalization of the Saint Venant incompatibility
Geometric incompatibility for a system of deformable blocks can be defined as
[A4]
It is easy to check that the value of G does not depend on the rate of movement of the coordinate system. Thus G is an invariant of the rate of deformation.
For rigid blocks, the integral in A4 vanishes, and the geometric incompatibility becomes
[A5]
similar to Eq. 3. This is an element of ![]() , the external square of the Lie algebra
, the external square of the Lie algebra ![]() of the orthogonal affine group. If K=0, this can be rewritten as
of the orthogonal affine group. If K=0, this can be rewritten as
G=V1∧V2+(V1+V2∧V3)
+…+(V1+…+Vn−2∧Vn−1), [A6]
similar to (Eq. 4). Otherwise, Vv should be modified as in (Eq. 5) to make K=0.
For a system of rigid blocks, an analog of the Stokes formula is valid for G: its value for a contour is equal to the sum of its values over the junctions within the contour, when the Saint Venant incompatibility is zero for all these junctions.
For a system of two-dimensional rigid blocks, let x=(x, y), and Vv(x, y)=(Xv−yωv, Yv+xωv). Here (Xv, Yv) is the relative displacement rate at the origin, and ωv is the relative rotation rate of the two blocks adjacent at xv. In this case, ![]() is three-dimensional, and the Saint Venant incompatibility has three components:
is three-dimensional, and the Saint Venant incompatibility has three components:
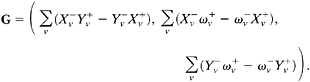
[A7]
The space ![]() is also three-dimensional. Accordingly, the geometric incompatibility G has three components:
is also three-dimensional. Accordingly, the geometric incompatibility G has three components:
[A8]
Here ![]() , define the operators
, define the operators ![]() in Eq. A5. Expression A6 can be rewritten similarly in terms of Xv, Yv, and ωv.
in Eq. A5. Expression A6 can be rewritten similarly in terms of Xv, Yv, and ωv.
This work was supported by National Science Foundation Grant no. 931650, and P.O. no. 56659 from University of Southern California, on behalf of the Southern California Earthquake Center. The first author (A.G.) was partly supported by the U.S. Army Research Office through the Mathematical Sciences Institute of Cornell University, Contract DAAL03–91-C-0027, and Department of Geological Sciences at Cornell University, under National Science Foundation Grant no. EAR-94–23818.
1. McKenzie, D.P. & Morgan, W.J. (1969) Nature (London) 224, 125–133.
2. Cronin, V.S. (1992) Tectonophysics 207, 287–301.
3. King, G.C.P. (1983) Pure Appl. Geophys. 121, 761–815.
4. King, G.C.P. (1986) Pure Appl Geophys. 124, 567–583.
5. Gerasimov, I. & Rantsman, E. (1973) Geomorphol. Res. 1, 1–13.
6. Alekseevskaya, M., Gabrielov, A., Gel’fand, I., Gvishiani, A. & Rantsman, E. (1977) J. Geophys. 43, 227–233.
7. Gelfand, I.M., Guberman, Sh. A, Keilis-Borok, V.I., Knopoff, L., Press, F., Ranzman, E.Y., Rotwain, I.M. & Sadovsky, A.M. (1976) Phys. Earth Planet. Int. 11, 227–283.
8. Guberman, Sh.I. & Rotwain, I.M. (1986) Izvestia Akad. Nauk SSSR 12, 72–74.
9. Feigl, K.L., Agnew, D.C., Bock, Y., Dong, D., Donnellan, A., Hager, B.H., Herring, T.A., Jackson, D.D., Jordan, T.H., King, R.W., Larsen, S., Larson, K.M., Murray, M.H., Shen, Z. & Webb, F.H. (1993) J. Geophys. Res. 98, 21677–21712.
10. Working Group on California Earthquake Probabilities (1995) Bull. Seis. Soc. Am. 85, 379–439.
11. Brune, J. (1968) J. Geophys. Res. 73, 777–784.
12. Fung, Y.C. (1965) Foundation of Solid Mechanics (Prentice-Hall, Englewood Cliffs, NJ), Chap. 4.
13. Minster, J.B. & Jordan, T.H. (1984) in Tectonics and Sedimentation Along the California Margin: Pacific Section, eds. Crouch, J.K. & Bachman, S.B. (Soc. Econ. Paleontol. Mineral., Los Angeles), Vol. 38, pp. 1–6.





