13 Comparative Perspectives on Plasticity in Human Aging and Life Spans
Caleb E. Finch
Introduction
Throughout the world, human life expectancy is increasing. Unprecedented numbers are reaching ages beyond the 10th decade and the maximum human life span is creeping up to break new records each year (Vaupel, Wilmoth, in this volume). I will discuss how these demographic shifts represent the plasticity found throughout the evolution of life histories. Similarly wide variations in life expectancy and maximum life spans are observed in animals and plants, within populations as well as between closely related species. The preceding chapters review the details of these increases and some of the mechanisms that may be involved. However, major unknowns remain about the nature of the aging process in humans and other organisms. The general information that is available from all sources gives a very limited basis for predicting further changes in human aging schedules and ultimate life spans.
The life history of multicellular organisms is built on the scheduling of functions during the life span. In sexually reproducing organisms, life history may be considered to begin with the gametes produced in the prior parental generation, which may exist for many decades before fertilization. Thus, the ova from which we arose were formed in our mothers' ovaries while she was a fetus in our maternal grandmothers' uterus, which allows environmental effects that span at least three generations in mammals (Finch, 1996; Finch and Loehlin, in press). Similarly, social insect queens store sperm acquired during their nuptial flights that remains viable for at least 7 years (Hölldobler and Wilson, 1990:146, 154). The prezygotic environment is a major unexplored domain of life history
that could have profound influences on characteristics of one or more ensuing generations.
More conventionally, the analysis of life history emphasizes the zygote and subsequent developmental stages through maturation and later postmaturational stages. At later postmaturational ages, mammals typically show declining reproduction and slowly manifest increasing physiological and functional losses that, in association with increasing mortality risk, define the phase of senescence.
One measure of the rate of senescence is the rate of increase of age-specific mortality, m(t). In many populations, m(t) increases exponentially after maturity according to the Gompertz formula: m( t) = exp[α(t)] (Finch and Pike, 1996; Finch et al., 1990; Mueller et al., 1995). A convenient basis for comparing mortality rate accelerations is the time required for mortality rates to double (MRDT = In 2/α), which is about 8 years in humans and about 0.3 year in laboratory rodents (Finch et al., 1990).
A huge body of work demonstrates many ways in which the phenomena of senescence are highly plastic and subject to modifications through environmental parameters, for example diet, as discussed below. This plasticity challenges traditional beliefs that the life spans of higher organisms are rigidly preprogrammed by their genes. I use the plural, life spans, to emphasize that there may be many statistically distinct life-history trajectories within a given human population, which are subject to myriad gene-environment interactions, including lifestyle choices (Finch and Tanzi, 1997). The plasticity of life histories is generally consistent with an evolutionary basis for the numeric life span as a life-history trait. The vast range of schedules shown by multicellular organisms, as described next, implies that the plasticity in life-history schedules and phenotypes is itself a general outcome of evolution by allowing multiple alternative adaptive schedules.
The Million-Fold Range Of Life Spans
The life expectancy of an individual in a population is not constrained by any known intrinsic feature of aging at the molecular or cellular level that is not open to evolution. As discussed by Tuljapurkar and by Rose (in this volume), for a species to survive, at least one of its populations must, on the average, maintain non-negative growth. This statistical outcome is achieved by balancing cumulative survival across adult ages by cumulative fecundity. The Euler-Lotka ''equation of state" for population dynamics does not lead to any predictions about the duration of the developmental stages that precede reproduction. Although time is a necessary dimension in the parameters that are used to describe population growth, evolutionary biologists generally conclude that the magnitude of duration for any life-history stage is free to increase without constraint and that there is no biological limit to the maximum life span.
Nonetheless, phenomena of senescence leading to characteristic life spans in a population are expected to be the norm. Rose, Partridge, and Tuljapurkar (in
this volume) summarize arguments from evolutionary theory that the force of natural selection diminishes at later ages, which therefore permits populations to accumulate germ-line mutations with delayed adverse consequences. This concept was developed in detail for sexually reproducing organisms (Haldane, 1941: Medawar, 1952; Hamilton, 1966; Williams, 1957; Charlesworth, 1994).
The plasticity of the life span was shown by artificial selection experiments in fruit flies. Life spans of outbred flies were lengthened during selection for individuals that could reproduce at later ages (see Rose, in this volume). Moreover, the increased life span could then be experimentally returned to starting values by selection for reproduction at younger ages. The rate of mortality acceleration (Gompertz coefficient α; see above) shows parallel changes to the maximum and median life spans in these genetic manipulations of the life span (Nusbaum et al., 1996). Because these bidirectional changes in life span and in reproductive history could be accomplished within 30 generations, it is likely that their genetic basis is shifts in genetic variations that pre-existed in the starting outbred population, rather than point mutations or chromosomal translocations. Natural populations of many organisms have genetic variations in neural and endocrine functions that regulate such quantitative life-history traits as the age at maturation and the frequency of reproduction (Finch and Rose, 1995). Indirectly, these parameters of the reproductive schedule are statistical determinants of the life span.
While the evolution of senescence in nonsexually reproducing organisms has been given less attention, clonal reproduction is well documented to coexist with senescence of the individual organism—e.g., two species of annelid worms (Martinez and Levinton, 1992). Mathematical modeling suggests that the evolution of senescence in organisms with the capacity for both sexual and clonal reproduction may depend on the age structure of the population (Orive, 1995) and the rates of sexual reproduction (Gardner and Mangel, 1997).
Existing organisms show a huge range in the life spans and reproductive schedules that implies the absence of evolutionary limits in life-history schedules, including the statistical life span in a population. The observed life spans in eukaryotes span a I million-fold range, with a short extreme from the 2-day life span of yeast cells (Saccharomyces ) up to the >1.8 × 106-day (5,000 year) life span of bristlecone pines (Pinus aristata) (Figure 13-1). Plant clones appear to exceed these examples several fold—e.g., the "King clone" of the creosote bush (Larrea tridentata), which is estimated to be >10,000 years old (Vasek, 1980).
These examples suggest that it is the physiological architecture of the species that determines the life span (Finch and Rose, 1995). Thus, the allocation of resources for regeneration and repair or for hormone-behavior changes during reproduction are fundamental determinants of mortality, either through risky behavior or pathophysiological side effects that can influence the rate of senescence. In contrast, certain other cellular characteristics show weak correlation
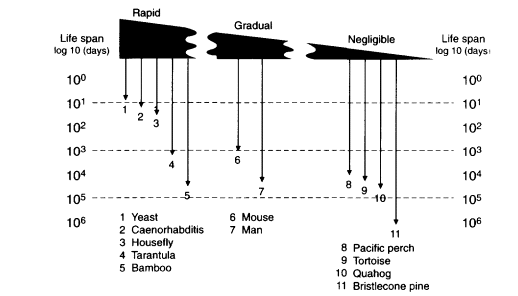
Figure 13-1
Life spans of sexually reproducing species rate of senescence in adult. Schema of the range of intensities of senescence on a spectrum from rapid to gradual to negligible, as indicated by thickness of the wedge. Durations of total life spans, embryo-to-adult life phase, are shown on the vertical scale as days in powers of 10. SOURCE: Life spans of individual organisms are taken from Finch (1990:chapters 2-4 and appendix 1).
with life span—e.g., nuclear DNA content and neuron oxygen utilization differ by <10 percent in rodents and humans (Hoffman, 1983; Finch, 1990:260,283).
The bidirectional plasticity of life-history schedules that is shown experimentally for fruit flies is consistent with evolutionary changes that can, in part, be traced in the fossil record. A striking example is found in mayflies, which are famous for their adult phases lasting as little as a few hours to a few days, depending on the species. Their total life span, however, may extend for up to 5 years and commonly includes 10 or more in stars. These ultrashort adult phases are a direct consequence of their physiological architecture, because mayflies from the 227-odd genera lack complete mouth parts as adults (Finch, 1990:4950). Because mayflies cannot eat during the intense activities of reproduction that ensue upon eclosion, nutritional reserves accumulated before maturation are rapidly depleted. The trait of adult aphagy is almost certainly a derived trait—i.e., recently evolved—because fossils of mayflies from the Paleozoic Era, 300 million years ago, show mouth parts as adults that were well developed for chewing. Some ancient mayflies were giants relative to the present diminutive species. For example, Bojophlebia had an 18-inch wingspan and is thought to
have been a fierce predator because of its well developed mandibles (Kukalova-Peck, 1985; Finch, 1990:583-584). Although it is not clear that the present mayflies have descended from gigantic ancestors, by the Eocene Epoch (57-36 million years ago) mayflies resembled those in modern families (Edmunds, 1972). The mayflies and many other examples are consistent with the idea that adult life spans, like adult body sizes, can become smaller as well as larger during evolution, depending on local ecological constraints.
Figure 13-1 also shows that nearly the same range of life spans is observed in sexual organisms that display very different rates of senescence and physiological characteristics. A scale of senescence is shown that approximates the rates of mortality acceleration in adults, ranging from rapid to gradual to negligible (Finch, 1990). Rapid senescence is observed in semelparous organisms that die within a year of maturation from causes that are typically relatively homogenous within the population. Typical mortality rate doubling times are less than 0.1 year. In these plants and animals, the very short adult phase is terminated by a rapid senescence after sexual reproduction that leads to death of the adult populations within one season. In general, such organisms display very similar pathophysiological changes that affect most members of the population, more-or-less concurrently (Finch, 1990: chapter 2; Finch, 1994). Rapid senescence is epitomized in the familiar example of spawning Pacific salmon, in which both genders rapidly develop symptoms like in Cushing disease that are caused by high blood cortisol levels. In marsupial mice (genus, Antechinus and Phascogale), males, but not females, show seasonal die-off soon after mating, also in association with elevated cortisol levels (Finch, 1990:95-97; Lee and Cockburn, 1985). The fruit fly Drosophila and the nematode Caenorhabditis are valuable laboratory invertebrate models for senescence, with life spans of up to several months that show extensive pathophysiological changes. Unlike the hyper-adrenocorticism of Pacific salmon, however, no single pathophysiological trigger has been identified in the senescence of Drosophila or Caenorhabditis. Thus, the senescence of Pacific salmon may be atypical of the physiology of senescence in other animals.
Depending on the species, rapid senescence nonetheless can occur after very long total life spans, because of prolonged juvenile prereproductive phases before rapid senescence. Examples of this life-history type are shown by the thick-stemmed bamboo species in the genus Phyllostachys that, depending upon the species, grow vegetatively for several decades or for more than 100 years before flowering and dying in one season (Janzen, 1976; Finch, 1990:101). As another example with a different physiology, the male tarantula matures at about 10 years and dies a few months later with a shrinking abdomen that indicates cessation of feeding. In contrast, female tarantulas live at least 25 years (Baerg, 1920; Finch, 1990:67-68).
Gradual senescence represents the intermediate range in rates of senescence and probably represents the bulk of species among plants and animals with life
spans of more than I year but that are more-or-less definite, depending on the population size and local conditions (Finch and Pike, 1996). Mortality rate doubling times range at least 100-fold, from about 0.3 year (mice, pond snail) to >27 years (river perch) (Finch, 1990:122-123). In general, gradual senescence is not associated with a homogeneous set of pathological changes throughout the population. Mammals have life spans ranging about 25-fold, from laboratory rodents with maximum life spans of about 5 years, to humans, presently at 122.4 years in the fleeting example of Jeanne Calment, who recently died. The increasing maximum life spans of humans from about 100 years in the best authenticated cases from the last century (Vaupel, in this volume) to the present >122 years may be considered as small relative to the full range of mammalian life spans.
In humans, midlife is marked by the increased incidence of numerous diseases (cancer, hypertension, vascular conditions, type II diabetes, etc.) that are major factors in the acceleration of mortality. Although the burden of various diseases may be associated with varying degrees of frailty and dependence, the presence of numerous sources of morbidity does not constitute a senium. or demarcated phase of morbidity during old age that precedes death, as once believed. For example in one population, >50 percent of those aged 65 of older were in apparent good health up to 1 year before their death (Brock et al., 1992). With the clear exception of the ovary (vom Saal et al., 1994), there is no general failure of cells throughout the body at a particular age. The dogma that mammals lose neurons throughout life during normal aging is being sharply challenged in studies of rodents and humans (Gallagher et al., 1996). Moreover, recent studies demonstrate that age-related dysfunctions in memory can occur without loss of neurons in the hippocampus (West, 1993; Rasmussen et al., 1996) and that impairments of hypothalamic control of gonadotrophins can occur without loss of gonadotropic-releasing-hormone neurons (Hoffman and Finch, 1986). The example of Madame Calment implies that the duration of functions of most organs do not have a predetermined upper age limit to functioning that would precipitate a general senile involution. At 122 years, she was, of course, postreproductive and recently became nearly blind and deaf. Yet, she was living independently until 10 years ago and showed no indications of dementia (informal accounts communicated to me by local observers).
Laboratory rodents have undergone increase in life spans during the past 50 years that parallel those of humans. Russell (1966) summarizes survival curves for highly inbred strains of mice—e.g., C57BL/6J strain—which was established in 1936 and has been since inbred for more than 100 generations. Several cohorts at the Jackson Laboratory showed progressive improvement in adult survival between 1948 and 1962, when the mean life span increased from about 560 days to 700 days, and maximum life spans increased from 800 to 900 days. Another cohort of this strain obtained from Jackson Laboratory by this author a few years later had markedly greater life spans, with a mean of 900 days and a maximum of 1460 days (Finch, 1971: Finch et al., 1969). The basis for this
increased life span is almost certainly not genetic in view of the extensive inbreeding and includes such environmental factors as improved nutrition and husbandry, particularly the major decreases in the incidence of Salmonella and other infections.
Chronic moderate food restriction, 10-50 percent ad libitum. can increase rodent life spans even more. Food-restricted rats lived up to 45 months in 1943 (McCay et al., 1943), whereas present food-restricted rodents (note, not the same genotype) can live at least 8 months longer than they did 50 years ago. The present record maximum life spans are 1742 days in mice (Harrison and Archer, 1987) and about 1600 days in rats (Sprott and Austad, 1996). Ongoing studies of food-restricted rodents may lead to even greater life spans. It might be informative to analyze historical trends for mortality rates and life spans of laboratory rodents since the beginnings of modern small animal husbandry. A midcentury segment of this history was helpfully summarized by Russell (1966).
At the further extreme of senescence (Figure 13-1) are even slower aging patterns that I have provisionally called negligible senescence. In these species, there is no evidence of physiological dysfunctions at advanced ages, no acceleration of mortality during adult life, and no recognized characteristic limit to life span (Finch, 1990: chapter 4). Although the demographic analyses by Promislow and colleagues identified some mammalian species that did not show the expected increase of mortality with adult age (Gaillard et al., 1994), these cases need further study for physiological and pathological traits of aging before it can be concluded that these species or populations lack senescence. This category of life histories warrants caution and unremitting scrutiny, because few individual organisms of authenticated great ages have been rigorously examined.
A promising example of negligible senescence from the vertebrates is the rockfish genus Sebastes, a scorpaenid with several species that achieve ages greater than 100 years. The age is estimated from measurements of otolith rings in conjunction with natural radioisotopes (Finch, 1990:217; Chilton and Beamish, 1982; Mulligan and Leaman, 1992; Leaman, 1991). The age-specific fecundity increases progressively during continued body growth after maturation at about 20 years. In remarkable contrast to mammals (vom Saal et al., 1994), there is no evidence of reproductive decline in males or females by 55 years or more. At necropsy, a few older fish (Sebastes aleutianus aged 50-80 years) appeared healthy on gross examination; their ovaries contained the usual seasonal complement of mature eggs by histological studies (X. de Bruin, R. Gosden, C. Finch. and B. Leaman, unpublished work). In Sebastes, the oldest fish are generally not the largest in the population, implying size-selective mortality—e.g., from predation or interactions of growth rate and mortality. Although the numbers of fish aged over 50 years are few, the statistical procedure of Mueller et al. (1995) might be used to evaluate the stability of mortality rates at advanced ages.
In contrast to Sebastes, the much shorter-lived fish Cynolebias. shows considerable gross pathology during aging under laboratory conditions in association
with accelerating mortality rates during its 2- to 3-year life span that approximate the schedule of senescence in laboratory rodents (Finch, 1990:137-138; Liu and Walford, 1969). Cynolebias is a cyprinodont from a different order than the scorpaeniform Sebastes (both belong to the same taxon of bony fishes, the superorder Acanthopterygii). Because Cynolebias shows age-related changes that are heterogeneous in the population with respect to the time of onset and the variations among individuals, we observe here a different phenomenon than the nearly synchronous senescence of spawning Pacific salmon. Although little is known about the age-related pathology of long-lived fish species, evidence like this does indicate a very wide range of phenomena.
Other examples of fish with very slow aging are the cod and sturgeon, which show increasing fecundity with age (Finch, 1990: chapter 4). Certain turtles also achieve life spans of at least 100 years. However, detailed microscopic or biochemical examination of tissues are lacking for any older specimens of very long-lived fish or other animals except for mammals. While these observations are consistent with very slow aging, much further work is needed to evaluate biochemical markers from mammals that are sensitive to slowly accumulated chemical changes in molecules with long life spans. Biochemical markers for future study could include the "I-spot" adducts formed on brain DNA nucleotides (Randerath et al., 1993) and the pentosidine glycooxidation products found on collagen from cartilage and skin (Miyata et al., 1996; Sell et al., 1996). Until we have data on such biochemical markers on aging and detailed histological studies, we should not assume that certain animals escape aging, even if senescence is not obvious. That is, age-related molecular damage could be slowly accumulated that might not be sufficient to cause age-related dysfunctions recognized as senescence. Whatever the future findings, some organisms clearly show even more gradual forms of senescence than observed in humans.
The putative category of negligible senescence merits a great deal more attention than given it so far because of its apparent challenge to the evolutionary theory that "senescence must always creep in" (Hamilton, 1966; Rose, in this volume). Important opportunities for study of life spans in natural populations are rapidly disappearing because of environmental disruptions from human population growth and, in the case of Sebastes and many other long-lived fish, because of commercial exploitation. The preservation of natural age-structured populations with multiple coexisting generations should be considered as a crucial aspect of the efforts to protect endangered species and biodiversity (Finch and Ricklefs, 1991). Investigators will encounter special statistical problems of sampling the few individuals of advanced ages to obtain estimates of the distribution of life spans and of age-related diseases. The size of later age groups will likely be small and could have different mortality characteristics from younger age classes, as observed for humans after 85 when mortality rates decline. For such subgroups, the population size will have a greater influence on estimates of
apparent maximum life span than for the estimates of mean life span (Finch and Pike, 1996).
Plasticity In Senescence
Three Examples from Semelparous Animals
The rapid senescence of Pacific salmon can be prevented by blocking reproduction—e.g.. by castrating juvenile kokanees, which then survive to 8 years, or about twice the usual life span associated with spawning (Robertson et al., 1961; Finch, 1990:90-92). A similar example is the extension of life in the normally semelparous male marsupial mice by castration before mating (Finch, 1990:97; Lee and Cockburn, 1985). Moreover, a segmented worm, the polychaete Nereis, was recently shown by experimental interventions to be capable of living twice its usual life span. When worms mature at 2 years of age, they stop feeding, lose the ability to regenerate ablated segments, and die soon after spawning (Golding and Yuwono, 1994). However, these changes can be postponed by transplanting cerebral ganglia from immature donors into adults; the worms then begin to feed and recover the ability to regenerate; the transplantation was repeated, thereby doubling the usual maximum life span. For other examples of life span extension from postponed reproduction in animals and plants, see Finch (1990: chapters 2 and 10; Finch, 1994) and Golding and Yuwono (1994).
These striking experiments demonstrate that somatic cells have a great deal more potential for function than available in the usual life span. In fact, the evolutionary theory of senescence does not require that the leading causes of death during senescence be synchronized with other aging processes (Rose, 1991:167).
This view is consistent with the historical trends for lengthened life spans in humans but without the compression of morbidity at later ages predicted by Fries (1980). Moreover, each species must be considered in terms of the physiological architecture that reflects its unique evolutionary history. For example, in blood-cortisol elevations common in vertebrates during reproductive stress, there may be a wide quantitative range of cell responses to a given elevation of blood cortisol, which result in different degrees of cell damage and its reversibility (C.V. Mobbs and C.E. Finch, unpublished work). Endocrine manipulations give a valuable experimental approach to resolving gene-environment interactions that trigger senescence in some semelparous and iteroparous species.
Examples from Mammalian Life Histories
Mammalian life histories are also subject to alternative schedules in the timing and rate of events and age changes, particularly through nutritional influences on the reproductive schedule. In laboratory rodents, food restriction to 10-
50 percent of ad libitum intake slows many age-related changes (Weindruch, 1996; Weindruch and Walford, 1988; Finch, 1990:506-536; Hopkin, 1995; Roth et al., 1995)—e.g., the mortality-rate doubling time, mean life spans, and maximum life spans of rodents are extended by 30 percent or more. Genotype-specific tumors are delayed, e.g., in the p53 "knock-out" mouse strain, which has a very high incidence of malignancy (Hursting et al., 1994). At necropsy, some very old food-restricted rats (nonmutant strains) lacked any display of gross pathology that could be assigned as a cause of morbidity or mortality (Maeda et al., 1985; Weindruch and Walford, 1988; Finch, 1990:518-519). The causes of death in these rats could include transients in blood pressure, cardiac rhythms, and blood glucose, which might not lead rapidly to gross organ pathology.
Food restriction also delays puberty and slows the age-related loss of ovarian oocytes in laboratory mice (Nelson et al., 1985). When mice are fed ad libitum, fertility recovers and is maintained to later ages than in fed controls. The effects of food restriction extend to delaying age-related impairments in key neuroendocrine functions, such as the preovulatory surge of gonadotrophins (McShane and Wise, 1996) and the pulsatile release of growth hormone (Sonntag et al., 1995). The ad libitum food intake of laboratory rodents may be atypical, because food resources are subject to seasonal and other fluctuations in natural populations. This plasticity in the reproductive schedule is hypothesized to be adaptive, because it would coordinate reproduction with food availability (Holliday, 1989; Harrison and Archer, 1989; Graves, 1993). In particular, Graves (1993) argues that these responses to food restriction demonstrate tradeoffs between energy expended on survival versus reproduction.
The generalizability of these effects of food restriction to humans is not clear. In ongoing studies with rhesus monkeys, chronic food restriction had effects on metabolism that, in part, resembled those observed in rodents. Food restriction decreased both blood glucose and insulin, (integrated 24-hour levels) and increased insulin sensitivity (Roth et al., 1995). This change might be expected to oppose the age-related trend in humans for subtle, but persistent, decreases in insulin sensitivity during aging, in association with age-related trends for increased levels of fasting blood glucose (Rowe et al., 1983; Harris et al., 1987).
I suspect that gene-environment interactions will eventually be identified that lead to vulnerability of particular organ systems for degeneration during aging, but that a great deal of plasticity will be observed in the age when a particular degree of impairment is manifested. A potential example of this is the strong statistical association of higher education with a lower incidence of Alzheimer disease at later ages, which is observed in five human populations on three continents (Katzman, 1993). Education, of course, may be a proxy (surrogate) variable for other primary environmental factors. The existence of at least four genetic risk factors for Alzheimer disease gives a basis for evaluating how
education and other environmental factors influence these risk factors at different ages.
Cell Proliferation And Life-History Plasticity
Against the above examples, we must also consider if there are changes at cellular and molecular levels that may not be readily reversible or open to intervention. The Hayflick phenomenon, or the limited proliferative life span of diploid human fibroblasts in serial culture, is often cited as an example of a built-in aging clock (Hayflick, 1977, 1994; Fries, 1980). In parallel with the loss of proliferative capacity, there is a loss of telomeric DNA at the ends, or telomeres, of chromosomes (Martin, 1994; Harley and Villaponteau, 1996). Telomere DNA loss during replicative senescence has been demonstrated so far only in human cells and in some ciliated protozoans. The enzyme telomerase that maintains telomere DNA is not found in most somatic cells but is expressed in malignant cells. These phenomena are manifested during aging in vivo—e.g., telomere loss is detected in cells cloned from blood vessels of older humans in which there has been local endothelial cell proliferation (Chang and Harley, 1995). A major question is the relationship between proliferative limits and telomere shortening. The impact of telomere shortening on the proliferative potential of bone marrow cells is unclear but may be pertinent to immunoproliferative responses and red blood cell production at later ages.
In contrast to these widely appreciated phenomena, a fundamental fact is less well known—that cell death does not ensue simply because fibroblasts have stopped dividing (Campisi, 1997). There is no general failure of biosynthesis of RNA and protein at the time when DNA synthesis ceases in fibroblasts, despite their unhealthy appearance with accumulations of lipids and pigments. In particular, postreplicative fibroblasts can still support full viral infections with undiminished yield of infective progeny (Tomkins et al., 1974; Holland et al., 1973). In view of the fact that neurons in our brains have been postreplicative for decades without detectible cell death (see above), it is not surprising that postreplicative fibroblasts can live for at least 3 years in culture if properly cared for (Smith and Pereira-Smith, 1996). The capacity for functional survival of postreplicative fibroblasts is well known to investigators of in vitro models for aging but is less known outside of this research community.
Another feature of cell proliferation in life histories is the unlimited somatic cell proliferation demonstrated by many species of animals and plants that can propagate by vegetative or asexual reproduction. Familiar examples are the vegetative propagation of plants by shoots and cuttings and the asexual propagation of flatworms by fission. This capacity, while widespread among plants, is scattered among the animals. Depending on the species, vegetative reproduction may be the primary mode, as well as an alternate life-history strategy. From its distri-
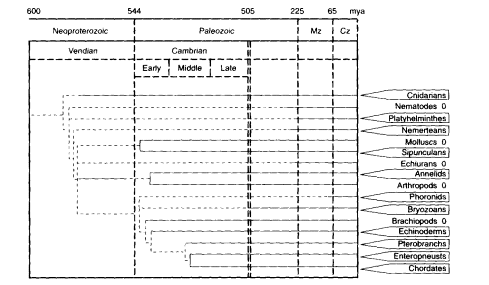
Figure 13-2
Schema showing distribution of phyla containing species that manifest vegetative reproduction in at least one species of a subphylum or order, as shown in boxes. Vegetative reproduction includes reproduction from somatic cells by budding or segmentation. In many examples, vegetative reproduction can prevail for many successive generations, without a required intermediate cycle of sexual reproduction. For examples, see Buss (1987) and Finch (1990: chapter 4). This capacity for extensive vegetative reproduction depends on an unlimited capacity for proliferation of somatic cells. Davidson et al. (1995) proposed that the evolution of animal development depended on an unlimited capacity for proliferation of embryonal cells. These phenomena markedly diverge from the finite proliferation of mammalian fibroblasts during serial culture, the ''Hayflick limit." The phylogenetic tree shows the depth of the fossil record (solid lines) and the minimum age of divergence: Mz, Mesozoic; Cz. Cenozoic; mya, million years ago. In the early-to-middle Cambrian, when most extant phyla are represented in the fossil record, one can find lines of descent that lead to phyla that show both the presence and absence of vegetative reproduction, as denoted by the boxes (report of at least one species showing vegetative reproduction in adults) or by O (its apparent absence). For example, annelids (box) and arthropods (0) diverged by the early Cambrian Period. Among chordates, urochordates (tunicates) (box), e.g., Botryllus (Grosberg, 1982: Sabbadin, 1979) and vertebrates (0) may also have diverged by the early Cambrian Period. It is likely that vegetative reproduction is a primitive trait in the animal phyla and that its absence, in any phylum, is a derived trait. These perspectives imply that finite clonal proliferation of diploid mammalian fibroblasts is also a derived trait. SOURCE: The phylogenetic tree is adapted from Davidson et al. (1995).
bution across all grades of organization, vegetative reproduction would appear to have existed in the earliest multicellular organisms (Figure 13-2).
An important example is found in the tunicates (urochordates), which have two-chambered beating hearts, a notochord, and a complex neural network. This lineage separated from other chordates about 500 million years ago. Botryllus. in particular, develops from a tadpole-like free-swimming larva, which settles down to form a sessile colony that can reproduce sexually or asexually, depending on the local conditions (Buss, 1987; Grosberg, 1982, 1988; Finch, 1990:106-108). Asexual reproduction by budding from the body wall of adult animals (e.g., Chang and Lauzon, 1995) has been observed as the exclusive mode of propagation for hundreds of vegetative asexual generations in the laboratory (Sabbadin, 1979), with no signs of a proliferative limit analogous to the Hayflick phenomena. Neighboring colonies of Botryllus and other tunicates may display asexual reproduction concurrently with sexual semelparity and iteroparity. Botryllus is also being studied as a model for synchronized apoptosis (Chang and Lauzon. 1995).
In animal embryos, an unlimited capacity for proliferation of undifferentiated cells is thought to be the basis for the development of larger structures from small initial numbers of cells (Davidson et al., 1995). A well-studied case of this is the vast proliferative capacity of larval fruit fly cells: after serial transplantation of imaginal discs for hundreds of doublings, exposure to ecdysone induces morphologically normal differentiated adult organs (Hadorn, 1966, 1968). During development in mammals, there may be a marked reduction of proliferative capacity during early development, since mouse blastocyst cells can be serially cultured from >250 cumulative doublings, or about 10-fold more than obtained with mouse fibroblasts derived from later-stage embryos (Suda et al., 1987). "Progenitor" cells from adult rat brains can be grown in culture for >2 years and >33 passages, when fibroblast growth factor (FGF-2) is present (Gage et al., 1995; Suohonen et al., 1996). During serial culture, the homogenous-appearing cells had doubling times of 2 days and then differentiated into several types of neurons when transplanted into adult brains. While each of these studies could involve extensive selection of minor cell subpopulations with very high proliferative capacity, there was no indication of a culture crisis or proliferative limit.
Provisionally, the acquisition of finite proliferative capacity as epitomized by mammalian fibroblasts may be regarded as a specialized, or evolutionarily derived, feature of cell differentiation, rather than a fundamental limitation of animal cells to which germ cells are an exception. Ongoing work may demonstrate whether the immortality of germ-cell lineages is an exclusive property of these special cells. From a comparative perspective, the plasticity of the human life span should not depend as much on the proliferative capacity of somatic cells as on changes in hormones and growth factors that modify cell functions.
The huge proliferative capacity of mouse cells when obtained from blasto-
cysts before the germ cells had differentiated (Suda et al., 1987) recalls Weissman's concept of "disposable soma" from the last century (Kirkwood and Cremer, 1982; Martínez and Levinton. 1992). According to the disposable soma concept, natural selection protects the immortality of the germ cells but does not protect against the evolution of somatic senescence. The capacity for indefinite somatic proliferation during asexual or vegetative reproduction weakens this dichotomy, because in these examples a subpopulation of somatic cells are equivalent to germ-line cells. However, the capacity for vegetative reproduction does not exclude somatic senescence, as observed in tunicates (see above), annelids, and flatworms (Martinez and Levinton, 1992).
If proliferative limits are considered as an aspect of organismic senescence, then it would be important to observe the timing during development of acquisition of finite cell proliferation in relation to germ-cell differentiation. However, cell differentiation does not confer inevitable proliferative senescence, as shown above by Hadorn's example of vast proliferation of imaginal discs in fruit flies: although these cells do not terminally differentiate until exposed to ecdysone, they were already differentiated by their capacity for hormonal responses.
There is no close link between the timing of germ-cell differentiation and the onset of somatic senescence. On one extreme are female mammals, in which germ-cell differentiation and proliferation are complete before birth (vom Saal et al., 1994). Ovarian senescence can be said to begin in utero, because the numbers of ovarian oocytes and primary follicles decrease exponentially after birth, so that more than half are lost by puberty. Eventually, the loss is complete at menopause, leading to decreases of estrogens that increase the risk of mortality from osteoporosis, vascular disease, and Alzheimer disease (e.g., Holinka, 1994; Schneider and Finch, 1997).
At the other extreme are flowering plants and some animals, in which germ-cell differentiation is delayed until just before reproduction, whether a species is semelparous or perennial (Finch, 1990:239-240). Bony fish give an important counter-example to mammals. Although their germ-cell differentiation begins early in development, as in mammals, unlike mammals, bony fish maintain de novo oogenesis as adults (vom Saal et al., 1994)—for example, the new seasonal stocks of oocytes found in chronologically old Sebastes that do not show indications of somatic or ovarian senescence, as described above.
Molecular Age Changes And Plasticity
At a molecular level, long-lived proteins and DNA are subject to diverse changes that may ultimately limit the plasticity of the life span. Proteins such as collagen and elastin slowly accumulate oxidative damage from a variety of chemical processes, including the formation of oxidation productions from glucose. The advanced glycation end-products or glycooxidation products arise from spontaneous (nonenzymatic) additions of glucose and other reducing
sugars to free amino groups, with the subsequent formation of pentosidine and other condensation products that can cross-link adjacent protein molecules (Cerami, 1996; Baynes, 1991; Sell and Monnier, 1995). Several different types of advanced glycation end-products have been shown to accumulate progressively, with a nearly linear time course from birth onward. In the skin, for example, pentosidine accumulates in skin collagen, at rates that are in proportion to the life spans of humans and other mammals of short- and intermediate life spans (Sell et al., 1996). In the human eye, a different oxidation product, LM-1, a blue fluorophore covalently associated with lens crystallins, accumulates linearly with age; in this case, the reducing sugar may be ascorbic acid rather than glucose (Nagaraj and Monnier, 1992). These examples suggest the complexity of the biochemistry of aging, where there are important variations between tissues and multiple substrates from intermediary metabolism.
Certain targets in tissues of glycoxidation by glucose and other reducing sugars can be modified through diet and drugs. For example, glycooxidation is accelerated by chronic elevations of blood glucose, as in diabetes (Schnider and Kohn, 1980). Correspondingly, food restriction, which lowers blood glucose, has been shown to decrease oxidative damage to proteins in rats (Reiser, 1994; Youngman et al., 1992). This finding points to the potential impact of nutrition across the life span on amount of damage that may accumulate in slowly replaced molecules. The nontoxic antioxidant aminoguanidine appears to block glycooxidation in animal studies and is in clinical trial (Cerami, 1996). Because minimum levels of blood glucose and other reducing sugars found both extra-and intracellularly are essential to physiological function, it would appear that glycooxidative damage to long-lived proteins may set some ultimate limit on plasticity of human life histories. The high blood sugar of birds (5- to 10-fold that of mammals) would predict intense glycooxidative damage to proteins (Monnier et al., 1990; Finch, 1990:405; Holmes and Austad, 1995). In view of their long life spans, special antioxidant mechanisms must have been evolved during the evolution of birds.
DNA damage from oxidation and a variety of other mechanisms is also observed in chromosomal and mitochondrial DNA of tissues with little cell replication like brain and muscle (Linnane et al., 1989; Randerath et al., 1993; Fraga et al., 1990; Soong et al., 1992; Mecocci et al., 1993). The age-related accumulation of mutations during aging is of unquestionable importance to one or more steps in malignant transformation and may be important to other dysfunctions of nondividing as well (Finch and Goodman, 1997).
Recent findings from van Leewen's group indicate that some mutational processes are under physiological control. The Brattleboro rat carries a germ-line mutation causing a frame-shift in the vasopressin gene. Remarkably, about one hypothalamic neuron per day reverts to acquire the normal vasopressin peptide: the reverted neurons accumulate in an age-related schedule from birth onward—
at least beyond middle age (Finch and Goodman, 1997; Evans et al., 1995). The molecular analysis so far shows that the reversions result from clustered replacements of amino acids. Moreover, if the mutant rats are given vasopressin hormone replacements, then the rate of reversion is slowed. Ongoing studies are evaluating whether other genes show these processes. The present findings point to an utterly different form of plasticity in molecular aging processes, which suggest that physiological manipulations could be used to intervene and reduce mutational changes in DNA.
Prospects For A Genetics Of Longevity
Many laboratories are actively pursuing genes that influence life spans in short-lived animal models of aging, particularly nematodes (Johnson and Shook, in this volume), fruit lies (Rose, in this volume) (reviewed in Finch and Tanzi, 1997). Efforts to breed long-lived mice by selecting for reproduction at later ages are showing some success (Ngai et al, 1995) in parallel with similar studies on fruit flies (Rose, in this volume). In humans, genes that cause specific age-related diseases that shorten the life span are continuing to be identified, as in familial breast cancer, vascular disease, and Alzheimer disease. One of the progerias, Werner syndrome, which is characterized by intensified atherosclerosis and malignancy (both proliferative disorders), has been mapped to a gene predicted to encode a helicase, an enzyme that, by modifying DNA structure, may alter telomere replication (Yu et al., 1996).
The genetics of centenarians promises to reveal alleles that may favor extreme longevity, including the apoE2 allele (Schächter et al., 1994) and certain HLA haplotypes (Schächter, in press). There may be other general classes of genes that promote longevity through similar physiological mechanisms in widely different organisms, so-called "longevity assurance genes" or "gerogenes" (Jazwinski, 1996; Johnson and Shook, in this volume). One class of such genes may prove to reduce the effects of oxidative damage, a challenge to all organisms that exist in an oxidizing atmosphere and must cope with the myriad by-products of oxidative metabolism, including the continuing production of free radicals through oxidative phosphorylation. Atmospheric oxygen concentration increased steadily, if not monotonically, during the great radiations of the extant animal phyla more than 550 million years ago (Figure 13-2) and progressed to a maximum of 35 percent during the late Paleozoic Era (Graham et al., 1995). The machinery for combating oxidative stress was presumably subject to strong evolutionary pressures long before ancestors of the present long-lived birds and mammals had evolved in the Mesozoic Era. There is every reason to expect a continuing parade of genes controlling such protective mechanisms from diverse organisms that can shorten or lengthen life span.
At present, we do not understand the basis for the striking recent historical trends in increased life expectancy at the oldest ages in humans. It is unlikely that
this can be attributed to a genetic change in chromosomal genes because of its broad occurrence throughout the world. Nonetheless, the role of outbreeding through migration and the impact of social changes on the degree of consanguineous marriage has not been systematically evaluated. Outbreeding could contribute to increased adult life spans through hybrid vigor, as observed, for example, in the offspring of laboratory inbred rats and mice (Storer, 1978; Finch, 1990:321 324). Moreover, the evidence for the roles of older individuals in socially organized long-lived mammals (Carey and Gruenfelder, in this volume), as well as humans (Kaplan. in this volume) give a basis for discussing whether genes that are permissive of long life spans in some environments might be subject to kin selection mechanisms. Nonetheless, the most obvious alternative causes of increased longevity are improvements in public health, including nutrition, reduction of infectious disease, and other aspects of medical technology. Intriguing questions remain open about whether these environmental advances can account for the increased numbers of centenarians in rural China (Yi, in press) as satisfactorily as they appear to account for increases of centenarians in North America. Increased population size is certainly another factor. Although population size does not have a major effect on maximum life span during the Gompertz acceleration of mortality, when mortality accelerations slow at very advanced ages, population size will be a greater determinant of maximum life span (Finch and Pike, 1996).
In conclusion, the biology of human aging allows few predictions about the ultimate limits to life spans in different environments. The available evidence from different species shows that organisms of whatever body construction have the potential for widely varying patterns of senescence, with respect to the intensity of any particular pathophysiological age change and its time course of occurrence. This enormous plasticity is completely consistent with the recent increases of human life spans.
Acknowledgment
This research was supported by a grant to C.E.F. from the National Institute on Aging (K07-AG-00729).
References
Baerg. W.J. 1920 The life cycle and mating habits of the male tarantula. Quarterly Review of Biology 3:109-116.
Baynes, J.W. 1991 Role of oxidative stress in development of complications in diabetes. Diabetes 40:405-412.
Brock, D.B., M.B. Holmes, D.J. Foley, and D. Holmes 1992 Methodological issues in the last days of life. Pp. 315-332 in The Epidemiologic Study of Aging. New York: Oxford University Press.
Buss, L.W. 1987 The Evolution of Individuality. New York: Princeton University Press.
Campisi, J. 1997 The biology of replicative senescence. European Journal of Cancer 35:703-709.
Cerami, A. 1996 Hypothesis. Glucose as a mediator of aging. Journal of the American Geriatrics Society 33:626-634.
Chang, E., and C.B. Harley 1995 Telomere length and replicative aging in human vascular tissues. Proceedings of the National Academy of Sciences U.S.A. 92:11190-11194.
Chang, W-T., and R.J. Lauzon 1995 Isolation of biologically functional RNA during programmed death of a colonial ascidian. Biological Bulletin 188:23-31.
Charlesworth, B. 1994 Evolution in Age-Structured Populations. Cambridge: Cambridge University Press.
Chilton, D.E., and R.J. Beamish 1982 Age determination methods for fishes studied by the groundfish program at the Pacific biological station. Canadian Special Publication of Fisheries and Aquatic Sciences 60.
Davidson, E.H., K.J. Peterson, and R.A. Cameron 1995 Origin of bilaterian body plans: Evolution of developmental regulatory mechanisms. Science 270:1319-1325.
Edmunds, G.F. 1972 Biogeography and evolution of Ephemeroptera. Annual Review of Entomology 17:21-42.
Evans, D.A.P., J.P.H. Burbach, and F.W. van Leeuwen 1995 Somatic mutations in the brain: relationship to aging? Mutation Research 338:173-182.
Finch, C.E. 1971 Comparative biology of senescence: Evolutionary and developmental considerations. Pp. 47-67 in Animal Models for Biomedical Research IV. Washington, DC: National Academy of Sciences.
1990 Longevity. Senescence, and the Genome. Chicago: University of Chicago Press.
1994 Commentary: Latent capacities for gametogenic cycling in the semelparous invertebrate Nereis. Proceedings of the National Academy of Sciences U.S.A. 91:11769-11770.
1996 Biological bases for plasticity during aging of individual life histories. Pp. 488-512 in D. Magnusson, ed., The Life span Development of Individuals: Biological and Psychosocial Perspectives, a Synthesis. Cambridge: Cambridge University Press.
Finch, C.E.. J.R. Foster, and A.E. Mirsky 1969 Aging and the regulation of cell activities during exposure to cold. Journal of General Physiology 54:690-712.
Finch, C.E., and Goodman, M.F. In press Relevance of adaptive mutations arising in non-dividing cells in microorganisms to neurobiological systems. Trends in Neuroscience.
Fince, C.E., and J. Loehlin lin press Environmental influences that may precede fertilization: A first examination of the prezygotic hypothesis from maternal age influences on twins. Behavior Genetics.
Finch, C.E., and M.C. Pike 1996 Maximum life span predictions from the Gompertz mortality model. Journal of Gerontology B183-B194.
Finch, C.E., M.C. Pike, and M. Witten 1990 Slow mortality rate accelerations during aging in animals approximate that of humans. Science 249:902-905.
Finch, C.E., and R.E. Ricklefs 1991 Age structure of populations (letter). Science 254:799.
Finch, C.E., and M.R. Rose 1995 Hormones and the physiological architecture of life history evolution. Quarterly Review of Biology 70:1-52.
Finch, C.E., and Tanzi, R.E. 1997. Genetics of aging. Science.
Fraga, C.G., M.K. Shinegaga, J.W. Park, P. Degan, and B.N. Ames 1990 Oxidants, antioxidants, and the degenerative diseases of aging. Proceedings of the National Academy of Sciences U.S.A. 87:4533-4537.
Fries, J.F. 1980 Aging, natural death, and the compression of morbidity. New England Journal of Medicine 303:130-135.
Gage, F.H., P.W. Coates, T.D. Palmer, H.G. Kuhn, L.J. Fisher, J.O. Suhonen, D.A. Peterson. S.T. Suhr, and J. Ray 1995 Survival differentiation of adult neuronal progenitor cells transplanted to the adult brain. Proceedings of the National Academy of Sciences U.S.A. 92:11879-11883.
Gaillard, J., D. Allaine, D. Pontier, N.G. Yoccoz, and D.E.L. Promislow 1994 Evolutionary patterns among measures of aging. Evolution 48:509-516.
Gallagher, M., P.W. Landfield, B.S. McEwen, M.J. Meaney, P.R. Rapp. R.M. Sapolsky, and M.J. West 1996 Hippocampal neurodegeneration in aging. Science 274: 484-485.
Gardner, S.N., and M. Mangel. 1997 When can a clonal organism escape senescence. American Naturalist.
Golding, D.W., and E. Yuwono 1994 Latent capacities for gametogenic cycling in the semelparous invertebrate. Proceedings of the National Academy of Sciences U.S.A. 91:11777-11781.
Graham, J.B., R. Dudley. N.M. Aguilar, and C. Gans 1995 Implications of the late paleozoic oxygen pulse for physiology and evolution. Nature 375:117-120.
Graves, J.L. 1993 The costs of reproduction and dietary restriction: Parallels between insects and mammals. Growth, Development and Aging 57:233-249.
Grosberg, R.K. 1982 Ecological, Genetical, and Developmental Factors Regulating Life History Variation Within a Population of the Colonial Ascidian Botryllus schlosseri (Pallas) Savigny. Unpublished Ph.D. dissertation, Yale University.
1988 Life history variation within a population of the colonial ascidian Botryllus schlosseri 1: The genetic and environmental control of seasonal variation. Evolution 42:900-920.
Hadorn, E. 1966 Konstanz, Wechsel, und Typus der Determination in Zellen aus mannlichen Genitalanlagen von Drosophila melanogaster durch Dauerkulter in vivo. Developmental Biology 13:424-509.
1968 Transdetermination in cells. Scientific American 219:110-114.
Haldane, J.B.S 1941 New Paths in Genetics. London: Allen and Unwin.
Hamilton, W.D. 1966 The moulding of senescence by natural selection. Journal of Theoretical Biology 12:12-45.
Harley. C.B.. and B. Villeponteau 1996 Telomeres and telomerase in aging and cancer. Current Biology 5:249-255.
Harris, M.I., W.C. Hadden, W.C. Knowler, and R.L. Bennett 1987 Prevalence of diabetes and impaired glucose tolerance and plasma glucose levels in U.S. population aged 20-74 yr. Diabetes 36:523-534.
Harrison, D.E.. and J.R. Archer 1987 Genetic differences in effects of food restriction on aging in mice. Journal of Nutrition 117:376-382.
1989 Natural selection for extended longevity from food restriction. Growth Development and Aging 53:3-6.
Hay flick, L. 1977 The cellular basis for biological aging. Pp. 159-188 in C.E. Finch and L. Hayflick, eds., Handbook of the Biology of Aging, 1st ed. New York: Van Nostrand.
1994 How and Why We Age. New York: Ballantine Books.
Hoffman. M.A. 1983 Energy metabolism, brain size, and longevity in mammals. Quarterly Review of Biology 58:495-512.
Hoffman, G.E., and C.E. Finch 1986 LHRH neurons in the female C57BL/6J mouse brain during reproductive aging: No loss up to middle-age . Neurobiology of Aging 7:45-48.
Holinka, C.F. 1994 Aspects of hormone replacement therapy. Annals of the New York Academy of Sciences 734:271-284.
Holland, J.J.. D. Kohne. and M.V. Doyle 1973 Analysis of virus replication in aging human fibroblasts. Nature 245:316-318.
Hölldolber, B., and E.O. Wilson 1990 The Ants. Cambridge. MA: The Belknap Press of Harvard University Press.
Holliday, R. 1989 Food, reproduction, and longevity: Is the extended life span of calorie-restricted animals an evolutionary adaptation'? Bioessays 10:125-127.
Holmes, D.I., and S.N. Austad 1995 Birds as animal models for the comparative biology of aging: A prospectus. Journal of Gerontology and Biological Science 50A:B59-B66.
Hopkin, K. 1995 Aging in focus: Caloric restriction may put the brakes on aging. Journal of NIH Research 7:47-50.
Hursting, S.D.. F.N. Perkins. and J.M. Phang 1994 Calorie restriction delays spontaneous tumorigenesis in p53 knock-out transgenic mice. Proceedings of the National Academy of Sciences U.S.A. 91:7036-7040.
Janzen, D.H. 1976 Why bamboos wait so long to flower. Annual Review of Ecological System. 7:347-391.
Jazwinski, M. 1996 Longevity-assurance genes and mitochondrial DNA alterations: Yeast and filamentous fungi. Pp. 39-54 in E.L. Schneider and J.W. Rowe. eds., Handbook of the Biology of Aging. 4th ed. San Diego: Academic Press.
Katzman, R. 1993 Education and the prevalence of dementia and Alzheimer's disease. Neurology 43:13-20.
Kirkwood, T.B.L.. and T. Cremer 1982 Cytogerontology since 1881: A reappraisal of August Weismann and a review of modern progress. Human Genetics 60:101 -112.
Kukalová-Peck, J. 1985 Ephemeroid wing veination based on new gigantic Carboniferous mayflies and basic morphology, phylogeny, and metamorphosis of pterygote insects (Insecta. Ephemerida). Canadian Journal of Zoology 63:933-955.
Leaman, B.M. 1991 Reproductive styles and life history variables relative to exploitation and management of Sebastes stocks. Environmental Biology of Fishes 30:253-271.
Lee. A.K., and A. Cockbum 1985 Evolutionary Ecology of Marsupials. New York: Cambridge University Press.
Linnane, A.W., S. Marzuki, T. Ozawa, and M. Tanaka 1989 Mitochondrial DNA mutations as an important contributor to ageing and degenerative diseases. Lancet 1:642-645.
Liu, R.K., and R.L. Walford 1969 Laboratory studies on life span, growth, aging, and pathology of the annual fish. Cynolebiasbellottii Steindachner. Zoologica 54:1-16.
Maeda, H., C.A. Gleiser, E.J. Masoro. I. Murata, C.A. McMahan. and B.P. Yu 1985 Nutritional influences on aging Fischer 344 rats. 2. Pathology. Journal of Gerontology 40: 671-688.
Martin, G.M. 1994 Genetic modulation of telomeric terminal restriction-fragment length: relevance for clonal aging and late-life disease. American Journal of Human Genetics 55:866-869.
Martinez, D.E., and J.S. Levinton 1992 Asexual metazoans undergo senescence. Proceedings of the National Academy of Sciences U.S.A. 89:9920-9923.
McCay, C.M., G. Sperling, and L.L. Barnes 1943 Growth, ageing, chronic diseases, and life span in rats. Archives of Biochemistry 2:469-479.
McShane, T.M.. and P.M. Wise 1996 Life-long moderate caloric restriction prolongs reproductive life span without interrupting maintenance of regular estrous cyclicity in rats: Evidence for central mechanisms. Biology of Reproduction 54:70-75.
Mecocci, P., U. MacGarvey, A.E. Kaufman, D. Koontz, J.M. Shoffner, D.C. Wallace. and M. Flint Beal 1993 Oxidative damage to mitochondrial DNA shows marked age-dependent increases in human brain. Annals of Neurology 34:609-616.
Medawar, P.B. 1952 An Unsolved Problem of Biology. London: H. K. Lewis
Miyata, T., S. Taneda, R. Kawai, Y. Ueda, S. Horiuchi, M. Hara. K. Maeda. and V.M. Monnier 1996 Identification of pentosidine as a native structure for advanced glycation and products in beta2-microglobulin-containing amyloid fibrils in patients with dialysis-related amyloidosis. Proceedings of the National Academy of Sciences U.S.A. 93:2353-2358.
Monnier, V.M., D. R. Sell, S. Miyata, and R.H. Nagara 1990 The Maillard reaction as a basis for a theory of aging. Pp. 393-414 in P.A. Finot. ed., Advanced Life Sciences, Proceedings of the Fourth International Symposium on the Maillard Reaction. Basel: Birkhausert-Verlag.
Mueller, L.D., T.J. Nusbaum, and M.R. Rose 1995 The Gompertz equation as a predictive tool in demography. Experimental Gerontology 30:553-569.
Mulligan, T.J., and B.M. Leaman 1992 Length-at-age analysis: Can you get what you see? Canadian Journal of Fisheries and Aquatic Science 49:632-643.
Nagaraj, R.H., and Monnier, V.M. 1992 Isolation and characterization of a blue fluorophore from human eye lens crystallins: In vitro formation from Maillard reaction with ascorbate and ribose. Biochimica Biophysica Acta 1116:34-42.
Nelson. J.F., R.G. Gosden, and L.S. Felicio 1985 Effect of dietary restriction on estrous cyclicity and follicular reserves in aging C57BL/6J mice. Biology of Reproduction 32:515-522.
Ngai. I., C.Y. Lin, and M.P. Sabour 1995 Lines of mice selected for reproductive longevity. Growth, Development and Aging 59:79-81.
Nusbaum, T.J., L.D. Mueller, and M.R. Rose 1996 Evolutionary patterns among measures of aging. Experimental Gerontology 31:507-516.
Orive, M.E. 1995 Senescence in organisms with clonal reproduction and complex life histories. American Naturalist 145:90-108.
Randerath, K., K.L. Putnam, H.H. Osterburg, S.A. Johnson, D.G. Morgan, and C.E. Finch. 1993 Age-dependent increases of DNA adducts (I-compounds) in human and rat brain DNA. Mutation Research 295:11-18,
Rasmussen, T., T. Schliemann, C. Sorensen. J. Zimmer, and M. J. West 1996 Memory impaired aged rats: No loss of principal hippocampal and subicular neurons. Neurobiology of Aging 17:143-147.
Reiser, K.M. 1994 Influence of age and long-term dietary restriction on enzymatically mediated crosslinks and nonenzymatic glycation of collagen in mice. Journal of Gerontology 49:B71-B79.
Robertson, O.H., B.C. Wexler, and B.F. Miller 1961 Degenerative changes in the cardiovascular system of the spawning Pacific salmon (Oncorhynchus tshawytscha). Circulation Research 9:826-834.
Rose, M.R. 1991 The Evolutionary Biology of Aging. New York: Oxford University Press.
Roth. G.S., D.K. Ingram, and M.A. Lane 1995 Slowing ageing by caloric restriction. Nature Medicine 1:414-415.
Rowe, J.W., K.L. Minaker, J.A. Pallotta, and J.S. Flier 1983 Characterization of the insulin resistance of aging. Journal of Clinical Investigation 71:1581-1587.
Russell, E.S. 1966 Life span and aging patterns. Pp. 51 1-519 in E.L. Green, ed., Biology of the Laboratory Mouse, 2nd ed. New York: McGraw-Hill.
Sabbadin, A. 1979 Colonial structure and genetic patterns in ascidians. Pp. 433-444 in G. Larwood and B.R. Rosen, eds., Biology and Systematics of Colonial Organisms. New York: Academic Press.
Schächter, F. In press Chronos Project in Longevity: To the Limits and Beyond. Foundation IPSEN: Paris, France.
Schächter, F., L. Faure-Delanef, F. Guénot. H. Rouger, P. Froguel, L. Lesueur-Ginot, and D. Cohen 1994 Genetic associations with human longevity at the ApoE and ACE loci. Nature Genetics 6:29.
Schneider. L.S., and C.E. Finch 1997 Can estrogen prevent neurodegeneration? Drugs and Aging 11:87-95.
Schnider, S.L., and R.R. Kohn 1980 Glucosylation of human collagen in aging and diabetes mellitus. Journal of Clinical Investigation 66: 179-1181.
Sell. D.R., M.A. Lane, W.A. Johnson, E.J. Masoro, O.B. Mock, K. Reiser, J.F. Fogarty, R.G. Cutler, D.K. Ingram, G.S. Roth. and V.M. Monnier 1996 Longevity and the genetic determination of collagen glycoxidation kinetics in mammalian senescence. Proceedings of the National Academy of Sciences U.S.A. 93:485-490.
Sell, D.R.. and V.M. Monnier 1995 Aging of long-lived proteins: Extra-cellular matrix (collagens, clastins, proteoglycans) and lens crystallins. Pp. 235-305 in E.J. Masoro, ed., Handbook of Physiology Section 11, Aging. New York: Oxford University Press.
Smith. J.R., and O.M. Pereira-Smith 1996 Replicative senescence: Implications for in vivo aging and tumor suppression. Science 273:63-67.
Sonntag, W.E., X. Ziaowei, R.L. Ingram, and A. D'Costa 1995 Moderate caloric restriction alters the subcellular distribution of somatostatin mRNA and increases growth hormone pulse amplitude in aged animals. Neuroendocrinology 61:601-608.
Soong, N.W., D.R. Hinton, G. Cortopassi, and N. Amheim 1992 Mosaicism for a specific somatic mitochondrial DNA mutation in adult human brain. Nature Genetics 2:318-323.
Sprott, R.L., and S.N. Austad 1996 Animal models for aging research. Pp. 3-23 in E.L. Schneider and J.W. Rowe, eds., Handbook of the Biology of Aging, 4th ed. San Diego: Academic Press.
Storer, J.B. 1978 Effect of aging and radiation in mice of different genotypes. Pp. 55-71 in D. E. Harrison and D. Bergsma, eds., Genetic Effects on Aging. New York: Liss.
Suda, Y., M. Suzuki, Y. Ikawa, and S. Aizawa 1987 Mouse embryonic stem cells exhibit indefinite proliferative potential. Journal of Cell Physiology 133:197-201.
Suohonen, J.O., D.A. Peterson, J. Ray, and F.H. Gage 1996 Differentiation of adult hippocampus progenitors into olfactory neurons in vivo. Nature 383:624-626.
Tomkins, G.A., E.J. Stanbridge, and L. Hayflick 1974 Viral probes of ageing in the human diploid strain. W1-38. Proceedings of the Society of Experimental Biology and Medicine 146:385-390.
Vasek, F.C. 1980 Creosote bush: Long-lived clones in the Mojave Desert. American Journal of Botany 67:246-255.
vom Saal, F.S., C.E. Finch, and J.F. Nelson 1994 The natural history of reproductive aging in humans, laboratory rodents, and selected other vertebrates. Pp. 1213-1314 in E. Knobil, ed., Physiology of Reproduction, 2nd ed., Vol. 2. New York: Raven Press.
Weindruch, R. 1996 Caloric restriction and aging. Scientific American, 274(1):46-52.
Weindruch, R.H., and R.L. Walford 1988 The Retardation of Aging and Disease by Dietary Restriction. Springfield, IL: C.C. Thomas.
West, M.J. 1993 Regionally specific loss of neurons in the aging human hippocampus. Neurobiology of Aging 14:287-293.
Williams, G.C. 1957 Pleiotropy, natural selection, and the evolution of senescence. Evolution 11:398-411.
Yi, Z. In press Han Chinese mortality at older ages and Chinese centenarians. In Longevity: To the Limits and Beyond. Paris, France: Foundation IPSEN.
Youngman. L.D., J-Y.K. Park, and B.N. Ames 1992 Protein oxidation associated with aging is reduced by dietary restriction of protein or calories. Proceedings of the National Academy of Sciences U.S.A. 89:9112-9116.
Yu, C-E., J. Oshima, Y-H. Fu, E.M. Wijsman, F. Hisama, R. Alisch, S. Matthews. J. Nakura. T. Miki, S. Ouais, G.M. Martin, J. Mulligan, and G.D. Schellenberg 1996 Positional cloning of the Werner's syndrome gene. Science 272:258-262.
























