3 In Search of Limits
John R. Wilmoth
Introduction
The dramatic rise in life expectancy during the past two or three centuries is arguably the greatest collective human achievement. Fragmentary evidence suggests that early levels of human life expectancy were around 25 years (Acsádi and Nemeskéri. 1970). At the beginning of the twentieth century, many poorer countries still had life expectancies in this range (Preston, 1980; Davis, 1951), although by 1900 the mean life span in the most advantaged countries had already risen to around 50 years (Preston, 1990). According to the latest estimates, life expectancy at birth is still in the low to mid 40s in some African countries but is almost universally above 50 years elsewhere; in Japan and a few other countries, the mean length of life is now around 80 years (Population Reference Bureau, 1995).
As we approach the end of the twentieth century, we are led to question whether this incredible progress has run its course. Is it plausible to believe that these well-documented gains in human longevity can continue? Are limits to the rise in human life expectancy imposed by the structure of the organism itself? Several authors have argued that such limits must exist, based on their understanding of biological mechanisms or a review of demographic evidence. Two common beliefs that have gained an almost mythical status are that human life expectancy is bounded by a limit of around 85 years and that the maximum human life span is around 120 years.
There are numerous means of approaching the question of whether such limits exist. In this chapter. I restrict the discussion to a review of relevant demographic evidence and do not address the many biological arguments related
to this issue. My approach is that of a demographer and statistician who attempts to define what limits might look like in terms of aggregate mortality data and then reviews the existing empirical evidence within that framework.
What would limits to human longevity look like?
If limits to human longevity exist, they must have both a mechanism and a manifestation. As noted already, I do not address the issue of mechanisms in this chapter but focus instead on the question of how limits might manifest themselves in aggregate mortality patterns. Based on a review of the literature and my own understanding of this topic, there appear to be three hypotheses about the age distribution of human mortality—and, in particular, about changes in the shape of that distribution over time—which may have a bearing on the issue of limits. In this section, I seek to explain these hypotheses clearly, to review some of the relevant literature, and to examine the most important empirical evidence in light of this theoretical framework. I also discuss briefly the logical connections between the three hypotheses. I conclude by offering a summary view of what a demographic perspective suggests at present about the limits of human longevity.
Notation
The three hypotheses can be stated using the notation of life tables or survival analysis. The former notation is most familiar to demographers and actuaries, while the latter is often used by statisticians, reliability engineers, and many biomedical researchers. To facilitate understanding by a diverse crowd, I will mention both sets of notation whenever convenient. I will favor the notation of survival analysis, however, because it is more general and probably more widely accessible to an interdisciplinary audience.
Mortality distributions can be effectively summarized by any one of several complementary functions. Three functions are particularly useful: the density function, the survival function, and the hazard function. Let X be a (positive) random variable representing the life span of an individual drawn at random from a population of newborns. Following standard statistical practice, let f(x) be the probability density function describing the distribution of life spans in this population. The cumulative density function, F(x), gives the probability (Pr) that an individual dies before surpassing age x:
The survival function, S(x), gives the complementary probability that an individual is still alive at age x:
The hazard function, h(x), is defined as the ratio of the density and survival functions:
Thus, the hazard function gives the probability density at age x conditional on survival to that age:
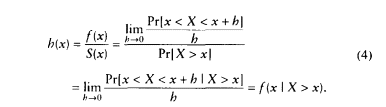
In life table notation, the probability of surviving to age x, S(x), would be denoted as lx/l0 (the radix of the life table, l0, may equal one by definition, although it is usually some large, arbitrary number like 100,000). The continuous density function, f(x), would be replaced by the discrete function, dx (or dx/l0), which gives the number (or proportion) of life table deaths in the age interval from x to x + 1. Finally, the hazard function, h(x), would be written in the life table as µx and is known to demographers and actuaries as the force of mortality.
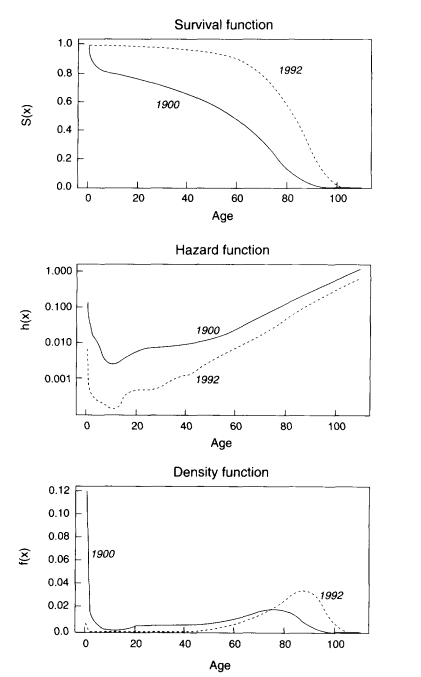
As an illustration, the survival, hazard, and density functions for U.S. females in 1900 and 1992 are shown in Figure 3-1. As the hazard function has fallen across the age range, the area under the survival curve has grown, and the density function has shifted to the right. Three hypotheses about possible limits to human longevity can be described in a similar way. These hypotheses, known as the limited-life span hypothesis, the compression-rectangularization hypothesis, and the limit-distribution hypothesis, are illustrated in Figures 3-2 to 3-4.
Limited-Life-Span Hypothesis
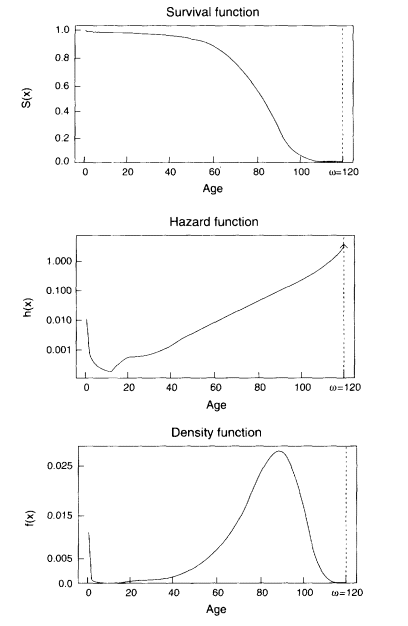
Perhaps the most common notion of a limit in the study of human longevity is the limited-life span hypothesis, which states that there exists some age w beyond which there can be no survivors. In the notation of survival analysis, this hypothesis can be expressed by any one of the following three formulas:
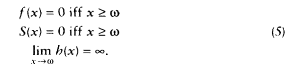
Each of these formulas implies the other two. This hypothesis is illustrated in Figure 3-2. These formulas may apply to an individual or to a population; if they
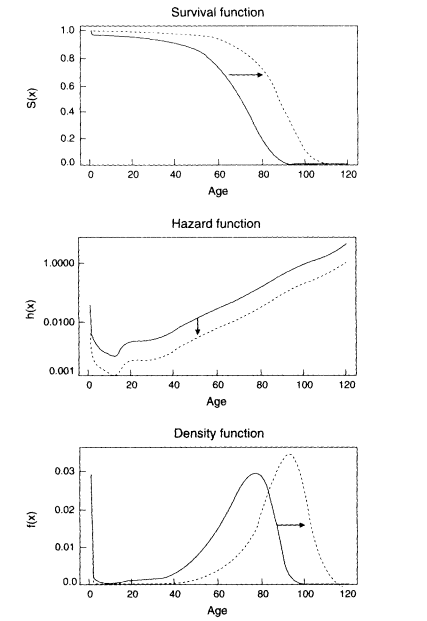
Figure 3-3
Mortality curves implied by the compression-rectangularization hypothesis. Note: Changes in these three curves are interrelated: over time the hazard function falls more rapidly at younger than older ages. the area under the survival function grows larger as the curve becomes more rectangular, and the density function shifts to the right and becomes more compressed. The distribution may or may not be truncated at some maximum age. Likewise, the dashed curves may or may not represent ultimate mortality limits.
refer to a heterogeneous population, then w is the maximum potential age at death for the most robust individual.
Intuitively, this hypothesis is not very satisfactory. It implies that it is possible to live up to age ω, but that survival to age w plus 1 day is impossible. The theoretical plausibility of such a truncated mortality distribution was criticized by the eminent probabilist William Feller (1950:8-9). Gavrilov and Gavrilova (1991), who are critical of the idea that there exists a species-specific maximum life span for humans or other animals, devote an entire chapter of their book to this topic.
It is quite clear that a habitual vagueness in the use of the term ''life span" has confused the discussion of human mortality limits. According to Webster's dictionary, life span is either "the longest period over which the life of any plant or animal organism or species may extend, according to the available biological knowledge concerning it," or "the longevity of an individual." Thus, the life span of an individual refers to his or her age at death; the life span of a species refers to the maximum potential length of life for the most robust member(s) of the species; and the mean life span (of individuals) is equivalent to the familiar concept of life expectancy.
Use of this term in the literature has been rather haphazard, however. This confusion has led to some rather remarkable empirical assertions. Economos (1985:110), for example, asserts that "it has long been recognized that the human maximum life span has remained constant, around 100 years, across time, races, and civilizations." I agree with Gavrilov and Gavrilova (1991:119) that this notion appears to have "become established through a long period of mutual citation . . . in the total absence of any convincing proof."
There appear to be two common demographic arguments that are thought to support the limited-life span hypothesis. One is the assertion that there has been no increase over time in the maximum age at death observed for human populations (Fries, 1980; Olshansky et al., 1990). This assertion is clearly false, however, as illustrated by a recent analysis of trends in the maximum age at death for five countries. Figure 3-5 reproduces a key finding from Wilmoth and Lundström (1996), showing that the maximum age at death for men and women in Sweden has risen steadily for at least 130 years.1 These authors document a similar trend in three other developed countries (France, England and Wales, and Japan), although only during more limited time periods when the quality of the data appears reliable.2 Of course, some portion of this upward trend is attributable to population growth, because the extreme values of a sample from any probability distribution are partly a function of sample size (Gumbel. 1937 and 1958). Popu-
|
1 |
Data for the earliest decade shown in Figure 3-5. 1851-1860. appear to be contaminated by a handful of exaggerated ages at death. Wilmoth and Lundström (1996) attribute the improvement in data quality around 1860 to the founding of Sweden's National Central Bureau of Statistics. |
|
2 |
It is not uncommon to observe a decrease in the maximum reported age at death, although in all known cases this trend can reasonably be attributed to an improvement in data quality rather than a genuine retraction in the tail of the age distribution of deaths. |
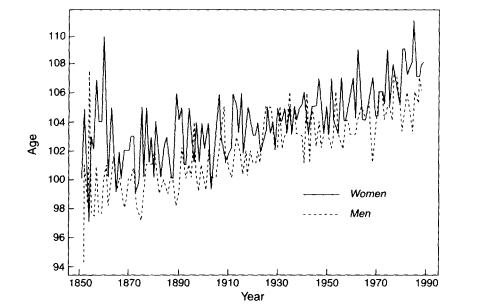
Figure 3-5
Maximum reported age at death in Sweden. women and men, 1851-1990. SOURCE: Wilmoth and Lundström (1996:69).
lation growth, however, is mostly a product of mortality decline, so it is difficult to separate conceptually the influence of these two factors.
One approach to this problem is to consider the causes of the rapid growth in the centenarian population of industrialized countries. This "proliferation" of centenarians is due mostly to an increasing probability of surviving into old age (say, until age 80) and, especially, of surviving from 80 until 100 years of age (Vaupel and Jeune, 1995). Then, for any underlying mortality function, the age of death of the oldest individual should rise partly as a function of the increasing number of persons who become centenarians. A complete analysis of the trend shown in Figure 3-5—breaking it into components related to the trend in births, the probability of survival until old age, and the probability of survival within old age—is still lacking. Nevertheless, if the mortality distribution were truncated on the right, this trend would be subject to an upper limit, regardless of the increasing size of the centenarian population. Therefore, its steady, almost linear rise over time suggests that the tail of the empirical age distribution has not yet arrived at such a limit. If the theoretical distribution is bounded on the right, we would expect this trend to level off as it approaches the limit. The apparent absence of deceleration in this upward trend suggests that the limit is at least not immediately in sight.3
The second demographic argument in support of the limited-life span hypothesis is the assertion that the exponential increase in mortality rates with age, as implied by the Gompertz curve, "ensures a finite life span" (Fries, 1980:131). This argument contains two fallacies. The first fallacy results from the mistaken notion that the Gompertz curve implies a finite life span (Gavrilov and Gavrilova, 1991; Wilmoth, 1992). As noted before, a finite life span results from a hazard function (or force of mortality) that rises abruptly toward infinity as age approaches w, the species-specific life span. The Gompertz model, on the other hand, implies that there is a non-zero probability of survival even to ages that are well beyond those previously observed (or even imaginable) for humans.4 Therefore, perhaps contrary to popular belief, the Gompertz mortality curve implies that the limited-life span hypothesis is false.
A second fallacy in this argument is that the Gompertz curve does not describe human mortality well at old ages. This point is well illustrated in Figure 3-6, which is taken from Gavrilov and Gavrilova (1991). Contrary to the prediction of the limited-life span hypothesis, observed death rates for humans do not rise abruptly toward infinity at some very high age. In fact, the age-related increase in the hazard rate, or force of mortality, is even less than the exponential rise implied by the Gompertz curve. The data presented in Figure 3-6 are for Swedish men during a limited time period, but all reliable evidence is consistent with the conclusion that the force of mortality continues to rise throughout adult life, but at a decreasing rate after the age of 75 or 80 (Horiuchi and Coale, 1990; Kannisto, 1994; Wilmoth, 1995; Horiuchi and Wilmoth, in press). A similar, or more extreme, finding exists for nonhuman species such as fruit flies (Drosophila melanogaster), medflies (Ceratitis capitata), and nematodes (Caenorhabditis elegans), whose mortality rates appear to level off in old age (Curtsinger et al., 1992; Carey et al., 1992; Fukui et al., 1993; Vaupel et al., 1994).
Of course, it is possible that there exists a maximum human life span at a point that is well beyond current experience. At present, it has been possible to compute reliable death rates for female populations up to a maximum age of around 109 years and for male populations to around 107 years (Kannisto, 1994). The oldest woman whose age has been reliably verified died recently at 122 years old (Robine and Allard, 1995); the oldest man has been verified as 1 15 years old (Wilmoth et al., 1996). Is it possible that an upper limit to the human life span lies just beyond these ages? We really have no way of denying or affirming this possibility, because verified observations of humans living (or dying) above 110 years of age are so few that we cannot compute reliable death rates in the tail of the distribution. As shown in Figure 3-2, the force of mortality could rise steadily
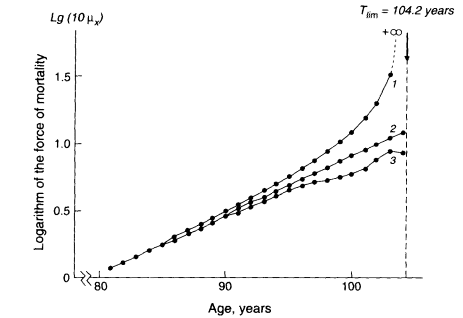
Figure 3-6
Force of mortality implied by the limited-life span hypothesis (1), compared with the Gompertz curve (2), and data for Swedish men during 1945-1967 (3). SOURCE: Gavrilov and Gavrilova (1991:128). Reprinted with permission from Harwood Academic Publishers.
until just before the upper limit of the life span and only then shoot abruptly toward infinity. However, such a situation—even if it were the reality—could never be observed and documented using our present methods.
In summary, the limited-life span hypothesis suggests that there exists a maximum age, ω, beyond which no human being can live. The theoretical plausibility of such a model is questionable, but the literature on this topic is confusing due to careless and inconsistent use of terminology. The hypothesis is not implied by the Gompertz curve or other common models of the age pattern of human mortality. A review of the empirical evidence also shows that the available demographic data provide no support for this hypothesis. We are led, therefore, to consider other means of conceptualizing a possible limit to human longevity.
Compression-Rectangularization Hypothesis
Another theoretical concept that has been associated with the study of limits to human longevity is the hypothesis of mortality compression, also known as
rectangularization of the survival curve. According to this hypothesis, the variance in life-table ages at death should decrease over time. Recalling that X is a random variable representing the life span of an individual drawn at random from a population of newborns, let Var(X,t) denote the variance of X at time t.5 In its strictest version, the compression hypothesis states that the following inequality holds for any choice of t1 < t2 < ... < tn :
Alternatively, compression could be defined in terms of the interquartile range of the distribution or some other measure. In general, the compression hypothesis implies that the dispersion in the density function of X,f(x), should diminish over time.
The notion of mortality compression, defined by a successive decrease in the variance of X, seems also to be associated with characteristic changes in the survival function, S(x), and the hazard rate function, h(x) (Wilmoth et al., 1995). Previous empirical analyses indicate that the rectangularity of the survival curve, S(x), is highly correlated with the standard error in the distribution of deaths, f(x). Furthermore, changes in these two characteristics of mortality curves appear to be linked to changes in the hazard function, h(x): a hazard function, h(x). that falls more precipitously at younger than older ages tends to be associated with a compression in the distribution of deaths, f(x), and a rectangularization of the survival curve, S(x), as depicted in Figure 3-3.
Because compression-rectangularization refers to the variability in the distribution of deaths, it is not immediately obvious that this hypothesis should be associated with a limit in the level of human longevity. It may be instructive to consider, therefore, an argument by Ryder (1975:10-11), which suggests a possible link between these two trends. Although the primary focus of Ryder's discussion was not the question of limits to human mortality, his comments provide some insight. In an article on stationary populations, he noted a strong linear relationship in West model life tables (of the Coale-Demeny system) between life expectancy and the coefficient of variation of ages at death (r2 = 0.9882 for females, and r2= 0.9834 for males). As life expectancy increases in these model life tables, the coefficient of variation declines. By extrapolation, the variability in age at death should diminish to nothing when equals 85.6 for females or 82.5 for males.
After performing this numerical exercise, Ryder remarks: "The phenomenon of declining coefficient of variation with increasing length of life would be the outcome of a model of survivorship in which one posits, as a species characteristic, a 'normal' life span close to invariant over all populations, with a small
but non-zero coefficient of variation; the principal source of variations in observed mean age at death would be the proportion of the population failing to achieve that life span—i.e., experiencing 'preventable' death." Without pushing this view as a prediction of future mortality trends, Ryder anticipated Fries' argument, with both authors suggesting that compression-rectangularization may reflect a process of convergence toward a characteristic human life span of around 85 years (Fries, 1980).
Although compression-rectangularization may be consistent with such a model of mortality change, a decrease in the variability of ages at death is not sufficient proof of the existence of mortality limits. It is certainly possible that the distribution of ages at death could become more and more compressed while also shifting further and further to the right. In such a situation, there might be no fixed life span or maximum life expectancy. Furthermore, there is no reason to believe that an extrapolation of the relationship between level and variability in Coale-Demeny model life tables is an accurate prediction of the course of future mortality change.6 Alternatively, it is at least theoretically possible that the variability in ages at death could decrease more slowly relative to the increase in life expectancy than predicted by the Coale-Demeny model tables. Thus, Figure 3-3 provides an example of the compression-rectangularization hypothesis in the absence of apparent limits on either the maximum life span or life expectancy.
Because the compression-rectangularization hypothesis suggests a limit in the variability of human longevity, not its level, it is only weakly related to the other two hypotheses considered in this paper. In a situation of mortality decline across the age range, the limited-life span hypothesis should result in a compression of mortality. Therefore, falling mortality in the absence of compression would suggest that the limited-life span hypothesis is false.7 Fries (1980) began by asserting that the limited-life span hypothesis was true and then concluded that rectangularization of the survival curve must result. In response, some authors have argued that compression-rectangularization has not been observed empirically as a means of countering the limited-life span hypothesis.
Some of these empirical analyses, however, have offered rather sweeping conclusions based on quite limited evidence. For example, Myers and Manton (1984) conclude that "there is no significant evidence that rectangularization has had a significant effect on the population and mortality dynamics of the elderly, at least through 1979." The empirical basis for this article, and for two other
papers that also refute the compression-rectangularization hypothesis (Rothenberg et al., 1991; Manton and Singer, 1994), is mortality data for the United States after 1962. Clearly, even a casual inspection of Figure 3-1 demonstrates that the U.S. survival curve has become more rectangular in shape during this century and that the distribution of ages at death has become more compressed.8 Therefore, Fries was not wrong to observe that human survival curves have become more rectangular over time, although the conclusion that this trend would continue—and any suggestion that it has implications for limits to human longevity—is questionable.
Another analysis of mortality trends in three countries, using up to 130 years of data, has concluded that "rectangularization is by no means a myth" and that "a significant compression of ages at death has clearly occurred over the long-term history of human mortality decline" (Wilmoth et al., 1995). Nevertheless, this study also noted a slowdown and even scattered reversals after 1950 in the compression-rectangularization trend for the countries considered (the United States, Sweden, and Japan). It seems possible and even likely that these trends—so prominent in the past—may not continue indefinitely into the future.
In summary, the compression-rectangularization hypothesis suggests that the variability in the distribution of ages at death should decline as life expectancy increases over time. This compression of the death distribution, f(x), tends to be associated with a progressive rectangularization of the survival curve, S(x), and with a pattern of decrease in the hazard rate, h(x), that is more pronounced at younger ages. An analysis based on model life tables suggests that there exists a consistent negative relationship between the increase in life expectancy and the decline in variability of ages at death; a simple linear extrapolation of this relationship suggests that the current increase in life expectancy at birth may reach a limit around 85 years of age. These calculations are not sufficient proof of limits to human longevity on their own, however, and the empirical evidence demonstrates that compression and rectangularization are by no means universal aspects of mortality decline. Overall, the compression-rectangularization hypothesis seems to have little relevance to questions about the biological limits of human mortality.
Limit-Distribution Hypothesis
A third hypothesis about limits to human longevity asserts that there exists a limiting distribution that mortality curves may approach but not surpass. In terms of the hazard function, this limiting distribution can be written as h*(x). Thus. h(x) ≥ h*(x) > 0 for all x in a large, random sample of humans at any point in time. This hazard function has a corresponding density function, f*(x). and survival
|
8 |
Although Figure 3-1 shows mortality curves for U.S. women only, the general pattern for U.S. men is quite similar. |
function, S *(x), which have similar interpretations. An example of convergence toward these limiting curves is illustrated in Figure 3-4. In this example, the survival curve may or may not equal zero (exactly) after some age, and the density function may or may not be right-truncated. Similarly, the variance in age at death may or may not decrease in a consistent manner as the distribution converges toward a limit.
Presumably, the limit implied by these curves is the product of some fundamental aspects of human biology in interaction with unavoidable environmental factors. By this argument, all large human populations in all environments should be subject to the same mortality limit. Clearly, the theoretical plausibility of this hypothesis demands some discussion. For example, given what is known about genetic and environmental variability, is it reasonable to suppose that there might be a universal mortality limit that applies to all human populations in all environments? Without this restriction, however, what is the meaning of the limit itself? If we made allowances for subpopulations that possess different mortality limits or environmental conditions that change the limit, it would be necessary to sacrifice the notion of a universal mortality limit.
Consider the issue of genetic variability. There are elements of the human phenotype that show almost no variability (two eyes, two legs, 10 fingers, 46 chromosomes), because in these situations most mutations are deleterious. There are other characteristics that show considerable variability (hair and skin color, height, intelligence), because Darwinian selection does not strongly favor one phenotype over another. In low-mortality populations, longevity probably falls into the latter category, because postreproductive survival can have only limited selective influence.
Empirically, we know from twin studies that roughly one quarter of the variability in individual ages at death may be due to genetic factors (McGue et al., 1993; Herskind et al., 1996). Therefore, it should be possible to find subgroups of the human population that have an unusual genetic endowment for longevity. For a selected subpopulation, we might observe average mortality levels that fall below the theoretical minimum, which applies to a random sample of the total human population. In addition, it is possible that this theoretical minimum could change over time, as a result of Darwinian selection, genetic drift, or conscious manipulation (selective breeding or genetic engineering).
Therefore, for the purpose of discussing ultimate mortality limits, I assume that the forces of Darwinian selection and genetic drift will have only a negligible impact on the genetics of human longevity over the time horizon of interest to demographers and social planners, which is perhaps 50-100 years. Furthermore, although it seems imprudent to speculate about the potential impact that the conscious manipulation of the human genome might have in this area, all statements about ultimate mortality limits must necessarily assume an absence of successful efforts to alter human longevity by this means. Finally, for this discussion, I also neglect the possibility that fundamental changes in the earth's ecosys-
tem (such as the climatic changes associated with geologic eras or human-induced "global warming") might have a significant effect on human mortality levels in the next century.
With these restrictions and qualifications in mind, it is reasonable to consider at least the possibility that some version of the limit-distribution hypothesis might be true. The question associated with the hypothesis might be stated as follows: Given the current genetic composition of the human population and the natural environment as it exists today, does there exist an irreducible mortality level, represented by h*(x), which thus implies an upper limit to the mean life span, or life expectancy (but not necessarily a finite maximum life span)?
As with the two hypotheses mentioned previously, there have been several discussions of this topic already in the literature. Bourgeois-Pichat (1952, 1978), Kannisto (1988), and Olshansky et al. (1990) have all used methods for theoretically eliminating certain causes of death as a means of exploring the lower limits of human mortality rates. The justification for such calculations is the belief that certain "exogenous" causes of death could theoretically be eliminated, while other "endogenous" causes may prove intractable.
There are several reasons to criticize the cause-elimination methodology, however. First, the method typically involves an assumption that the various causes operate independently of one another (Keyfitz, 1985), which is not plausible in many situations (Manton et al., 1991). Furthermore, the theoretical distinction between "endogenous" and "exogenous" causes is rather dubious. Mortality rates due to so-called exogenous causes (e.g., infectious disease, accidents, suicide) tend to increase with age, perhaps reflecting an increased propensity to succumb to these causes as a result of internal degeneration. Empirical evidence also demonstrates that mortality rates due to so-called endogenous causes are highly variable, both over time and across populations. Thus, it seems likely that almost all causes of death are both "exogenous" and "endogenous" in nature. Similarly, the notion of death due exclusively to "old age'' or "senility," which Fries (1980) referred to as "natural death," has been sharply criticized (Schneider and Brody, 1983).
Nevertheless, cause-elimination models are not the only means of exploring the notion of a mortality limit distribution. Other, mostly ad hoc methods have also been used to estimate one or more parameters of this hypothetical distribution. For example, Fries (1980) derived his estimate of the maximum achievable human life expectancy by extrapolating the total life expectancy at age ![]() . at various ages. Because
. at various ages. Because ![]() has traditionally been rising much less rapidly at older than at younger ages, the extrapolated curves must eventually intersect. According to Fries, this intersection will occur around the year 2045 for the U.S. population, when an "ideal average life span" of around 85 years should be achieved. This maximum life expectancy corresponds to Fries' "ideally 'rectangular' survival curve" and thus to a limiting mortality distribution.
has traditionally been rising much less rapidly at older than at younger ages, the extrapolated curves must eventually intersect. According to Fries, this intersection will occur around the year 2045 for the U.S. population, when an "ideal average life span" of around 85 years should be achieved. This maximum life expectancy corresponds to Fries' "ideally 'rectangular' survival curve" and thus to a limiting mortality distribution.
Fries' argument, however, seems to ignore the problem of a discontinuity at
the limit itself. Why would the various values of ![]() follow separate, linear paths until the point of convergence but then merge and remain constant (around 85 years) thereafter? Equally consistent with the empirical evidence—and more plausible theoretically—is a prediction that the values of
follow separate, linear paths until the point of convergence but then merge and remain constant (around 85 years) thereafter? Equally consistent with the empirical evidence—and more plausible theoretically—is a prediction that the values of ![]() may move closer over time along curvilinear paths but never become equal. From this perspective, these curves might or might not be thought to possess an upper limit.
may move closer over time along curvilinear paths but never become equal. From this perspective, these curves might or might not be thought to possess an upper limit.
Most evidence from demographic trends seems inconsistent with the notion of a finite mortality limit, but there are some important questions of interpretation. If there exists a non-zero lower bound for age-specific death rates, how would we know if it were approaching? Most authors seem to assume that the approach to a limit would be characterized by a slowdown in the rate of mortality decline over time. The absence of deceleration in the rate of mortality decline, then, is taken as evidence that we are not currently approaching a lower limit in mortality rates.
For example, the reduction in age-specific death rates for most developed countries has been a stable, long-term process. This conclusion is illustrated for the United States in Figure 3-7, which shows age-adjusted death rates for women and men during 1900-1992 based on Social Security data (Bell et al., 1992). This figure is drawn using a semilogarithmic scale to conform with standard practice. Thus, it is the relative, not absolute, rate of mortality decline that has been stable.
If Figure 3-7 showed trends in death rates for separate age groups, the general conclusion (of stable decline) would not change. It would be evident, however, that the rate of decrease has varied enormously by age: although the pattern has changed in recent years, death rates have typically fallen much more rapidly at younger than at older ages. When making mortality projections, it is typical to assume that the differences by age in the pace of mortality decline will continue into the future (Pollard, 1987; Lee and Carter, 1992).
Thus, the trend in Figure 3-7 is influenced by the enormous decline in infant and child mortality, and also by smaller reductions in death rates at older ages. Over the time period shown here, the relative importance to the overall mortality decline of changes in younger and older age groups has reversed itself. As discussed below, the most rapid decreases in mortality are now occurring at older ages, whereas the opposite was true in earlier eras of mortality decline. Thus, it is all the more remarkable that the trend in Figure 3-7, which is a composite of trends across the age range, moves downward with such regularity.
The pace of overall mortality decline has not, however, been constant. From Figure 3-7, it is evident not only that there have been periods of acceleration and deceleration but also death rates have moved steadily downward over the long run. Perhaps the most curious feature of Figure 3-7 is the plateau that appears from around 1954 to 1968, especially for men. A detailed discussion of this phenomenon is given by Crimmins (1981), who analyzes these trends in terms of underlying causes of death. The period around the 1940s was characterized by very rapid mortality decline, owing at least in part to the increased use of drug
therapies, primarily antibiotics and sulfa drugs, in the treatment of infectious diseases. By the mid 1950s, however, the potential for further reduction by this means was nearly exhausted, and so the pace of overall mortality decline slowed considerably for women and came to a veritable halt for men.
Crimmins points out that the trend in male mortality around the 1960s was also affected by a mild increase in violent deaths, in particular, deaths due to homicide and suicide. The resumption of rapid mortality decline in the United States after 1968, however, resulted from a new set of changes affecting cardiovascular mortality (i.e., deaths due to heart disease, cerebrovascular disease, and arteriosclerosis). These changes included both life style (exercise, diet, smoking) and medical factors (access to treatment through federal programs, surveillance and treatment of hypertension, pharmaceutical and surgical interventions). Owing to these developments, the relative size of the decline in U.S. mortality rates during 1968-1977 was greater at ages 85 and above than for all other age groups except infants (Crimmins, 1981:230).
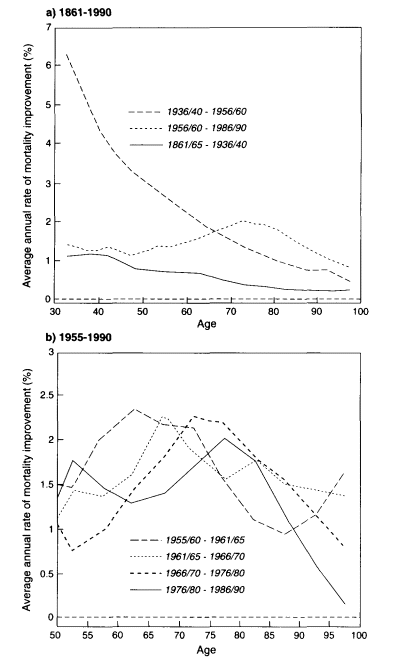
What was happening in other developed countries during this time period? A slower pace of mortality decline during the late 1950s and 1960s, especially for men, was characteristic of most developed countries (United Nations, 1982; Spiegelman and Erhardt, 1974; Anderson and Silver, 1994). There is also evidence that the pace of mortality decline in developed countries has quickened in recent decades, especially at older ages (Kannisto et al., 1994). Figure 3-8 shows
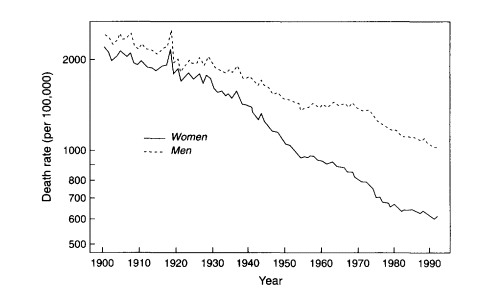
Figure 3-7
Age-adjusted death rates, U.S. women and men, 1900-1992.
SOURCE: Bell et al. (1992:3-4), updated by the author. Total death rates were standardized using the 1980 census population.
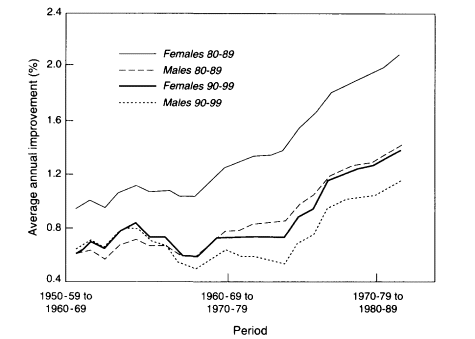
Figure 3-8
Average annual rates of mortality decline, women and men, ages 80-89 and 90-99 combined, for an aggregate of nine countries.
SOURCE: Kannisto et al. (1994:802). Reprinted with permission. Each observation in this graph gives the annualized rate of mortality improvement over successive 10-year time periods; for example, the last point on the curve gives the improvement between 1972-81 and 1982-91. The nine countries included in the aggregate analysis are Austria. Belgium, England and Wales, France, West Germany, Japan, Scotland, Sweden, and Switzerland.
the average annual reduction in death rates (in percent) for ages 80-89 and 90-99 in an aggregate of eight European countries plus Japan from the 1950s through the 1980s. Rather than slowing down, mortality decline at older ages in industrialized countries seems to have accelerated.
The evidence from the recent study by Kannisto and his colleagues is corroborated by the work of Horiuchi and Wilmoth (1995), who have documented an "aging of mortality decline" for several countries. This trend is illustrated in Figure 3-9 using Swedish data for the period 1861-1990. These graphs demonstrate that the age pattern of mortality decline has evolved over time, with the most recent period characterized by an increase in the age of the most pronounced decline (thus, an "aging of mortality decline"). The more detailed graph in Figure 3-9b shows that this change has continued at least until 1990.
Another empirical result worth mentioning here is the apparent absence of a strong correlation between level of mortality and speed of mortality decline.
Figure 3-10 shows a scatter plot of average death rates for ages 80-99 in the 1970s versus the average annual rate of improvement during the 1970s and 1980s, again taken from a study of 27 developed countries (Kannisto et al., 1994). The correlations associated with these graphs are negative: -0.10 for males and -0.35 for females. If the Eastern European countries (shown in darker type) are omitted, these correlations become slightly positive: 0.30 for males and 0.07 for females. In either case, these data do not provide strong evidence of a slowdown in the rate of mortality decline associated with lower mortality levels. Furthermore, it is notable that the values for females lie to the "northwest" of those for males, indicating that women enjoy both lower mortality levels and faster rates of mortality decline.
Kannisto and his colleagues argue (p. 802): "If mortality among the oldest-old were approaching biological or practical limits, then countries that have the lowest death rates would be closer than other countries to such limits. Rates of mortality improvement, however, are only weakly related to levels of mortality. . . ." Thus, the failure to demonstrate a positive correlation between mortality level and rate of improvement is taken as evidence against the limit-distribution hypothesis—but this argument, too, must be qualified by the observation that a limit distribution could still exist but is not currently in sight.
In summary, then, the limit distribution of human mortality is represented by a hazard function, h*(x), and associated density and survival functions, f*(x) and S*(x), which signify the hypothetical level of mortality that would be achieved by a large, random sample of individuals from the present human population if those individuals lived their entire lives under optimal environmental conditions. The most common means of estimating the limit distribution implied by these curves has been some form of cause-elimination, although the validity of this framework is itself questionable, both because of the interdependence between competing causes of death and because of problems in distinguishing between exogenous and endogenous, or between senile and nonsenile, causes of death.
The parameters of a limiting-mortality distribution have also been estimated by extrapolating past trends until some form of convergence is achieved, such that further reductions in mortality may appear improbable, but such arguments are not convincing if they imply a discontinuity at the point of convergence. Empirical studies of trends in total mortality contain no suggestion that human mortality is approaching a lower bound. Contrary to the predictions of the mortality limit hypothesis, mortality decline is accelerating in the oldest age groups in several low-mortality countries, and there is no evidence of a positive correlation between mortality level and the pace of mortality decline.
Conclusion
The demographic debate about the limits of human longevity can be expressed in terms of three hypotheses: limited life span, compression-rectangu-
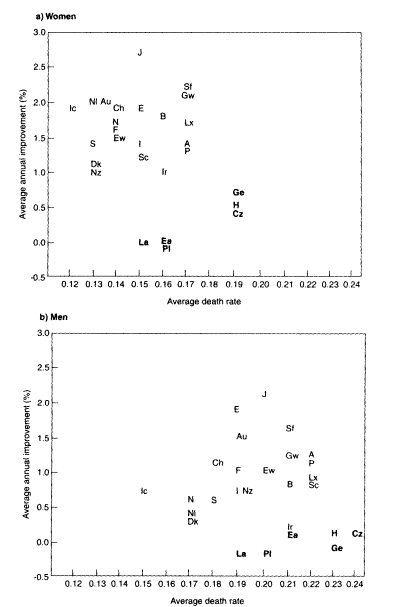
Figure 3-10
Average death rate in the 1970s plotted against the average annual rate of mortality decline from the 1970s to 1980s, women and men, ages 80-99 combined, 27 developed countries.
SOURCE: Kannisto et al. (1994:803). See source for explanation of country abbreviations. Abbreviations for Eastern European countries are printed in darker type.
larization, and limit distribution. These hypotheses can be stated precisely in the language of statistical survival analysis as limits regarding, respectively, the maximum age attainable by humans, the variability in individual life spans, and the age pattern of human mortality.
Intuitively, the limited-life span hypothesis is unappealing because it suggests that it is possible to survive to some maximum age, w, but not to w plus 1 day. Empirical research provides two pieces of relatively strong evidence that the limited-life span hypothesis is false (more precisely, that a finite human life span limit is not presently within sight). First, rather than rising abruptly toward infinity as predicted by the hypothesis, within the measurable range the rise in the human death rate decelerates with age. In some nonhuman species such as fruit flies, medflies, and nematodes, a more extreme pattern is observed, in that death rates seem to level off at advanced ages. It is possible, however, that we simply have not measured the force of mortality at ages near enough to the limit. A second, perhaps more convincing, piece of evidence that humans are not currently approaching an ultimate life span limit is the observation that the maximum age at death for some national populations has risen and continues to rise in a steady, almost linear fashion. If we were close to observing a biological maximum, intuition suggests that this trend would show some sign of deceleration, although none is evident.
The compression-rectangularization hypothesis describes a trend of decreasing variability in individual life spans that has probably been observed throughout most of the history of human mortality decline. Nevertheless, it is not certain that this trend continues in all low-mortality populations today or that it will be observed there in the future. The failure to observe a continuing pattern of compression-rectangularization seems to deny further the validity of the limited-life span hypothesis, although the empirical basis for this conclusion is not strong, and its theoretical basis needs more careful consideration as well. Overall, the relevance of the compression-rectangularization hypothesis to the current debate about the limits of human longevity is somewhat dubious.
The most general, and perhaps useful, of these three hypotheses is the limit-distribution hypothesis. It asserts that the age pattern of human mortality possesses an irreducible lower limit (in a large, randomly selected population). This hypothesis implies limits in the mean life span, or life expectancy, and in other parameters of the probability distribution of ages at death, including the median, the variance, and so forth. There have been several attempts to derive this limit distribution by separating causes of death into two mutually exclusive categories—either endogenous versus exogenous or senile versus nonsenile—and then computing the distribution that would result from the hypothetical elimination of exogenous or nonsenile causes. These methods do not appear to be well-grounded in theory, however, and some of their predictions have already been overturned. Attempts to derive a single parameter of the limit distribution—for example, life expectancy—through extrapolation of past trends also lack a firm theoretical
justification and are plagued by logical inconsistencies, particularly with regard to discontinuities at the limit.
Three empirical observations provide important evidence in opposition to the limit-distribution hypothesis: (1) the historical stability of rates of mortality decline, (2) the acceleration of mortality decline at older ages, which are now characterized by the fastest age-specific rates of decline currently seen in some populations; and (3) the absence of a strong, positive correlation between levels of mortality and rates of improvement over time. Nevertheless, the link between these patterns and the limit-distribution hypothesis relies on intuition rather than firm theoretical results. Logically, mortality decline might or might not decelerate as the hazard rate approaches an irreducible lower bound.
In any case, demographic evidence can suggest only that we are not close to a limit at present, not that no ultimate limit exists. If the data contain no suggestion of a limit, a facile response is to assert that the limit may still be out there but that we are just not close enough to be able to observe it. In my view, however, proving or disproving the existence of limits that lie far beyond current experience is not a pressing task: the question of interest to policy makers is whether we are now approaching a biological limit to longevity, not whether such a limit exists. Furthermore, any hypothesis about a limit that lies far from current experience would not be falsifiable: anyone could assert or deny that such a limit exists, and there could be no basis for disputing that assertion empirically. Therefore, rather than merely asking, "Are there limits to human longevity?," we should inquire, "Are limits to human longevity presently in sight?" Of course, we should also be asking ourselves, ''How good is our eyesight?"
References
Acsádi. G., and J. Nemeskéri 1970 History of Human Life Span and Mortality. Budapest: Akadémiai Kiadó.
Anderson, B.A., and B.D. Silver 1994 A comparison of Soviet mortality in the working ages: 1959-1988. Pp. 295-338 in W. Lutz, S. Scherbov, and A. Volkov, eds., Demographic Trends and Patterns in the Soviet Union before 1991. London: Routledge.
Bell, F. C., A.H. Wade, and S.E. Goss 1992 Life Tables for the United States Social Security Area 1900-2080. Actuarial Study No. 107, SSA Publication No. 11-11536.
Bourgeois-Pichat, J. 1952 Essai sur la mortalité "biologique" de l'homme. Population 7(3):381-394.
1978 Future outlook for mortality decline in the world. Population Bulletin of the United Nations, No. 11.
Carey, J.R., P. Liedo, D. Orozco, and J.W. Vaupel 1992 Slowing of mortality rates at older ages in large medfly cohorts. Science 258:457-463.
Crimmins, E.M. 1981 The changing pattern of American mortality decline, 1940-1977, and its implications for the future. Population and Development Review 7(2):229-254.
Curtsinger, J.W., H.H. Fukui, D. Townsend, and J.W. Vaupel 1992 Demography of genotypes: Failure of the limited life span paradigm in Drosophila melanogaster . Science 258:461-463.
Davis, K. 1951 The Population of India and Pakistan. Princeton, NJ: Princeton University Press.
Economos, A.C. 1985 Rate of aging. rate of dying and non-Gompertzian mortality-Encore .... Gerontology 31:106-111.
Feller, W. 1950 An Introduction to Probability Theory and its Applications. New York: John Wiley & Sons.
Fries, J.F. 1980 Aging, natural death, and the compression of morbidity. New England Journal of Medicine 303:130-135.
Fukui, H.H., L. Xiu, and J.W. Curtsinger 1993 Slowing of age-specific mortality rates in Drosophila melanogaster. Experimental Gerontology 38:585-599.
Gavrilov, L.A., and N.S. Gavrilova 1991 The Biology of Life Span: A Quantitative Approach. New York: Harwood.
Gumbel, E.J. 1937 La Durée Extrême de la Vie Humaine. Paris: Hermann.
1958 Statistics of Extremes. New York: Columbia University Press.
Herskind, A.M., M. McGue, N.W. Holm, T.I. Sorensen, B. Harvald, and J.W. Vaupel 1996 The heritability of human longevity: A population-based study of 2872 Danish twin pairs born 1870-1900. Human Genetics 97:319-323.
Horiuchi, S., and A.J. Coale 1990 Age patterns of mortality for older women: An analysis using the age-specific rate of mortality change with age. Mathematical Population Studies 2(4):245-267.
Horiuchi, S.. and J.R. Wilmoth 1995 The Aging of Mortality Decline. Presented at the annual meetings of the Population Association of America, San Francisco, April 6-8, and the Gerontological Society of America, November 15-19.
1995 Deceleration in the age pattern of mortality at older ages. Demography.
Kannisto, Väinö 1988 On the survival of centenarians and the span of life. Population Studies 42:389-406.
1994 Development of Oldest-old Mortality, 1950-1990: Evidence from 28 Developed Countries. Odense, Denmark: Odense University Press.
Kannisto, Väinö, J. Lauritsen. A.R. Thatcher, and J.W. Vaupel 1994 Reduction in mortality at advanced ages. Population and Development Review 20:793-810.
Keyfitz, N. 1985 Applied Mathematical Demography. New York: Springer-Verlag.
Lee, R.D., and L.R. Carter 1992 Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87:659-671.
Manton, K.G., and B. Singer 1994 What's the fuss about compression of mortality? Chance 7(4):21-30.
Manton, K.G., E. Stallard, and H.D. Tolley 1991 Limits to human life expectancy: Evidence, prospects, and implications. Population and Development Review 17(4):603-637.
Manton, K.G.. and H.D. Tolley 1991 Rectangularization of the survival curve: Implications of an ill-posed question. Journal of Aging and Health 3(2):172-193.
McGue, M., J.W. Vaupel, N. Holm, and B. Harvald 1993 Longevity is moderately heritable in a sample of Danish twins born 1870-80. Journal of Gerontology 48:B237-244.
Myers, G.C., and K.G. Manton 1984 Compression of mortality: Myth or reality? The Gerontologist 24(4):346-353.
Olshansky, S. J., B.A. Cames, and C. Cassel 1990 In search of Methuselah: Estimating the upper limits to human longevity. Science 250:634-640.
Pollard, J.H. 1987 Projection of age-specific mortality rates. Pp. 55-69 in Population Bulletin of the United Nations No. 21/22.
Population Reference Bureau 1995 World Population Data Sheet. Washington, DC: Population Reference Bureau.
Preston, S.H. 1980 Causes and consequences of mortality declines in less developed countries during the twentieth century. Pp. 289-360 in R. A. Easterlin, ed., Population and Economic Change in Developing Countries. Chicago: University of Chicago Press.
1990 Sources of variation in vital rates: An overview. Pp. 335-350 in J. Adams, D. Lam, A. Hermalin, and P. Smouse, eds., Convergent Issues in Genetics and Demography. Oxford: Oxford University Press.
Robine, J., and M. Allard 1995 Validation of the exceptional longevity case of a 120 year old woman. Pp. 363-367 in B.J. Vellas, J.L. Albarede, and P.J. Garry, eds., Long-Term Care. Facts and Research in Gerontology. New York: Springer Publishing Company.
Rothenberg, R., H.R. Lentzner, and R.A. Parker 1991 Population aging patterns: The expansion of mortality. Journal of Gerontology: Social Sciences 46(2):S66-S70.
Ryder, N.B. 1975 Notes on stationary populations. Population Index 41:3-28.
Schneider, E.L., and J.A. Brody 1983 Aging, natural death, and the compression of morbidity: Another view. New England Journal of Medicine 309(14):854-856.
Spiegelman, M., and C.L. Erhardt 1974 International comparisons of mortality and longevity. Pp. 39-64 in C.L. Erhardt and J.E. Berlin, eds., Mortality and Morbidity in the United States. Cambridge. MA: Harvard University Press.
United Nations 1982 Levels and Trends of Mortality since 1950. New York: United Nations.
Vaupel, J.W., and B. Jeune 1995 The emergence and proliferation of centenarians. In B. Jeune and J.W. Vaupel, eds., Exceptional Longevity. Odense, Denmark: Odense University Press.
Vaupel, J.W., T.E. Johnson, and G.J. Lithgow 1994 Rates of mortality in populations of Caenorhabditis elegans. Science 266:826.
Wilmoth, J.R. 1992 The Demographer's Crystal Ball: How Long Will We Live During the 21st Century? Presented to the Bay Area Colloquium in Population, October 7.
1995 Are mortality rates falling at extremely high ages? An investigation based on a model proposed by Coale and Kisker. Population Studies 49(2):281-295.
Wilmoth, J.R., J.W. Curtsinger, and S. Horiuchi 1995 Rectangularization Revisited: Survival Curves for Humans and Fruit Flies. Presented at the annual meeting of the Population Association of America, San Francisco. April 6-8.
Wilmoth, J.R., and H. Lundström 1996 Extreme longevity in five countries: Presentation of trends with special attention to issues of data quality. European Journal of Population 12(1):63-93.
Wilmoth, J.R., A. Skytthe, D. Friou, and B. Jeune 1996 The oldest man ever? A case study of exceptional longevity. The Gerontologist 36(6):783-788.