4 The Evolution of Senescence
Shripad Tuljapurkar
Introduction
This paper suggests directions for developing an evolutionary theory of senescence with the aim of producing testable predictions or theoretically based tools for data analysis. The evolutionary view of mortality defined by Medawar (1952), Williams (1957), and Hamilton (1966) made the key points that mortality is a fitness component and that the age pattern (which I will call the shape) of mortality is probably under the influence of evolutionary forces (selection, mutation, drift, etc.). These writers also made the important prediction that immortality (or, at least, indefinite extension of life) is unlikely to be the end result of evolution by selection. Recent analyses of experimental data (e.g., Carey et al., 1992, Curtsinger et al., 1992 and 1994; Gaillard et al., 1994) have provided detailed information about the shape of mortality within species and comparisons among species. To understand and analyze this information as well as to predict at an appropriate level of detail will require that we move beyond the classical theories.
Theoretical advance hinges on defining what we wish to understand and how we will proceed. I center my discussion on the concept of an evolutionary equilibrium for a life history, which includes the shape of fertility and mortality and possibly other features such as growth rates. A theory focused on equilibria is limited by the assumption that the forces of evolution have operated long enough that the characters we study are close to their equilibrium states. A nonequilibrium theory is much more difficult, because the characters of interest may be in some transient state that depends on initial conditions unknown to us.
Understanding equilibria is an essential step toward a nonequilibrium theory and should provide greater insights than we now possess.
I first discuss different theoretical approaches to the definition of evolutionary equilibria. Next I consider the classical theory and define two special equilibria: the "salmon" limit, and the "bacterium" limit. These equilibria reveal critical issues concerning the assumptions and structure of the theory. The consequences of some specific generalizations of the classical theory will then be reviewed. Finally, I outline a program of theoretical work that should lead to a more useful evolutionary theory of senescence.
Evolutionary Equilibria
Consider the dynamics of a population phenotype under the action of selection and mutation. At any time, there is some frequency distribution of the phenotype (among individuals) and an underlying distribution of genotypes. Genotypes map into phenotypes, and phenotypes map into fitness. Fitness differences, mutation, and random drift can lead to a change in the relative numbers of different genotypes and thus to changes in phenotype distribution. Any theoretical analysis makes assumptions about each step in this process. Given such assumptions, an evolutionary equilibrium (EE) is defined as a phenotypic distribution for a population that remains unchanged under the above dynamic process.
For an age-structured population, the individual phenotype of interest is a vector z = (µ, m). The components µ(x) and m(x) of the two vectors listed on the right are, respectively, the mortality rate and fertility at age x. For a size-structured population, we would add size-specific growth rate g(s) at size s, and make µ(s) and m(s) size-dependent to get z = (µ, m, g). Suppose that time is measured in discrete units (e.g., generations) and that the frequency distribution of the phenotype in the population is given by ft(z) at time t. The evolutionary dynamic process above changes this distribution, in one time step, into a new one, ft+1(z). An evolutionary equilibrium is a distribution F( z) that remains unchanged under the dynamics. We are mainly interested in stable equilibria: the analysis of stability properties can be difficult, although this paper does consider the stability of some special equilibria. Unstable equilibria can also be interesting, typically in situations where one asks if a newly introduced phenotype can increase in frequency in a population from which it was previously absent. Such invasion analyses are used here to examine the effects of random environments on the evolution of mortality patterns.
There are three ways of modeling the dynamics of a phenotype distribution, and I consider them in turn. In each case, I direct attention to the assumptions and limits of the method. The reader should note that the results of the theory depend not only on the assumptions within each method below but also that different methods can produce different answers.
Evolutionarily Stable Strategy
Evolutionarily stable strategy (ESS) models assume that every genotype maps to a single phenotype and (typically) that the population displays one common phenotype. Instead of a frequency distribution of phenotypes, a single phenotype applies to every individual. An underlying set Z of possible phenotypes is considered, and the dynamics consist of competition between phenotypes. In the usual set-up, a rare (infrequent) phenotype ZR is assumed to compete with a common phenotype zC. If the rare type can increase in frequency, it is said to invade the population. The object of the theory is to identify a subset ZE of the best competitors among the possible phenotypes Z. The set ZE may contain several phenotypes that are equally competitive, or a single "best" phenotype; in either case, the ESS model consists of subset ZE
How is competitive success (i.e., fitness) defined here? The definition depends on the population dynamics of competition. The original model of Hamilton (1966) was (implicitly) of this sort and assumed exponential growth in a constant environment, so that fitness equaled the Lotka (intrinsic) rate of increase r = r(z). If we change the model of competition, a different fitness measure may apply. For example, Orzack and Tuljapurkar (1989) assumed exponential growth in a stochastic environment, so their fitness equaled the long-run stochastic growth rate a = a(z). With different fitnesses, the competitive ranking of phenotypes in the same underlying set Z can change.
In this type of model, the ESS depends on the initial set Z of possible phenotypes. Suppose, for example, that the fitness measure is r from classical demography. Then we know that r increases with an increase in fertility at any age. Absent any constraints, the ESS phenotypes would cluster at the point of maximum fertility in the set Z. Absent an upper bound on fertility in the set Z, we would be led to ridiculous conclusions. The set Z of possible phenotypes must contain constraints: one example would be the imposition of correlations between fertility and mortality and another would be the imposition of a maximum fertility (or other measure of reproductive output). I will later discuss a particular model of correlations that has been analyzed in different ways.
A shortcut approach to the ESS is sometimes used, based on the idea that if there is a single fitness for each phenotype z, then the ESS set ZE is simply that set which yields a maximum of the fitness. This approach works when there is a single maximum but can fail when multiple fitness maxima occur.
Evolutionary Genetic Stability
Evolutionary genetic stability (EGS) is a term coined by Eshel and Feldman (1982) and is a relative of ESS. In this approach, the genetic basis of the phenotypes of interest is taken to be more complex. Eshel and Feldman typically consider two- or three-locus models. As with ESS, there is a set of possible
phenotypes, but here competition is described by the dynamics of a rare "modifier" gene at one of the loci. Typically, the modifiers are chosen from a set, and each modifier in the set maps into a phenotypic variant. If a rare modifier gene can invade a given genetic configuration, by increasing in frequency, the genetic configuration is unstable. When a genetic configuration is found such that it cannot be invaded by any modifiers in the set, that configuration is said to be at EGS.
This approach has not been used for life-history characters but rather has been used for characters that are not components of fitness. Examples of the latter are mutation rate and rate of recombination between loci. A virtue of this method is that it forces attention to the genotypic structure. Such attention is conspicuously absent in the literature on the evolution of life-history characters; possible reasons for its absence are the complexity of analysis in EGS theory and the relative dearth of good information on the genetic basis of life-history traits.
Selection-Mutation Equilibrium
The preceding methods do not explicitly invoke mutation. They do implicitly assume that the phenotype set Z is generated by mutational events, but there is no dynamical representation of the mutational process. (This restriction applies to ESS and EGS models for life-history traits; obviously, an EGS model for modifiers of mutation rate will include mutational dynamics, as in Liberman and Feldman, 1986.) However, mutation is central to most arguments about the evolution of mortality rates, and it is clearly important to examine the joint dynamics of mutation and selection.
The first paper to do this, as far as I know, was Charlesworth (1990), following earlier work by Lande (1982). His approach points the way in which, I believe, the theory should go, and I will review it in a little more detail. A central assumption is that the components of the life-history phenotype z are determined by the additive action of many loci that are loosely linked. This, plus an assumption that selection is weak, allows the phenotypic dynamics to be described by the mean and variance of the phenotype distribution (in effect, the phenotype distribution is approximated by a normal distribution). Further, the dynamics of the mean phenotype are independent of the dynamics of the phenotypic variance. Changes in the mean phenotype are driven by selection and mutation.
The selective force acting here is simple competition between phenotypes that differ in mortality, fertility, and so on and is measured in terms of Lotka intrinsic growth rate r and the generation time T. In these models, a selective change in gene frequency first shows up in the youngest age class (new offspring) and then propagates through the population as these offspring, in turn, age and produce further young. As a result, the generation time T is a characteristic time scale for change in the population distribution of genes and phenotypes. The effectiveness of selection also depends on correlations between components of
the phenotype; for example, increased fertility may be accompanied by decreased survival.
The Lande-Charlesworth approach summarizes these facts in an equation for the dynamics of the population-average of the life-history phenotype vector. The equation has the form
Mutational change in the average life-history phenotype is taken to be the result of mutations at each of the many underlying loci that additively determine the phenotype.
Equation 1 provides an equation for the equilibrium mean phenotype that will be maintained under the combined effects of selection and mutation. This is an important feature because it provides an explicit mapping from assumptions about mutation and the phenotype set to the equilibrium state. Such a mapping is essential if we are to make testable predictions. This approach does not, however, resolve the problems of defining the phenotype set; the problems noted above for ESS also occur here, as I will illustrate later.
In contrast to ESS models, this approach yields predictions for equilibrium phenotypes. These predictions can then be confronted with data in an unambiguous way. When mutation is not directly modeled, theory leaves us with no clear guide to possible sources of discrepancy between predictions and observations, because one can always appeal to unspecified mutational effects. Unfortunately, the predictions of a mutationally based theory are also difficult to check because mutational effects are difficult to measure (see Mukai et al., 1972, and Partridge, in this volume).
Two Evolutionary Equilibria
The simplest dynamic process for the evolution of the shape of mortality is based on classical demography, with r as fitness. I now show, in this case, that there are two obvious evolutionary equilibria for life-history phenotypes. These equilibria are derived under the assumptions of the classical theory of senescence—i.e., that there is exponential growth in a constant environment. It is helpful, first, to recall two well-known results from classical demography.
We use discrete ages, survival from age x to x + 1 is p(x), survival from birth to age x is l(x), and the stable (Lotka) growth rate is r. Then
where T is mean length of generation, and
Note that ![]() r/
r/![]() p(x) is constant at the ages before reproduction starts, declines after that until reproduction stops, and is zero postreproduction. However,
p(x) is constant at the ages before reproduction starts, declines after that until reproduction stops, and is zero postreproduction. However,![]() r/
r/![]() m(x) always decreases with age if r > 0.
m(x) always decreases with age if r > 0.
The Salmon Limit
Assume that there is a fixed age ß after which reproduction ceases, so that m(x) = 0 for x > ß. Assume also that mutations affecting survival are always deleterious. Then for x > ß there is no selection to balance the mutational pressures, and it must follow that survival rate will evolve to zero. This is what I will call the salmon limit for mortality, because it corresponds to a catastrophic increase in mortality beyond age ß.
It is important to note that this result is unaffected by several changes in the assumptions. First, suppose that we have antagonistic pleiotropy, defined specifically by saying that some mutations have a beneficial effect early in life (i.e., before age ß) and also have deleterious effects late in life. Such mutations will be favored, but they will only accelerate the accumulation of postreproductive deleterious effects. Therefore the salmon limit is stable under such mutations.
Second, remove the assumption of a fixed age of last reproduction and allow a tradeoff between mortality and fertility at every age, so that a positive change in p(x) comes at the expense of a negative change in m(x). Such a tradeoff alters the values of the derivatives in Equations 2 and 3 but does not alter the fact that the selective pressure measured by [![]() r/
r/![]() m(x)] declines with age x. Consequently, with deleterious mutations affecting survival there will always be some age ß past which the mutation-selection balance will be dominated by mutations and survival will fall catastrophically. This is precisely the pattern observed by Charlesworth (1990).
m(x)] declines with age x. Consequently, with deleterious mutations affecting survival there will always be some age ß past which the mutation-selection balance will be dominated by mutations and survival will fall catastrophically. This is precisely the pattern observed by Charlesworth (1990).
The Bacterium Limit
For a different limit, let us constrain total reproduction, so that, for example, the total lifetime reproduction is fixed. Now assume that there are both beneficial and deleterious mutations affecting survival and fertility. Because of the age pattern of the selection coefficients, mutations with beneficial effect on early fertility will be most strongly selected. In other words, selection will act to increase early reproduction even at the cost of late reproduction. As long as a supply of some mutations that can increase early reproduction exists, the mortality schedule will be compressed toward earlier ages, leading to a collapse into a one-age-class life cycle. This is what I call the bacterium limit.
Shortcomings of the Classical Theory
Although it is certainly true that we can observe both salmon and bacteria
and thus the equilibria described by these limits are observable, most examples that interest us are not described by these limits. Yet these limits are the only equilibrium states possible under the specific assumptions stated, and this fact is rarely discussed. Clearly, theoretical analyses that yield different patterns must make other assumptions. That is the subject of the next section.
Other Equilibria
I now discuss several models that yield ESS patterns or mutation-selection equilibria that depart from the salmon type of mortality pattern, yielding patterns of the kind suggested by Carey et al. (1992).
Tradeoffs: One View
Abrams and Ludwig (1995) have presented an elegant analysis of an ESS model in which the life history is described by the vector z = (µ,m). They assume that there is a tradeoff at each age between a component of mortality at that age a(x) and fertility at that age. Specifically,
The tradeoff is contained in the assumption that fertility is an increasing function of a(x); thus, fertility only increases at the expense of increased mortality. To find the ESS, they maximize reproductive value (equivalent to maximizing r). They then present results of ESS trajectories of m(x) as a function of age x, given different functional relationships between fertility and a(x). Their paper focuses on the conditions under which µ(x) is or is not of Gompertz form. Here I will point to a different feature of their results. In all the results they present, there is a non-zero trajectory of values of a(x); in some cases a(x)→ a constant as x increases; in others a(x) increases with increasing x. Notice that Equation 4 implies, in these respective cases, that m(x) → a constant as x increases: or m(x) increases with age. Thus in their model there is no prediction of declining reproduction with age, which is surely a correlate of increasing age and/or increasing mortality in most cases. This result is not surprising when we note that they do not include mutation.
Tradeoffs: Another View
Charlesworth (1990) uses a tradeoff model that is similar in spirit to that of Abrams and Ludwig (1995), except that in his model there is no accumulative effect of mortality. He does, however, explicitly include mutation. His model
measures the tradeoff at each age x by a reproductive-effort phenotype e(x), and the level of fertility at each age is scaled to a phenotypic value e(x), so that
The parameter k is fixed and measures the convexity of the tradeoff. He says (p. 528), ''there is directional selection on [a(x)] . . . . There is assumed to be a net negative effect on the means of the [a(x)] values, consistent with the assumption of directional selection." On the other hand, he takes e(x) to be under optimizing selection.
Although this model contains considerably more detail, it is still governed by the sensitivity of classical demography. In agreement with my discussion of the salmon limit, Charlesworth finds in every case that there is a catastrophic onset of high mortality at some age. The age of onset is determined by the mutation rate and other parameters of the model.
Positive Pleiotropy
Curtsinger (1995 and personal communication) has argued that the existence of an equilibrium that displays a high mortality plateau at later ages may be due to positive pleiotropy between mutations affecting early and late ages. This assumption gets past the salmon limit by adducing a positive selection pressure (due to early-age effects) on mutations with pleiotropic beneficial late-age effects. In essence, a catastrophic mortality decline is averted because of the accumulation of mutations that "hitch-hike" on a positive effect of selection early in life.
Variable Environments
A different explanation for the evolution of mortality rates is found in the analysis of life-history evolution in the common situation when vital rates depend on a randomly varying external environment. Tuljapurkar and Boe (1993) examined selection in a environment that affects the age-specific probability of successful reproduction. They model the timing of fertility in two different ways. The first of these is the classical approach in which we specify the age pattern of fertility and examine the impact of shifting the entire schedule of fertility to later ages; the second approach uses the demographic notion of parity progression: individuals make transitions from maturity to states where they have reproduced once, twice, thrice, etc. They assume that a random environment affects the probability of a successful parity transition, so that in severe environments reproduction is very difficult, whereas in favorable environments reproductive success is high.
In the presence of random variation, the relative fitness of phenotypes is
measured by a stochastic growth rate a. The value of a is determined by two factors—the growth rate corresponding to the average vital rates and the impact of variability, which is modulated by the generation time. These factors are summarized in an approximate expansion
Here r is the Lotka growth rate for the time-averaged vital rates, Si,j is the derivative of r with respect to vital rate (i, j), and σij,kl is the covariance between vital rates (i, j) and (k, 1). Therefore fitness depends on the generation length and the age pattern of variability in fertility and mortality.
Results from both formulations of the stochastic model show that phenotypic combinations that differ with respect to the age pattern of fertility can be equally "fit" in a range of stochastic environments. It follows that stochastic selection can produce a range of equally fit phenotypes. This paper concludes that phenotypic polymorphism for the length of reproductive life can be readily maintained by temporally varying selective regimes.
The practical consequence of such polymorphism will be that mortality will not be observed to fall catastrophically but rather will show some kind of plateau at late ages.
Size-Structured Models
An important class of biologically useful models has sensitivity properties that are always very different from the sensitivity properties that underlie age-structured demography. This class of models is based on size and physical growth rate. These models define fitness as do age-based models, but they enforce a correlation between mortality and fertility, because there is usually a positive value to age delays that allow the organism to grow to larger size. Such models have been analyzed by Caswell (1985) and Tuljapurkar and Boe (1993).
In a typical size-structured model, the size s of an individual depends on its age x via a physical growth function,
and mortality µ(s) and fertility m(s) depend on size. The Lotka equation of classical demography is replaced by a size-structured analog,
where
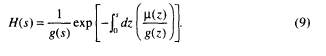
In typical biological situations the physical growth rate g(s) starts at some high value when the organism is at its minimum (birth) size and then decreases until a maximum size is reached. In consequence, [1/g(s)] is an increasing function of size. In Equation 8, then, the exponential factor in H(s) decreases with size s, whereas [1/ g(s)] increases with size. The result is that the function H first increases and then decreases with size, typically displaying a maximum at some non-zero size. Hence increases in fertility will have progressively greater positive effect until the organism reaches some size s*, beyond which fertility will have progressively smaller effect. The sensitivity to mortality first decreases with size to some minimum value and then increases with size.
These selective pressures on mortality and fertility show a dramatically different qualitative pattern as compared with classical age-structured models. Therefore in size-structured models, different patterns in the timing ("early" versus "late") of reproduction can lead to equivalent fitness, just as in models with temporally varying vital rates. In other words, we have here another mechanism for the existence of equilibrium mortality patterns that are not salmon-like.
Directions
The preceding sections suggest the elements of a research program that should yield substantially improved insight into the evolution of equilibrium patterns of life-history phenotypes. I will discuss these below and conclude with some suggestions for work on the analysis of empirical data.
Mutation-Selection Equilibria
It should be clear by now that models must incorporate mutation explicitly if they are to provide unambiguous predictions. The work of Charlesworth (1990) shows how this can be done, at least for some models. An important line of research is the embedding of different dynamical and ESS models in a mutations-election framework. Such models include models of tradeoffs between different components of the life-history phenotype, models of temporally varying selection, and models of size-structured dynamics.
The assumptions of the mutational dynamics need to be explored carefully, with a clear statement of assumptions. In principle, one can classify all mutations by their age pattern of effects on fertility and mortality. Given such a classification, a mutational variance-covariance matrix will describe any particular assumed pattern of mutational events. It is highly desirable to use such a general framework so that the results of different assumptions can be usefully compared. A careful analysis of the literature on mutations, especially the extensive body of work on fitness-related mutations in Drosophila, should help in this regard.
Tradeoffs in Life History
There is growing experimental and theoretical interest in the nature of tradeoffs. Abrams and Ludwig (1995), for example, use a different kind of tradeoff than does Charlesworth (1990), even though there are similarities. It would be useful here to classify tradeoffs in terms of covariances between life-history components. As with mutations, this would provide a systematic framework for comparisons between theoretical studies. Here, too, a careful assessment of the empirical data on plants and animals would be worthwhile.
Temporally Varying Environments
Models of temporal variation predict stable polymorphisms among a range of life-history phenotypes. It would be valuable to extend this theory to a model for quantitative traits using the methods of quantitative genetics and to examine the nature of equilibrium phenotypic distributions that would be predicted by such models.
Size-Structured Models
These models have been relatively little explored in the context of life-history evolution, although considerable work has been done on their application to the modeling of population dynamics. The study of such models is promising because they express ontogenetic correlations between fertility and mortality and may yield new insights into the determinants of evolutionary equilibrium phenotypes. These models, too, need to be extended to incorporate quantitative genetics.
Strong Selection
The quantitative theory of mutation-selection dynamics is based on the assumption of weak selection, under which the demography of the population is always close to equilibrium. It is well known that demographic characters strongly influence dynamics when the population is not in demographic equilibrium. Therefore, it would be very interesting to extend this theory to incorporate the interaction between selection and demographic disequilibrium. Such a theory should reveal similarities with the theory of temporally varying selection, because the latter also deals with demographic disequilibrium.
Empirical Issues
The work of Gaillard et al. (1994) shows that it is possible and necessary to examine field data on populations using careful longitudinal methods where possible. While demographers have the relative luxury of conducting new surveys
with more covariates and higher resolutions, ecologists often do not. Demographers could help ecologists by examining the issues that confront the latter when examining field data. In particular, work is needed on the effect of age/size and time resolutions on estimates of mortality, and on practical assessment of senescent patterns (when does senescence occur?). Analyses of comparative data also must to be done with great care and pose interesting statistical questions.
A different direction in comparative analysis is suggested by the work of Sibley and Ahlquist (1990) on bird phylogeny. Using a massive application of DNA-DNA hybridization, they constructed a new phylogeny of birds. Along with the phylogenies, they summarize information on demographic differences between birds. With the increasing accumulation of molecular data leading to phylogenies in many other plants and animals, there is a mine of information on the evolutionary development of demographic differences. This would be a valuable place to look for estimates on the rate at which demographic characters diverge during evolution. Such estimates would add to a broader and more accurate perspective on the evolution of mortality and fertility in humans.
Acknowledgments
I thank the Morrison Institute for Population and Resource Studies, Marc Feldman, and Jean Doble at Stanford University; the National Institutes of Health for support from HD 16640 and HD 32124; the National Science Foundation for support from DEB 9420153; and Carl Boe, Jim Curtsinger, Ken Wachter, Jim Vaupel, Daniel Promislow, Jim Carey, Mike Rose, and Peter Abrams for useful discussions.
References
Abrams, P., and D. Ludwig 1995 Optimality theory, Gompertz' Law, and the disposable soma theory of senescence. Evolution 49:1055-1066.
Carey, J., P. Liedo, D. Orozco, and J. Vaupel 1992 Slowing down of mortality rates at older ages in large Medfly cohorts. Science 258:457-463.
Caswell, H. 1985 The evolutionary demography of clonal reproduction. Pp. 187-224 in J.B.C. Jackson, L.W. Buss, and R.E. Cook, eds., Population and Evolution of Clonal Organisms. New Haven. CT: Yale University Press.
Charlesworth, B. 1990 Optimization models, quantitative genetics, and mutation. Evolution 44:520-538.
Curtsinger, J.W. 1995 Density, mortality, and the narrow view. Genetica 96:187-189.
Curtsinger, J.W., H. Fukui, D. Townsend, and J.W. Vaupel. 1992 Demography of genotypes: Failure of the limited life span paradigm in Drosophila melanogaster. Science 258:461-463.
Curtsinger, J.W., H. Fukui, A. Khazacli, L. Xiu, and S. Pletcher 1994 Rates of mortality in populations of Caenorhabditis elegans. Science 266:826.
Eshel, I., and M.W. Feldman 1982 On the evolutionary genetic stability of the sex-ratio. Theoretical Population Biology 21:430-439.
Gaillard, J-M., D. Allaine, D. Pontier, N.G. Yoccoz, and D. Promislow 1994 Senescence in natural populations of mammals. Evolution 48: 509-516.
Hamilton, W.D. 1966 The moulding of senescence by natural selection. Journal of Theoretical Biology 12:1245.
Lande, R. 1982 A quantitative genetic theory of life history evolution. Ecology 63(3):607-615.
Liberman, U., and M.W. Feldman 1986 Modifiers of mutation rate: A general reduction principle. Theoretical Population Biology 30:125-142.
Medawar, P.B. 1952 An Unsolved Problem of Biology. London: H.K. Lewis.
Mukai, T., S.I. Chigusa, L.E. Mettler, and J.F. Crow 1972 Mutation rate and dominance of genes affecting viability in Drosophila melanogaster. Genetics 72:335-355.
Orzack, S., and S. Tuljapurkar 1989 Population dynamics in variable environments VII. The demography and evolution of iteroparity. American Naturalist 133:901-923.
Sibley, C., and J.E. Ahlquist 1990 Phylogeny and Classification of Birds: A Study in Molecular Evolution. New Haven, CT: Yale University Press.
Tuljapurkar, S., and C. Boe 1993 No Senescence Before Its Time: Life History and Mortality. Paper presented at the annual meeting of the Population Association of America.
Williams, G.C. 1957 Pleiotropy, natural selection, and the evolution of senescence. Evolution 11:398-411.













