Applying the Model to the Biomedical and Behavioral Science Workforce
In this workforce analysis, each individual is classified as being in one of three possible states:
- Employed in the biomedical or behavioral workforce
- Employed, but in the nonbiomedical or nonbehavioral workforce
- Not employed8
Multi-state life tables are used to model the flows and the distribution of the workforce among these states.
The basic model used to generate projections of the workforce was a standard demographic model in which the future workforce in period t+1 (WFt+1) was defined as the current (or base) workforce in period t (WFt) plus gross inflows experienced between period t and period t+1(INFt) minus comparable gross outflows (OUTt):
Gross inflows between periods t and t+1 include new entrants to the workforce (NEt), mobility from other fields (MOBINt), immigration from abroad (IMMt), and mobility from outside the workforce (WINt). Gross outflows between periods t and t+1 include deaths (Dt), retirements (Rt), mobility to other fields (MOBOUTt), emigration to other countries (EMIt), and those who leave the workforce for reasons other than death or retirement (WOUTt).9
Because satisfactory data were not available, IMMt and EMIt were omitted from the model. Although it is possible that these omissions offset each other, the panel believes, on balance, that they produce an understatement of NEt immigration; hence the model probably understates the rates of growth and the sizes of the workforces.10 WINt and WOUTt are also not included.
|
8 |
"Not employed" includes respondents who report they are either not employed and looking for work (i.e., unemployed) or not employed and not looking for work (i.e., retired, disabled, etc.). |
|
9 |
In the model that is estimated below, neither WINt nor WOUTt were included, although they should be if the model is to be used for projections |
|
10 |
See Appendix A for a more detailed examination of the zero immigration assumption. |
To approximate likelihoods or rates, the model generally expresses these flows as fractions of some relevant stock variable (e.g., the workforce).11 For example, among the outflows the likelihood of a member of the workforce dying (or death rate (dt)) was defined as the ratio of Dt to WFt. Comparable definitions were used for retirement rates (rt) and rates of mobility to other fields (moboutt).12 Only one inflow variable—mobility from other fields (mobint)—was expressed as a likelihood or transition rate. The stock used to deflate this inflow was the workforce of scientists and engineers in other fields (NONt) (e.g., nonbiomedical or nonbehavioral). New entrants (NEt) was treated as an endogenous variable, determined by the model, and was not deflated by a stock variable.
Given the assumptions about immigration and emigration, and given the transformations of numbers to rates, the workforce model can be summarized by the following equation:
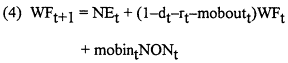
An important issue for determining training needs is the number of new entrants that will be needed to support the workforce (i.e., to replace those who leave and to provide for adequate workforce growth). Equation (4) can be transformed to solve for this number. Solving for NEt, the equation becomes
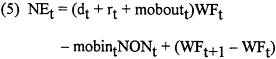
The model assumes that the rates summarized in equation (4) (i.e., dt, rt, mobint, and moboutt) remain constant.13
The model presented above shows the calculation of the number of new entrants under the assumption that there is only one cohort, or, equivalently, that the entire population is the same age. In actual application, in a population consisting of a number of cohorts, NEt is calculated for each cohort and summed to get new entrants for the entire system.14


