3
The Gravity Field as a Tool For Science
In the chapters following this one we address specific fields of research that we believe will particularly benefit from a satellite gravity mission. In this chapter, we mention some of the ways in which gravity field data are vital to the basic infrastructure of science. The gravity field is an essential part of the reference frame used for locating points on the Earth. The gravity equipotential surface, called the "geoid," is essentially equivalent to the "mean sea level" to which elevations on land are referred and the shape that the ocean surface would have if there were no currents flowing. The direction of gravity determines the directions of "horizontal" and ''vertical" and anomalies in the direction ("deflections of the vertical") affect the location of points on land by classical astronomic surveying. Gravity anomalies also perturb the orbits of Earth satellites and accurate gravity field models are required to correctly locate the position of an orbiter above the Earth. The limiting factor in the accuracy of some remotely sensed data is the uncertainty in the orbit produced by uncertainty in the gravity field. For example, synthetic-aperture-radar interferometry would be enhanced if the spacecraft's orbit could be computed with an across-track accuracy of a few centimeters; satellite altimetry would have improved accuracy if orbits could be computed with a radial error under 30 mm. In this chapter we discuss some of the ways in which accurate gravity-field information is a vital part of the Earth reference frame and the value a satellite mission would have in the calibration and validation of existing data from gravity-field surveys.
REFERENCE FRAME (1): THE FOUNDATION FOR MEASURING THE CHANGING EARTH
The gravity field has conventionally played a critical role in the definition of reference frames that provide the basis for measurement of periodic and stochastic motions in the Earth's atmosphere, hydrosphere, lithosphere, and deep interior. Indeed, the establishment of precise geodetic reference frames is necessary to quantify the dynamic Earth system. The global gravity field is useful as the fundamental reference for two reasons: (a) the conformance of mean sea level to a (nearly) equipotential surface allowed a height reference system based on the geoid to be established worldwide before the advent of satellite-based positioning systems; and (b) the only directions that could be defined globally were the directions of plumblines, which are perpendicular to the equipotential surface. With the advent of spaced-based measurements of positions that use range or range-rate determinations (and are thus independent of the angle relative to the direction of gravity), both of these reference-frame issues have become moot to some degree. It is now possible to position points geometrically without any direct reference to the gravity field. However, there is still a need to realize a coordinate system through some means, and the gravity field is a natural basis. Moreover, many countries would like to have a geoid model that is sufficiently accurate to be combined with satellite positioning to
give direct estimates of elevations above sea level, without traditional leveling surveys.
To define an instantaneous coordinate system for the Earth, six parameters are needed (assuming that scale is not a serious issue with the measurement system): three translations and three rotations. Nearly all measurement systems derive their orientation from the rotation axis of the Earth or a suitably averaged measure of this axis. However, the rotation axis of the Earth moves by several meters every year with respect to the crust of the Earth due to atmospheric, oceanic and, to a lesser extent, solid-Earth dynamical motions. In practice, the current definitions of the orientations of coordinate systems are based on the minimization of the difference in orientation between coordinates at different times.
For some measurement systems based on monitoring of extraterrestrial sources such as quasars, the same applies to translations (i.e., the system is not sensitive to translations of the coordinate system because the observed objects are so distant that the frame can be arbitrarily translated between measurements). However, systems that make measurements of Earth-orbiting bodies cannot be freely translated because the bodies are orbiting around the center of mass of the Earth. For these measurement systems, the gravity field plays a critical role in the definition of the coordinate system. Of particular significance in this regard is that these types of systems can make absolute measurements of the changes in heights of points independently of the orientation of the coordinate system. Thus the gravity field provides the center of the coordinate system for making measurements of phenomena such as post-glacial rebound. Of concern is the possible motion of the center of mass of the Earth with respect to the center of figure, but these motions (expected to be <10 mm) are themselves geophysical signals. In a fully consistent analysis of measurements to Earth-orbiting satellites, the coordinates of the site and changes in the first-degree harmonic terms of the gravity field should be estimated in the same solution. These gravity-field coefficients can be estimated equivalently as translations of the coordinate system with time. In this case, the measurement is of changes of the center of figure relative to the center of mass.
It is clear that a major limitation in detecting subtle but important changes in the Earth, particularly those that arise from coupled interaction of discrete parts of the geosystem, is the accuracy of the absolute reference frame. Establishing even more accurate reference coordinate systems will be required in future efforts to characterize the Earth quantitatively as a complex system.
REFERENCE FRAME (2): THE GEOID, FLUID CIRCULATION, AND SATELLITE ALTIMETRY
As stated in the Introduction, the "gravity" experienced on the rotating Earth combines the effects of attraction and rotation. If the fluids of the atmosphere and oceans were to cease their motions and come to rest in a state of hydrostatic equilibrium upon the (uniformly rotating) solid Earth, then surfaces of constant pressure within the fluids would conform to equipotential surfaces of the gravity field. In that condition, the interface between the oceans and the atmosphere would lie on a particular equipotential surface called the "geoid." Since the geoid is defined as an equipotential of gravity, it can be extended through areas on land occupied by rock; it is not restricted to the oceans only. The shape of the geoid is approximately an ellipsoid. A reference ellipsoidal shape is adopted for the Earth, and "geoid anomalies" are defined as displacements of the geoid above or below the ellipsoid; these have root-mean-square amplitudes of about 30 m. (This mean ellipsoid differs from the hydrostatic figure by 29 m rms.) The geoid defines the ''mean sea level" to which heights on land have been classically referred, as discussed above.
Since the fluids in the atmosphere and oceans are in motion with respect to the solid Earth, the actual position of the sea surface is vertically displaced from the geoid through a dynamic equilibrium involving the fluid motions. These departures are on the order of 1-2 m and are referred to as dynamic heights. Through the techniques of satellite altimetry, one can measure the shape of the ocean surface with respect to the ellipsoid (that is, the combined effects of the geoid plus the dynamic displacement) with an accuracy currently approaching 40-50 mm (Fu et al., 1994). The current limit on accuracy is the ability to model the orbital height of the altimeter satellite above the ellipsoid; the distance between the altimeter and the ocean surface has a precision of 20-30 mm, and its absolute accuracy depends on corrections for delays in the atmosphere, which are known or can be modeled to a few centimeters. Thus, satellite altimetry measures the sum of the geoid anomalies plus the dynamics of fluid circulation with an accuracy much better than is needed to study either one; however, it cannot separate the two effects.
The trade-off between spatial and temporal resolution discussed in Chapter 2 applies to all satellite remote-sensing missions, including satellite altimetry. Most satellite altimeters are operated in "exact repeat" orbits, which sacrifice spatial resolution to achieve temporal resolution. For example, the NASA/Centre Nationale d'Etudes Spatiales' TOPEX/Poseidon spacecraft measures the sea-surface height every 10 days along a pattern of ground tracks spaced 315 km apart at the equator. This allows oceanographers to study the time variations in sea-surface height, which are caused by variations in the ocean circulation. The absolute circulation cannot be studied without independent knowledge of the geoid. In Chapter 4 we describe the science that could be done by combining a dedicated satellite gravity mission with a satellite altimeter sea-height mission.
Two satellite altimeters have operated in "geodetic" orbits in which the sea-surface elevation is measured only once along a densely-spaced network of ground tracks. Over an 18-month period in 1985-1986 the U.S. Navy's Geosat surveyed the ocean height with a track spacing of approximately 5 km at the equator, whereas in an 11-month period in 1994-1995, the European Space Agency's European Remote-Sensing Satellite-1 (ERS-1) surveyed the ocean height with a track spacing of approximately 8 km at the equator. These data have been combined to produce a map of the variation of gravity over the oceans (Smith and Sandwell, 1995a; Sandwell and Smith, 1997); however, this map is not a correct characterization of gravity because of errors and oceanographic dynamic effects (Smith and Sandwell, 1995b). Marks (1996) found root-mean-square differences of 3 to 5 mGal between the Smith-Sandwell gravity field and the best available marine gravity surveys, with coherency only at wavelengths exceeding 20 km or so. This level of resolution (about 90% of the total signal) is sufficient to allow reconnaissance of ocean-floor tectonic features, but it is not as accurate as could be achieved with state-of-the-art marine (Bell and Watts, 1986) or airborne (NRC, 1995) gravimetry.
DATA CALIBRATION AND VERIFICATION: GIVING OLD DATA NEW VALUE
Conventional gravity surveys on land, at sea, and in the air are made with gravimeters, which yield only relative values and so must be calibrated by "known" values to yield complete information. In many cases this has been done inaccurately, or the "known" values have been in error. Furthermore, when surveys are contributed to data banks, the documentation about calibration and reference frames (including the standard ellipsoidal gravity model to which anomalies are referred) is frequently not supplied. When one attempts a global synthesis of the various data in data banks, a peculiar patchwork quilt emerges, with significant discrepancies at the borders between countries and land surveys. Errors in marine surveys are particularly large, as evidenced by the discrepancies at their crossings (Wessel and Watts, 1988). The relative changes in gravity measured by all these surveys over short horizontal distances (less than a few hundred kilometers) are potentially very accurate—much more accurate than a satellite mission could achieve—so one would like to be able to tie these surveys together into a seamless regional or global synthesis.
A satellite gravity mission would provide spatially (nearly) uniform coverage and error distribution, and it would allow correct calibration of archival survey data, adding enormous value to existing data. As the resolving power of the satellite data increases, so would the statistical reliability of the calibration. An important calibration of gravity survey data could be made with a satellite mission that has a resolution of a few hundred kilometers and a precision of 1 mGal.
The calibration problem is particularly severe for marine data. Marine gravimeters are calibrated when the ship is in port, and recent investigations of the accuracy of these data suggest that incorrect port calibrations are a major source of error (Wessel and Watts, 1988; Smith and Sandwell, 1995c). A typical situation is shown in Figure 3.1, where a sequence of shipboard gravity measurements is plotted against the distance the ship traveled between ports (bottom panel). This example is a 1985 cruise of the R/V Conrad between two ports on the South China Sea. For comparison, the gravity anomalies estimated from satellite altimetry by Smith and Sandwell (1995a) are also shown (bottom panel, dotted). The difference between the two profiles (top panel) shows a linear trend starting out around 42 mGal and decreasing by more than 1 mGal per day of the cruise. Shipboard gravimeters do not drift this rapidly; the difference is most easily explained by supposing that the shipboard data were calibrated to one wrong value in the port of origin and a different wrong value in the port of arrival, producing the apparent drift. (Superimposed on this linear drift are short-wavelength differences. These are expected, due to a variety of effects: real short-wavelength signals that can be measured by the ship-
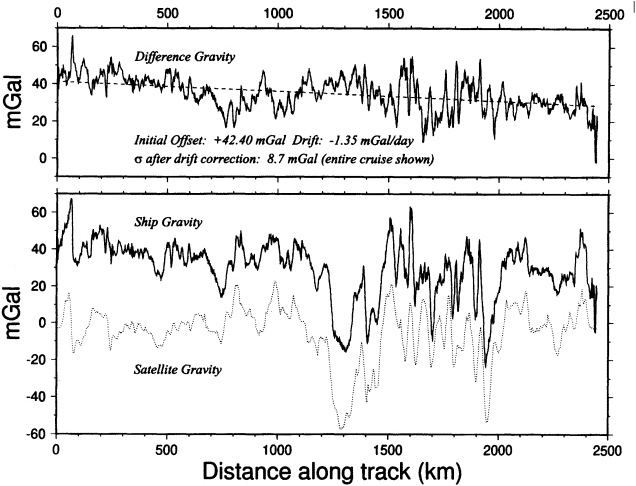
FIGURE 3.1 Gravity anomaly versus distance traveled for a ship survey (bottom panel, solid line) and gravity anomaly estimated from satellite altimetry (bottom panel, dashed line) for comparison. Top panel: the differences between the two appear to show a linear trend, probably due to errors in calibrating the ship instrument to correct values in port. Figure from Smith and Sandwell (1995c).
board gravimeter but not by a satellite; errors in the shipboard data due primarily to navigational errors in the Eötvös correction [Wessel and Watts, 1988]; and errors in the satellite data due to the dynamic ocean topography.)
Calibration errors as large as those shown in Figure 3.1 are detectable—but not correctable—either through examination of errors at crossing ship tracks (Wessel and Watts, 1988) or through comparison with gravity anomalies estimated from satellite altimetry, as shown here. Wessel and Watts (1988) estimated corrections for the mean level and apparent drift of marine survey data by minimizing the errors at crossing ship tracks. This left the global mean value of their data set after correction undetermined, since any constant could then be added to all the marine surveys without adding a crossing error; they found their global mean differed from other gravity fields by 9 mGal. Their technique would also leave wavelengths longer than the typical distance between port calls poorly determined. Although Figure 3.1 seems to suggest it, one should not try to fix the marine data simply by adjusting them to a gravity field derived from satellite altimetry, because that field has errors caused by assuming that the sea-surface height determined by the altimeter is the geoid height One ultimately would like to use the correctly calibrated marine gravity data to make a gravimetric geoid that can be compared with the altimeter-derived sea
surface to study the oceans. Use of the satellite data shown in Figure 3.1 to correct the shipboard data would not yield a geoid measurement that is independent of altimetry. Therefore, only a satellite gravity mission, such as investigated in this report, can adequately calibrate and validate the existing marine gravity database.
CONCLUSIONS
Satellite gravity measurements are useful for complementing and supporting other types of measurements. All four mission scenarios considered in this report offer significant improvements in measuring the static gravity field, which is vital in a variety of fundamental ways. These include:
-
Determination of the reference frame for defining position coordinates;
-
Calculation of orbits for other remote sensing applications (e.g., altimetry, synthetic-aperture-radar interferometry);
-
Determination of the geoid as the hydrostatic reference level to which absolute ocean circulation is referred (this is discussed further in Chapter 4); and
-
Verification and calibration of regional and shorter-scale terrestrial, marine, and airborne gravity-survey data.






