4
Ocean Dynamics and Heat Flux
STATIC FIELD
The primary direct benefit of an improved static geoid for ocean circulation studies is in the determination, in conjunction with precise-satellite altimeter measurements, of the geostrophic surface currents. These, in turn, can become the basis of calculations of such quantities as near-surface advective heat transport, can be assimilated into general circulation models (GCMs), and can be used with in situ data in inverse calculations of mass, heat, salt, and other transports at intermediate and deep levels. The importance of determining the deep ocean circulation derives from its role in regulating the Earth's climate on decadal and longer time scales (Box 4.1). It is therefore fundamentally important to the understanding and prediction of future climate change that the dynamical and thermodynamical processes of the ocean be studied and modeled. With the advent of satellite systems, we are now able to obtain nearly synoptic global measurements of key variables such as surface temperature, sea level, and wind stress. Satellite altimetry measures sea level, which is a parameter for both ocean currents and heat storage. As is discussed below, a precise gravity model is necessary to obtain full benefit from altimetry in determining the mean surface circulation.
The surface geostrophic velocity is proportional to the slope of the dynamic topography, which is the departure of the sea-surface elevation (measured by altimetry) from the static marine geoid. (Assuming that the geoid is static, a change in the sea-surface elevation equals a change in the dynamic topography, so the altimeter data are widely used to study temporal oceanic variability on all scales.) The geostrophic calculation will be valid where the uncertainty of the marine geoid is negligible compared to the magnitude of the undulations of the mean dynamic topography. As shown below, the latter can be estimated with dynamic heights derived from historical oceanographic-atlas data, such as that of Levitus et al. (1994) and Levitus and Boyer (1994), or from a state-of-the-art numerical ocean general circulation model, such as the Parallel Ocean Circulation Model (POCM) described by Semtner and Chervin (1992) and Stammer et al. (1996). Figure 4.1 indicates that this condition is satisfied to about degree 20-25 (1600-2000 km wavelength) with the EGM96 geoid errors. The state of the art of gravity modeling and existing satellite tracking is not likely to offer significant reductions in geoid error to improve oceanographic calculations at shorter wavelengths. In contrast, the satellite gravity missions will offer major improvement to degree 100 or greater (~400 km and shorter wavelength), with the exception of the GPS scenario, which will not provide significant improvement for oceanographic purposes.
The classical method for computing dynamic topography is to integrate the specific volume of sea water vertically to obtain the steric height, or vertical separation between isobaric surfaces. It is generally assumed that the slopes of deep isobaric surfaces are small, so that the variation of the steric height of the sea surface relative to a deep surface nearly represents
|
Box 4.1 The Ocean's Role In Global Change The ocean influences climate change on seasonal, interannual, and longer time scales in a variety of important ways. Half of the solar radiation reaching the Earth's surface is first absorbed by the ocean (Peixoto and Oort, 1992). The ocean stores or transports this heat before it is eventually released to the atmosphere through evaporation and longwave radiation, providing the major source of energy for atmospheric motions and thus for the Earth's climate (NRC, 1994). Surface currents influence the exchange of heat across the air-sea interface and thus indirectly influence how the oceans regulate climate change. The moderation of the northern European climate by the warm waters carried in the Gulf Stream and North Atlantic Current is a well known example. Conversely, a southward shift in the flow axis of the North Atlantic is believed to have been responsible for cooling events in the geologic past. Changes in the deep circulation caused by warming in the polar latitudes can also affect the primary productivity of the oceans by changing the area and intensity of upwelling of water from deeper layers (IPPC, 1996). This would have profound impacts on fish species production—marine mammals and sea birds, in turn, would be affected as centers of food production shift Finally, the El Niño-Southern Oscillation (ENSO), which occurs when warming in the eastern and central tropical Pacific Ocean becomes coupled with a seesaw in atmospheric mass, is the most significant source of interannual variability in weather and climate (IPCC, 1996). ENSO events, which occur every 3 to 10 years, have far-reaching climatic and economic consequences. For example, it has been estimated that improved forecasts of ENSO events could lead to savings in agricultural production that exceed $100 million per year in the United Stares alone (Subcommittee on Global Change Research, 1997). |
the variation of the sea surface relative to the geoid. When the deep surface also has a slope, which it generally does, then that slope must be added to the steric estimate for the surface in order to obtain the absolute dynamic topography. In this context, we refer to the barotropic component of the pressure field as that which is the same at all levels. Determining a reference-level pressure field, or barotropic term, is a long-standing problem in dynamical oceanography. The World Ocean Circulation Experiment (WOCE) is producing a global, but still very sparse, network of conventional transoceanic sections and measured deep ocean currents. Efforts are under way to use observations to constrain models of ocean circulation. However, because of the limited array of observations in the deep ocean and the lack of direct control of the circulation by the atmosphere, our knowledge of deep ocean pressure and circulation will retain significant uncertainty.
The question is whether such a calculation will be as good an estimate for the surface dynamic height as that obtained from a gravity mission coupled with satellite altimetry. Put another way, will a gravity mission offer substantially new information about the ocean given what we already know? As shown below, the answer is "yes" for spatial scales ranging from 300 to 3000 km. The observed sea-surface elevation is the sum of the geoid and the ocean dynamic height signals. While the problem is usually viewed as the ocean being the unknown, it is equally valid to state that a geoid can be estimated with an ocean model and an altimeter (Ganachaud et al., 1997). At present, it seems that our knowledge of the ocean provides a better estimate of the geoid than vice versa.Figure 4.2 shows the differences between an ocean model and a mean surface determined by altimetry and the JGM3 gravity model. Biases as large as 20-30 cm over large expanses are clearly spurious in the geoid and not the model, particularly the large >50 cm anomaly near Indonesia, because otherwise they would imply vigorous circulation features that are known to be absent from the real ocean.1 A spaceborne estimate of dynamic height can be used as a reference from which the pressure field and velocity at all depths can be determined from the steric calculations. Ganachaud et al. (1997) considered
|
1 |
The JGM3 gravity model (Tapley et al., 1996b) used by Rapp et al. (1996) in the analysis shown in Figure 4.2 is a predecessor of the EGM96 model discussed throughout this report. EGM96 differs from JGM3 over the oceans in that marine gravity anomalies estimated from altimetric data were included in EGM96. These additional data cause EGM96 to partially absorb dynamic topography signals into the EGM96 geoid at degrees larger than 70 (the maximum degree included in JGM3). It is necessary to have a precise geoid model obtained independently from altimeter measurements to obtain a better measure of the ocean circulation. An investigation similar to that of Rapp et al. (1996), but using the EGM96 gravity model is under way and the results are expected to be somewhat different (R. Rapp, personal communication). |
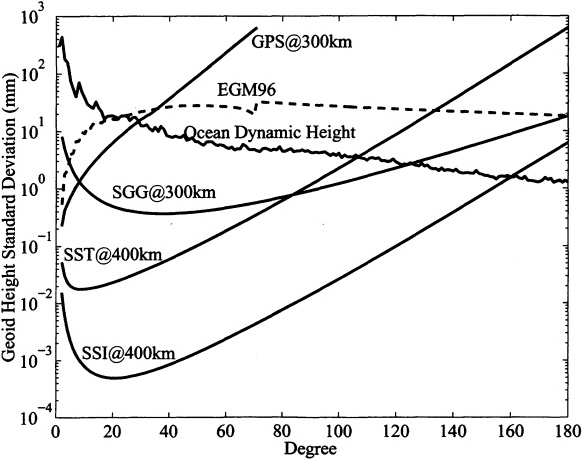
FIGURE 4.1 Geoid height and mission error spectra from Figs. 2.3-2.6 based on 90-day missions (see Chapter 2), plotted along with the degree spectrum of mean ocean surface dynamic height derived from the Parallel Ocean Circulation Model, POCM-4B, (Stammer et al., 1996). The degree variances were based on an orthonormal expansion (Rapp et al., 1996) to degree 20 and spherical harmonic expansion for degree 21 and higher (Courtesy of R. Rapp, Ohio State University). The EGM96 errors exceed the oceanographic signal higher than about degree 20-25. All missions except GPS will yield significant improvement in the static marine geoid.
this problem very rigorously using the accuracy of heat fluxes derived from inverse methods, and concluded that the JGM3 model coupled with altimetry did not reduce the uncertainty of the heat flux estimates, but that a more precise geoid could reduce uncertainties by as much as a factor of two in large data-sparse regions, such as the Antarctic Circumpolar Current (ACC) and portions of the Pacific. Such calculations were based on box-inverse methods set up such that the unknown quantities were computed at the same locations where high quality hydrographic data had been collected, densely along track, with large gaps between cruise profiles. Minster and Legrand (1996) argue that errors will be larger when the estimates are computed in the large gaps between cruises, and that the technique chosen by Ganachaud et al. (1997) must make a single barotropic correction at all depths between each station pair, rather than allow a vertical profile of velocity corrections (which introduces a non-linearity in the problem). While they also find small reduction in total heat and mass transport errors, they argue that the primary benefit from a gravity mission will be improved estimates of upper-ocean baroclinic transports rather than the reference velocity and barotropic terms.
Hasselmann and Giering (1996) suggest that data assimilation with a coupled ocean-atmosphere general
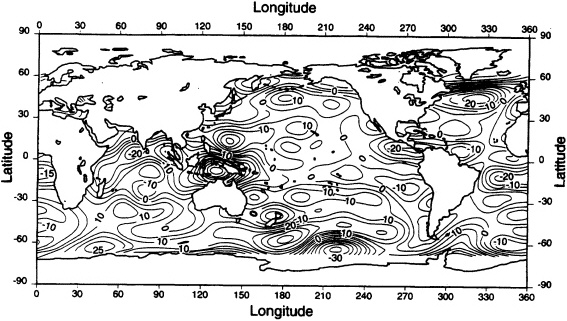
FIGURE 4.2 Difference in cm between the dynamic topography derived from TOPEX/Poseidon and JGM3 geoid model and a numerical general circulation model (from Rapp et al., 1996). Note the large discrepancies, particularly around Indonesia, which are the result of geoid model errors.
circulation model (GCM) is a preferred approach to the box inverse-closure methods employed by Ganachaud et al. (1997). Indeed, we can expect that various GCM, assimilation, and inverse methods and data sets will continue to improve and reduce the uncertainty of the mean circulation estimates and deliver high-resolution gridded analyses. A major difficulty at present, however, is understanding the uncertainties of GCM simulations, which impedes our ability to assess the relative improvement to be gained from a gravity mission.
Another important source of error is the contemporaneousness of measurements (Ganachaud et al., 1997). Oceanographic data collected over several decades to estimate a mean sea surface do not represent the same state of the ocean, in the presence of significant interannual to interdecadal variability, as a few years of satellite altimeter data. Likewise, higher frequency ocean variability can cause estimates of steady-state properties from individual temperature and salinity hydrographic sections to be uncertain by tens of percent (Wunsch, 1996). These uncertainties must be carried through inverse calculations as error sources. Satellite gravimetry with simultaneous altimetry provides a significant advantage by providing a snapshot of the state of the surface dynamic topography. This will then serve as a datum for all co-registered altimeter data obtained before and after a precise gravity mission from which the absolute as well as time-varying surface geostrophic flow can be computed.
To further evaluate the potential payoff for a gravity mission, it is useful to examine the scales over which we are likely to obtain important new information. Since we are dealing with two measurement systems—the altimeter to measure sea level and the gravity mission to derive the geoid—both must have errors smaller than the static ocean signal we wish to measure. Ideally, we would like each error to be at least an order of magnitude smaller than the mean dynamic topography signal. That is generally the case for the altimeter, except for the longest resolution lengths. If the two errors are of the same order, we cannot distinguish them and the errors are compounded as the root sum square. If one is an order of magnitude smaller than the other, it is effectively eliminated as an error source. Thus, another practical criterion for geoid-slope accuracy is that it be an order of magnitude better than the satellite-altimeter accuracy and thus be eliminated as an error source over the range of spatial scales of interest.
An estimated mean-slope error for altimetry is plotted versus separation distance as a line in Figure 4.3. This assumes that a 10-mm uncertainty in the dif-
ference between two mean height measurements is attainable by altimeter systems in the near future, taking into account tropospheric, ionospheric, tidal, wave-height, orbit-error, and other corrections. Figure 4.3 also shows the gravity-anomaly uncertainty for EGM962 and for 400-km-altitude 90-day missions of the SGG, SST, and SSI concepts. The right-hand axis gives the equivalent surface-slope accuracy (1 mm/km is equivalent to 10-6 = 1 mGal/g). The EGM96 error exceeds the altimeter error at horizontal resolutions shorter than about 3000 km by 1 to 2 orders of magnitude. With the advent of any of the gravity missions, the situation reverses and the gravity error becomes insignificant for a range of resolutions of importance to oceanography. The geoid-error curves for SGG, SST, or SSI missions indicate they will provide at least an order of magnitude lower contribution than altimetry to the total error budget for the estimation of geostrophic currents on spatial scales greater than ~400 km; the SST and SSI missions offer additional orders of magnitude improvement over SGG. At shorter scales, the SGG, SST, and SSI geoid-slope errors increase rapidly, crossing the altimeter-slope error curve at resolutions of 200-300 km; SGG and SSI provide the best small-scale accuracy. The payoff for the static ocean problem appears to be in the range of about 300-3000 km where the gravity error is dominant without a gravity mission and becomes insignificant with a gravity mission. Uncertainties in inverse calculations are of the same order as altimeter errors (Ganachaud et al., 1997). As noted above, GCM uncertainties have not been quantified, but they are not likely to be smaller than those of inverse calculations or altimetry. Consequently, in this 300-3000 km scale range, the gravity mission offers substantially better geoid information than can be inferred from altimetry and an ocean model. The improved geoid data could therefore be used to improve the ocean model.
Ocean geostrophic currents are dependent on surface slope, so the ability to resolve currents accurately will be limited by slope error. As indicated in Figure 4.3, this will require ~10-9 slope accuracy on basin-wide current (denoted BASIN) scales >1000 km. The slope resolution required for the 500-1000 km [width] scales of the ACC and 50-100 km scales of typical Western Boundary Currents (WBC) are likewise shown. The SGG, SST, and SSI gravity-mission concepts will allow BASIN and ACC scales to be resolved accurately. At the short WBC scales, the gravity uncertainties will be near the same order as the dynamic height slope, which may limit the accuracy of WBC estimates. It may turn out that airborne gravimetry has advantages in regions such as this because of its ability to resolve smaller scales. On the other hand, our gain of knowledge from the satellite gravity mission will be greater for basin scales and regions where there are few conventional data, such as the Antarctic Circumpolar Current.
Eliminating the gravity model as a significant source of surface-slope uncertainty over these spatial resolutions allows a number of issues to be addressed. The dynamic-topography surface determined by altimeter and gravity measurements represents the sum of the barotropic and steric height terms, and from this the total surface geostrophic current can be calculated. The regions where the barotropic component is strong but difficult to obtain will benefit significantly. The recirculation cells in the western subtropical gyres are presently poorly defined because they are significantly barotropic (Marchese and Gordon, 1996). In the western Atlantic, these circulations have transport volumes 2 or 3 times that of the Florida Current. The seasonal and interannual variability of these recirculation cells influences the large-scale heat transport and climate variability of the North Atlantic. Such recirculations exist in the North Pacific Kuroshio Current, the Agulhas Current, and possibly the weaker Brazil Current of the South Atlantic. The Antarctic Circumpolar Current is estimated to be about 30% barotropic (A. Gordon, personal communication). This current tends to appear in several narrow parallel filaments about 50 km wide, rather than as a broad flow. The gravity missions considered here will not resolve the individual filaments but will provide constraints for the transport sum across these filaments over 300-km and larger widths.
As noted above, time changes in the geostrophic circulation can be studied by altimetry without the benefit of an accurate geoid. However, both the mean and variable components are essential for heat and freshwater budget calculations. Budgets of the upper ocean mixed layer are balanced by the net flux of heat and water across the air-sea interface. Estimates of these fluxes have large errors and are important climatological variables. Divergences of surface temperature and salinity are important terms in these balances. Thus, accurate determination of surface currents is critical to closing both the heat and freshwater budgets
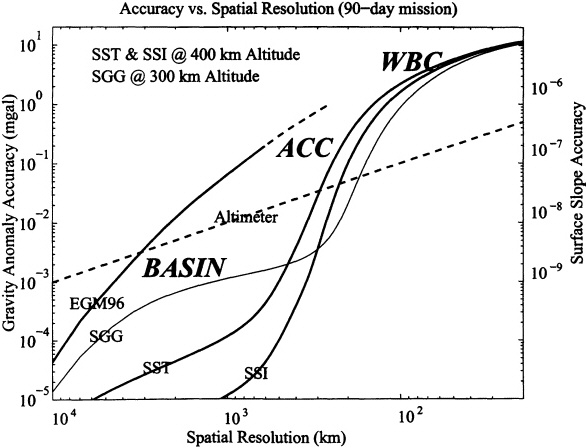
FIGURE 4.3 Errors versus spatial resolution for the SGG 300-km mission, the SST and SSI 400-km missions, and the EGM96 gravity model (see Chapter 2). The surface-slope scale is shown on the right-hand axis and the approximate slope magnitude and spatial scales of basin-wide currents (BASIN), the Antarctic Circumpolar Current (ACC) and Western Boundary Currents (WBC) are indicated. The dashed line indicates the slope error versus separation distance assuming a 10-mm uncertainty in altimeter height differences. The payoff for the static ocean problem appears to be in the range of about 300 to 3000 km where the gravity error is dominant without a gravity mission and becomes insignificant with a gravity mission.
of the coupled ocean-atmosphere system. For example, an uncertainty in the net surface flux of less than 10 Wm-2 is desirable for climate studies. Sea-surface-temperature anomalies in the mid-latitude North Pacific have significant climatological variations on interannual to decadal time scales that may be related to changes in advection. Typical sea-surface-temperature gradients are of the order of 10° C per 1000 km. Assuming a 50m-deep mixed layer, the implied uncertainty in the surface current requires a slope error equivalent to about 0.05-mGal gravity error at around 40 degrees latitude (see Chapter 1). In the tropics, the uncertainty will need to be an order of magnitude smaller for similar temperature gradients. It can be seen from Figure 4.3 that the altimeter and various gravity-mission uncertainties at 300-1000 km resolution will be smaller in either case. Thus we can expect to calculate the advective terms in the heat budget of the mixed layer to better than 10 Wm-2 with the proposed gravity missions.
TIME-DEPENDENT MEASUREMENTS
Most of what is known about the ocean occurs in the upper 500 meters. Time-dependent gravity measurements have the potential to provide a global estimate of
processes that occur deeper in the water column. For example, gravity measurements could revolutionize ocean circulation studies in at least two ways. The first is that they will allow a reasonably direct way of estimating bottom pressure variations, and thus variations in oceanic mass and deep ocean currents, from space. (Currently, oceanographers rely on indirect integrative constraints, such as those based on 14C tracer measurements [Broecker and Peng, 1982]. Such tracer measurements are limited in that they cannot resolve changes in ocean circulation but indicate the time it takes for a water mass to move along an unknown trajectory.) The second is that, when combined with altimetry from a mission such as TOPEX/Poseidon, gravity measurements will allow the separation of steric changes in sea level associated with changes in density from nonsteric changes. Thus the combination of gravity and altimetry places a powerful constraint on models of ocean circulation. At the end of this section we discuss the important issue of the accuracy with which different geophysical effects may be separated.
The Earth's gravity field is mostly determined by the density distribution within the solid Earth. The total mass of the ocean, for example, is only about 0.02% of the mass of the solid Earth. However, because the ocean is far more mobile than the solid Earth, it provides significant contributions to time-dependent variations in gravity (see Figure 4.4 for the annual variation). As a result, observations of time-dependent gravity can provide information about changes in the total vertically-integrated mass in oceanic water columns. Even in the presence of horizontal mass and pressure and surface topography differences that propel ocean currents, the ocean can be treated theoretically as being hydrostatic in the vertical direction. This assumption is valid at spatial scales greater than 10 km because vertical accelerations on these scales are small compared with gravity. Because the ocean is very nearly hydrostatic, variations in gravity are directly related to time-varying bottom pressure. Satellite gravity observations function, in effect, as a global network of bottom pressure gauges providing estimates of pressure changes over spatial scales of a few hundred kilometers. The accuracy of these measurements increases with increasing spatial and temporal scales, the former because of the smaller uncertainties in the satellite-gravity measurements at larger scales, and the latter because of the availability of multiple samples. Improvement in the sensitivity of the measurements at longer periods, as well as the research community's interest in seasonal and longer time scales suggests that a multi-year mission is desirable.
Bottom Pressure and Mass
To illustrate the accuracy in bottom pressure that could be achieved with a gravity mission, we consider the annual cycle, which is of particular interest because of its high amplitude (<= 7.5 mbar, Tsimplis and Woodworth, 1994) and broad spatial scales. Figure 4.5 depicts estimates of the degree amplitudes of several annually-varying signals, including signals from the ocean, together with the uncertainties of the generic SGGE, SST, and SSI missions (these results are estimated as described in Appendix B, equation B5 for the degree variance of equivalent water thickness. The improvement in variance estimation in the 5-year data set is a result of improved sampling). The water thickness results can be converted to bottom pressure by noting that a 10 mm increase of water corresponds to a 1 mbar increase of pressure. For Figure 4.5 we assumed a 5-year mission length and a 400-km satellite altitude. The 5-year SGG case is labeled as SGGE in this figure. This figure shows that after 5 years of data, the degree amplitudes of the annually-varying ocean signal are larger than the uncertainties of SST at all degrees below 25 (corresponding to half-wavelengths larger than 800 km) and are larger than the uncertainties of SSI at degrees less than 40+ (corresponding to a 500-km half-wavelength). By contrast, the oceanic signal lies well below the SGGE error bars, even assuming a 5-year mission. Figure 4.6 shows that if the objective is to determine the annually-varying signal one year at a time, the SST and SSI uncertainties are still well below the oceanic signal at low degrees.
As described in Appendix B, however, a degree amplitude comparison does not do full justice to a satellite's ability to detect geographically fixed signals. Direct observations of the annual cycle of bottom pressure fall in the range of 0.5-5 mbar (Cartwright et al., 1987; Woodworth et al., 1996). The usefulness of the missions to detect geographically fixed signals can be better assessed using the results shown in Figures B.1-B.4 in Appendix B. Figure B.2 shows that with 5 years of data, the annual variation of bottom pressure can be determined over a square with a side of length 500 km with a precision of 0.1 mbar for SSI and of 1 and 3 mbar, respectively, for SST and SGGE. At longer (1000 km) scales, the detection limit for SSI approaches an astonishing 0.01 mbar, while the detection limit for SST is 0.1 mbar. The limit for SGGE remains above 1 mbar for squares of up to 2000 km. This result suggests that accurate determination of the annual cycle of bottom pressure may be difficult with SGGE.
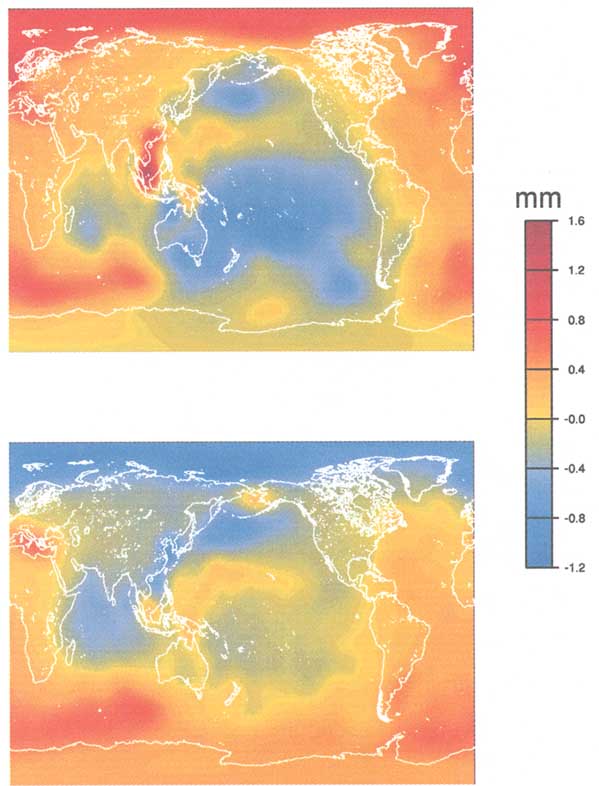
FIGURE 4.4 The annually-varying contributions to the geoid from oceanic variability, as estimated from output from NCAR runs of the Los Alamos POP ocean general circulation model. Top panel: the amplitude of cosine(ωt), where ω = 1 cycle/yr and t = 0 on January 1. Bottom panel: the amplitude of sine(ωt).
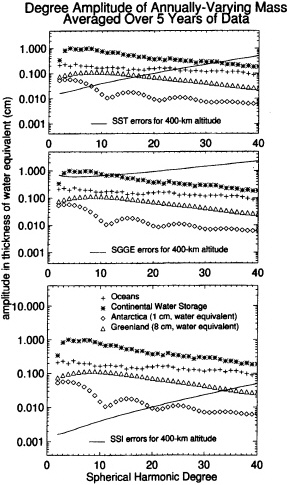
FIGURE 4.5 The degree amplitudes in mass, expressed as the thickness of a water layer, for the annually-varying terms (averaged over 5 years of data) from continental hydrology, oceanography, and changes in Antarctic and Greenland ice mass, computed as described in the text (see Appendix A; conversion to equivalent thickness of water is described in Appendix B). To estimate the Antarctic and Greenland contributions, we assumed annually-varying changes in thickness of 1 cm and 8 cm, respectively, for the two ice sheets, which are in reasonable agreement with the results of Bromwich et al. (1993, 1995).
Currently, less than 20 direct measurements of bottom pressure are available from in situ gauges. These are generally distributed at a few ''choke points," primarily in the Southern Ocean. Even at these locations current technology limits the periods detectable by the measurements to 12 months or less because of compression effects on sensor accuracy performance that result from the high pressure of the benthic environment (Woodworth et al., 1996). Thus, the current suite of in situ bottom pressure measurements represent a complementary data set that could provide "ground truth" for the time-dependent gravity data. Its use in this capacity, however, may be limited to deployments with sufficient spatial coverage.
Gravity data provide a direct estimate of the change of total mass within an oceanic basin or large sea. These data could open up a completely new set of applications of which we can suggest only a few possibilities. The semi-enclosed Arctic Ocean, for example, is subject to an enormous increase in freshwater input during summer due to continental runoff. The residence time of the freshwater along the continental shelves at the southern margins of the Arctic Ocean is likely to be a month or longer. The increase in mass could potentially raise the geoid by 15 mm. Gravity data could provide an important constraint on this increase, and thus on the residence time of the freshwater (see, for example, Aagaard and Carmack, 1989).
Another example is determining changes in the oceanic conveyor belt that supplies deep and bottom water to the major ocean basins. Deep geostrophic currents are proportional to the gradient of bottom pressure. Thus, gravity measurements provide the possibility of directly estimating changes in the poleward and equatorward transports in the lower limb of the conveyor. At this time, we can only put forward "back of the envelope" calculations in support of this statement. However, choosing scales from the North Atlantic, formation rates of North Atlantic Deep Water suggest basin-averaged meridional velocities of ~2 × 10-3 m/s. Integrated zonally across 4000 km, this meridional transport implies a pressure difference across the basin of approximately 1 mbar, corresponding to a surface slope of 2 × 10-9. The accuracy versus spatial resolution comparison in Figure 4.3 shows that the SST and SSI missions are sufficiently accurate to measure annual and secular variations in this transport if the variations are assumed to be 10% or greater of the mean transport.
Steric Changes
Another way in which gravity measurements can contribute to improved understanding of ocean circulation is through their complementary relationship to altimetry and in situ measurements of temperature and salinity. The difference between the observed sea level
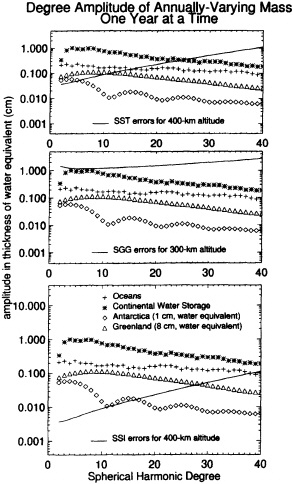
FIGURE 4.6 The degree amplitudes in mass, expressed as the thickness of a water layer, for the annually-varying terms (using 1 year of data) from continental hydrology, oceano-graphy, and changes in Antarctic and Greenland ice mass.
and the bottom pressure variations will equal the change in sea level due solely to changes in density (the steric effect). Figure 4.3 was introduced above to illustrate the improvement in the static gravity field. It also shows, however, that for spatial scales greater than 400 km all three missions (SGG, SST, and SSI) will improve the accuracy of bottom pressure variations to such an extent that determination of the time-dependent steric effect will be limited by the accuracy of altimetry rather than gravity. This improvement extends down to scales of 250 km for SSI.
Knowledge of bottom-pressure and steric variations would provide powerful constraints on models of ocean circulation and on efforts to improve model estimates through data assimilation. In data assimilation we use observations as a constraint on the evolving fields of an ocean model to provide an improved estimate of the true state of the ocean. Altimetry provides a particularly useful constraint because in many regions sea-level changes are dominated by steric changes. In the tropical Pacific, for example, changes in the depth of the thermocline have a correlation of greater than 80% with changes in sea level. In other regions, such as the recirculation region of the North Atlantic, however, nonsteric variations are large and poorly correlated with sea level. By combining altimetry with gravity data, we can estimate the steric variations more precisely and, thus, provide a tighter constraint on the ocean thermal field in regions with large nonsteric variations. The use of bottom pressure has received little attention so far because the existing data coverage is far too sparse to be useful for this purpose.
Accuracy
The accuracy estimates described in Chapter 2 and in Appendix B, and the degree amplitude comparison shown in Figures 4.5 and 4.6 describe the sensitivity of the generic satellite missions to surface-mass changes. They do not address the problem of separating the gravitational effects of different geophysical processes, however, which can be critical in determining how well a satellite gravity mission could constrain a specific process.
The problem for oceanographic applications is best understood by noting that the most effective way to use the gravity data for oceanography will probably be to sum together the spherical harmonic geoid coefficients to construct mass anomalies (equivalent to bottom pressure anomalies) averaged over discs of some chosen radius. A method for estimating the errors in the disc averages is described in the appendixes and in Chapter 2. Briefly, discs of larger radius are less affected by satellite errors, because they are less dependent on the high-angular-order (and more poorly known) geoid coefficients. The precision with which a disc mass can be determined from the satellite data is shown in Figures B. 1-B.4 as a function of spatial scale.
For determining the time-varying oceanographic gravity signal, the most serious source of contamina-
tion is likely to come from changes in the distribution of continental water (including snow and ice). This will probably be a negligible source of error in the open ocean, but could be potentially serious for determining changes in oceanic mass close to shore. For example, suppose the objective is to obtain bottom pressure estimates averaged over discs of radius 500 km covering the world's oceans. It is reasonable to expect that those estimates might be contaminated by the effects of continental water/snow/ice when the disc is centered within ~300 km of the shore (which would place about 15% of the disc's area over the continent); though the contamination could be more serious near continental areas that have considerable hydrological activity.
Contamination by atmospheric pressure fluctuations is not likely to cause problems for most oceanographic applications. The ocean's response to pressure is likely to be nearly that of the "inverted barometer," which means that for every millibar of pressure increase the ocean surface is depressed by 10 mm, so there is no net change in pressure below the surface of the ocean. The gravitational effects of atmospheric pressure are thus balanced by the effects of the ocean's response to that pressure, so that there is no net effect on the gravitational field. The ocean, in effect, removes that signal itself. The ocean's response will, of course, not exactly accord with the inverted barometer solution (see, for example, Wunsch and Stammer, 1997). Thus, there will be a residual effect on sea-floor pressure due to the combination of atmospheric pressure and oceanic response. But that is a real bottom pressure variation, contributing to bottom currents, and so is probably best left in the data for most applications. Thus, it would probably be best in most cases if atmospheric pressure data were not used to remove the geoid signal caused by atmospheric pressure over the ocean. In contrast, altimetry will still need to be corrected for atmospheric pressure variations. As a result, errors in atmospheric pressure will still enter the estimates of steric height obtained from combining altimetry and gravity.
CONCLUSIONS
-
SGG, SST, and SSI missions at 400-km altitude offer dramatic improvements in our knowledge of absolute dynamic topography and surface circulation from satellite altimetry. The most significant improvement will come at basin scales (~300-3000 km), effectively eliminating the geoid as an error source on these spatial scales. For phenomena with scales less than ~100 km, such as western boundary currents, gravity uncertainties (the error) will be on the same order as ocean dynamic height slopes (the signal). For features with intermediate length scales of 100-300 km, missions with the lowest orbits will offer the best improvement.
-
Interesting and detectable signals are expected for climate-related phenomena with seasonal to interannual time scales. For these phenomena a multi-year mission lifetime is required. This requirement gives priority to SST or SSI over an SGG-type mission.
-
Satellite measurements of time-dependent gravity provide global estimates of changes in sea-floor pressure averaged over spatial scales of a few hundred kilometers and larger. Results are likely to have reduced accuracy within a few hundred kilometers of shore, due to the gravitational effects of changes in water and snow on the continents. Contamination from other geophysical processes is apt to be minimal.
-
Studies suggest that gravity data will reduce the uncertainty in our knowledge of deep circulation, heat, and mass transport by a factor of two or more. Part of this reduction in uncertainty comes from an improvement in estimates of surface current. For example, the geostrophic advective terms in the mixed-layer heat budget would be resolvable to less than 10 Wm-2 uncertainty.
-
Studies in ocean regions with strong nonsteric fluctuations of sea level will benefit from knowledge gained from the static geoid. These include the recirculation cells in the western subtropical gyres of the western Atlantic, the Kuroshio Current in the North Pacific, the Agulhas Current in the southwest Atlantic, and the Antarctic Circumpolar Current.
-
In regions of strong nonsteric fluctuations in sea level, the combination of gravity and altimetry data will provide a much more powerful constraint on the ocean circulation than altimetry alone. Combining altimetry and gravity will allow separation of the time-dependent steric and nonsteric components of sea level. This separation will substantially increase the usefulness of sea level in testing ocean models and constraining ocean circulation through data assimilation.












