5
Solid Earth Processes
Accurate determination of the Earth's gravity field over a wide range of spatial scales is of fundamental importance for understanding the structure and dynamics of the solid Earth. Gravity is used in combination with topography at commensurate resolution to resolve the compositional, thermal, and mechanical structure of the deep crust and upper mantle, and to elucidate fundamental aspects of the plate tectonic process (shown schematically in Figure 5.1), such as the nature of ridges and trenches, the dynamics of mountain building, and the planform of mantle convection. Results of such analyses bear directly on attempts to understand the dramatic surface manifestation of tectonic forces, i.e., earthquakes and volcanism.
The requirements for measuring the static gravity field as it relates to understanding the solid Earth were summarized schematically in Figure 1.1 (bottom panel). Those requirements have been well established in numerous previous reports (NRC, 1979, 1982; NASA, 1987, 1991) and the literature (e.g., Nerem et al., 1995). Here we present a synopsis of those results, with updates as appropriate, especially with regard to the utility of various mission approaches in achieving objectives. In addition, in Chapter 3 we discussed the importance of using satellite gravity measurements to "tie down" observations from surface gravimetry that are poorly referenced, but of high resolution, and that have application in many studies of continental and seafloor tectonics.
In this chapter, we discuss applications that reflect fundamental processes that are consequences of the dynamic nature of the Earth; namely, mantle convection and plumes, post-glacial rebound, tectonic activity, and earthquakes. Note that gravity measurements used in applications to the fluid Earth are commonly expressed in terms of the geoid, whereas many solid-Earth applications traditionally use gravity anomalies. We follow this convention. Figure 5.2 shows an overlay of the expected gravity-anomaly recovery accuracy from the generic GPS, SGG, SST, and SSI missions on a schematic of measurement requirements. Three of the four missions (SGG, SSI, and SST) are significantly more accurate than the best current gravity model (EGM96) (Lemoine et al., 1996), permitting new insights on a number of phenomena at finer resolution. The GPS mission only yields marginal improvement and only at the longest wavelengths (resolution >1,000 km). From 500 to 10,000 km, the SSI mission would give the greatest sensitivity, followed by SST and then by SGG. This new measurement regime will enable a better understanding of mantle convection in the 200 to 1,000 km range and permit improved insights into the structure of continental roots and mountain building.
MANTLE CONVECTION AND PLUMES: UNDERSTANDING THE EARTH'S HEAT ENGINE
Most of the heat loss from the Earth occurs via mantle convection—the process by which the Earth loses the bulk of its internal heat and which drives the plate-tectonic cycle. The primary manifestations of plate tectonics—volcanism and faulting—occur along plate boundaries. Understanding plate tectonics and its physical consequences requires knowledge of the driving mechanism. Satellite gravity measurements
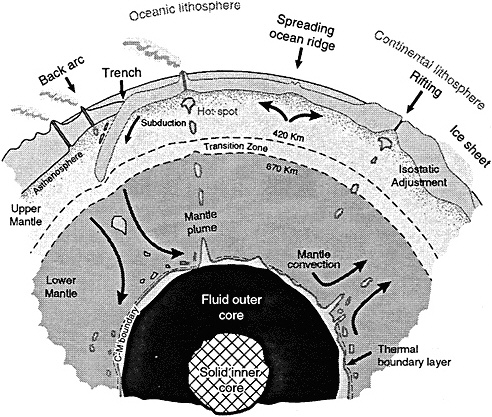
FIGURE 5.1 Schematic illustration showing internal structure and major dynamical processes associated with the solid Earth. Heat loss from the deep interior results in motion of mantle material via convection and mantle plumes. The manifestation of the Earth's internal dynamics is the interaction of surface plates at trenches and mid-ocean ridges in oceanic seafloor and rift zones and mountain belts in the continents. Isostatic adjustment of continental lithosphere associated with melting of major ice sheets results in slow vertical rebound indicative of mantle viscosity structure. Figure from ESA (1996).
achieve sufficient accuracy at long to intermediate wavelengths to constrain the nature of mantle convection. Relevant length scales span the range from the sizes of plates to the thickness of the Earth's convecting layer (Figure 5.2). Given the range of plate size and the possibility of convection at various scales—from small scale to whole mantle—spatial resolutions needed range approximately from 200 to 3,000 km.
Significant progress has been made in recent years in relating spatial variations in the gravity field to mantle convection (e.g., Hager and Richards, 1989; King and Masters, 1992; Forte et al., 1993; Phipps Morgan and Shearer, 1993; Ricard et al., 1993). While there is general agreement on the existence of an appreciable increase of viscosity with depth from the upper to the lower mantle, there is less agreement on the details of either the inferred viscosity structure or the predicted gravity field. The differences among models are largely the result of differences in assumptions of how to relate seismic velocity heterogeneity to density heterogeneity in the upper mantle. The question is whether the velocity variations result only from temperature variations, and can be directly interpreted as density variations, or whether there are compensating differences in composition, particularly under cratons, so that the seismic velocities could even have an inverse correlation with density.
Combined investigation of the changes in gravity and seismic velocity associated with continent-ocean and craton boundaries would provide a way to resolve this issue. Figure 5.3 shows a representative global model of seismic velocity heterogeneity at 200-km depth, expanded through degree and order 16 (Masters et al., 1996) and the global gravity field, expanded through degree and order 150 (Lemoine et al., 1996). The largest contrasts in seismic velocity are between shields and oceans (e.g., West African continental margin) or between shields and tectonically active

FIGURE 5.2 Measurement requirements for the Earth's static gravity field. Adapted from NASA (1991).
areas, such as the Canadian Shield and Western Cordillera. At this depth, in cold regions such as continental roots, the coupling between density heterogeneities and surface deformation is essentially isostatic, so that knowledge of density structure and gravity variations, rather than non-uniqueness in mantle flow models, are the limiting factors. Neither this seismic model nor the existing gravity field are sharp enough (~200 km resolution) to define precisely the geophysical transitions between geologic provinces. Seismologists are rapidly improving the spatial resolution of their models; if the improvement in the accuracy of the gravity field can keep pace, this type of investigation should be a frontier area of geodynamics in the next decade.
Other key questions in mantle dynamics concern the nature of mantle plumes, which are a major source of intraplate volcanism and enhanced heat flow. Gravity changes within plates that could be associated with mantle plumes can be as large as 10 mGal, but resolutions of approximately 1 mGal at the shorter wavelength limit down to ~10-2 mGal at the longer wavelength limit need to be obtained to characterize smaller, though important, variations in thermal structure and to distinguish between various models of mantle structure. For a mission flown at 400 km, the ~10-2 mGal accuracy level is met by SGG and SST for resolutions of 400 km and larger, and by SSI for resolutions of 300 km and larger. Separation of the longer-wavelength mantle structure effects from those caused by other phenomena will clearly be a challenge with current technology. However, the situation is more favorable for questions that require shorter wavelength measurements, such as the depths of origin of mantle plumes. To constrain plume depths it will be necessary to isolate the effects of dynamic upwelling from signals associated with lithospheric processes, which will require gravity resolution of approximately 1 mGal over length scales of order 100 km. As shown in Figure 2.13, three of the generic missions (SGG, SST, and SSI) at 400 km would provide 1-mGal-level measurements down to the necessary resolution levels of 100-200 km.
POST-GLACIAL REBOUND
During the last ice age, the extensive ice loads over Canada and Scandinavia caused deep depressions in the Earth's surface. Although this ice had mostly
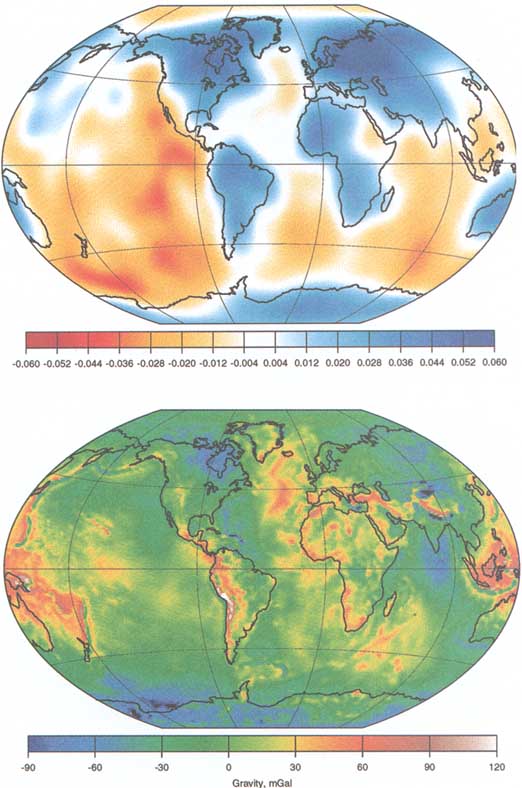
FIGURE 5.3 Top: shear wave velocity heterogeneity (dVs/Vs) at a depth of 200 km for global tomograhic model S16B30 (Masters et al., 1996). Fast areas are blue and slow areas are red. Bottom: free air gravity anomalies relative to the hydrostatic reference figure for the gravity model of Lemoine et al. (1996). Courtesy of B. Hager, MIT.
vanished by about 9,000 years ago, the depressions have not yet completely disappeared; they are partially filled by Hudson Bay and the Baltic Sea. The Earth's surface continues to rise as a result of horizontal inflow of mass from the surrounding regions, because over long periods of time, the Earth behaves more as a viscous fluid than as an elastic solid. This process of readjustment is referred to as post-glacial rebound. (The elastic response of the Earth to present-day changes in polar ice is not considered in this chapter, but is included in Chapter 7.)
A primary goal of post-glacial-rebound studies is to provide constraints on the viscosity profile of the mantle. The community that models post-glacial rebound, however, has yet to reach a consensus on the results, particularly on how much the viscosity of the lower mantle (i.e., at depths below 670 km) increases. Progress has been hampered by the difficulty of finding observational constraints that are both sensitive to lower-mantle viscosity and unaffected by other geophysical processes. For example, the 40-50 mGal depression in the Earth's static gravity field over northern Canada has sometimes been interpreted as a measure of incomplete post-glacial rebound, but it has also been argued to reflect mass anomalies related to large-scale convection in the mantle (see, for example, Cathles, 1975; Peltier et al., 1992; Forte and Mitrovica, 1996). Similarly, a secular drift in the position of the Earth's rotation axis, a non-tidal acceleration of the Earth's rotation rate, and secular changes in the lowest-order zonal spherical harmonic components of the Earth's gravity field (e.g., C20) have all been observed and could all be partly due to post-glacial rebound (Yoder et al., 1983; Rubincam, 1984; Yuen et al., 1982; Peltier and Jiang, 1996; Peltier, 1985). But there could also be important effects from other geophysical processes, including changes in polar ice mass (e.g., Sabadini et al., 1988; Mitrovica and Peltier, 1993; Trupin, 1993; James and Ivins, 1995) and the steady mass-redistribution caused by convective flow in the mantle (which could contribute to the secular drift of the rotation axis; see for example, Sabadini and Spada, 1995; Richards et al., 1995). (The effects of mantle convective flow on the secular terms in the gravity field are probably about two orders of magnitude smaller than the effects of post-glacial rebound [M. Richards, personal communication]. They are unlikely to be a significant source of error when using satellite gravity results to learn about the rebound process.) Crustal-uplift rates, as determined mainly from geological dating of raised beaches, are probably the least ambiguous data type in terms of their relative insensitivity to other processes and form the basic observational foundation of post-glacial-rebound studies. Still, it is difficult to unravel the competing effects of lower-mantle viscosity, upper-mantle viscosity, lithospheric thickness, and uncertainties in the time history and spatial distribution of the ice sheets, using this data set alone (see, for example, Lambeck et al., 1990; Mitrovica and Peltier, 1992; Han and Wahr, 1995).
There are other methods of inferring the Earth's viscosity profile from observational data. Most useful are attempts to explain the observed long wavelength geoid by modeling the Earth's response to internal mass loads (e.g., Richards and Hager, 1984; Ricard et al., 1993). The loads are estimated from seismic tomographic maps or tectonic models of the Earth, and the Earth's response to those loads depends on the viscosity contrast from one region of the Earth to another. These studies have their own characteristic set of difficulties and can only provide ratios of viscosities between regions, rather than absolute viscosity values. Nevertheless, they provide a useful complement to the post-glacial-rebound estimates. In fact, there has been recent progress in using both tomography and modeling techniques in a joint inversion (Forte and Mitrovica, 1996).
It is clear that post-glacial-rebound studies could benefit greatly from more unambiguous observational constraints. Measurements of the secular change in the gravity field using a dedicated gravity satellite could provide such constraints. The portion of the gravity signal relatable to the secular changes in the low-degree zonal components observed with satellite laser ranging to LAGEOS, for example are not, by themselves, sufficient to distinguish post-glacial rebound from other geophysical effects. More spherical harmonic coefficients, including a significant number of nonzonal terms, are needed and can only be obtained from a dedicated gravity mission.
The top and middle panels of Figure 5.4 show map views of the secular change in the geoid over North America as predicted by two versions of the model described in Appendix B. Both versions assume an upper-mantle viscosity of 1.0E21 Pa-sec and a lithospheric thickness of 120 km and use model ICE-3G of Tushingham and Peltier (1991) to represent the melting of the ice during the Pleistocene. The difference is that the lower-mantle viscosity is taken to be 10.E21 Pa-sec in the top panel and 50.E21 Pa-sec in the middle panel. The pattern of the geoid fluctuation depends largely on the ice-sheet model. Because the same model (ICE-3G) has been used in both cases, the patterns are similar, although the amplitudes are different The top panel predicts a rate of change as large as 2.3 mm/yr over the center of Hudson Bay, whereas the corresponding
amplitudes in the middle panel are about two-thirds that size (i.e., 1.5 mm/yr).
For satellite gravity measurements to be useful, they must be accurate and complete enough to be able to resolve differences between competing viscosity models and to allow separation of the post-glacial-rebound signal from the effects of other processes. In Figure 5.5, the degree amplitudes of the secular change in the geoid caused by the rebound beneath Canada (the effects of ICE-3G from Antarctica, Greenland, and Scandinavia are not included in these results) are compared with uncertainties for the SST, SSI, and SGGE generic missions described in Chapter 2. For these comparisons we have assumed that each mission length is 5 years. The short (<1 year) length of an SGG mission makes it impractical for studying post-glacial rebound or other secular processes, and the GPS mission has not been included, because its relatively poor performance at all but the very lowest degrees make it far less useful than the other missions for this application. All three missions shown in Figure 5.5 are assumed to orbit the Earth at 400-km altitude, which is likely to be the minimum altitude compatible with any long-lifetime mission.
The results for a lower-mantle viscosity of 10.E21 Pa-sec (Figure 5.5, plus symbols) are at or above the SST satellite errors for degrees below 28 (corresponding to half-wavelengths of 740 km and longer) and above the SSI errors at degrees below 40 (half-wavelengths longer than 500 km). This suggests that the post-glacial-rebound signal could readily be seen with the SST or SSI missions. The SGGE mission, however, has uncertainties much higher than the rebound effects for all but the very largest wavelengths (i.e., smallest degrees) and so would be far less useful for post-glacial rebound studies.
An SST or SSI mission could also provide data needed to resolve differences between models of lower-mantle viscosity and to separate the effects of post-glacial rebound from the effects of other processes, such as changes in ice sheets and in ground and surface water. Figure 5.5 shows the predicted degree amplitudes of the difference between results for 10.E21 and 50.E21 Pa-sec lower-mantle viscosities (triangle symbols). The degree amplitudes of the difference between the two lower-mantle-viscosity models lie above the SST uncertainty levels up to about degree 12 (half-wavelengths greater than about 1700 km) and above the SSI uncertainties up to degree 18 (half-wavelengths in excess of 1100 km). At higher degrees, the results for the two lower-mantle-viscosity values converge because the Earth's response at those shorter wavelengths does not penetrate into the lower mantle.
Satellite gravity measurements would be less effective for inferring the trade-off between upper-mantle viscosity and lithospheric thickness. Those parameters tend to have significant effects only at the higher degrees, where even the SST and SSI uncertainties begin to rise above the predicted signal. On the other hand, this means that uncertainties in those parameters would probably have little impact on estimates of lower-mantle viscosity derived from the satellite data.
It is possible that errors in the Pleistocene ice model could map into errors in the inferred lower-mantle viscosity. It is not clear how large these ice-load errors might be. Fortunately, only the large-scale components of the ice model are important for lower-mantle studies. Thus, the problem of separating ice-sheet and viscosity parameters is less of an issue for the interpretation of gravity data than it is for the interpretation of geological crustal uplift data, where short-wavelength terms in the load are more important.
The other issue is whether a satellite mission could differentiate between the effects of Canadian post-glacial rebound and the effects of other processes. A 5-year SST or SSI mission would be able easily to separate the Canadian rebound from the effects of any ongoing secular change in the volume of Greenland ice. This requires only that the effects of the rebound rise above the satellite uncertainties for values of l up to about l = 4 or 5 (the half-wavelength of an l = 4 spherical harmonic is 45°, which is about equal to the angular separation between Greenland and Hudson Bay). This criterion is satisfied by both SST and SSI (see Figure 5.5).
It is harder to assess the possible contamination from changes in surface water and groundwater over this region of Canada and from changes in the total water content of Hudson Bay. Seasonal effects would presumably average out over a 5-year mission. Longer-period effects could be partially absorbed into a viscosity estimate, if their spatial patterns are similar to the rebound pattern.
To estimate the hydrologic effects, we used five years (1987-1991) of monthly output from the global soil moisture/surface water model described in Chapter 6 and Appendix B. The geoid was computed for each month of output. Although the results are dominated by seasonal terms, there is also interannual variability that could leak into the secular solution, particularly since the solution is based on only five years of data.
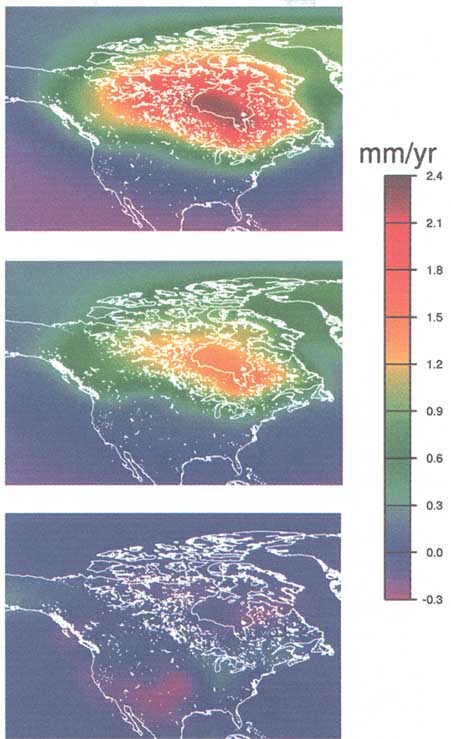
FIGURE 5.4 The secular geoid signal over North America due to post-glacial-rebound for two lower-mantle viscosity values: vlm = 10.E21 Pa-sec in the top panel, and = 50.E21 Pa-sec in the middle panel. In both cases the upper-mantle viscosity is l.E21 Pa-sec, the lithospheric thickness is 120 km, and ICE-3G is used as the Pleistocene ice load. The bottom panel shows the secular signal in the geoid due to changes in continental water storage during 1987-1991, as inferred from the soil moisture data described in the text. The amplitude of this hydrological signal can be as large as 0.2 mm/yr, which is about 10% of the rebound signal. But the spatial patterns are quite different, suggesting that the hydrology is not apt to have much of an impact on the solution for the rebound.
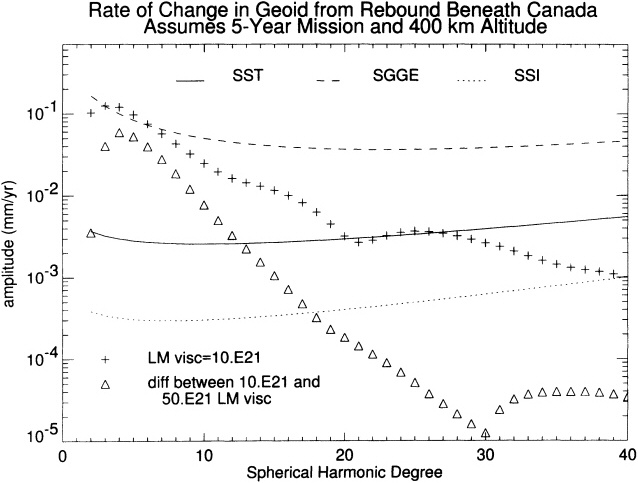
FIGURE 5.5 The degree amplitudes for post-glacial rebound in North America for a lower-mantle viscosity of 10.E21 Pa-sec and for the difference between results for viscosities of 10.E21 and 50.E21 Pa-sec, compared with degree variances from 3 generic missions.
To estimate that leakage, the geoid was fit with a linear function of time. The bottom panel of Figure 5.4 shows the portion of the hydrological signal over North America that would have affected post-glacial-rebound estimates from a 1987-1991 satellite gravity mission. The amplitude of the geoid perturbation from the hydrology in this region is about 0.2 mm/yr, only about 10% of the post-glacial-rebound amplitudes shown in the other panels of Figure 5.4. Because the hydrological and post-glacial-rebound contributions have different spatial patterns, the hydrological effects on the inferred rebound signal would be further reduced. For example, fitting the post-glacial-rebound geoid patterns from the top two panels in Figure 5.4 to the hydrological pattern shown on the bottom panel, we find that the hydrology perturbs the regression coefficient by 1% or less, which is far smaller than the 30-40% difference between the 10.E21 and 50.E21 Pa-sec lower-mantle-viscosity models.
The effect of a linear increase in the water mass of Hudson Bay is also likely to be small. Suppose, as a worst-case scenario, that Hudson Bay is rising, due to water inflow, at a rate of 3 mm/yr, which is probably a little more than twice the global estimate inferred from
tide-gauge data, after removing the estimated effects of thermal expansion (see Chapter 7). This would produce a secular geoid perturbation with an amplitude of about 0.07 mm/yr, centered over Hudson Bay. This is about 3% of the rebound signal shown in the top panels of Figure 5.4. The spatial pattern of the Hudson Bay geoid is similar to that of the rebound, but is of somewhat smaller scale. When the rebound signal is fit to this Hudson Bay geoid, the regression coefficient is slightly less than 0.01. This implies that an unmodeled 3 mm/yr increase in Hudson Bay would have about a 1% effect on the rebound signal inferred from satellite gravity, which in turn is far smaller than the effects of different viscosity models.
The implicit basis of this discussion has been largely a uniform linear rheology. The more accurate data from a gravity mission should be an important step toward inferring lateral heterogeneities and, possibly, non-linear effects in the rheology.
REGIONAL DEFORMATION AND STRUCTURE: THE SURFACE MANIFESTATION OF PLATE TECTONICS
Post-glacial rebound is mainly a transitory perturbation on a mantle with irregularities that are much larger, but less inferable because their causes are much more obscure in their spatial and temporal distribution than the geologically recent glaciation. The convection causing the irregularities is thus much more complex, entailing non-linear rheology, differentiation, and interaction with the thermal (lithosphere) and compositional (crust) boundary layers. Hence, the subsequent discussion is more qualitative and dependent on indications from other data types.
Despite decades of observations of the Earth's interior, the fundamental question of the thickness of the continents is still debated. Resolving the discrepancies between estimates of the depths of continental roots at length scales of 500-1,000 km requires gravity measurements at the mGal level (Figure 5.2), which would be feasible from all four generic mission types. On the regional scale, variations in the thermal and mechanical properties of the crust preserve the record of the history of tectonics. Gravity data, in conjunction with topography, have been applied in increasing detail and refinement to infer the tradeoffs between elastic and buoyant support of topography and the extent of buried loads. The thermal and mechanical structure of continental lithosphere is commonly studied by flexural analysis of a thin elastic plate that may contain surface and subsurface loads. The pertinent parameter is the effective elastic thickness, which is a measure of the mechanical competence of the lithospheric plate and can be directly related to its thermal structure (McNutt, 1984). In analyses of this genre, gravity and topography measurements provide the observational basis for the load estimation. The observed power spectral ratio of gravity to topography as a function of wave number (or wavelength) is compared to that predicted for an elastic plate with the observed loads. Figure 5.6a plots the correlation coefficient of Bouguer gravity and topography, termed the coherence, as a function of wavenumber for a model of an elastic plate of various effective elastic thicknesses assuming equal amounts of surface and subsurface loading. The basis of the estimation of elastic thickness using the coherence (Forsyth, 1985) is that at short wavelengths the lithosphere supports loads by its elastic strength and so gravity and topography are uncorrelated. In contrast, at long wavelengths a load deflects the lithosphere and produces a gravity anomaly indicative of the compensation of the load, so gravity and topography are correlated. The wavelength of the transition between coherent or correlated and incoherent or uncorrelated loads provides a measure of the effective elastic thickness.
The coherence approach to characterizing the thermomechanical structure of the continents is illustrated for the Australian lithosphere in Figure 5.6b, where the large (130-km) thickness estimate is consistent with that continent consisting largely of old, thermally cool craton (Zuber et al., 1989). However, smaller tectonic subregions of the continents display varying ages and thermal states and so in a regional sense thickness variations occur. In regions of dense gravimetry, such as Australia and North America (Bechtel et al., 1990), there has been a fairly complete mapping of lithospheric thicknesses on the regional scale. However, note in Figure 5.6a that for thick lithospheres the transition from high to low coherence occurs at long wavelengths so gravity and topography data with high geodetic integrity are required. In contrast, for thin lithospheres the transition occurs at short wavelengths so data with high spatial resolution is required. Also note that in addition to high quality gravity, topography at commensurate resolution is required. While some local areas have high enough quality topography and gravity data to have been studied in a systematic sense (e.g., McNutt et al., 1988; Bechtel et al., 1987; Lowry and Smith, 1994), there remains a need for detailed analysis of interesting tectonic regions, such as orogenic provinces, conti-
nental rift zones, and sedimentary basins. Mechanisms of support of surface and subsurface loads provided by the gravity and topography constrain models of continental evolution. To contribute further, properly referenced gravity should have a resolution that is at least comparable to the thicknesses of the structural layers, which may be as thin as 10-30 km; the latter range would not be obtainable with satellite gravity alone and are appropriate applications for high-resolution airborne gravimetry (Brozena, 1991; NRC, 1995).
Topography must be at the same resolution as gravity to be useful in geophysical studies. Current data resolution varies considerably. In well sampled areas such as North America, Europe, and Australia, the spatial resolution is higher than the resolution that can be expected from a new satellite gravity mission. But in parts of Asia, South America, and Africa, topographic coverage is poor. NASA's Shuttle Radar Topography Mission, which is scheduled to be launched on the space shuttle in 1999, will map land topography south of about 60° latitude at 30-m spatial resolution. Topography obtained from that mission will have a higher spatial resolution than that expected from an SST mission.
There are appreciable regions of interest where even moderate resolution is lacking, such as the Andes-Altiplano region, where recent studies have attempted to isolate the effects of plate subduction, magmatism, and erosion in controlling the style of mountain building (Isacks, 1988; Kono et al., 1989; Masek et al., 1994). On the regional scale, data gaps would best be filled in using measurements of the gravity field provided by airborne platforms (e.g., NRC, 1995). Detailed corrections to such gravity measurements to assure geodetic integrity will require accurate knowledge of spacecraft position provided by GPS, as well as a precise record of aircraft velocity. The recent availability of gravity data from former communist nations will help elucidate some interesting structures, such as the Himalayas and the Tibetan Plateau, particularly as related to the dynamics of the India-Eurasia collision zone and the mechanism of strain accumulation (Jin et al., 1994; Willet and Beaumont, 1994). Here, satellite data may help to put both the gravity and topographic observations on a unified datum through the calibration and rescue discussed in Chapter 3. The continuity of gravity data from continents into the oceans is also a matter of great need in addressing the structure of continental margins (e.g., Karner and Watts, 1982), and a satellite gravity mission would be helpful in tying land and marine surveys to a common datum. Passive margins are of great importance because they represent the transition of continental to oceanic lithosphere and they also contain sedimentary basins that hold the record of macroscale continental erosion. In addition, they are often the source of petroleum reserves of economic interest.
The seafloor produced at mid-ocean ridges has a thermal structure that reflects both the mechanical structure of the lithosphere and the coupling of the lithosphere to the convecting mantle below. Heat-flow measurements are often corrupted by local processes such as hydrothermal circulation (Sclater et al., 1980), so gravity measurements with regional-scale integrity can make a significant contribution to understanding the lithosphere structure from a thermal point of view as well as a compositional one. The basic characterization of mid-plate swells in the oceanic lithosphere on length scales of ~1,000 km has been accomplished from the altimetric geoid. At shorter wavelengths gravitational data have contributed greatly to understanding the evolution of the oceanic lithosphere in the seafloor spreading process. The recent release of Geosat Geodetic-Mission and European Remote Sensing Satellite (ERS-1) altimetry has helped greatly to provide high-quality, short-wavelength marine gravity (Sandwell and McAdoo, 1990; Sandwell, 1992; Smith and Sandwell, 1995a), so that now the limiting factor for detailed studies of oceanic structure in many areas is accurate, high resolution bathymetry. In these studies, attention is focused on processes such as rifting, subduction, and volcanism. One particular question to which globally referenced satellite gravity may contribute significantly is in resolving whether there exists a straightforward relationship between lithospheric age and plate thickness (Watts et al., 1980), as has been suggested by flexural analysis of trench and seamount loads (Calmant and Cazenave, 1987; Smith et al., 1989; Wessel, 1992; Smith and Sandwell, 1994) or whether there has been significant reheating of oceanic lithosphere to reset thermal age (McNutt, 1984) in areas affected by hot spots. A complete gravity data set from a satellite mission could be used to investigate the nature of the flexural strength of the lithosphere, the isostatic compensation of seamounts, and the role of thermal anomalies in the lithosphere associated with the south Pacific and other areas. Wavelength resolution of ~100 km and gravity measurement accuracy to ~3-4 mGals (for rifts) and 10 mGals (for subduction zones) are required; these requirements can be met by the SGG, SSI, and SST missions.
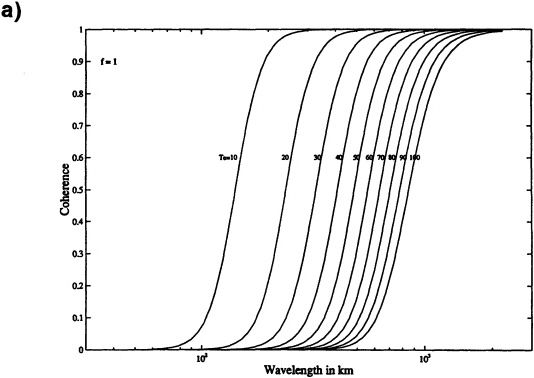
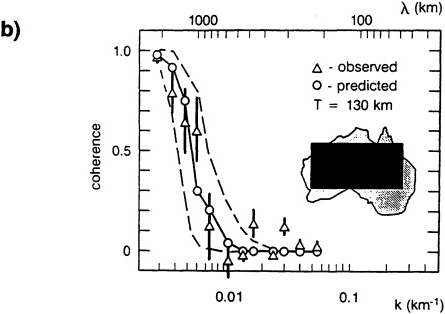
FIGURE 5.6 (a) Theoretical coherence, the correlation coefficient between Bouguer gravity and topography, for an elastic plate equally loaded from at the surface and bottom. The transition wavelength or wave number from high coherence to low coherence provides a measure of the elastic thickness of the lithospheric plate that can be related to the thermomechanical state of the lithosphere. Courtesy of Y. Jin.
(b) Observed coherence pattern for Australia indicating a thick elastic lithosphere. The black box on the Australia figure shows the region from which data for the coherence calculation was gathered. Figure from Zuber et al. (1989).
EARTHQUAKES
Earthquakes release in a few seconds the elastic strain energy accumulated over decades, centuries, or millennia. Most of the world's earthquakes occur near plate boundaries and result from strain associated with motions of a few centimeters per year. Earthquakes, occasionally quite large, occur much less often in plate interiors. The study of earthquakes and associated precursory and post-seismic phenomena is of great societal importance.
Seismology furnishes a means of locating earthquakes, imaging rupture surfaces, estimating energy release, and so on. GPS, along with tilt meters and strain meters, can monitor surface displacements and strains at instrumented points. SAR interferometry can furnish areal images of surface displacements. Such approaches represent the methods of choice for characterizing short-term Earth deformation. The contribution of a satellite gravity mission to these existing techniques would probably be limited to a volume-integrated measure of displacements of mass.
Mass displacements associated with earthquakes arise from surface deformation (Freund and Barnett, 1976; Savage, 1983) and internal densification (Singh, 1970; Jovanovitch et al., 1974). Models of these phenomena can be used to estimate the changes in the Earth's gravity field associated with an earthquake (Walsh and Rice, 1979; Savage, 1984). The details of the expected signal depend on the width and dip of the rupture surface and the slip on it. Since a satellite gravity mission would be largely insensitive to structures with wavelengths shorter than the orbital altitude, only those earthquakes with rupture surfaces extending over a few hundred kilometers will generate detectable signals. For the largest known earthquakes, such as the 1960 Chile and 1964 Alaska events, the expected signals are of order 0.3 mGal of gravity change or 3 cm of geoid change with wavelengths of a few hundred kilometers. Such signals would be near the limit of resolvability for even the most sensitive mission scenarios studied here. We thus conclude that the deformation accompanying interseismic and coseismic processes is more readily monitored from near the fault zone using measurements of surface gravity, strain, and displacement. The scales and rates of earthquake processes, and more so those of volcanic eruptions, is evidently too small for a significant increase in our understanding to be developed from the gravity field observed from orbiting satellites.
CONCLUSIONS
-
Satellite gravity measurements from four generic missions (SGG, SGGE, SSI, and SST) would constrain the nature of mantle convection on spatial scales of 200-1,000 km. An accuracy of ~10-2 mGal at resolutions larger than 300-400 km would suffice to characterize the variations in thermal structure that distinguish between various models of mantle structure. Observations with 1 mGal accuracy at length scales of 500-1,000 km would resolve discrepancies between estimates of the depths of continental roots and would distinguish between models of mantle flow. Gravity resolution of approximately 1 mGal over length scales of order ~120 km would help constrain the depths of origin of hotspot mantle plumes, which are a major source of intraplate volcanism and enhanced heat flow.
-
The medium- to long-wavelength effects of post-glacial rebound could be resolved at the 1% level by a 5-year SST or SSI mission at 400-km altitude. Measuring these effects is important for providing increased understanding of the Earth's interior, particularly the viscosity of the lower mantle. The SGGE mission is less useful because of its lower accuracy at long wavelengths. A multi-year mission is highly desirable for post-glacial rebound studies.
-
Recent availability of gravity data from former communist nations will help elucidate interesting structures in areas of active continental deformation, such as the Himalayas-Tibetan Plateau. Satellite data from any of the generic missions would permit these data to be put on a unified datum, which will be essential for understanding the subsurface structure and dynamics of these regions.
-
The best satellite missions for regional studies of ocean tectonics are SGG, SSI, and SST. For a 300-km mission, the SGG mission provides marginally better resolution over the SST mission for resolutions finer than 300 km. GPS-guided airborne gravimetry is ideal for obtaining regional high-resolution measurements.
-
Continuity of gravity measurements across the continent-ocean boundary is badly needed to address the structure of passive margins. All the generic gravity missions would provide information that would assist significantly in tying together oceanic and continental observations.












