1
Introduction
Scientific Overview
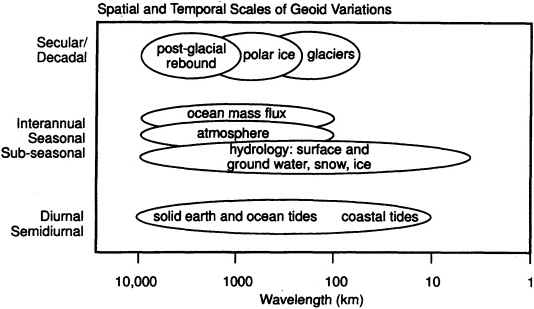
The Earth is a dynamic system—it has a fluid, mobile atmosphere and oceans, a continually changing distribution of ice, snow, and groundwater, a fluid core undergoing hydromagnetic motion, a mantle undergoing both thermal convection and rebound from glacial loading of the last ice age, and mobile tectonic plates. These processes affect the distribution of mass in the Earth and produce variations in the Earth's gravitational field on a variety of spatial and temporal scales (Figure 1.1). Highly accurate measurements of the Earth's gravity field made with appropriate spatial and temporal sampling can thus be used to better understand the processes that move mass within the Earth, and on and above its surface.
In this report the Committee on Earth Gravity from Space explores the scientific questions that could be addressed with a better global gravity field. Traditionally, the gravity field has been treated as essentially steady-state, or "static," over human lifetimes because over 99% of the departure of the field from a rotating fluid figure of the Earth's mass, mean radius, and moment-of-inertia is static in historic time. The static field is dominated by irregularities in the solid Earth caused by convective processes that deform the solid Earth on time scales of thousands to millions of years. Spaceborne gravity measurements have already led to dramatic advances in recent years in the understanding of the structure and dynamics of the core and mantle, the thermal and mechanical structure of the lithosphere, ocean circulation, and plate tectonics. The substantial improvements in the accuracy of static field measurements that would result from the satellite gravity missions we discuss in this report would allow geophysically important smaller-scale features to be resolved and, by improving the geodetic reference frame, would greatly enhance other types of satellite measurements as well.
Nevertheless, it is not in the improved measurement of the static field that we envision the most dramatic advances arising from the next generation of gravity satellites, but in the examination of the remaining 1% of the departure of the gravity field, which is caused by processes that vary on time scales ranging from hours to thousands of years. Temporal variations are caused by a variety of phenomena that redistribute mass, including tides raised by the Sun and Moon, and post-glacial rebound (i.e., creep in the mantle in response to the geologically recent removal of ice sheets) (Figure 1.2). The hydrosphere-oceans, lakes, rivers, groundwater—is the source of much of the irregular variations in the time-varying mass distribution from sub-daily (tides) to long-term (aquifer depletion). Variations of mass within the atmosphere are manifested as surface pressure and contribute significantly at seasonal and other time scales. The cryosphere—the part of the Earth's surface that is perennially frozen—also has seasonal and interannual variations, as well as a long-term secular effect. Particularly exciting is the potential to study sea level changes, post-glacial rebound, deep circulation of the
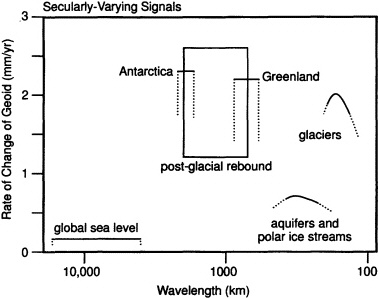
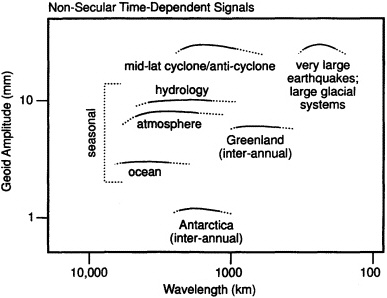
FIGURE 1.2 (Above) This figure indicates some of the expected sources of variability in the Earth's gravity field that would appear to vary linearly in time over a few years of observations. Each mechanism is represented in the figure by the amplitude of its contribution to the rate of change in the geoid (given on the y axis), and by the typical horizontal wavelengths that characterize its contribution to the geoid (the x-axis). For localized mass anomalies (e.g., aquifers, glaciers, etc.), we have chosen the approximate radius of the anomaly as the measure of the horizontal resolution. There can be a considerable spread in the geoid contributions within any one of the indicated categories. For example, there are many glacier systems around the globe, some that cause a notable secular change in the geoid and some that do not. The curve in the figure that represents the effects of glaciers is meant to indicate a crude upper bound of the likely effects of the different glacier systems. (Below) Similar to above figure, except that these are the sources of geoid variability that would not appear to vary linearly in time over a few years.
oceans, and changes in groundwater levels. Many of these have application to issues of importance to society like global change and the availability of natural resources.
The phenomena that produce static and temporally-varying gravity field signatures occur at spatial scales ranging from a few kilometers to tens of thousands of kilometers (Figures 1.1 and 1.2). At the longest spatial scales, large-scale processes such as sea-level change, mantle convection, and ocean and atmosphere circulation are important, whereas studies of lithospheric features (e.g., ridges, fracture zones, swells, trenches), ice-sheet flow and mass-balance, western boundary currents, and aquifers require resolutions of about 500 km or better. High resolutions, of course, require relatively low satellite orbits. On the other hand, determination of temporally varying phenomena improves as the time span of the measurements increases. Consequently, as we discuss further in this report, there are trade-offs to be evaluated, in selecting orbital parameters for a specific mission, that depend on the particular purposes and goals of that mission.
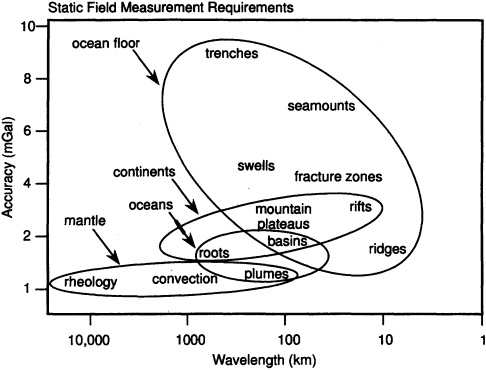
Throughout much of this report we consider gravity effects expressed as a spectrum with amplitudes as functions of wavelength, as in the previous paragraph and in Figures 1.1 and 1.2. However, the most significant influence on the magnitude of a variation in the gravity field is the causative mass. Figure 1.3 is a schematic representation of the masses that cause various features of the gravity field. This representation allows a rough comparison of magnitudes, which makes it evident that the static gravity field must be determined precisely in order to infer the much smaller time-varying effects.
In this report we identify the terrestrial mass variations that produce gravity signals usefully detectable from space and show how improved gravity-field data can be used to achieve a better understanding of a wide variety of earth-science processes. There is perhaps no other kind of experiment that can simultaneously advance the study of so many different levels of the Earth, from the asthenosphere through the atmosphere.
THE ATMOSPHERE AS A POTENTIAL SOURCE OF NOISE FOR TIME-DEPENDENT APPLICATIONS
A gravity satellite would determine the Earth's gravity field at regular time intervals. Because gravity is caused by mass, the satellite results would provide
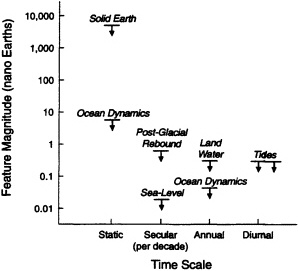
FIGURE 1.3 Estimates of the masses associated with deviations of the Earth's gravity field from a fluid equilibrium state. The unit of mass shown is the ''nano-Earth," 10-9 of the Earth's total mass, or approximately 6×1015 kg. The time variations shown represent the mass involved in a periodic (annual or diurnal) motion, or the mass which flows during a decade (secular motion). Note that time-varying gravity field signals are caused by mass flows which are 3 to 5 orders of magnitude smaller than the solid Earth sources of static field anomalies. Temporal variations at periods other than annual or daily are not shown. These generally involve even smaller masses, and are likely to have continuous frequency spectra difficult to schematize in this figure.
information on time-dependent changes in the Earth's mass distribution. However, inverting gravity data to calculate a mass distribution is an inherently nonunique process. It is impossible, using gravity data alone, to determine uniquely both the depth-dependence and the latitude- and longitude-dependence of a density anomaly.
Most of the non-secular variability in mass can be assumed to occur in a thin layer at the Earth's surface, consisting of the atmosphere, the oceans and, on the continents, the groundwater plus the water/snow/ice on the Earth's surface. This layer of variable mass is thin enough that gravity data could be used to determine unambiguously the change in mass, integrated vertically through that layer, as a function of latitude and longitude, but the vertical location of the mass anomalies cannot be inferred.
Over a continental region, for example, one could not distinguish between changes in the atmosphere and changes in the continental water-bearing layer. Whether the gravity data would be more useful for studying the atmosphere or the continental water would depend on which is better known from independent data. In most cases, it is the atmospheric mass that is better known. Pressure fields are accurate to about 0.1-0.3 mbar for seasonal periods, and perhaps 0.5 mbar at non-seasonal periods, which translates into about 1-3 mm equivalent water thickness for seasonal periods and to about 5 mm at non-seasonal periods. As will be apparent in later chapters, this level of inaccuracy would sometimes be the largest source of error in a hydrological or glaciological estimate. Except in a few cases, however, it is not likely to seriously limit the scientific value of those estimates. Precise knowledge of the atmospheric surface pressure uncertainty on seasonal, annual, and secular time scales becomes increasingly important as gravity measurements become increasingly accurate.
There are a few areas, such as parts of the Southern Hemisphere, where the atmospheric pressure errors may be larger than the uncertainties in the hydrological estimates. In that case, mass anomalies derived from satellite gravity observations could be useful for learning more about atmospheric pressure variations.
The atmospheric pressure uncertainties may be larger still over much of the ocean. However, as will be discussed in Chapter 4, uncertainties in atmospheric pressure, whatever their amplitude, are not apt to be a limitation for oceanic studies.
HISTORY OF SATELLITE GRAVITY
Over the first three decades of space techniques, the emphasis of gravimetry was to obtain a more detailed determination of spatial variations in the Earth's static gravity field (Table 1.1). All of these variations also affect the elevation of the Earth's surface, which is usually easier to measure than the gravitational field. However, there are differences of effect reflecting the depths of the causative density variations, and hence their nature. Consequently, since the inference of isostasy well over a century ago, gravity has always been analyzed in conjunction with topographic elevation.
While measurement accuracy steadily improved, the need to lower orbits to obtain better resolution was always frustrated by the greatly increased expense of maintaining orbits against atmospheric drag (see Nerem et al., 1995 and references therein). As measurements became more precise, it became possible to detect temporal variations in the gravity field, which are typically less than 10-6 g in amplitude. The first significant temporal measurement was in 1983, when it became possible to measure secular variations in the gravity field associated with changes in the overall shape of the Earth probably arising from a combination of post-glacial rebound and changes in the mass of polar ice (Table 1.1). Temporal variations in ocean tides have been incorporated into gravity field determinations since 1987. Today, scientists are exploring processes that vary over seasonal, interannual, decadal, and secular (i.e., varies linearly over the mission lifetime) changes in the gravity field.
The development of new technologies, such as satellite laser ranging systems with sub-centimeter accuracy, high-accuracy Global Positioning System (GPS) receivers designed for use onboard orbiting satellites, and the successful operation of several geodetic satellite missions (e.g., Laser Geodynamics Satellite [LAGEOS] 1 and 2) has led to new advances in gravity modeling and interpretation (Nerem et al., 1995). However, many of the goals of the earth-science community have not been achieved due to the lack of a dedicated gravity mission. Several mission concepts have been studied and advanced over the last two decades, but none has been realized. Although these missions did not fly, they stimulated a vigorous development of gravity instruments and left a legacy of an improved understanding of the accuracy and resolution required to meet the goals of the scientific community. Three important factors have come into play:
-
. the availability of new low-cost (e.g., on the order of $100 M) mission designs;
-
. the need to improve the geodetic reference system for other satellite measurements; and
-
. the realization that there are significant temporal variations of longer wavelengths measurable from higher altitude orbiters, which would allow nontraditional and interdisciplinary applications to be addressed.
Two categories of mission designs are currently being considered: (1) gradiometry in a single satellite; and (2) tracking between two satellites. The Spaceborne Gravity Gradiometer (SGG) combines pairs of accelerometers in close proximity along a common axis to measure components of the gravity gradient tensor along the axis of each pair. By combining three pairs in
TABLE 1.1 Milestones in Gravitational Satellite Geodesy
|
Year |
Event |
Implications |
|
1958 |
Determination of the oblateness from tracking of Sputnik |
• Definitive determination of the Earth's oblateness: the largest difference of the real Earth from fluid equilibrium |
|
1959 |
Determination of the "pear shape" (odd zonal harmonic) of the Earth |
• First determination of a gravity term not associated with rotation • Showed that the Earth has major density variations not associated with isostatic topographic compensation, as predicted by Jeffreys (1952) |
|
1963 |
Longitudinal variations from camera tracking included in gravity field determination |
• Confirmed the "10-5/l2" rule for the decline in magnitude of variations in gravity with harmonic degree l; ±27 meters rms error in the geoid |
|
1965 |
Doppler tracking from U.S. Navy TRANET network included in gravity field determination |
• Significantly improved gravity-field accuracy to ± 12 meters rms error in the geoid |
|
1968 |
Effective satellite-to-satellite tracking, i.e., Earth to lunar satellite |
• Mapped the front-side field of the Moon to better accuracy than contemporary measurements of the Earth |
|
1975 |
The first altimetric satellite Geodetic Satellite Mission (GEOS-3) |
• Measured sea-level height at the 1-m level, an order-of-magnitude improvement in the ocean geoid |
|
1979 |
Incorporation of laser ranging data into gravity field solutions |
• Significantly reduced systematic error and improved accuracy of the geopotential field |
|
1979 |
Gravity field of Mars determined from Mariner Orbiters |
• Showed a gravity field twice as great in its irregularities as predicted from the Earth's field, and the dominance by a great high over the Tharsis province, a planet-scale locus of high topography, volcanism, and tectonism |
|
1981 |
Gravity field of Venus determined from Pioneer Orbiter |
• Showed a gravity field of much greater geoid:topography ratio than the Earth's, implying depths of compensation greater than 100 km |
|
1983 |
Generation of marine gravity field from Seasat data |
• Revealed major uncharted tectonic features of the ocean floor (Haxby et al., 1983) |
|
1983 |
Detection of the change in the Earth's oblateness (dJ2/dt) from high LAGEOS spacecraft |
• Implied an increasing spin rate consistent with the long-term post-glacial motion of matter toward the rotation axis |
|
1987 |
Incorporation of tidal variations in gravity-field determinations |
• Provided important constraints on ocean-tide solutions and improved the accuracy of the static field |
|
1987 |
Analysis of monthly gravity data from LAGEOS and complementary atmospheric pressure data |
• Linked seasonal variations of the geopotential with atmospheric pressure variations |
|
1993 |
Comprehensive solution incorporating altimetry, surface gravimetry, and GPS tracking (Joint Gravity Model [JGM3]) |
• Determined the gravity field to the 70th degree, plus tides, to an estimated geoid accuracy of ±0.5 meters |
|
1995 |
Mass of asteroid 243 Ida determined from Galileo spacecraft Doppler tracking |
• Bulk density consistent with "rubble-pile" model of asteroids |
|
1995 |
Inference of tidal Love number of Venus from Magellan Doppler tracking |
• The high value (0.27) indicated that Venus has a completely fluid core, consistent with the absence of an energy source for a Venusian magnetic field |
|
1995 |
Geodesy Satellite altimetry (ERS-1 acquired; Geosat declassified) |
• Led to a global map of the oceanic gravity field with a resolution of 20 km |
|
1996 |
Measurement of the ellipsoidal fields of the Galilean satellites |
• Moments-of-inertia indicated big iron cores in Ganymede and Europa, a modest core in Io, and no core in Callisto |
orthogonal directions, the trace of the gradient tensor can be measured. Existing technologies permit missions of one-year duration, whereas five-year duration missions utilizing improved miniaturization and cryogenic techniques are expected around 2010. Three types of tracking between satellites are considered in this report: (1) high-low GPS tracking; (2) low-low microwave tracking between two satellites (SST); and (3) low-low laser interferometry between two satellites (SSI). There are tradeoffs between mission lifetime, altitude, and resolution (e.g., long missions are higher altitude and have lower resolution than short missions), and between temporal and spatial sampling.
The compact size, low weight, and low power consumption of the instrumentation proposed for future gravity missions allows the use of newly available low-cost launch vehicles. The development of compact, highly accurate accelerometers and gradiometers eliminates the need for the expensive "drag-free" system included in many of the earlier gravity-mission designs. In all of the current gravity-mission proposals, modern, highly capable, compact GPS flight receivers will provide access to the rich information content of the dual-frequency navigation signals of the GPS constellation. These improvements will allow several types of gravity missions to be flown at low cost.
The proposed missions will have different capabilities and thus will have application to different scientific problems. In discussing the scientific issues, we note the accuracies that could be obtained by each type of gravity mission.
"GRAVITY" AS USED IN THIS REPORT
Newton's laws of motion apply to inertial reference frames, whereas terrestrial motions are observed in a non-inertial coordinate system rotating with the Earth. In accordance with standard practice among geodesists, we will use the term "gravity" to mean the combination of Newtonian gravitational attraction with the effect of the Earth's rotation at a point stationary with respect to the Earth's surface; it has the physical dimension of acceleration. The rotational effect is included in the definition of the standard ellipsoidal model of the reference gravity field for the Earth. "Gravity anomalies" are departures from this reference model at points fixed relative to the Earth and are thus identical to the anomalies of attraction only, the rotation being common to both the reference field and the observed values. The ''anomalous potential" is the difference between the potentials of the real and reference gravity fields, consequently, gravity anomalies are related to the gradient of the anomalous potential. The "geoid" is the equipotential surface of the real gravity field that coincides, on average, with mean sea level. A "gravity mission" is an observational satellite program designed to sense these gravity anomalies.
There are three different ways that deviations from the reference gravity-field model are commonly expressed; each has its convenience. "Gravity anomalies" are anomalies in the magnitude of the acceleration and, from long habit, are commonly expressed in milli-Galileos (mGal). One mGal = 10-5 m/s2 and is approximately 10-6 of the total gravity acceleration. "Deflections of the vertical" are anomalies in the direction of gravity, measured as angles and conveniently described in micro-radians (µrad), a slope of 1 µrad being a 1 mm rise in a 1 km run. "Geoid anomalies" or "geoid heights" are elevations of the geoid above or below the standard ellipsoidal reference shape of the Earth and are conveniently measured in meters. Root-mean-square (rms) magnitudes are about 42 m for geoid height, 30 mGal for gravity anomaly, and 30 µrad for deflections of the vertical with respect to a hydrostatic figure.
Geoid anomalies can be calculated from gravity anomalies, and vice versa. Spatial derivatives of the anomalous potential in different coordinate directions are related to one another through Laplace's equation. By combining these two relations, one can relate horizontal derivatives (slopes) of the geoid to gravity anomalies, and thus obtain the convenient result that a 1 mGal gravity anomaly approximately corresponds to a 1-µrad slope in the geoid. Furthermore, at mid-latitude values of the Coriolis parameter, a slope of 1 µrad in the dynamic ocean height implies a surface-current velocity of 0.1 m/s. This is important for oceanographers to bear in mind, because if a gravity anomaly as determined by a satellite mission has an uncertainty of x mGal, it means that the slope of the geoid is also uncertain by x µrad, hence that the calculated slopes of the oceanic dynamic topography will also be uncertain by x µrad. In this way, the gravity anomaly uncertainties described in this report may be scaled into uncertainties in derived ocean circulation.
ORGANIZATION OF REPORT
In this report we evaluate the capabilities of the next generation of satellite gravity missions for improving the global gravity field and explore the scientific questions that could be addressed with better gravity data. The applications of the static field are important; however, they have been discussed extensively in the literature (e.g., National Research Council [NRC], 1979, 1982; National Aeronautics and Space Administration [NASA], 1987; Nerem et al., 1995). Here, we summarize and update these findings. In contrast, application of the time-varying field to geophysical processes is an emerging frontier of science and requires significantly more detail in this report. Because little systematic work has been done in this area, it was necessary to develop forward models to determine which phenomena could be detected from space. The models are described in Appendix B.
In Chapter 2 (Mission Scenarios and Measurement Techniques), we describe the measurement techniques needed to advance the state of the art in gravity research. Here, we focus on the expected results of five possible missions, which are described in a generic format, and illustrate the trade-offs between mission duration and spatial resolution. In Chapter 3 (The Gravity Field as a Tool for Science) we describe the utility of gravity data (e.g., the geoid) to a broad range of scientific disciplines. In the remainder of the report we examine what new insights can be gained with improved gravity measurements, with an emphasis on understanding "processes." Both static (i.e., constant in historic time) and time-varying phenomena are described. Within the time-varying category, we distinguish among those that are secularly-varying and those that are expected to fluctuate, some shorter and some longer than one mission lifetime. The focus of Chapter 4 (Ocean Dynamics and Heat Flux) is oceanic processes, with a particular emphasis on ocean circulation and the ocean's role in global change. Chapter 5 (Solid Earth Processes) contains a discussion of mantle convection and plumes, tectonics and crustal deformation, post-glacial rebound, and earthquakes. Monitoring of one of the most important renewable resources, water, is discussed in Chapter 6 (Water Cycling). In Chapter 7 (Sea-Level Change) we consider how rates of sea-level rise can be constrained using space geodetic measurements, an issue of profound concern to coastal societies. Chapter 8 (The Dynamic Atmosphere) is a description of the synergistic benefits of space gravity measurements when studied with more conventional meteorological data and, on the other hand, the need for accurate atmospheric pressure data to deconvolve other sources of gravitational variations. Finally, in Chapter 9 we summarize our conclusions.