Moreover, sufficient predictability in the control loop delay is necessary for the receiver to perform policing. After issuing a flow control command to the sender, the receiver will need to start policing the traffic according to the new condition only after the control loop delay. If control loop delay cannot be bounded, it is impossible for the receiver to decide when to start policing.
Per-VC Queueing to Achieve a High Degree of Fairness
To achieve fairness between bursty VCs sharing the same output, it is necessary to have separate queueing for individual VCs. With a fair round-robin scheduling policy among these queues, cells from different VCs will be sent out in a fair manner.
Per-VC queueing provides firewall protection against VCs interacting each other. Technology advances have lowered the cost of implementing per-VC queueing. There are more and more per-VC queueing switches available on the market. Fore System's ASX200WG is one example. Per-VC queueing will be the future trend for ATM technology.
Rate-Based Flow Control
It is instructive to consider rate-based flow control schemes [3, 4], in contrast to the credit-based approach described above. Rate-based flow control consists of two phases: rate setting by sources and network, and rate control by sources. These two phases correspond to the buffer allocation and credit control phases in credit-based flow control.
Rate control is a shaping function for which various implementations are possible. For example, when a cell of a VC with a given rate r arrives, the cell will be scheduled for output at time 1/r after the previous output of the same VC. By sorting arriving cells into buckets according to their departure times, rate control can be implemented without per-VC queueing (although per-rate-bucket queueing may be needed).
Suppose that traffic is so smooth that it is possible to set the rate for each VC perfectly against some performance criteria, and that these rates need not change over time to sustain the target performance. Then, if the VCs are shaped at the sources according to the set rates, the rate-based flow control method should work perfectly well. There would be no need for link-by-link flow control and per-VC queueing in the network. The buffer in a switch could also be kept at the minimum, almost as in a synchronous transfer mode (STM) switch.
However, setting rates perfectly or near optimally is a complicated matter. Consider, for example, the configuration in Figure 12, known at the Traffic Management Group of the ATM Forum in 1994 as Generic Fairness Configuration (GFC) [20]. All traffic sources are assumed to be persistently greedy and can transmit at the peak link rate when bandwidth is available. Links
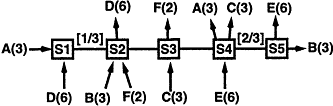
Figure 12
Generic Fairness Configuration (GFC). [ ]: Link bandwidth; link bandwidth = 1 if not indicated. (k): Number of virtual circuits (VCs) in the VC group.
have various propagation delays. The actual values of the propagation delays are not important to the discussion here, and thus are not listed.
Note that both traffic B and E share the same link between S4 and S5, and the source of E is closer to the link than that of B. This is analogous to a parking lot scenario in which E starts from a position closer to the exit than B. In a normal, real-world parking lot, E would have an unfair advantage over B by being able to move itself in front of B and get out first. However, in a good ATM network with separate virtual circuits for B and E, they ought to share fairly the bandwidth of the link, as long as they are not bottlenecked elsewhere in the network.
With this fairness objective in mind, we naturally consider the performance criterion described below, which is sometimes called "max-min" fairness [3, 4, 6] in the literature. First, the VCs on the most congested link will share the link bandwidth equally, and this determines the rates to be set for these VCs. Then, apply the procedure to the other VCs with the remaining bandwidth of the network. Continue repeating the procedure until rates for all the VCs have been assigned. Table 1 shows the resulting rates assigned to individual VC groups.
Translating the above mathematical rate-setting procedure into an efficient and robust implementation is a major challenge. First, with highly bursty ABR traffic, because load changes rapidly, there would be no static rate-setting that could be ideal for any significant period of time. When traffic changes, "optimal" rates to be assigned to the affected VCs must change accordingly.
For this reason, adaptive rate-setting is necessary for bursty traffic and has been the subject of intensive research for many years. The Enhanced Proportional Rate-Control Algorithm (EPRCA) [18], one of the schemes considered at the 1994 ATM Forum, represents the kind of adaptive rate-setting schemes this paper assumes.
Rate adaptation cannot be so precise that the newly derived rates will be exactly right with respect to current load, for at least two reasons. First, information and measurements based on which particular adaptation is performed cannot be totally complete or up to date due to various cost and implementation constraints. Second, the feedback control time that the adaptation takes to inform sources can vary because of disparities in propagation delay and link speed, congestion conditions, scheduling policies, and many other factors.
More interesting, perhaps, is that rate adaptation should not be precise either. To achieve high utilization with bursty traffic, it is necessary that the total assigned rate for all the VCs over a link be higher than the peak link rate. Consider the simple scenario shown in Figure 13 involving only two VCs, A and B. Assume that the two VCs share the same switch output link
TABLE 1
Expected Rates for VC Groups in Generic Fairness Configuration (GFC) of Figure 12
|
Group |
Bandwidth |
Bottleneck Link |
|
A |
1/27 = 0.037 |
S1-S2 |
|
B |
2/27 = 0.074 |
S4-S5 |
|
C |
2/9 = 0.222 |
S3-S4 |
|
D |
1/27 = 0.037 |
S1-S2 |
|
E |
2/27 = 0.074 |
S4-S5 |
|
F |
1/3 = 0.333 |
S2-S3 |


