Two Traffic Models
Any prediction of how well a flow control scheme will work requires a model for the behavior of network traffic. A full-blown model might involve characteristics of applications and higher-level protocols. For our discussion here, it is enough to distinguish between smooth and ''bursty'' traffic.
A smooth traffic source offers a constant and predictable load, or changes only on time scales that are large compared to the amount of time the flow control mechanism takes to respond. Such traffic is easy to handle well; the sources can be assigned rates corresponding to fair shares of the bottleneck bandwidth with little risk that some of them will stop sending and lead to underutilized links. Furthermore, switches can use a small amount of memory, since bursts in traffic intensity are rare.
Sources of smooth traffic include voice and video with fixed-rate compression. The aggregate effect of a large number of bursty sources may also be smooth, particularly in a WAN where the loads from a large number of traffic streams are aggregated and the individual sources have relatively low bandwidth and arc uncorrelated.
Bursty traffic, in contrast, lacks any of the predictability of smooth traffic, as observed in some computer communications traffic [8]. Some kinds of bursts stem from users and applications. A World Wide Web browser clicking on a link, for instance, wants to see a page or image as soon as possible. The network cannot predict when the clicks will occur, nor should it smooth out the resulting traffic, since doing so would hurt the user's interactive response.
Other sources of bursts result from network protocols that break up transfers into individual packets, windows, or RPCs, which are sent at irregular intervals. These bursts are sporadic and typically do not last long enough on a high-speed link to reach steady state over the link round-trip time.
Designing flow control systems for bursty traffic is obviously much more difficult than designing control systems for smooth traffic. In supporting computer communications, which are generally bursty, we will have no choice but to face the challenge of designing effective flow control for bursty traffic.
A Flood Control Principle
An old principle for controlling floods suggests an approach to controlling network congestion. Dams on a river for holding floods are analogous to buffers in a network for holding excessive data.
To control floods, dams are often built in series along a river, so that an upstream dam can share the load for any downstream dam. As depicted in Figure 6, whenever a dam is becoming full, its upstream dams are notified to hold additional water. In this way, all the upstream dams can help reduce flooding at a downstream congestion point, and each upstream dam can help prevent flooding at all downstream congestion points. The capacity of every dam is efficiently used.
Credit-Based Flow Control
An efficient way of implementing flow-controlled ATM networks is through the use of credit-based, link-by-link, per-VC (virtual circuit) flow control [12, 14, 17]. As depicted in Figure 7, credit-based control works like the method of controlling floods described above. Each
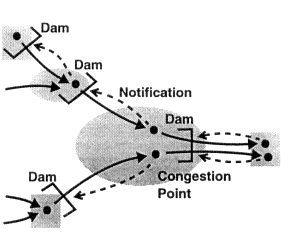
Figure 6
Flood control analogy. All the dams (or buffers) on the path leading to the congestion point can help prevent flooding (or cell loss). Notifications are denoted by dashed arrows.
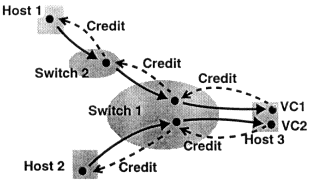
Figure 7
Credit-based flow control. Black dots stand for virtual circuit (VC) buffers.
downstream-to-upstream notification is implemented with a credit record message. The scheme generally works over a VC link as follows. A link can be a physical link connecting two adjacent nodes, or a virtual circuit connecting two remote nodes. Before forwarding any data cell over the link, the sender needs to receive credits for the VC from the receiver. At various times, the receiver sends credits to the sender indicating availability of buffer space for receiving data cells of the VC. After having received credits, the sender is eligible to forward some number of data cells of the VC to the receiver according to the received credit information. Each time the sender forwards a data cell of a VC, it decreases its current credit balance for the VC by one.
There are two phases in flow controlling a VC [15]. In the first buffer allocation phase, the VC is given an allocation of buffer memory in the receiver. In the second credit control phase, the sender maintains a non-negative credit balance to ensure no overflow of the allocated buffer in the receiver.
Credit Update Protocol
The Credit Update Protocol (CUP) [12] is an efficient and robust protocol for implementing credit control over a link. As depicted in Figure 8, for each flow-controlled VC the sender keeps a running total Tx_Cnt of all the data cells it has transmitted, and the receiver keeps a running total Fwd_Cnt of all the data cells it has forwarded. (If cells arc allowed to be dropped within the receiver, Fwd_Cnt will also count these dropped cells.) The receiver will enclose the up-to-date value of Fwd_Cnt in each credit record transmitted upstream via a credit cell. When the sender receives the credit record with value Fwd_Cnt, it will update the credit balance, Crd_Bal, for the VC:
where Buf_Alloc is the total number of cells allocated to the VC in the receiver.
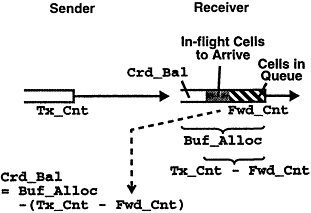
Figure 8
Credit Update Protocol (CUP). The dotted arrow indicates a credit record, transmitted upstream, containing the current value of Fwd_Cnt at the receiver.
Note that the quantity computed by the sender, Tx_Cnt - Fwd_Cnt, represents the "outstanding credits" corresponding to those cells of the VC that the sender has transmuted but the receiver has not founded. As depicted in Figure 8, these cells are "in-flight cells to arrive" and "cells in queue" at the time when the receiver sends credit record Fwd_Cnt to the sender. Thus Crd_Bal computed by the sender using Equation (1) is the proper new credit balance, in the sense that, as long as the sunder transmits no more than Crd_Bal cells, it will not overrun the VC's allocated buffer in the receiver. See [12] for a scheme of using credit_check cells periodically sent from the sender to the receiver, to recover from possible loss of data or credit cells due to link errors.
The frequency at which the receiver sends credit records for a VC depends on the VC's progress. More precisely, each time after the receiver has founded a certain number of cells, "N2" cells [14] for some positive integer N2, the receiver will send a credit record upstream. The value of N2 can be set statically or adaptively (see Equation (4) below).
The Buf_Alloc value given to a VC determines the maximum bandwidth allowed to the VC by credit flow control Without loss of generality, we assume that the maximal peak bandwidth of any link is 1, and represent the rate of a VC as a fraction of 1. For the rest of this section, we also make a simplifying assumption that all links have the same peak bandwidth of 1. Let RTT be the round-trip time, in cell transmission time, of the link between the sender and the receiver (see Figure 8), including both link propagation delays and credit processing time. Assume that the receiver uses a fair scheduling policy between VCs with Crd_Bal > 0, when forwarding cells out from its output link. Then, if there are N active VCs competing for the same output link, the maximum average bandwidth over RTT that the VC can achieve is
Note that when there is only one VC using the output port, i.e., N = 1, the VC's bandwidth (BW) can be as high as Buf_Alloc / (RTT + N2).
The CUP scheme is a lower-level and lighter-weight protocol than are typical sliding window protocols used in, e.g., X.25 and TCP. In particular, CUP is not linked to retransmission of lost packets. In X.25 or TCP, loss of any packet will stop the advancing window until the dropped packet has been retransmitted successfully. To implement this, each data packet carries a
sequence number. In contrast, in CUP the sender does not retransmit lost data cells, the receiver does not reorder received cells, and data cells do not carry sequence numbers. This simplicity is made possible because CUP need only work for ATM VCs that preserve cell order.
It can be shown [14] that CUP produces the same buffer management results as the well-known "incremental" credit updating methods (see, e.g., [7, 9]). In these other methods, instead of sending Fwd_Cnt values upstream the receiver sends incremental credit values to be added to Crd_Bal at the sender.
Static vs. Adaptive Credit Control
We call a credit-based flow control either static or adaptive depending on whether the buffer allocation is static or adaptive. In a static credit control, a fixed value of Buf_Alloc is used for the lifetime of a VC. Requiring only the implementation of CUP, or some equivalent protocol, the method is extremely simple.
There are situations, however, where adaptive credit control is desirable. In order to allow a VC to operate at a high rate, Equation (2) implies that Buf_Alloc must be large relative to RTT + N2*N. Allocating a small buffer to a VC can prevent the VC from using otherwise available link bandwidth. On the other hand, committing a large buffer to a VC can be wasteful, because sometimes the VC may not have sufficient data, or may not be able to get enough scheduling slots, to transmit at the desired high rate. The proper rate at which a VC can transmit depends on the behavior of traffic sources, competing traffic, scheduling policy, and other factors, all of which can change dynamically or may not be known a priori. In this case, adaptive credit control, which is static credit control plus adaptive adjustment of Buf_Alloc of a VC according to its current bandwidth usage, can be attractive.
Generally speaking, for configurations where a large Buf_Alloc relative to RTT + N2*N is not prohibitively expensive, it may be simplest just to implement static credit control. This would give excellent performance. Otherwise, some adaptive buffer allocation scheme, as described below, may be used to adjust Buf_Alloc adaptively. To maximize flexibility, the adaptation can be carried out by software.
Adaptive Buffer Allocation
Adaptive buffer allocation allows multiple VCs to share the same buffer pool in the receiver node adaptively, according to their needs. That is, Buf_Alloc of a VC is automatically decreased if the VC does not have sufficient data to forward, cannot get sufficient scheduling slots, or is back-pressured due to downstream congestion. The freed-up buffer space is automatically assigned to other VCs that have data to forward and are not congested downstream.
Adaptive buffer allocation can be implemented at the sender or receiver node. As depicted in Figure 9, in a sender-oriented adaptive scheme [12, 17] the sender adaptively allocates a shared input-buffer at the receiver among a number of VCs from the sender that share the same buffer pool. The sender can allocate buffer for the VCs based on their measured, relative bandwidth usage on the output port p [12].
Receiver-oriented adaptation [13] is depicted by Figure 10. The receiver adaptively allocates a shared output-buffer among a number of VCs from one or more senders that share the same buffer pool. The receiver can allocate buffer for the VCs based on their measured, relative bandwidth usage on the output port q [13].
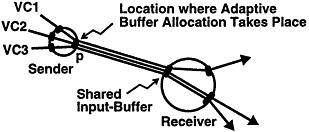
Figure 9
Sender-oriented adaptation. The circles are switches. Each darkened bar denotes a switch point.
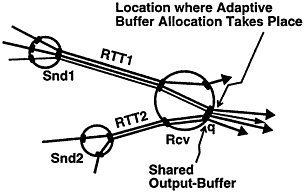
Figure 10
Receiver-oriented adaptation.
Receiver-oriented adaptation is suited for the case where a common buffer pool in a receiver is shared by VCs from multiple upstream nodes. Figure 10 depicts such a scenario: the buffer pool at output port q of the receiver switch Rcv is shared by four VCs from two switches Snd1 and Snd2. Note that the receiver (Rcv for Figure 10) can observe the bandwidth usage of the VCs from all the senders (that is, Snd1 and Snd2). In contrast, each sender can observe the bandwidth usage only of those VCs going out from the same sender. Therefore, it is natural to use receiver-oriented adaptation in this case.
Moreover, receiver-oriented adaptation naturally supports the adaptation of N2 values for individual VCs, in order to minimize credit transmission overhead and increase buffer utilization. Since only the receiver needs to use N2 values, it can conveniently change them locally, as described in the next section.
Receiver-oriented Adaptive Buffer Allocation
We describe the underlying idea of the receiver-oriented adaptive buffer allocation algorithm [13]. In referring to Figure 10, let RTT be the maximum of all the RTTs and M be the size, in cells, of the common buffer pool in the receiver.
For each allocation interval, which is set to be at least RTT, the receiver computes a new allocation and an N2 value for each VC according to its relative bandwidth usage. Over the allocation interval, let VU and TU be the number of cells forwarded for the VC and that for all the N active VCs, respectively. Then for the VC, the new allocation is:
and the new N2 value is
where TQ is the total number of cells currently in use in the common buffer pool at the receiver. For exposition purposes this section ignores floor and ceiling notations for certain quantities, such as those in the right-hand sides of the above two equations. See [13] for precise definitions and analysis of all quantities.
It is easy to see that the adaptive formula of Equation (3) will not introduce cell loss. The equation says that for each allocation interval, the VCs divide a buffer of size M/2 - TQ - N according to their current relative bandwidth usage VU/TU. Thus, the total allocation for all the VCs is no more than (M/2 - TQ - N) + N or M/2 - TQ, assuming that each of the N VCs is always given at least one cell in its allocation. Since allocation intervals are at least RTT apart, after each new allocation, the total number of in-flight cells is bounded by the total previous allocation. Note that the total previous allocation is no more than ![]() , where TQprev is the TQ value used therein. Therefore the total memory usage will never exceed (M/2 - TQ) + M/2 + TQ or M. Consequently, adaptive buffer allocation will not cause cell loss. This analysis also explains why M is divided by 2 in Equation (3).
, where TQprev is the TQ value used therein. Therefore the total memory usage will never exceed (M/2 - TQ) + M/2 + TQ or M. Consequently, adaptive buffer allocation will not cause cell loss. This analysis also explains why M is divided by 2 in Equation (3).
Equation (4) allows the frequency of transmitting credit cells of the VC, i.e., the N2 value, to adapt to the VC's current Buf_Alloc, or equivalently, its relative bandwidth usage. That is, VCs with relatively large bandwidth usage will use large N2 values. This will reduce their bandwidth overhead in transmitting credit records upstream. (In fact, by adapting N2 values and by packing up to 6 credits in each transmitted credit cell, the transmission overhead for credit cells can be kept very low. Simulation results in [13] show that this overhead is generally below a few percent, and sometimes below 1 percent.) On the other hand, an inactive VC could be given an N2 value as small as 1. With a smaller N2 value, the receiver can inform the sender about the availability of buffer space sooner, and thus increase memory utilization. The N2 value would increase only when the VC's bandwidth ramps up. Thus the required memory for each VC could be as small as one cell.
From Equations (2), (3), and (4), we can show that the adaptive scheme guarantees that a VC will ramp up to its fair share. A sufficient condition is that a fair scheduling policy is employed, the switch buffer size
or larger is used, and a significant portion of the switch buffer is not occupied, e.g.,
The condition of Equation (6) holds if those VCs that are blocked downstream do not occupy much buffer space at the current node. The adaptive buffer allocation scheme is indeed designed in such a way that inactive or slow VCs will be allocated the very minimum or a small buffer space, respectively.
Assume that there are N - 1 active VCs that in aggregate already get the full link bandwidth of an output port of the receiver. Now a new VC using the same output port starts and wishes to get its fair share, i.e., 1/N, of the link bandwidth. Suppose that the VC's current buffer allocation X is insufficient for achieving this target bandwidth. That is, by Equations (2) and (4),
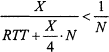
or, equivalently,
Note that with the current allocation X, by Equation (2) the relative bandwidth that the VC can achieve satisfies:
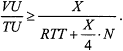
Since TQ < 2*RTT/3, it follows from Equation (5) and the last two inequalities above that:
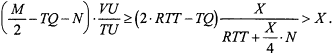
Thus the new allocation for the VC computed by Equation (3) will be strictly larger than X. In this way the buffer allocation for the VC will keep increasing after each round of new allocation, as long as the achievable bandwidth allowed by the current Buf_Alloc X is less than 1/N and the total queue length TQ is less than 2*RTT /3.
In fact, the ramp up rate for a VC is exponential in number of allocations initially, when the bandwidth allowed by the credit control is small and when TQ is small. We can easily explain this exponential ramp up, using the last inequality expression above, for the simplifying case that TQ = 0. When RTT is large and X*N/4 is much smaller than RTT, the middle term is about a factor-of-two larger than the third term. That is, X is ramped up roughly by a factor of two for every new allocation. In general, from the inequality expression we see that if M = 2*α*RTT + 2*N, then the ramp up factor for each allocation is about α. Therefore, the larger α or M is, the faster the ramp up will be.
Rationale for Credit-based Flow Control
We discuss some key reasons behind the credit-based approach to flow control. The same rationale, perhaps formulated in a different form, is applicable to any flow control scheme.
Overallocation of Resources to Achieve High Efficiency
For reasons of efficiency, the size M of the total allocated buffer in the receiver generally needs to be larger than RTT. This is overallocation in the sense that if traffic is 100 percent steady state, M need only be RTT for sustaining the peak bandwidth of the output link. However, for bursty traffic, M needs to be larger than RTT to allow high link utilization and reduce transmission time.
First consider static credit control. If the required memory cost is affordable, we can let Buf_Alloc be RTT + N2 for every one of the N active VCs. Then by Equation (2) the maximum bandwidth the VC can achieve is at least 1/N for any value of N. When a scheduling slot for the output link becomes available, an "eligible" VC at the sender that has data and credit can transmit instantly at the peak link rate. When there are no other competing VCs, i.e., when N =
1, any single VC can sustain the peak link rate by Equation (2). Thus, link utilization is maximized and transmission time is minimized.
Now consider adaptive credit control. As in the static case, M needs to be large for increased link utilization and reduced transmission time. For adaptive buffer allocation, M needs to be large also for fast ramp up [15] as explained above.
Intuitively, receiver-oriented adaptation needs more buffer than does sender-oriented adaptation, because receiver-oriented adaptation involves an extra round-trip delay for the receiver to inform the sender of the new allocation. Thus the minimum buffer size for receiver-oriented adaptation is increased from RTT to 2*RTT. Suppose that the total memory size is larger than the minimum 2*RTT, e.g., as given by Equation (5). Then the part of the memory that is above the minimum 2*RTT will provide "headroom" for each VC to increase its bandwidth usage under the current buffer allocation. If the VC does increase its bandwidth usage, then the adaptation scheme will notice the increased usage and will subsequently increase the buffer allocation for the VC [12].
The receiver-oriented adaptive buffer allocation scheme in [13] uses M given by Equation (5). Analysis and simulation results have shown that with this choice of M the adaptive scheme gives good performance in utilization, fairness, and ramp up [13].
Link-By-Link Flow Control to Increase Quality of Control
Link-by-link flow control has shorter and more predictable control loop delay than does end-to-end flow control. This implies smaller memory requirements for switching nodes and higher performance in utilization, transmission time, fairness, and so on.
Link-by-link flow control is especially effective for handling transient "cross" traffic. Consider Figure 11, where T is an end-to-end flow-controlled traffic using some end-to-end transport-level protocol such as TCP and X is high-priority cross traffic. If X uses the whole bandwidth of the Switch3's output link, then the entire window of T for coveting the end-to-end round-trip delay would have to be buffered to avoid cell loss. With link-by-link flow control, all the buffers on the path from the source of T to Switch3 can be used to prevent cell loss. In contrast, without link-by-link flow control, only the buffer at the congestion point (i.e., Switch3 in this case) can be used for this purpose. The argument for making efficient use of buffers is similar to that for making efficient use of dams in the flood-control analogy described above.
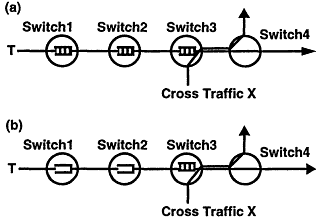
Figure 11
(a) With link-to-link flow control, all buffers on the path leading to the congestion point (Switch3) where traffic T meets cross traffic X can be used for preventing cell loss; (b) without link-by-link flow control, only the buffer in Switch3 can help.








