2
Cycles That Effect Change
Roger W. Brockett
Division of Applied Sciences Harvard University
|
New generations of motors are needed for applications where, due to small dimensions, a need for high torque, a need for precise control, or all of these factors, conventional electric or internal combustion motor technology cannot be used. In some instances, engineers desire suitable analogs to the high force and precise control provided by muscle tissue. We discuss the geometrical ideas that underlie a new generation of precisely controllable high-force actuators based on suitably patterned high-frequency vibrations. Current and planned applications of such actuators include their use in automatic focusing lenses and in endoscopic surgery. |
INTRODUCTION
Prevailing modes of thought in subjects, ranging from economics to biology, show the influence of ideas originating in the study of feedback control. The linear analysis that underlies the theory of single and multiple feedback loops has played an important role in explaining both stable regulation and exponential growth. There are, however, a variety of problems involving automatic control that cannot be explained on the basis of this body of results. For example, at least since the work of Graham Brown in 1911, it has been recognized that some provision for pattern generation must be incorporated in the neural circuitry used to generate and control various animal movements such as walking, breathing, blood circulation, and peristalsis. Pattern generation also plays an important role in the design of mechanical and electrical systems. The wheels of a steam locomotive should rotate steadily, yet their motive power comes from periodic processes involving the filling and emptying of the cylinders with steam and the corresponding motion of the pistons. In fact, both conventional piston-type steam engines and internal combustion engines depend on a carefully orchestrated, repetitive motion pattern as an intermediate step in the generation of steady rotational motion; the recently introduced vibratory motors depend on an even more subtle type of pattern generation. Similar ideas play a role in certain types of electrical circuits. Technologically important examples include parametric amplifiers, switched capacitor
Note: This work was supported in part by the National Science Foundation under grant NSF D CDR-8803012 (Engineering Research Center Program), and by the U.S. Army Research Office under grant DAAL03-86-K-0171 (Center for Intelligent Control Systems).
filters, and DC to DC transformers that make use of periodic switching to transform the voltage available from some supply, such as a battery, to the voltage required by the transistor or motor that is being powered. In many cases, the explanation of the behavior of these types of examples is much more subtle than the explanation of ordinary linear regulation. In this paper we use examples from various domains to illustrate the mathematical ideas that lie at the heart of these problems.
Perhaps the most fundamental arguments as to why periodic processes are required to produce nonperiodic effects seem to be based on considerations of kinematics and force amplification. Animals and automobiles need to cover distances that far exceed the longest linear dimension in their makeup. They cannot simply reconfigure their bodies to cover the distances involved. Moreover, muscles, magnets, and expanding gases can only generate their significant force over a limited range of displacements. Having generated a force over this range, it is necessary to reconfigure before being able to generate the same level of force again. Among the possible temporal patterns of reconfiguration, some are more effective than others. Having found an effective one, it can be repeated over and over, giving a cyclic process that enables the coverage of large distances by means of repeated short distance movements.
Within this overall paradigm there is a further important distinction to be made. Certain periodic processes operate with a fixed amplitude, piston engines being a good example. Other periodic processes, such as the motion of an inchworm and the swimming motion of a fish, can operate at a variety of amplitudes. In the case of variable amplitude devices it may happen that the mechanical advantage increases as the amplitude decreases. Theories dealing with nonlinear controllability provide considerable insight into the capabilities of systems of this latter type. Understanding the dynamics of their regulatory processes requires more study, and only recently has there been an appropriate mathematical formulation of a control problem in which pattern generation plays a decisive role. We touch on this in our final section.
ORDER SOMETIMES MATTERS
In choosing from various possible actions that one may take, it sometimes happens that a particular set of actions applied in one order has an overall effect that is different from that obtained when the same set of actions is applied in a different order. The order in which we make deposits and withdrawals in a checking account does not affect the end-of-the-month balance. Driving in a city laid out on a rectangular grid, we can go north for one block then east for one block and get to the same location as we would if we first went east for one block and then north for one block. On the other hand, there are situations in which order matters very much. The most obvious examples, such as opening a door and then walking though it versus walking through the door and then opening it, do not lead to very interesting, or general, mathematical models. However, the situation shown in Figure 2.1 does embody a rather general mathematical/physical principle. Because it is illustrative of several of the main points we will analyze it in detail.
The illustration depicts a pair of tanks. The top tank holds fluid in a vessel that is fitted to create a sealed chamber below it. The lower chamber is full of fluid. Fluid can be pumped into or out of the tanks. For the purposes of exposition, we suppose that there are individual agents responsible for the
management of the flow rates u and ν. One agent, associated with the flow rate u, adds or removes fluid to the top tank. The second, associated with flow rate ν, adds or removes fluid to the lower chamber. One of the fundamental ideas in hydrostatics is that the pressure produced by a column of fluid is independent of the shape of the column and is proportional to the height of the column. The power required to pump a fluid is the flow rate times the pressure. Applying these facts to the situation at hand, we see that, when expressed in suitable units, the energy supplied by the agent responsible for the flow u must provide energy at the rate u(x + y) per unit time whereas the agent responsible for flow ν must provide energy at rate ν(x + y) per unit time.
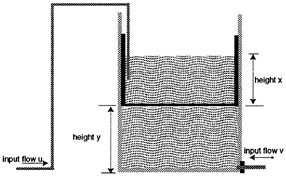
FIGURE 2.1 A simple flow-level model of a nonholonomic system.
The virtue of having a model that can be visualized this concretely is thin the differential equation description can be related to common sense in a direct way. For example, it is clear that the time rate of change of y, the height of the fluid in the bosom chamber measured from the base, is proportional to the flow rate ν. The time rate of change of x, the height of the fluid in the top tank, measured from the bosom of thin tank, is proportional to u. Denoting the time rate of change of a variable x by means of an overdot, e.g., ![]() , we may summarize the statements about flow rate and levels as
, we may summarize the statements about flow rate and levels as
Now suppose that the agents are concerned with the energy they must expend to manage the levels in the ranks. The corresponding equations describing the time rate of change of the energy that must be expended by the agent controlling u, call it eu, and the time rate of change of the energy that must be expended by the agent controlling ν, eν satisfy the equations
Simple as this system is, by analyzing the flow of energy one comes to conclusions that are not entirely obvious. To begin with, it is clear that if it is necessary to bring the levels in the tanks to specific values, the bottom tank to the level y = yo, and the top tank to x = xo, different courses of action on the part of individual agents will result in different expenditures of energy by the individual agents. For example, if the tanks are initially empty and if the bottom tank is filled to the level y = 1 while the top tank remains empty and then the top tank is filled to the level x = 1 while the bottom tank remains at y = 1, then agent u supplies energy 1/2 and agent ν supplies energy 3/2. If we reverse the order, i.e., if agent ν fills the top tank first and then agent u fills the bottom tank, it follows that the energy requirements of the agents are just reversed. A similar analysis applies to pumping fluid from the tanks.
By making use of periodic filling and emptying, the difference between the energy requirements for u and ν can be made as large as one wants and can favor either agent. There is no limit on the energy difference. We can find filling policies that take an arbitrary amount of energy e from agent u and take energy 2- e from agent ν. We can use this device as a way to transfer energy from one agent to the other. The important point is that the difference between the energy supplied by u and the energy supplied by ν is not just a function of the final state, but rather depends on the order, now interpreted in some infinitesimal sense, in which the tanks are filled. This is an example of what is meant by the phrase path dependent. The infinitesimal relationships between x, y and eu-eν are nonintegrable. In a mechanical context they could be said to define a nonholonomic system.
Before leaving this example we want to recast, slightly, the energy equations. First of all, because the sum of the energies supplied by the two agents is just the difference between the initial and final value of x + y, there is no need to keep track of the sum of the energies supplied by the agents. However, the difference in the energies supplied by the agents is dependent on the path and, therefore, requires us to use a differential equation to keep track of it. This means that we can use just three equations for the levels and the energy relationships, not four. Finally, it will simplify the equations if we focus on the difference in the supplied energy plus the difference in the energy available to the individual agents, should they wish to empty their tanks. With this in mind, we define z as z = eu-eν + x2-y2 / 2 and describe the system by
Expressed in this form, the energy flow relationships of the situation depicted in Figure 2.1 can be explained in terms of a remarkably simple geometric picture to be developed in the next section.
SIMPLE MACHINES AND THE AREA RULE
We emphasized, in the case just analyzed, that the difference between the energy supplied by u and the energy supplied by ν is strongly dependent on the path taken to accomplish the task. In fact, the way that it depends on the path is particularly simple: the difference between the amount of energy
supplied by u and the amount of energy supplied by ν is proportional to the area of the closed path defined by going around a cycle in (u, ν)-space. It is characteristic of the simplest class of nonholonomic systems to exhibit such a proportionality. (See Figure 2.2.)
Physically speaking, the area in (u, ν)-space has the units of flow rate squared. To equate this to energy flow one needs a constant factor having suitable units. This factor can be expressed in terms of the value of a certain component of the Lie bracket of two vector fields; as u and ν vary in a cyclical way, z increases monotonically with a rate proportional to the product of this factor and the area in (u, ν)-space.
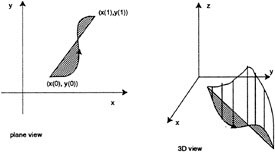
FIGURE 2.2 The area rule in x-y and x-y-z coordinates.
The tank analysis carried out above may seem far removed from mechanics and the basic mechanisms of mechanical engineering. However, there are mechanical realizations of the same mathematical model based on spheres rolling on planes. In Figure 2.3 we illustrate an elementary and useful mechanical device, consisting of a screw engaging a slider having regularly spaced gear teeth. This configuration couples the rotational motion of the screw to the horizontal motion of the slider. If z represents the position of the slider and if x and y are the coordinates of a point on the crank handle, then the equations relating x, y, and z are just a rescaled version of the ones introduced above. More precisely, if the screw has p threads per unit length, then we may describe the kinematics by
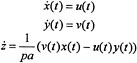
subject only to the constraint that x2 + y2 = a2. Thus a suitably restricted version of the equations relating height and energy flow in the tanks also describes the relationship between the rotational motion and the translational motion of this mechanical system.
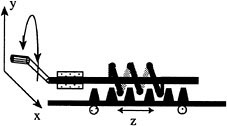
FIGURE 2.3 Converting rotational motion to rectilinear motion with a screw and slider.

FIGURE 2.4 Rotating wheels and the corresponding covering space.
Of course the fact that this screw and slider mechanism represents only the case in which x2 + y2 = a2 means that the overall behavior of this system is just a subset of the possible behaviors of the tank system. In this case we can say that for each point on the circle x2 + y2 = a2 there are (in the case of an infinitely long slider extending in both directions) a countably infinite number of possible locations for the slider and that these locations are discrete, separated by the distance that the slider travels when the screw rotates by one full turn. Thus this mechanism displays a kind of discrete path dependence. In the language of topology, one would say that the space of possible z coordinates forms a coveting space for the space of possible (x, y) values. We illustrate this idea in a somewhat simpler setting also involving the kinematics of machines. In Figure 2.4 we show two wheels, one having twice the diameter of the other, rolling on each other without slipping. If we are told that a particular mark on the small wheel lies at 9 o'clock then we can say that a particular mark on the bigger wheel lies at one of two possible locations, separated by 180 degrees. Again, the space of possible configurations of the bigger wheel forms a covering space for the set of configurations of the smaller one.
A significant difference between the way the set of configurations of the slider covers the set of configurations of the screw versus the way that the set of configurations of the large wheel covers the set of configurations of the small wheel is illustrated on the tight side of Figure 2.4, which shows that there are only two points "sitting over" each point on the small circle, not a countably infinite number as in the screw-slider case. Of course the situation represented by the basic nonholonomic model is even more extreme. In that case there is a continuum of z-values corresponding to a given value of x and y. In fact, any z value can sit above a given value of x and y. In this sense we can think of the nonholonomic system as having the capability of generating any relationship between these variables, containing any fixed-gear ratio system as a special case.
VIBRATIONAL, ROTARY, AND LINEAR MOTION
It is a familiar story that Hero of Alexandria invented a simple steam engine in the first century AD. The drawings of it found in history books show it spinning smoothly over the fire, producing motion but not much torque. Hero's invention did not enable any industrial revolution; the greater part of two thousand years elapsed before that occurred. And when steam power did become useful, it was through the more indirect designs of Newcomen and Watt, based on the generation of reciprocating motion that proved to be effective. In fact, there are a great many examples, ranging from biped locomotion to ratcheting, in which the generation of motion involves the conversion of force developed by a periodic process into some desired steady translation or rotation.
The standard way to convert rotational motion into reciprocating motion is by means of a crank and slider mechanism illustrated in Figure 2.5. As the crank turns in a circle, steadily advancing, the connecting rod connected to the crank moves back and forth. Thought of from the opposite point of view, as the connecting rod moves back and forth, the crankshaft rotates in a steady advance. Thus the same mechanism converts reciprocating motion to circular motion. Figure 2.6 illustrates a different means for converting rotary motion into translational motion. These ideas are relevant to a discussion of nonholonomic systems because they provide a useful basis for comparison to the way in which nonholonomic systems convert oscillatory inputs into steady unidirectional motion.
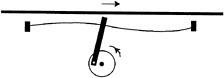
Recently there has been renewed interest in a variety of rather different mechanisms for the generation of motion. Figure 2.7 provides some insight into the nature of one of these new ideas. An elastic member is shown supported at each end in such a way as to permit it to vibrate in two different modes. The first of these may be characterized as a general vertical motion, larger in the middle and smaller toward the supports. The second mode is an asymmetrical motion characterized by a shape such that when the elastic is raised on the fight it is lowered on the left and vice versa. If these modes were to vibrate at the same frequency and with the correct phase relationship, the overall motion of the tip protruding upward from the center would produce an elliptical path as shown at the bottom of the figure. Just as it takes two agents to manipulate the energy flow in the tank example, it takes two modes having the same frequency and appropriate phase relationship to generate the elliptical motion with nonzero area.
In Figure 2.8 we illustrate how this type of two-mode motion can be coupled to a rigid member in such a way as to generate translational motion. The operation of the vibratory motors referred to in the introduction can be explained in this way.
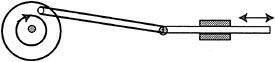
FIGURE 2.5 Converting rotary to reciprocating motion.
ELECTRICAL CIRCUITS WITH SWITCHES
The scope of the above arguments, based as they are on simple geometric ideas, is quite wide and can be applied in a variety of circumstances. One of the especially important areas is that of electrical networks whose behavior is controlled by switches. Nearly every personal computer contains one or more subsystems of this type to provide electrical power at the various voltage levels appropriate for memory chips, disk drive motors, etc. In the recent past, different, more expensive, and less efficient methods based on linear analysis were used. Although our treatment here is brief, we will try to give the reader a feeling for this type of application by recasting some of the arguments given above in terms of electrical circuits.
Electrical engineers often deal with periodic signals such as sine waves and square waves. In some cases it is natural to think of smoothly modulated vector fields, as suggested by
whereas in other cases it might be more useful to think of
with the understanding that csq (ωt) is a square wave, taking on the values =1 and -1 and having a sign that agrees with that of cos (ωt). Similarly, ssq (ωt) is a square wave whose sign always agrees with the sign of sin (ωt). The above system can be thought of as one whose time evolution is governed by two vector fields. In operation, one switches periodically among the set g1 + g2, g1-g2,-g1 + g2, and-g1-g2. According to the area rule, the response to the sinusoidal system and the response of the square wave system will be nearly the same, provided that the inputs are scaled so as to make the area, in the sense described in the section ''Simple Machines and the Area Rule,'' the same.
Electrochemical batteries generate a steady voltage, which, in the presence of suitable external circuit, will cause a current to flow through them, always in the same direction. By contrast, in almost all cases, electrical power from utility companies is distributed to customers in the form of alternating current, that is, in the form of a current that alternates between the two possible directions of flow many times per second. In some important applications, such as powering electronic equipment and charging rechargeable batteries, it is necessary to convert this alternating current into direct current before it can be used. This process of conversion, called rectification, used to be a relatively inefficient and expensive process, requiting bulky equipment and producing unwanted heat. Today there exist solid state electronic devices capable of providing elegant and efficient solutions to this problem at modest cost. A pervasive problem in electronics is that of producing the required voltages for various applications from a given source. In some cases this means converting battery voltage of 1.5 volts to 12 volts as required for typical electronics applications. To do this one now uses switching converters , which can be thought of as electrical analogs of the problems we have been discussing. In electrical terms, we may say that their operation is based on a sort of "inverse rectification" in which switches are used to generate alternating current. Figure 2.9 shows a circuit with two switches, two inductors, a capacitor, and a battery. The switches allow one to control the evolution of the divers variables that describe the network. The labels u
and ν refer to the two switches and denote variables that represent the position of the switches in the diagram.
The time evolution of this network is governed by a set of equations that are similar to those describing the tanks, although the meaning of the control terms is now different. In terms of the assignments given below, they take the form
If the switch labeled u is closed to the left, then u = 0; if it is closed to the right, then u = 1. We use the same convention for ν. We attach no meaning to other values of u and ν. The variables x, y are the currents through the inductors. The variable z is the voltage across the capacitor. For simplicity, we take the voltage on the battery to be one. If the voltage across the capacitor is small compared to the voltage on the battery, then the νz term in the first equation and the uz term in the second equation can be ignored and, after a relabeling of the controls, the equations become identical to those discussed above.
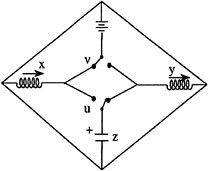
FIGURE 2.9 An electrical network controlled by switches.
THREE THINGS FROM TWO THINGS
One important aspect of nonholonomic systems, not brought out in our discussion above, is the extraordinary possibility of using a relatively small number of inputs to force the system to follow paths in a high dimensional space with small error. We begin our discussion with an analogy from telecommunications.
A single pair of telephone wires can carry many distinct conversations at the same time. Years ago, engineers demonstrated that it is possible to superimpose multiple signals, send them to their
destination, and then disentangle them for delivery to their intended recipient. This is accomplished by recognizing that a speech signal carries most of its useful information in a limited frequency range whereas copper wires can reliably carry signals whose energy occupies a much wider range of frequencies. By mapping different telephone conversations into different, nonoverlapping frequency bands at the sending end, and then reversing the process at the receiving end, one can use the transmission line more efficiently. This is an example of a more abstract circle of ideas involving a general theory of multiplexing, i.e., combining many independent signals into one, and demultiplexing, i.e., separating one signal into many independent ones.
The model nonlinear system we have been using for the purposes of this exposition displays a capability for demultiplexing. It is possible to use it to extract three signals, having a surprisingly high degree of independence, from the two inputs. In Figure 2.10 we diagram the relationship between the various causes and effects represented by the differential equations of our standard model. This type of block diagram differs from the usual physical diagrams, such as that shown in Figure 2.1, in that one does not attempt to be faithful to the physics or spatial relationships but, as happens when one represents natural phenomena in terms of equations, attempts to express the abstract relationships clearly. In this sense such diagrams are just mathematics all over again but now arranged in such a way as to make certain types of interrelationships more obvious.
This diagram depicts a system with two independent inputs and three outputs. Intuition, in many cases backed up by theorems in topology, suggests that one should not be able to control three things with two things. Indeed, if the spaces are finite dimensional and/or the relationships are linear, this idea can be made into a precise statement and proven. The present situation is different. We can get some feeling for it by examining the response to a class of inputs of a particularly simple type. Suppose that we apply the inputs
Assuming the appropriate initial conditions, the resulting response is

This shows that the effect of such an input on x and y can be made as small as we wish by increasing the frequency ω, whereas its effect on z is independent of ω. In fact, one may see here the shadow of a very general fact proven by Liu and Sussmann showing that, in our language, a very wide class of nonlinear controllable systems can act as demultiplexers.
One of the possible interpretations of this idea is that systems such as the two-input, three-output system in Figure 2.10 have approximate inverses. In this case the inverse takes the form of a three-input, two-output precompensator, such that the overall precompensated system is, for low-frequency inputs,
nearly the identity operator. One interesting aspect of these inverse systems is that they are necessarily time-varying even though the original system is described by time-invariant differential equations. This can be interpreted as supporting the need for pattern generation. When one approaches the difficult problem of designing stabilizing feedback control laws for nonholonomic systems from this point of view, it often becomes much easier to understand.
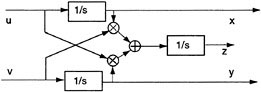
FIGURE 2.10 A block diagram representation of the basic system.
CONCLUSIONS
New ways of thinking about nonlinear systems have lead to new ways of taking advantage of their properties. Nonholonomic systems, a particularly interesting class of nonlinear systems that were once cause for alarm because of their counterintuitive properties, are now being incorporated in practical systems. Some ideas from differential geometry, algebra, and other areas of mathematics have played an important role in this process. In the not too distant future we expect to see some of these ideas being applied to new problems in biological motion control, mechanical design, electronics, and in areas we cannot yet anticipate.
BIBLIOGRAPHY
Brockett, R.W., 1989, "On the Rectification of Vibratory Motion," Sensors and Actuators 20 91-96.
Brockett, R.W., 1983, "Asymptotic Stability and Feedback Stabilization." In: Differential Geometric Control Theory, R.W. Brockett, R. Millman, and H. Sussmann (eds.), Boston: Burkhauser.
Brockett, R.W., 1981, "Control Theory and Singular Riemannian Geometry." In: New Directions in Applied Mathematics, pp. 11-27, P. Hilton and G. Young (eds.), New York: Springer-Verlag.
Brown, G., 1911, "Intrinsic Factors in the Act of Progression of the Mammal," Proc. R. Soc. London 84, 308-319.
Krishnaprasad, P.S., 1990, "Geometric Phases and Optimal Reconfiguration of Multibody Systems," Proceedings of the 1990 Automatic Control Conference, 2440-2444.
Liu, W. and H.J. Sussmann, 1991, "Limits of Highly Oscillatory Controls and the Approximation of General Paths by Admissible Trajectories," Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, England, Dec., 437-442.
Murray, R.M. and S.S. Sastry, 1991, "Steering Nonholonomic Systems Using Sinusoids," Proceedings of the 29th IEEE Conference on Decision and Control, New York.
Severns, R. and E. Bloom, 1987, DC to DC Converters, New York: Van Nostrand.
Shapere, A. and F. Wilczek, 1989, Geometric Phases in Physics, Singapore: World Scientific.
von Euler, K., 1985, "Central Pattern Generation During Breathing." In: The Motor System in Neurobiology, E. Evarts, S. Wise, and D. Bousfield (eds.), Amsterdam: Elsevier Biomedical Press.