1
Geometric Foundations of Motion and Control
Jerrold E. Marsden
Department of Control and Dynamical Systems California Institute of Technology
|
Some interesting aspects of motion and control, such as those found in biological and robotic locomotion and attitude control of spacecraft, involve geometric concepts. When an animal or a robot moves its joints in a periodic fashion, it can rotate or move forward. This observation leads to the general idea that when one variable in a system moves in a periodic fashion, motion of the Whole object can result. This property can be used for control purposes; the position and attitude Of a satellite, for example, are often controlled by periodic motions of parts of the satellite, such as spinning rotors. One of the geometric tools that has been used to describe this phenomenon is that of connections, a notion that is used extensively in general relativity and other parts of theoretical physics. This tool, part of the general subject Of geometric mechanics, has been helpful in the study of both the stability and instability of a system and system bifurcations, that is, changes in the nature of the system dynamics, as some parameter changes. Geometric mechanics, currently in a period of rapid evolution, has been used, for example, to design stabilizing feedback control systems in attitude dynamics. Theory is also being developed for systems with rolling constraints such as those found in a simple rolling wheel. This paper explains how some of these tools of geometric mechanics are used in the study of motion control and locomotion generation. |
INTRODUCTION
We describe below a geometric framework that leads to a better understanding of locomotion generation and motion control in mechanical systems. This introduction provides some basic examples that motivate and set the stage for this framework.
Perhaps the most popular example of the generation of rotational motion is the failing cat, which is able to execute a 180º reorientation, all the while having zero angular momentum. It achieves this by manipulating its joints to create shape changes. To understand this, one has to remember that the angular momentum of a rotating rigid object is its moment of inertia times its instantaneous angular velocity; this
is the angular version of the familiar relation ''momentum equals mass times velocity.'' Shape changes result in a change in the cat's moment of inertia and this, together with the constancy of the angular momentum, creates the overall orientation change. However, the exact process by which this occurs is subtle, and intuitive reasoning can lead one astray. While this problem has been long studied (e.g., by Kane and Shur, 1969), recently new and interesting insights have been discovered using geometric methods (see Enos, 1993; Montgomery, 1990, and references therein).
Astronauts who wish to reorient themselves in a free space environment can similarly do so by means of shape changes. For example, holding one of their legs straight, they can swivel it at the hip, moving their foot in a circle. When they have achieved the desired orientation, they merely stop their leg movement. Similar movements for robots and spacecraft can be controlled automatically to achieve desired objectives (see, for example, Walsh and Sastry, 1995). One often refers to the extra motion that is achieved as the geometric phase.
The history of this phenomenon and its applications is a long and complex story. We shall only mention a few highlights. Certainly the shift in the plane of the swing in the Foucault pendulum as the earth rotates once around its axis is one of the earliest examples of this phenomenon. Anomalous spectral shifts in rotating molecules are another. Phase formulas for special problems such as rigid body motion and polarized light in helical fibers were understood already in the early 1950s. Additional historical comments and references can be found in Berry (1990), and Marsden and Ratiu (1994). Gradually the subject became better understood, but the first paper to clarify and emphasize the ubiquity of the geometry behind all these phenomena was Berry (1985). It was also quickly realized that the phenomenon occurs in essentially the same way in both classical and quantum mechanics (Hannay, 1985), and that the phenomenon can be linked in a fundamental way with the presence of symmetry (Montgomery, 1988; Marsden et al., 1990).
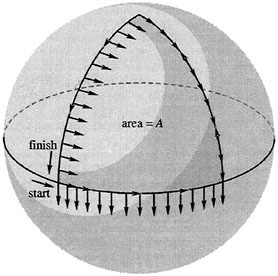
The theory of geometric phases has an interesting link with noneuclidean geometry, a subject first invented for its own sake, without regard to applications. A simple way to explain this link is as follows. Hold your hand at arm's length, but allow rotation in your shoulder joint. Move your hand along three great circles, forming a triangle on the sphere, and during the motion, keep your thumb "parallel," that is, forming a fixed angle with the direction of motion. After completing the circuit around the triangle, your thumb will return rotated through an angle relative to its starting position (see Figure 1.1). In fact, this angle (in radians) is given by Θ = Δ-π where Δ is the sum of the angles of the triangle. The fact that ![]() is of course one of the basic facts of noneuclidean geometry—in curved spaces, the sum of the angles of a triangle is not necessarily z (i.e., 180º). This angle is also related to the area A enclosed by the triangle through the relation Θ = A/r2, where r is the radius of the sphere.
is of course one of the basic facts of noneuclidean geometry—in curved spaces, the sum of the angles of a triangle is not necessarily z (i.e., 180º). This angle is also related to the area A enclosed by the triangle through the relation Θ = A/r2, where r is the radius of the sphere.
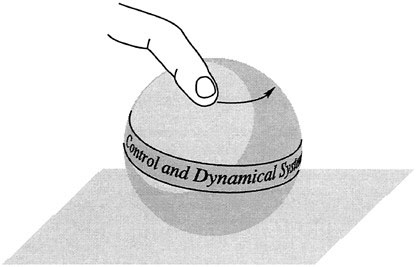
The examples presented so far are rather different from what one finds in many other mechanical systems of interest in one crucial aspect—the absence of constraints of rolling, sliding, or contact. For example, when one parks a car, the steering mechanism is manipulated and movement into the parking spot is generated; obviously the rolling of the wheels on the road is crucial to the maneuver. When a human or a robot manipulates an object in its fingers (imagine twirling an egg in your fingers), it can reorient the object through the rolling of its fingers on the object. This can be shown in a demonstration I learned from Roger Brockett: roll your fingers in a rotating motion on a ball resting on a table—you will find that the ball reorients itself under your finger! The amount of rotation is again related to the amount of area you capture in the rotating motion. You have generated rotational motion! (See Figure 1.2.)
In all these cases, cyclic motion in one set of variables (often called the internal variables) produces motion in another set (often called the group variables). This idea is central to the basic geometric framework described in ensuing sections.
One can generate translational motion as well as rotational motion. For example, microorganisms and snakes generate translations by a very specific cyclic manipulation of their internal variables (Shapere and Wilczek, 1987). The reason for this is, in a superficial sense, that in these examples, translation is kinematically possible (translations are available as group variables) and the controls are such that these variables are activated. Often translational motion and rotational motion are coupled in interesting ways, as in the snakeboard, a modification of the familiar skateboard. This modification allows the rider to rotate the front and back wheels by rotating his feet and this, together with the rotary motion of the rider's body, allows both translational and rotational motion to be generated. Such motion can be controlled with the objective that desired motions be generated. We will discuss this example in a little more detail in the section entitled "The Snakeboard," below.
The generation of motion in small robotic devices is very promising for medical applications. In this context, one seeks devices that can move in confined spaces under variable conditions (flexible walls, tight comers, etc.). In fact, this general philosophy is one of the reasons one hopes that medical operations in the future will be much less intrusive than many of them are now.
There are similar links between vibratory motion and translational and rotational motion (e.g., the developments of micromotors) (Brockett, 1989), on the one hand, and, on the other hand, motion generation in animals (e.g., the generation and control of waves from coupled oscillators, as seen in the swimming of fish and in the locomotion of insects and other creatures).
A central question to address in this area is, How should one control motions of the internal variables so that the desired group (usually translational and rotational) motions are produced? To make progress on this question, one needs to combine experience with simple systems and strategies—such as steering with sinusoids, as in Murray and Sastry (1993)—with a full understanding of the mathematical structure of the mechanical systems, both analytical and geometrical. We also mention the work of Brockett (1981), which shows that for certain classes of control systems that are controllable via first level brackets, steering by sinusoids is, in fact, optimal.
CONNECTIONS AND BUNDLES
One of the fruitful ideas from geometry that has been used in the investigation of mechanical systems is that of a connection. While the notion of a connection is quite precise, connections have many personalities. On the one hand, one thinks of them as describing how curved a space is; in fact, in the classical Riemannian setting used by Einstein in his theory of general relativity, the curvature of the space is constructed out of the connection (in that case, also called the Christoffel symbols). In other, but related, settings developed by Eli Cartan, the connection is what is responsible for a corrected measure of acceleration; for example, if one is on a rotating merry-go-round, one has to correct any measurement of acceleration to take into account the acceleration of the merry-go-round, and this correction can be described by a connection.
In the general theory, connections are associated with mappings, called bundle mappings, that project larger spaces onto smaller ones, as in Figure 1.3. The larger space is called the bundle and the
smaller space is called the base. Directions in the larger space that project to zero are called vertical directions. The general definition of a connection is a specification of a set of directions, called horizontal directions, that complements at each point the space of vertical directions.
In the example of parallel transport of the thumb around the sphere, the larger space is the space of all tangent vectors to the sphere, and this space projects to the sphere itself by projecting a vector to its point of attachment to the sphere. The horizontal directions are the directions with zero acceleration within the intrinsic geometry of the sphere; that is, the directions determined by great circles.
In the thumb example, we saw that going around the triangle produces a change in the orientation of the thumb on return. The thumb is parallel transported, that is, it moves in horizontal directions with respect to the connection. The thumb has undergone a rotational shift from the beginning to the end of its journey.
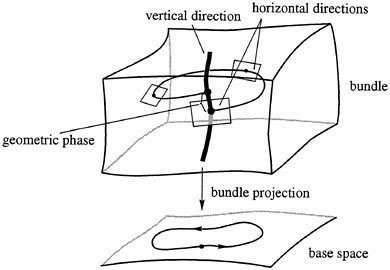
Figure 1.3 A connection divides the space into vertical and horizontal directions.
In general, we can expect that if we have a horizontal motion in the bundle and if the corresponding motion in the base is cyclic, then the horizontal motion will undergo a shift, which we will call a phase shift, between the beginning and the end of its path. The shift in the vertical direction is often given by an element of a group, such as a rotation or translation group. In many of the examples discussed so far, the base space is the control space in the sense that the path in the base can be chosen by suitable controls. The path above it in the bundle is regarded as being determined by the condition of horizontality. This condition therefore determines its phase.
This setting of connections provides a framework in which one can understand the phrase we started with: when one variable in a system moves in a periodic fashion, motion of the whole object can result. Here, the "motion of the whole object" is represented by the geometric phase. Coming along with
this notion are plenty of lovely theorems and calculational tools; for example, one of these (based on Stokes' theorem) shows how to calculate the geometric phase in terms of the integral of the curvature of the connection over an area enclosed by the closed curve on the base. This is one reason that areas so commonly appear in geometric phase formulas.
Connections are ubiquitous in geometry and physics. For example, connections are one of the main ingredients in the modem theory of elementary particles, and are the primary fields in Yang-Mills theory, a generalization of Maxwell's electromagnetic theory. In fact, in electromagnetism, the equation ![]() for the magnetic field may be thought of as an expression for the curvature of the connection (or magnetic potential) A.
for the magnetic field may be thought of as an expression for the curvature of the connection (or magnetic potential) A.
CONSTRAINTS: ANGULAR MOMENTUM AND ROLLING
In many mechanical systems, there are conditions called "constraints." For our purposes, these are of two fundamentally different sorts. The first is typified by the constraint of zero angular momentum for the falling cat. The cat, once released, and before it reaches the ground, cannot change the fact that its angular momentum is zero, no matter how it moves its body parts. We choose the cat's base space to be its shape space, which does indeed literally mean what it says—the collection of all the shapes of its body, which can be specified by giving the angles between its body parts. The bundle in this case consists of these shapes together with a rotation and translation to specify the position and orientation in space. Since the cat is free to manipulate its shape using its muscles, it can perform maneuvers, some of them cyclic, in shape space. Meanwhile, how the cat turns in space is governed by the law of conservation of angular momentum. It turns out that this law exactly defines the horizontal space of a connection! The connection in this case is called the "mechanical connection." That this corresponds to a connection was discovered through the combined efforts of Smale (1970), Abraham and Marsden (1978), and Kummer (1981). Thus, when one puts together the theory of connections with this observation, and throws in control theory, one has the beginnings of the "gauge theory of mechanics." This theory has been extended and developed by many workers since then.
Observation of the motions of a mechanical system in its shape space shows a relation to the theory of reduction, a theory that seeks to make the configuration space of a mechanical system smaller by taking advantage of symmetries. This method has led to many interesting and unexpected discoveries about mechanics, including, for example, the explanation of the integrability of the Kowaleskaya top in terms of symmetry by Bobenko et al. (1989). (An algebraic-geometric construction with similar goals was found by Haine, Horozov, Adler, and van Moerbeke around the same time.) Observing the motion in shape space alone is similar to watching the shapes change relative to an observer riding with the object. In such a frame, one sees what seem to be extra forces, namely the Coriolis and centrifugal forces. In fact, these forces can be understood in terms of the curvature of the mechanical connection. Then the problem of finding the original complete path is one of finding a horizontal path above the given one. This is sometimes called the "reconstruction problem." We conclude that the generation of geometric phases is closely linked with the reconstruction problem.
One of the simplest systems in which one can see these phenomena is called the planar skater. This device consists of three coupled rigid bodies lying in the plane. They are free to rotate and translate in the plane, somewhat like three linked ice hockey pucks. This has been a useful model example for a
number of investigations, and was studied fairly extensively in Oh et al. (1989), and Krishnaprasad (1989) and references therein. The only forces acting on the three bodies are the forces they exert on each other as they move. Because of their translational and rotational invariance, the total linear and angular momentum remains constant as the bodies move. This holds true even if one applies controls to the joints of the device; this is because the conservation of momentum depends only on externally applied forces and torques. See Figure 1.4.
The planar skater illustrates well some of the basic ideas of geometric phases. If the device starts with zero angular momentum and it moves its arms in a periodic fashion, then the whole assemblage can rotate, keeping, of course, zero angular momentum. This is analogous to our astronaut in free space who rotates his arms or legs in a coordinated fashion and finds that he rotates. One can understand this simple example directly by using conservation of angular momentum. In fact, the definition of angular momentum allows one to reconstruct the overall attitude of the device in terms of the motion of the joints using freshman calculus. Doing so, one gets a motion generated in the overall attitude, which is indeed a geometric phase. This example is sufficiently simple that one does not need the geometry of connections to understand it, but nonetheless it provides a simple situation in which one can test the ideas. For more complex examples, such as the falling cat, the geometric setting of connections has indeed proven useful.
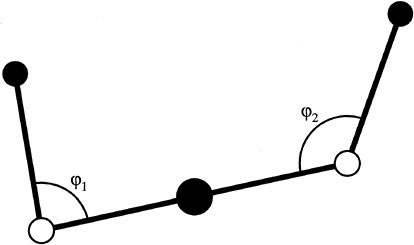
FIGURE 1.4 The planar skater consists of three interconnected bodies that are free to rotate about their joints.
To indicate some of the flavor of three-dimensional examples, we discuss the rigid body. Each position of the rigid body is specified by a Euclidean motion giving the location and orientation of the body. The motion is then governed by the equations of mechanics in this space. Assuming that no external forces act on the body, conservation of linear momentum allows us to solve for the components of the position and momentum vectors of the center of mass. Passage to the center of mass frame reduces one to the case where the center of mass is fixed, so only pure rotations remain. Each possible orientation corresponds to the specification of a proper orthogonal matrix A. Back in 1740, Euler parametrized the
matrix A in terms of three (Euler) angles between axes that are either fixed in space or are attached to symmetry planes of the body's motion.
We regard the element ![]() giving the configuration of the body as a mapping of a reference configuration to the current configuration. The matrix A takes a reference or label point X to a current point x = A(X). For a rigid body in motion, the matrix A is time dependent and the velocity of a point of the body is
giving the configuration of the body as a mapping of a reference configuration to the current configuration. The matrix A takes a reference or label point X to a current point x = A(X). For a rigid body in motion, the matrix A is time dependent and the velocity of a point of the body is ![]() . Since A is an orthogonal matrix, we can write
. Since A is an orthogonal matrix, we can write ![]() , which defines the spatial angular velocity vector ω .The corresponding body angular velocity is defined by Ω; = A-1ω, so that Ω; is the angular velocity as seen in a body-fixed frame. The kinetic energy is given by integrating the kinetic energy expression for particles (one-half the mass density times the square of the velocity) over the reference configuration. In fact, this kinetic energy is a quadratic function of Ω;. Writing
, which defines the spatial angular velocity vector ω .The corresponding body angular velocity is defined by Ω; = A-1ω, so that Ω; is the angular velocity as seen in a body-fixed frame. The kinetic energy is given by integrating the kinetic energy expression for particles (one-half the mass density times the square of the velocity) over the reference configuration. In fact, this kinetic energy is a quadratic function of Ω;. Writing  defines the (time independent) moment of inertia tensor I, which, if the body does not degenerate to a line, is a positive definite 3 × 3 matrix, or better, a quadratic form. Every calculus student learns how to calculate moments of inertia as illustrations of the process of multiple integration.
defines the (time independent) moment of inertia tensor I, which, if the body does not degenerate to a line, is a positive definite 3 × 3 matrix, or better, a quadratic form. Every calculus student learns how to calculate moments of inertia as illustrations of the process of multiple integration.
The equations of motion in A space define certain equations in Ω; space that were discovered by Euler: ![]() . The body angular momentum is defined, analogous to linear momentum p = mv, as Π = IΩ;. In terms of Π, the Euler equations read Π = Π × Ω;. This equation implies that the spatial angular momentum vector π = AΠ is fixed in time. One may view this fact as a conservation law that results from the rotational symmetry of the problem. These and other facts given here are proven in every mechanics textbook, such as Marsden and Ratiu (1994).
. The body angular momentum is defined, analogous to linear momentum p = mv, as Π = IΩ;. In terms of Π, the Euler equations read Π = Π × Ω;. This equation implies that the spatial angular momentum vector π = AΠ is fixed in time. One may view this fact as a conservation law that results from the rotational symmetry of the problem. These and other facts given here are proven in every mechanics textbook, such as Marsden and Ratiu (1994).
Viewing the components (Π1,Π2,Π3) of Π as coordinates in three-dimensional space, the Euler equations are evolution equations for a point in this space. A constant of motion for the system is given by the square length of the total angular momentum vector: ![]() . This follows from conservation of π and the fact that
. This follows from conservation of π and the fact that ![]() or can be verified directly from the Euler equations by computing the time derivative of
or can be verified directly from the Euler equations by computing the time derivative of ![]() .
.
Because of conservation of ![]() , the evolution in time of any initial point Π(0) is constrained to the sphere
, the evolution in time of any initial point Π(0) is constrained to the sphere ![]() . Thus we may view the Euler equations as describing a two-dimensional dynamical system on an invariant sphere. This sphere is called the reduced-phase space for the rigid body equations. Another constant of the motion is the Hamiltonian or energy:
. Thus we may view the Euler equations as describing a two-dimensional dynamical system on an invariant sphere. This sphere is called the reduced-phase space for the rigid body equations. Another constant of the motion is the Hamiltonian or energy: ![]() . Since solutions curves are confined to the sets where H is constant, which are in general ellipsoids, as well as to the invariant spheres where
. Since solutions curves are confined to the sets where H is constant, which are in general ellipsoids, as well as to the invariant spheres where ![]() = constant, the intersection of these surfaces is precisely that of the trajectories of the rigid body, as shown in Figure 1.5.
= constant, the intersection of these surfaces is precisely that of the trajectories of the rigid body, as shown in Figure 1.5.
Let us briefly indicate how geometric phases come into the rigid body example. Suppose we are given a trajectory Π(t) on Pμ that has period T and energy E. After time T the rigid body has rotated in physical 3-space about the axis μ by an angle given by
Here Λ is the solid angle enclosed by the curve Π(t) on the sphere and is oriented according to the right-hand rule, and k is an integer (reflecting the fact that we are really only interested in angles up to multiples of 2π).
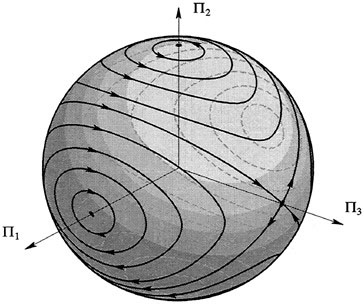
FIGURE 1.5 The solutions of Euler's equations for rigid body motion.
An interesting feature of this formula is the fact that Δθ splits into two parts. The term A is the purely geometric quantity, the geometric phase. It does not depend on the energy of the system or the period of motion, but rather on the fraction of the surface area of the sphere that is enclosed by the trajectory. The second term, the dynamic phase, depends on the system's energy and the period of the trajectory.
Geometrically we can picture the rigid body as tracing out a path in its phase space; that is, the space of rotations (playing the role of positions) and corresponding momenta with the constraint of a fixed value of the spatial angular momentum. The phase space plays the role of the bundle, and the projection map to the base, the momentum sphere, is the map we described earlier that takes the orientation A and its velocity (or momentum) to the body momentum sphere. As Figure 1.5 shows, almost every trajectory on the momentum sphere is periodic, but this does not imply that the original curve of rotations was periodic, as is shown in Figure 1.6. The difference between the true trajectory and
a periodic trajectory is given by the geometric plus the dynamic phase. Although this figure is given in the context of rigid body dynamics, its essential features are true for any mechanical system with symmetry.
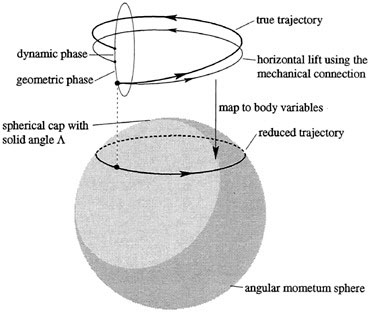
FIGURE 1.6 The geometric phase formula for rigid body motion.
This formula for the rigid body phase has a long and interesting history. It was known in classical books, such as that of Whittaker, in terms of quotients of theta functions, but not in terms of areas, as above. This aspect was discovered in the 1950s independently in work of Ishlinskii and of Goodman and Robinson. Montgomery (1991b,c) and Marsden et al. (1990) showed, following the lead of Berry and Hannay, that the formula can be interpreted in terms of holonomy of a connection. Further historical details may be found in Marsden and Ratiu (1994).
It is possible to observe some aspects of the geometric phase formula for a rigid body with a simple experiment. Put a rubber band around a book so that the cover will not open. (A tall thin book works best.) With the front cover facing up, gently toss the book in the air so that it rotates about its middle axis. Catch the book after a single rotation and you will find that it has also rotated by 180º about its long axis; that is, the front cover is now facing the floor.
In addition to its use in understanding phases, the mechanical connection has been helpful in stability theory. For example, when a rigid body such as a satellite tumbles about its long or short axis, it does so stably, but it is unstable when it rotates about the middle axis. When one takes into account small dissipative effects such as a vibrating antenna, then the rotational motion about the long axis becomes
unstable as well, but this effect is more delicate. Corresponding statements for systems like rigid bodies with flexible appendages or interconnected rigid bodies are more subtle than the dynamics of a single rigid body. There is a powerful method for determining the stability of such solutions called the energy momentum method. This method is an outgrowth of basic work of Riemann, Poincaré, and others in the last century and more recently by Arnold; further recent developments were made by Simo et al. (1991), and Bloch et al. (1994, 1996) and references therein. Here the main problem is to split the variables properly into those that correspond to internal, or shape, changes, and to those that correspond to rotational and translational motions. Interestingly, the mechanical connection plays a key role in the solution of this problem and it makes many otherwise intractable problems soluble.
This gauge theory of mechanics has been successful for a number of important problems, such as the falling cat problem, as we shall discuss below. Nevertheless, there is another important class of problems that it does not apply to as stated, namely, mechanical systems with rolling constraints, typified by the constraint that a wheel or ball rolls without slipping on a plane. One very simple idea ties this type of problem to the zero angular momentum constraint problem that was just described. This idea is that of realizing the constraint as the horizontal space of a connection. In fact, the constraint itself defines a connection by declaring the constraint space to be the horizontal space. This, in effect, defines the connection. In the case of rolling constraints, we call this connection the kinematic connection to avoid confusion with the mechanical connection described earlier. This point of view for systems with rolling (and rolling type) constraints was developed by Koiller (1992) and by Bloch et al. (1997). For example, the equations of motion expressed on the base space again involve the curvature of the kinematic connection. This shows again that the links with geometry are strong at a very basic level.
Things get even more interesting when the system has both rolling constraints and symmetry. Then we have the kinematic connection as well as the symmetry group to deal with, but now they are interlinked. One of the things that makes systems with rolling constraints with symmetry different from free systems is that the law of conservation of angular momentum is no longer valid for them. This is already well illustrated by a toy called the rattleback, a canoe-shaped piece of wood or plastic. When the rattleback rocks on a flat surface like a table, the rocking motion induces a rotational motion, so that it can go from zero to nonzero angular momentum about the vertical axis as a result of the interaction of the rocking and rotational motion and the rolling constraint with the table. One can say that the forces of constraint that enforce the condition of rolling can upset the balance of angular momentum. This is also the case for the snakeboard discussed below, but nonetheless, this rams out to be a key point in understanding locomotion generation for this system. One of the interesting aspects of this is that, as shown by Bloch et al. (1996), there is a very nice equation satisfied by a particular combination of the linear and angular momentum, which they call the momentum equation. Because of that success, one can imagine that this understanding will be important for many other similar systems as well.
STABILIZATION AND OPTIMAL CONTROL
Control theory is closely tied to dynamical systems theory in the following way. Dynamical systems theory deals with the time evolution of systems by writing the state of the system, say z in a general space P, and writing an evolution equation
for the motion, where μ includes other parameters of the system (masses, lengths of pendula, etc.). The equations themselves include things like Newton's second law, the Hodgkin-Huxley equations for the propagation of nerve impulses, and Maxwell's equations for electrodynamics, among others. Many valuable concepts have developed around this idea, such as stability, instability, and chaotic solutions.
Control theory adds to this the idea that in many instances, one can directly intervene in the dynamics rather than passively watching it. For example, while Newton's equations govern the dynamics of a satellite, we can intervene in these dynamics by controlling the onboard gyroscopes. One simple way to describe this mathematically is by making f dependent on additional control variables u that can be functions of t, z, and μ. Now the equation becomes
and the objective, naively stated, is with an appropriate dependence of f on u to choose the function u itself to achieve certain desired goals. Control engineers are frequently tempted to overwhelm the intrinsic dynamics of a system with the control. However, in many circumstances (fluid control is an example—see, for example, the discussion in Bloch and Marsden, 1989), one needs to work with the intrinsic dynamics and make use of its structure.
Two of the basic notions in control theory involve steering and stabilizability. Steering has, as its objective, the production of a control that has the effect of joining two points by means of a solution. One imagines manipulating the control, much the way one imagines driving a car so that the desired destination is attained. This type of question has been the subject of extensive study and many important and basic questions have been solved. For example, two of the main themes that have developed are, first, the Lie algebraic techniques based on brackets of vector fields (in driving a car, you can repeatedly make two alternating steering motions to produce a motion in a third direction) and, second, the application of differential systems (a subject invented by Elie Cartan in the mid-1920s whose power is only now being significantly tapped in control theory). The work of Tilbury et al. (1993) and Walsh and Bushnell (1993) typify some of the recent applications of these ideas.
The problem of stabilizability has also received much attention. Here the goal is to take a dynamic motion that might be unstable if left to itself but that can be made stable through intervention. A famous example is the F-15 fighter, which can fly in an unstable (forward wing swept) mode but which is stabilized through delicate control. Flying in this mode has the advantage that one can execute tight turns with rather little effort—just appropriately remove the controls! The situation is really not much different from what people do everyday when they ride a bicycle. One of the interesting things is that the subjects that have come before—namely, the use of connections in stability theory—an be turned around to be used to find useful stabilizing controls, for example, how to control the onboard gyroscopes in a spacecraft to stabilize the otherwise unstable motion about the middle axis of a rigid body (see Bloch et al., 1992; Kammer and Gray, 1993).
Another issue of importance in control theory is that of optimal control. Here one has a cost function (think of how much you have to pay to have a motion occur in a certain way). The question is
not just if one can achieve a given motion but how to achieve it with the least cost. There are many well-developed tools to attack this question, the best known of these being what is called the Pontryagin Maximum Principle. In the context of problems like the falling cat, a remarkable consequence of the Maximum Principle is that, relative to an appropriate cost function, the optimal trajectory in the base space is a trajectory of a Yang-Mills particle. The equations for a Yang-Mills particle are a generalization of the classical Lorentz equations for a particle with charge e in a magnetic field B:
where v is the velocity of the particle and where c is the velocity of light. The mechanical connection comes into play though the general formula for the curvature of a connection; this formula is a generalization of the formula ![]() expressing the magnetic field as the curl of the magnetic potential. This remarkable link between optimal control and the motion of a Yang-Mills particle is due to Montgomery (1990, 1991a).
expressing the magnetic field as the curl of the magnetic potential. This remarkable link between optimal control and the motion of a Yang-Mills particle is due to Montgomery (1990, 1991a).
One would like to make use of results like this for systems with rolling constraints as well. For example, one can (probably naively, but hopefully constructively) ask what is the precise connection between the techniques of steering by sinusoids mentioned earlier and the fact that a particle in a constant magnetic field also moves by sinusoids, that is, moves in circles. Of course if one can understand this, it immediately suggests generalizations by using Montgomery's work. This is just one of many interesting theoretical things that requires more investigation. One of the positive things that has already been achieved by these ideas is the beginning of a deeper understanding of the links between mechanical systems with angular momentum type constraints and those with rolling constraints. The use of connections has been one of the valuable tools in this endeavor. One of the papers that has been developing this point of view is that of Bloch et al. (1997). We shall see some further glimpses into that point of view in the next section.
THE SNAKEBOARD
The snakeboard is an interesting example that illustrates several of the ideas we have been discussing (see Lewis et al., 1997). This device is a modification of the standard skateboard, the most important of which is that riders can use their feet to independently turn the front and back wheels—in the standard skateboard, these wheels are of course fixed to the frame of the skateboard. In addition, one can manipulate one's body using a swivelling motion and this motion is coupled to the motion of the snakeboard itself. We show the snakeboard schematically in Figure 1.7.
One of the fascinating things about the snakeboard is that one can generate locomotion without pedaling, solely by means of internal motions. When the user's feet and body are moved in the right way, rotational and translational motion of the device can be generated. The snakeboard is simple enough that one can study many parts of it analytically and numerical simulations of its motion are reasonably economical to implement. On the other hand, it seems to have all of the essential features that one would want for more complex systems, the main one for the present goals being its ability to generate rotational and translational motion. From the mathematical and mechanical point of view, it is rich in geometry and
in symmetry structure, which also makes it attractive. Thus, it provides a good testing and development ground for both theoretical and numerical investigations.
From the theoretical point of view, one feature of the snakeboard that sets it truly apart from examples like the planar skater and the falling cat is that even though it has the symmetry group of rotations and translations of the plane, the linear and angular momentum is not conserved. Recall that for the planar skater, no matter what motions the arms of the device make, the values of the linear and angular momentum cannot be altered. This is not true for the snakeboard and this can be traced to the presence of the forces of constraint, just as in the rattleback mentioned earlier. Thus, one might suspect that one should abandon the ideas of linear and angular momentum for the snakeboard. However, a deeper inspection shows that this is not the case. In fact, one finds that there is a special component of the angular momentum, namely that about the point P shown in Figure 1.8.
If we call this component p, one finds that, due to the translational and rotational invariance of the whole system, there is a ''momentum equation'' for p of the form
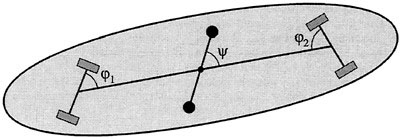
FIGURE 1.7 The snakeboard has three movable internal parts, the front and back wheels and the angle of the rider's body.
where x represents the internal variables of the system (the three angles shown in the preceding figure). The point is that this equation does not depend on the rotational and translational position of the system. Thus, if one has a given internal motion, this equation can be solved for p and, from it, the attitude and position of the snakeboard calculated by means of another integration. This strategy is thus parallel to that for the falling cat and the planar skater.
With this set-up, one is now in a good position to identify the resulting geometric phase with the holonomy of a connection that is a synthesis of the kinematic and mechanical connection. Carrying this out and implementing these ideas for more complex systems is in fact the subject of current research.
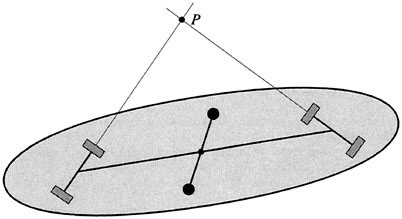
FIGURE 1.8 The angular momentum about the point P plays an important role in the analysis of the snakeboard.
ACKNOWLEDGMENTS
Thanks are extended to John Tucker, Tony Bloch, Roger Brockett, Joel Burdick, P.S. Krishnaprasad, Andrew Lewis, Richard Montgomery, Richard Murray, Jim Ostrowski, Tudor Ratiu, Shankar Sastry, Greg Walsh, and Jeff Wentlandt for their kind advice and help.
REFERENCES
Abraham, R. and J.E. Marsden, 1978, Foundations of Mechanics, Second Edition, Reading, Mass.: Addison-Wesley.
Berry, M., 1990, "Anticipations of the geometric phase," Physics Today, December, 34-40.
Berry, M., 1985, "Classical adiabatic angles and quantal adiabatic phase," J. Phys. A. 18, 15-27.
Bloch, A.M., P.S. Krishnaprasad, J.E. Marsden, and R.M. Murray, 1997, "Nonholonomic systems with symmetry," Arch. Rat. Mech. Anal. (to appear).
Bloch, A.M., P.S. Krishnaprasad, J.E. Marsden, and T.S. Ratiu, 1996, "The Euler-Poincaré equations and double bracket dissipation," Commun. Math. Phys. 175, 1-42.
Bloch, A.M., P.S. Krishnaprasad, J.E. Marsden, and T.S. Ratiu, 1994, "Dissipation Induced Instabilities," Ann. Inst. H. Poincaré, Analyse Nonlinßaire 11, 37-90.
Bloch, A.M., P.S. Krishnaprasad, J.E. Marsden, and G. Sánchez de Alvarez, 1992, "Stabilization of rigid body dynamics by internal and external torques," Automatica 28, 745-756.
Bloch, A.M. and J.E. Marsden, 1989, "Controlling homoclinic orbits," Theor. Comput. Fluid Mech. 1, 179-190.
Bobenko, A.I., A.G. Reyman, and M.A. Semenov-Tian-Shansky, 1989, "The Kowalewski Top 99 years later: A Lax pair, generalizations and explicit solutions," Commun. Math. Phys. 122, 321-354.
Brockett, R.W., 1989, "On the rectification of vibratory motion," Sensors and Actuators 20, 91-96.
Brockett, R.W., 1981, "Control theory and singular Riemannian geometry." In: New Directions in Applied Mathematics, P.J. Hilton and G.S. Young (eds.), Berlin, Heidelberg, New York: Springer-Verlag.
Enos, M. (ed.), 1993, "Dynamics and Control of Mechanical Systems: The Falling Cat and Related Problems," Fields Institute Communications , Vol. 1, Providence, RI: American Mathematical Society.
Hannay, J., 1985, "Angle variable holonomy in adiabatic excursion of an itegrable Hamiltonian," J. Phys. A 18, 221-230.
Kammer, D.C. and G.L. Gray, 1993, "A nonlinear control design for energy sink simulation in the Euler-Poinsot problem," J. Astron. Sci. 41, 53-72.
Kane, T.R., and M. Shur, 1969, "A dynamical explanation of the falling cat phenomenon," Int. J. Solid Structures 5, 663-670.
Koiller, J., 1992, "Reduction of some classical nonholonomic systems with symmetry," Arch. Rat. Mech. Anal. 118, 113-148.
Krishnaprasad, P.S., 1989, "Eulerian many-body problems," Cont. Math. AMS 97, 187-208.
Kummer, M., 1981, "On the construction of the reduced phase space of a Hamiltonian system with symmetry," Indiana Univ. Math. J. 30, 281-291.
Lewis, A., R.M. Murray, J.P. Ostrowski, and J. Burdick, 1997, "Nonholonomic mechanics and locomotion: the snakeboard example," IEEE Intern. Conf. on Robotics and Automation, to appear.
Marsden, J.E. and T.S. Ratiu, 1994, "An Introduction to Mechanics and Symmetry" Texts in Applied Mathematics, Berlin, Heidelberg, New York: Springer-Verlag.
Marsden, J.E., R. Montgomery, and T.S. Ratiu, 1990, "Reduction, symmetry, and phases in mechanics," Memoirs AMS 436.
Montgomery, R., 1991a, "Optimal Control of Deformable Bodies and Its Relation to Gauge Theory." In: The Geometry of Hamiltonian Systems , T. Ratiu (ed.), Berlin, Heidelberg, New York: Springer-Verlag.
Montgomery, R., 1991b, "How much does a rigid body rotate? A Berry's phase from the 18th century," Am. J. Phys. 59, 394-398.
Montgomery, R., 1991c, "Optimal control of deformable bodies and its relation to gauge theory," In The Geometry of Hamiltonian Systems , T. Ratiu (ed.), Berlin, Heidelberg, New York: Springer-Verlag.
Montgomery, R., 1990, "Isoholonomic problems and some applications," Commun. Math. Phys. 128, 565-592.
Montgomery, R., 1988, "The connection whose holonomy is the classical adiabatic angles of Hannay and Berry and its generalization to the non-integrable case," Commun. Math. Phys. 120, 269-294.
Murray, R.M. and S.S. Sastry, 1993, "Nonholonomic Motion Planning: Steering Using Sinusoids," IEEE Trans. Autom. Control 38, 700-716.
Oh, Y.G., N. Sreenath, P.S. Krishnaprasad, and J.E. Marsden, 1989, "The Dynamics of Coupled Planar Rigid Bodies Part 2: Bifurcations, Periodic Solutions, and Chaos," Dynamics and Differential Equations 1, 269-298.
Shapere, A. and F. Wilczek, 1987, "Self-propulsion at low Reynolds number," Physical Review Letters 58, 2051-2054.
Simo, J.C., D.R. Lewis, and J.E. Marsden, 1991, "Stability of relative equilibria I: The reduced energy momentum method," Arch. Rat. Mech. Anal. 115, 15-59.
Smale, S., 1970, "Topology and Mechanics," Invent. Math. 10, 305-331, 11, 45-64.
Sreenath, N., Y.G. Oh, P.S. Krishnaprasad, and J.E. Marsden, 1988, "The dynamics of coupled planar rigid bodies. Part 1: Reduction, equilibria and stability," Dynamics and Stability of Systems 3, 25-49.
Tilbury, D., R. Murray, and S. Sastry, 1993, "Trajectory generation for the N-trailer problem using Goursat normal form," Proc. IEEE Control and Decision Conf., San Antonio, Dec. 1993.
Walsh, G. and L. Bushnell, 1993, "Stabilization of multiple input chained from control systems," Proc. IEEE Control and Decision Conf ., San Antonio, Dec. 1993.
Walsh, G. and S. Sastry, 1995, "On reorienting linked rigid bodies using internal motions," IEEE Trans. on Robotics and Automation 11 (1), 139-146.