4
Motion Control and Coupled Oscillators
P. S. Krishnaprasad
Department of Electrical Engineering and Institute for Systems Research University of Maryland
|
It is remarkable that despite the presence of large numbers of degrees of freedom, motion control problems are effectively solved in biological systems. While feedback, regulation, and tracking have served us well in engineering as useful solution paradigms for a wide variety of control problems, including motion control, it appears that nature gives prominent roles to planning and coordination as well. There is also complex interplay between sensory feedback and motion planning to achieve effective operation in uncertain environments (in movement on uneven terrain cluttered with obstacles, for example). Recent investigations by neurophysiologists have brought to increasing prominence the idea of central pattern generators (a class of coupled oscillators) as sources of motion "scripts" as well as a means for coordinating multiple degrees of freedom. The role of coupled oscillators in motion control systems is currently under intense investigation. In this paper we examine some unifying themes relating movement in biological systems and machines. An important insight in this direction comes from the natural grouping of degrees of freedom and time scales in biological and engineering systems. Such grouping and separation can be treated from a geometric viewpoint using the formalisms and methods of differential geometry, Lie groups, and fiber bundles. Coupled oscillators provide the means to bind degrees of freedom either directly through phase locking or indirectly through geometric phases. This point of view leads to fresh ways of organizing the control structures of complex technological systems. |
INTRODUCTION
In optics, lithography applications in microelectronics, and in a variety of other contexts, the need for high-resolution motion control with high accuracy is met by specialized actuators that are quite different in their principles of operation from everyday devices such as electromagnetic motors. One
such device, manufactured by Burleigh Instruments under the trademark INCHWORM™, is illustrated in Figure 4.1.
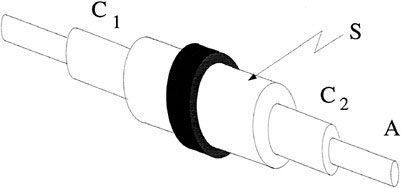
FIGURE 4.1 INCHWORM™ clamps C1, C2, stretcher S, and armature A.
This actuator, consisting of three sleeves/tubes made from piezoelectric material mounted on a frame and enclosing a linear armature, works on the physical principle that the piezoelectric material deforms under electrical stimulus (the outer sleeves independently clamp down, and the middle sleeve stretches in length). Running the actuator through a succession of clamp-stretch-unclamp-unstretch cycles, one generates incremental motion of the armature in a specified direction. It is possible to make linear movements as small as 4 nanometers. Other actuators based on piezoelectric effects are increasingly finding their way into consumer products, including ultrasonic motors for autofocusing in cameras based on surface wave excitation (see Ueha and Tomikawa, 1993, for detailed discussions of these devices). A common design principle in these devices is a type of rectification of small cyclical motions to produce gross motions.
Turning to the natural world, much attention has been devoted to the systematic understanding of how various microscopic organisms move in fluids under various conditions. Since movement is essential to reaching food particles, efficiency considerations have also been of interest (see Childress, 1981, for related discussion). Apparently, the paramecium gets around in a fluid under conditions of a very low Reynolds number through a process of cyclical change in its boundary contour (or more precisely, the envelope determined by the oscillating cilia that make up the contour). (See Figure 4.2.) In the work of Shapere and Wilczek (1989) this has been shown, under appropriate fluid mechanical assumptions, via the mathematics of gauge theory (which has played an important role elsewhere in modem physics and geometry over the last three decades). Here again a type of rectification is at work.
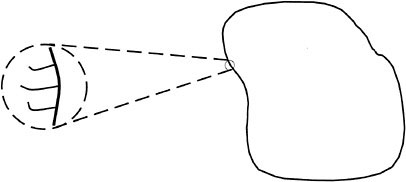
Figure 4.2 Illustration of paramecium in a fluid.
Although the low Reynolds number regime permits an essentially kinematic treatment of the paramecium, in other contexts of animal movement dynamic influences play an important part, e.g., in walking, trotting, and galloping gaits of quadrupeds (Alexander, 1968), in the swimming movement of the lamprey (Bowtell and Williams, 1991), etc. A rather striking illustration of this occurs in the Basiliscus plumifrons, a type of lizard found in Central America that is capable of engaging in short bursts (less than 10 meters) of walking on water, supporting itself by rapidly pushing down (at 30 Hz frequency) its hind feet on the water. The reaction forces thus generated are sufficient for support (see Lambert, 1994).
Our examples are meant to underscore the principle of movement generation by repetitive, cyclical variation in certain degrees of freedom (of a machine or an organism) while constrained by interactions with the environment (e.g., ground contact, friction). Understanding this principle has had an important influence on recent research in control theory and in robotics, as also explained by the companion papers of R.W. Brockett, J.E. Marsden, and R.M. Murray in this report. Turning this principle into a quantitative tool requires an understanding of the rectification mechanism mentioned above. It is precisely this mechanism, variously associated with geometric phases, area rules, and Lie bracket generation, that has had a crucial role as a tool for designing machines and algorithms to control them. In the context of motion generation, Brockett's paper (1989) appears to be the first to state clearly and prove a version of the rule (see Murray et al., 1994; Murray and Sastry, 1993).
Placing the rectification principle in the broader context of motion control architectures for systems with many degrees of freedom is one of the goals of this paper. To clarify matters further, an example is given in the following section, "From Shape Change to Global Movement," involving a unicycle and oscillations.
There is already a rich tradition in the biology and neuroscience of modeling movement via coupled oscillators. It is noteworthy that even in the presence of large numbers of degrees of freedom, motion control problems are effectively solved in biological systems of extraordinary variety. The work of Brown (1914) on half-centers, and the fundamental investigations, starting in the 1930s, of Bernstein (1967) on strategies for motion control, continue to have an influence in modem work (see Pearson,
1993, for a modern perspective). Bernstein clearly identified a role for planning (i.e., feedforward control) along with feedback, regulation, and tracking in motion control. In Bernstein's scheme, adaptive restructuring of motion programs on the fly, through the use of afferent feedback pathways from mechanoreceptors and other sensory modalities, had a prominent place. More recent work of neurophysiologists has focused attention on central pattern generators (CPGs) in the nervous system as key to understanding the control of movement and posture (Cohen, 1988; Cohen et al., 1982, 1988; Kopell and Ermentrout, 1988; Kopell, 1988). As mathematical objects, CPGs are networks of coupled oscillators and can be incorporated in the control architecture of a complex machine. Thus, if the state variables of the nodes of a CPG are in turn coupled to the degrees of freedom of the system to be controlled, it is possible to achieve coordination of the latter by prescribed phase coherence of the oscillators. The system to be controlled may be a multilegged walking machine or a multifingered, anthropomorphic mechanical hand with built-in tactile sensors on the fingers. Sensory feedback paths to correct CPG dynamics would be necessary to provide a level of robustness to changes in the environment (e.g., obstacles, failures). These elements lead us to the architecture of Figure 4.4, discussed further in ''Scripts and Oscillators'' below.
In the section on "Unifying Geometry," we present a unifying geometric-mechanical picture of the ideas on rectification. The language of principal bundles and connections goes hand in hand with the mechanical notions of configuration spaces, symmetries, and constraints. Complementing the perspectives presented in the companion papers in this report, we focus attention on the notion of averaging in Lie groups and its relation to rectification. In the section below on "Some Interesting Machines," we discuss novel machines that illustrate the main ideas of this paper and point the way to further extensions.
FROM SHAPE CHANGE TO GLOBAL MOVEMENT
Our purpose here is to show how suitable notions of shape, together with cyclical shape change, can yield global movement. In the case of the INCHWORM™ actuator, the concept of shape can be identified with two pieces of information: the continuous elongation/contraction of the middle sleeve and the discrete state of the clamp-pair (which one is on or off?). For each such "shape," there is an associated holonomic constraint, and coordinated shape change together with switching of constraints leads to rectification and the travel of the armature. In a setting more natural for geometric arguments, piecewise holonomic constraints may be replaced by nonholonomic constraints. This is best illustrated by classical mechanical examples involving the constraint of no sliding of a knife edge or rolling without slipping of a wheel on a surface. Consider, for instance, the geometry of motion of a unicycle with rider, as shown in Figure 4.3. The kinematic equations of the unicycle are given by
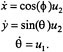
(4.1)
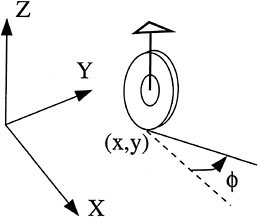
FIGURE 4.3 Geometric model of a unicycle.
Here x and y denote the position of a fixed reference point on the unicycle and ![]() denotes the orientation of the unicycle relative to a fixed laboratory/observer frame. Further, u1 denotes the steering speed and u2 denotes the heading speed, and these are assumed to be controllable by the unicyclist. From equation 4.1, it is clear that the constraint of no sliding
denotes the orientation of the unicycle relative to a fixed laboratory/observer frame. Further, u1 denotes the steering speed and u2 denotes the heading speed, and these are assumed to be controllable by the unicyclist. From equation 4.1, it is clear that the constraint of no sliding
(4.2)is maintained at all times.
Equations 4.1 and 4.2 can also be recast in the following equivalent form:
(4.3)
where
(4.4)
evolves in the group of rigid motions in the plane, with
(4.5)
Imagine a typical unicyclist implementing pedaling and steering maneuvers that give rise to ui(t) = ε fi(t), where fi(.) are zero-mean periodic functions of time with a common period T, and ε > 0 is a small amplitude parameter. In this instance, the "shape variables" ![]() are also periodic/oscillatory. Where does the unicycle end up? To get a decent approximation to the exact solution, one resorts to averaging theory (Leonard and Krishnaprasad, 1994a; Leonard, 1994). In fact, g(t) is approximated up to quadratic terms in ε by the formula
are also periodic/oscillatory. Where does the unicycle end up? To get a decent approximation to the exact solution, one resorts to averaging theory (Leonard and Krishnaprasad, 1994a; Leonard, 1994). In fact, g(t) is approximated up to quadratic terms in ε by the formula
(4.6)
where, for i = 1, 2,
(4.7)
and
(4.8)
Here, the ![]() are initial conditions, and the matrix
are initial conditions, and the matrix
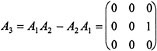
is the Lie bracket of A1 and A2, and
is the area of the loop in shape space executed by the unicyclist in the course of the chosen oscillatory maneuver.
Equation 4.6 predicts a secular drift in the direction of the Lie bracket A3 and, following 4.8 and 4.9, illustrates the rectification principle as an area rule. By a succession of oscillatory maneuvers, the unicyclist can get around anywhere and manage parallel parking! (For related ideas and references, see the paper by Murray in this report.) This hinges on the fact that the constraint (4.2) is nonholonomic or, equivalently, the Lie bracket A3 is linearly independent of A1 and A2, the directions trivially controllable by the unicyclist. It is, however, important that the phase relations between the pedaling
oscillations and the steering oscillations be right, or else the Area1,2 (T) will vanish, killing the secular drift. This brings up the need for coupled oscillations. Appropriate shape variations may be drawn from solutions to variational problems.
The unicycle example illustrates a geometric interpretation of shape and shape change. For a six-legged insect (or machine) with legs capable of lift and swing, the shape space may be a submanifold of a 6 × 3-dimensional toms. Shape change in that case is achieved via successively lifting and swinging the legs before returning to ground contact.
SCRIPTS AND OSCILLATORS
Area rules of the type discussed in the last section have been used in developing computer programs to synthesize feedforward control laws (motion scripts) in Leonard and Krishnaprasad (1994a) and Leonard (1994). We think of such programs as script generators, producing detailed streams of instructions to machines. One such program is used to control an underwater vehicle (Leonard and Krishnaprasad, 1994b; Leonard, 1994). Integrating script generators into a larger framework for intelligent control of movement is a major challenge (the framework has to accommodate uncertainty, limited sensing of the environment, obstacles that move about, rough terrain, etc.) and we argue that there is much insight to be gained from deeper study of biological motion control systems.
The Russian physiologist N. Bernstein, in his studies of the movement problem, proposed a variety of architectural principles. Given the large numbers of degrees of freedom involved in even elementary motor acts, binding (or synchronization) of the degrees of freedom into groups is necessary. Such binding has to be dynamic to accommodate varying stages in a movement. Bernstein viewed rhythm generators or oscillators as the means to implement binding. Bernstein also viewed as central to motor control the ability to change a motor program in the middle of a movement, possibly based on data from afferent sensory pathways. Much work since Graham Brown's proposal of half-centers has gone into understanding how neural circuitry could be organized to produce temporal patterns of neuronal firings that seem to be responsible for rhythmic movements. See, for instance, the compendium of papers in Cohen et al. (1988). The oscillations in the temporal patterns are assumed to be in correspondence with actual movements produced, for instance, a particular gait, i.e., rhythmic stepping, in a quadruped. A complex movement could be segmented into distinctive gaits and modules capable of piecing together such segments prior to initiation of a movement and altering them "on the fly" are essential to intelligent control. Further, it is plausible that in biological systems, the higher cognitive elements engaged in movement control pay attention primarily to a symbolic description of movement, ignoring detailed timing information. For instance, in the case of a six-legged insect, by identifying the legs on the left and right sides of the body with the symbols Li and Ri, where the index i rims from 1 to 3 (3 stands for the hind legs, 2 for the middle legs, and 1 for the front legs), one can refer to a gait pattern by a string of symbols, as in
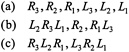
These strings are to be interpreted as defining the sequence in which each leg is lifted from the ground, and symbols in a group not separated by a comma correspond to synchronized leg-lifts. Thus string (c) above represents the so-called alternating tripod gait, being the fastest, and string (a) above stands for the slowest. Both timing and step length information are hidden, although it is experimentally observed that swing times are independent of gait. A suitable control framework would need to be able to accommodate descriptions of movement both at the symbolic and at the detailed timing level. In fact, one can even work out an admissible language for movements by stringing together "words" as in (a) (b)(c).
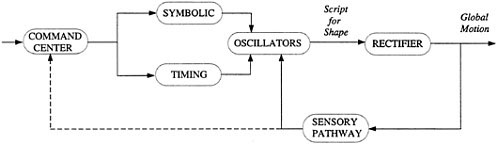
FIGURE 4.4 Architecture for motion control.
Based on these insights from biology, one is led to a possible architecture for intelligent control of movement as in Figure 4.4. Here the command center communicates a prescribed global movement command to be transformed into symbolic and timing instructions, which are then implemented by a network of coupled oscillators that produce the script for shape change. The rectification path produces the desired global movement. Sensory information is returned to the command center and possibly to the oscillators to modify/correct the motion commands and scripts. In practice, in legged animals or machines, this afferent pathway may lead to script change (gait switching). For a robust, model-independent approach to gait switching on the basis of bifurcation theory in the presence of symmetries, see Collins and Stewart (1993). In our own work, the change in control authority that accompanies the failure of actuators is one of the sources of script change (Leonard and Krishnaprasad, 1994b).
The architecture sketched out here gives prominence to what may be a missing ingredient in much of the discussion of rhythmic movements in biology, namely, the rectification module. In his paper in the present volume, Brockett takes the view that rectification is a tool for "approximate inversion" of motion specifications over time and shows how oscillators do the job. It may be possible to suggest some biological experiments to determine if indeed such approximate inverses are learned from repeated trials,
thereby lessening the need to store motion scripts. Finally, it should be added that there is some software involved in the control architecture we discussed that corresponds to current thinking in reconfigurable software for robotics (Stewart et al., 1993).
We close this section by pointing out exciting new developments toward incorporating a combination of pattern-generating oscillators, elastomechanics-based models of body movement and muscle response, and models of fluid interaction with the skin to capture the complexities of lamprey movement (Bowtell and Williams, 1991). In at least one machine that we have studied (see "Some Interesting Machines"), all these ingredients prove to be necessary for complete understanding.
UNIFYING GEOMETRY
The model (4.3) of the unicycle is not so special as it might seem at first glance. In practice, the models of mechanics governing the behavior of a wide variety of machines admit certain unifying geometric elements. The possible system configurations constitute the space Q. There is always the symmetry of Newtonian mechanics, namely, indifference of the dynamics to change of inertial observer. More generally, one has a Lie group G of invertible transformations acting on Q that leave the Lagrangian of the system invariant and possibly any applicable constraints as well. The equivalence classes defined by the orbits of G can be brought to one-to-one correspondence with the space S = Q/G of shapes. The triple (Q,G,S) is known as a principal bundle. Most of the examples one encounters in mechanical settings can be given the structure of a trivial principal bundle, i.e., the configuration space looks like a product of S × G, a simplification we shall assume from here on. Each configuration will then be a pair q = (x,g).
If sufficiently many independent constraints (analogous to the constraint of no sliding in the unicycle example) are present then, it is possible to construct a well-defined splitting of the space of velocities (tangent bundle TQ of the configuration space) at every configuration, into a set of symmetry directions along group orbits (also called vertical directions) and a set of complementary directions (called horizontal directions) isomorphic to the space of directions along which one can change the shape. One then says that the bundle (Q,G,S ) has acquired a principal connection (see Figure 4.5 for a sketch of the geometric set-up). The curvature of the connection has a great to deal to say about the following question. In analogy with the unicyclist's problem, where do we end up in the configuration space Q when we make a cyclic movement in the space of shapes? The constraints are sufficient to determine a relation between the evolution of g(t) and the shape trajectory x(t), of the form
(4.10)
where ξ represents the connection form and is linear in ![]() . Despite the complication arising from the connection form, equation 4.10 is a good deal like equation 4.3. The concept of holonomy in differential geometry gives a formal answer to the above question. Drift in the group variables can be built up by repetitively traversing the same loop in shape space. If the shape velocity is of the form
. Despite the complication arising from the connection form, equation 4.10 is a good deal like equation 4.3. The concept of holonomy in differential geometry gives a formal answer to the above question. Drift in the group variables can be built up by repetitively traversing the same loop in shape space. If the shape velocity is of the form ![]() , where ε is a small amplitude parameter, then, as discussed above in "From Shape Change to Global Movement," one can give an approximate solution to equation 4.10 using the theory of averaging. This is
, where ε is a small amplitude parameter, then, as discussed above in "From Shape Change to Global Movement," one can give an approximate solution to equation 4.10 using the theory of averaging. This is
done in Leonard and Krishnaprasad (1994a,b) and in Leonard (1994), leading to area rules. Once again the area rules yield constructive procedures for generating suitable movements in shape space to achieve required transport in configuration space.
The unifying geometric point of view of this section is very useful in formulating answers to constructive controllability questions arising in the study of maneuvers of space-based robotic devices (Krishnaprasad, 1990), the problem of the paramecium at low Reynolds number studied by Shapere and Wilczek (1989), and a wide variety of nonholonomically constrained problems. There is much that needs to be done to integrate this geometric viewpoint into the control architecture presented above in "Scripts and Oscillators." In particular, the capability to adapt motion scripts in this level of generality, based on sensory inputs, probably needs new mathematical apparatus.
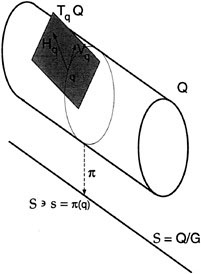
FIGURE 4.5 Principal bundle with connection.
SOME INTERESTING MACHINES
Some of the ideas we presented here have been tested in the laboratory and in simulation. In the thesis of Manikonda (1994), motion planning for nonholonomic robots in the presence of obstacles is investigated from a perspective close to the one we discuss. Over the years, there has been growing interest in robotic machines that exploit principles of movement found in biological systems. The excellent book of Hirose (1993) contains many examples of successful designs and algorithms. Encouraged by certain designs for redundant manipulators developed by Joel Burdick and his students at
Caltech, we investigated a variety of machines that could be controlled via shape change. One such instance is the nonholonomic variable geometry truss (NVGT) in Figure 4.6. This machine consists of a pair of modules on idle wheels, rolling without slipping on a surface, with deformable bodies. The intent is to drive this machine entirely by deformations of the body using the connecting links, without any direct actuation of the wheels.
The NVGT fits nicely into the framework of this paper. The configuration space is the Cartesian product of three copies of the rigid motion group SE(2), and the symmetry group is also SE(2). Thus the shape space is S = SE(2) × SE(2), representing the freedom to alter the shape by changing the lengths of the connecting links in each module. Apart from certain singular configurations, determined as those for which all three axles intersect (possibly at infinity), the unifying geometry discussed previously applies and the "no sliding" constraints fix a principal connection. Cyclical shape changes produce snake-like movement of the machine (Krishnaprasad and Tsakiris, 1994; Tsakiris, 1995).
It should be clear that additional modules could be attached to the NVGT of Figure 4.6, thereby increasing the number of constraints and the number of degrees of freedom. In that case, as shown in Krishnaprasad and Tsakiris (1994b), and Tsakiris (1995), the problem becomes over constrained, thus limiting the allowable shape changes. This in itself is not a disadvantage in selecting shape change scripts.

FIGURE 4.6 Two-module nonholonomic variable geometry tress. Reprinted, by permission, from Krishnaprasad and Tsakiris, 1995. Copyright © 1995 by Institute of Electrical and Electronics Engineers.
Suppose now that one of the modules in Figure 4.6 is detached and we are left with just one module. In this case the problem is under constrained, and one does not quite have the unifying geometry described above. One does not obtain a principal connection from the "no sliding" constraints alone. There is a subtler symmetry in the problem that arises from the interaction between the original Newtonian symmetry and the constraints, which yields a new momentum equation that the trajectories of the system must obey. The main ideas behind this new symmetry have only recently become clear in the work of Bloch et al. (1996). To illustrate this, a machine modeled on the patented toy Roller Racer (U.S. patent # 3663038 of May 16, 1972) was built (see Figure 4.7). This device is a special case of the single module nonholonomic variable geometry truss on wheels, with only a single degree of shape freedom.
The shape space in this case is the circle S1. It is remarkable that in this case the full theory of nonholonomic momentum equation applies and using this extra equation, one formulates a principal connection on the bundle (S1 × SE(2), SE(2), S1). Motion control by periodic forcing of one degree of shape freedom is accomplished. Details can be found in Tsakiris (1995).
The last-mentioned example uses dynamical information in an essential way, and in some sense there are parallels between this investigation and the work of Bowtell and Williams (1991) on the lamprey. The rich variety of global motions can be best understood by the proper synthesis of kinematic, geometric, and dynamic information, and the principle of rectification applied to cyclical shape variations is an effective guide even in this mathematically complex setting. An intelligent control architecture based on such synthesis would be of great interest. Again nature would have taught us to build better machines.

FIGURE 4.7 Computer-controlled roller racer.
ACKNOWLEDGMENTS
It is a pleasure to acknowledge fruitful collaborations on the subject matter of this paper with Anthony Bloch, Roger Brockett, Naomi Leonard, Vikram Manikonda, Jerrold Marsden, Richard Murray, Dimitris Tsakiris, and Rui Yang. Conversations with Joel Burdick and Avis Cohen on the subject of rhythmic movement have been a source of inspiration. The theses of Mishra and Marvin were influential in the development of the ideas here. Tom Finan got us thinking about the Roller Racer. This research was supported in part by the National Science Foundation's Engineering Research Centers Program, NSFD CDR 8803012; by the AFOSR University Research Initiative Program under grant AFOSR-90-0105 and by grant AFOSR-F49620-92-J-0500; and by the Army Research Office under Smart Structures, URI Contract No. DAAL03-92-G-0121.
REFERENCES
Alexander, R., 1968, Animal Mechanics, Seattle: University of Washington Press.
Bernstein, A., 1967, The Coordination and Regulation of Movements, Oxford: Pergamon Press.
Bloch, A.M., P.S. Krishnaprasad, J.E. Marsden, and R.M. Murray, 1996, "Nonholonomic Mechanical Systems with Symmetry," Archive for Rational Mechanics and Analysis (in press).
Bowtell, G. and T.L. Williams, 1991, "Anguilliform Body Dynamics: Modelling the Interaction Between Muscle Activation and Body Curvature," Philos. Trans. R. Soc. Lond. B. Biol. Sci. 234, 385-390.
Brockett, R.W., 1989, "On the Rectification of Vibratory Motion," Sensors and Actuators 20(1-2), 91-96.
Brown, T.G., 1914, "On the Nature of the Fundamental Activity of the Nervous Centres, Together with an Analysis of the Conditioning of Rhythmic Activity in Progression and a Theory of Evolution of Function in the Nervous System," J. Physiol. Lond. 48, 18-46.
Childress, S., 1981, Mechanics of Swimming and Flying, Cambridge: Cambridge University Press.
Chirikjian, G. and J.W. Burdick, 1995, "Kinematics of Hyper-redundant Locomotion with Applications to Grasping," Proceedings of the IEEE International Conference on Robotics and Automation, New York: IEEE, 720-727.
Cohen, A.H., 1988, "Evolution oft he Vertebrate Central Pattern Generator for Locomotion." In: Neural Control of Rhythmic Movements in Vertebrates , A.H. Cohen, S. Rossignol, and S. Grillner (eds.), New York: John Wiley and Sons Inc.
Cohen, A.H., P.J. Holmes, and R.H. Rand, 1982, "The Nature of the Coupling Between Segmental Oscillators of the Lamprey Spinal Generator for Locomotion: A Mathematical Model," J. Math. Biol. 13, 345-369.
Cohen, A.H., S. Rossignol, and S. Grillner (eds.), 1988, Neural Control of Rhythmic Movements in Vertebrates, New York: John Wiley and Sons Inc.
Collins, J.J. and I. Stewart, 1993, "Hexapodal Gaits and Coupled Nonlinear Oscillator Models," Biol. Cybern. 68, 287-298.
Hirose, S., 1993, Biologically Inspired Robots: Snake-Like Locomotors and Manipulators, Oxford: Oxford University Press.
Kopell, N., 1988, "Toward a Theory of Modelling Central Pattern Generators." In: Neutral Control of Rhythmic Movements in Vertebrates, A.H. Cohen, S. Rossignol, and S. Grillner (eds.), New York: John Wiley and Sons Inc.
Kopell, N. and G.B. Ermentrout, 1988, "Coupled Oscillators and the Design of Central Pattern Generators," Math. Biosci. 90, 87-109.
Krishnaprasad, P.S., 1990, "Geometric Phases and Optimal Reconfiguration of Multibody Systems," Proceedings of the American Control Conference , American Automatic Control Council, Philadelphia, 2440-2444.
Krishnaprasad, P.S. and D.P. Tsakiris, 1994a, "2-Module Nonholonomic Variable Geometry Truss Assembly: Motion Control," Proceedings of the 4th IFAC Symposium on Robotics Control, 263-268.
Krishnaprasad, P.S. and D.P. Tsakiris, 1994b, "G Snakes: Nonholonomic Kinematic Chains on Lie Groups," Proceedings of the 33rd IEEE Conference on Decision and Control, IEEE, New York, 2955-2960.
Krishnaprasad, P.S. and D.P. Tsakiris, 1995, ''Oscillations, SE(2)-snakes and Motion Control,'' Proceedings of the 34th IEEE Conference on Decision and Control, IEEE, New York, 2806-2811.
Lambert, C., 1994, "To Run Atop the River," Harvard Magazine, May-June, 14-15.
Leonard, N.E., 1994, Averaging and Motion Control of Systems on Lie Groups, Ph.D. thesis (Institute for Systems Research Technical Report, Ph.D. 94-09), University of Maryland, College Park.
Leonard, N.E. and P.S. Krishnaprasad, 1994a, "Motion Control of Drift-Free Left-Invariant Systems on Lie Groups: Parts I & II," Institute for Systems Research Technical Reports, 94-8 and 94-9, University of Maryland, College Park. (Also IEEE Transactions on Automatic Control 40(9), Sept. 1995, 1539-1554.)
Leonard, N.E. and P.S. Krishnaprasad, 1994b, "Motion Control of Autonomous Underwater Vehicle with an Adaptive Feature," Proceedings of a Symposium on Autonomous Underwater Vehicle Technology, IEEE Oceanic Engineering Society, 283-288, IEEE, New York.
Manikonda, V., 1994, A Hybrid Control Strategy for Path Planning and Obstacle Avoidance with Nonholonomic Robots, M.S. thesis, Institute for Systems Research Technical Report, M.S. 94-8, University of Maryland, College Park.
Murray, R.M., Z. Li, and S.S. Sastry, 1994, A Mathematical Introduction to Robotic Manipulation, Boca Raton, FL: CRC Press.
Murray, R.M. and S.S. Sastry, 1993, "Nonholonomic Motion Planning: Steering Using Sinusoids," IEEE Transactions on Automatic Control 38(5), 700-716.
Pearson, K.G., 1993, "Common Principles of Motor Control in Vertebrates and Invertebrates," Annu. Rev. Neurosci. 16, 265-297.
Shapere, A. and F. Wilczek, 1989, "Geometry of Self-Propulsion at Low Reynolds Number," J. Fluid Mech. 198, 557-589.
Stewart, D.B., R.A. Volpe, and P.K. Khosla, 1993, "Design of Dynamically Reconfigurable Real-Time Software using Port-Based Objects," Carnegie Mellon University Tech. Report CMU-RI-TR-93-11, July.
Tsakiris, D.P., 1995, Motion Control and Planning for Nonholonomic Kinematic Chains, Ph.D. thesis, University of Maryland, College Park.
Ueha, S. and Y. Tomikawa, 1993, Ultrasonic Motors: Theory and Applications , Oxford: Clarendon Press.















