9
Uses of Dietary Reference Intakes
OVERVIEW
In the past, Recommended Dietary Allowances (RDAs) in the U.S. and Recommended Nutrient Intakes (RNIs) in Canada were the only values available to health professionals for planning and assessing diets of individuals and groups and for making judgments about excessive intake. However, the RDAs and RNIs were not ideally suited for many of these purposes (IOM, 1994). The Dietary Reference Intakes (DRIs) developed in this report—Estimated Average Requirements (EARs), RDAs, Adequate Intakes (AIs), and Tolerable Upper Intake Levels (ULs)— are a more complete set of reference values. Each type of DRI has specific uses. The most widespread uses of DRIs—diet assessment and planning—are described in this chapter. EARs, RDAs, AIs, and ULs refer to average daily intake over 1 or more weeks.
Three of the DRIs—the EAR, RDA, and AI—were set with reference to a specific criterion of adequacy. The criterion of adequacy may be the same for each gender and life stage group, but sometimes it is not. For example, the criterion of adequate calcium intake is desirable calcium retention for most age groups, but calcium balance is the criterion for men and women ages 31 through 50 years. Desirable calcium retention, in itself, would not be used to determine adequacy. Instead, it is the presumed relationship between desirable calcium retention and reduced risk of fracture in later life that provides a basis for selection of this indicator. Reduced fracture risk is the functional outcome chosen as the hall-
|
Dietary Reference Intakes (DRIs) *
|
mark of adequacy for calcium, and its indicator is desirable calcium retention to the extent that retention can be affected by dietary intake. Each nutrient chapter (Chapter 4, Chapter 5, Chapter 6, Chapter 7 through Chapter 8) identifies the primary indicator or criterion that defines adequacy for the specific life stage and gender group. (See also Table S-1, Table S-2, Table S-3, Table S-4 and Table S-5.)
USING RECOMMENDED DIETARY ALLOWANCES
Nutrient Recommendations for Individuals
The RDA is the value to be used in guiding individuals to achieve adequate nutrient intake. RDAs are given separately for specified life stage groups and by gender if applicable; they are intended to apply to healthy individuals. Due to the large variation in intakes, the RDAs are seldom appropriate for planning diets for or assessing the nutrient intakes of free-living groups (Beaton, 1994).
The RDA for each nutrient is set at a value that should be adequate for 97 to 98 percent of all individuals in a life stage group, given a specified definition of adequacy. The RDA is a target or recommended intake. Nutrient intake that is less than the RDA does not necessarily indicate that the criterion of adequacy has not been met by a given individual.
The RDA is expressed as a single absolute value and not in rela-
tion to weight or height. For example, from Chapter 5, the RDA and thus the recommended daily intake of phosphorus for women aged 19 through 30 years is 700 mg (22.6 mmol)/day. This would be the case for a woman in this age range weighing 50 kg (110 lb), 55 kg (121 lb), or 70 kg (154 lb).
One would expect larger individuals to have larger skeletal mass and therefore a greater requirement for calcium, phosphorus, magnesium, vitamin D, and fluoride. However, given the variety of research designs and subject variability used in the studies that provided the data for deriving the DRIs, it would be somewhat misleading to express them per kilogram of body weight or per centimeter of height. This would imply a greater precision in the estimate than is possible, given the available data. Reference weights are provided (Table 1-3) to allow a calculation, when necessary, of the amount per unit of body weight for individuals who are outside the typical range of body size. For some nutrients (for example magnesium), requirements may be closely related to lean tissue; for others, the relationship is weak.
Needs for energy are not necessarily useful for adjusting nutrient needs for this group of nutrients. For example, the RDA for phosphorus would be the same for an 18-year-old long-distance runner whose energy needs were 4,000 kcal/day and an 18-year-old sedentary individual with energy needs of 2,000 kcal/day.
From Chapter 6, the RDA for magnesium is 130 mg (5.4 mmol)/day for healthy boys and girls ages 4 through 8 years. This recommended intake, consumed on a daily basis, on average, would allow essentially all children to achieve the positive magnesium balance needed for normal growth. Because the RDA was based on studies of requirements in children or adolescents with a normal range of body weights for their age, a reference weight and height for the age group are given. It is thus possible to determine the amount of the nutrient per kilogram of body weight that is recommended and to use this value for adjusting the RDA for individuals in the age category whose weights and heights deviate substantially from the reference. This might be done, for example, for small 4-year-old children or for large 8-year-old children.
Assessing the Adequacy of Nutrient Intakes of an Individual
The RDA is of limited use in assessing the adequacy of an individual 's nutrient intake. An individual's nutrient requirement is never known with certainty. If the individual 's intake, on average, meets or exceeds the RDA, there is good assurance that the intake is ade -
quate for the specified criterion, given current knowledge. When an individual's intake is less than the RDA, the risk of an inadequate intake is present. The risk increases as the intake falls further below the RDA. At 2 standard deviations (SD) below the EAR, it would be nearly certain that the individual's requirements would not be met (NRC, 1986). Neither reported dietary intake nor any other single criterion can be used, by itself, to evaluate the nutritional status of individuals. A usual intake that is well below the RDA may be an indication of the need for further assessment of nutritional status by biochemical tests or clinical examination.
USING ADEQUATE INTAKES
An AI is based on observed or experimentally determined approximations of the average nutrient intake, by a defined population or subgroup, that appears to be sufficient to sustain a defined nutritional state in the specified population. It is emphasized that, in contrast to the EAR, which is an estimate of the requirement that applies to individuals, the AI is usually derived from mean intakes of groups —the group rather than the individual is the unit of observation. The AI is therefore higher than the EAR would be, if it could be determined, since by definition, the EAR is the intake that meets the nutrient need of only 50 percent of the individuals in a group. Because of uncertainties about the relationship of the AI to the actual average requirement, the AI provides an imprecise basis for the assessment of nutrient intakes of population groups. Thus, the applications of the AI must be quite different from those of the EAR. However, healthy individuals with an intake at or above the AI are assumed to have a low risk of intake inadequate for a defined state of nutrition.
USING TOLERABLE UPPER INTAKE LEVELS
The UL is the highest level of daily nutrient intake that is likely to pose no risk of adverse health effects to almost all individuals in the general population. As intake increases above the UL, the risk of adverse effects increases. In most cases it applies to usual intakes from all sources, but in the case of magnesium, it does not apply to intake from food or local water supplies.
Similar to the situation for nutrient requirements, the intake at which a given individual will develop adverse effects as a result of taking high amounts of a nutrient from food and/or nonfood sources cannot be known with certainty. If the individual's intake is
below the UL, there is good assurance that the intake will not cause adverse effects, given current knowledge. At intakes above the UL, the risk of adverse effects increases. Although there is no established benefit for healthy individuals associated with consumption of nutrients or food components above the RDA or AI, there is little concern of an increased risk of harmful effects of consumption up to the UL.
Ordinarily, the UL refers to intake from food, fortified food, water, and supplements. Nutrients are often available from a variety of food and nonfood sources. For fluoride, for example, intake from all sources must be considered, including water and dental products. Combined with other sources of fluoride, the over-use of fluoride-containing dental products may place many young children at risk of dental fluorosis.
To avoid exceeding the adult UL for calcium of 2.5 g (62.5 mmol)/day, intake from food, fortified food, and supplements must all be considered. The UL for calcium was determined based in part on studies in which hypercalciuria was related to both dietary and supplemental intakes of calcium. For phosphorus, intakes from both food and supplements are to be considered when comparing intakes with the UL of ~4.0 g (130 mmol)/day for adults. However, for individuals requiring very high energy intakes, phosphorus intake from diet alone may exceed the UL without adverse effects.
To avoid exceeding the UL for vitamin D of 50 µg (2,000 IU)/day, considering intake from all sources is important, but ordinarily only intake from food, fortified food, and nutrient supplements provides notable amounts. (Apart from fatty fish and liver, high concentrations of vitamin D do not occur naturally in commonly eaten foods in the United States and Canada.) Individuals who have high intakes of vitamin D-fortified foods (such as milk and margarine) and of vitamin D supplements (in multivitamin preparations, alone, or in fish oil) should keep the combined average daily intake below the UL of 50 µg (2,000 IU)/day to minimize the risk of developing hypercalcemia.
For many nutrients, such as magnesium, adverse effects associated with high levels of intake from food sources have not been reported. The UL of 350 mg (14.6 mmol)/day was set for magnesium from nonfood, over-the-counter pharmacologic products. This is the intake at which an individual might first experience an adverse effect (diarrhea) from ingestion of a nonfood source of magnesium for at least 1 week. Since the UL for magnesium applies only to nonfood sources, individuals should not be concerned with trying
to avoid excessive amounts of magnesium from that occurring naturally in food or water.
USING ESTIMATED AVERAGE REQUIREMENTS
The EAR is particularly useful for evaluating the possible adequacy of nutrient intakes of population groups and for planning intakes of groups. In 1986, the National Research Council (NRC) proposed an approach to calculating the prevalence of inadequate nutrient intakes among a population group, using the mean (or EAR) and SD of the requirement (NRC, 1986). Beaton (1994) has noted that the prevalence of inadequate nutrient intakes can be estimated by the proportion of the population with intakes below the EAR, assuming that the variance of the intakes is greater than the variance of the EAR (which is generally the case). The EAR may also be used in setting a recommended mean intake for a population group, such that only 2 to 3 percent of the population falls below the EAR. These methods are described briefly below. A more detailed explanation of the methodology is given in Beaton (1994) and by the World Health Organization, Food and Agriculture Organization of the United Nations, and International Atomic Energy Agency (WHO/FAO/IAEA) Expert Consultation in Trace Elements in Human Nutrition and Health (WHO, 1996). It is anticipated that methods of using the EAR for these purposes will be addressed in a subsequent Food and Nutrition Board report.
Assessing the Adequacy of Nutrient Intake of Groups
An estimate of the prevalence of inadequate intakes of a nutrient by a specific gender or life stage group can be obtained by determining the percentage of the individuals in the group whose usual intakes are less than the EAR (Beaton, 1994) (see Figure 9-1). The estimate is most accurate if the requirements are symmetrically distributed and the SD of intakes is at least twice as large as the SD of requirements. It is also important that the intake data reflect usual intakes; methods have been developed to remove the day-to-day variance in the distributions of intake data (Nusser et al., 1996). This adjustment narrows the distribution and thus gives a better estimate of the proportion of the group with intakes below the EAR. This concept is illustrated in Figure 9-2. Estimates of the prevalence of inadequate intakes also can be affected by biases in the intake data (such as underreporting). (See Chapter 2 for a discussion of the many potential sources of error in self-reported dietary data.)
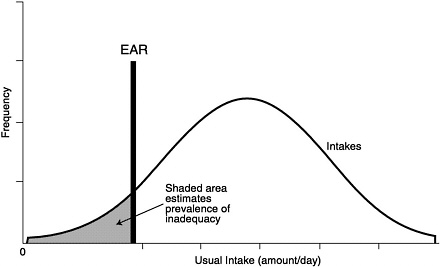
FIGURE 9-1 Prevalence of inadequate intakes in a population group. Adapted from Beaton (1994).
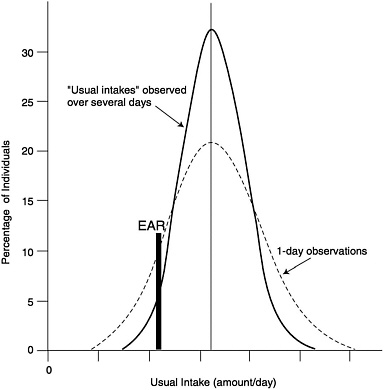
FIGURE 9-2 Effect of multiple days of observation on the apparent distribution of nutrient intake and how it changes the prevalence of inadequacy as estimated by comparison to EAR. Adapted from Hegsted (1972).
TABLE 9-1 Adjusted and Unadjusted Phosphorus Intakes (mg/day) of Young Women and Adolescent Boys in the United States
|
Percentile |
|||||||||
|
Category |
Mean |
SEb |
5th |
10th |
25th |
50th |
75th |
90th |
95th |
|
Females 20–29a (n = 272) |
|||||||||
|
Unadjusted |
1,098 |
54 |
342 |
465 |
694 |
1,041 |
1,376 |
1,722 |
2,066 |
|
Adjusted |
1,097 |
61 |
703 |
780 |
917 |
1,080 |
1,259 |
1,436 |
1,551 |
|
Males 12–19 (n = 286) |
|||||||||
|
Unadjusted |
1,619 |
53 |
565 |
745 |
1,077 |
1,416 |
1,932 |
2,610 |
3,350 |
|
Adjusted |
1,612 |
54 |
976 |
1,091 |
1,300 |
1,564 |
1,871 |
2,194 |
2,413 |
|
a Females include pregnant and lactating women. b Standard error of the mean. |
|||||||||
SOURCE: One-day unadjusted intake data from the 1994 CSFII, providedby USDA/ARS Food Survey Research Group, 1996. The data have beenadjusted using the method developed by Nusser et al. (1996).
Table 9-1 illustrates the importance of adjusting distributions before calculating intake percentiles for groups. The means and seven percentiles of intakes of phosphorus from the 1994 CSFII are shown for teenage boys and for young women, with and without adjustment for usual intake using the Nusser et al. procedure (1996). If unadjusted 1-day intake data are used to estimate the prevalence of inadequate phosphorus intakes for young women, the actual prevalence of usual intakes below an EAR of 580 mg (18.7 mmol)/day will be overestimated. As shown in Table 9-1, between 10 and 25 percent of 1-day intakes fall below 580 mg (18.7 mmol)/day, while less than 5 percent of the adjusted intakes are below the EAR. For teenage boys, less than 10 percent would have inadequate intakes using the adjusted distribution and an EAR of 1,055 mg (34 mmol)/day, while almost 25 percent would have inadequate intakes if only the unadjusted distribution were examined.
The adjustment procedure is also crucial when examining the percentage of the population that is above the UL. Using an unadjusted distribution for adolescent boys, 5 percent of the population would have phosphorus intakes above 3,350 mg (108.1 mmol)/day, a level that is approaching the UL of 4,000 mg (129 mmol)/day. This might be considered unacceptably high unless the adjusted
distribution were also examined: the ninety-fifth percentile of usual intakes is just 2,413 mg (77.8 mmol)/day implying that intakes seldom exceed the UL.
When assessing the intake of populations, a number of other questions need to be considered:
-
To what extent does the nutrient requirement affect intake? Such a relationship, described by WHO/FAO/IAEA (WHO, 1996), would limit the validity of the probability approach.
-
What kinds of adjustments can be made, if any, for biases in the food intake data?
-
What factors should be considered in interpreting the findings in different populations?
-
What is the allowable level of inadequate intake in a population before concern is raised?
Planning Nutrient Intakes of Groups
The EAR also may be used as a basis for planning or making recommendations for the nutrient intakes of free-living groups. If nutrient intakes are normally distributed, a target intake for a population group can be estimated based on the EAR and the variance of intake. The objective might be to set a value for the mean intake of the group that will ensure that most individuals (usually 97 to 98 percent) meet their nutrient requirement. In order that less than 2 to 3 percent of intakes fall below the EAR, a group's mean intake must be at least two SDs of intake above the EAR. Because the SD usually varies in relation to the magnitude of intake, the coefficient of variation (CV) of intake is used to calculate the target mean intake. The following formula has been derived for this calculation (see Beaton [1994] and WHO [1996] for more details):
Target mean intake for a group = EAR/(1 − [2 × CV of intake])
Where CV = SD of intake/mean intake.
For example, if a group of women in a nursing home had phosphorus intakes with a CV of 0.16, and intakes were normally distributed, achieving a group mean intake of 853 mg (27.5 mmol)/day would ensure that only 2 to 3 percent would have intakes below the EAR of 580 mg (18.7 mmol)/day (580/1−[2 × 0.16]) = 853). If intakes are not normally distributed, other mathematical approaches will be needed.
Another approach would be to implement programs that focus on increasing intakes at the lower end of the distribution, rather than trying to shift the entire distribution of intakes upward. For example, in a nursing home, persons with low phosphorus intakes could be given foods especially high in phosphorus, or meal planning could focus on increasing intakes of phosphorus from many sources. Although it is beyond the scope of this report, an evaluation of the various approaches that could be used to reduce the prevalence of inadequate intakes in population subgroups should be pursued. Such approaches include nutrition education, meal planning, nutrient fortification, and nutrient supplementation. The most efficient and effective strategy would vary from nutrient to nutrient and depend on the distribution of current intakes compared to the EAR.
The use of the EAR in planning intakes for groups is a process that involves a number of key decisions and analysis of questions such as the following:
-
Should actual or ideal distributions of populations intakes be used to calculate recommendations for groups? (Actual distributions are seldom normally distributed.)
-
What factors should influence the selection of the degree of risk that can be tolerated when planning for groups?
-
Should other adjustments be made for factors that would reduce or increase actual intake of the nutrients?
OTHER USES OF DIETARY REFERENCE INTAKES
For many years, the U.S. Recommended Dietary Allowances and the Canadian Recommended Nutrient Intakes have been used by many national and federal agencies for a variety of purposes. For example, they have been considered in setting regulations for feeding programs, setting standards for feeding in group facilities (nursing homes, school cafeterias, correctional facilities), developing recommended intakes for the military, and setting reference values for food labels. They have been used for comparative purposes in many computer programs for nutrient analysis and by dietitians in modifying diets for patients. Guidance for using DRIs for these and many other purposes is beyond the scope of this report, but should be addressed in future reports.
ADDRESSING DISCREPANCIES BETWEEN USUAL INTAKE AND THE AI
Chapter 4 reveals major discrepancies between estimates of usual intakes of calcium and the AI for calcium for some of the life stage groups. For example, mean calcium intake from foods for U.S. females aged 9 years and older is about 650 mg (16.3 mmol)/day, but the AI for calcium ranges from 1,000 to 1,300 mg (25 to 32.5 mmol)/day, depending on the age group. However, this discrepancy does not necessarily mean that dietary intakes are generally inadequate because the relationship between the AI and the distribution of requirements for the nutrient is not known. Nevertheless, for individuals who wish to increase their calcium consumption, there are several possible strategies. These include increasing intake of foods high in calcium, such as low- or nonfat milk products, and increasing consumption of foods fortified with calcium, such as calcium-fortified orange juice or breakfast cereals. For those individuals at high risk, use of calcium supplements may be desirable in order to meet the AI. Identifying the most appropriate strategies to improve nutrient intake should be the focus of a research agenda.
SUMMARY
The correct reference value must be used for its intended purpose, which usually involves either planning for an adequate intake or the assessment of adequacy of intake. It is anticipated that future publications will address the interpretation and appropriate uses of DRIs in more detail in order to assist both the health professional and those interested in nutrition policy and analysis.











