There was a problem loading page 128.
Overview
For many experienced and prospective teachers, tasks like those in High School Mathematics at Work pose several inter-related challenges involving curriculum, pedagogy, and assessment.
- In planning the class: How can I tell if a task is appropriate for my students? How would such tasks fit in my curriculum? After choosing a task, what are the mathematical concepts and big ideas that can be approached with the task?
- During class: How do I get students working on the task I've chosen? What can I expect from classroom discussion? How can I engage all students in the big mathematical ideas?
- After class: What can I expect from student work? What should I expect from student work? How should I provide feedback?
These questions speak to the broad demands that today's students and curricula place on teachers. To respond adequately to these demands, teachers must be very resourceful and must have the skills and inclinations to create an intellectual community in their classrooms. What is needed is teachers who are mathematically confident and have the tools to learn mathematics as they
need it, so that they and their students may thrive when either the curriculum or the students take them into uncharted territory. Furthermore, teachers need professional support in creating learning communities of teachers in their schools, districts, and states.
Working with both preservice and inservice teachers, the authors of the essays in Part Four find that tasks like those in this document have changed teachers' ideas about students' capabilities, about how a curriculum might be organized, and about what it means to do mathematics. In each case, such change requires time and support.
The Professional Standards for Teaching Mathematics (National Council of Teachers of Mathematics, 1991) acknowledges the important role that teachers have in choosing tasks in their curriculum. Under the heading "Worthwhile Mathematical Tasks," it asserts that
The teacher of mathematics should pose tasks that are based on—
- sound and significant mathematics;
- knowledge of students' understandings, interests, and experiences;
- knowledge of the range of ways that diverse students learn mathematics. (p. 25)
In her essay, Glenda Lappan suggests that "teachers are architects of curriculum," for what is learned depends upon the context in which it is taught. She acknowledges that the use of complex problems creates more complexity in classrooms, and she notes that if preservice teachers work through complex problems themselves, they receive some of the background and confidence they need to handle such complexity. After describing problem-centered teaching and some of the issues that it raises, Lappan suggests that "teachers will find that learning alone is unlikely to be as powerful as engaging in dialogue with other teachers."
Like Lappan, Gilbert Cuevas acknowledges that with scant experience solving complex mathematical tasks, many preservice teachers are uncertain about using such tasks in their classrooms. He presents five principles for the preparation of teachers, such as providing "opportunity for reflection about their tasks and their implementation with students," and emphasizing communication, discussion, and orientation toward problems.
Paul LeMahieu and Marshá Horton note that assessments alone are not effective agents of educational reform. When extended, open-ended tasks are included in assessment, however, there is an opportunity for a different and powerful role, if teachers are involved in the evaluation of student work responding to these items. LeMahieu and Horton discuss how teachers develop consensus about quality and rigorous expectations for quality through discussions of student work on assessments. Furthermore, they note,
inservice teachers' expectations for students change when they participate in such scoring.
The tasks in Part Four might be used in the professional development of teachers, both as a site for discussion of student work, as suggested by LeMahieu and Horton, and as a complex task for their own exploration, as suggested by Lappan and Cuevas. Because these tasks are more open-ended than most in previous sections, the mathematical analysis sections do not include complete solutions, but instead suggest some of the mathematical and pedagogical issues and some sources of data or other useful information. Estimating Area (p. 145) brings to light mathematical ideas such as the distinction between distance, area, and volume, scaling factors, and estimation, possibly leading to calculus ideas such as limit and integration. Like the tasks in Part Three, this is a task that may be fruitfully revisited several times in a student's career.
Timing Traffic Lights (p. 147) concerns a workplace situation usually considered by town and city planners. The ideas are similar to the ideas behind scheduling trains, airplanes, and canal-boats. The potential interest for students is that city planners' solutions (both the good and the bad) can be seen in everyday life. This task may be used to explore mathematical ideas such as distance, rate, time, velocity, modeling, and representation.
Buying a Used Car (p. 153) is an everyday situation about which people do not often think mathematically. Yet, by considering in the analysis not only estimates of the purchase price and repair costs but also insurance, taxes, depreciation, interest on a loan, and inflation, there is high potential for rich mathematical discussion.
Reference
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
13—
Pedagogical Implications for Problem-Centered Teaching
GLENDA T. LAPPAN
Michigan State University
No other decision that teachers make has a greater impact on students' opportunity to learn and on their perceptions about what mathematics is than the selection or creation of the tasks with which the teacher engages the students in studying mathematics. Here the teacher is the architect, the designer of the curriculum:
The activity in which knowledge is developed and deployed … is not separate from or ancillary to learning and cognition. Nor is it neutral. Rather, it is an integral part of what is learned. Situations might be said to co-produce knowledge through activity. (Brown, Collins, & Duguid, 1989)
In order to develop productive notions about mathematics, students must have opportunities to be actually involved in doing mathematics—to explore interesting situations that can in some way be mathematicized; to look for patterns; to make conjectures; to look for evidence to support their conjectures; to make logical arguments for their conjectures; to make predictions or reach conclusions supported by evidence; to invent new ways to use their mathematical knowledge and tools to solve problems; and to abstract from experiences with solving problems the common mathematical concepts, ideas, skills, procedures, and structures that have more universal application.
In selecting a mathematical task, a teacher judges how well the task represents
the embedded concepts and procedures that are the goals of instruction, how likely the students are to bump into the mathematics in the course of investigating the task, how well the task represents what is entailed in doing mathematics, and what skill development the task will or can support. An experienced teacher asks the question, "With what mathematics does the task surround the students?" Teachers also have to balance their selection of mathematical tasks to include tasks that allow and promote the usefulness of mathematics in solving authentic problems with all of their inherent messiness.
Here is an example of such a task. Consider the data in Table 13-1, taken from an advertisement in a Florida newspaper.
TABLE 13-1: Monthly charges for various Internet access providers
|
ACCESS PROVIDER |
MONTHLY RATE |
HOURS INCLUDED |
COST OF ADDITIONAL HOURS |
|
TDO Online |
$24.94 |
100 |
$2.00 |
|
America Online |
$9.95 |
5 |
$2.95 |
|
CompuServe (Basic) |
$9.95 |
5 |
$2.95 |
|
CompuServe (Super Value) |
$24.95 |
20 |
$1.95 |
|
Prodigy (Basic) |
$9.95 |
5 |
$2.95 |
|
Prodigy (30/30) |
$30.00 |
30 |
$2.95 |
Suppose you are in the market for an Internet access provider. Which of the services in the table would be the best option for you to choose? The answer to this question is, "It depends!" One way to approach the problem would be to build tables and form graphical representations of each plan for different number of hours of use. Creating representations that allow comparisons is desirable. Tools such as graphing calculators or spreadsheets could be used. The solution is, of course, not a resounding endorsement for one of the services, but a more serious analysis of what ifs; an analysis that shows which plan is optimal when a desired number of hours of access is specified.
If teachers make the decision to use such a task in their classrooms, they have the responsibility to determine its mathematical potential. What mathematics can students learn from analyzing this situation? What mathematics are they most likely to use? Each of the plans can be represented by a piecewise linear relationship between cost and hours of use. This engages students in identifying variables and writing equations describing relationships that are constant for a number of hours and that change in a predictable fashion after that time. This is the essence of mathematical modeling. After modeling the situation with equations, tables of values, or graphs, students have to
analyze the representation to make comparisons. They are likely to have to find points of intersection for the relationships. They may look at rates of change or slopes of lines. The important thing is that the task is rich with important, useful, connected, applicable mathematics.
Teaching Through Bigger Problems
While the payoff for students can be very great, teaching through big problems increases the complexity of classroom instruction for teachers who are often imbued with the traditional view that mathematics is a well-ordered sequence of rules and procedures, mostly concerned with numbers and number operations. Many prospective and some practicing teachers do not expect mathematics to make sense, but they do expect to be able to remember a rule from which a solution can be swiftly found. They view the role of the teacher as explaining how to do the tasks and telling students when they are correct. Teachers with the traditional view can teach traditional classes confidently if they know the rules, the procedures, and when to apply them. Unless the teacher's mathematical understanding is deep and connected, however, such an approach often misses opportunities to make connections with other mathematics and with student thinking.
It takes a great deal of effort, and time, to create a new vision of what mathematics learning could be. Experience in working on "big problems" helps change how preservice teachers see themselves as learners of mathematics. "We were trained for so many years," reported Tamara, an older woman with weak mathematical background. "This is the way you do it. It becomes a way of thinking. This was the way I had always done mathematics so I've had to totally reorient myself. You have to restructure your whole way of thinking about mathematics and that alone is a big job. … To know mathematics means being able to say, 'this would make sense.' To know why something works and to be able to express it, you have to be able to communicate it. … You have to experience math, interact with it. You have to struggle to put things together and take them apart. If something doesn't work, you just try something else. … You need to experience it and talk about it, not just memorize it." (Schram, 1992, pp. 26, 34)
Another prospective teacher, Kim, struggled throughout the first two courses in her program. In her later courses, she began to gain confidence in her ability to think about the problems posed. "Math 201 was the hardest of the courses in the sequence because I really struggled with trying to think about math differently. … Now I am willing to continue working on a problem for a long time. Before, just forget it, if I didn't know the answer when I looked at a problem. I didn't even try further." (Schram, 1992, p. 32)
Preservice and inservice teachers who work on big problems become more willing to persevere with them. They develop mathematical resources, both intellectual and personal, that give them confidence in their ability to tackle
real problems. They move from approaching mathematics as a technical subject to approaching mathematics as a sense-making enterprise based on careful observation, invention, making connections, gathering data, making conjectures, and seeking evidence.
Teachers face enormous complexities in attempting to create environments for learning mathematics in which students engage in making sense, individually and in groups, of big problems. Problem-centered teaching is demanding and requires of teachers an understanding of mathematics that will enable them to help students in their search to make sense of and use mathematics. Such instruction values students' thinking. Students are seen as "thinkers with emerging theories about the world" (Brooks & Brooks, 1993) rather than as passive recipients of information.
Problem-Centered Teaching
As the nature of the mathematical tasks changes, teachers must develop new classroom roles. If students are to have opportunities to explore rich problems within which mathematics will be confronted, teachers have to learn how to be effective in at least four new roles:
- Engaging students in the task;
- Pushing student thinking while the exploration is proceeding;
- Helping students to make the mathematics more explicit during whole-class and group interaction and synthesis;
- Using and responding to the diversity of the classroom to create an environment in which all students feel empowered to learn mathematics.
A reflective teacher realizes that engaging students in a task does not mean just having fun with its context. It is important, of course, for students to understand the context. But having an inclination to seek ways to mathematicize the situation they are exploring is critical. The teacher has to work with the students to help them understand which questions mathematics can help answer in the situation. This means keeping an eye on the mathematical goal in posing the task. This does not mean that the teacher structures the mathematical questions so that no thinking or work is left to the student. It means that the teacher keeps the focus on the big question embedded in the task and uses his or her judgment about whether this is a time when the students are to formulate questions for themselves or to find answers to problems in the situation that are posed by the situation or the teacher.
As the students work on the task posed—often in groups, always using tools such as calculators, computers, and physical manipulatives, as well as intellectual tools such as analogies—the teacher can assess what sense the students are making of the task and of the mathematics. By circulating among groups of
students the instructor can ask students for evidence to support their conjectures and can redirect groups that are off-task or floundering. Here the teacher is a coach, a guide, an interlocutor, and an assessor of student progress and problems.
After groups have made progress on the task, the teacher and the class can come together to look at the different answers, to examine the data collected, to look at the strategies used, to examine the conjectures the groups have made and their supporting evidence, and to look at the proposed solutions and the reasoning to support the conclusions reached. It is during group sense-making that the teacher must be alert to the mathematical goals embedded in the task—to bring the mathematics alive, to help students make it more explicit and powerful, and to help students connect what they have learned to things they already know. This is where the teacher can work most effectively to set high expectations, both for students' mathematical performance and for the ways in which students engage in discussions with each other.
For teachers, it is daunting to examine what they need to know in order to help develop mathematical power for all students. Few teachers know enough to feel comfortable with this type of self-examination. However, a first step is to recognize that we all have things to learn. As students often learn most effectively in groups, so teachers will find that learning alone is unlikely to be as powerful as engaging in dialogue with other teachers. In order to get started, teachers need motivation for engaging in a daily search for tasks, materials, questions, and responses that will enable students to learn. Teachers have to focus on what students are learning rather than on simply ''covering" the curriculum. Part of this has to do with the professionalism of teachers. Being professional includes managing the dilemmas of teaching in a thoughtful way, constantly trying to get smarter about the possibilities.
References
Brooks, J. G. & Brooks, M. G. (1993). The case for constructivist classrooms. Alexandria, VA: Association for Supervision and Curriculum Development.
Brown, J. S., Collins, A., & Duguid, P. (1989). Situated cognition and the culture of learning. Educational Researcher, 18(1), 32-42.
Schram, P. (1992). Learning mathematics to teach: What students learn about mathematical content and reasoning in a conceptually oriented course. Unpublished doctoral dissertation, Michigan State University, East Lansing.
GLENDA T. LAPPAN is a Professor in the Department of Mathematics at Michigan State University. Her research interests are in the related areas of teaching and learning mathematics and supporting teachers to improve their practice. She is currently Vice Chair of the Mathematical Sciences Education Board and is President of the National Council of Teachers of Mathematics (NCTM), 1998-2000. She is Co-Director of the National Science Foundation funded Connected Mathematics Project and a member of the National Education Research Policy and Priorities Board. She chaired the development of the grades 5-8 part of the NCTM Curriculum and Evaluation Standards for School Mathematics and was the overall Chair for the development of the NCTM Professional Standards for Teaching Mathematics.
14—
The Role of Complex Mathematical Tasks In Teacher Education
GILBERT J. CUEVAS
University of Miami
The NCTM Curriculum and Evaluation Standards promotes increased emphasis on problem solving, mathematical communication, thinking, and reasoning. The resulting gap between a "traditional" and a reform-based approach to mathematics instruction poses a challenge for teacher educators as they develop strategies to help both preservice and classroom teachers implement the Standards. To help teachers become thoroughly familiar with the kinds of instructional activities that reflect the Standards, mathematics educators in teacher preparation programs can focus on processes similar to those recommended for students. The use of complex mathematical tasks can play a very important role in closing the gap between what teachers have traditionally done in the mathematics classroom and the approaches emphasized in the Standards.
A primary purpose of such tasks is to engage students in meaningful and worthwhile activities that lead to understanding of mathematics as a subject matter that has real-life applications. Complex mathematical tasks have several noteworthy aspects. First, they can be thought of as instructional activities that focus on specific sets of ideas and skills. Second, they demand active involvement by both students and teachers. Finally, such tasks should provide opportunities for expansion and reinforcement of learning. This learning should focus on the exploration of concepts being addressed in class, on the reinforcement of skills and ideas, on connections between ideas, and on the promotion of student communication through discussion, justification of solutions, and explanations of mathematical processes.
My personal experience in teaching mathematics methods courses has convinced me that the use of complex tasks helps teachers become oriented toward a Standards-based approach. Such tasks encourage classroom teachers to explore instructional strategies that reflect a problem-solving approach to mathematics education. In addition, they help teachers to see the value of classroom discourse for student learning and also to develop strategies that will assist students in improving their communication skills. Just as students need time to acquire the knowledge, strategies, and skills needed to deal effectively with tasks at different levels of complexity, teachers also need opportunities to develop a mental picture of how such tasks can be integrated into typical classroom activities.
Teachers who have limited experience with complex tasks regularly raise certain questions primarily concerning their desire to know how to implement these instructional activities in their classrooms effectively and how to help students get the most out of the experiences. Teachers ask questions such as the following:
- How can I know if the level of the mathematics addressed by the task is too difficult for my students?
- How can I help my students see that a task may be approached in more than one way?
- In what ways can I incorporate complex tasks into the curriculum that I am supposed to teach?
- How do I grade students on this?
- How do I make sure that all the skills and concepts in the curriculum are addressed?
Other questions have focused on helping students learn from the tasks:
- How do I know that the approaches the students have used are appropriate and lead to correct solutions?
- How do I provide feedback to students on their performance?
- What do I do if students cannot begin the task or are not able to describe what they have done, to draw conclusions, or to justify their solutions?
In the search for the answers to these questions I have found five guiding principles for the preparation of teachers. They are as follows.
Model a problem-oriented classroom environment. In methods courses for preservice teachers, complex tasks and "big problems" can be used throughout. They can be integrated into classroom activities to begin the study of particular mathematical topics. For example, the following task introduces the number concept:
Suppose a friend told you she had a suitcase large enough to hold one million one-dollar bills. She asked you to help her bring the suitcase to a bank. Could you lift such a suitcase?
Complex tasks also can be used to summarize and reinforce ideas and concepts dealt with at different times during the course. Some tasks are used for assessment purposes. Preservice students work in small groups on these tasks and, upon completion, present their solutions to the class. Members of the class provide the group with evaluation feedback through the use of a predetermined rubric.
Provide experiences with tasks at all levels of mathematical complexity . Some secondary students will find certain tasks difficult for reasons ranging from inexperience with the activities involved to lack of appropriate mathematical background. Teachers should develop strategies to identify tasks that provide a challenge to students without being impossible to complete. Such strategies and sensitivity to the level of task difficulty can be acquired through exposure to a variety of mathematical tasks of different levels of complexity. Preservice as well as classroom teachers need to have numerous opportunities to engage in mathematical tasks, to analyze their mathematical content, and to develop solution strategies. Throughout these experiences, teachers must be guided to develop a framework by which they make decisions about the mathematical content of a task and its difficulty level. I have found that this is best accomplished when teachers reflect on and discuss the tasks.
Promote discussion of mathematical tasks, their content, and solutions . I have found three successful approaches to promote classroom discourse: small-group exploration and discussion of a given task, individual or group presentations of solutions to the whole class, and class discussion of students' approaches and solutions to tasks. For the latter, I present the class with samples of student work that I have collected in the local schools. The preservice teachers first analyze the work individually, then discuss it in small groups, and, finally, present their comments to the whole class. These experiences provide teachers with opportunities to explore a variety of student approaches to
the tasks—some more effective than others—and to identify errors in mathematics or reasoning. Also, these exercises allow teachers to construct feedback as if they were communicating with the students whose work was examined.
Emphasize development of communication skills. Communication skills and the promotion of classroom discourse in mathematics should be approached developmentally. We cannot assume that if we give students an unstructured task such as "use data from current newspaper advertisements to examine the economics of buying a car versus leasing" that they will give complete explanations of procedures, solutions, and conclusions. Teachers should guide students in the development of mathematical communication until students achieve the skills and comfort level to communicate mathematical ideas effectively. A teacher using the buying versus leasing task might structure communication with a framework such as the following:
- Describe the facts stated in the newspaper advertisements.
- Describe the differences and similarities in the facts among these advertisements.
- Describe the factors you need to take into account to begin your comparison of buying versus leasing.
- Describe how you decide whether it is more economical to buy or lease a car.
- Write your conclusions and your reasons that support your conclusions.
Provide opportunities for reflection about the tasks and their implementation with students. Teachers need time to reflect on the mathematical content, thinking and reasoning requirements, student solutions, and communication demands of each task. In this way, teachers will develop strategies to address the concerns posed earlier in this essay. In methods courses, I require students to write reflections about tasks they have completed. These reflections are then shared in small groups during class time. In workshops, I give participants opportunities to reflect on task features and possible implementation strategies.
Rather than concluding with a personal thought on the role of complex mathematical tasks in teacher education, I will share a comment made by a teacher on this matter: "By working through the tasks, I became confident of my mathematical ability, developed ideas for using them with students, and I am now more sensitive to the difficulties and obstacles students may have in their learning of mathematics."
GILBERT J. CUEVAS is a Professor of Mathematics Education in the School of Education at the University of Miami. He has directed a number of professional teacher development projects in bilingual, mathematics, and science education. He has also served as a member of the Mathematical Sciences Education Board.
15—
Assessment Conversations as a Tool for Reform
PAUL G. LEMAHIEU
University of Delaware and Delaware Department of Education
MARSHÁ T. HORTON
Delaware Department of Education
What role might extended, open-ended tasks play in assessment? Through the good efforts of many individuals and the reform of large-scale assessment initiatives, we have begun to ask such questions. While there is yet much to be done to bring technical quality and intellectual rigor to this particular aspect of a more general reform movement, it is clear that we will never again think of assessment in precisely the same terms as those that have dominated our thinking for the past century or more. What is less certain is what role assessment should play in order to maximize its contribution to broader reform efforts.
Some see assessment as an agent of reform, as a lever that, when properly applied, lifts the system (and the individuals within it) to improved performance by increasing accountability. This view is based on a well-established logic about the force and influence of assessment and accountability: clear articulation of goals will make public the expectations for individuals and the education system; appropriate and adequate assessments will reveal the performance of individuals, schools, and systems; and appropriate sanctions and rewards will provide the motivation to improve effectiveness and productivity.
This "lever view" is plausible and quite possible. We are not too optimistic, however, about assessments (reformed or otherwise) used solely in this way and detect an underlying cynical assumption: that those who work in our schools have the skills and the capacities to help their students learn better, but for some reason choose not to do so. Our experience within schools does not support this cynical view. We have encountered some who (sad to say) lack the requisite familiarity with national, state, or local standards for student learning; more who have not had the opportunity to develop or refine the skills necessary to ensure their students' success; and still more who are constrained by a lack of intellectual or material support from their school districts or systems for the kinds of practice necessary to prefigure accomplishment of the standards. We have not encountered many who willfully choose not to perform well.
However, tasks like the ones in this volume, if we assume that these are assessment tasks, do offer a potentially powerful but very different role for assessment in reform. They might play an "instrumental" role, in which teachers work with such tasks in a variety of ways that challenge their practice. First and most obvious is the signaling function, helping to make the standards concrete. This is particularly important as the concepts (curricular and instructional) underlying the standards become more complex and more subtle.
There is a second instrumental use for tasks like those documented here, also related to teachers' growth and development. Such tasks can be strategically used to stimulate and discipline what we have come to term the "assessment conversation." Making these tasks (as well as the student work that they elicit) central to professional discourse can challenge teachers' notions of students' capacities. Appropriate professional development focused on the use of these tasks can powerfully shape teachers' notions about what constitutes high-quality student work and what serves as adequate evidence of such quality. Our experience with the instrumental use of tasks like these is instructive: assessment and the development and use of tasks such as these can be approached so as to maximize the beneficial impact on instructional practice.
Just as standards-based reform requires so much more by way of professional judgment, there is a need to warrant that judgment. Given the very complex systems within which educational professionals work, faith and trust must be located somewhere. That confidence can be placed in the people who work within the system or can be placed in mechanisms designed to control people and their behaviors. The current reform movement places faith in people rather than mechanisms. Whether one considers local democratization and site-based management; teacher empowerment and shared-decision making; the increased role of teachers in curriculum definition and selection; efforts at organizational development founded upon continuous improvement and learning community ideals; or the advent of assessment approaches that more explicitly privilege human judgment—in all of these cases the trust and the hopes for a high-performing system are vested in the teachers and other professionals who serve within it.
However, the call for placing our trust in the empowerment of professionals requires that serious action be taken to warrant that trust. This is the basis for the persistent urging for investment in capacity building at the system level and in the professional development of individuals. As part of that professional development, we are optimistic about the potential of well-designed "assessment conversations" as instruments to shape teachers' expectations, beliefs, and practices.
Assessment systems offer important opportunities to show that our trust in teachers is warranted and thereby facilitate beneficial change. Well constructed assessment activities and the efforts to employ them strategically in professional development activity permit teachers to engage in review of student work; develop shared notions of high-quality student performance; determine what constitutes adequate evidence of high quality; and ultimately to reflect upon the kinds of learning experiences that challenge traditional practice and produce the desired performances.
We see immense potential for the use of tasks, such as those in this volume, as assessments within a process of ongoing and sustained development designed to support professional growth. We have done so involving large numbers of teachers who meet regularly (at least monthly for up to two days at a time) over an extended period (two years) to develop assessment tasks and to pilot and refine them in their classrooms. In these assessment-development conversations, teachers share and closely examine students' work. A professional discourse is provoked by the simple guiding question, "What can we tell about this student as a learner in mathematics?"
The ensuing discussions are closely documented and analyzed for "points of evaluative judgment." These points of judgment represent the beginnings of a framework or rubric for evaluating student work. Over time, insights grow in number, depth, and sophistication, and are synthesized into a framework that teachers use and refine.
Can an evaluative framework derived from one collection of student work be applied meaningfully to others? Will it hold up across a diverse array of students (with respect to abilities, levels of performance, cultural and linguistic backgrounds, gender, etc.)? Can it be applied with discipline and consistency (yet insight and sophistication) by many teachers? These and similar questions are addressed by taking the evaluative framework and applying it to new and broader collections of student work. At the same time that an evaluative perspective is being validated in this way, the sophistication, consistency, and reliability of shared interpretations are also being refined. Over time, these conversations, begun with a group of teachers involved in assessment development, are replicated in professional development activities on a broader and more extensive scale.
In our experience, two things have invariably been realized through these "assessment conversations." First, all who participate in them leave with
higher and more clearly articulated aspirations for student performance. This should not be the least surprising, as the derivation of criteria and expectations for quality in mathematical performances is essentially additive. One teacher sees certain things in a piece of student work, while the next recognizes some (but perhaps not all) of them and adds others. These assessment conversations proceed until the final set of aspirations (criteria of quality) are far greater than the initial one or that of any one teacher at the outset. Simply put, these assessment conversations increase the expectations of all those who participate in them.
The second effect of these assessment conversations is that a shared framework for interpreting and evaluating student work emerges. The aspirations and expectations associated with this framework become commonly understood by the teachers and more consistently applied to all their students. Again, the nature of these conversations (long-term shared encounters and reflections) supports this outcome.
These two outcomes of assessment conversations—elevated aspirations and more consistently held and applied aspirations—are key ingredients in a recipe for beneficial change. Educational research is nowhere more compelling than in its documentation of the relationship between expectations and student performance. Where expectations are high and represent demanding yet attainable goals, students strive to respond and, ultimately, they do achieve. Assessment conversations, focused upon tasks such as those in this volume and student work produced in response to them, provide a powerful device through which to warrant investment in the human side of the educational system. It is when assessment is used to provoke conversations of this kind that we find cause for optimism about the role of assessment in reform.
PAUL G. LEMAHIEU currently serves as Director of the Delaware Education Research and Development Center and as Associate Professor of Educational Studies at the University of Delaware. He is currently the principal investigator of Delaware's Statewide Systemic Initiative for Mathematics and Science Reform. He also holds a senior staff appointment in the Delaware Department of Education as Special Undersecretary of Education for Policy Research and Development. LeMahieu has received a number of major awards for his contributions to educational theory and practice from the American Educational Research Association, the Evaluation Research Society, the Buros Institute of Measurement, the National Association of Test Directors, and the Association for Supervision and Curriculum Development. He is a former member of the Mathematical Sciences Education Board, having served on its Executive Committee and as Chair of its National Forum on School Mathematics.
MARSHÁ T. HORTON is the Associate State Superintendent of Assessments and Accountability for the Delaware Department of Education. In this position, Horton coordinates the design and implementation of the Delaware State Testing Program and coordinates the department's teacher certification and licensure responsibilities. She has served on the National Reading Research Center National Advisory Board, the Sweet Briar College Board of Directors, and the New Standards Project Literacy Advisory Panel. She recently co-authored a paper with Dr. Paul LeMahieu on standards-based accountability and has served as a consultant to many school districts and national organizations.
Estimating Area
Task
In medicine, calculation of body surface area is sometimes very important. For example, severe burns are usually described as covering a percentage of the body surface area. Some chemotherapy drug dosages are based on body surface area. How might body surface area be measured? What factors influence the accuracy of the estimates?
Commentary
Three main mathematical themes could be emphasized in this task: estimation, partitioning, and successive approximation. These need to be combined with an understanding of the relationships among measurements of distance, area, volume, and weight. This task might also be used as an introduction to the calculus topic of integration.
In everyday life, we estimate area in order to determine how much paint to use in painting our homes, how much carpet to buy for a room, how many plants to buy for a garden, or how much grass seed or fertilizer to buy for our lawns. Some approaches to this task can also lead to discussion of proportion and scale. Highway designers, landscape designers, interior designers, and architects all make and interpret diagrams drawn to scale.
An important component of this task is estimating the error in measurement—perhaps finding both upper and lower bounds, which lays some of the groundwork for calculus. In some cases, upper and lower bounds may lend themselves to further refinement.
Mathematical Analysis
There are many possible avenues of approach for this task. One possibility is to consider the human body as a collection of cylinders. Each limb, the head, and the midsection, for example, might be approximated as cylinders. Finding the sum of the lateral surface area of each of these would give a good first approximation. This procedure could be refined by adding the areas of the "ends" of the cylinders and subtracting the areas where the cylinders are attached together. The procedure could be further refined by considering, for example, the head and the neck to be a sphere and a cylinder, respectively, and eventually by approximating the fingers as individual cylinders.
A very different approach would be to take pictures of a person—front, lateral, and top views—and to superimpose a flat grid on the pictures to approximate the surface area. This approach would require additional discussion of proportions due to the scale of the picture. The accuracy would depend not only on the size of the grid relative to the dimensions of the person in the picture, but also on the reasonableness of projecting a three-dimensional human onto two-dimensional pictures to estimate surface area. Using smaller and smaller grids to achieve successively better approximations foreshadows some of the ideas of calculus.
An approach that also foreshadows calculus but doesn't involve scaling is to cover the body with patches of cloth of known area. If the pieces of cloth are all the same size, the accuracy of the approximation would depend on the size of the pieces. Covering the body with cloth suggests a very elegant approach that doesn't involve calculus at all. If the entire body is clothed with close-fitting, non-stretch cloth of consistent thickness and density, the surface area may be determined by weighing the cloth and then dividing by the weight of a piece of cloth of unit area.
From any of the above approximations, students would be afforded experience and data from which to discuss the adequacy of the standard medical practice of approximating surface area by using the following formula:
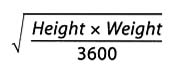
where height is measured in centimeters and weight is measured in kilograms. The result of the calculation gives an approximation for body surface area in square meters. Thus, for example, a person who is 5'10'' (177.8 cm) tall and weights 180 lbs. (81.8 kg) has a surface area of approximately 177.8 × 81.8/3600 = 2 square meters. This calculation is based in part on the assumption that, for humans, weight is roughly proportional to volume, an assumption that is also worthy of investigation. The formula has a certain dimensional consistency in that the product of height (one-dimensional) and weight (three-dimensional) gives a four dimensional quantity. Taking the square root then gives a two-dimensional result, consistent with the fact that surface area is a two-dimensional quantity.
Extensions
Given a map of the United States, students might estimate the area in square miles of the states of Colorado, Texas, Florida, and Vermont and compare their estimates to the actual area of each state given in an almanac or an encyclopedia. The students might discuss the accuracy of their estimates and why the process is easier for some states than for others. If the students are using a square grid to do the approximation, they can ask: What size grid is needed to estimate the area to a given accuracy?
Using a map causes another kind of measurement error. Because a map is a flat representation of the curved surface of the earth, there is some inevitable error in the way it shows angles or areas. How big an area on the earth must be considered before such errors are measurable? Understanding the reason for this distortion and some of the projections used by map makers involves solid geometry and spherical trigonometry.
Students also could explore the extent to which a state's topography affects its surface area. Is the surface area of a 100-mile square section of western Colorado the same as a 100-mile square section of eastern Colorado? This leads to interesting questions about how surveyors actually calculate the area of steeply sloped land.
Other extensions might concern volume or perimeter, estimating, for instance, the amount of air in a school building to determine how often the ventilation system refreshes the air. Approximating the perimeter of a territory can lead to some interesting findings. When the coastline of Britain on a geographical map is approximated by line segments corresponding to 500 km on the map, the result is 2600 km. When the coastline is approximated by segments corresponding to 17 km, the result is 8640 km—more than a three-fold increase. In contrast, when the border of Utah is measured in the same ways, the estimated length goes from 1450 km to about 1890 km—not even a two-fold increase. Fractal dimension is concerned with characterizing differences like these (Peitgen et al., 1992).
Reference
Peitgen, H.-O. et al. (1992). Fractals for the classroom. New York: Springer-Verlag.
Timing Traffic Lights
Task
A stretch of a suburban road lined with shopping plazas carries heavy commuter traffic. The road has 15 traffic signals, unevenly spaced, at the intersections with cross streets and mall entrances. Figure out how to time the lights in order to maximize the flow of commuter traffic.
Commentary
One approach to this task uses a very powerful geometric technique to model the situation. The technique combines the information for cars (given by two-dimensional position versus time graphs) with the information given for traffic lights (given by one-dimensional time graphs showing how long they are red, green, and yellow). Similar diagrams are used in the planning of highways, railroad schedules, and canals. This task and the techniques in the solution below provide opportunities for geometric thinking, reasoning from graphs, and connections between slope and velocity.
Mathematical Analysis
Rather than a complete solution, which would require precise data about placement of lights and about typical traffic flow and consideration of many alternatives, this section discusses a solution for a simple case. This simple case can provide understanding of the geometric model and insights into the general case.1
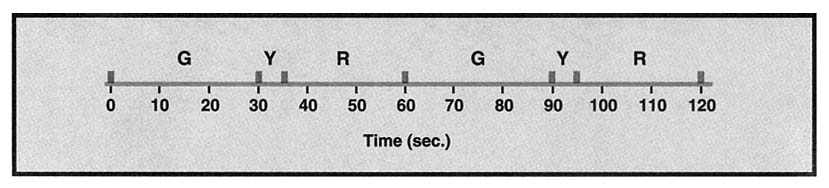
FIGURE 1: The green-yellow-red cycle of light A
Suppose the road travels north-south and has only three lights. Label the lights A, B, and C, and suppose that lights B and C are 0.25 and 0.38 miles north of light A, respectively. First consider only light A. Suppose that it follows a 1-minute cycle—green for 30 seconds, yellow for 5 seconds, and red for 25 seconds. The pattern of the light can be represented graphically on a line (Figure 1).
To show the position of cars over time, the distance from light A may be represented on a vertical axis with time represented on a horizontal axis as in Figure 1. For smooth traffic flow, cars going a moderate speed should be able to go through all three lights without stopping. Consider first only cars traveling north and assume that all cars travel at a constant speed of 30 mph. Figure 2 shows possible positions of 12 north-bound cars over the first 120 seconds after the beginning of a cycle of light A. The first car goes through light A 5 seconds after it turns green and the sixth goes through at 30 seconds, just as the light turns yellow. The white space in the middle of the graph shows that light A, when it is red, causes "spaces" in the traffic flow, if traffic entering from other roads is ignored. In this representation, the slope of a line is equal to the speed of the car it represents. Here, the slopes are 0.5 miles/60 seconds, or 30 mph.
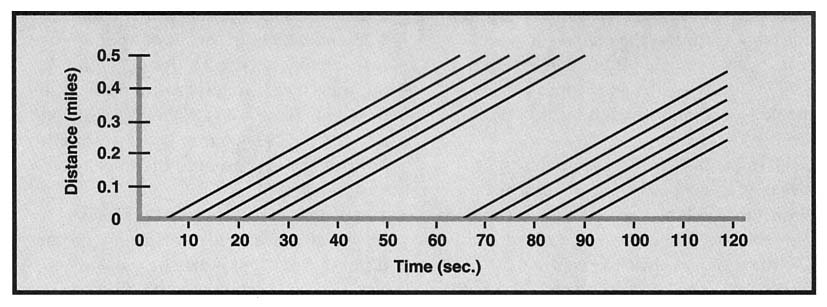
FIGURE 2: Cars going north through light A when it is green
The lines are parallel because all of the cars are assumed to be traveling at the same speed.
Lights B and C are represented as horizontal lines in Figure 3. The lines have been partially dotted to show "windows"—time intervals during which the light should be green to allow unimpeded flow of the 12 cars from Figure 2. Each light should turn green shortly before the first car arrives at the light so that the car will not need to slow down
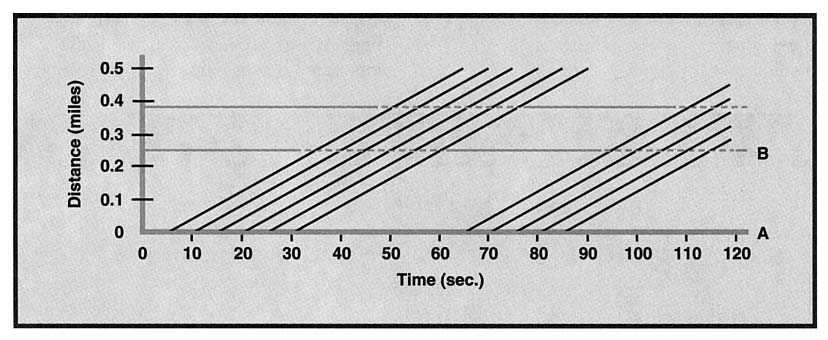
FIGURE 3: Determining when lights B and C should be green for north-bound traffic
before reaching the light. The diagram shows that light B should be green from about 30 until 60 seconds and again from 90 until 120 seconds. Allowing for a 5-second yellow light, this implies a 25-second red light between the green intervals. Thus, light B should follow the same cycle as light A, but the cycle is shifted in phase by 30 seconds. Light C should be green between about 45 and 75 seconds and then again at 105 seconds. Thus, this light should also follow the same cycle, but phase shifted by 45 seconds.
This is a sufficient one-directional solution for three lights. In fact, with this sort of phase-shifting of the same light pattern, any number of lights could be added to this road and still allow for unimpeded flow of traffic in the north-bound direction. Lights on one-way streets are often timed in a manner similar to this, although the expected speed may be different from the 30 mph used here.
Allowing for similarly smooth flow of traffic in two directions is much more difficult. Figure 4 shows both north-bound traffic as in Figure 2 and also some south-bound traffic that would go through light A when it is green. Note that if light B uses the same green intervals as in Figure 3, it will allow both north- and south-bound traffic to flow unimpeded. In order to allow all the north- and south-bound traffic to flow through light C, however, it must be green all the time, which would not be practical.
One solution to this dilemma is to give priority to the north-bound traffic and time the lights as indicated in Figure 3. Then north-bound traffic can flow unimpeded, but the south-bound traffic will always have to stop at at least one of the lights. Alternatively, priority could be given to the south-bound traffic.
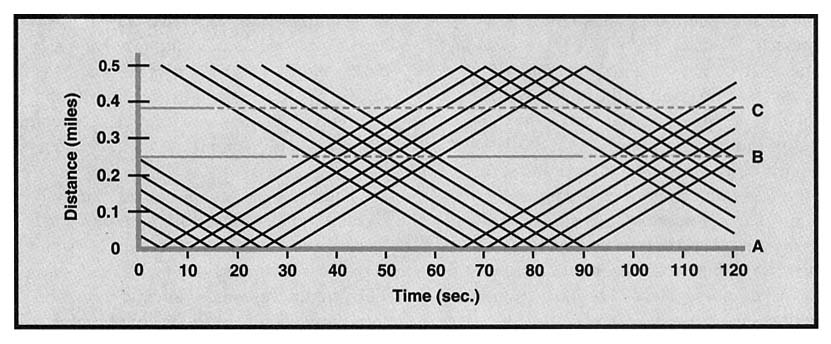
FIGURE 4: Determining when lights B and C should be green for two-way traffic
Another approach is to change the period of the light cycles. If the lights are on a 90-second rather than a 60-second cycle, then light C can be timed to accommodate both north- and south-bound traffic, as shown in Figure 5. Now, however, light B needs an excessively long green interval to accommodate both directions of traffic.
Neither a 60-second light cycle (Figure 4) nor a 90-second light cycle (Figure 5) can accommodate traffic in both directions at both lights B and C. Figures 4 and 5 do, however, suggest a compromise: a 75-second light cycle.
Figure 6 shows that with a 75 second light cycle, if both lights B and C are green from about 30 to about 75 seconds after the beginning of light A's cycle, most of the north- and south-bound traffic will flow unimpeded.

FIGURE 5: Two-way traffic, assuming a 90 second light cycle2
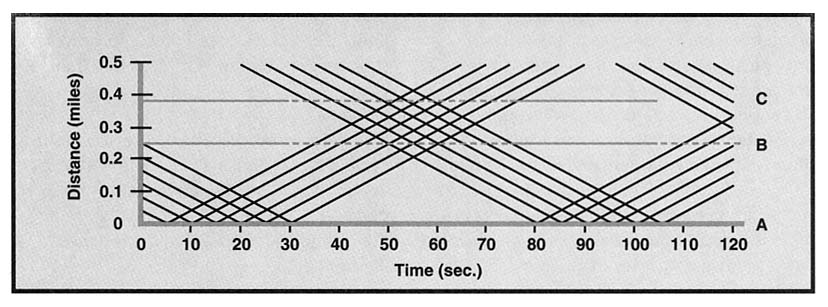
FIGURE 6: Two-way traffic, assuming a 75 second light cycle
Extensions
The discussion and diagrams above suggest that when there are only two lights or when the lights are evenly spaced, the light cycle may be adjusted to accommodate good traffic flow in both directions. When there are more than two lights and they are unevenly spaced, however, it is not always possible to allow for stop-free traffic in both directions on a two-way road. Is it possible to ensure that all cars stop at at most one of three lights? Some drivers get frustrated when they must stop at two or more consecutive lights. On a road with many unevenly spaced lights is it always possible to time the lights so this won't happen? On some two-way streets, five or more consecutive lights change as a group, allowing for most cars to pass through all the lights in the group without stopping. How does this approach compare to more flexible optimization?
The above discussion has not taken into account the east-west traffic. How should these requirements be factored in? If some of the east-west roads are major roads with much traffic, these requirements should be considered in any decisions about timing the
lights. On the other hand, if they are minor roads, it is probably safe to assume that traffic from these roads will not benefit from long red signals on the north-south road.
The discussion above began with positions of the lights and tried to find a reasonable way to time the lights for traffic going 30 mph. What about the reverse? Given the timing of some traffic lights, what are the speeds that must be traveled so that cars do not have to stop? As shown in Figure 7, cars can be given positions by tilting the lines to fit the "windows" represented by green lights. The trick is to find slopes that correspond to appropriate driving speeds.
Under the scenario represented by the solid line in Figure 7, it takes the car 60 seconds to travel from light A to light B. If B – A represents the distance between the two lights, then the speed is (B – A)/60 feet per second (fps). If the distance between A and B is 2400 feet, then the speed is 40 fps, which is about 27 mph, and that's fine. But suppose the distance between A and B is 6000 feet. Then the speed would be 100 fps, or about 70 mph, and that's not sensible. In this case, the dotted line in Figure 7 might represent a more realistic possibility. Passing through the second "window" in the line representing light B corresponds to allowing two cycles of the lights to get from A to B. This doubles the time that it takes for the car to travel from light A to light B and cuts the speed in half to about 35 mph, which might be acceptable. In general, if N is a positive integer representing a number of cycles of light B, then the speed will be (B – A)/(60N) feet per second. Just pick N to get the speed into a sensible range.
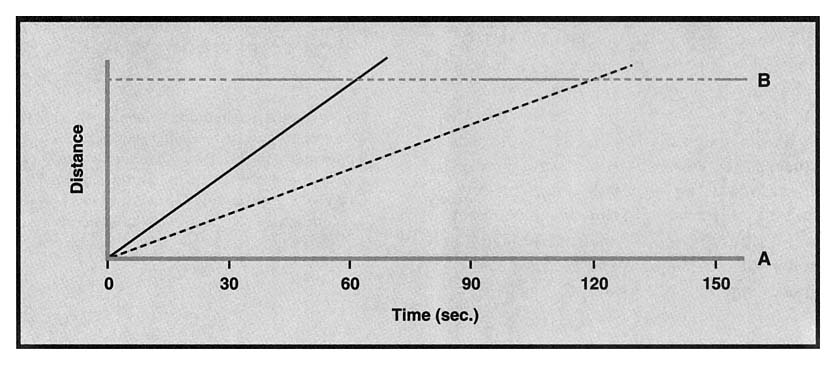
FIGURE 7: Two scenarios for a car traveling from light A to light B
What if the road carries heavy commuter traffic northbound in the mornings and southbound in the evenings? Would it make sense to have different timings of the lights for the different rush hours? Does it make sense in very heavy traffic to slow down the expected speed of travel? What needs to happen to the timing of the lights to accommodate the slower speeds?
Much of the discussion has aimed to allow cars to pass through many lights without
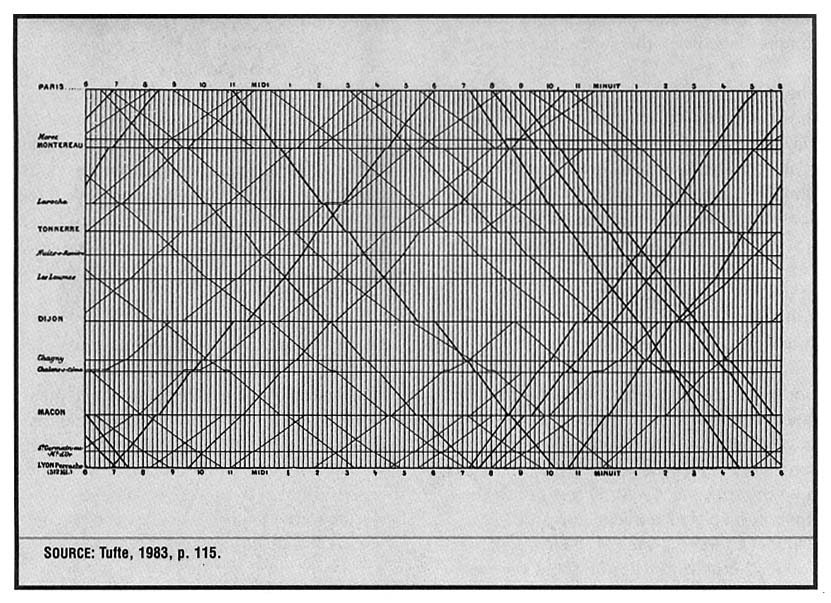
FIGURE 8: Marey's train schedule
stopping. What about maximizing the capacity of the road? Will the solution be the same or different?
This sort of diagram is used in other situations, such as train scheduling (see Figure 8). For a one-track railroad line, or a canal like the Suez Canal which is one-way much of the way, you locate sidings (bypasses) on the distance axis where traffic in opposing directions can pass, and schedule trains (convoys) to get there at the right times. The planners of traffic for the Suez Canal use a similar diagram, but with the time and distance axes interchanged for historical reasons.
References
Tufte, E. (1983). The visual display of quantitative information. Cheshire, CT: Graphics Press.
Walker, J. (1983). Amateur scientist: How to analyze a city traffic light system from the outside looking in. Scientific American, 248 (3), 138-145.
Notes
-
1.
For other ideas and approaches, see Walker (1983).
-
2.
A 90-second light cycle would likely include a longer green portion, allowing for more than 6 cars, at 5-second intervals, to pass through the green light. Nonetheless, Figure 5 includes only 6 cars through each cycle to allow for easier comparison with the other figures.
Buying A Used Car
Task
How does the age of a used car affect its price? How does its age affect its repair costs? What is the best age at which to buy a used car?
Commentary
Many people in the United States are dependent on cars, and students are no exception. This task may be particularly meaningful to students as they become consumers of cars.
Although this task begins with data collection, it leads quickly to other important mathematics, including graphs and scatter-plots, linear regression, amortization, and optimization—to balance rising repair costs against falling purchase prices.
Mathematical Analysis
Data for this task may be collected from consumer magazines, from car buying guides, or from the Internet. If data are gathered about prices and repair costs for used cars, they reveal opposite trends: newer cars tend to have lower repair costs, but older cars generally have lower purchase prices. Purchase price is a one-time cost, and repair costs are likely to be on-going. So to combine this information, students might first convert it to a common basis—either annual expenses (if the purchase price is paid out over time) or total costs (by adding up total expected repairs for the likely life of the car).
Once these data are combined, either in a spreadsheet or on a graph, it should be clear visually where the total costs are least. This may be somewhere in the middle of the age or price range being examined, or it might be at one end or the other. For example, among cars older than ten years, it might be that the newest cars are the best buy because repair costs rise more rapidly than the drop in price as cars age.
Many people who are buying a used car may expect that their incomes will rise. In that case, they may not want to minimize the total cost but might be willing to bear larger repair expenses down the road in return for a lower purchase price.
Extensions
What is the relation between age and mileage? How much more value is there in a low-mileage car of a certain age? By collecting repair costs and plotting them by age and by mileage, it is possible to determine whether age or mileage is the better indicator of the reliability of the car. (Such data may be available—at least for specific brands—from the computerized repair records of automobile dealers.) Other extensions could look at differences between cars repaired at dealers' shops or at independent garages or in different regions of the country.
Another question a prospective car-buyer might want to consider is whether to buy or lease.
Finally, if the data are available, it would be interesting to find out how old a car needs to be before its price begins to rise—because it is becoming an antique.
There was a problem loading page 154.




























