| This page in the original is blank. |
Overview
Any discussion of curriculum assumes, whether implicitly or explicitly, one of many views of curriculum. College admissions requirements, for example, sometimes describe a high school mathematics curriculum as little more than a list of course titles. Toward the other end of specificity, some might point to a textbook, looking especially at its table of contents. For the purposes of this document, a curriculum is a detailed plan for instruction, including not only the materials used by teachers and students, but also understandings of how they fit together and of the important mathematical concepts embedded within them. Thus, a mathematics curriculum might include—but must not be limited to—tasks such as those in this volume. The essays in Part Three in particular go beyond a list of topics, beyond a collection of tasks, to discuss how curricula might be constructed—how tasks, topics, and ''habits of mind" might be knit together as themes or strands to create a curriculum with coherence, depth, and rich opportunity for student learning, sense making, and connections to students' ways of thinking about the world.
In his essay, Zalman Usiskin discusses the importance of applying knowledge to new situations. When designing curriculum, he begins with a key concept and seeks models—settings, often from the workplace or everyday life, which embody the mathematical ideas. Of course, for many users of mathematics,
it is more common to go in the other direction—to begin with a real-world setting and seek a mathematical model of that setting, perhaps with graphs or formulas. Chazan and Bethell (p. 35) describe such an approach earlier in this volume. They put students into the workplace and asked them to find the mathematics. Thus, whether the mathematics models the world or the world models the mathematics depends upon where you begin. Ultimately, both directions might be necessary for students to make strong connections between mathematics and their worlds. In discussing the role of tasks in curriculum, Usiskin suggests organizing curriculum around sequences of such models and problems that range over many years.
Albert Cuoco takes another approach to organizing curriculum. He suggests that mathematics is more than a collection of topics organized under broad headings such as geometry and number but, rather, is about ways of thinking, or habits of mind, such as algorithmic thinking, proportional reasoning, and reasoning through thought experiment. Habits of mind, he suggests, can be threads that help organize curriculum, for without habits of mind, higher order skills will remain elusive.
Harvey Keynes' essay discusses a key theme in this document: effectively preparing students for work and for higher education. Keynes asks two important questions: First, what are characteristics of tasks that can prepare students both for the workplace and for post-secondary education? Second, what are the requirements for effective use of tasks like these in the classroom? Keynes suggests conditions of appropriateness for tasks that can develop both concrete and abstract thinking.
The tasks in Part Three differ from those in other parts to illustrate that they may be fruitfully approached at many different times in a student's mathematical career. The discussions of these tasks include multiple solutions, many extensions, and more connections to other mathematical ways of thinking. Some of this discussion is quite deep mathematically, not to suggest that such depth is appropriate for all students at the same time, but, rather, to suggest that these tasks can provide opportunity for engagement in rich and deep mathematics to students when they are interested and ready. Tasks that are sufficiently rich and that satisfy Keynes' conditions for appropriateness can fit more than once into a curriculum that is organized around Cuoco's "habits of mind" or Usiskin's sequences of models.
The Lottery Winnings (p. 111) task may be solved at one level with spreadsheets, for students having little formal algebraic experience, and it may be used to motivate students to see a need for the general symbolic language that algebra provides. At another level, students who are more experienced with the symbolism of algebra might be expected to express the task's spreadsheet relationships in standard algebraic notation. Students with even more sophistication might be expected to find the general formula. In a precalculus course, students might explore these lottery winnings with annual,
semi-annual, monthly, weekly, and daily payments as excellent background for the important calculus idea of successive approximation.
The other tasks in this part are similarly rich. In addition to discussion of probability and Simpson's paradox, Hospital Quality (p. 115) can lead to exploration of ideas about rates, ordered pairs, and vectors. Rounding Off (p. 119) provides opportunities for exploring ideas in algebra and arithmetic, while serving as an introduction to the idea of using geometry to represent probability. Rules of Thumb (p. 123) can lead to discussion of modeling and comparison of linear models, or linear and quadratic models. The many avenues of approach to these tasks may be exploited by teachers to maximize connections to students' thinking and experience.
The idea of periodically revisiting tasks sounds rather like Bruner's spiral curriculum (Bruner, 1965/1960), an idea that some might argue has lost its usefulness. Data from the Third International Mathematics and Science Study (TIMSS) (Schmidt, McKnight, & Raizen, 1996) suggest, however, that there has been a degeneration of the spiral curriculum as Bruner saw it. The point of Bruner's spiral curriculum was not that topics should be repeated for several years until they "stick" but that, when an idea is revisited in a new setting or with new tools, if students have opportunity to connect the new encounter to their understandings of their previous encounters with the idea (along with all the intervening experiences), then their understanding can grow.
There are dangers in any statements of standards or suggested visions of school mathematics, for there is no clear path indicating what should happen in classrooms. Cuoco warns that the statement, "Students should be able to solve problems like these," can become "Students should be able to solve these problems." But such a conclusion is contrary to the intention of this volume. The goals are for students to learn mathematics and to learn to appreciate the power that mathematics holds for us. Any task or collection of tasks is merely intended to be a means to those ends. Furthermore, teaching any task as only a procedure to be memorized will destroy its richness. Our point—especially in evoking the image of the spiral curriculum—is that there is value in revisiting tasks such as these at various points in a student's career, each time aiming for more sophisticated analysis and deeper mathematics.
In summary, the tasks in this volume cannot comprise a high school mathematics curriculum; no small collection of tasks could. These tasks have been chosen for their illustrative richness rather than for any collective curricular coherence. Individually and collectively, these tasks together with the essays might instead serve as inspiration for those interested in curriculum, but, as curriculum designers know, there is a lot of work to be done between first noting that there is mathematics in some real-world context and finally developing good curricular materials.
10—
Fitting Tasks to Curriculum
ZALMAN USISKIN
University of Chicago
When I first taught high school, I used to tell my students—even the average ones—that the real test of learning was not whether they could answer questions like those they had seen in their textbooks but whether they could apply their knowledge to new situations they had not encountered. This aphorism is only partially true and was patently unfair. In applying the principle of the aphorism, when I would make up a test, I would purposely choose items that students had not encountered, items for which they would not have studied. Those items were not a test of what had been learned from the class but what had not been learned from the class. They tested some natural or acquired competence beyond the course.
Those who wish students to apply, synthesize, analyze, and evaluate (to use the language of higher mental processes found in Bloom's Taxonomy of Educational Objectives [1956]) have always found it difficult to invent representative items. Those for whom a problem is "a situation which we want to resolve but for which we do not have an algorithm" (to use the common researcher definition) have a similar dilemma, for once a problem is solved, the astute solver has an algorithm to use for the next problem of that type. Inventing good problems has always been an art.
The quandary presented by the desire to have students apply their knowledge
and not just parrot it has been felt by all those whose goals involve more than routine skills. In the 1970's, when in a reaction to one of the weaknesses of the "new math" we began to design curricula in which a main goal was to have students apply what they knew in real-world situations, the same dilemma appeared in only slightly different clothing. We felt strongly that students were not able to apply algebra because they were not taught the applications. But if we taught the applications, then were we not changing "application" from a higher level process to a lower one?
We decided that the goal of learning to apply was more important than how that learning had been attained; that is, we decided to teach the applications. For example, consider the following problem, introduced in Algebra Through Applications with Probability and Statistics (Usiskin, 1979).
In Chicago there are two monthly rates for local telephone service. Choice 1 has a base rate of $11.25 for 200 calls plus .0523 for each call over 200. Choice 2 is $24.50 for an unlimited number of calls. How do you decide which plan is better?
Students were asked to write a sentence that would help them decide. The goal was to think of the sentence 11.25 + .0523(x - 200) > 24.5 (When is choice 1 better?) or 11.25 + .0523(x - 200) < 24.5 (When is choice 2 better?). This is not an easy task for students who have never studied problems like these. But we wanted to make solving such problems routine because they abound in the real world. The lesson contained similar items involving teacher salaries (compare $9,000 plus $500 for each year's experience with $9,750 plus $350 for each year) and rental cars (compare $15.95 a day plus 14¢ a mile with $12.95 a day plus 15¢ a mile). Fitting the title of the lesson, "Decision-Making Using Sentences," students were not asked to solve the sentences they wrote. The problems were employed to motivate the next lesson, in which students were shown an algorithm for solving ax + b < cx + d, and were given additional problems of the type.
"Problems of the type" is an important phrase to consider. What type is involved here? A current view is that it is unwise to sort problems by their context, such as has been the tradition in algebra with coin problems, mixture problems, distance-rate-time problems, age problems, and so on. Yet, on the other hand, Polya's advice is also commonly accepted: "If you cannot solve the proposed problem try to solve first some related problem" (Polya, 1957). When is a problem to be considered as "related''? How should we group problems for study?
The consequences of grouping related problems reach far beyond explication of types. With respect to problem solving, the power of mathematics lies in its ability to solve entire classes of problems with similar techniques. The Chicago telephone-cost problem is not an earth-shaking context for mathematics, but it exemplifies a class of constant increase problems that lead to equations and functions involving the algebraic form ax + b. Put another way, if we expect
students to come up with a mathematical model for a real situation, they need to know the attributes of the situation that would cause a particular mathematical model (linear, quadratic, exponential, sine wave, etc.) to be appropriate.
So, in developing the University of Chicago School Mathematics Project curricula that give strong attention to applications, we have often begun with the mathematical concept and sought the key mathematical models of that concept (University of Chicago School Mathematics Project, 1989-97; Usiskin, 1991). In a few instances, the content is standard in the curriculum, as with growth and decay models for exponential functions. In other cases, the mathematical conceptualizations of the topic need to be broadened; as with angle, for example, which in geometry is traditionally "the union of two rays," but which in applications may be better conceptualized as a "turn" or as a "difference in directions." Freudenthal (1983) has done many analyses of this kind.
In a few cases, we have found that the standard approach to the problem type to be inhibiting. Consider the following problem, which originates from an actual situation:
A city charges 8% tax and a restaurant in the city gives a 5% discount for paying cash. Is it better for a diner if the discount is given first and the tax charged on the discounted price, or if the tax is charged on the discounted price, and then the discount taken?
Students are customarily taught that taxes (discounts) are added to (subtracted from) original prices to determine total cost. Thinking this way, working from a meal with original cost M, the first option is represented by the expression
If, instead, students are taught to think of taxes and discounts as factors, i.e., to think multiplicatively, that same option is represented by 1.08(.95M). The multiplicative representation is not only simpler but makes transparent the desired generalization from doing this sort of problem: it makes no difference what the specific discounts and taxes are; if they are fixed they can be done in any order.
Fitting tasks to curriculum involves more than assuring that the scope of the curriculum is broad enough to accommodate the tasks. There is also the question of the sequence of topics. The mathematics you will see illustrated in the Lottery Winnings (p. 111) task involves the general idea of annuities, which can be viewed as the sums of compound interest expressions, which themselves trace back to the same multiplicative idea in the restaurant example given immediately above, which in turn requires that a student have the notion that multiplication by a number larger than 1 serves to enlarge a quantity, and multiplication by a number between 0 and 1 serves to contract it.
In the past, the mathematics curriculum has been carefully sequenced either by algorithmic considerations (to perform long division, you must be able
to subtract and multiply, so these operations must precede division) or by logical considerations (one proof of the Pythagorean Theorem involves similar triangles, so these must be studied before the Pythagorean Theorem can be considered). The above analysis suggests that the development of problem-solving among the populace would be aided by the development of sequences of models and problems that range over many years of study.
Here is an example of such a development. Begin in the primary grades with the use of subtraction for comparison and the specific example of change. When division is introduced, cover the wide range of rates such as students/class, km/hr, and people/mi2. In middle school, use negative numbers to represent measures in situations that have two opposing directions, such as gain and loss, up and down, or north and south, and picture them on the number line. Introduce ordered pairs, not only for cataloguing the locations of objects but also for recording pairs of data. Then, by asking how fast something has changed, introduce the concept of rate of change, picture this in the coordinate plane, and use both the application and the picture to lead into the idea of slope. In high school, study situations in which the rate of change is not constant. Use these to consider limits of rates of change. There is reasonable evidence that such an approach is far more effective in leading to understanding of the pure and applied mathematics involved than traditional approaches, in which the idea of slope is introduced by a definition as (y2 - y1)/(x2 - x1) with no prior buildup or connection to rate of change.
Another example is geometric. In the elementary grades, use the familiar coordinate square grid to obtain areas of rectilinear figures and associate the product xy with the area of a rectangle with dimensions x and y. But also modify the square or rectangular grid to generate tessellations. Point out that a two-dimensional object that tessellates can be cut from a large sheet without wasting space. In the middle grades or early high school, use finer and finer grids to provide better and better estimates of the areas of regions. In high school, graph the speed of a car or other object over time, and interpret the area between the graph and the x-axis as the product of the speed and the time, i.e., as the distance traveled. This paves the way for the many situations representable with integrals.
It is significant that the long sequences described in the preceding two paragraphs are embedded in the traditional content of arithmetic, algebra, geometry, and elementary analysis. We have yet, however, to develop long sequences for the teaching of statistics, as it has had a shorter lifetime in the high school curriculum. To incorporate tasks like those in this volume into the experience of students is a curricular problem that is currently being undertaken by some of the mathematics reform curricula.
Even with the analysis of individual tasks and their setting in the curriculum, there remain two particularly knotty curricular problems. First, there are tasks that involve a range of mathematics too wide to be classified by
a single mathematical model or even a family of related models. Incorporating these tasks into a curriculum is on the one hand easy because they can fit in so many places. On the other hand, without such a broader context in which to embed them, such tasks become unwieldy if students are not well versed in the prerequisites to them.
Second is the issue with which this essay began. While a fundamental goal of mathematics education must remain for students to acquire the competencies to solve simple and complex problems they are likely to encounter in their lives, students must also have opportunities to approach problems the likes of which they have not seen before. A task for curriculum developers is to accommodate these two competing needs. The corresponding task for philosophers and policy makers is to consider whether it is fair for everyday classroom assessments to test students on the latter.
References
Bloom, B. (Ed.). (1956). Taxonomy of educational objectives. Handbook I: Cognitive domain. New York: David McKay.
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Polya, G. (1957). How to solve it. (Second ed.). Princeton, NJ: Princeton University Press.
University of Chicago School Mathematics Project. (1989-97). Transition mathematics. Algebra. Geometry. Advanced Algebra. Functions, statistics, and trigonometry. Glenview, IL: Scott Foresman.
Usiskin, Z. (1979). Algebra through applications with probability and statistics. Reston, VA: National Council of Teachers of Mathematics.
Usiskin, Z. (1991). Building mathematics curricula with applications and modelling. In M. Niss, W. Blum, & I. Huntley (Eds.), Teaching of mathematical modelling and applications, (pp. 30-45). London: Ellis Horwood, Ltd.
ZALMAN USISKIN is Professor of Education at the University of Chicago and Director of the University of Chicago School Mathematics Project. He is a member of the Board of Directors of the National Council of Teachers of Mathematics, of the Mathematics/Science Standing Committee of the National Assessment of Educational Progress, and of the United States National Commission on Mathematical Instruction. He has served as a member of the Mathematical Sciences Education Board.
11—
Mathematics as a Way of Thinking about Things
ALBERT A. CUOCO
Education Development Center
I didn't always feel this way about mathematics. When I started teaching high school, I thought that mathematics was an ever-growing body of knowledge. Algebra was about equations, geometry was about space, arithmetic was about numbers; every branch of mathematics was about some particular mathematical objects. Gradually, I began to realize that what my students (some of them, anyway) were really taking away from my classes was a style of work that manifested itself between the lines in our discussions about triangles and polynomials and sample spaces. I began to see my discipline not only as a collection of results and conjectures but also as a collection of habits of mind.
This realization first became a conscious one for me when my family and I were building a house at the same time I was researching a problem in number theory. Now, pounding nails seems nothing like proving theorems, but I began to notice a remarkable similarity between the two projects. The similarity did not come from the fact that house-building requires applications of results from elementary mathematics (it does, by the way); rather, house-building and theorem-proving are alike, I realized, because of the kinds of thinking they require. Both require you to perform thought experiments, to visualize things that don't (yet) exist, to predict results of experiments that would be impossible to actually carry out, to tease out efficient algorithms from
seemingly ad hoc actions, to deal with complexity, and to find similarities among seemingly different phenomena.
This focus on mathematical ways of thinking has been the emphasis in my classes and curriculum writing ever since, and I'm now convinced that, more than any specific result or skill, more than the Pythagorean Theorem or the fundamental theorem of algebra, these mathematical habits of mind are the most important things students can take away from their mathematics education (see Cuoco, Goldenberg & Mark, 1996; Cuoco, 1995; and Goldenberg, 1996 for more on this theme). For all students, whether they eventually build houses, run businesses, use spreadsheets, or prove theorems, the real utility of mathematics is not that you can use it to figure the slope of a wheelchair ramp, but that it provides you with the intellectual schemata necessary to make sense of a world in which the products of mathematical thinking are increasingly pervasive in almost every walk of life. This is not to say that other facets of mathematics should be neglected; questions of content, applications, cultural significance, and connections are all essential in the design of a mathematics program. But without explicit attention to mathematical ways of thinking, the goals of "intellectual sophistication" and "higher order thinking skills" will remain elusive.
The habits of mind approach seems to be gaining acceptance among other mathematics educators. Everybody Counts (NRC, 1989) describes it this way: "Mathematics offers distinctive modes of thought which are both versatile and powerful. … Experience with mathematical modes of thought builds mathematical power—a capacity of mind of increasing value in this technological age. …"
A curriculum that uses workplace and everyday tasks to support the goal of developing mathematical thinking is less likely to use the tasks as the curriculum; it is less likely to let the message "high school graduates should be able to solve problems like these" evolve into "high school graduates should be able to solve these problems." Conversely, a curriculum firmly rooted in concrete problems is less likely to turn the goal of developing mathematical habits of mind into a "mathematics appreciation" curriculum, that studies little more than lists of mathematical ways of thinking. The dialectic between problem-solving and theory-building is the fuel for progress in mathematics, and mathematics education should exploit its power. Problems can be both sources for and applications of methods, theories, and approaches that are characteristically mathematical. For example, through the work of Descartes, Euler, Lagrange, Galois, and many others, techniques for solving algebraic equations developed alongside theory about their solutions. (See, e.g., Kleiner, 1986.)
What does it mean to organize a curriculum around mathematical ways of thinking? One way to think about it is to imagine a common core curriculum for all students lasting through, say, grade 10. Students would work on problems, long-term investigations, and exercises very much as they do now, except the activities would be aimed at developing specific mathematical approaches.
In contrast to other kinds of organizers currently in use (applications, everyday situations, whimsy, even computational skill), the benchmark for deciding whether or not to include an activity in a curriculum would be the extent to which it provides an arena in which students can develop specific mathematical ways of thinking, such as:
- Algorithmic thinking: Constructing and using mechanical processes to model situations.
- Reasoning by continuity: Thinking about continuously varying systems.
- Combinatorial reasoning: Developing ways to "count without counting."
- Thought experiment: Learning to imagine complex interactions.
- Proportional reasoning: Thinking about scaling, area, measure, and probability.
- Reasoning about calculations: Developing algebraic thinking about properties of operations in various symbol systems.
- Topological thinking: Generalizing notions of closeness and approximation to non-metric situations.
These themes would run throughout the K-10 experience. They would be discussed explicitly in class, in diverse contexts, while students were working on problems. For example, an investigation involving topological reasoning might ask students to improve on the way users are allowed to organize their desktops in Macintosh and Windows environments.
After a decade of this core curriculum, students could choose from a set of electives that would vary from school to school and from year to year. Courses in probability, geometry, physics, history, algebra, cryptography, linear algebra, art, data-analysis, accounting, calculus, computer graphics, trigonometry, and whatever else interests teachers and students are all candidates. If students have a solid foundation in mathematical thinking, they will be prepared for a wide array of high-powered courses designed to meet the interests and needs of the entire spectrum of students. This is a genuine alternative to the current system of tracking: it would give students a choice and a chance to pursue their interests (16-year-old students do have well-developed interests). But no matter what choices they made, students would be assured of a substantial mathematics program that built on a core curriculum centering around mathematical habits of mind.
Such a curriculum would help students develop general strategies for doing mathematics, establish underlying mathematical (not just contextual) connections among the tasks, and help students develop the intellectual prowess necessary to deal with the kinds of problems they'll face after graduation. For example, a strand on algorithmic thinking would be a good context
for investigating problems such as Lottery Winnings (p. 111) or Buying on Credit (p. 87). Whereas the contextual similarity of these tasks is evident even at a superficial level, they also share a deeper mathematical similarity based on a kind of algorithmic thinking that is somewhat removed from the mathematics backgrounds of most adults.
Show a group of eighth graders a table like Table 11-1. Then ask these eighth graders to describe what is going on. Their responses will be quite different from those of most adults who have been schooled in algebra. Adults immediately search for a "rule"—a procedure that can be performed to the "Input" column to produce the "Output" numbers. (In this case, multiplying by 5 and subtracting 1 does it). Young students are much more likely to see other patterns (the last digits on the right, for example), and very often they'll notice that every number in the right-hand column is 5 more than the one preceding it. This is the germ of recursive thinking, a very important way of looking at things. Rather than extinguish it during high school, a strand on algorithmic thinking would develop it in tandem with the more traditional "closed form" (multiply by 5 and subtract 1) way of modeling the data. Recursive approaches are ideal ways to build spreadsheets and model processes using computer algebra systems like Mathematica. And investigating the connections between recursive and closed form models can become a theme that organizes a great many of the topics in traditional high school mathematics.
TABLE 11-1: An input/output table
|
INPUT |
OUTPUT |
|
1 |
4 |
|
2 |
9 |
|
3 |
14 |
|
4 |
19 |
|
5 |
24 |
|
6 |
29 |
Recursive thinking also gives students genuine intellectual power. Listen to a group of adults discussing the question, "How does the bank figure out the monthly payment on my car loan?" You'll hear qualitative statements, but you'll seldom hear a satisfactory mathematical description of what goes on behind the button on the calculator. Students accustomed to thinking in algorithms would ask themselves how the bank constructs a spreadsheet for computing the balance owed at the end of each month. They'd articulate an algorithm something like, "The amount you owe at the end of a month is the amount you owed at the beginning, plus 1/12 of the yearly interest on that amount, minus whatever you make for a payment." This simple model is easily executed on a spreadsheet, and it quickly leads to an algorithm for calculating the monthly payment on a loan. This can be refined in calculus to the method that is used in practice, and it can be modified well before calculus is known to handle tasks like those in this volume.
The usefulness of this kind of algorithmic thinking transcends the analysis of a particular context; algorithmic thinking is used by chefs, construction workers, librarians, and people surfing the Internet. A curriculum that focuses
on developing similar mathematical habits will go a long way toward achieving the goal of preparing students for challenges that don't yet exist. And it offers a mathematical framework that meets the goal of providing tasks that prepare students both for the world of work and for post-secondary education, that "exemplify central mathematical ideas," and that "convey the rich explanatory power of mathematics."
References
Cuoco, A. (1995). Some worries about mathematics education. Mathematics Teacher, 88(3), 186-187.
Cuoco, A., Goldenberg, E. P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curriculum. The Journal of Mathematical Behavior, 15(4), 375-403.
Goldenberg, E. P. (1996). "Habits of mind" as an organizer for the curriculum. Boston University Journal of Education, 178(1), 13-34.
Kleiner, I. (1986). The evolution of group theory: A brief survey. Mathematics Magazine, 59(4), 195-215.
National Research Council. (1989). Everybody counts: A report to the nation on the future of mathematics education. Washington, DC: National Academy Press.
ALBERT A. CUOCO is Senior Scientist and Director of the Mathematics Initiative at the Education Development Center (EDC). Before coming to EDC, he taught high school mathematics for 24 years to a wide range of students in the Woburn, Massachusetts, public schools, chairing the department for the last decade of his term. A student of Ralph Greenberg, Cuoco received his Ph.D. in mathematics from Brandeis in 1980. His mathematical interest and publications have been in algebraic number theory, although his recent work in high school geometry is gradually convincing him that geometric visualization has a place in mathematical thinking.
12—
Preparing Students for Post-secondary Education
HARVEY B. KEYNES
University of Minnesota
The goals of High School Mathematics at Work are broad and ambitious as well as somewhat novel. This collection of essays discusses issues and potential themes for mathematical curricula that might be appropriate for both those students heading to the world of work and those headed into post-secondary education in the mathematical sciences. These issues and themes are illustrated by tasks that are intended to "exemplify central mathematical ideas" and "convey the rich explanatory power of mathematics."
One can hardly argue with any of these goals. But we also expect that the use of mathematics in the world of work by students who have completed their mathematics education in high school will probably be different (though not necessarily easier) than for students continuing in post-secondary education. In the first instance, technical workers might be expected to do concrete multi-step computations using numerical methods, probably with technological support, and to understand and use some algebraic and geometric methods, and symbolic arguments that are job-specific. They generally will not be expected to abstract and symbolically model mathematics embedded in work situations, to reason and communicate symbolically, or to use abstract mathematical reasoning or advanced mathematical tools in applications to other disciplines.
On the other hand, students moving on to post-secondary education, especially in careers that use mathematics in a professional capacity, will be expected to have these more conceptual skills as well as the some of the same concrete skills of students who enter the work force. Certainly in college courses, many of these more conceptual and abstract skills will be prerequisites. So a major issue for post-secondary preparation is whether tasks such as those in this volume can be used to effectively prepare students to engage in symbolic and abstract mathematical reasoning in algebra, geometry, and analysis as well as to explore concrete and numerical methods.
When selecting or designing tasks for inclusion in a curriculum, one must ask not only whether the tasks are based on rich and deep mathematics but also whether they can be used effectively in the typical classroom to exemplify central mathematical ideas and to contribute to an integrated whole. Can the rich and deep mathematical ideas embedded in tasks be exposed and effectively explored conceptually, visually, and analytically, as well as numerically and technologically, so that they contribute in meaningful ways to students' preparation for college calculus, combinatorics, and linear algebra? These questions depend on (a) the classroom teacher's interest and capability, (b) the mathematics curriculum, (c) classroom dynamics, (d) school and family expectations, and (e) the inherent mathematical ideas embedded in the tasks themselves. Any task must be viewed in this larger perspective to see if it can really be useful in helping students learn mathematics at both the concrete/computational and symbolic/conceptual levels.
It does not take very long to realize the difficulty of finding tasks that can effectively illustrate the major objectives of this document. Such tasks must, at a minimum,
- be presented in a practical context in language that is easily understood but precise;
- be amenable to analysis on several different levels: numerically, geometrically, symbolically, and conceptually;
- be based at least partially on mathematics that is of central importance in the high school curriculum; and
- allow for more extended mathematical interpretations.
The first point, which concerns linguistic style and clarity of mathematical goals, needs some amplification. Poorly worded and mathematically vague tasks actually discourage students from seeking to develop and analyze the mathematical models behind these questions and encourage them simply to resort to ad hoc or strictly computational solutions. If high school students were really able to interpret mathematically these verbal descriptions, many of the widespread student difficulties with ''story" problems would suddenly vanish.
One needs to remember that the abstraction of the mathematical phenomena described by seemingly straightforward language is one of the most difficult tasks of applied mathematics, even for professional mathematicians.
In examining a task, our primary concern is to determine what mathematics students can learn from it. Many of the tasks in this document have the capacity to be mathematically analyzed both concretely and conceptually at levels that support both work force and post-secondary goals. Lottery Winnings (p. 111) is an excellent illustration: one can feel reasonably confident that many teachers will encourage students both to explore numerical solutions and also to conceptualize the important mathematical ideas embedded in this task.
Given a collection of tasks, one important measure is the breadth of mathematics present in the tasks. Clearly, any small collection of tasks will necessarily need to make choices and de-emphasize certain aspects. As a whole, the tasks in this volume use classical geometric patterns and some level of pictorial representations. Algebraic reasoning at a classical level is also addressed. On the other hand, newer uses of geometric and visual reasoning—information embedded in pictures or graphs—are downplayed. Moreover, the breadth required for vocational training or direct entry into the work world is certainly different for students who will become professional users of mathematics. These tasks can provide a piece of the picture but not the entire spectrum of mathematical expectation for all post-secondary students.
Many of the tasks in this document meet conditions listed above. Here are three more tasks:
- You are installing track lighting in an old warehouse that is being remodeled into a restaurant. The lights can adequately illuminate up to 15 feet from the bulbs and, at that distance, illuminate a circle with a 6 foot diameter. Figure out where to place the tracks and the bulbs for maximum illumination of the customer area. This task uses geometry, trigonometry, solid geometry (looking at the cone of illumination from a constrained light bulb), and proportional reasoning. It could be modeled with computer software or solved analytically. All of the mathematics involved is within the scope of the high school curriculum.
- Your employer at your first job has given you a choice of where to invest your retirement funds: in a mutual fund that is expected to grow at 10% per year or at the local bank, which charges a 1% yearly service rate for a similar fund, also rated at 10%. You would like to deal with your local bank but don't want to lose too much money. Suppose you expect to put $1,000 each year into the fund. How much will you lose over 10 or 20 or 30 years if you invest at your local bank? This task, which can be modeled in many different ways, illustrates the famous rule that a 1% difference in interest grows very rapidly in
- compounding over time. It can also lead to some interesting graphs and comparisons of growth rates of functions. Finally, it can be explained in language appropriate for a high school classroom.
- Analyze a contour map with peaks and flat areas. This will provide an opportunity to study curves and shapes in two-dimensions, explore rates of change (closely packed contours), preview functions and graphs on the plane, and examine the geometry of three-space. Practical aspects from cartography and local area maps can provide an everyday context.
The overall goal of High School Mathematics at Work—to call attention to rich and compelling manifestations of high school mathematics all around us—is enticing and potentially very important. And, in addressing a broad and diverse set of students, it is reasonable to downplay the role of abstraction. Yet many mathematicians and mathematics educators would argue that mathematics without abstraction is not mathematics. While this dictum could be argued as applying to all students, it is probably less controversial to apply it to post-secondary students who will be professional users of mathematics.
The process of developing tasks with "real life" contexts that are relevant and mathematically significant both for students directly entering the technical work force and for students going on to mathematics-based careers is both difficult and daunting. We must continue to discuss issues and directions, such as scope, breadth, language, and complexity of the mathematics. The tasks in this volume do, however, provide an excellent core framework and standard of quality in which to continue the discussion.
HARVEY B. KEYNES received his B.A. in 1962 from the University of Pennsylvania and the Ph.D. in 1966 from Wesleyan University. His research interests are in dynamical systems. He has directed the following projects: University of Minnesota Talented Youth Mathematics Program (UMTYMP, state and private funding); the National Science Foundation's (NSF) Teacher Renewal Project; the NSF-supported Minnesota Mathematics Mobilization; the Ford Foundation Urban Mathematics Collaborative; the NSF-supported Mathematics in Education Reform Network; the NSF-supported Young Scholars Project; the Bush Foundation to increase female participation in UMTYMP; and the NSF-funded Early Alert Initiative. He is the recipient of the 1992 Award for Distinguished Public Service of the American Mathematical Society. He is published extensively in mathematics education journals.
Lottery Winnings
Task
A lottery winner died after five of the twenty years in which he was to receive annual payments on a $5 million winning. At the time of his death, he had just received the fifth payment of $250,000. Because the man did not have a will, the judge ordered the remaining lottery proceeds to be auctioned and set the minimum bid at $1.3 million. Why was the minimum bid set so low? How much would you be willing to bid for the lottery proceeds?
Commentary
This task engages students in exploration of interest rates, exponential growth, and formulating financial questions in mathematical terms. These ideas introduce students to an important way of thinking about decisions they will have to make throughout their lives. For example, students will need to decide whether they can afford to buy a car and, if so, whether it would be better to lease; or whether to go to college now versus working first. Later in life, sound decisions can come from an understanding of annuities and, more generally, the present value of future money. Many will live in homes for which funds need to be saved for future repairs; others will need to consider the pros and cons of renting versus buying. Students should learn to consider all aspects of such decisions, including cost of loans, loss of earning power, and effects of inflation.
These issues bear directly on civic life as well. Every community thinks about bond issues that provide money for capital improvements. This involves, among other things, depreciation of capital expenditures. How do you think about borrowing vs. paying up front? Consideration and discussion of these issues can make students better citizens and more informed voters.
The mathematical formulation of the problem depends on recursive thinking, an important tool in many applications of mathematics. This task is especially appropriate because it can be explored at many levels of mathematical sophistication. The solution presented below, however, assumes only enough algebra to be able to enter formulas in a spreadsheet.
Mathematical Analysis
One way to think about this problem is to imagine an equivalent scenario. Suppose you make an initial deposit in a bank account at a fixed rate of interest and then withdraw $250,000 each year for 15 years. This is equivalent because buying the lottery proceeds will produce the same stream of payments. The question, then, is how much must be deposited at the beginning so that there will be enough to last exactly 15 more years.
There are 15 remaining payments of $250,000 each, totaling $3,750,000. But a deposit of $3.75 million would be more than is necessary because it would collect a substantial amount of interest, especially in the beginning years. In order to make some specific calculations, one can assume a fixed interest rate of 8% and then ask whether the judge's suggested $1.3 million will be enough. Since the year five payment has just been made, one can reasonably assume that the year six payment will occur exactly one year later. At year six, then, the initial deposit will have accrued 8% interest, which amounts to .08 × $1,300,000 = $104,000. At the same time that interest payment is made, however, one would be withdrawing the year six payment of $250,000. That leaves $1,300,000 + $104,000 - $250,000 = $1,154,000 remaining in the account at year six. A spreadsheet
can be used to continue these calculations for subsequent years. If the initial payment is in cell C5, the formula for cell C6 is C5+C5*. 08-250000. That formula may then be copied to cells C7 and below.
TABLE 1: Remaining principal by year, first attempt
|
YEAR |
PAYMENT |
PRINCIPAL REMAINING |
|
5 |
|
$1,300,000.00 |
|
6 |
$250,000 |
$1,154,000.00 |
|
7 |
$250,000 |
$996,320.00 |
|
8 |
$250,000 |
$826,025.60 |
|
9 |
$250,000 |
$642,107.65 |
|
10 |
$250,000 |
$443,476.26 |
|
11 |
$250,000 |
$228,954.36 |
|
12 |
$250,000 |
-$2,729.29 |
Table 1 shows that if the initial deposit is $1.3 million, and the interest rate is 8%, there will not be enough to make the payment in year 12, never mind years 13 through 20. Note that although 1.3 million could provide only a little more than 5 payments of $250,000 if there were no interest, it can provide almost 8 payments at an interest rate of 8%. Thus, The judge's initial bid is lower than $3.75 million in order to account for the interest that will accrue. If an interest rate of 8% is reasonable, however, $1.3 million is far too low.
What we want to find is an initial deposit that will leave exactly $0 at the end of the year 20. We know that $3.75 million is too high, and $1.3 million is too low. By choosing initial deposit amounts between these, and keeping track of which are too low and which are too high, we can "zero in" on the desired value. According to Table 2, $2,139,869.67 almost works. In fact, to the closest penny, it is the best answer.
Thus, assuming a fixed 8% interest rate, this stream of payments is worth $2,139,869.67 today. Another way to say this is that assuming an 8% discount rate, the present value of the payments is $2,139,869.67.
One of the nice features of this task is that there are many answers, depending upon the interest rate chosen, and many approaches to solutions, depending upon the students' knowledge. The discussion above, for example, can be phrased in more sophisticated mathematical notation. The spreadsheet formula might be written Dn+1 = (1+i) Dn - P, where i is the annual interest rate, P is the $250,000 annual payment the lottery winner was receiving and Dn is the amount of money still invested at year n in order to produce the annual payments. Then the goal would be to find what initial investment in year five, D5, just covers the 15 years of payments, leading to D20 being $0.
Students who are prone to exploring the capabilities of their spreadsheet software might find a "Present Value" function which gives the desired initial investment directly. Other students, after studying geometric series, might derive or use the present value formula,
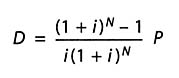
where N is the number of payments, and the other variables are as above. Many
TABLE 2: Remaining principal by year, final attempt
|
YEAR |
PAYMENT |
PRINCIPAL REMAINING |
|
5 |
|
$2,139,869.67 |
|
6 |
$250,000 |
$2,061,059.24 |
|
7 |
$250,000 |
$1,975,943.98 |
|
8 |
$250,000 |
$1,884,019.50 |
|
9 |
$250,000 |
$1,784,741.06 |
|
10 |
$250,000 |
$1,677,520.35 |
|
11 |
$250,000 |
$1,561,721.97 |
|
12 |
$250,000 |
$1,436,659.73 |
|
13 |
$250,000 |
$1,301,592.51 |
|
14 |
$250,000 |
$1,155,719.91 |
|
15 |
$250,000 |
$998,177.50 |
|
16 |
$250,000 |
$828,031.71 |
|
17 |
$250,000 |
$644,274.24 |
|
18 |
$250,000 |
$445,816.18 |
|
19 |
$250,000 |
$231,481.48 |
|
20 |
$250,000 |
-$0.01 |
mathematics of finance texts contain derivations of this formula. This task could be used to motivate such formulas and functions.
Extensions
Explore what the necessary initial payment would be when different interest rates are assumed. Does the initial payment go up or down as the interest rate goes up? Why does the answer make sense? Find the interest rate, if possible, for which the judge's suggested bid of $1.3 million makes sense.
Assuming that students use a "search" procedure for finding the initial payment, ask about the efficiency of different methods of searching. Some students, for example, might try $1.4 million, $1.5 million, $1.6 million, and $1.7 million—clearly an inefficient approach when $1.3 million was already known to be far too low. Explore the mathematics behind the binary search method, in which the next guess is always the average of the best high and low guesses so far. Explore the mathematics behind the linear interpolation search method, in which the next guess is determined by finding the intercept of the line between the best high and low guesses so far.
If students are impatient with a "search" procedure, ask them to use algebra to find a formula. The algebra involved in the derivation of the formula requires use of some standard facts about geometric series, and might provide motivation for the usefulness of such formulas.
Suppose a student inherits money or wins a lottery. This money provides a certain annual income for a fixed number of years. How much of the income should be put aside so that the winner will still have savings long after the annual payments cease? Can it last a lifetime? Can it last indefinitely? It is also interesting to consider the impact of taxes and inflation. (These are serious problems. A research study of the early winners of lotteries showed that more than 75% were broke 20 years after winning.)
This task and its extensions can provide opportunities for exploration and discussion of other financial instruments, such as annuities, pensions, mortgages, and other savings and borrowing plans, and also economic issues, such as interest rates, other rates of return, the trade-off between risk and expected return, and the liquidity of an investment. Rather than leading to a unit on finance, questions about these issues can lead students to be interested in the mathematics behind them.
Hospital Quality
Task
As health care director for your company, your job is to select which of two local hospitals you will send your employees to in case of emergency. Mercy Hospital is the larger of the two and a local emergency care facility. It had 2,100 surgery patients last year, many of whom entered the hospital in poor condition. Of its surgery patients, 63 died. Excelsior is smaller. It had 800 surgery patients last year, a smaller percentage entered in poor condition, and 16 of its surgery patients died. The detailed information is given in Table 1.
TABLE 1: Patient mortality, two hospitals
|
|
MERCY HOSPITAL |
EXCELSIOR HOSPITAL |
||
|
|
PATIENTS |
DEATHS |
PATIENTS |
DEATHS |
|
In Good Condition |
600 |
6 |
600 |
8 |
|
In Poor Condition |
1,500 |
57 |
200 |
8 |
|
Combined Total |
2,100 |
63 |
800 |
16 |
The director of public relations at Excelsior claims that the overall death rate at Excelsior is smaller than the overall death rate at Mercy and that the intimacy of a small hospital is preferable to the hustle and bustle of a large facility. The director of public relations at Mercy claims that if you look at the death rates more carefully, you will see that they are a better facility—they simply treat a lot of patients who are more seriously ill.
Analyze the given data and make a recommendation to your board of directors. Make the recommendation in the form of a memo in which you clearly justify your decision, knowing that the director of the hospital you do not choose may appeal your decision.
Commentary
This is a decision-making situation that might actually arise in the workplace, but its relevance is much broader. Drawing sound conclusions in such situations requires understanding and careful thinking. In the news and in everyday life, we are inundated with statistics supporting various positions. Thus, it is important that students learn to look for complexities that are often hidden behind the statistics.
Both directors of public relations are correct, despite their seemingly contradictory statements. These data provide an example of an occurrence known in probability as Simpson's paradox; it can also occur in other situations involving "weighted averages." Similar apparent paradoxes arise, for example, in situations where women or minorities in various jobs earn about the same as their male counterparts, but their overall average earnings may be far less. (This can happen if most women are employed in low paying jobs, for example.)
Because of the apparent paradox, this task provides an intriguing context for discussing more fundamental notions, such as probability, rates, and weighted averages. Working through such examples can sensitize students to the need to understand the
numbers and trends that give rise to statistics. It will also give them a better sense of what to believe and what to question when confronted with statistical assertions.
Mathematical Analysis
To check the directors' assertions, one must compute death rates. For example, the death rate for patients in good condition at Mercy is 6/600 or 1%. The other results are shown in Table 2.
TABLE 2: Patient mortality, two hospitals, with rates
|
|
MERCY HOSPITAL |
EXCELSIOR HOSPITAL |
||||
|
|
PATIENTS |
DEATHS |
RATE |
PATIENTS |
DEATHS |
RATE |
|
In Good Condition |
600 |
6 |
1% |
600 |
8 |
1.33% |
|
In Poor Condition |
1500 |
57 |
3.8% |
200 |
8 |
4% |
|
Combined Total |
2100 |
63 |
3% |
800 |
16 |
2% |
Looking only at the combined death rate, it looks like Excelsior is the better hospital, for a 2% death rate is better than 3%. Looking at the separate death rates, however, the picture is different. For patients in good condition, the death rate is lower at Mercy. Similarly, a patient in poor condition is better off at Mercy. So the public relations director at Mercy is correct: Mercy Hospital has a better success rate both with patients in good health and with those in poor health. The reason Mercy loses more patients overall is that it treats many more seriously ill patients.
Here's an easy way to see how averages based on aggregates can deliver a different message than averages based on components. Suppose a company, in an attempt to recruit women into all positions, pays them more than men in all positions. If it is easy to recruit women for the low-paying positions, and hard to recruit them for the high-paying positions, it is possible that the average salary for women will still be lower than the average salary for men, seemingly contradicting the company's intent to pay women more.
Extensions
Students might find and analyze employment and salary patterns in various professions. They might look at admissions rates at a university by gender or by race, for the university as a whole, and then separated by college or by department. Such assignments should not be given, however, without allowing for discussion of equity issues that can be raised by such data.
Students might construct data that illustrates analogous paradoxes in contexts that appeal to them. In baseball, for example, it is possible for a batter to have the best batting average before the all-star break and the best average after the all-star break and yet fail to have the best average for the whole season.
Students might also explore other instances of weighted averages, perhaps first as simple ways of computing more familiar averages. For example, if a teacher explains that homework counts 50%, each of three exams count 10%, and the final exam counts 20%, a student
can determine his or her average going into the final as follows:
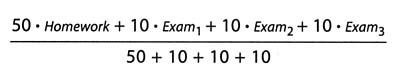
The arithmetic in this task deserves comment. If one thinks of the death rates as fractions, then one might consider the relationship between the separate death rates and the combined death rate to be like addition. In the case of Mercy hospital, the "addition" looks as follows, where the ⊕ indicates that this is not the standard addition of fractions.
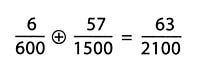
Notice that this "addition" is performed by adding the numerators and adding denominators—one of the mistakes that students make when they are supposed to perform the standard addition of fractions. Yet, this "addition" is used in many contexts, from computing batting averages in baseball to computing terms in Farey sequences, an advanced topic in number theory.
Students might be asked, "Why does this 'addition' make sense here?" "What is the difference between this and the standard addition of fractions?" "What is different about the contexts that gives rise to a different kind of addition?" Discussion of such questions can provide for a firmer understanding of the concepts of fraction, rate, and average.
This kind of "addition by component" is reminiscent of addition of vectors, which gives us a geometric model of the situation. The data for patients in good condition at Mercy (600 patients, 6 deaths) can be represented as the vector (600, 6) which can be represented geometrically as an arrow from the origin to the point (600, 6) on a coordinate plane. (See Figure 1.) Then the death rate, 6/600, is precisely the slope of the vector. By similarly representing the data for patients in poor condition as the vector (1500, 57), the sum of the vectors is given by adding the components of the vectors. That is, (600, 6) + (1500, 57) = (2100, 63). Geometrically, the sum of these vectors is the diagonal of the parallelogram formed by the vectors. (See Figure 1.) Note that because the death rate is represented by the slope of the vector, a steeper vector corresponds to a higher death rate. We can similarly represent the data from Excelsior Hospital (Figure 2).
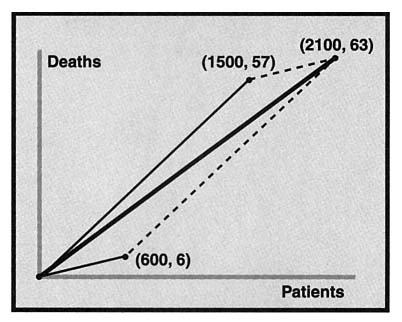
FIGURE 1: Patient mortality at Mercy Hospital
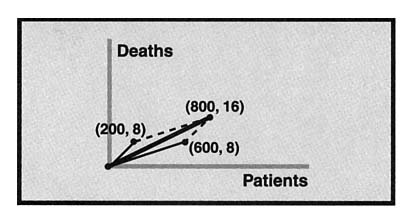
FIGURE 2: Patient mortality at Excelsior Hospital
Superimposing the data from Excelsior Hospital upon that from Mercy (Figure 3) shows that the sides of the Excelsior parallelogram are steeper than the corresponding sides of the Mercy parallelogram, but Mercy has a steeper diagonal. To gain a spatial and kinesthetic sense of this paradox, students might use dynamic geometry software to draw such a picture to construct data that exhibit this paradox.
Observe that the diagonal representing the sum must be between the two vectors, indicating that the slope of the sum must be between the other slopes. This provides a compelling geometric argument for the algebraic fact that ![]() defined as above, is always between the two fractions a/b and c/d, as long as a, b, c, and d are all positive. Proving this algebraically, on the other hand, requires some non-obvious techniques.
defined as above, is always between the two fractions a/b and c/d, as long as a, b, c, and d are all positive. Proving this algebraically, on the other hand, requires some non-obvious techniques.
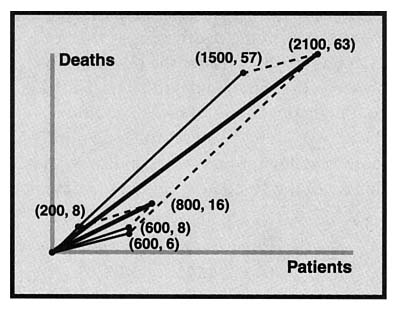
FIGURE 3: Patient mortality, two hospitals
Rounding Off
Task
In a certain multi-million dollar company, Division Managers are required to submit monthly detail and summary expense reports on which the amounts are rounded, for ease of reading, to the closest $1,000. One month, a Division Manager's detail report shows $1,000 for printing and $1,000 for copying. In the summary report, the total for ''printing and copying" is listed as $3,000. When questioned about it by the Vice President, he claims that the discrepancy is merely round-off error. In subsequent months, the Vice President notices that such round-off errors seem to happen often on this Division Manager's reports. Before the Vice President asks that the Division Manager re-create the reports without rounding, she wants to know how often this should happen.
Commentary
We are often quoted rounded numbers that do not then turn out to be quite exact. Even a bank's approximate computational program for principal and interest can eventually drift far enough off the actual payment for the difference to be important. In any problem, we have to be concerned about which numbers are exact and about the accuracy of those that are not.
People don't often realize how huge the consequences of rounding numbers can be. Suppose, for example, that a company's board of directors has received a report indicating that each of the machines manufactured by their company will take up 2% of the freight capacity of their cargo planes, and the board wants to know how many machines can be shipped on each plane. In our standard notation, 2% represents a number somewhere between 1.5% and 2.5%. Solving the problem with each of these two exact percentages yields answers that are quite different. Using 1.5%, the board will find that the plane can hold 100% ÷ (1.5%/machine) = 66 machines; but by using 2.5%, the board will find that the plane can hold 100% ÷ (2.5%/machine) = 40 machines. So, in truth, all the board can say is that the answer is between 40 and 66 machines! Clearly, the report has not supplied accurate enough information, especially if the profitability of the shipment depends strongly on the number of machines that can be shipped.
If, on the other hand, the report had indicated that the board could assume another decimal place of accuracy, by stating that each machine accounted for 2.0% of the plane's capacity, then, with rounding, the board can be sure that the exact portion is somewhere between 1.95% and 2.05%. Using these exact percentages, the board can conclude that the plane can hold between 48 and 51 machines. One decimal place of additional accuracy in the reported data reduced the uncertainty in the answer from 26 machines to 3.
This problem is important for another reason as well, for its solution introduces a useful mathematical connection: the notion of geometric probability, where the range of options (technically, the "sample space") is represented by a geometric figure so that the probability of certain events correspond to the areas of certain portions of that figure. Geometric probability enables us to use our knowledge of the area (or length or volume) of geometric figures to compute probabilities.
Mathematical Analysis
Fundamental to an understanding of geometric probability is the idea that on a portion of a
line, probability is proportional to length, and on a region in a plane, probability is proportional to area. For example, suppose that in Figure 1, the areas of regions A, B, and C are 2, 1, and 3 respectively, for a total area of 6. Then a point picked at random from these regions would have probability of 2/6, 1/6, and 3/6 of being in regions A, B, and C respectively.
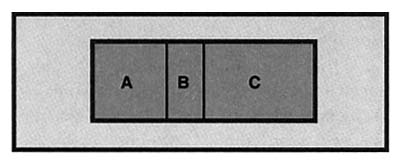
FIGURE 1: An area model for probability
Note that the boundaries of the regions are not significant in the calculations because they have no area. Ideally (as opposed to in a physical model) these boundaries are lines with no thickness. Thus, the probability that a point from this rectangle will lie exactly on one of these boundaries, rather than close to a boundary, is zero.
In order to answer the question at hand, it must be stated more mathematically: Given a pair of numbers that both round to 1, and assuming that all such pairs are equally likely, find the probability that their sum rounds to 2. This assumption may or may not be reasonable in a particular business and would require some knowledge of typical expenses and some non-mathematical judgment.
A number that rounds to 1 is somewhere between .5 and 1.5. These numbers may be represented by a line segment, shown as the shaded portion of the number line in Figure 2.
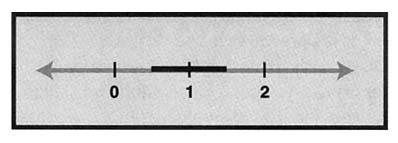
FIGURE 2: A linear representation of numbers that round to 1
To state this a bit more formally, a number x will be rounded to 1 if .5 < x < 1.5. (Again, we can ignore the boundaries, 5 and 1.5, because the probability that a number will be exactly on the boundary is zero.) Suppose y also rounds to 1, so that .5 < y < 1.5. If we consider a coordinate plane with points (x, y), these two inequalities determine a square of side 1. This square (Figure 3) represents all pairs of numbers where both could be rounded to 1. For example, point A represents (.8, .6), B represents (1.1, 1.1), and C represents (1.3, 1.4).
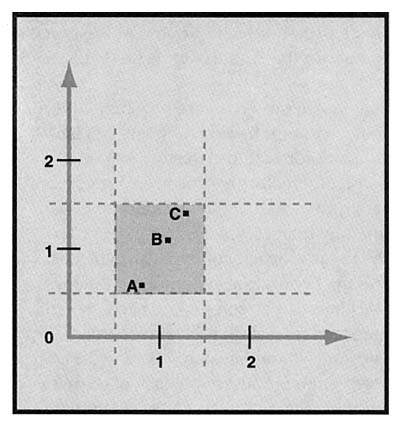
FIGURE 3: An area representation for 1 + 1
What can we say about x + y for points inside the square? Most of the time, x + y will round to 2, but sometimes it will round to 3, and sometimes it will round to 1. Note that the components of A add to 1.4, which rounds to 1; the components of B add to 2.3, which rounds to 2; and the components of C add to 2.7, which rounds to 3.
The probability that 1 + 1 rounds to 1 is the fraction of the square containing pairs that, when added, round to 1. Now, x + y rounds to 1 if x + y < 1.5, which will occur for points below the line x + y = 1.5. Similarly, x + y rounds to 3 for points above the line x + y = 2.5. These conditions each cut off a triangular corner of the square (shown as the darker shaded regions in Figure 4).
The legs of these right triangles are each of length 1/2, so they each have area 1/8. Thus, the probability that 1 + 1 = 3 is 1/8, and the probability that 1 + 1 = 1 is also 1/8. Finally the probability that 1 + 1 = 2 is 3/4, the remaining fraction of the square.
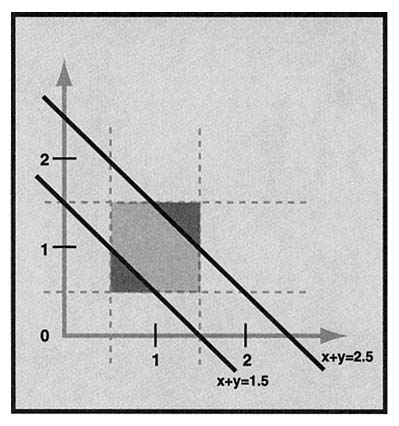
FIGURE 4: An area representation for 1 + 1, with rounding boundaries
Extensions
What's the probability that 1 × 1 = 2? This requires calculating the portion of the square that satisfies xy > 1.5 (Figure 5). Is this bigger or smaller than 1/8, calculated as the area of the upper triangle in Figure 4? A comparison of Figures 4 and 5 shows remarkable similarity. What is the precise relationship between the line x + y = 2.5 and the curve xy = 1.5? Solving the first equation for y and substituting into the second yields x(x - 2.5) = 1.5, a quadratic which simplifies to -x2 + 2.5x - 1.5 = 0 or 2x2 -5x + 3 = 0. This second equation factors easily as (2x - 3)(x - 1) = 0, yielding solutions x = 1.5 and x = 1. These solutions imply that the line x + y = 2.5 and the curve xy = 1.5 intersect the square at the same points. By the concavity
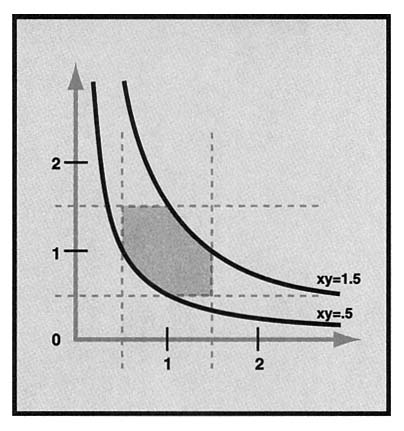
FIGURE 5: An area representation for 1 × 1, with rounding boundaries
of the curve xy = 1.5, the curve must lie below the line inside the square. So the answer should be a little bigger than 1/8 = .125.
Calculus allows us to calculate the shaded area as precisely:
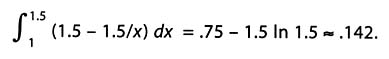
Similarly, if x = .6 and y = .7, then xy = .42 < .5, which would round to 0. The probability that xy rounds to 0 is .5 in 2 - .25 < .097.
What about 1/1? It rounds to 0 with probability .0625, to 1 with probability .75, to 2 with probability .175, and to 3 with probability .0125. These calculations require only geometry, no calculus.
Rules Of Thumb
Task
Some drives learn the rule of thumb, "Follow two car lengths behind for every 10 miles per hour." Others learn, "Stay two seconds behind the car ahead." Do these two rules give the same results? Is one safer than the other? Is one better for roads with speed limits of 45 or 50 miles per hour and another for highways on which the speed limit is 65 or 70 miles per hour?
Commentary
Obtaining a driver's license has become one of the "rites of passage" in the U.S. On almost every written driver's test, applicants are asked how closely one driver should follow another on the highway. We all appreciate the dangers of tailgating—not enough stopping time and not enough space to avoid an accident. However, it is not clear that there is agreement about what actually constitutes tailgating—how far apart cars should be.
Rules of thumb are helpful guidelines—sometimes derived from experience—that are calculated using easily available measurements. Often they are developed under particular conditions and may be extremely inaccurate if those conditions are not fulfilled. The existance of two rules of thumb for the same situation suggests a natural question: Are the two rules simply two different ways of saying the same thing or are they offering different advice? As stated, the rules may provide visual images of how far to stay behind another car, but translating that understanding into practice on the road may be quite a different matter. The exercise of interpreting rules of thumb and comparing their results with real data could help students realize that the rules they use have implications for their actions. Also, there is the reality of high incidences of automobile accidents among new drivers. This exercise may help students examine and improve their driving habits.
In order to do the task, students need to know what it means to make a comparison. They have to identify the quantities needed in order to calculate the following distances given by the two rules and represent the rules mathematically. There are many ways to do this—written descriptions, tables, equations, or graphs, all basic tools of mathematical literacy. A comparison requires that the two representations use the same units of measurement—hence some conversions are necessary from the units used in the original rules of thumb. Such conversions are an essential part of many everyday situations, both at work and at home.
Mathematical Analysis
To begin, students might be well advised to consider the case in which two automobiles are traveling at a steady rate. The information presented is not complete and students will find that they have to seek out missing data. Naturally, what students seek will depend on their interpretation of the task. One necessary piece of information may be average car length.
The units for the car-length rule are miles per hour and car lengths, and the units for the two-second rule are miles per hour and seconds. To compare the two rules, both need to be written in the same units. A typical sedan is about 14 feet, so the car-length rule might be translated as "follow about 28 feet behind for every 10 miles per hour" or as the equation y = 28(x/10), where x is the speed of the car in miles per hour and y is the following distance in feet.
If a car is traveling at x mph, then it travels x miles in one hour—in other words, x/3600
miles in one second. The two-second rule is then "if your speed is x mph, follow about 2x/3600 miles behind." As an equation, it is z = 2(x/3600), where x is again the speed of the car in miles per hour, but this time z is the following distance in miles (not feet as in the previous equation), and we use a different letter to distinguish it from y above.
Now the rules are both in terms of miles per hour and units of distance but not the same units of distance. The car-length rule is as follows:
where y is the following distance in feet. The two-second rule is
where z is the following distance in miles.
where z is the following distance in miles. Simplifying the car-length rule gives
where y is the following distance in feet. Simplifying the two-second rule gives
Now it's a matter of converting z to feet (or y to miles). There are 5,280 feet in a mile, so x/1800 miles is 5280(x/1800) feet. That's about 2.93x feet—very close to the distance given by the car-length rule!
Some driver's manuals give data on the distance cars travel before they are able to come to a complete stop. Often the distance is broken into two components, the reaction distance and the braking distance. The reaction distance is the distance traveled while the driver reacts to a situation and hits the brakes. The braking distance is the distance traveled from the time the brakes are applied until the car comes to a stop. A simplified version is given in Table 1.
TABLE 1: Reaction and braking distances for various speeds
|
SPEED |
REACTION DISTANCE |
BRAKING DISTANCE |
|
20 mph |
20 feet |
20 feet |
|
30 mph |
30 feet |
45 feet |
|
40 mph |
40 feet |
80 feet |
|
50 mph |
50 feet |
125 feet |
|
60 mph |
60 feet |
180 feet |
This table allows a comparison of the distances given by the rules of thumb with actual stopping distances. But the stopping distances are the distances required for a car to stop before hitting an immovable object blocking the road, whereas the rules of thumb assume that the car in front is also moving forward. This table suggests some questions about the rules of thumb: How much reaction time does each rule allow? Why are the rules of thumb linear and the stopping distances non-linear—and does this matter?
Extensions
In 1977, a National Observer article stated, "The usual rule of thumb in the real-estate business is that a family can afford a house 2 to 2 1/2 times its income." Incomes and housing prices have changed considerably since 1977, and real-
estate agents' rules of thumb may have changed as well. Every subject—from shop to physics, from auto mechanics to economics—introduces rules of thumb that work well in appropriate situations. Even in mathematics, practices that students don't understand may acquire the status of rules of thumb for them and may be misapplied.
The original rule of thumb gave the measurement of a person's waist in terms of the measurements of their thumb, wrist, or neck. "Twice around the thumb is once around the wrist. Twice around the wrist is once around the neck. Twice around the neck is once around the waist." (The Dutch refer to "rules of fist," possibly for similar reasons.) The differences in body proportions at different ages (see Figure 1) suggest that this rule may have been developed for adults and may not be useful in designing clothes for young children. Students can be asked to
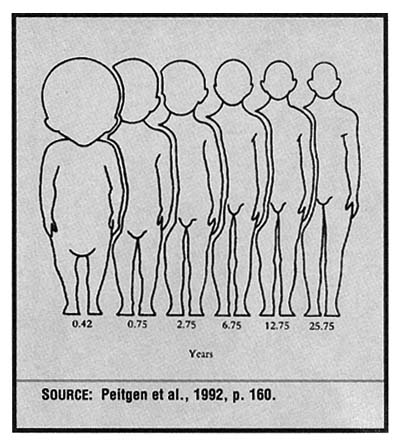
FIGURE 1:
Changes in shape between infancy and adulthood, by age in years
create a rule that would work for young children. Because children's proportions change so rapidly with age, such a rule might include age as a variable.
There are numerous other rules of thumb: "The rule of 72" in finance, "Double the tax to get the tip" in a restaurant, "Magnetic north is true north" in navigation, and so on. Students can compare the results of these rules with actual data or investigate the accuracy and derivation of such rules in their areas of interest. For instance, The Joy of Cooking provides the following rule of thumb for cooking turkeys, "allow 20 to 25 minutes per pound for birds up to 6 pounds. For larger birds, allow 15 to 20 minutes per pound. For birds weighing over 16 pounds, allow 13 to 15 minutes per pound. In any case, add about 5 minutes to the pound if the bird you are cooking is stuffed'' (Rombauer & Becker, 1976). Students could explore the reasonableness of such predictions: might one conclude that a 5.9 pound bird requires (5.9) × (25) = 147.5 minutes, while a 6.1 pound bird requires no more than (6.1) × (20) = 122 minutes?
There are many other natural variations on the original problem as well. How sensitive is the car-length rule to what is assumed about the length of a car? Is the difference in average length of European versus U.S. sedans important to this rule of thumb? How should the two rules be modified for use on wet pavement? Questions might be raised about what happens if one car is traveling faster than the other or about the relationship between age and reaction time. In a state with a large number of retirees such as Florida, should the rules of thumb be the same as those in states with younger populations?
Another issue concerns the usability of the two rules for following distance. If the two rules give essentially the same advice, is one easier to use in practice than the other? Is it easier to think in terms of distance measured in car lengths, picturing the space filled with cars, or to pick a marker such as a road sign or billboard, and count seconds? Opinions will vary as to which is the easier method.
References
Peitgen, H.-O. et al. (1992). Fractals for the classroom. New York: Springer-Verlag.
Rombauer, I.S. & Becker, M. R. (1976). The joy of cooking. New York: Bobbs-Merrill Company.




































